Deformation Behavior and Processing Map of AlCoCrFeNiTi0.5 High-Entropy Alloy at High Temperature
Abstract
:1. Introduction
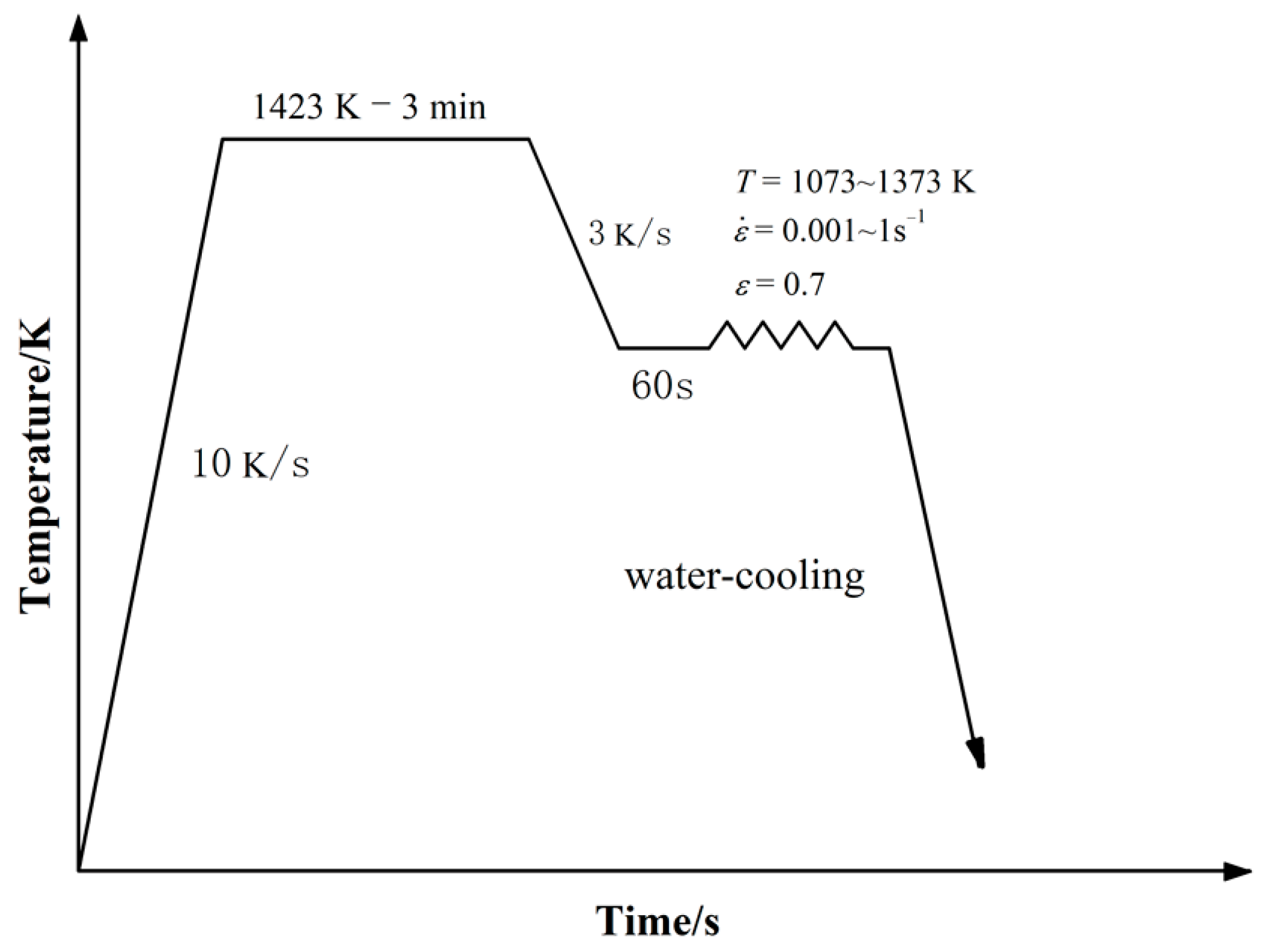
2. Experiments
3. Results
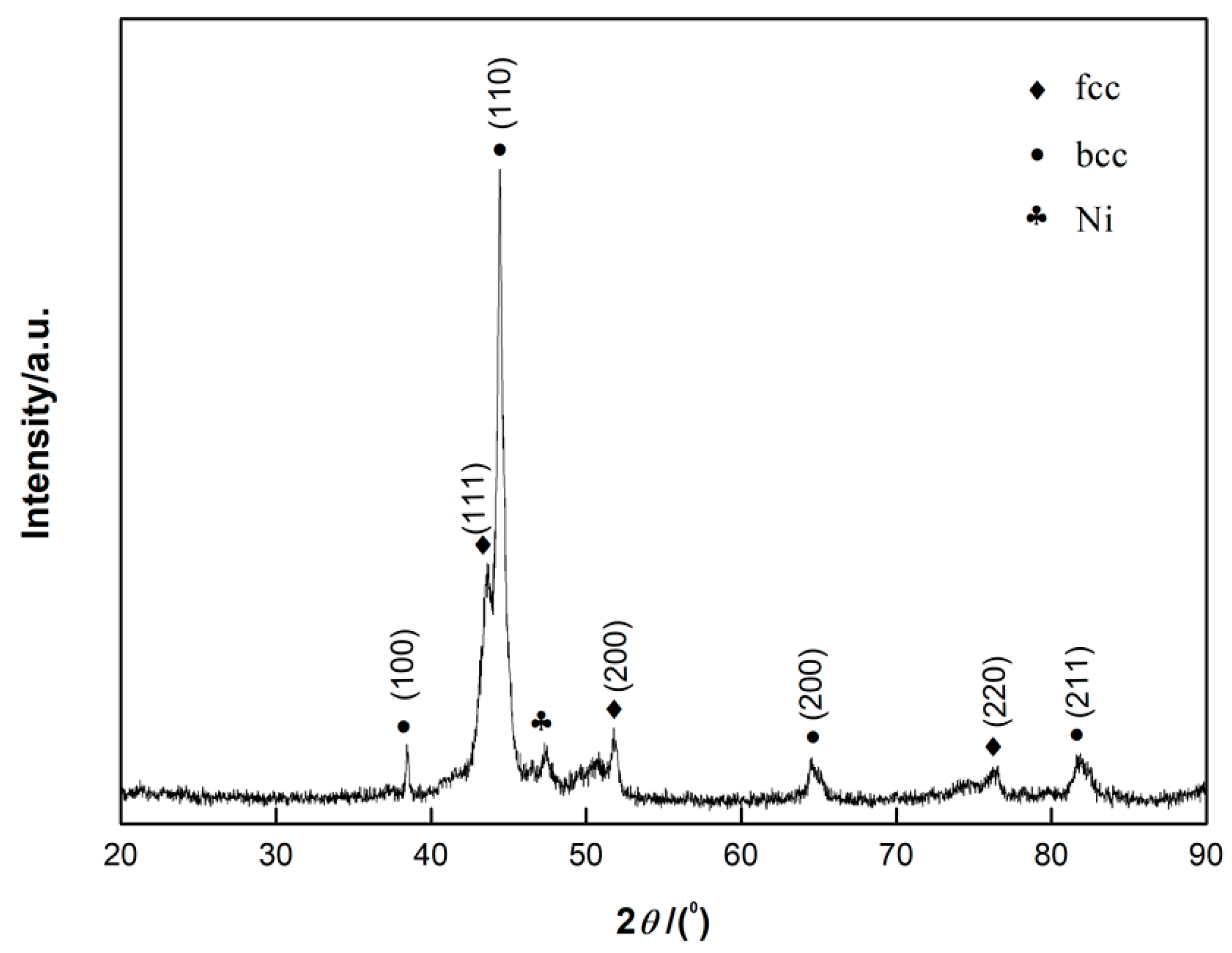
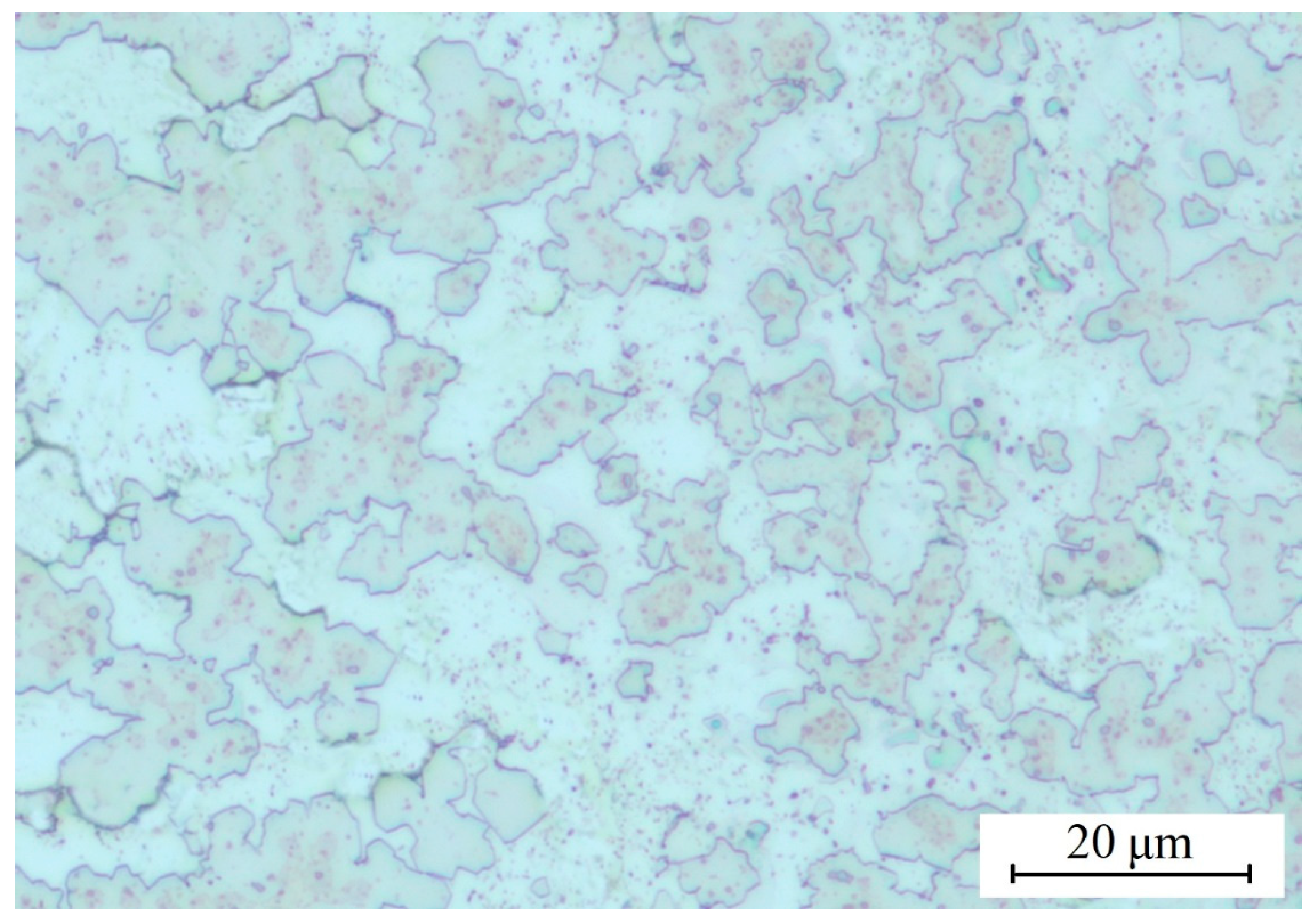
3.1. Microstructure
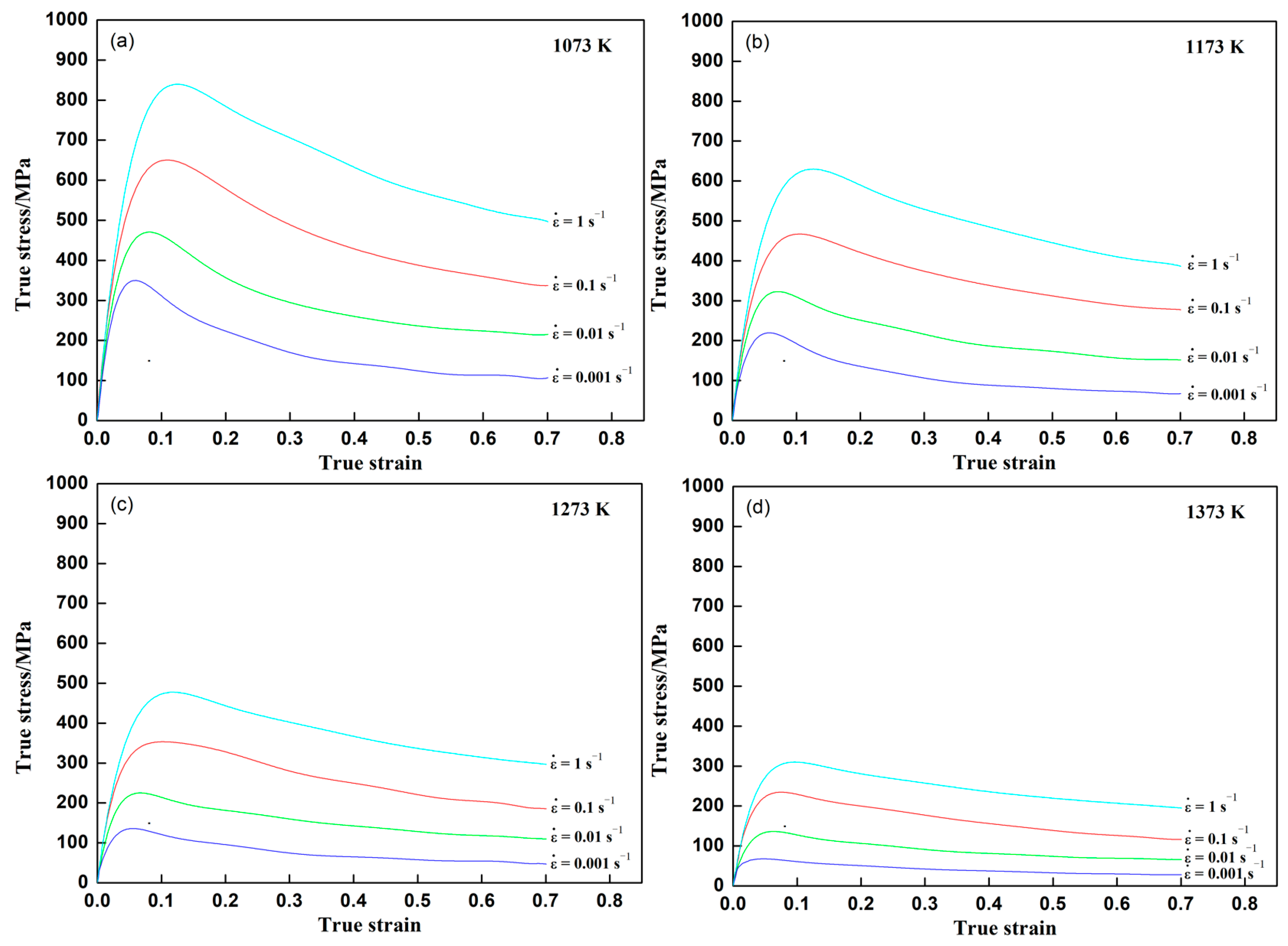
3.2. Analysis of Stress–Strain Curve
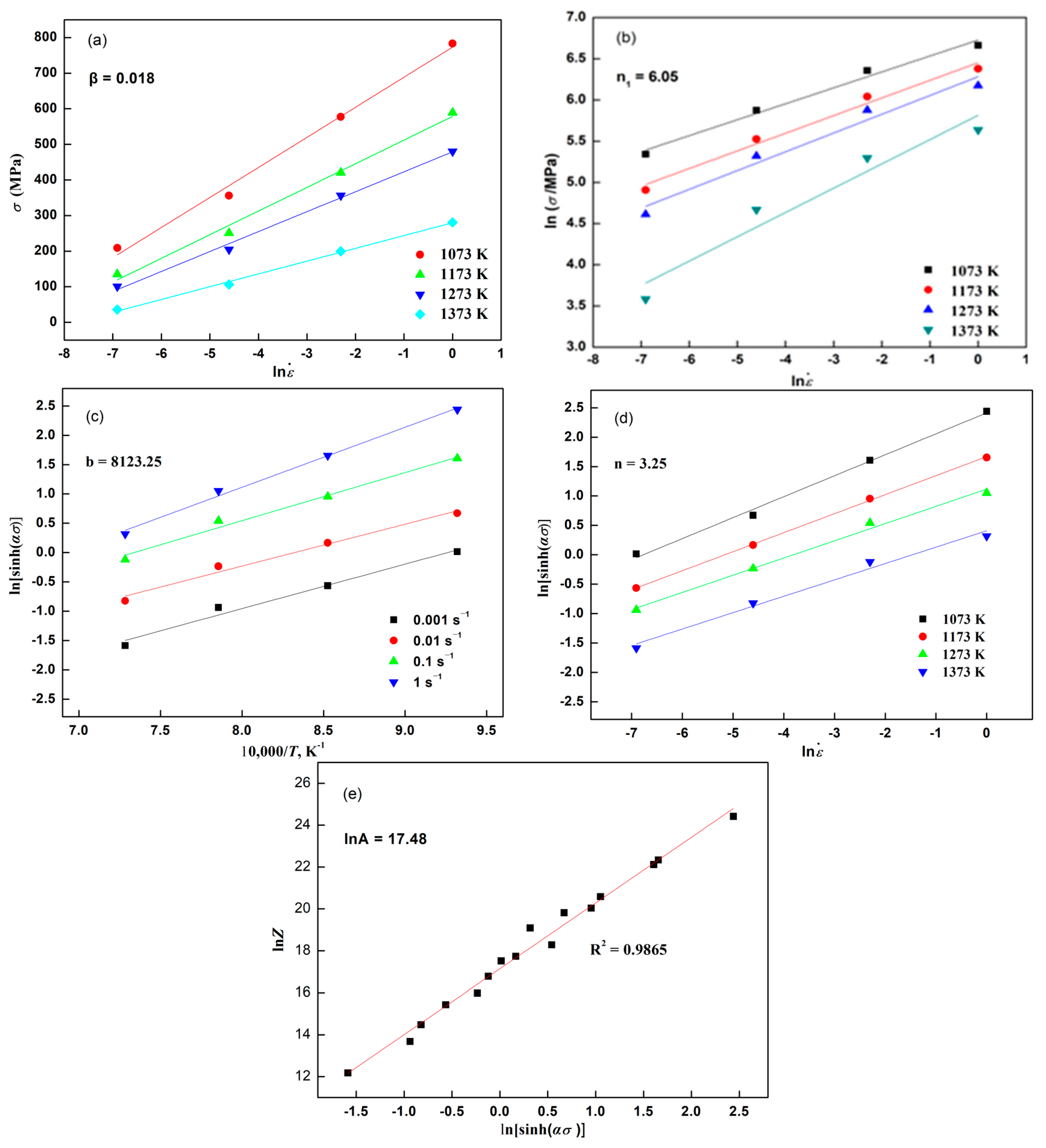
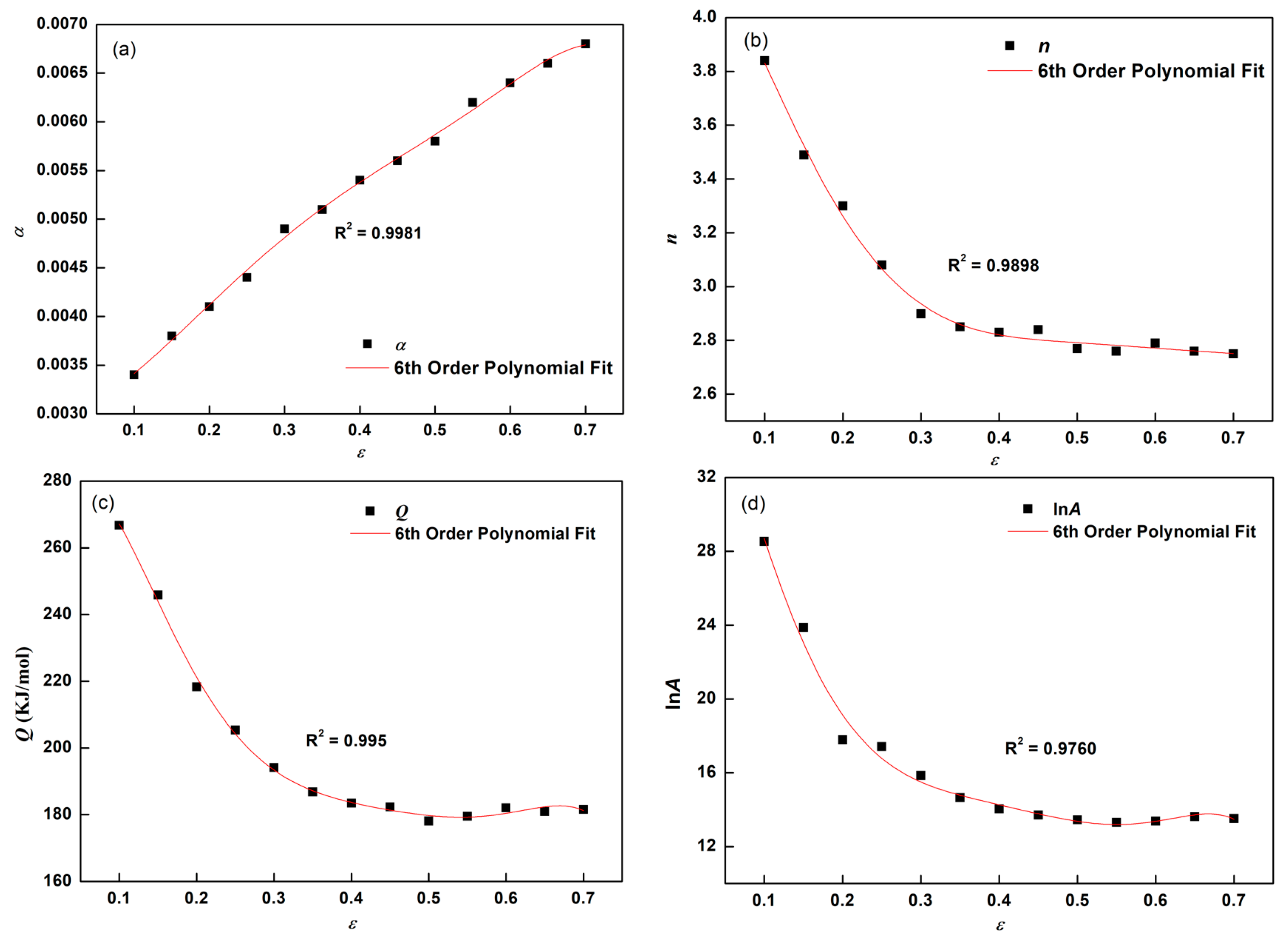
3.3. Establishment of Constitutive Equation
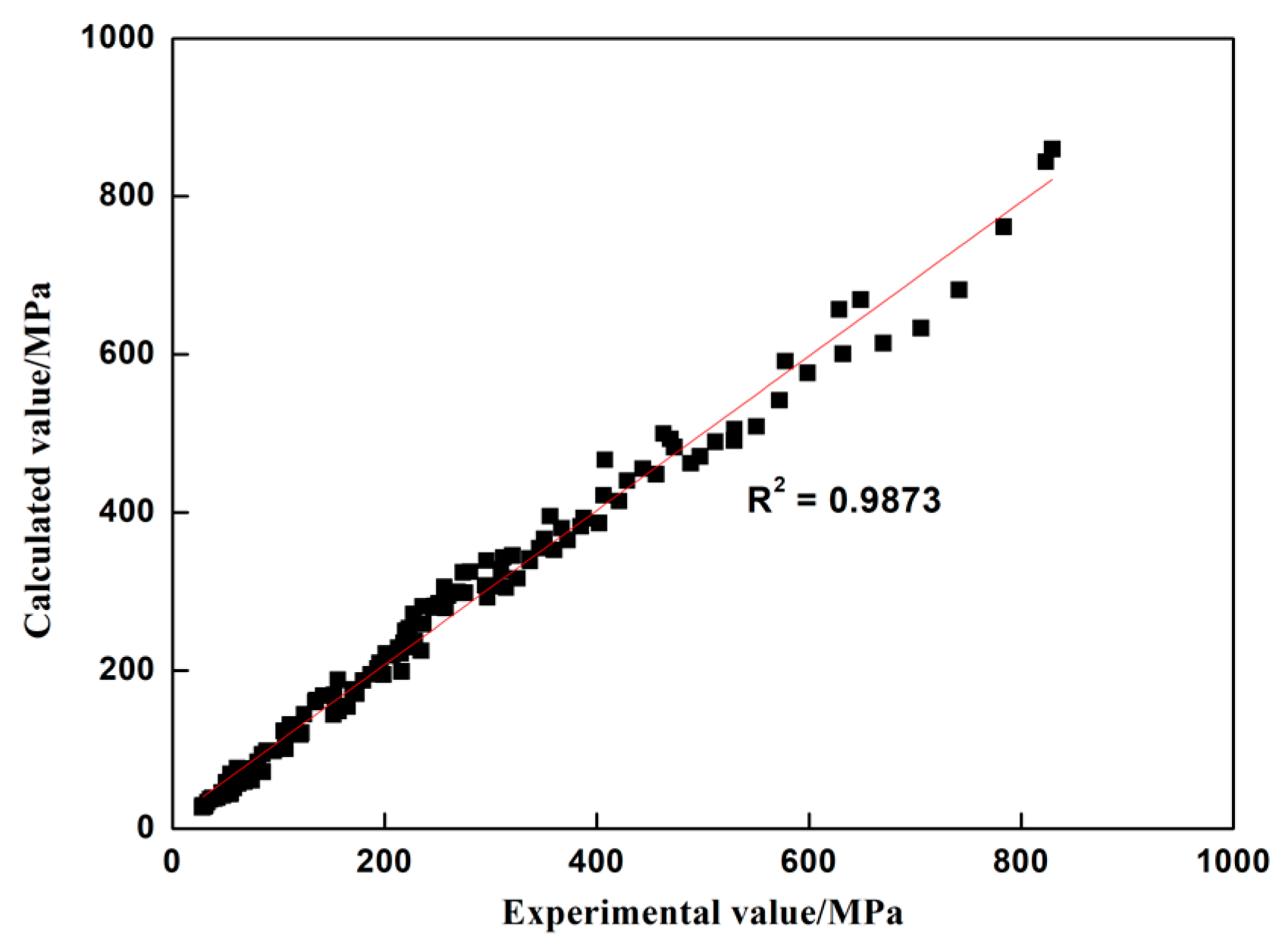
3.4. Verification of Constitutive Equation
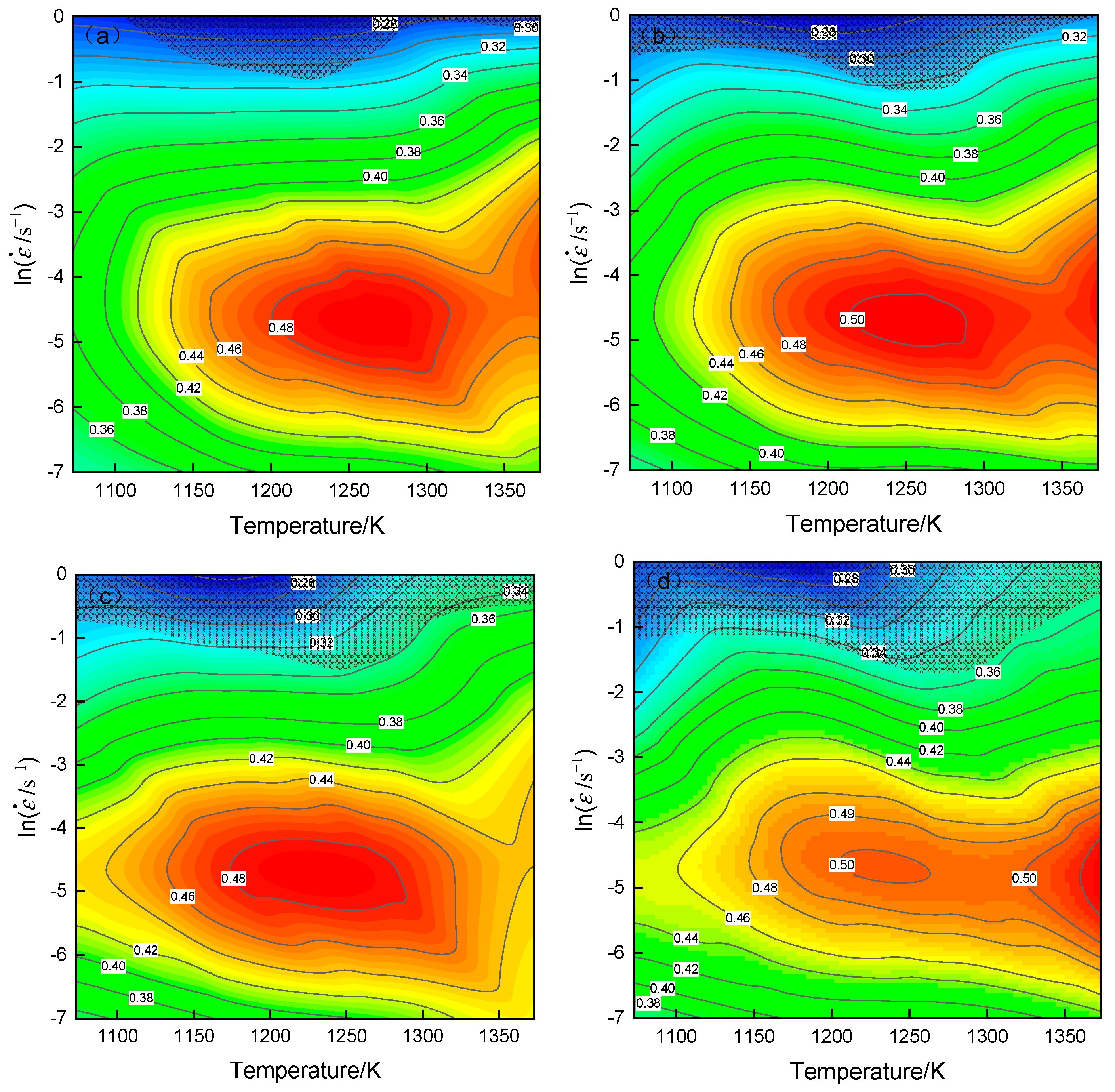
3.5. Processing Map
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Zuo, T.T.; Tang, Z.; Michael, C.G.; Karin, A.D.; Peter, K.L.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Yi, J.J.; Wang, L.; Zeng, L.; Xu, M.; Tang, S. Excellent strength-ductility synergy in a novel single-phase equiatomic CoFeNiTiV high entropy alloy. Int. J. Refract. Met. Hard Mater. 2020, 95, 105416. [Google Scholar] [CrossRef]
- Parakh, A.; Vaidya, M.; Kumar, N.; Chetty, R.; Murty, B.S. Effect of crystal structure and grain size on corrosion properties of AlCoCrFeNi high entropy alloy. J. Alloys Compd. 2020, 863, 158056. [Google Scholar] [CrossRef]
- Bhattacharjee, T.; Wani, I.S.; Sheikh, S.; Clark, I.T.; Okawa, T.; Guo, S.; Bhattacharjee, P.P.; Tsuji, N. Simultaneous Strength-Ductility Enhancement of a Nano-Lamellar AlCoCrFeNi2.1 Eutectic High Entropy Alloy by Cryo-Rolling and Annealing. Sci. Rep. 2018, 8, 3276. [Google Scholar] [CrossRef]
- Shabani, M.; Indeck, J.; Hazeli, K.; Jablonski, P.D.; Pataky, G.J. Effect of Strain Rate on the Tensile Behavior of CoCrFeNi and CoCrFeMnNi High-Entropy Alloys. J. Mater. Eng. Perform. 2019, 28, 4348–4356. [Google Scholar] [CrossRef]
- Samoilova, O.; Shaburova, N.; Samodurova, M.; Pashkeev, K.; Moghaddam, A.O.; Doubenskaia, M.; Sova, A.; Trofimov, E. Microstructural evolution of Al0.25CoCrFeNi- Cu and Al0.45CoCrFeNiSi0.45 high-entropy alloys during laser cladding. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2022, 236, 1806–1813. [Google Scholar]
- Liu, Q.; Wang, X.Y.; Huang, Y.B.; Xie, L.; Xu, Q.; Li, L.H. Effect of Mo Content on Microstructure and Corrosion Resistance of CoCrFeNiMo High Entropy Alloy. Chin. J. Mater. Res. 2020, 34, 868–874. [Google Scholar]
- Zhang, A.; Han, J.; Meng, J.; Su, B.; Li, P. Rapid preparation of AlCoCrFeNi high entropy alloy by spark plasma sintering from elemental powder mixture. Mater. Lett. 2016, 181, 82–85. [Google Scholar] [CrossRef]
- Chuang, M.H.; Tsai, M.H.; Wang, W.R.; Lin, S.J.; Yeh, J.W. Microstructure and wear behavior of AlxCo1.5CrFe Ni1.5Tiy high-entropy alloys. Acta Mater. 2011, 59, 6308–6317. [Google Scholar] [CrossRef]
- Guo, L.; Ou, X.; Ni, S.; Liu, Y.; Song, M. Effects of carbon on the microstructures and mechanical properties of FeCoCrNiMn high entropy alloys. Mater. Sci. Eng. A 2019, 746, 356–362. [Google Scholar] [CrossRef]
- Verma, A.; Tarate, P.; Abhyankar, A.C.; Mohape, M.R.; Gowtam, D.S.; Deshmukh, V.P.; Shanmugasundaram, T. High emperature Wear in CoCrFeNiCux High Entropy Alloys: The Role of Cu. Scr. Mater. 2019, 161, 28–31. [Google Scholar] [CrossRef]
- Qin, G.; Chen, R.R.; Zheng, H.T.; Fang, H.Z.; Wang, L.; Su, Y.Q.; Fu, H.Z. Strengthening FCC CoCrFeMnNi high entropy alloys by Mo addition. J. Mater. Sci. Technol. 2019, 35, 578–583. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Hossam, M.Y.; Ahmed, S.A.M.; Ahmed, E.E.N.; Omayma, A.E. Effect of Copper Addition on the AlCoCrFeNi High Entropy Alloys Properties via the Electroless Plating and Powder Metallurgy Technique. Crystals 2021, 11, 540. [Google Scholar]
- Zhao, P.B.; Zhu, J.P.; Yang, K.J.; Li, M.L.; Shao, G.; Lu, H.X.; Ma, Z.; Wang, H.L.; He, J.L. Outstanding wear resistance of plasma sprayed high-entropy monoboride composite coating by inducing phase structural cooperative mechanism. Appl. Surf. Sci. 2023, 616, 156516. [Google Scholar] [CrossRef]
- Zhao, P.B.; Zhu, J.P.; Li, M.L.; Shao, G.; Lu, H.X.; He, J.L. Theoretical and experimental investigations on the phase stability and fabrication of high-entropy monoborides. J. Eur. Ceram. Soc. 2023, 43, 2320–2330. [Google Scholar] [CrossRef]
- Yu, L.Y.; Wang, C.; Zhu, L.L.; Zhang, H.; Huang, H.L.; Ruan, J.J.; Zhang, S.Z.; Jiang, L.; Zhou, X. Microstructure and properties of AlxCoCrFeNi high entropy alloys fabricated by laser additive manufacturing. J. Mater. Eng. 2023. (In Chinese) [Google Scholar]
- Deng, C.; Li, R.D.; Yuan, T.C.; Niu, P.D. Influence of Al Content on Microstructure and Nanoindentation of Selective Laser Melting AlxCoCrFeNi(x = 0.3, 0.5, 0.7, 1.0). J. Mater. Eng. 2022, 50, 27–35. (In Chinese) [Google Scholar]
- Zhang, P.; Wang, S.X.; Lin, Z.Y.; Yue, X.J.; Gao, Y.R.; Zhang, S.T.; Yang, H.J. Investigation on the mechanism of micro-milling CoCrFeNiAlX high entropy alloys with end milling cutters. Vacuum 2023, 211, 111939. [Google Scholar] [CrossRef]
- Wu, Y.; Li, Z.; Feng, H.; He, S. Atomic Interactions and Order-Disorder Transition in FCC-Type FeCoNiAl1-xTix High-Entropy Alloys. Materials 2022, 15, 3992. [Google Scholar] [CrossRef]
- Ye, H.M.; Yang, W.C.; Pang, X.Z. Effect of titanium content on wear resistance of CoCuFeNiVTix high-entropy alloys. J. Guangxi Univ. (Nat. Sci. Ed.) 2017, 42, 1187–1191. [Google Scholar]
- Zhang, L.; Sha, M.H.; Zhang, J.W.; Chen, Z.S.; Li, S.L. Effect of Titanium on the Microstructure and Wear Resistance of AlCoCrFeNiTi0.5 Alloy Coating Prepared by Laser Cladding. Mater. Prot. 2022, 55, 24–30. [Google Scholar] [CrossRef]
- Shun, T.T.; Chang, L.-Y.; Shiu, M.H. Microstructure and Mechanical Properties of Multiprincipal Component CoCrFeNiMox Alloys. Mater. Charact. 2012, 70, 63–67. [Google Scholar] [CrossRef]
- Liu, Z.; Xiong, Z.P.; Chen, X.W. Large-size high-strength and high-ductilityAlCoCrFeNi2.1 eutectic high-entropy alloy produced by hot-rolling and subsequent aging. Mater. Lett. 2022, 315, 131933. [Google Scholar] [CrossRef]
- Savaedi, Z.; Motallebi, R.; Mirzadeh, H. A review of hot deformation behaviorand constitutive models to predict flow stress of high-entropy alloys. J. Alloys Compd. 2022, 903, 163964. [Google Scholar] [CrossRef]
- Gao, P.F.; Fu, M.W.; Zhan, M.; Lei, Z.N.; Li, Y.X. Deformation behavior and microstructure evolution of titanium alloys with lamellar microstructure in hot working process: A review. J. Mater. Sci. Technol. 2020, 39, 56. [Google Scholar] [CrossRef]
- Dong, F.Y.; Yuan, Y.; Li, W.D.; Zhang, Y.; Liaw, P.K.; Yuan, X.G.; Huang, H.J. Hot deformation behavior and processing maps of an equiatomic MoNbHfZrTi refractory high entropy alloy. Intermetallics 2020, 126, 106921. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K. Dynamic materials model: Basis and principles. Metall. Mater. Trans. 1996, 27, 235. [Google Scholar] [CrossRef]
- Xiao, B.L.; Huang, Z.Y.; Ma, K.; Zhang, X.X.; Ma, Z.Y. Research on hot deformation behaviors of discontinuously reinforced aluminum composites. Acta Metall. Sin. 2019, 55, 59. [Google Scholar]
- Liu, X.B.; Wu, G.L.; Zhou, C.Y. Constitutive modeling of dynamic recrystallization behavior and processing map of Cr5 steel. J. Cent. South Univ. 2016, 23, 3065–3071. [Google Scholar] [CrossRef]
- Jeong, H.; Kim, W.J. Deformation Mechanisms and Processing Maps for High Entropy Alloys (Presentation of Processing Maps in Terms of Zener–Hollomon Parameter): Review. Materials 2023, 16, 919. [Google Scholar] [CrossRef] [PubMed]
- Mcqueen, H.J.; Ryan, N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A 2002, 322, 43–46. [Google Scholar] [CrossRef]
- Trusov, P.; Kondratev, N.; Podsedertsev, A. Grain structure rearrangement by means the advanced statistical model modified for describing dynamic recrystallization. Metals 2023, 13, 113. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comput. Mater. Sci. 2008, 42, 470. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136. [Google Scholar] [CrossRef]
- Lin, Y.C.; Wen, D.X.; Deng, J.; Liu, G.; Chen, J. Constitutive models for high temperature flow behaviors of a Ni-based superalloy. Mater. Des. 2014, 59, 115. [Google Scholar] [CrossRef]
- Ferdowsi, M.R.G.; Nakhaie, D.; Benhangi, P.H.; Ebrahimi, G.R. Modeling the high temperature flow behavior and dynamic recrystallization kinetics of a medium carbon microalloyed steel. J. Mater. Eng. Perform. 2014, 23, 1077–1087. [Google Scholar] [CrossRef]
- Ebrahimpourghandi, B.; Mahmudi, R. Hot deformation constitutive analysis and processing maps of the as-cast and wrought Mg-2.5Gd-0.5Zr alloy. J. Alloys Compd. 2023, 942, 169133. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Seshacharyulu, T. Modelling of hot deformation for microstructural control. Int. Mater. Rev. 1998, 43, 243. [Google Scholar] [CrossRef]
- Sun, F.C.; Li, J.S.; Han, J.K.; Peng, Y.H.; Zhou, K.; Chen, L.J.; Cao, X. Hot deformation behavior and processing map of AlFeCoNi-Mo0.2 high-entropy alloy. J. Netshape Form. Eng. 2021, 13, 91–97. (In Chinese) [Google Scholar]
- Sumit, G.; Mahesh, C.S.; Daria, S.; Suhrit, M. Elucidation of deformation mechanisms and construction of processing maps for a Ti+Nb stabilized IF steel. Mater. Sci. Eng. A 2020, 790, 139648. [Google Scholar]
- Lou, Y.; Chen, H.; Ke, C.X.; Long, M. Hot tensile deformation characteristics and processing map of extruded AZ80 Mg alloys. J. Mater. Eng. Perform. 2014, 23, 1904–1914. [Google Scholar] [CrossRef]
- Sui, D.S.; Wang, T.; Zhu, L.L.; Ga, L.; Cui, Z.S. Mathematical modeling of high-temperature constitutive equations and hot processing maps for as-cast SA508-3 steel. JOM 2016, 68, 2944–2951. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Gegel, H.L.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, K.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. 1984, 15, 1883. [Google Scholar] [CrossRef]

| Element | Al | Co | Cr | Fe | Ni | Ti |
|---|---|---|---|---|---|---|
| Content | 17.69 | 18.21 | 18.60 | 18.63 | 18.28 | 8.59 |
| Strate Rate, s−1 | Deformation Temperature, K | |||
|---|---|---|---|---|
| 1073 | 1173 | 1273 | 1373 | |
| 0.001 | 208.73 | 135.38 | 100.67 | 35.98 |
| 0.01 | 356.08 | 250.93 | 204.53 | 106.53 |
| 0.1 | 577.51 | 420.55 | 356.68 | 199.74 |
| 1 | 783.40 | 589.19 | 480.24 | 280.40 |
| ε | α | n | lnA | Q/(kJ·mol−1) |
|---|---|---|---|---|
| 0.10 | 0.0034 | 5.6 | 21.88 | 266.725 |
| 0.15 | 0.0038 | 3.84 | 17.79 | 245.83 |
| 0.20 | 0.0041 | 3.49 | 17.42 | 218.359 |
| 0.25 | 0.0044 | 3.3 | 15.85 | 205.404 |
| 0.30 | 0.0049 | 3.08 | 14.65 | 194.146 |
| 0.35 | 0.0051 | 2.899 | 14.05 | 186.814 |
| 0.40 | 0.0054 | 2.85 | 13.71 | 183.435 |
| 0.45 | 0.0056 | 2.83 | 13.45 | 182.321 |
| 0.50 | 0.0058 | 2.84 | 13.31 | 178.158 |
| 0.55 | 0.0062 | 2.77 | 13.37 | 179.514 |
| 0.60 | 0.0064 | 2.76 | 13.62 | 182.07 |
| 0.65 | 0.0066 | 2.79 | 13.52 | 180.963 |
| 0.70 | 0.0068 | 2.76 | 13.5 | 181.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Li, T.; Wang, Y.; Kong, X.; Zhao, C. Deformation Behavior and Processing Map of AlCoCrFeNiTi0.5 High-Entropy Alloy at High Temperature. Coatings 2023, 13, 1811. https://doi.org/10.3390/coatings13101811
Liu X, Li T, Wang Y, Kong X, Zhao C. Deformation Behavior and Processing Map of AlCoCrFeNiTi0.5 High-Entropy Alloy at High Temperature. Coatings. 2023; 13(10):1811. https://doi.org/10.3390/coatings13101811
Chicago/Turabian StyleLiu, Xinbin, Tiansheng Li, Yong Wang, Xianghua Kong, and Chenyang Zhao. 2023. "Deformation Behavior and Processing Map of AlCoCrFeNiTi0.5 High-Entropy Alloy at High Temperature" Coatings 13, no. 10: 1811. https://doi.org/10.3390/coatings13101811
APA StyleLiu, X., Li, T., Wang, Y., Kong, X., & Zhao, C. (2023). Deformation Behavior and Processing Map of AlCoCrFeNiTi0.5 High-Entropy Alloy at High Temperature. Coatings, 13(10), 1811. https://doi.org/10.3390/coatings13101811





