Abstract
The blades of some airborne equipment are prone to icing under supercooled cloud conditions. In this paper, we propose an anti-deicing spray method to prevent blades from icing at low temperatures. Using computational fluid dynamics modeling and orthogonal experimental methods, we investigated the effects of the blade angle of attack, inlet wind speed, and nozzle mass flow rate on the thickness and coverage of the liquid layer of spray material and examined the use of deflectors in this study. We found the magnitude and change rule of the influence of the previously mentioned parameters on the liquid film thickness and coverage of sprayed material to be the nozzle mass flow rate is greater than the blade angle of attack and greater than the inlet wind speed. Under the optimal combination of conditions of α = 30°, u0 = 6 m/s, and Q = 0.003 kg/s, the liquid film thickness was maximized, and the liquid film thickness was 0.037 mm; under the optimal combination of conditions of α = 60°, u0 = 6 m/s, and Q = 0.003 kg/s, the liquid film coverage was maximized, and the liquid film coverage was 99.81%. The anti-deicer spraying method proposed herein for use on blades is effective when considered from a number of perspectives. It provides an innovative and feasible solution to the wind turbine blade freezing problem. However, the method must be explored and modified to maximize its chances of general application, and other factors must also be considered to fully optimize the sprinkler de-icing technique to improve the performance and reliability of blades.
1. Introduction
In recent years, as a result of the escalating carbon emission problem [1] and the recurrent energy crisis [2], people have progressively realized the significance of developing new renewable energy sources [3]. Among the many applications of renewable energy technologies, wind power has a significant advantage due to its mature technology, good infrastructure, relatively low cost, and its inherent cleanliness [4,5]. It has the potential to become a significant contributor to the growing global demand for clean energy [6]. Nevertheless, the current wind energy technology is plagued by numerous issues, such as condensation in low-temperature environments.
Many wind farms in coastal or mountainous regions are susceptible to blades ice during winter [7,8,9]. Minor blades icing may reduce the capacity of the wind turbine and lead to the inaccuracy of instruments such as anemometers [10,11]. At the same time, severe wind turbine icing leads to wind turbine shutdown, ice on the blades can cause severely unbalanced loads on the wind turbine, and severe safety hazards will be near roads, houses, electric wires, and transportation pipelines [12,13,14]. Therefore, choosing an appropriate anti-icing method for Blades of airborne operational equipment such as aircraft or wind turbines is crucial. Currently, electrothermal de-icing [15,16,17], electric pulse de-icing [18,19], mechanical de-icing [20,21], and anti-icing coating are the most prevalent anti-icing technologies. These techniques are typically characterized by a high energy consumption, low de-icing effectiveness, and environmental pollution [13,22,23]. Anti-icing coating technology is the application of anti-icing coating or hydrophobic coating on solid surfaces, which has the advantages of a low energy consumption, environmental friendliness, and a wide range of applications [19,24,25]. Although it cannot wholly prevent icing under severe icing conditions, it is the most cost-effective option of the numerous technologies [25].
Currently, numerous researchers, including Jiaqiang et al. [26] and Wu et al. [27], have developed a variety of anti-icing coatings, which has led to the resolution of the material issue of anti-icing coatings; however, research is still needed to determine how to apply anti-icing coatings effectively. Drone technology has been used in pesticide spraying [28,29]. The Norwegian University of Science and Technology (NTNU) recently conducted an informal study of wind turbine anti-ice spraying in the Arctic using drones [30]. Aerones claimed to have developed a drone that is capable of being applied to the spraying of de-icing fluids on wind turbines [31]. Villeneuve et al. developed a UAV de-icing system, and Gidinceanu et al. [32] further validated the potential of UAV technology in the field of wind turbine de-icing, but due to the immaturity of the technology, more research is needed to deal with the day-to-day work [32]; Ernez et al. [33], in 2019, presented for the first time an Eulerian–Lagrangian CFD model and mentioned, several times, the feasibility of spraying an anti-de-icer in the field of aircraft ground de-icing [33,34], and due to the similarity between aircraft wings and wind turbine blades, the technology also has the potential to be applied in the field of wind turbine blade de-icing.
In this paper, an anti-deicing spraying model has been developed and particle spraying calculations have been carried out for the blade of NREL5MW airfoil shape, simulates the anti-icing liquid spraying working condition based on an orthogonal experimental method, and combines simulation and experimental results to investigate critical parameters such as the optimal spraying angle of attack and the nozzle flow rate of the anti-icing coating technology, as well as the feasibility and development of the model. In Section 2, we establish the simulation model, verify the grid independence, and describe the parameter settings for the model and the simulation parameters. In Section 3, we present the experimental results and analysis. In Section 4, the conclusion and discussion are presented.
2. Modeling and Grid-Independent Verification
2.1. Materials and Models
In this paper, liquid water is used to simulate spray coating, and the spraying scheme is modeled under the static state of the balde of NREL 5MW airfoil shape, which are 2.82 m in length and 27.3 m from the tip position. A spraying device for blades anti-ice liquid is constructed. This spraying device consists of a tower crawler, a spraying frame, and a deflector plate. The spraying frame is equipped with ten pre-film atomizing nozzles, the nozzle spraying cone angle is 30°, and the precise structure and operating principle are depicted in Figure 1. The device is mounted on a suitable wall of the equipment with blades. When the equipment with blades (in the case of a wind turbine) is stopped due to icing, the blades are rotated to a parallel tower position and remain stationary, clamping the rotating arms together to provide non-contact clamping of the blades. The injectors are uniformly oriented in the direction of the blade axis, and the effect of ice melting is accomplished by the continuous sprinkling of anti-icing agents, as shown in Figure 1b.
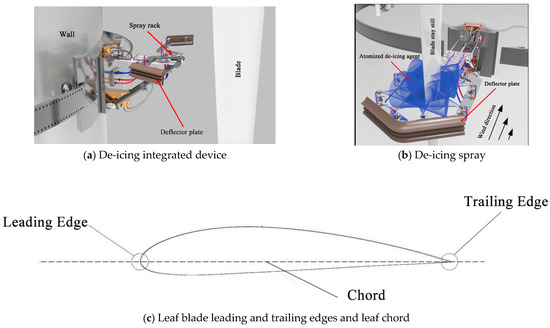
Figure 1.
Device design and operating principle.
2.2. Regulating Equations
Physical conservation laws govern the fluid flow, and fundamental conservation laws include the laws of the conservation of mass, momentum, and energy, which are collectively referred to as the controlling equations of the fluid flow. CFD’s governing equations consist primarily of the continuity conservation equation, the momentum conservation equation, and the energy conservation equation [35,36], which can be rewritten as follows:
In Equation (1), denotes the density, t denotes the time, div is the result of the scattering calculation, and U is the velocity vector.
In Equation (2), represents the general variables, which can be expressed as u, v, and w, while u, v, and w represent the components in the x, y, and z directions, respectively, Γ represents the diffusion coefficients, grad is the result of the scattering calculations, and represents the source item.
In Equation (3), T denotes temperature, k denotes the heat transfer coefficient of the fluid, cp denotes the specific heat capacity, and ST denotes the viscous dissipation item.
2.3. Choice of Boundary Conditions
Boundary conditions are prerequisites for solving the governing equations and are essential to accurately simulate the sprinkling process on the blades. In the simulation, we set the number of time steps to 650, the time step to 0.008 s, the maximum number of iterations to 20, and the total simulation time to 5.2 s. We added a description of this in the main text. Due to the relative complexity of the blade and spray structure, Ansys ICEM CFD was chosen to construct the global three-dimensional tetrahedral computational mesh, while local meshing is used to mitigate the computational effort by setting different mesh densities in different regions. Due to the brief duration of the sprinkling simulation and the short-term stability of the wind turbine’s external conditions, the Realise k-Model [37] was chosen as the turbulence model. This extensively used method for simulating turbulence exhibits high accuracy and applicability in current turbulence research. Moreover, to obtain valuable insight into the behavior of spray particulates and the deposition of spraying liquid film on blade surfaces, we developed the Discrete Phase Model (DPM) [38]. The DPM allows us to precisely trace the motion path of aerosol particles within the airflow, providing crucial data for analyzing the formation and distribution of the liquid deposit on the blades of wind turbines.
We simplified the air’s properties to maintain computational efficiency while maintaining the simulation’s physical accuracy. We can represent the air as stable and incompressible ideal air because the ventilation velocity and temperature fluctuations are relatively small. Additionally, we accounted for the effect of gravity in the simulation. The configuration of the inlet and outlet boundary conditions is also crucial for accurate simulation results. To ensure a seamless flow at the domain boundaries, we configured the inlet as a velocity and the outflow as a pressure outlet. In order to depict irregular flow effects during the spraying process, we set the initial state of the simulation to be stable, which will later transition to a transient state. Table 1 displays the specific model and parameter configurations.

Table 1.
Model configuration and boundary conditions.
In the simulation, we set the number of time steps to 650, the time step to 0.008 s, the maximum number of iterations to 20, and the total simulation time to 5.2 s. The density of the fluid was 1.226 kg/m3. The initial velocity of the nozzle jet was 140 m/s, and there was no slip condition on the wall surface because this study needs to consider the particle distribution of the particles on the wall surface.
2.4. Grid-Independent Verification
To ensure the accuracy of the numerical simulation and the independence of the grids, for the wind turbine blade model depicted in Figure 1, we investigated the thickness of the liquid film of the sprayed material and the liquid film coverage at the leading and trailing edge positions and in the profile parallel to the blade chord plane under the following conditions: blade angle of attack, α = 0°; inlet incoming wind speed, u0 = 5 m/s; and nozzle mass flow rate, Q = 0.001 kg/s. To acquire reliable results, three distinct quantities of meshes were employed, and the numerical simulation results are presented in Table 2.

Table 2.
Comparison of grid-independent validation data.
Table 2 shows that the difference in the liquid film thickness between the three cases is minor, but there was a significant difference between Case 1, Case 2, and Case 3 at the leading edge position. Case 1 had a thin liquid film thickness, with an average liquid film thickness of 0.007 mm and a liquid film coverage of 67.28 percent. In contrast, the thickness of the liquid deposit at the leading edge of Case 2 and Case 3 was substantially increased, and the difference between the two operating conditions was negligible. The difference in the liquid film thickness between Case 2 and Case 3 at the downstream margin was less than 2%.
To acquire a higher mesh resolution and a lower computational cost in the subsequent numerical simulations, we choose Case 2’s mesh density. The total number of meshes and nodes for Case 2 were 37,345,291 and 6,652,215, respectively. Such a grid configuration can ensure the accuracy of the calculation results and enhance the computational efficiency, providing a solid numerical foundation for our in-depth investigation of the blades spraying process.
3. Result and Discussion
3.1. Influence of a Single Variable on Liquid Film Thickness and Coverage
3.1.1. Single-Factor Effect Parameter Configuration
This section describes the parameter settings used to investigate the effects of single-factor variations on the liquid film thickness and liquid film coverage of the blade discharge material. Table 3 details the parameter configurations for various operating conditions. A total of three influencing factors were set up: α, u0, and Q. The fundamental parameters were α = 30°, u0 = 9 m/s, and Q = 0.001 kg/s. Only the value of a single variable was altered when investigating the effect of a single variable’s change on the liquid film thickness and liquid film coverage. In contrast, the other variables remained unchanged as the above fundamental parameters.

Table 3.
Changes in single-factor independent variables and their parameters.
3.1.2. Influence of Blade Strike Angle Variation
Figure 2 and Table 4 compare the liquid film thicknesses obtained by varying the blade attack angle, as well as the average liquid film thickness and liquid film coverage. Figure 2 reveals that the distribution of the dispersed material at various angles of attack differs significantly, and that Case 1-3 has a significant advantage in terms of the liquid film coverage. Table 4 reveals that the average liquid film thickness and average liquid film coverage are the lowest when the angle of attack is 90°, and that the 30° angle of attack and the 60° angle of attack produce the highest average liquid film thicknesses and average liquid film coverages, respectively, among the four angles of attack. The average liquid film thickness under a 30° angle of attack is 0.017 mm, which is 0.006 mm greater than that under a 90° angle of attack. The average liquid film coverage at an angle of attack of 60° is 87.42%, which is a 15.27% increase compared to that of an angle of attack of 90°.

Figure 2.
Liquid film distribution at different blade angles of attack.

Table 4.
Average liquid film thickness and liquid film coverage at different leaf attack angles.
3.1.3. Influence of Variable Inlet Air Velocity
Figure 3 and Table 5 compare the liquid film thicknesses obtained by varying the inlet flow wind speed and the average liquid film thickness and coverage. Figure 3 reveals that, due to the presence of the deflector plate, the inlet flow wind speed has less of an effect on the liquid film thickness, and the overall change is not significant; however, as the wind speed increases, the liquid film thickness decreases marginally. By examining Table 5, it can be seen that the fluctuation of the data from Case 2-1 to Case 2-4 is small; with the increase in the wind speed from 6 m/s to 15 m/s, the average liquid film thickness is reduced by only 0.003 mm, and the average liquid film coverage is also gradually reduced with the increase in the wind speed, but the reduction gradually decreases. The reductions in the average coverage from Case 2-1 to Case 2-4 are 2.18%, 2.17%, and 1.68%. The cause of the above phenomenon is that the airflow that should have entered the spraying field was guided to the upper and lower ends due to the airflow guidance effect of the deflector plate. However, as the wind speed increased, the deflector plates’ flow-inducing effect gradually decreased, and the airflow guided to the upper and lower ends was restored earlier, resulting in a lower thickness and coverage of the liquid film at high wind speeds.
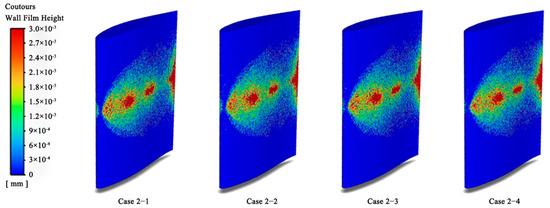
Figure 3.
Liquid film distribution at different incoming wind speeds.

Table 5.
Average liquid film thickness and liquid film coverage at different incoming wind speeds.
3.1.4. Influence of Changes in Nozzle Mass Flow Rate
Figure 4 and Table 6 compare the liquid film thicknesses obtained by varying the nozzle mass flow rate and the average liquid film thickness and coverage. By observing Figure 4, it is evident that as the nozzle mass flow rate increases, the liquid film thickness and the liquid film coverage increase significantly. With the nozzle mass flow rate increasing, the average liquid film thickness and coverage gradually increase, as shown in Table 6. The average liquid film thickness and liquid film coverage of Case 3-4 were improved by 0.025 mm and 43.23%, respectively, compared with those of Case 3-1. However, the growth rate was gradually reduced: from Case 3-1 to Case 3-2, the mass flow rate was improved by 0.0005 kg/s, and the average liquid film thickness and coverage increased by 0.009 mm and 18.57%, respectively; from Case 3-3 to Case 3-4, the average liquid film thickness was improved by 0.0005 kg/s, and the average liquid film thickness and coverage increased by 0.005 mm and 9.17%, respectively, representing a significant reduction in the increase. Therefore, it can be concluded that the use of a nozzle with a higher mass flow rate can effectively improve the liquid film thickness and coverage of the material sprayed for de-icing; however, the magnitude of the improvement decreases as the mass flow rate increases, and the liquid film thickness and coverage reach their maximum values when the mass flow rate reaches 0.003 kg/s and above.
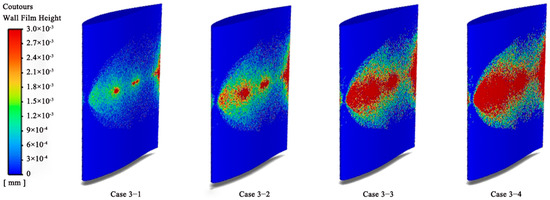
Figure 4.
Liquid film distribution at different mass flow rates.

Table 6.
Average liquid film thickness and liquid film coverage at different mass flow rates.
3.2. Effects of Multi-Factor Changes on Liquid Film Thickness and Coverage
In the preceding section, the effects of three factors on the liquid film thickness and liquid film coverage were studied separately. However, in practice, the cross-influence between various factors can result in significant variations in the liquid film thickness and liquid film coverage; thus, this section will investigate the optimal combination of working conditions under the influence of multiple factors to optimize the de-icing spraying technology. To investigate the effects of all parameters on the average power output of wind farms with the shortest simulation time and the lowest arithmetic cost possible, the orthogonal test method is introduced due to the large number of working conditions to be investigated.
In this section, simulation measurements and analyses of the dispersed liquid film thickness and liquid film coverage will be conducted using the orthogonal test method with three influencing factors, α, u0, and Q. The three influential factors are denoted by the letters A, B, and C. At the same time, the levels range from 1 to 4. The orthogonal test parameter settings are detailed in Table 7.

Table 7.
Parameter setting of orthogonal test.
This orthogonal test utilized the three-factor, four-level orthogonal table of L1643, and 16 test situations were set up. Table 8 displays the results of the experiment. According to Table 8, the polar analysis of the average liquid film thickness and the average liquid film coverage indicates the degree of influence of the various factors. R represents the difference between the optimal level of the parameter and the lowest level of power, K1 through K4 represent the sum of the average data for levels 1 through 4, and k1 through k4 represent the average liquid film thickness or liquid film coverage based on K1 through K4. The extreme variance analysis outcomes are detailed in Table 9 and Table 10.

Table 8.
Results of orthogonal test.

Table 9.
Extreme variance analysis of mean liquid film thickness.

Table 10.
Extreme variance analysis of liquid film coverage.
From the analysis of extreme deviation, it can be seen that the degree of influence on the average liquid film thickness of the spraying material is ranked as C > A > B, and the optimal combination to maximize the liquid film thickness is A2B1C4. The degree of influence on the average liquid film coverage of the spraying material is ranked as C > A > B, and the optimal combination to maximize the liquid film coverage is A3B1C4. The optimal working conditions for enhancing the liquid film thickness and coverage are not identical. However, the change rule is the same as the result derived from the single-factor influence section. The optimal liquid film thickness is 0.037 mm, and the optimal liquid film coverage is 99.81% based on simulations of the two theoretically optimal working condition combinations.
3.3. Verification of Deflector Effect
In this section, the performance of the deflector is analyzed, and the liquid film thickness and liquid film coverage of the sprayed material are compared for both cases with and without the deflector to verify the deflecting effect of the deflector, as mentioned above. The numerical simulation uses three basic parameters to investigate the influence of a single factor, i.e., α = 30°, u0 = 9 m/s, and Q = 0.001 kg/s. The simulation results are shown in Figure 5 and Figure 6. Figure 5a reveals that, due to the airflow guiding effect of the flow guide plate, the gases that are supposed to enter the spray field can be guided towards the upper and lower ends. At the same time, the gases that are exported through the middle part of the plate push the gases at the upper and lower ends of the plate to flow in directions farther away from the spray field. At the same time, the gas that is exported from the center of the deflector plate pushes the gas at the upper and lower ends of the deflector plate to flow in a direction farther away from the spraying field, forming a virtuous cycle. A comparative analysis of Figure 5b,c reveals that the presence of the deflector plate enables the formation of a static fluid space in the rear spray field, which helps the de-icer to become atomized by the nozzle to move towards the surface of the blade and improves the effect of spraying onto a film.

Figure 5.
Secondary deflector flow field streamlines and velocity distribution. (a) Deflector plate flow field flow line. (b) Velocity distribution cloud of the deflector plate cross section. (c) Velocity distribution in the cross section without deflector plate.

Figure 6.
Liquid film distribution with/without deflector.
Figure 6 provides a detailed illustration of the deflectors’ essential function in the atomized sprinkling process. Without a deflector, the paint particulates that are expelled from the nozzle are powerfully deflected before they contact the blade. Consequently, the liquid film thickness is considerably reduced, particularly in the middle section of the blade, where the deflection away from the distribution frame is significantly greater. The inclusion of a primary and effective deflector improves the discharge efficacy. The deflector installation resulted in a considerable increase of 0.003 mm in the average film thickness and an increase of 3.56% in the film coverage, representing a significant improvement.
4. Conclusions
The anti-deicing spray effect demonstrated by this method is affected by a number of factors. This study aims to optimize the blades anti-ice liquid spraying technology, proposes a new de-icing scheme, and, by using the orthogonal experimental method and a CFD numerical simulation, investigates the influence of multiple factors on the liquid film thickness and liquid film coverage, as well as the effect of the deflector plate and the viability of the modified scheme.
- (1)
- Upon studying the effects of the blade angle of attack separately, the inlet incoming wind speed, and the nozzle mass flow rate on the liquid film thickness and liquid film coverage, the following laws were derived: a 30° angle of attack and a 60° angle of attack produce the highest liquid film thickness and coverage, respectively. In contrast, a 90° angle of attack produces the lowest liquid film thickness and coverage. In terms of the inlet incoming air velocity, lower air velocities result in a greater film thickness and coverage, with the film thickness and coverage diminishing as the air velocity increases. In terms of the nozzle mass flow rate, using a nozzle with a higher mass flow rate can effectively improve the liquid film thickness and coverage, but as the mass flow rate increases, the magnitude of the improvement diminishes.
- (2)
- Using the orthogonal experimental method to determine the level of influence of the factors on the liquid film thickness and coverage, as well as the optimal combination of working conditions, the results demonstrate the following: In descending order, the influences on the liquid film thickness and coverage are the nozzle mass flow rate, blade angle of attack, and inlet inflow wind speed. The liquid film thickness was maximized at 0.037 mm for the optimal combination of conditions of α = 30°, u0 = 6 m/s, and Q = 0.003 kg/s, and the liquid film coverage was maximized at 99.81% for the optimal combination of conditions of α = 60°, u0 = 6 m/s, and Q = 0.003 kg/s.
- (3)
- Using CFD simulation, the flow-guiding effect of the deflector plate was validated. The deflector plate can cause the discharged liquid to form a benign cycle, effectively enhance the liquid film thickness and coverage, and increase the average liquid film thickness by 21.43% and the average liquid film coverage by 3.56%.
In conclusion, this study provides an in-depth analysis and optimization of the anti-icing liquid sprinkling technology for baldes, which can be used to improve the anti-icing effect and efficacy of the blades. However, it is essential to note that this study simulates the spray coating using only liquid water and does not account for the influence of other variables, such as the chemical properties of the spray material and the ambient temperature. Future research will further enhance the model, consider additional practical factors, and conduct an experimental verification to increase the dependability and practicality of the anti-icing liquid spray coating technology for b. However, it is worthwhile to note that there has not been any theoretical research similar to this paper, and the reality also happens to lack an environmentally friendly, stable, and efficient way to de-ice blades; this study will make an innovation in this field, which has a high application and commercial value.
Author Contributions
Conceptualization, G.L. (Gang Lei); G.L. (Guohao Li); F.F. Conceptualization, F.F.; methodology, G.L. (Guohao Li); software, G.L. (Guohao Li); validation, G.L. (Gang Lei), and F.F.; formal analysis, G.L. (Guohao Li); investigation, G.L. (Gang Lei), and F.F.; resources, F.F.; data curation, G.L. (Guohao Li); writing—original draft preparation, G.L. (Guohao Li); writing—review and editing, G.L. (Gang Lei); G.L. (Guohao Li); F.F.; visualization, G.L. (Gang Lei), and F.F.; supervision, F.F.; project administration, G.L. (Gang Lei), and F.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by “Academic Backbone” of Northeast Agricultural University Fund, grant number 20XG20.T.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| cp | Specific heat capacity | ST | Viscous dissipation term |
| I | Turbulence intensity | x, y, z | Cartesian space coordinates |
| g | Gravity | u, v, w | The velocity components in the x, y, and z directions, respectively |
| HL | Wall film height of leading edge of blade | u0 | Inlet incoming air velocity |
| HM | Average wall film height of blade | α | Blade angle of attack |
| HT | Wall film height of trailing edge of blade | ρ | Density |
| k | Heat transfer coefficient of fluid | Φ | General variables, which can represent u, v, and w |
| p0 | Outlet gauge pressure | Γ | Diffusion coefficient |
| Q | Mass flow | T | Temperature |
| SΦ | Source item | U | Velocity vector |
References
- O’Neill, B.C.; Dalton, M.; Fuchs, R.; Jiang, L.; Pachauri, S.; Zigova, K. Global demographic trends and future carbon emissions. Proc. Natl. Acad. Sci. USA 2010, 107, 17521–17526. [Google Scholar] [CrossRef] [PubMed]
- Manieniyan, V.; Thambidurai, M.; Selvakumar, R. Study on energy crisis and the future of fossil fuels. Proc. SHEE 2009, 10, 2234–3689. [Google Scholar] [CrossRef]
- Dincer, I. Renewable energy and sustainable development: A crucial review. Renew. Sust. Energ. Rev. 2000, 4, 157–175. [Google Scholar] [CrossRef]
- Leung, D.Y.; Yang, Y. Wind energy development and its environmental impact: A review. Renew. Sust. Energ. Rev. 2012, 16, 1031–1039. [Google Scholar] [CrossRef]
- Sesto, E.; Casale, C. Exploitation of wind as an energy source to meet the world’s electricity demand. J. Wind. Eng. Ind. Aerodyn. 1998, 74, 375–387. [Google Scholar] [CrossRef]
- Veers, P.; Dykes, K.; Lantz, E.; Barth, S.; Bottasso, C.L.; Carlson, O.; Wiser, R. Grand challenges in the science of wind energy. Science 2019, 366, eaau2027. [Google Scholar] [CrossRef]
- Fortin, G.; Perron, J. Wind turbine icing and de-icing. In Proceedings of the47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; p. 274. [Google Scholar] [CrossRef]
- Martini, F.; Contreras Montoya, L.T.; Ilinca, A. Review of wind turbine icing modelling approaches. Energies 2021, 14, 5207. [Google Scholar] [CrossRef]
- Etemaddar, M.; Hansen MO, L.; Moan, T. Wind turbine aerodynamic response under atmospheric icing conditions. Wind. Energy 2014, 17, 241–265. [Google Scholar] [CrossRef]
- Bose, N. Icing on a small horizontal-axis wind turbine—Part, 1: Glaze ice profiles. J. Wind. Eng. Ind. Aerodyn. 1992, 45, 75–85. [Google Scholar] [CrossRef]
- Parent, O.; Ilinca, A. Anti-icing and de-icing techniques for wind turbines: Critical review. Cold Reg. Sci. Technol. 2011, 65, 88–96. [Google Scholar] [CrossRef]
- Hochart, C.; Fortin, G.; Perron, J.; Ilinca, A. Wind turbine performance under icing conditions. Wind. Energy 2008, 11, 319–333. [Google Scholar] [CrossRef]
- Wei, K.; Yang, Y.; Zuo, H.; Zhong, D. A review on ice detection technology and ice elimination technology for wind turbine. Wind. Energy 2020, 23, 433–457. Available online: https://publons.com/publon/10.1002/we.2427 (accessed on 12 October 2022). [CrossRef]
- Gao, L.; Tao, T.; Liu, Y.; Hu, H. A field study of ice accretion and its effects on the power production of utility-scale wind turbines. Renew. Energy 2021, 167, 917–928. [Google Scholar] [CrossRef]
- Lewis, J.P. De-Icing Effectiveness of External Electric Heaters for Propeller Blades; (No. NACA-TN-1520); NASA: Washington, DC, USA, 1948. [Google Scholar]
- VonGlahn, U.; Blatz, R.E. Investigation of Power Requirements for Ice Prevention and Cyclical De-Icing of Inlet Guide Vanes with Internal Electric Heaters; (No. NACA-RM-E50H29); NASA: Washington, DC, USA, 1950. [Google Scholar]
- Yugulis, K.; Chase, D.; McCrink, M. Ice Accretion Analysis for the Development of the HeatCoat Electrothermal Ice Protection System. In Proceedings of the Aiaa Aviation 2020 Forum, Virtual, 15–19 June 2020; p. 2834. [Google Scholar] [CrossRef]
- Mayer, C.; Ilinca, A.; Fortin, G.; Perron, J. Wind tunnel study of electro-thermal de-icing of wind turbine blades. Int. J. Offshore Polar Eng. 2007, 17. [Google Scholar]
- Dalili, N.; Edrisy, A.; Carriveau, R. A review of surface engineering issues critical to wind turbine performance. Renew. Sust. Energy Rev. 2009, 13, 428–438. [Google Scholar] [CrossRef]
- Schulz, M.; Sinapius, M. Evaluation of Different Ice Adhesion Tests for Mechanical Deicing Systems; (No. 2015-01-2135); SAE International: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Laforte, J.L.; Allaire, M.A.; Laflamme, J. State-of-the-art on power line de-icing. Atmos. Res. 1998, 46, 143–158. [Google Scholar] [CrossRef]
- Frohboese, P.; Anders, A. Effects of icing on wind turbine fatigue loads. J. Phys. Conf. Ser. 2007, 75, 012061. [Google Scholar] [CrossRef]
- Laakso, T.; Holttinen, H.; Ronsten, G.; Tallhaug, L.; Horbaty, R.; Baring-Gould, I.; Tammelin, B. State-of-the-art of wind energy in cold climates. IEA Annex XIX 2003, 24, 53. [Google Scholar]
- Jiaqiang, E.; Jin, Y.; Deng, Y.; Zuo, W.; Zhao, X.; Han, D.; Zhang, Z. Wetting models and working mechanisms of typical surfaces existing in nature and their application on superhydrophobic surfaces: A review. Adv. Mater. Interfaces 2018, 5, 1701052. [Google Scholar] [CrossRef]
- Peng, C.; Xing, S.; Yuan, Z.; Xiao, J.; Wang, C.; Zeng, J. Preparation and anti-icing of superhydrophobic PVDF coating on a wind turbine blade. Appl. Surf. Sci. 2012, 259, 764–768. [Google Scholar] [CrossRef]
- Wang, Z. Recent progress on ultrasonic de-icing technique used for wind power generation, high-voltage transmission line and aircraft. Energy Build. 2017, 140, 42–49. [Google Scholar] [CrossRef]
- Wu, X.; Fu, Q.; Kumar, D.; Ho JW, C.; Kanhere, P.; Zhou, H.; Chen, Z. Mechanically robust superhydrophobic and superoleophobic coatings derived by sol–gel method. Mater. Design. 2016, 89, 1302–1309. [Google Scholar] [CrossRef]
- Faiçal, B.S.; Freitas, H.; Gomes, P.H.; Mano, L.Y.; Pessin, G.; de Carvalho, A.C.; Ueyama, J. An adaptive approach for UAV-based pesticide spraying in dynamic environments. Comput. Electron. Agr. 2017, 138, 210–223. [Google Scholar] [CrossRef]
- Cervantes, A.; Garcia, P.; Herrera, C.; Morales, E.; Tarriba, F.; Tena, E.; Ponce, H. A conceptual design of a firefighter drone. In Proceedings of the 2018 15th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 5–7 September 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Villeneuve, E.; Karmouch, E.; Boulerice, X. Development of a small and transportable de-icing/anti-icing drone-mounted system. Part 1: System design. Drone Syst. Appl. 2022, 10, 155–177. [Google Scholar] [CrossRef]
- Aerones. Aerones DRONE Solutions. 2022. Available online: https://www.aerones.com/ (accessed on 12 October 2022).
- Gidinceanu, C.P. De-Icing and Maintenance of Wind Turbines with Drones. Master’s Thesis, Aalborg University, Aalborg, Denmark, 2019. [Google Scholar]
- Ernez, S.; Morency, F. Eulerian–Lagrangian CFD model for prediction of heat transfer between aircraft deicing liquid sprays and a surface. Int. J. Numer. Method H 2019, 29, 2450–2475. [Google Scholar] [CrossRef]
- Ernez, S.; Morency, F. A multi-region CFD model for aircraft ground deicing by dispersed liquid spray. Energies 2022, 15, 6220. [Google Scholar] [CrossRef]
- Amini, Y.; Nasr Esfahany, M. CFD simulation of the structured packings: A review. Sep. Sci. Technol. 2019, 54, 2536–2554. [Google Scholar] [CrossRef]
- Kim, K.; Yoon, J.Y.; Kwon, H.J.; Han, J.H.; Son, J.E.; Nam, S.W.; Lee, I.B. 3-D CFD analysis of relative humidity distribution in greenhouse with a fog cooling system and refrigerative dehumidifiers. Biosyst. Eng. 2008, 100, 245–255. [Google Scholar] [CrossRef]
- Lew, A.J.; Buscaglia, G.C.; Carrica, P.M. A note on the numerical treatment of the k-epsilon turbulence model. Int. J. Comput. Fluid D 2001, 14, 201–209. [Google Scholar] [CrossRef]
- Zahari, N.M.; Zawawi, M.H.; Sidek, L.M.; Mohamad, D.; Itam, Z.; Ramli, M.Z.; Rashid, M. Introduction of discrete phase model (DPM) in fluid flow: A review. In AIP Conference Proceedings; AIP Publishing: Woodbury, NY, USA, 2018; Volume 2030. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).