Abstract
The permeability of fiber-based materials and general medical textiles is very important, and it is commonly believed that air permeability and water permeability are correlated. This property is expressed as the breathability of the material. Knowing the air permeability is helpful in predicting the water vapour permeability as well, but whether this really works for textiles at different pressures and humidities still needs to be explored. In this study, this hypothesis is examined, and it is discovered that this phenomenon does not show significant corelation. Moreover, the non-standardised unit of measurement of breathability makes the comparison much more complex in terms of textiles. The articles focuses on any possible relationship between the air and water vapour permeability of textiles.
1. Introduction
The breathability of textiles is one of the most important factors in realising a garment’s functional behaviour and its final usage. The breathability includes air permeability and water vapour resistance. There are multiple standard methods evalutating breathability, the most commonly used being ISO 9237 to measure the volume of air crossing the material per unit of time. On the other hand, the water vapour permeability can be measured by multiple methods, considering either the resistance to water vapour crossing the fabric or the amount of water vapour in grams that crosses the material per unit of time. These phenomena look very similar, and considering the porous structure of the textile, both can be true. Many researchers [1,2,3,4,5,6,7] have worked to find the relationship between both factors of breathability. The wetting, or water drop movement, is generally achieved through capillary action, whereas the water vapour exchange generally occurs due to the partial pressure gradient. The air permeability measurement is quick and economical, so it would be beneficial to find a corelation between air and water vapour permeability, if possible.
Air Permeability
The air permeability of a textile sample is defined as the volumetric airflow through the sample area:
V/S = (m3/s)/m2 = m/s
Simply put, it is the velocity of the airflow through the sample area. The gas volume depends on its stated quantities following the general gas law:
where:
p · v = r · T resp. p · V = m · r · T
- p (Pa) = absolute pressure;
- v (m3/kg) = specific volume;
- T (K) = absolute temperature;
- r (J/(kg · K)) = gas constant;
- m (kg) = mass;
- V (m3) = volume.
Generally, it is better to use the mass flow through the sample area in (kg/s)/m2. It is independent of state quantities; thus, the conversion is simple:
where:
m = V/v = V · p/(r · T) = V · (B ± Δp)/(r · T)
- B (Pa) = barometric pressure;
- ±Δp (Pa) = variance in barometric pressure.
The barometric pressure changes with both altitude and weather, as well as if the air is pressed or pulled through the sample during the measuring process. The air permeability of a sample is proportional to the absolute pressure.
The device used to measure low pressure differences (up to 250 Pa) in textiles used for clothing materials sucks air through a tested sample, and the flow volume is measured in the depression; this means that the measured air volume is a little higher than the actual air volume (see the general gas law above).
The device to evaluate high pressure differences (up to 2000 to 5000 Pa) is used for various building materials by pressing air through the sample. The volume flow is measured in the overpressure, which means that the measured air volume is lower than the actual air volume.
To achieve an exact comparison of the results obtained by both devices, it is necessary for the measured values to be corrected to some standard, for instance, to the pressure of the surroundings, adjusting the general gas law (4) as:
where the index:
pm · vm/Tm = pc · vc/Tc
- M = measured value;
- C = calibration value (or any standard value).
Note:
Using high pressure, the measured textile sample deforms into the shape of a spherical segment, which means that the blown sample area is increasing. The area of such a segment is:
where:
S = 2 · π · r · v
- r (m) = the radius of the relevant sphere;
- v (m) = the height of the relevant segment.
The radius of the measured circular sample is a < r, so the radius of the relevant sphere is:
r = (a2 + v2)/(2 · v).
Now, it is possible to state that the increase in the flow area of the concaved segment (with pressure) compared to the area of the flat sample (no pressure) is given by the relationship of (v/a)2; moreover, for example, when v/a = 0.01, the increase in the flow area of the spherical segment compared to the initial flat circle is 0.01%, which can also be neglected. For v/a = 0.1, the increase in the segment area is 1%, which is also in the range of the usual measurement error.
- (1)
- The diffusion flow J is proportional to the gradient of concentration ∂c/∂x, with proportionality constant D (m2/s) as the so-called diffusion coefficient:J = D · ∂c/∂x
D depends on temperature T, as well as on the dynamic viscosity of the fluid and on the size R of the diffusing particles:
D = k · T / (6 · π · η · R).
- (2)
- The characteristics of the concentration change over time. Some argue that in the used device, both of the concentrations, before and after sampling, remain constant (at least theoretically; however, this has not been verified).
Theoretical explanation:
The water vapour permeability of the sample—in contrast to the air permeability—is defined as the vapour’s mass flow (kg/s) through the sample area (m2). As for the airflow above the sample, when measuring the air permeability of gases, it is better to use mass flow instead of volume flow. For values in g/(m2 · day), as measured by the device, it is necessary to recalculate them into legitimate SI measuring units as kg/(m2 · s). This is the same for air permeability. The relation between mass and volume flow is given by (3). Instead of such a simple quantity, the standard [8] contains a complicated quantity for “evaporating resistance” Ret (m2 · Pa/W), and probably more precisely, “the resistance of the vapour flow through the sample”. Using basic SI units, the resistance Ret is in (s/m), which is the reciprocal value of the vapour flow through the sample. This is the vapour permeability for the sample. This result is logical since flow and flow resistance are reciprocal values.
The same standard also gives a feature of a textile material (without further specification): water vapour permeability Wd = 1/(Ret · q), with the mentioned unit of g/(m2 · h · Pa). It is the reciprocal value of the evaporating resistance above and divided by the so-called latent heat; this heat is the evaporative heat q (J/kg), generally used in thermo-mechanics. It is the heat that is necessary for the evaporation of water at the saturation limit (boiling) into the saturated vapour. So, suddenly, here is the heat (enthalpy) mentioned, contained in the passing vapour, which can be understood as the heat passed through the sample, as well as some cooling. Introducing legal SI measuring units, the result is simple (s/m); in addition, the dimensions of such vapour permeability Wd are the same as for the evaporating resistance Ret, more precisely, the flow resistance. However, according to the standard, the two reciprocal values have the same dimensions.
On a common carousel, the used automatic device holds 12 cups filled with water; textile samples with an area of 50 cm2 are fixed above the water’s surface at the upper edge of the cups. The carousel is turning so that every 5 min, one cup is weighed to determine the mass (water) in order to determine the water vapour permeability. In the beginning, the samples are initially conditioned for the time of half an hour. The unit is permanently shut air-tight and isothermally, which means that no condensation of the diffused vapour can take place. In the inner volume, the adjusted and required air temperature and relative humidity are kept, i.e., the lower pressure of unsaturated air behind the sample and higher pressure of saturated vapour over the water level in the cup before the sample. The penetrated vapour is led away by airflow, the velocity of which is also reputedly defined. However, the air velocity is controlled by a simple flap, only in the range of one order.
The water temperature before the samples is 40 °C (saturated vapour of pressure 7375 Pa) for all realized measurements, and the relative humidity behind the samples is set and kept in the range of 20–90% R.H. and at the same temperature of 40 °C. In this way, the pressure gradient is set up to 6000 Pa for the penetration of the vapour through the samples.
The measuring process is very long; it usually takes more than 24 h. Nevertheless, the device producer recommends that the permeability values be read as soon as 2 h after the process started. The characteristics of individually measured permeability curves are different for each set and pressure gradient; for relative humidity behind a sample of 20, 30, 60, and 90%, the corresponding pressure gradients for the temperature of 40 °C are 5900, 5163, 2951, and 739 Pa, respectively. The probable reason for the different characteristics of the individual graphs could be the measurement technique used, the determination of the evaporated mass, the maintenance of the microclimate and flow characteristics in the device, etc. Furthermore, it is not correct to indicate the flow turbulence as the standard deviation of the mean flow velocity (along the sample surface) during the measurement process. The turbulent fluctuations, leading away the passing vapour from the area over (behind) the sample, are the cross components of velocity! Moreover, the flow characteristics along the sample surface can be different and will differ according to what position the cup is in on the carousel inside the device, i.e., concerning the predominant flow direction. This measurement is fully theoretical; it is necessary to warn once again that the permeability measurement is realized isothermally. However, in reality, the temperature behind the sample (i.e., in the surroundings) is usually lower than before the sample (near the body’s surface). This means that if the practically saturated wet air passes through the sample, a part of the aerial humidity will condense inside the sample volume, and the sample mass is therefore going to be wet; thus, its thermal resistance is decreasing and the flow resistance is increasing. Presumably, there are high differences between the theoretical results of laboratory measurements and reality.
2. Materials and Methods
For the experiment, two samples are selected to observe their air permeability, water vapour resistance, and the basic physical properties (Table 1).

Table 1.
Parameters of tested samples.
The pore structure and distribution are important for the flow of air and vapours. Porosity is measured using Skyscan 1272 desktop computerized microtomography (Bruker, Billerica, MA, USA) and is shown in Figure 1 and Figure 2.
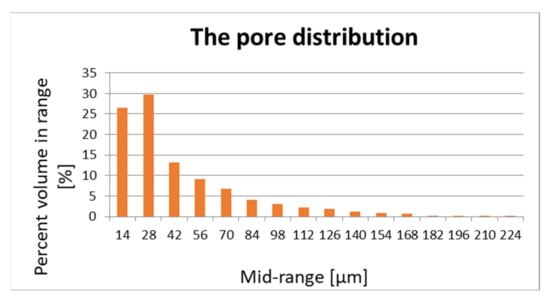
Figure 1.
Pore distribution of sample 1.
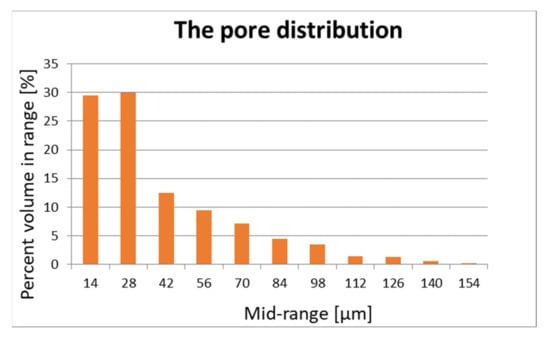
Figure 2.
Pore distribution of sample 2.
2.1. Air Permeability of Sample No. 1
For the first measurement, only sample No. 1 was used. Generally, the airflow resistance is a quadratic function of the velocity Δp = f(w2, w), see, e.g., [9]. At low velocities, the linear term is prevailing (Darcy’s law for slow flow in porous structures). On the contrary, at higher velocities, the influence of the quadratic term is increasing (Nikuradse’s or Moody’s law for flows through orifices, flows around bodies, etc.). The real flow through the textile sample is a combination of both terms.
Figure 3 shows the preliminary result of air permeability measurement for small pressure gradients (50–250 Pa) where the dependence is perfectly linear.
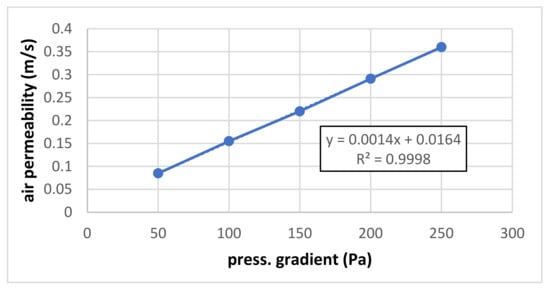
Figure 3.
Air permeability for small pressure gradients.
Figure 4 shows the air permeability for higher pressure gradients (200–2000 Pa). Compared with Figure 3, the linearity is slightly worse and the absolute term is a little higher. The lower slope (coefficient value of linear term) compared to small pressure gradients is probably given by the flow being measured at the pressure side, whereas, for small pressure gradients, the flow is measured at the suction side. Some deviations from the ideally linear course are probably given by some errors in measurement or evaluation.
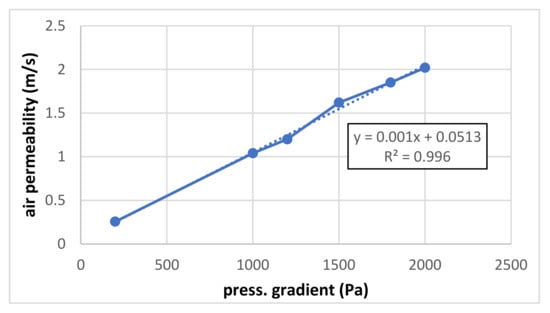
Figure 4.
Air permeability for higher pressure gradients.
The results of both measurements are summarized in Figure 3 and Figure 4. The air permeability for both lower and higher pressure gradients (up to 250 and 2000 Pa, respectively) is linear, and the influence of a possible quadratic term is negligible.
It can be seen that the slope of the measured linear dependence is higher for lower pressure gradients (measured under pressure) than for higher pressure gradients (measured in overpressure). Correcting the flow by recalculating it for the same pressure level (barometric) should be suitable.
The linear correlation is very good a shown in Figure 5. To verify it, the quadratic correlation is also mentioned because, theoretically, the flow resistance is increasing linearly for low flows and quadratically for higher flows. Nevertheless, it can be seen that the quadratic term is probably negligible, and both linear and quadratic terms are nearly identical for both correlations. It is necessary to add that the absolute term should be equal to zero because when the pressure is zero, the flow gradient is zero, too. The reason for the error (in measurement or evaluation) should be identified to realise how such an error can be removed.
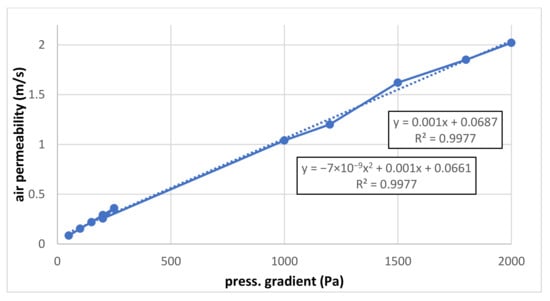
Figure 5.
Common graph for both air permeability measurements (low- and high-pressure gradient).
2.2. Water Vapour Permeability for Sample No. 1
Water vapour permeability measurements are summarized in the set of four graphs in Figure 6, Figure 7, Figure 8 and Figure 9. The measurement is isothermal (40 °C) for a relative humidity (R.H.) of 100% before the sample and of 20, 30, 60, and 90% behind the sample (subsequently, from top to bottom). The relevant pressure gradients are 5900, 5163, 2951, and 739 Pa.
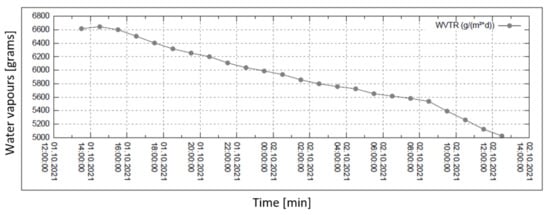
Figure 6.
Permeability of water vapour over 24 h with 20% external humidity.
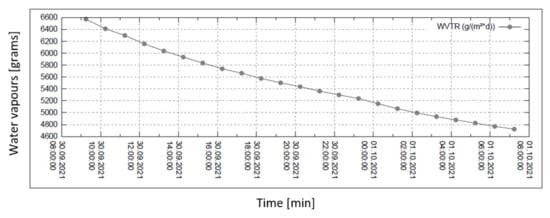
Figure 7.
Permeability of water vapour over 24 h with 30% external humidity.
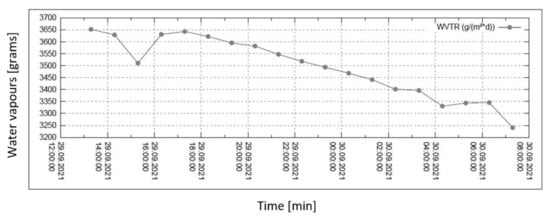
Figure 8.
Permeability of water vapour over 24 h with 60% external humidity.
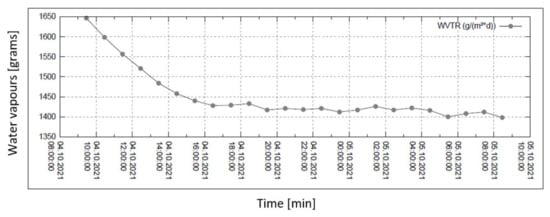
Figure 9.
Permeability of water vapour over 24 h with 90% external humidity.
In all graphs, the permanent decrease in water vapour permeability during the entire measuring process (24 h) is evident. This should mean that the permeability of the same sample is decreasing (providing that the partial pressures of water vapour before and after the sample remain constant during the whole measuring process). It might also mean that the samples are progressively clogged, most probably by humidity.
The third measured point for the case of 60% relative humidity is completely different from the general trend of the graph—probably caused by an error in measurement or evaluation.
For the case of 90% humidity, only, the permeability value comes to a final value after approx. 8 h. It looks as if the sample is being saturated by something, and as the measuring process continues, it shows that the vapour permeability reaches a constant (minimal) value. No other cases of higher pressure gradients reach such an effect even after 24 h of the measuring process! The question remains why the device producer recommends recording the permeability value after just 2 h from the start of the measuring process.
Figure 6, Figure 7, Figure 8 and Figure 9 shows the long-term isothermal measurement (24 h, 40 °C) of the sample’s water vapour permeability. From top to bottom, the relative humidities behind the sample are 20, 30, 60, and 90%, and the relevant pressure gradients are 5900, 5163, 2951, and 739 Pa, respectively. It is also observed that in order to receive comparable permeability values for both air and water vapour, the values of vapour mass flow g/(m2 · day) are recalculated into the volume flow (m3/(m2 · s) = m/s) using the specific volume of the saturated vapour v″ = 19.55 m3/kg (for 40 °C).
3. Results
For the measured points of vapour permeability in the sample (m/s), linear and quadratic correlations are set. These correlations are practically identical, so for the next processing step, the linear correlation is enough. For validation, the cubical correlation is realized—it is perfect, but only because just four points through which the cubical curve passes are are disposable. Among these four points, significant deviations are visible. This should mean that the water vapour permeability of the sample is not proportional to the used pressure gradient. Cubical correlations should have more measured points. It should be noted here again that the absolute term should be zero since, for zero pressure, the gradient of the flow is zero, too.
3.1. Correlation of Air–Vapour
Based on the measurement results above for sample No. 1, Figure 10 and Figure 11 present the test results of the correlation between air permeability and water vapour permeability. In the graphs, the necessary high values for air are not measurable by the used device and were extrapolated from the correlation result for vapour; the necessary low values for vapour are also not measurable by the used device and were extrapolated from the correlation results for air.
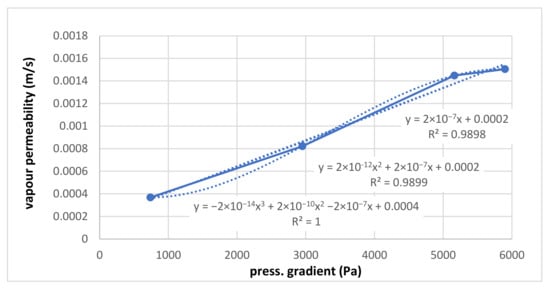
Figure 10.
Water vapour permeability at different pressure gradients.
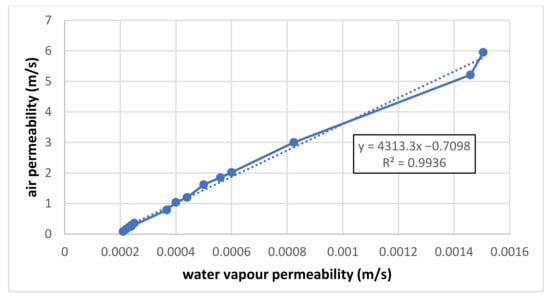
Figure 11.
Common graph of linear correlation between air and vapour permeability.
The absolute term of the resulting correlation should be zero because, for a pressure gradient of zero, the flow is zero, too. It would be desirable to find the reason for the non-zero value of any measurement or evaluation error to see the partial results for air and vapour above. If our above-defined hypothesis is correct, the coefficient of the linear term in correlation (4313) means that for sample No. 1, the air permeability (=y) is 4313 times higher than the vapour permeability (=x) of the same sample. The results should be verified by the measurement of other samples using the same procedure. The following questions arise: “Is this relation valuable for other measurements too? Or is there another trend? Or are the results randomly different?” To answer these questions, other samples should be measured and evaluated, too. At the same time, it is necessary to be aware of the fact that the unrealistically high values can be reached by extrapolating from the pressure gradient of the air permeability up to values of the vapour permeability! A pressure gradient of 200 Pa is used for the air permeability measurement, and the corresponding air (wind) velocity is 18.2 m/s = 66 km/h, which is an acceptable value for clothing. Generally speaking, the kinetic energy of this velocity is partially converted into the flow resistance of the tested sample; the sample’s real permeability is lower as well.
Analogously, the air velocity corresponding to the use of a higher pressure gradient of 2000 Pa, probably used for the testing of building and insulating materials, is 58 m/s = 208 km/h, which represents an unrealistically high value for clothing. For building materials, such pressure could be the reason for destruction, too. Extrapolating values at a pressure gradient of 6000 Pa, used after measuring the vapour permeability, the corresponding air velocity of 100 m/s is too high for practical use in reality. Probably, the use of vapuour values extrapolated from the pressure gradient for air is not suitable.
Thus, the proposed simple correlation of air–vapour permeability is quite unrealistic.
3.2. Permeability Measurement at Higher Pressure Gradients
Subsequently, the air permeability was measured up to 5000 Pa for samples 1 and 2. The summary of the results for both samples are shown in Figure 12, completed by the former results of sample No. 1 for pressure gradients up to 2000 Pa. The quadratic correlation for the measured points is perfect and in accordance with the theoretical combination of linear (Darcy) and quadratic (Weissbach, Moody) terms. The absolute term of one sample is correctly equal to zero (for zero flow, there is zero flow resistance), and a non-zero value of the second sample means a measurement or evaluation error.
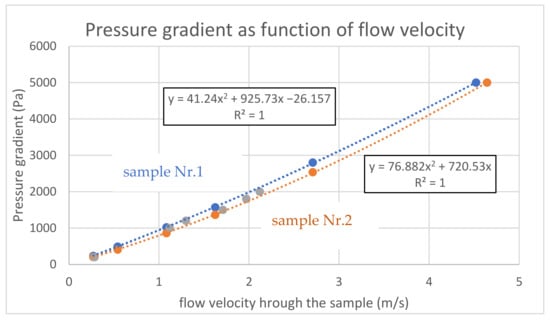
Figure 12.
Air permeability up to 5000 Pa.
3.3. Checking Measurement of Water Vapour Permeability
In the scope of the above-mentioned measurement, the next set of isothermal (40 °C) validation measurements of water vapour permeability was realized for higher numbers of relative humidity behind the samples:
20, 30, 45, 60, 75, and 90% r.h.
The corresponding pressure gradients are
5900, 5163, 4060, 2951, 1848, and 739 Pa.
The following four samples were used:
Free water level, a metallic sieve, and samples 1 and 2.
The results are shown in Figure 13. The vapour permeability for the free water level is the highest, and with any added sample, the permeability decreases. The second highest value is for the metallic sieve—probably due to the relatively low filling of the sample area by the metallic wire. The results of both clothing textile samples are practically identical, but the soft-shell material is slightly worse and is apparently very permeable to water vapour.
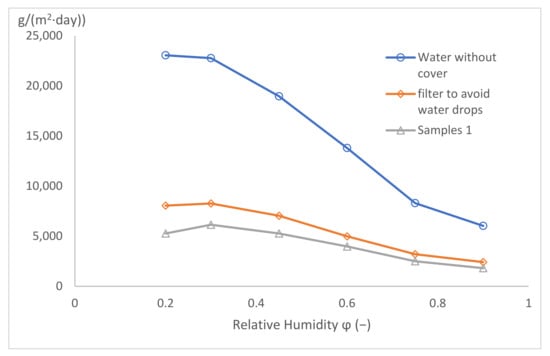
Figure 13.
Water vapour permeability for different samples.
The characteristics of all the measured curves are identical, i.e., the water vapour permeability decreases with the decreasing driving pressure gradient. For the high-pressure gradients (i.e., low relative humidity of 20% and 30% behind the sample), the water vapour permeability values remain practically constant. Similar results were estimated for low-pressure gradients, too (i.e., for a relative humidity of 90% and more behind the sample). Between those limiting values of pressure gradients, the water vapour permeability decreases after an S-shaped curve.
The curves in Figure 13 have a shape typical of a cubical parabola; therefore, in Table 2, cubical correlations for the measured values for all four samples are presented, together with very high correlation coefficients.

Table 2.
Samples’ water vapour permeability (y) as a function of pressure gradient (x).
To complete the information, for the sample “water”, the following quadratic and linear correlations are also presented:
- y = −7168.7x2 − 19,091x + 28,129R2 = 0.9782;
- y = −26,926x + 29,841R2 = 0.9755.
Although the correlation coefficient is a little worse, the course of both correlations is practically linearly decreasing, but without an evident inflex point, which is visible in all tested samples in Figure 13.
The measurement results show that the courses measured for all five samples have practically ideal cubical dependence of the water vapour permeability on the pressure gradient. The correlation, as expected, shows a linear dependence after Par. 5 and is acceptable, but it does not correspond exactly with the course of the measured values.
3.4. Vapour Diffusion
The passing of water vapour through porous materials is given by the following diffusion law:
where:
m = S · δ · t/d · Δp
- m (kg) diffused vapour;
- S (m2) sample area;
- D (m) sample thickness;
- t (s) time of diffusion;
- Δp (Pa) pressure gradient;
- δ (s) diffusion coefficient.
This means that the passing of water vapour through the sample is proportional to the pressure gradient (i.e., the difference in partial vapour pressures before and behind the sample) because all other quantities are constant—it is assumed that the diffusion coefficient is constant, too. This different from a quadratic dependence for air permeability through a sample (Par. 3).
The building tables in [9] present the values of the diffusion coefficients for water vapour as δ = 0.178 × 10−9 in the air at 0 °C or 0.125–0.179 × 10−9 in rock wool. Another source presents a value of 0.1 × 10−9 for glass wool. Therefore, all available values are in the range of one order, but the relative differences are quite high, within 25–78%. The vapour diffusion directly in the air also corresponds to the upper limit of the range, presented for fibrous insulating materials. At a temperature of 0 °C, as was used in [3], the pressure of saturated water vapour is 611 Pa. This is more than of one order less than the temperature of 40 °C (7375 Pa) used in isothermal clothing tests.
(1) The average temperature during the heating period (October–April) for central Europe (50° N, 375 m above sea level) is +2 °C, which is close to the value of 0 °C used in [9]. Diffustion coefficient values for other air temperatures were not found; it is possible that with the increase in temperature, the diffusion coefficient increased, too (i.e., the driving pressure gradient for diffusion increases with temperature).
(2) The diffusion coefficients of various standard building materials and foils are generally several orders lower. It is possible that diffusion coefficients for the tested textile samples (fibrous, relatively permeable) are of the same order as the diffusion coefficient of air. However, the clothing industry needs data that are more precise.
(3) Sometimes the so-called diffusion resistance, Rd = d/δ (m/s), is also used, in which the resistance of individual layers is summed up for a multilayer sample.
To validate these findings, the unknown diffusion coefficient is determined using measured data from Figure 14 recalculated in the unit system SI in an adapted version of Equation (8) as follows:
δ = m · d/S · t · Δp
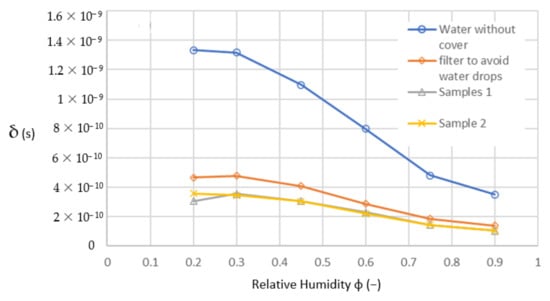
Figure 14.
Diffusion coefficient calculated from measured data.
In (10), only the mass of the diffused vapour is changed; other parameters remain constant. Therefore, the shape of the diffusion curves in Figure 14 is the same as the curves of the diffused vapour in Figure 13, with another scale in the y-axis only. Hence, the diffusion coefficient should be changing nonlinearly with the driving pressure gradient of diffusion as shown in Table 3.

Table 3.
Calculated diffusion coefficients (s).
The results of validating the samples from Figure 14 were used for the evaluation of the next validating parameter m/Δp. After the diffusion Equation (8), this parameter for should be constant for a certain sample because all other quantities (S · δ · t/d) are constant as well. Moreover, the diffusion coefficient is supposed to be constant, too. This validating parameter is independent from the driving pressure gradient. The result is shown in Figure 15—generally said, the checking parameter:
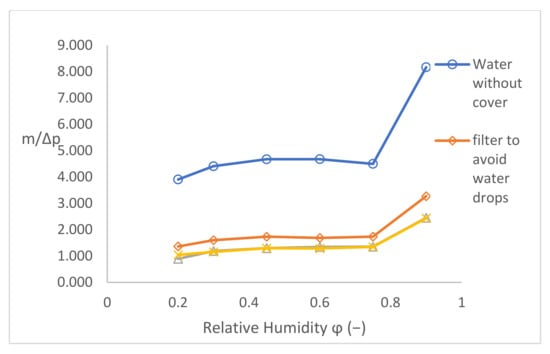
Figure 15.
Validation parameter m/Δp.
- -
- Slightly increases with the increase in φ for low-pressure gradients (low φ);
- -
- Is practically constant for medium-pressure gradients;
- -
- Increases by a jump for φ = 90%.
Therefore, it is possible that there is an error in the measurement method, in the measurement device, or in something else.
Alternatively, the diffusion coefficient is not constant; rather, it is nonlinearly changing with the driving pressure gradient. Values of the diffusion flow of water vapour are logically decreasing with the decrease in the driving pressure gradient and with the permeability of the tested sample, too. The values of the diffusion coefficient here are of the same order as the value of the diffusion coefficient in [10]. To determine the possible influence of temperature (for instance, at 30°/20°/10 °C), further measurement should be performed.
Providing that the diffusion coefficient of water vapour is materially constant, the validation parameter m/Δp in Figure 15 should be constant, too. Nevertheless, for the set temperature of 40 °C and for the pressure gradients of 5900−1848 Pa corresponding to the relative humidity of 20–75% behind the sample, the coefficient is slightly increasing, even at 90% (739 Pa), where a large jump is visible.
4. Conclusions
The initial hypothesis about the explicit correlation between air and water vapour permeability in the same sample has not been verified. The results of individual steps to test the possible correlation between the air and water vapour permeability of the sample are presented in their relevant paragraphs. It is expressed that the verification of the hypothesis about the correlation between the samples’ air and water vapour permeability is not exact, and several unanswered questions remain.
(1) The strange units used for measuring the both air and water vapour permeability should be replaced by identical units, as defined in thermo-mechanics. This means that for the fluid flow through the area, the density of mass flow (kg/(m2 · s) or density of volume flow (m3/(m2 · s), modified as (m/s), should be used.
The inverse unit, the flow resistance, has a reciprocal format. too: (m2 · s/kg) and (s/m), respectively.
(2) Units of volume are dependent on the state quantities of gas. For a mutual comparison of published results from different laboratories, the recalculation under any standard using general gas law (2) is necessary. It is important to remember that a temperature change of 3 K or a pressure change of 1 kPa means a volume change of 1%. Real changes, due to the weather or altitude, are usually higher.
(3) Air permeability, i.e., the airflow through a sample, depends on the sample’s flow resistance (generally, the quadratic function of the flow velocity). Water vapour permeability is a diffusive process, and according to Fick’s laws, it is a linear function of the pressure gradient. Based on the realized measurement and the evaluation and comparison of the measurement results, it can be assumed that it is not possible to simply compare flows of two different media based on different physical principles.
Obviously, it is not suitable to extrapolate airflow through the sample unless high values of pressure gradients are reached, such as those usually used for water vapour diffusion through the same sample.
(4) By measuring water vapour permeability, several unclarified data were found:
- -
- Setting, reading, and evaluation of measurement;
- -
- From the measured values, variable values of the diffusion coefficient for different pressure gradients were found.
Probably, the primary reason for this problem is the undefined flow inside the device along the sample’s surface, which should take away the vapour diffused through the sample in a constantly defined manner.
(5) The vapour mass, measured by diffusion through the tested sample, is a linear function of the driving pressure gradient. The air mass, measured by the flow through a tested sample, is a quadratic function of the flow velocity. Therefore, it should be assumed that a simple correlation between air and water vapour permeability through the sample is not possible to be set and verified.
Author Contributions
Conceptualization, K.A.; idea, A.H.; management, Z.K.; drafting, methodology, and article writing, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Adámek, K.; Havelka, A.; Kůs, Z.; Mazari, A. Correlation of Air Permeability to Other Breathability Parameters of Textiles. Polymers 2022, 14, 140. [Google Scholar] [CrossRef] [PubMed]
- Gidik, H.; Vololonirina, O.; Ghantous, R.M.; Ankou, A. Impact of test parameters on the water vapor permeability of textiles. Int. J. Cloth. Sci. Technol. 2019, 31, 350–361. [Google Scholar] [CrossRef]
- Baczek, M.B.; Hes, L. The effect of moisture on thermal resistance and water vapour permeability of Nomex fabrics. J. Mater. Sci. Eng. A 2011, 1, 358. [Google Scholar]
- Kumar, V.; Sampath, V.R.; Prakash, C. Investigation of stretch on air permeability of knitted fabrics part II: Effect of fabric structure. J. Text. Inst. 2016, 107, 1213–1222. [Google Scholar] [CrossRef]
- Tang, K.P.M.; Kan, C.W.; Fan, J.T. Evaluation of water absorption and transport property of fabrics. Text. Prog. 2014, 46, 1–132. [Google Scholar] [CrossRef]
- Mazari, A.; Havelka, A.; Naeem, J.; Adamek, K. Comparative Study on the Water Vapour Permeability of Textile by a Standard and Novel device. Fibres Text. East. Europe 2021, 43, 59–64. [Google Scholar] [CrossRef]
- Sivri, Ç. A Comprehensive Thermophysiological Comfort Analysis of Breathable Membrane Laminated Fabrics. Gazi Univ. J. Sci. 2022, 35, 346–358. [Google Scholar] [CrossRef]
- ČSN EN ISO 11092:2014; Měření Tepelného Odporu a Výparného Odporu za Stálých Podmínek (Measurement of Thermal and Water-Vapour Resistance under Steady-State Conditions). ÚNMZ: Prague, Czech Republic, 2015.
- Šeligová, M. Construction Design of a Warehouse Module for Preparations with Crane Loading. 1988. [Google Scholar]
- Adamek, K. Breathability of textile layers. In Proceedings of the International Conference Application of Experimental and Numerical Methods in Fluid Mechanics, Liberec, Czech Republic, 7 April 2008; p. 6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).