Dynamics of Colloidal Mixture of Cu-Al₂O₃/Water in an Inclined Porous Channel Due to Mixed Convection: Significance of Entropy Generation

Abstract

The unavailability of energy has become a major challenge to industry in the last years, as an important percentage of the generated energy is dissipated as heat in transport. Since heat transfer processes are irreversible, the role of entropy generation minimization in nanofluid flow and heat transfer cannot be neglected. The present paper was dedicated to the study of entropy generation for the problem of steady mixed-convection flow in a porous inclined channel filled with a hybrid nanofluid (Cu-Al₂O₃/water). A symmetrical uniform heat flux was considered at the walls and a constant flow rate was given through the channel. The mathematical model, consisting of a system of equations with given boundary conditions, was transformed in terms of dimensionless variables and the proposed analytical solution was found to be valid for all the cases of the inclined channel. The solution was validated by comparison with previously published results. The behavior of the velocity and temperature of the hybrid nanofluid were studied together with the entropy generation inside the channel by considering the influence of different important parameters, such as the nanoparticle volume fraction, the mixed-convection parameter and the inclination angle of the channel from horizontal. The results were focused to prevent the dissipation of energy by calculating the maximum thermal advantage at a minimum entropy generation in the system.

1. Introduction

Any solid with vacant space(s), or space not occupied by most atoms that make up the solid’s structure, is called porous material. Fluid flow through a porous material has received much attention in the last decades owing to its use in many fields of science and engineering, such as geophysical problems, electronic cooling, drying processes, solar collectors, hydrology, nuclear reactors, food stuffs, solar power collectors, etc. An important problem related to energy transport within a porous material is the mixed-convective flow through a channel, a chamber or past a given plate embedded in a fluid-saturated porous medium. Earlier studies were reported by Cheng [1] and Bejan [2]. Various practical applications of porous materials in industry and nature have been studied and published concerning the considered topic for different flow configuration models in books by Nield and Bejan [3], Ingham and Pop [4,5,6], Pop and Ingham [7] and Vafai [8]. In addition, Bear [9] recently published a study related to the phenomena of flow and transport in porous media.

The convective heat transfer characteristics of conventional fluids, including water, oil and ethylene glycol mixtures, are poor, since the thermal conductivity of these fluids is very important for the heat transfer coefficient between the heat transfer surface and the heat transfer medium. In the last decades, a widely used technique to improve heat transfer has been that of suspending nanoscale particles in a base fluid. Choi [10] has introduced the term nanofluid, which refers to these kinds of fluids. Nanofluids have attracted much interest due to their potential for a high rate of heat exchange incurring either little or no penalty in the pressure drop. Comprehensive references on nanofluids can be found in the book by Das et al. [11] and in the review paper by Buongiorno [12]. Several numerical and experimental papers on nanofluids include thermal conductivity, see Kang et al. [13], separated flow, see Abu-Nada [14], and convective heat transfer [15,16,17]. Recent papers have been related to natural convection of a nanofluid in a horizontal semi-cylinder, see Dogonchi et al. [18], Gowda et al. [19] have studied the binary chemical reaction and activation energy of the Marangoni flow of a non-Newtonian nanofluid and Grosan et al. [20], the behavior of a nanofluid-saturated porous media in a cavity. Karvelas et al. [21] investigated the efficiency of mixing iron oxide nanoparticles and water, and a non-Darcy mixed convection from a horizontal plate was studied by Rosca et al. [22]. In addition, important mixed-convection flow problems related to nanofluids have been published including a stability analysis, see Bakar et al. [23] and Salleh et al. [24].

Hybrid nanofluids are a new group of heat transfer liquids with tiny metal or non-metal particles (sizes are less than 100 nm) used in energy transport applications, see Huminic and Huminic [25]. These “smart” liquids include two or three kinds of particles, while the base conventional liquids could be water, ethylene glycol or a water–ethylene glycol mixture, kerosene, engine oil, vegetable oil or paraffin oil. In the last years, hybrid nanofluids have been employed in different thermal transmission applications such as heat pipes, mini channel heat sinks, solar collectors, heat exchangers, etc. Comprehensive reviews on hybrid nanofluids have been presented by Sarkarn et al. [26], Sidik et al. [27] and Babu et al. [28]. Recent studies were reported by Kumar et al. [29] and Aly and Pop [30]. However, the first paper concerning the thermophysical properties of hybrid nanoliquids was prepared by Jana et al. [31]. Different mathematical models describe the flow and heat transfer within a porous medium, such as Darcy, Darcy–Brinkman and Darcy–Brinkman–Forchheimer, and these approaches can be found in the book by Nield and Bejan [3]. In recent works, Rosca et al. [32] have examined a mixed-convection stagnation-point flow of a hybrid nanofluid past a vertical flat plate, Waini et al. [33] have reported the Hiemenz flow of hybrid nanofluid over a shrinking sheet and others have studied the MHD natural convection of hybrid nanofluids in an open wavy cavity, see Reza and Alireza [34], or the slip effects on MHD non-Newtonian nanofluids flow over a stretching cylinder in a porous medium, see Tlili et al. [35].

In addition, several papers have studied hybrid nanofluids in enclosures [36,37,38,39] and others have published results about hybrid nanofluids in channels [40,41]. Moghadassi et al. [42] recently studied the influences of nanofluids (water-based Al₂O₃) and hybrid nanofluids (Al₂O₃-Cu) and observed that hybrid nanofluids have a higher coefficient of convection heat transfer. The neoteric class of nanofluids is given by hybrid nanofluids, which contain a small amount of metal nanoparticles and non-metallic nanoparticles. The addition of metallic nanoparticles in a base fluid, such as Cu, Zn, Al, has reported high thermal conductivities, but their use has restrictions such as stability or reactivity. In contrast, nonmetallic nanoparticles, such as Al₂O₃, Fe₃O₄ or CuO, give lower thermal conductivities compared to metallic nanoparticles, but they have important properties such as stability or chemical inertness. Thus, as reported by Suresh et al. [43] and Tayebi and Chamkha [44], it was observed that by adding a small amount of Cu nanoparticle volume fraction to an Al₂O₃/based nanofluid, the thermophysical characteristics of the resulting hybrid nanofluid could be increased without reducing the stability. In addition, Devi and Devi [45] examined a Cu-Al₂O₃/water hybrid nanofluid using a mathematical approach. They compared their results with experimental results and found an excellent agreement.

In the last decades, the important efforts of researchers have been focused on the optimization of energy systems. An important way of obtaining this achievement is to study the entropy generation minimization for designing a thermal system. The fundamentals of entropy generation were reported by Bejan [46] and Narusawa [47]. Recently, several papers reported numerical results of MHD fluids and nanofluid sand the study of entropy generation, such as, Yusuf et al. [48] referred to a Sisko fluid through inclined walls with a porous medium, Hamzah et al. [49] considered a wavy lid-driven porous enclosure and Atashafrooz [50], an inclined duct.

An analytical result for a hybrid nanofluid flow influenced by magnetic induction effects towards a stretching sheet was recently reported by Khan et al. [51].

The aim of this research is to investigate the mixed convection, see [1,2,3,4,5,6,7], of a hybrid nanofluid, see [26,27,28,29,30,31], in an inclined porous channel with uniform heated walls by continuing the work of Cimpean and Pop [52]. The study is focused on the minimization of entropy generation in the considered system. The mathematical model was written for Cu-Al₂O₃/water hybrid nanofluid and a nondimensional analysis was used. The analytical (exact) solution was found by considering a new approach. The validity of this new solution was confirmed by a comparison with previously published results. Moreover, two hybrid nanofluid models were applied for the presented solutions and the results are in very good agreement. Considering the literature review and the authors knowledge, no study with these findings has been reported before in the literature.

Since entropy is one of the several reasons for the wastage of energy in heat transfer processes, often it becomes necessary to measure entropy generation in a very accurate way. With this idea in mind, this study is focused on answering to the following questions:

• Is it a thermal advantage to use a Cu-Al₂O₃/water hybrid nanofluid instead of using a regular Al₂O₃/water nanofluid in a porous inclined channel?
• Is the obtained analytical solution the most appropriate solution to calculate the entropy generation rate in the channel?
• Does the addition of the Cu nanoparticle volume fraction in the Al₂O₃/water nanofluid enhance the heat transfer in all the cases of the inclination angle of the channel?
• Is it significant to change the influence of free convection over forced convection into the channel to improve the thermal performance of the system?
• Is it relevant to change the main parameters, such as the nanoparticle volume fraction, the mixed-convection parameter and the inclination angle of the channel from horizontal, to obtain the maximum thermal advantage at a minimum of the entropy generation rate in the system?

2. Mathematical Model

The problem of mixed convection for a hybrid nanofluid flow in an inclined infinitely long two-dimensional porous channel bounded by impermeable parallel plane walls is presented in this paper. The x axis is considered lengthways and the y axis is oriented perpendicular to the channel walls, as shown in Figure 1. The fluid has a uniform streamwise velocity distribution U₀ at the channel entrance and the walls are heated by a uniform heat flux q_w. The flow is assumed to be fully developed and steady. The Boussinesq approximation was employed and the homogeneity and local thermal equilibrium in the porous medium were considered. The hybrid nanofluid mixture consisted of nanoparticles of Al₂O₃ which were the first added to the base fluid (water) with 0.1 vol. solid volume fraction, and this was fixed throughout the problem. Then, Cu nanoparticles were added with various volume fractions to obtain the hybrid nanofluid mixture, namely Cu-Al₂O₃/water. The hybrid nanofluid was assumed to saturate the solid matrix and both are in thermodynamic equilibrium.

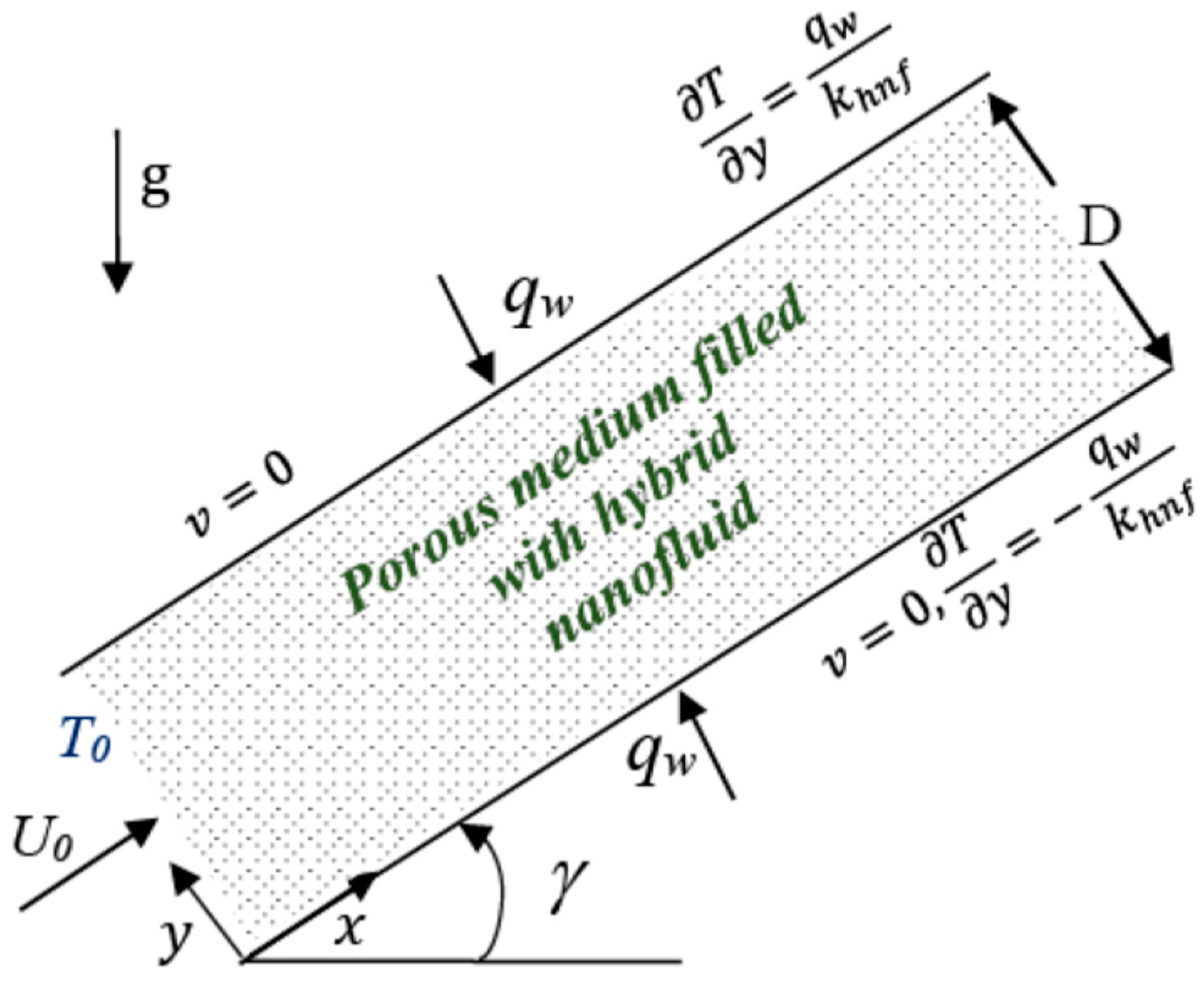
2.1. Basic Equations and Boundary Conditions

The basic equations were considered by using the model of Tiwari and Das [15]. The continuity equation, Darcy’s Law and energy equation, see [52], were written in Cartesian coordinates $x$ and $y$ by considering the hybrid nanofluid model, such that:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$\frac{{\mu }_{hnf}}{K}u=-\frac{\partial p}{\partial x}+{\left(\rho \beta \right)}_{hnf}g\sin \gamma \left(T-T_0\right)$$

(2)

$$\frac{{\mu }_{hnf}}{K}v=-\frac{\partial p}{\partial y}+{\left(\rho \beta \right)}_{hnf}g\cos \gamma \left(T-T_0\right)$$

(3)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial v}={\alpha }_{hnf}\left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}\right)$$

(4)

where $u$ and $v$ are the Cartesian velocity components and T is the hybrid nanofluid temperature. The coefficients are: β, the thermal expansion and ρ, the density corresponding to the hybrid nanofluid. K is the specific permeability of the porous medium, ${\mu }_{hnf}$ is the viscosity of the hybrid nanofluid and ${\alpha }_{hnf}$ is the thermal diffusivity of the hybrid nanofluid. The angle of the inclination of the channel, measured counterclockwise from horizontal, is denoted by γ and $T_0$ represents the given uniform fluid temperature at the inflow.

As a fully developed flow was assumed and a uniform heat flux was considered at both walls of the channel (lower and upper), the boundary conditions are given by

$$\begin{gathered} v=0, \frac{\partial T}{\partial y}=-\frac{q_w}{k_{hnf}} \mathrm{on} y=0 \\ v=0, \frac{\partial T}{\partial y}=\frac{q_w}{k_{hnf}} \mathrm{on} y=D \end{gathered}$$

(5)

and from the continuity equation, the forced flow condition is

$${{\displaystyle \int }}_0^{D}u dy=Q$$

(6)

where D is the width of the channel and Q is a prescribed constant that represents the inflow at the channel entrance. The streamwise velocity is $u=u\left(y\right)$, as a fully developed flow was considered. From Equation (1) and boundary conditions (5), $v \equiv 0$ is obtained, and then the pressure is eliminated by cross differentiation. The temperature was considered to be a linear function of $x$ and an arbitrary function of $y$, and the Equations (2)–(4) become

$$\frac{\partial u}{\partial y}=\frac{K}{{\mu }_{hnf}}{\left(\rho \beta \right)}_{hnf}g\left(\frac{\partial T}{\partial y}\sin \gamma -\frac{\partial T}{\partial x}\cos \gamma \right)$$

(7)

$$u\frac{\partial T}{\partial x}={\alpha }_{hnf}\frac{{\partial }^{2}T}{\partial y^2}$$

(8)

2.2. Thermophysical Models of Hybrid Nanofluids

Two thermophysical models of hybrid nanofluids, reported in the literature, were considered and used to obtain and validate the results of the problem.

The 1st model of the hybrid nanofluid has thermophysical parameters in the following form Ghalambaz et al. [53] and Bagheri et al. [54]:

-

Hybrid nanofluid density

$${\rho }_{hnf}={\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}{\rho }_{{\mathrm{Al}}_2{\mathrm{O}}_3}+{\phi }_{\mathrm{Cu}}{\rho }_{\mathrm{Cu}}+\left(1-{\phi }_{\mathrm{Cu}}-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right){\rho }_f$$

-

Hybrid nanofluid buoyancy coefficient

$${\left(\rho \beta \right)}_{hnf}={\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}{\left(\rho \beta \right)}_{{\mathrm{Al}}_2{\mathrm{O}}_3}+{\phi }_{\mathrm{Cu}}{\left(\rho \beta \right)}_{\mathrm{Cu}}+\left(1-{\phi }_{\mathrm{Cu}}-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right){\left(\rho \beta \right)}_f$$

-

Hybrid nanofluid heat capacitance

$${\left(\rho c\right)}_{hnf}={\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}{\left(\rho c\right)}_{{\mathrm{Al}}_2{\mathrm{O}}_3}+{\phi }_{\mathrm{Cu}}{\left(\rho c\right)}_{\mathrm{Cu}}+\left(1-{\phi }_{\mathrm{Cu}}-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right){\left(\rho c\right)}_f$$

-

Hybrid nanofluid thermal conductivity

$$\begin{gathered} \frac{k_{hnf}}{k_f}=\left\{\frac{{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}{k}_{{\mathrm{Al}}_2{\mathrm{O}}_3}+{\phi }_{\mathrm{Cu}}{k}_{\mathrm{Cu}}}{{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}+{\phi }_{\mathrm{Cu}}}+2k_f+2\left({\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}{k}_{{\mathrm{Al}}_2{\mathrm{O}}_3}+{\phi }_{\mathrm{Cu}}{k}_{\mathrm{Cu}}\right)-2\left({\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}+{\phi }_{\mathrm{Cu}}\right)k_f\right\} \\ \times {\left\{\frac{{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}{k}_{{\mathrm{Al}}_2{\mathrm{O}}_3}+{\phi }_{\mathrm{Cu}}{k}_{\mathrm{Cu}}}{{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}+{\phi }_{\mathrm{Cu}}}+2k_f-\left({\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}{k}_{{\mathrm{Al}}_2{\mathrm{O}}_3}+{\phi }_{\mathrm{Cu}}{k}_{\mathrm{Cu}}\right)+\left({\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}+{\phi }_{\mathrm{Cu}}\right)k_f\right\}}^{-1} \end{gathered}$$

-

Hybrid nanofluid viscosity

$${\mu }_{hnf}={\mu }_f{\left(1-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}-{\phi }_{\mathrm{Cu}}\right)}^{-2.5}$$

The 2nd model of the hybrid nanofluid has thermophysical parameters in the following form Devi and Devi [45], and Manjunatha et al. [55]:

-

Hybrid nanofluid density

$${\rho }_{hnf}=\left(1-{\phi }_{\mathrm{Cu}}\right)\left[\left(1-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right){\rho }_f+{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}{\rho }_{p_1}\right]+{\phi }_{\mathrm{Cu}}{\rho }_{p_2}$$

-

Hybrid nanofluid buoyancy coefficient

$${\left(\rho \beta \right)}_{hnf}=\left(1-{\phi }_{\mathrm{Cu}}\right)\left[\left(1-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right){\left(\rho \beta \right)}_f+{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}{\left(\rho \beta \right)}_p{}_1\right]+{\phi }_{\mathrm{Cu}}{\left(\rho \beta \right)}_p{}_2$$

-

Hybrid nanofluid heat capacitance

$${\left(\rho c\right)}_{hnf}=\left(1-{\phi }_{\mathrm{Cu}}\right)\left[\left(1-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right){\left(\rho c\right)}_f+{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}{\left(\rho c\right)}_p{}_1\right]+{\phi }_{\mathrm{Cu}}{\left(\rho c\right)}_p{}_2$$

-

Hybrid nanofluid thermal conductivity

$$\begin{gathered} \frac{k_{hnf}}{k_{bf}}=\frac{k_{p_2}+\left(n-1\right)k_{bf}-\left(n-1\right){\phi }_{\mathrm{Cu}}\left(k_{bf}-k_{p_2}\right)}{k_{p_2}+\left(n-1\right)k_{bf}+{\phi }_{\mathrm{Cu}}\left(k_{bf}-k_{p_2}\right)}, \\ \mathrm{where} \frac{k_{bf}}{k_f}=\frac{k_{p_1}+\left(n-1\right)k_f-\left(n-1\right){\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\left(k_f-k_{p_1}\right)}{k_{p_1}+\left(n-1\right)k_f+{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\left(k_f-k_{p_1}\right)} \end{gathered}$$

-

Hybrid nanofluid viscosity

$${\mu }_{hnf}={\mu }_f{\left[\left(1-{\phi }_{\mathrm{Cu}}\right)\left(1-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right)\right]}^{-2.5}$$

Here, $n$ = 3 is for spherical nanoparticles.

Both models were considered to obtain and discuss the results of the problem. For the hybrid nanofluid mixture, the nanoparticle of Al₂O₃ was considered to be the first added to the base fluid (water) with a 0.1 vol. solid volume fraction (i.e., ${\phi }_1={\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}=0.1$), which was fixed throughout the problem. Then, Cu nanoparticles were added with various volume fractions (${\phi }_2={\phi }_{\mathrm{Cu}}=0.02-0.06)$ to form the hybrid nanofluid, namely Cu-Al₂O₃/water.

The basic thermophysical properties of the liquid and Al₂O₃ and Cu nanoparticles are given in the

Table 1. Thermophysical properties of fluid (at $25 °\mathrm{C}$) and nanoparticles [45,52,54].

Physical Characteristics	Host Liquid (Water)	Al2O3	Cu
c (J·kg−1·K−1)	4179	765	385
ρ (kg·m−3)	997.1	3970	8933
k (W·m−1·K−1)	0.613	40	400
β × 10−5 (K−1)	21.0	0.85	1.67

.

2.3. Nondimensionalization Method

Further, we introduced the non-dimensional variables, see [52]:

$$X=\frac{x}{D}, Y=\frac{y}{D}, U=\frac{u}{U_0}, \tau =\frac{\left(T-T_0\right)}{∆T}$$

(9)

where $∆T=\frac{q_{w}D}{k_f}.$ Further, consider the nondimensional velocity and temperature in the form:

$$U=U\left(Y\right) \mathrm{and} \tau \left(X,Y\right)=CX+F\left(Y\right)$$

(10)

where C is an arbitrary constant.

By substituting in Equations (7) and (8) expressions (9) and (10), the equations of the problem become

$$\frac{dU}{dY}-\lambda \frac{A_1}{A_2}\left(\frac{dF}{dY}\sin \gamma -C\cos \gamma \right)=0$$

(11)

$$CPeU-A_3\frac{d^{2}F}{d{Y}^2}=0$$

(12)

and the boundary conditions from (5) and (6) are now:

$$\frac{dF}{dY}=-1 \mathrm{on} Y=0 \mathrm{and} \frac{dF}{dY}=1 \mathrm{on} Y=1$$

(13)

$${{\displaystyle \int }}_0^{1}U\left(Y\right)dY=1$$

(14)

By integrating Equation (12) and using conditions (13) and (14) we obtain $C=\frac{2A_3}{Pe}$.

Finally, an ordinary differential equation of the 3rd order is obtained from the system

$$\frac{d^{3}F}{d{Y}^3}-2\lambda \frac{A_1}{A_2}\sin \gamma \frac{dF}{dY}+4\lambda \frac{A_1{A}_3}{A_{2}Pe}\cos \gamma =0$$

(15)

The parameters involved in the equations are the mixed-convection parameter, $\lambda$, the Peclet number denoted by $Pe$ and the the Rayleigh number, $Ra$, defined as: $\lambda =\frac{Ra}{{\alpha }_{f}Pe}$, $Pe=\frac{U_{0}D}{{\alpha }_f}$, $Ra=\frac{Kg{q}_w{\left(\rho \beta \right)}_f{D}^2}{{\mu }_f{k}_f}$.

In addition, the functions A₁–A₃ are dependent on the nanoparticle volume fractions and have the following forms, corresponding to the considered hybrid nanofluid models:

For the 1st hybrid nanofluid model:

$$A_1={\left(1-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}-{\phi }_{\mathrm{Cu}}\right)}^{2.5}\left[\left(1-{\phi }_{\mathrm{Cu}}-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right)+{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\frac{{\left(\rho \beta \right)}_{{\mathrm{Al}}_2{\mathrm{O}}_3}}{{\left(\rho \beta \right)}_f}+{\phi }_{\mathrm{Cu}}\frac{{\left(\rho \beta \right)}_{\mathrm{Cu}}}{{\left(\rho \beta \right)}_f}\right]$$

$$A_2=\frac{k_{hnf}}{k_f}$$

$$A_3=A_2{\left[\left(1-{\phi }_{\mathrm{Cu}}-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right)+{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\frac{{\left(\rho c\right)}_{{\mathrm{Al}}_2{\mathrm{O}}_3}}{{\left(\rho c\right)}_f}+{\phi }_{\mathrm{Cu}}\frac{{\left(\rho c\right)}_{\mathrm{Cu}}}{{\left(\rho c\right)}_f}\right]}^{-1}$$

For the 2nd hybrid nanofluid model:

$$A_1={\left[\left(1-{\phi }_{\mathrm{Cu}}\right)\left(1-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right)\right]}^{2.5}\left[\left(1-{\phi }_{\mathrm{Cu}}\right)\left(1-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right)+{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\left(1-{\phi }_{\mathrm{Cu}}\right)\frac{{\left(\rho \beta \right)}_p{}_1}{{\left(\rho \beta \right)}_f}+{\phi }_{\mathrm{Cu}}\frac{{\left(\rho \beta \right)}_p{}_2}{{\left(\rho \beta \right)}_f}\right]$$

$$A_2=\frac{k_{hnf}}{k_f}$$

$$A_3=A_2{\left[\left(1-{\phi }_{\mathrm{Cu}}\right)\left(1-{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\right)+{\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}\left(1-{\phi }_{\mathrm{Cu}}\right)\frac{{\left(\rho c\right)}_p{}_1}{{\left(\rho c\right)}_f}+{\phi }_{\mathrm{Cu}}\frac{{\left(\rho c\right)}_p{}_2}{{\left(\rho c\right)}_f}\right]}^{-1}$$

3. Analytical Solution

An analytical solution assumes framing the problem in a well-understood form to obtain the exact solution. It is different from a numerical procedure, which is making guesses at the solution and testing if the problem is solved well enough (with a reasonable accuracy) to stop. So, an analytical solution, if it exists, is stronger than other approaches. The present paper is related to a hybrid nanofluid flow in a channel and proposes a new different procedure of finding the analytical solution (the first was given in [52] for regular nanofluid flow), which is valid for all the cases of the inclination of the channel.

The linear 3rd order ordinary differential Equation (16) is solved here. To simplify the form of the solutions, the system is considered as follows:

$$F^{‴}\left(Y\right)-a{F}^{\prime }\left(Y\right)=-b$$

(16)

$$2U\left(Y\right)-F^{″}\left(Y\right)=0$$

(17)

which are subject to the boundary conditions (13) and the additional condition:

$${{\displaystyle \int }}_0^{1}F\left(Y\right)U\left(Y\right)dY=0$$

(18)

where $a=2\lambda \frac{A_1}{A_2}\sin \gamma$ and $b=4\lambda \frac{A_1{A}_3}{A_{2}Pe}\cos \gamma .$

3.1. The Solution for the General Case of $a>0$

The inclination of the channel is considered here, where $\gamma \in (0,\frac{\pi }{2}].$ Then, for the general case of positive values of a, the general solutions of the temperature, F and velocity, U, profiles are obtained in the form:

$$F\left(Y\right)=C_1+C_2{e}^{-\sqrt{a}Y}+C_3{e}^{\sqrt{a}Y}+\frac{b}{a}Y$$

(19)

$$U\left(Y\right)=\frac{a}{2}\left(C_2{e}^{-\sqrt{a}Y}+C_3{e}^{\sqrt{a}Y}\right)$$

(20)

Then, the temperature, $\tau ,$ in a nondimensional form, has the expression:

$$\tau \left(X,Y\right)=\frac{2A_3}{Pe}X+C_1+C_2{e}^{-\sqrt{a}Y}+C_3{e}^{\sqrt{a}Y}+\frac{b}{a}Y$$

(21)

The constants considered in the solutions are obtained from the given conditions and have the form:

$$\begin{gathered} C_1=\left[\frac{C_2^2}{2}(e^{-2\sqrt{a}}-1)-\frac{C_3^2}{2}\left(e^{2\sqrt{a}}-1\right)-2\sqrt{a}{C}_2{C}_3\right]{\left(C_2-C_3-C_2{e}^{-\sqrt{a}}+C_3{e}^{\sqrt{a}}\right)}^{-1} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{b}{a}{\left(C_2-C_3-C_2{e}^{-\sqrt{a}}+C_3{e}^{\sqrt{a}}\right)}^{-1}\left[C_2\left((e^{-\sqrt{a}}+\frac{e^{-\sqrt{a}}}{\sqrt{a}}-\frac{1}{\sqrt{a}}\right)-C_3\left((e^{\sqrt{a}}-\frac{e^{\sqrt{a}}}{\sqrt{a}}+\frac{1}{\sqrt{a}}\right)\right] \\ {C}_2=\frac{1}{\sqrt{a}\left(e^{\sqrt{a}}-e^{-\sqrt{a}}\right)}\left[\left(\frac{b}{a}+1\right)e^{-\sqrt{a}}+1-\frac{b}{a}\right]+\frac{1}{\sqrt{a}}\left(\frac{b}{a}+1\right), C_3=\frac{1}{\sqrt{a}\left(e^{\sqrt{a}}-e^{-\sqrt{a}}\right)}\left[\left(\frac{b}{a}+1\right)e^{-\sqrt{a}}+1-\frac{b}{a}\right]. \end{gathered}$$

3.2. The Solution for $a=0$

If $a=0$, two situations are possible. The first is related to the horizontal channel (when $\gamma =0$) and the second is for the forced convection limit (when $\lambda =0$).

3.2.1. The Solution for a Horizontal Channel ($\gamma =0$)

The solutions of this case, considering the mixed-convection parameter $\lambda \ne 0,$ are obtained in the form:

$$F\left(Y\right)=c_1+c_{2}Y+c_3{Y}^2-\frac{b}{6}{Y}^3$$

(22)

$$U\left(Y\right)=c_3-\frac{b}{2}Y$$

(23)

$$\tau \left(X,Y\right)=\frac{2A_3}{Pe}X+c_1+c_{2}Y+c_3{Y}^2-\frac{b}{6}{Y}^3$$

(24)

Here, $c_1=\frac{2}{3}{\left(1+\frac{b}{4}\right)}^2-\frac{b}{6}\left(\frac{3}{4}-\frac{3}{80}b\right), c_2=-1 \mathrm{and} c_3=1+\frac{b}{4}.$

3.2.2. The Solution for the Forced Convection Limit ($\lambda =0)$

The solutions $F\left(Y\right)$ and $U\left(Y\right)$, for all inclinations of the channel, correspond here to the case of a regular nanofluid, as given in [52]. The temperature, $\tau ,$ in a nondimensional form, is given by:

$$\tau \left(X,Y\right)=\frac{2A_3}{Pe}X+Y^2-Y+\frac{1}{6}$$

(25)

4. Entropy Generation

The entropy generation in a system is caused by the non-equilibrium state of the fluid, resulting from the thermal gradient between the two media. For the present problem, the exchange of energy and momentum within the hybrid nanofluid-saturated porous medium and at the solid boundaries give the nonequilibrium conditions, which cause the entropy generation in the flow field of the channel. This entropy generation is due to the irreversible nature of heat transfer and to viscosity effects within the fluid and at the solid boundaries. This paper focused on the optimization of the energy in the considered system by obtaining the relevant minimization of entropy generation.

From the temperature and velocity fields, the volumetric entropy generation can be calculated by the following equation, see Baytas [56] and Bejan [57]:

$$S_g=\frac{k}{T_0^2}{\left(\nabla T\right)}^2+\frac{\mu }{K{T}_0}\left(u^2+v^2\right)$$

(26)

In (27) at the right-hand side, the first term of the sum is the local entropy generation due to heat transfer across a finite temperature difference and the second term is the local entropy generation due to fluid friction.

To describe the dimensionless number for the local entropy generation rate, the local volumetric entropy generation rate must be divided into a characteristic entropy generation rate, see Yazdi et al. [58]:

$$S_{g_0}=\frac{k\mathsf{\Delta }{T}^2}{D^2{T}_0^2}$$

(27)

where $\mathsf{\Delta }{T}^2={\left(\frac{q}{k}\right)}^2$. Then, by using the non-dimensional variables (9) in the formula $N=S_g/S_{g_0}$, we obtain the dimensionless entropy generation number, N:

$$N=\frac{1}{P{e}^2}{\left(\frac{\partial \tau }{\partial X}\right)}^2+{\left(\frac{\partial \tau }{\partial Y}\right)}^2+\mathsf{\Phi }{U}^2$$

(28)

After using (21) and (22) in (29) the entropy generation number has the form:

$$N=\frac{4A_3{}^2}{P{e}^4}+{\left(\frac{b}{a}-\sqrt{a}{C}_2{e}^{-\sqrt{a}Y}+\sqrt{a}{C}_3{e}^{\sqrt{a}Y}\right)}^2+\mathsf{\Phi }\frac{a^2}{4}{\left(C_2{e}^{-\sqrt{a}Y}+C_3{e}^{\sqrt{a}Y}\right)}^2$$

(29)

Here, $\mathsf{\Phi }$ is called the irreversibility distribution ratio, see Baytas [54], and is given by the expression $\mathsf{\Phi }=$ $\frac{\mu T_0}{k}\left[\frac{{\alpha }_f^2}{K\mathsf{\Delta }{T}^2}\right].$

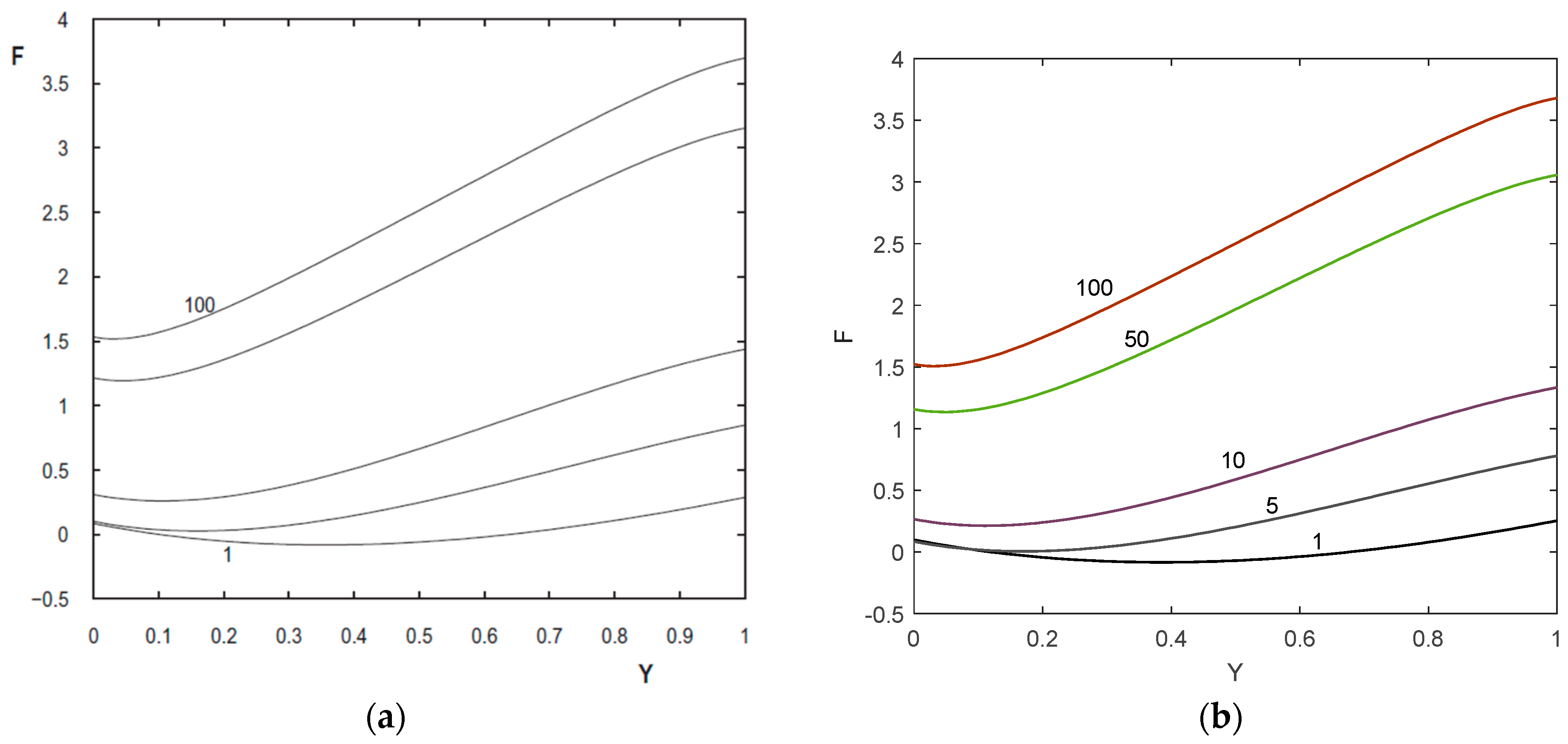
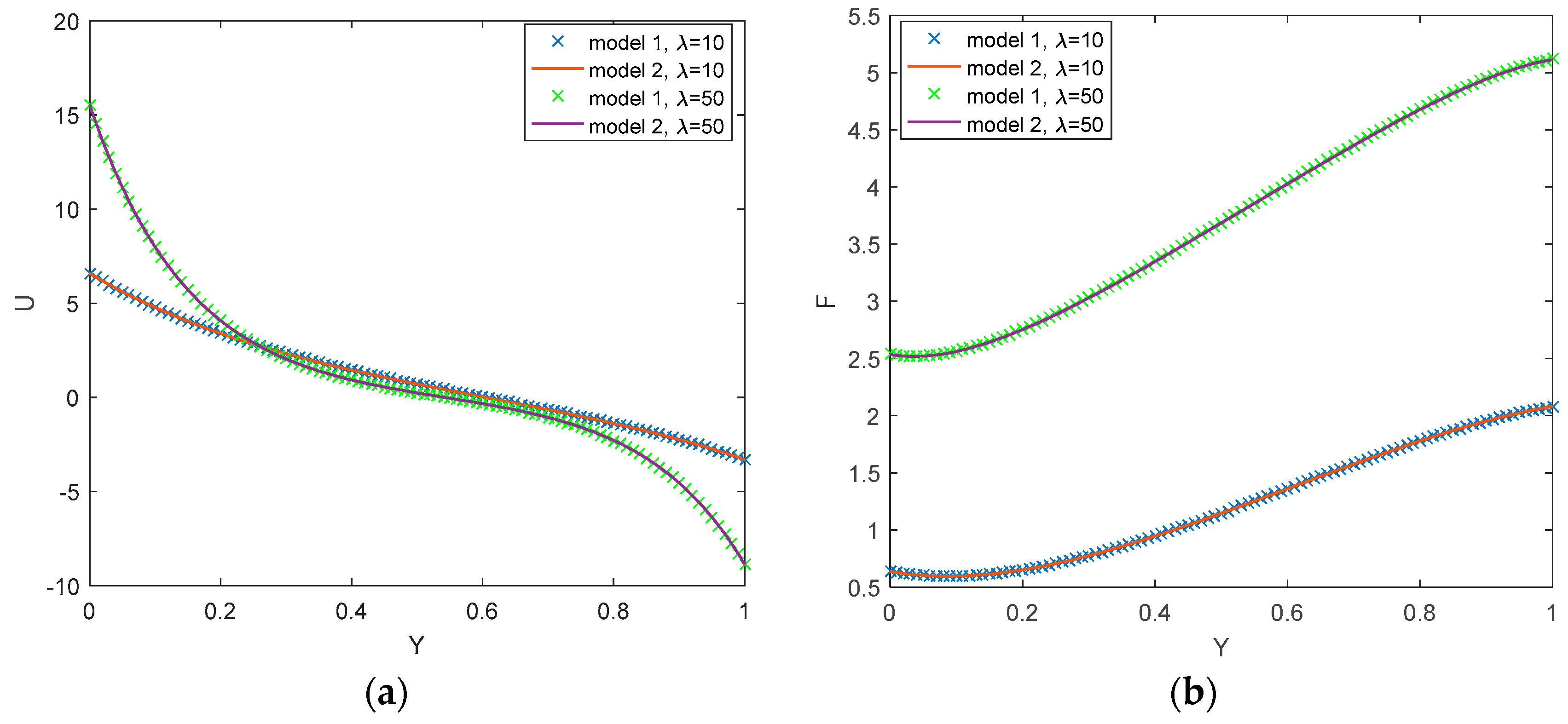
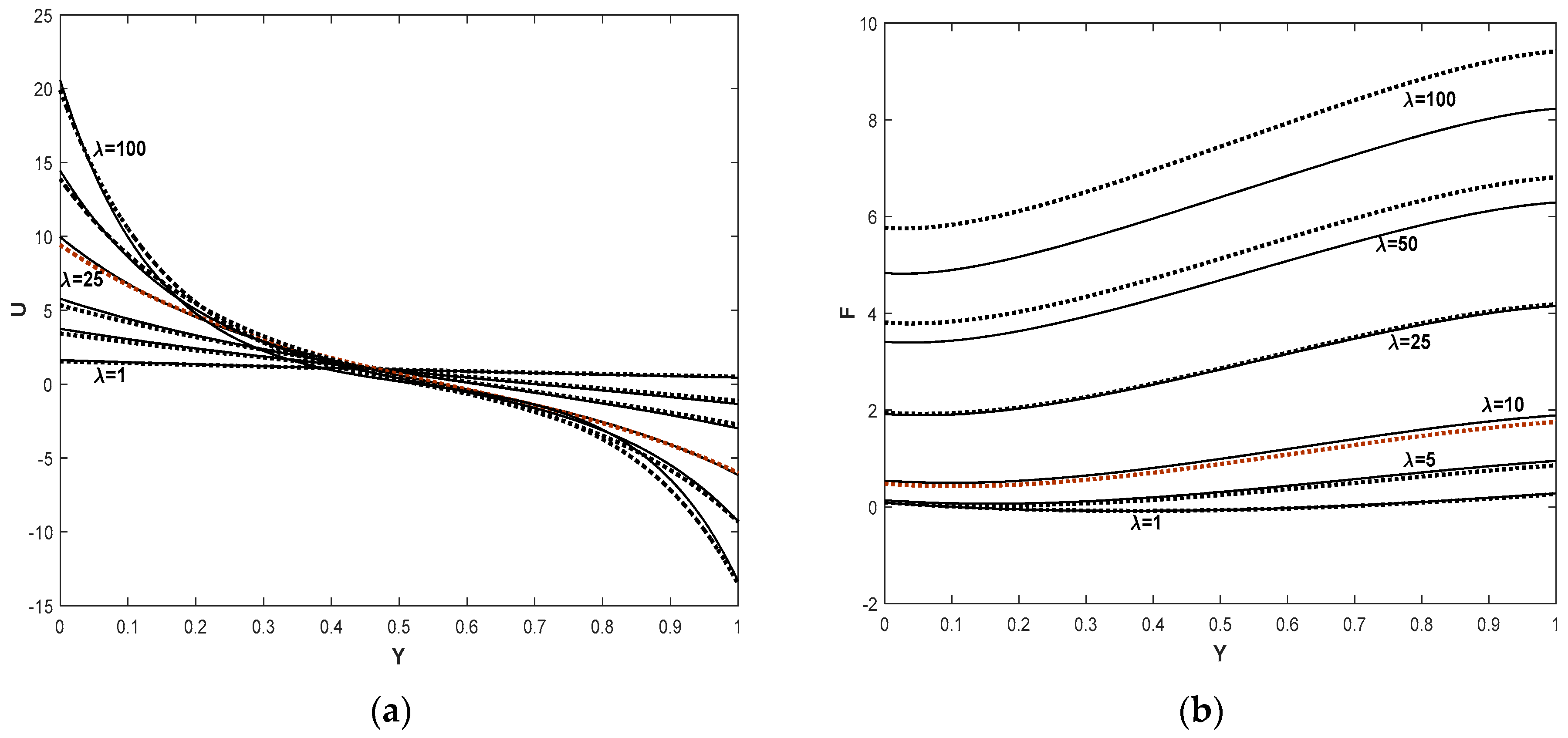
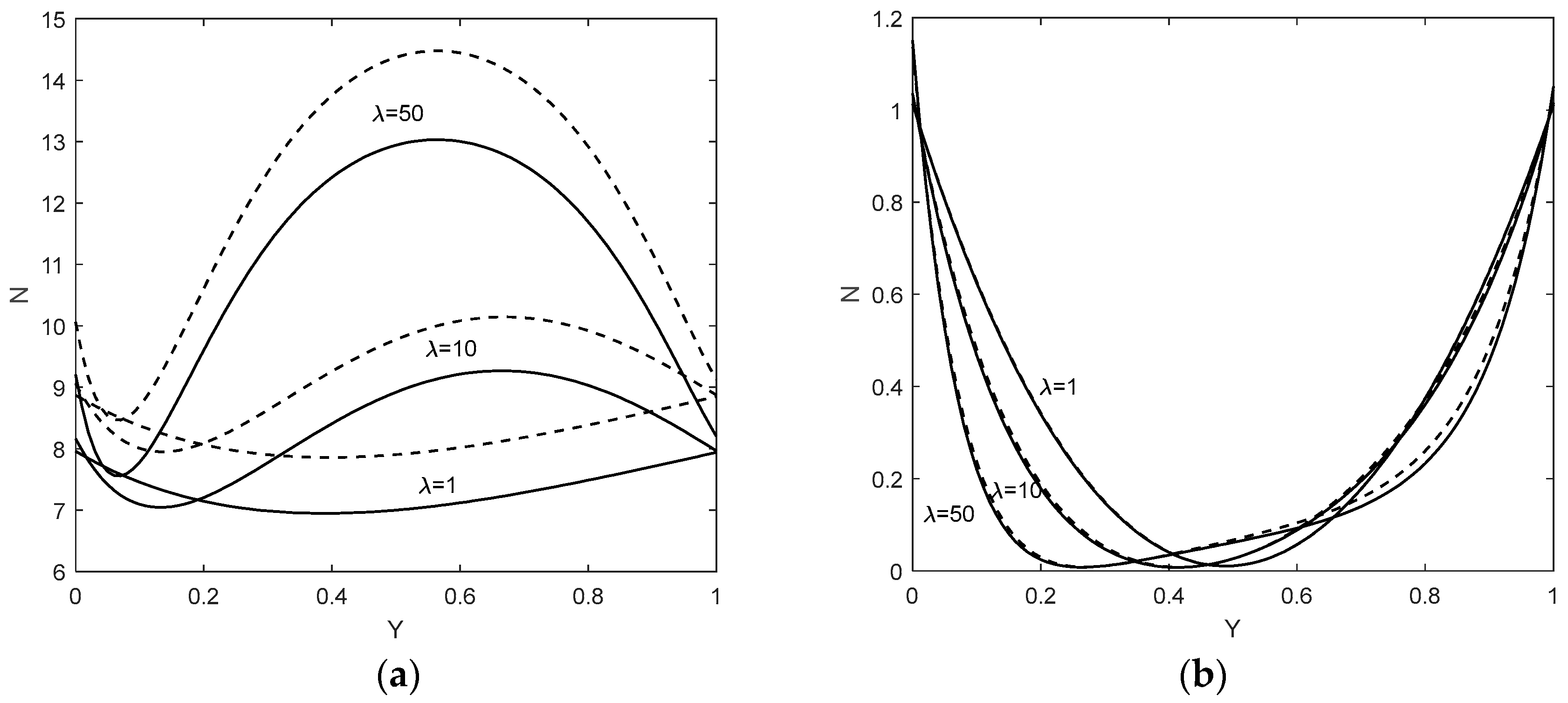
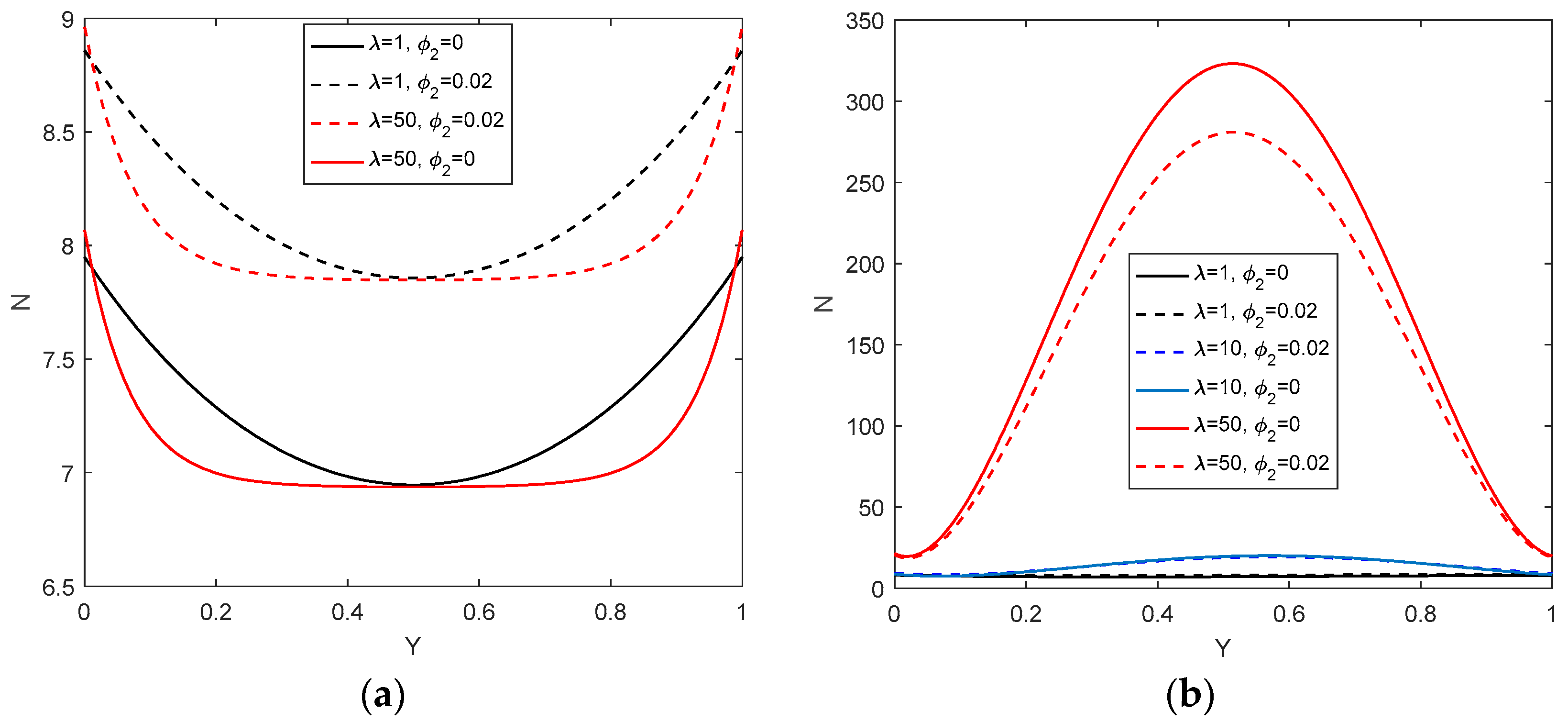
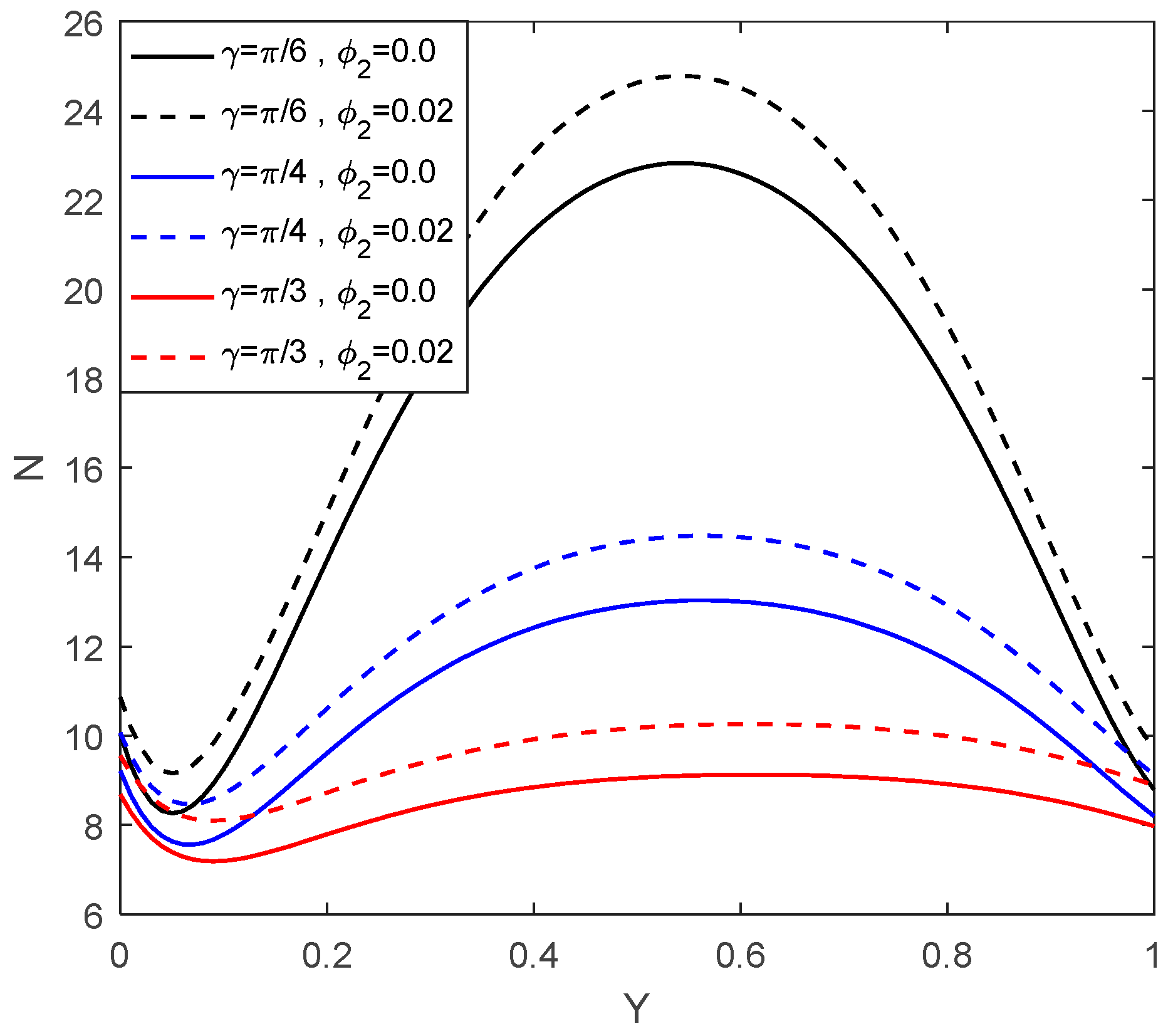
5. Results and Discussion

The two models of the hybrid nanofluids, as presented before, were used to investigate the results of the problem, and the differences between the results of the models were observed and they were not significant. In the proposed approach, initially, the Cu-Al₂O₃/water hybrid nanofluid was considered for investigation. For the problem of mixed-convection hybrid nanofluid flow in a porous inclined channel, the analytical solutions were obtained and plotted. The behavior of the velocity and temperature for different relevant parameters were obtained and discussed. In the presented results, the inclination angle of the channel $\gamma \in \left[0, \frac{\pi }{2} \right]$ was considered. The entropy generation of the system was also calculated for the relevant parameters in order to find its minimum and to obtain the best energy performance.

The results were validated by comparison with previous published results, see [52], for simple nanofluid flow in an inclined channel by considering, for the present solution, the simple Cu/water nanofluid (taking the copper nanoparticle volume fraction of ${\phi }_1=0.1$ and considering ${\phi }_2=0.0$), for $\gamma$ = $\pi$/4, $\lambda =1, 5, 10, 50, 100$ and Pe = 1. From Figure 2, very good agreement between the previous results (Figure 2a) and the present work (Figure 2b) was observed.

The two hybrid nanofluid models, first see [53,54] and second [45,55], are compared in Figure 3a,b by using the solutions of the problem, for $\gamma =\frac{\pi }{6}, {\phi }_1={\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}=0.01, \mathrm{and} {\phi }_2={\phi }_{\mathrm{Cu}}=0.01$. Very good agreement was observed between the models for the velocity and temperature profiles of the presented problem.

The behavior of the fluid flow inside the channel was observed by considering different concentrations of the nanoparticle volume fraction. For the considered hybrid nanofluid model, in the simple nanofluid Al₂O₃/water with a concentration of alumina oxide nanoparticles ${\phi }_1={\phi }_{{\mathrm{Al}}_2{\mathrm{O}}_3}=0.1$, the second nanoparticle volume fraction (cooper) was added gradually with different concentrations ${\phi }_2={\phi }_{\mathrm{Cu}}=0.02, 0.04, 0.06$. The influence of the second nanofluid volume fraction addition is shown in Figure 4a–d for the mixed-convection parameter $\lambda =10, 50$ and the inclination of the channel $\gamma =\pi /6$. The velocity profiles did not show a significant change when the hybrid nanofluid was considered (Figure 4a,b) but the temperature reported important changes. The velocity U(Y) reported changes for an increased mixed-convection parameter from 10 (Figure 4a) to 50 (Figure 4b). This was due to the increasing effect of free convection over forced convection at the lower wall of the channel. U(Y) took negative values from the middle of the channel (Y = 0.5) to the upper wall (Y = 1), reporting a region of reversed flow for all the values of the parameters. This behavior confirmed the influence of free convection obtained by the heated walls of the channel.

As the second nanoparticle volume fraction was added in the fluid mixture, for the higher mixed-convection parameter ($\lambda =50$), the temperature increased gradually, with the lowest temperature being seen for simple nanofluid flow (${\phi }_2=0.0$). For an increased influence of free convection over forced convection (the mixed-convection parameter increasing from 10 to 50), a significant increase in temperature was seen as the nanoparticle volume fraction ${\phi }_2$ increased.

In the horizontal channel, for small additions of the nanoparticle volume fraction ${\phi }_2$, the hybrid nanofluid flow influence was significant. The velocity decreased with adding small quantities of ${\phi }_2$ at the simple nanofluid flow for the bottom part of the channel and reversed-flow behavior was seen in the upper part of the channel (see Figure 5a). The temperature decreased with an increase in the Cu-nanoparticle volume fraction ${\phi }_2$ (see Figure 5b).

The velocity and temperature profiles for the different values of the mixed-convection parameter $\lambda =1, 5, 10, 25, 50, 100$ are plotted in Figure 6a,b for $\gamma =\pi /6$ and Peclet number $Pe=1$. The velocity had higher values near the lower wall of the channel and reported a reversed flow from the middle of the channel (U(Y) < 0) as the mixed-convection parameter increased. This confirms the influence of free convection (given by the heat flux) over forced convection (due to the inflow at the channel entrance) (Figure 6a).

Here, the cyclic flow encountered in natural convection was observed better. To explain the physical phenomenon of free convection (dominating forced convection as λ increases) we followed the evolution of a fluid packet through the imaginary closed duct that holds the cellular flow. Starting from the bottom of the heated wall, the fluid was heated by the wall and expanded as it rose to lower pressures in the hydrostatic pressure field maintained by the reservoir. Then, along the downflowing branch of the cycle, the fluid packet was cooled by the reservoir (T₀) and compressed as it reached the depths of the reservoir (initial cold medium).

The influence of hybrid nanofluid (considered for ${\phi }_2=0.04$) over simple nanofluid flow (${\phi }_2=0.0$) was not important for the velocity behavior.

The hybrid nanofluid reported important changes as the mixed-convection parameter increased, such that, for small values of $\lambda =1, 5, 10$ (see Figure 6b), the temperature of simple nanofluid is higher than for hybrid nanofluid. Over this value, the temperature of the hybrid nanofluid increased, becoming higher than the temperature of the nanofluid. A significant temperature increase was reported over $\lambda =25$ when the second nanoparticle volume fraction was added in the fluid mixture. This behavior was also due to the influence of free convection over forced convection.

A very important parameter of the study was the angle of inclination of the channel from horizontal, $\gamma$. The new proposed analytical solution also covered the horizontal channel case, so, for relevant results, the angle was considered $\gamma \in \left[0,\pi /2\right]$.

Figure 7 shows the velocity (a,b) and temperature (c,d) profiles for Pe = 1, $\lambda =10, 50$ for ${\phi }_1=0.1, {\phi }_2=0.04$ and different inclinations of the channel $\gamma =\frac{\pi }{6},\frac{\pi }{4},\frac{\pi }{3},\frac{\pi }{2}.$ For all inclinations, except $\gamma =\pi /2$ (vertical channel), a reversed flow was seen to start after the middle of the channel (Y = 0.5).

The velocity decreased as the angle of the inclination increased, and higher values of velocity were reported for a smaller inclination at the lower wall. Similar behavior but with higher values was seen when $\lambda$ increased ($\lambda =50$, Figure 7b). For the vertical channel, the velocity and temperature were symmetrical about the center line of the channel (Y = 0.5). The temperature profile F(Y) decreased as the angle $\gamma$ increased (Figure 7c,d). This behavior was similar for the simple nanofluid flow model, see [52].

Entropy Generation for the Hybrid Nanofluid Flow

This study focused on obtaining the minimum entropy generation at maximum thermal performances in order to obtain the best energetic performance of the system. In Figure 8, the entropy generation number for $Pe=1$ (Figure 8a) and for $Pe=10$ (Figure 8b) is presented for different values of the mixed-convection parameter $\lambda =1, 10, 50$ and $\gamma =\frac{\pi }{4} .$ It was observed that, for a small Peclet number, a very small addition of Cu nanoparticle volume fraction (${\phi }_2=0.02)$ greatly increased the entropy generation in the channel compared to the regular nanofluid with ${\phi }_1=0.1, {\phi }_2=0.0$ (regular nanofluid), see Figure 8a. This behavior was insignificant for a higher Peclet number, see Figure 8b. As for a higher Pe = 10, the thermal performance was not significant, and the small entropy generation obtained in this case was obvious but did not have much importance. Since the mixed-convection parameter increased, the entropy generation number, N, increased for small Pe = 1, and this confirmed the domination of free convection over forced convection as λ increased in the system. Then, by cumulating the results from Figure 4, Figure 6, Figure 7 and Figure 8, we conclude that, for smaller values of λ (<25), a simple nanofluid flow reported better thermal performances than a hybrid nanofluid at a minimum entropy generation rate. This information could be useful in improving the applications dedicated to solar power collectors.

Figure 9 presents the entropy generation number, N, for the particular cases of a vertical (Figure 9a) and a horizontal channel (Figure 9b). For the vertical channel (Figure 9a), an important increase in the entropy generation for all the values of mixed-convection parameter was observed when a hybrid nanofluid acted in the system (${\phi }_2=0.02).$ A very different behavior was seen for the horizontal channel. Here, only for higher values of the mixed-convection parameter ($\lambda$ > 25) (see Figure 9b for $\lambda =50$), the entropy generation was relevant compared to the regular nanofluid case. However, in this scenario, the entropy generation for the hybrid nanofluid flow was the most minor compared to the conventional nanofluid flow. Returning to Figure 5b, we see that the thermal performance of the hybrid nanofluid decreased when the second particle was introduced into the original nanofluid flow. As a result, the hybrid nanofluid characteristics were appropriate for producing cooling performances of the energetic systems in this circumstance.

Figure 10 presents the entropy generation number N, for different inclinations of the channel $\gamma =\frac{\pi }{6}, \frac{\pi }{4}, \frac{\pi }{3},$ for relevant values of the Peclet number and the mixed-convection parameter $Pe=1, \lambda =50$. A small decrease in the values of the entropy generation number was observed for the regular nanofluid since the values increased for the hybrid nanofluid flow for all inclinations of the channel. Also observing Figure 4d and Figure 7d, we conclude that a balanced choice of $\gamma =\frac{\pi }{6}$ and a very small addition of the nanoparticle volume fractions in the hybrid nanofluid obtained a good thermal performance with no important increase in entropy in the system.

6. Conclusions

The entropy generation minimization for the mixed-convection flow of a Cu-Al₂O₃/water hybrid nanofluid in an inclined infinitely long two-dimensional porous channel bounded by impermeable parallel plane walls was examined in this paper. The system of the governing equations of the hybrid nanofluid was written following the model of Tiwari and Das [15]. The system of partial differential equations, together with the boundary conditions, was changed to a system of linear ordinary differential equations by using non-dimensional transformations. Two hybrid nanofluid models were used to observe the behavior of the solution in the channel and the results were found in very good agreement.

The important findings of the current investigation are as follows:

• The obtained analytical solution of the problem includes for the first time, all the cases: the inclined, the horizontal and the vertical channel, respectively. This new solution is the most appropriate for an accurate calculating of entropy generation since it is an analytical (not an approximate) solution. Moreover, this exact solution was used to observe the thermal advantage of the hybrid nanofluid for mixed-convective flow in a porous channel.
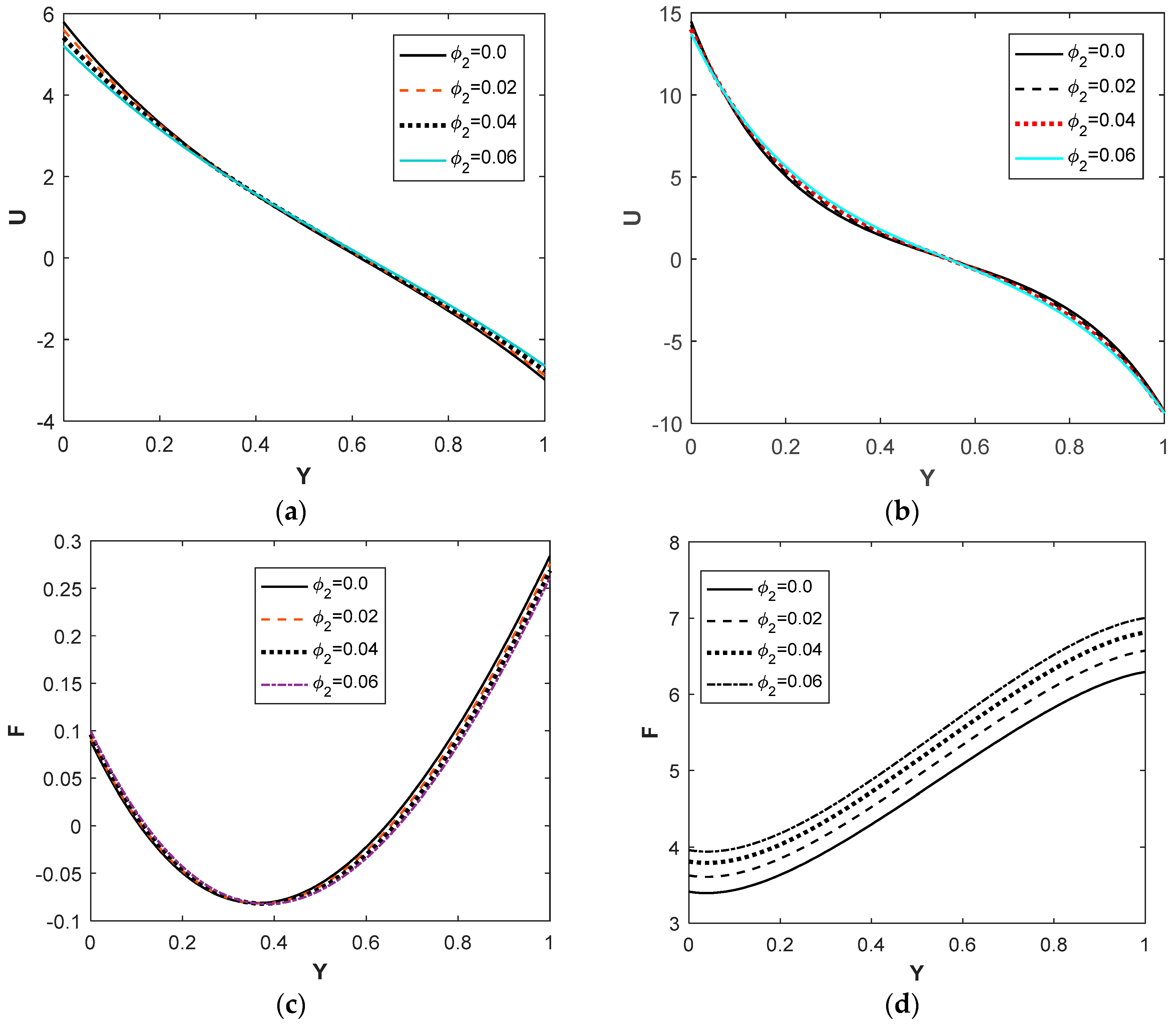
• The thermal properties of the fluid were enhanced considerably by adding small concentrations of the Cu nanoparticle volume fraction in the regular nanofluid Al₂O₃/water, but the velocity was not significantly affected by this change. This behavior was only relevant for values of the mixed-convection parameter λ > 25.
• The use of a Cu-Al₂O₃/water hybrid nanofluid instead of a regular Al₂O₃/water nanofluid in the porous inclined channel was not always a thermal advantage. For smaller values of the mixed-convection parameter (λ < 25), a simple nanofluid model has increased thermal properties at a minimum entropy generation in the system. This result could be useful to improve the systems dedicated to solar power collectors.
• The inclination angle of the channel from horizontal has an important role on the behavior of the hybrid nanofluid flow inside the channel. Reversed flow was reported for balanced conditions of the heat transfer by fluid motion over the heat transfer by thermal conductivity, Peclet number Pe = 1, for all the values of the inclination angle of the channel. In addition, the temperature increased with a decrease in the inclination angle of the channel. The cumulated results could be used in thermal transmission applications such as heat pipes, etc.
• In the case of the horizontal channel, the hybrid nanofluid flow decreased the thermal performance of the system compared to a regular nanofluid and the entropy generation had minimum values for a higher mixed-convection parameter (λ < 25). This case could be suitable for cooling energetic systems, for example, electronic equipment.

To summarize, the achievements of this paper could be easily applied to obtain a minimum entropy generation for maximum thermal effectiveness in several engineering devices.