Theoretical Analysis of Hybrid Metal–Dielectric Nanoantennas with Plasmonic Fano Resonance for Optical Sensing
Abstract
1. Introduction
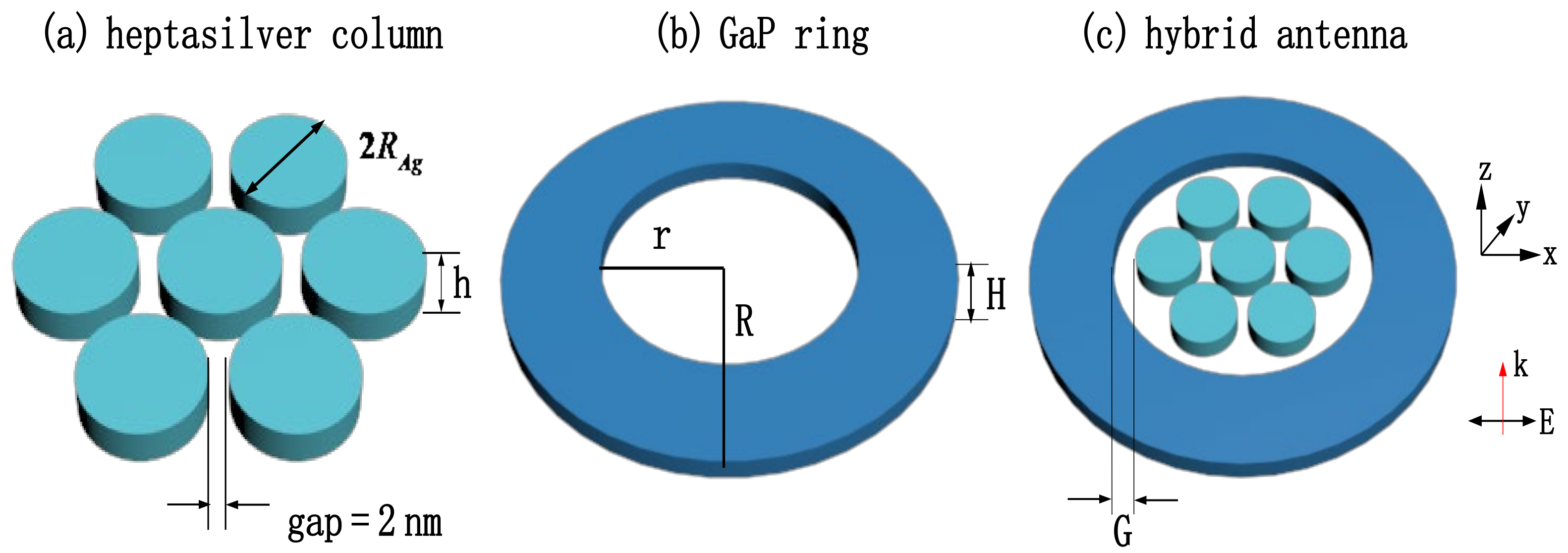
2. Materials and Methods
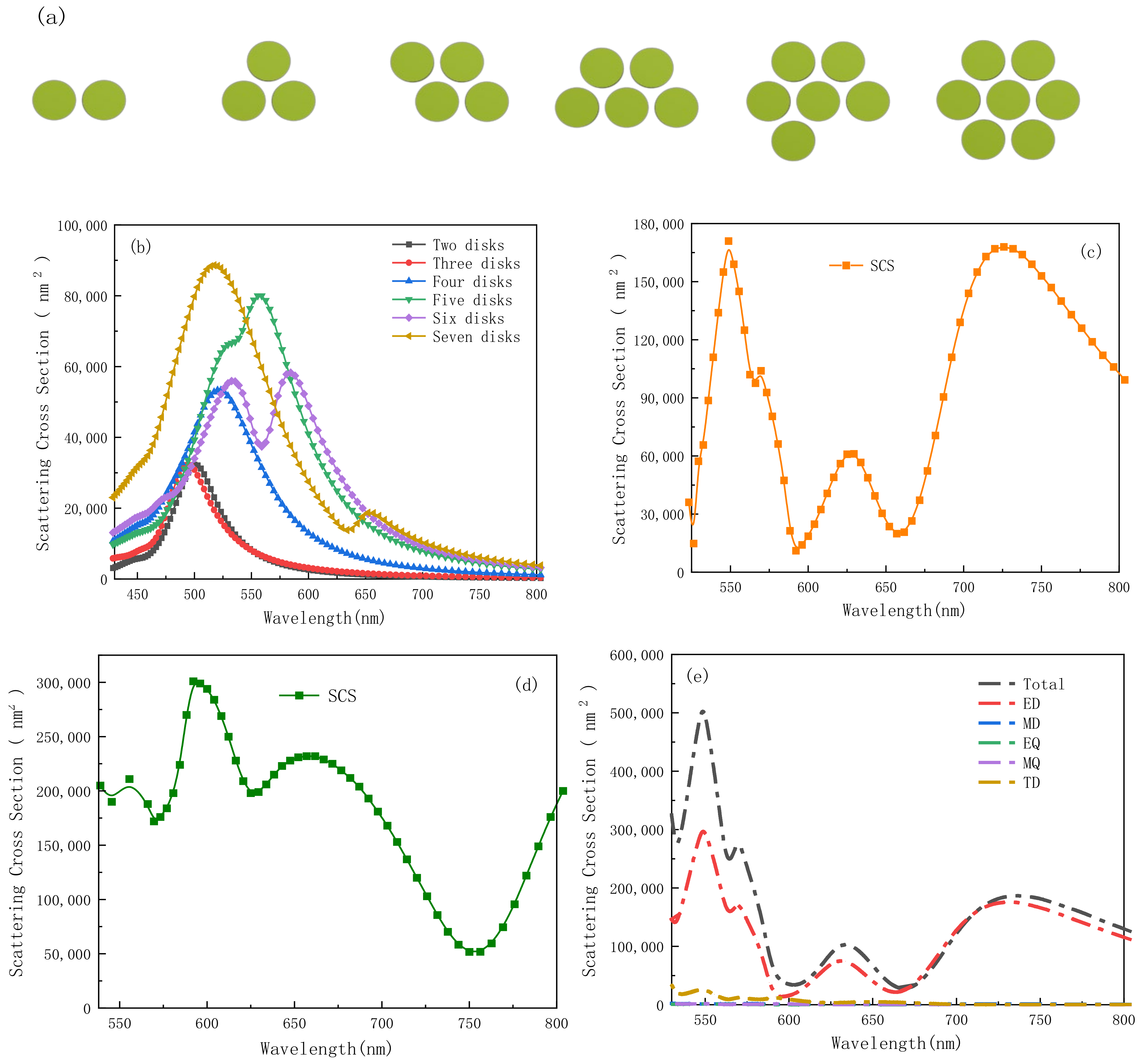
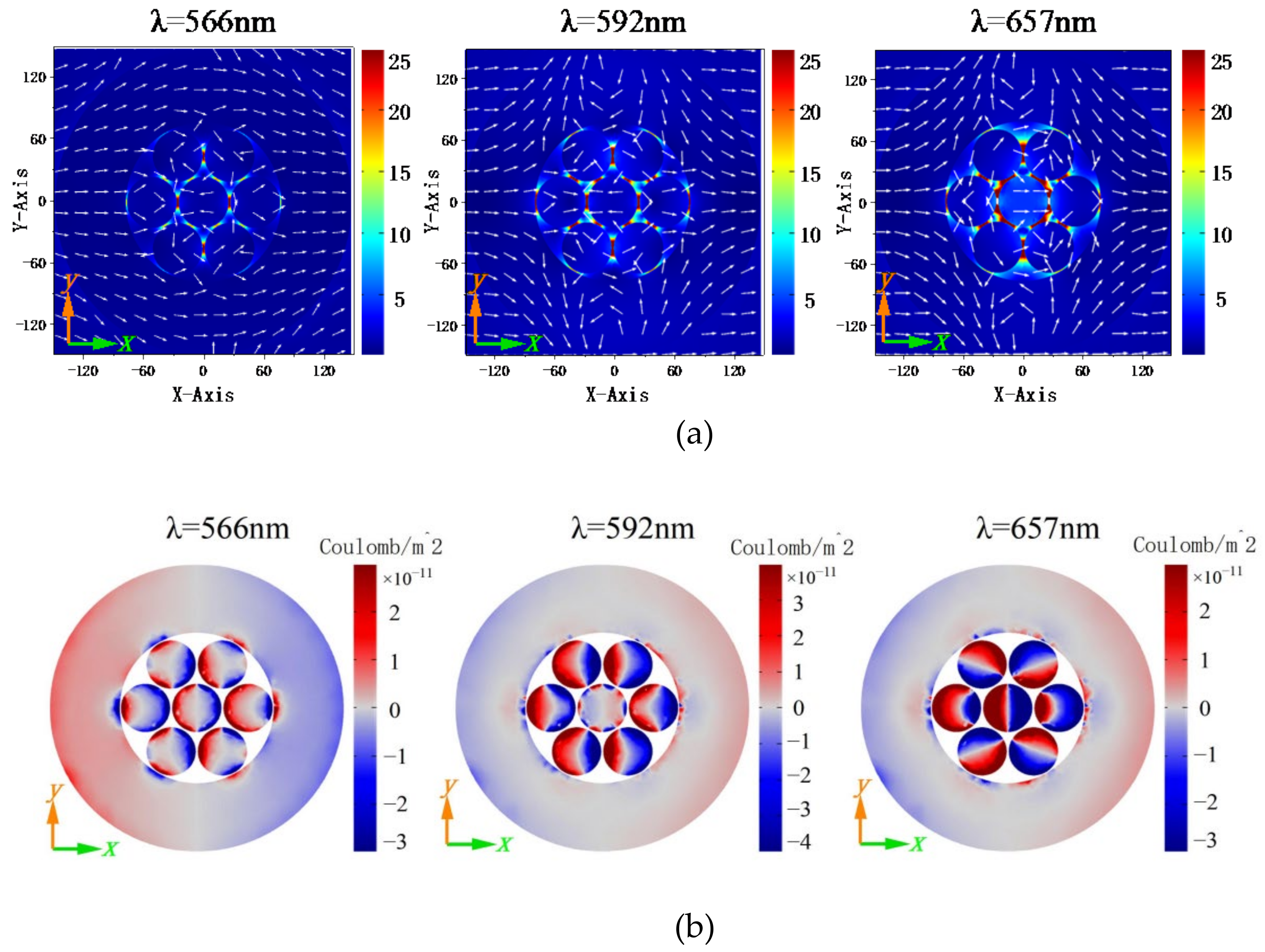
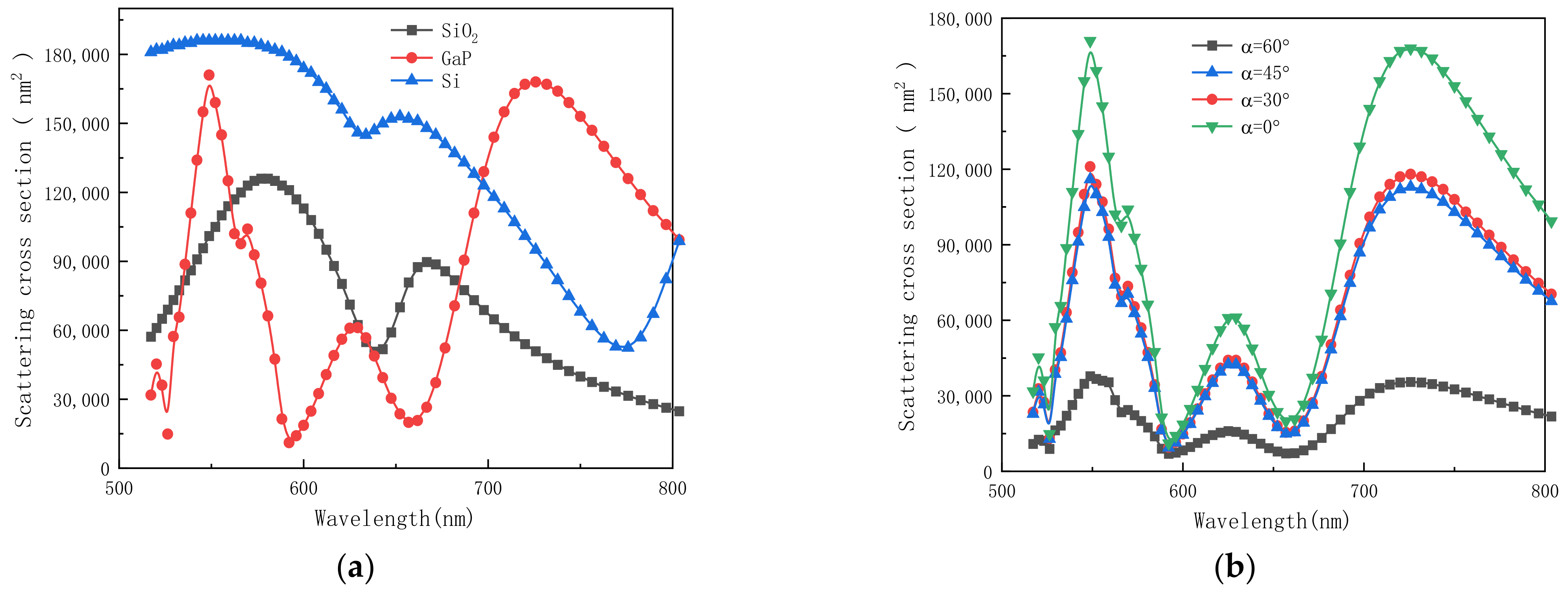
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, Q.; Pan, C.; Chen, Y. Nano-optical antenna sensor based on localized surface plasmon resonance. In Proceedings of the 2016 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Chengdu, China, 19–22 September 2016; pp. 1–4. [Google Scholar]
- Nikitin, A.; Remezani, M.; Rivas, J.G. Luminescent Metamaterials for Solid State Lighting. ECS J. Solid State Sci. Technol. 2015, 5, 3164–3169. [Google Scholar] [CrossRef][Green Version]
- Liu, J.X.; He, H.; Xiao, D.; Yin, S.T.; Ji, W.; Jiang, S.Z.; Luo, D.; Wang, B.; Liu, Y.J. Recent Advances of Plasmonic Nanoparticles and Their Applications. Materials 2018, 11, 1833. [Google Scholar] [CrossRef] [PubMed]
- Su, K.H.; Wei, Q.H.; Zhang, X.; Mock, J.J.; Smith, D.R.; Schultz, S. Interparticle Coupling Effects on Plasmon Resonances of Nanogold Particles. Nano Lett. 2003, 3, 8. [Google Scholar] [CrossRef]
- Pineider, F.; Pedrueza-Villalmanzo, E.; Serri, M.; Adamu, A.M.; Smetanina, E. Plasmon-enhanced magneto-optical detection of single-molecule magnets. Mater. Horiz. 2019, 6, 1148–1155. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, X.Y.; Li, D.L.; Wang, T.T.; Ma, F.; Zhang, C.Y. Construction of a gold nanoparticle -based single-molecule biosensor for simple and sensitive detection of Argonaute 2 activity. J. Mater. Chem. B 2022, 10, 5594–5601. [Google Scholar] [CrossRef]
- Yang, A.K.; Wang, D.Q.; Wang, W.J.; Odom, T.W. Coherent Light Sources at the Nanoscale. Annu. Rev. Phys. Chem. 2017, 68, 83–99. [Google Scholar] [CrossRef] [PubMed]
- Sakai, K.; Kitajima, H.; Sasaki, K. Plasmonic nanostructures for shrinking structured light to access forbidden transitions. Nanophotonics 2022, 11, 11. [Google Scholar] [CrossRef]
- Zhang, R.X.; Du, C.L.; Sun, L.; Rong, W.X.; Li, X.; Lei, M.X.; Shi, D.N. Individual Split Au Square Nanorings for Surface-Enhanced Raman and Hyper-Raman Scattering. Plasmonics 2022, 17, 965–971. [Google Scholar] [CrossRef]
- Kamimura, R.; Kondo, T.; Motobayashi, K.; Lkeda, K. Surface-Enhanced Electronic Raman Scattering at Various Metal Surfaces. Phys. Status Solidi B Basic Solid State Phys. 2021, 2100589. [Google Scholar] [CrossRef]
- Juan-Colas, J.; Parkin, A.; Dunn, K.E.; Scullion, M.G.; Krauss, T.F.; Johnson, S.D. The electrophotonic silicon biosensor. Nat. Commun. 2016, 7, 12769. [Google Scholar] [CrossRef]
- Chau, Y.F.; Chou Chao, C.T.; Jumat, S.Z.B.H.; Kooh, M.R.R.; Thotagamuge, R.; Lim, C.M.; Chiang, H.-P. Improved Refractive Index-Sensing Performance of Multimode Fano-Resonance-Based Metal-Insulator-Metal Nanostructures. Nanomaterials 2021, 11, 2097. [Google Scholar] [CrossRef]
- Limonov, M.F.; Rybin, M.V.; Poddubny, A.N.; Kivshar, Y.S. Fano resonances in photonics. Nat. Photonics 2017, 11, 543–554. [Google Scholar] [CrossRef]
- Wan, Y.; Tan, Y.X.; Yang, Y.; Chong, H.N.; Meng, Z.Z.; Wang, J. Actively Tunable Fano Resonance in H-Like Metal-Graphene Hybrid Nanostructures. Plasmonics 2022, 17, 843–849. [Google Scholar] [CrossRef]
- Yang, Z.J.; Zhao, Q.; He, J. Fano interferences of electromagnetic modes in dielectric nanoblock dimers. J. Appl. Phys. 2019, 125, 063103. [Google Scholar] [CrossRef]
- Ye, J.; Wen, F.; Sobhani, H.; Lassiter, J.B.; Van Dorpe, P.; Nordlander, P.; Halas, N.J. Plasmonic nanoclusters: Near field properties of the Fano resonance interrogated with SERS. Nano Lett. 2012, 12, 1660–1667. [Google Scholar] [CrossRef]
- Zuev, D.A.; Makarov, S.V.; Milichko, V.A.; Starikov, S.A.; IMukhin, I.S.; Morozov, I.A.; Shishkin, I.I.; Krasnok, A.E.; Belov, P.A. Fabrication Of Hybrid Nanostructures Via Nanoscale Laser-Induced Reshaping For Advanced Light Manipulation. Adv. Mater. 2016, 28, 3087–3093. [Google Scholar] [CrossRef]
- Zarrabi, F.B.; Moghadasi, M.N. Investigated the Fano resonance in the nano ring arrangement. Optik 2017, 138, 80–86. [Google Scholar] [CrossRef]
- Dutta, A.; Alam, K.; Nuutinen, T.; Hulkko, E.; Karvinen, P.; Kuittinen, M.; Toppari, J.J.; Vartiainen, E.M. Influence of Fano resonance on SERS enhancement in Fano-plasmonic oligomers. Opt. Express 2019, 27, 21. [Google Scholar] [CrossRef]
- Torres, M.U.; Klausen, K.O.; Sitek, A.; Erlingsson, S.I.; Gudmundsson, V.; Manolescu, A. Electromagnetic field emitted by core–shell semiconductor nanowires driven by an alternating current. J. Appl. Phys. 2021, 30, 034301. [Google Scholar] [CrossRef]
- Chou Chau, Y.F.; Chou Chao, C.T.; Huang, H.J.; Kooh, M.R.R.; Kumara, N.T.R.N.; Lim, C.M.; Chiang, H.P. Perfect Dual-Band Absorber Based on Plasmonic Effect with the Cross-Hair/Nanorod Combination. Nanomaterials 2020, 10, 493. [Google Scholar] [CrossRef]
- Zubaidah, S.; Chou Chao, C.T.; Chou Chau, Y.F.; Mahadi, A.H.; Kooh, M.R.R.; Kumara, N.T.R.N.; Chiang, H.P. Plasmonic refractive index sensor based on the combination of rectangular and circular resonators including baffles. Chin. J. Phys. 2021, 71, 286–299. [Google Scholar] [CrossRef]
- Sung, M.J.; Ma, Y.F.; Chau, Y.F.; Huang, D.W. Surface plasmon resonance in a hexagonal nanostructure formed by seven core shell nanocylinders. Appl. Opt. 2010, 49, 920–926. [Google Scholar] [CrossRef] [PubMed]
- Fedorov, V.V.; Koval, O.Y.; Ryabov, D.R. Nanoscale Gallium Phosphide Epilayers on Sapphire for Low-Loss Visible Nanophotonics. ACS Appl. Nano Mater. 2022, 5, 8846–8858. [Google Scholar] [CrossRef]
- Khmelevskaia, D.; Markina, D.I.; Fedorov, V.V. Directly grown crystalline gallium phosphide on sapphire for nonlinear all-dielectric nanophotonics. Appl. Phys. Lett 2021, 118, 201101. [Google Scholar] [CrossRef]
- Zhou, Y.; Meng, Y.J.; Huang, W.X.; Li, K.G. Application scope of multipole method for decomposition of plas monic spectrum. Results Phys. 2022, 39, 105742. [Google Scholar] [CrossRef]
- Radescu, E.E.; Vaman, G. Exact calculation of the angular momentum loss, recoil force, and radiation intensity for an arbitrary source in terms of electric, magnetic, and toroid multipoles. Phys. Rev. E 2002, 65, 046609. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S.; Lin, Z.; Sun, H.B.; Chan, C.T. Optical force on toroidal nanostructures: Toroidal dipole versus renormalized electric dipole. Phys. Rev. A 2015, 92, 043804. [Google Scholar] [CrossRef]
- Evlyukhin, A.B.; Fischer, T.; Reinhardt, C.; Chichkov, B.N. Optical theorem and multipole scattering of light by arbitrarily shaped nanoparticles. Phys. Rev. B 2016, 94, 205434. [Google Scholar] [CrossRef]
- Ray, D.; Kiselev, A.; Martin, O.J.F. Refractive index data for 150 nm Ag measured with ellipsometry [Data set]. Zenodo 2021. [Google Scholar] [CrossRef]
- West, P.; Ishii, S.; Naik, G.; Emani, N.; Shalaev, V.; Boltasseva, A. Searching for better plasmonic materials. Laser Photonics Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: New York, NY, USA, 1985. [Google Scholar]
- Yang, M.; Chen, X.; Wang, Z.; Zhu, Y.; Pan, S.; Chen, K.; Wang, Y.; Zheng, J. Zero→Two-Dimensional Metal Nanostructures: An Overview on Methods of Preparation, Characterization, Properties, and Applications. Nanomaterials 2021, 11, 1895. [Google Scholar] [CrossRef]
- Hüttenhofer, L.; Tittl, A.; Kühner, L.; Cortés, E.; Maier, S.A. Anapole-Assisted Absorption Engineering in Arrays of Coupled Amorphous Gallium Phosphide Nanodisks. ACS Photonics 2021, 8, 1469–1476. [Google Scholar] [CrossRef]
- Zhao, X.; Wen, J.; Zhu, A.; Cheng, M.; Zhu, Q.; Zhang, X.; Wang, Y.; Zhang, Y. Manipulation and Applications of Hotspots in Nanostructured Surfaces and Thin Films. Nanomaterials 2020, 10, 1667. [Google Scholar] [CrossRef]
- Dregely, D.; Hentschel, M.; Giessen, H. Excitation and tuning of higher-order Fano resonances in plasmonic oligomer clusters. ACS Nano 2011, 5, 8202–8211. [Google Scholar] [CrossRef]
- Torres, U.M.; Sitek, A.; Manolescu, A. Anisotropic light scattering by prismatic semiconductor nanowires. Opt. Express 2019, 27, 25502–25514. [Google Scholar] [CrossRef]
- Liu, W.; Shi, Y.; Yi, Z.; Liu, C.; Wang, F.M.; Li, X.L.; Lv, J.W.; Yang, L.; Chu, P.K. Surface plasmon resonance chemical sensor composed of a microstructured optical fiber for the detection of an ultra-wide refractive index range and gas-liquid pollutants. Opt. Express 2021, 29, 25. [Google Scholar] [CrossRef]
- Melwin, G.; Senthilnathan, K. High sensitive D-shaped photonic crystal fiber sensor with Vgroove analyte channel. Optik 2020, 213, 164779. [Google Scholar] [CrossRef]
- Ghodsi, F.; Dashti, H.; Shokouh, J.A. Design of a multilayer nano-antenna as a hyperbolic metamaterial with Fano response for optical sensing. Opt. Quantum Electron. 2020, 52, 316. [Google Scholar] [CrossRef]

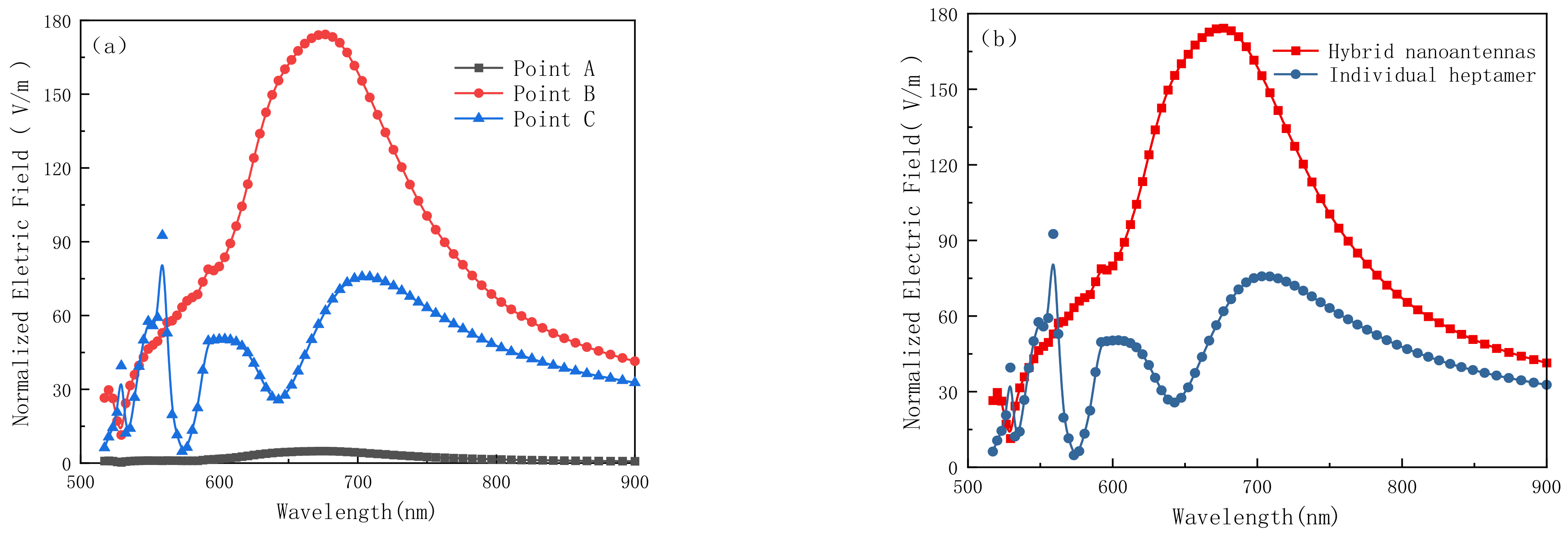
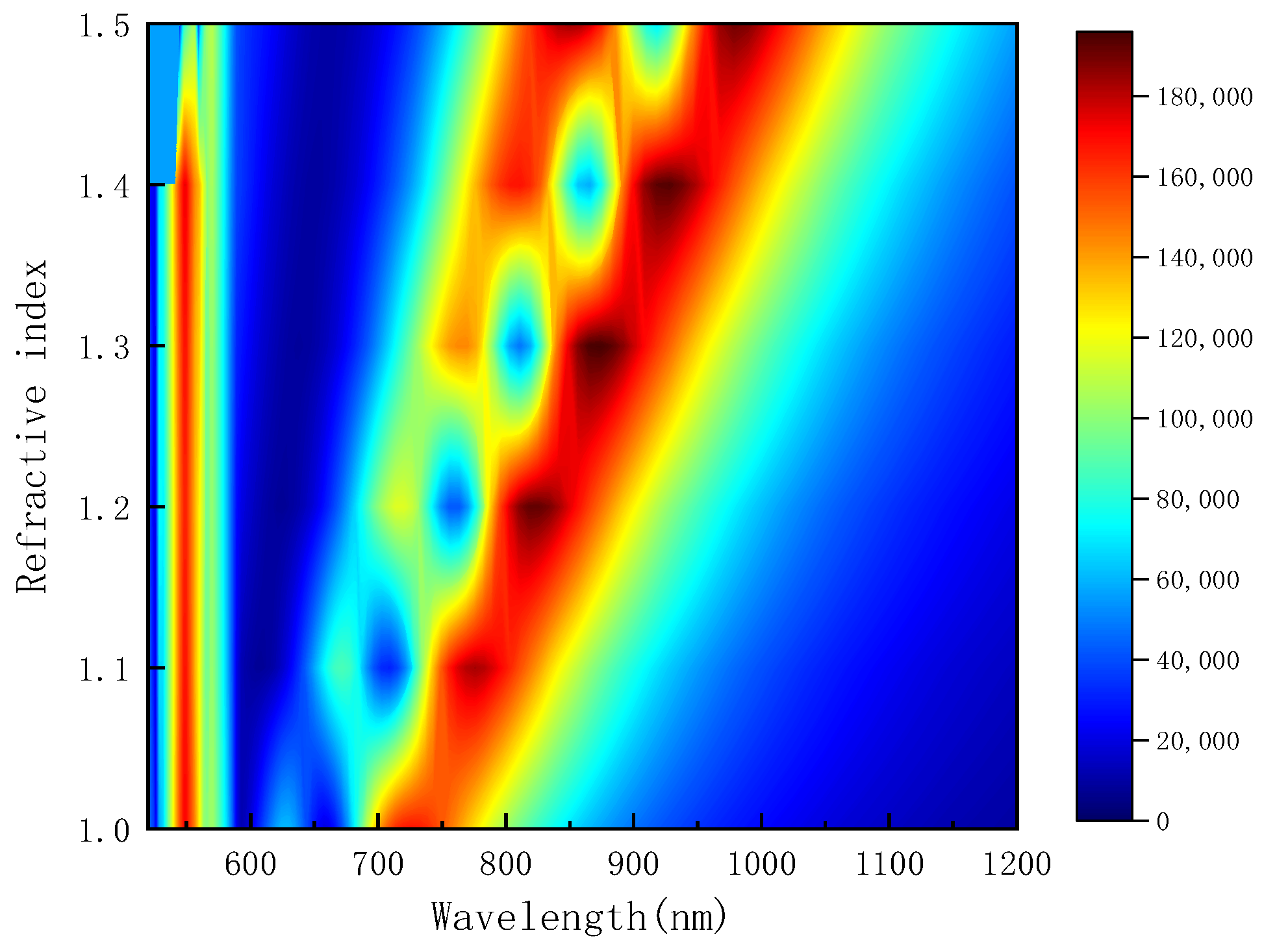
| Fano Dips | First Dip | Second Dip | Third Dip | |
|---|---|---|---|---|
| n = 1.0 | — | — | — | — |
| n = 1.1 | Δn | 0.1 | 0.1 | 0.1 |
| Δλ (nm) | 0 | 16 | 52 | |
| S (nm/RIU) | 0 | 160 | 520 | |
| n = 1.2 | Δn | 0.1 | 0.1 | 0.1 |
| Δλ (nm) | 0 | 17 | 47 | |
| S (nm/RIU) | 0 | 170 | 470 | |
| n = 1.3 | Δn | 0.1 | 0.1 | 0.1 |
| Δλ (nm) | 0 | 13 | 55 | |
| S (nm/RIU) | 0 | 130 | 550 | |
| n = 1.4 | Δn | 0.1 | 0.1 | 0.1 |
| Δλ (nm) | 0 | 14 | 54 | |
| S (nm/RIU) | 0 | 140 | 540 | |
| n = 1.5 | Δn | 0.1 | 0.1 | 0.1 |
| Δλ (nm) | 3 | 10 | 53 | |
| S (nm/RIU) | 30 | 100 | 530 |
| Fano Dips | First Dip | Second Dip | Third Dip | |
|---|---|---|---|---|
| n = 1.0 | — | — | — | — |
| n = 1.1 | S (nm/RIU) | 0 | 160 | 520 |
| FWHM (nm) | 7 | 42.1 | 40 | |
| FOM (RIU−1) | 0 | 3.8 | 13 | |
| n = 1.2 | S (nm/RIU) | 0 | 170 | 470 |
| FWHM (nm) | 7 | 54.8 | 54 | |
| FOM (RIU−1) | 0 | 3.1 | 8.7 | |
| n = 1.3 | S (nm/RIU) | 0 | 130 | 550 |
| FWHM (nm) | 7 | 72.2 | 50 | |
| FOM (RIU−1) | 0 | 1.8 | 11 | |
| n = 1.4 | S (nm/RIU) | 0 | 140 | 540 |
| FWHM (nm) | 8 | 82.4 | 53.5 | |
| FOM (RIU−1) | 0 | 1.7 | 10.1 | |
| n = 1.5 | S (nm/RIU) | 30 | 100 | 530 |
| FWHM (nm) | 1.7 | 100 | 98.1 | |
| FOM (RIU−1) | 17.5 | 1 | 5.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, J.; Wang, D.; Liu, C.; Wang, J.; Yang, L.; Liu, W.; Liu, Q.; Mu, H.; Chu, P.K. Theoretical Analysis of Hybrid Metal–Dielectric Nanoantennas with Plasmonic Fano Resonance for Optical Sensing. Coatings 2022, 12, 1248. https://doi.org/10.3390/coatings12091248
Lv J, Wang D, Liu C, Wang J, Yang L, Liu W, Liu Q, Mu H, Chu PK. Theoretical Analysis of Hybrid Metal–Dielectric Nanoantennas with Plasmonic Fano Resonance for Optical Sensing. Coatings. 2022; 12(9):1248. https://doi.org/10.3390/coatings12091248
Chicago/Turabian StyleLv, Jingwei, Debao Wang, Chao Liu, Jianxin Wang, Lin Yang, Wei Liu, Qiang Liu, Haiwei Mu, and Paul K. Chu. 2022. "Theoretical Analysis of Hybrid Metal–Dielectric Nanoantennas with Plasmonic Fano Resonance for Optical Sensing" Coatings 12, no. 9: 1248. https://doi.org/10.3390/coatings12091248
APA StyleLv, J., Wang, D., Liu, C., Wang, J., Yang, L., Liu, W., Liu, Q., Mu, H., & Chu, P. K. (2022). Theoretical Analysis of Hybrid Metal–Dielectric Nanoantennas with Plasmonic Fano Resonance for Optical Sensing. Coatings, 12(9), 1248. https://doi.org/10.3390/coatings12091248







