Deflection Prediction of Rehabilitation Asphalt Pavements through Deep Forest
Abstract
:1. Introduction
2. Literature Review
3. Data Acquisition and Preprocessing
3.1. LTPP Database
- (1)
- Improvement thickness was used to indicate the rehabilitation level.
- (2)
- The annual kilo equivalent standard axle load (ESAL) was chosen to represent the traffic level.
- (3)
- The climatic factors were the annual average precipitation and average freeze index.
- (4)
- The pavement structural characteristic were the structural number, asphalt layer thickness, base thickness, base type (granular base and treated base), and sub-base thickness.
- (5)
- The FWD test conditions were drop load, layer temperature, and the depth of the measured temperature.
- (6)
- Pavement service age.
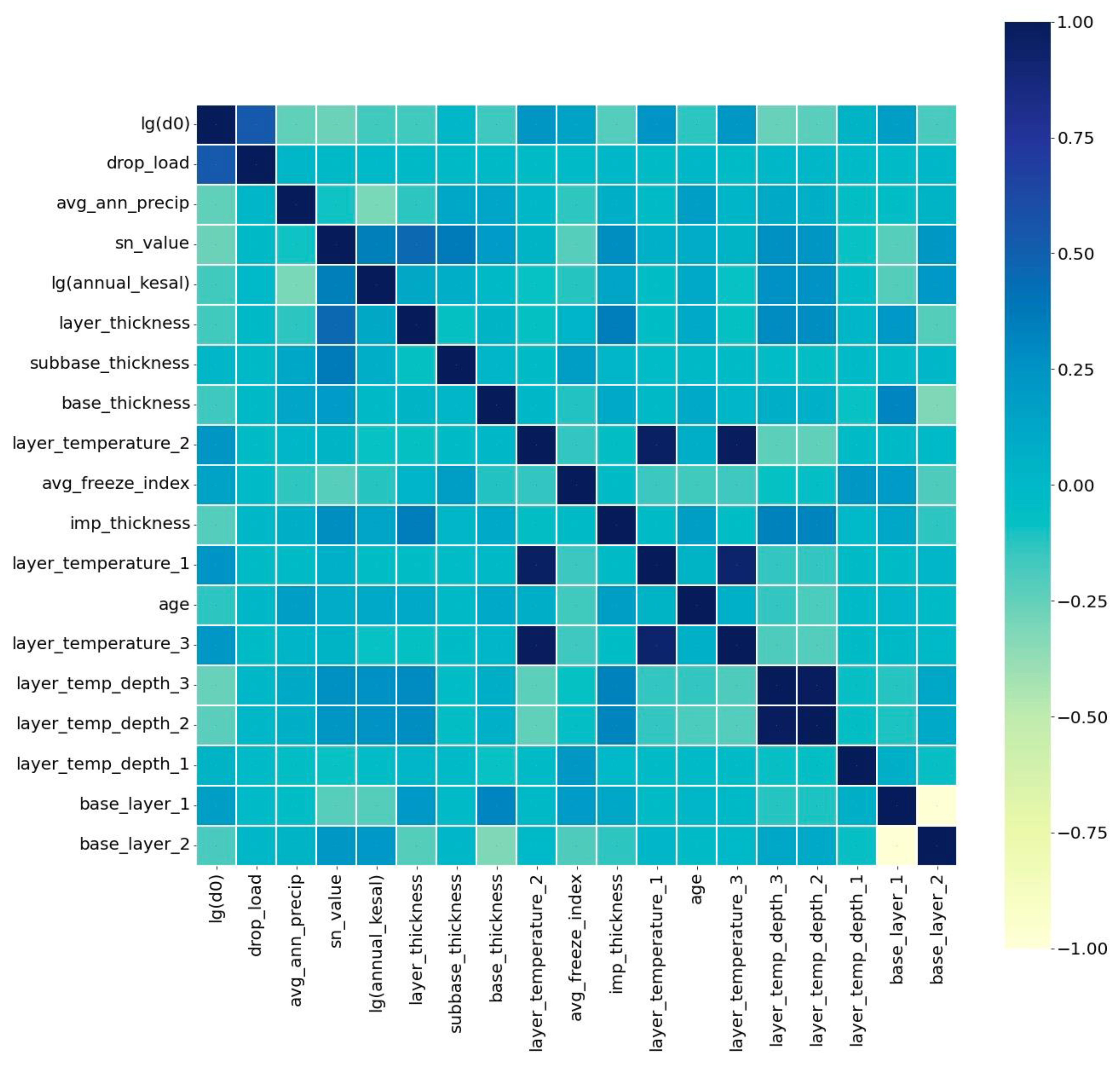
3.2. Data Preprocessing
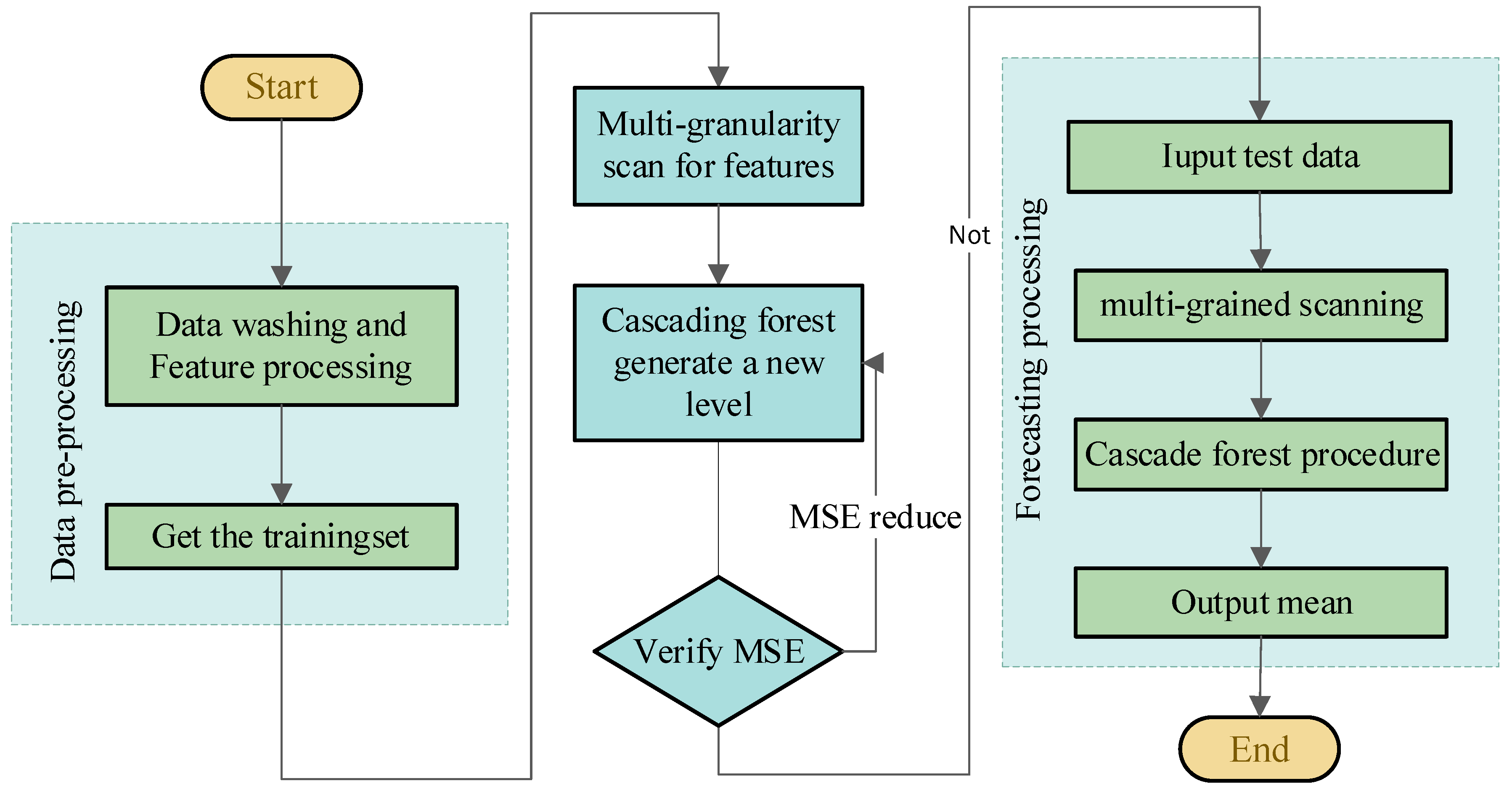
4. Methodology
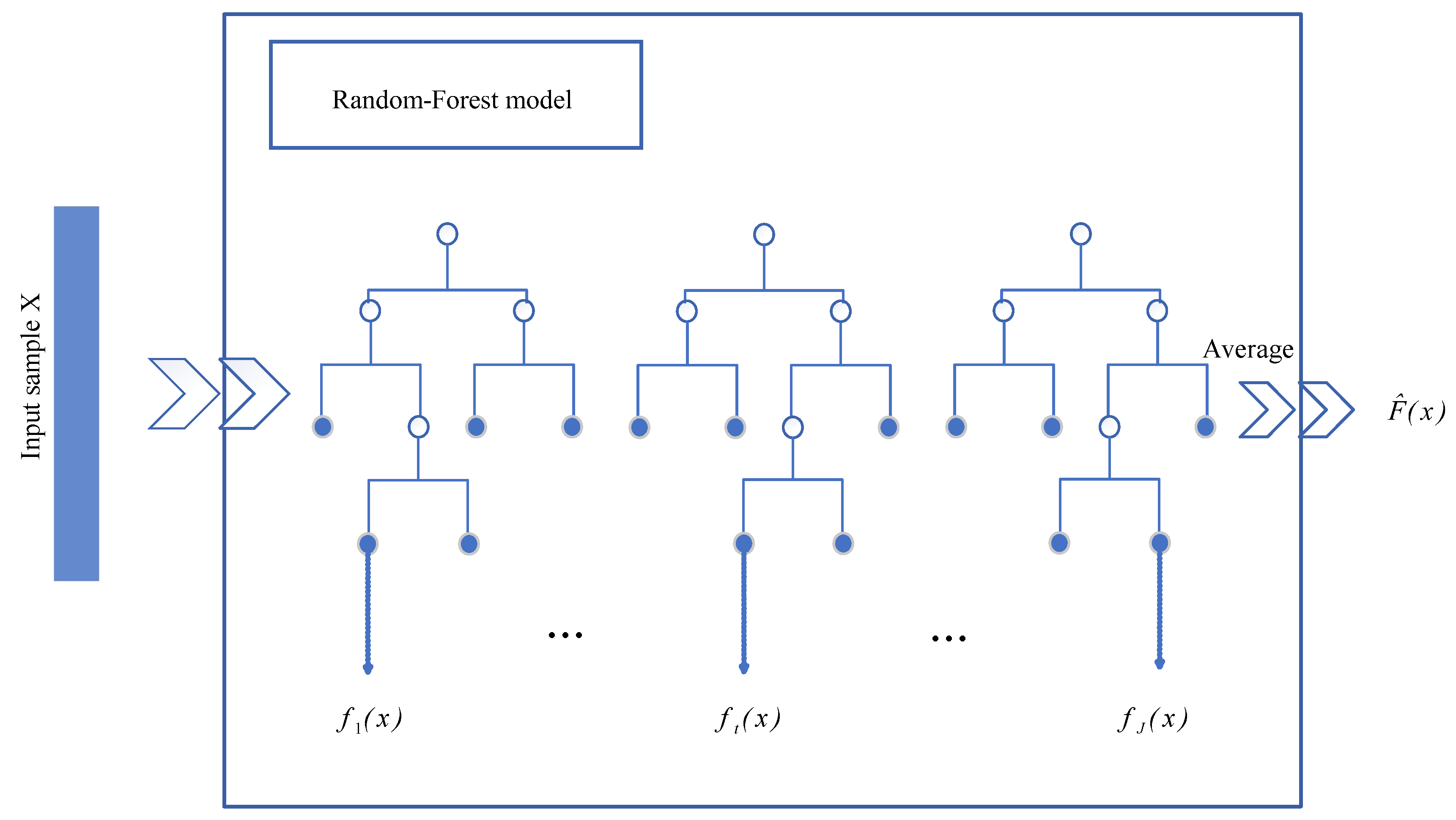
4.1. Random Forest Algorithm
- (1)
- Specify the training set as , where N represents the number of samples and M represents the number of feature dimensions. The minimal loss function is defined as follows.
- (2)
- Iterate through each segmentation node j and the segmentation value z of each node. Select the segmentation point by calculating the minimal damage function to divide the sample space into R1 and R2. c1 and c2 are the corresponding output values of R1 and R2 spaces.
- (3)
- Find the partition point again until it is impossible to continue to divide the subspace.
- (4)
- The sample space is lastly divided into M parts, and the model can be represented as ; I is taken as 1 when .
- (1)
- J training sets of same size are extracted by the bagging method (BM) and treated as inputs of the tree model. M features are randomly selected as candidate features to participate in the traversal when the tree model is split. Then, J independent regression trees are born.
- (2)
- Allow each regression tree to grow to its maximal height without pruning.
- (3)
- The average value of all samples falling on each leaf node is used as the prediction value of the leaf node, and Step (2) is repeated to finish building the J-tree regression tree.
- (4)
- The RF regression algorithm integrates J regression trees and can be represented as:
4.2. Deep Forest Algorithm
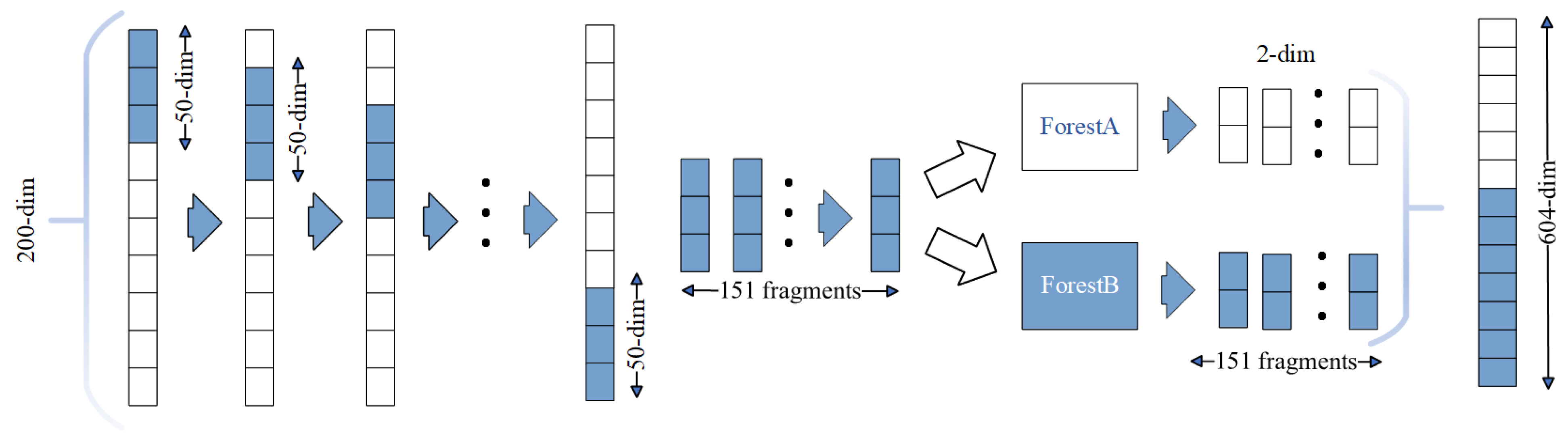
4.2.1. Multigranularity Scanning
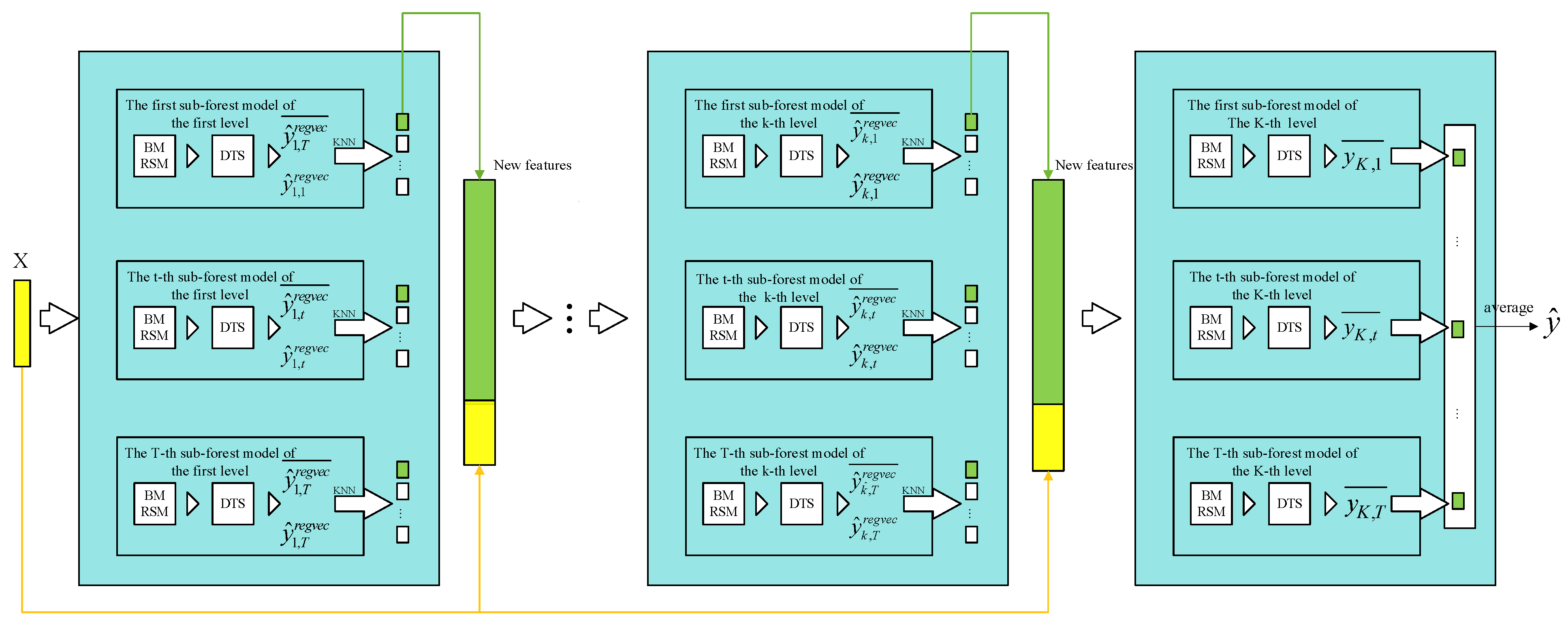
4.2.2. Cascade Forest
- (1)
- The transformed feature vectors after multigranularity scanning are used as the original feature vector X at one level in the cascade forest. X through each DTS in the subforest generates the regression vector (where 1 represents the first level of the cascade forest, and t represents the t-th subforest module).
- (2)
- The adjacent values of the average regression vector are selected by the K-nearest-neighbor method to obtain the augmented layer regression vectors, and then the augmented regression vectors are combined with the initial vectors to obtain new features.
- (3)
- Using the new features as the input vector of the next level, the output of the second cascade level is obtained in the same way as the input level. The number of born cascade layers is adaptively adjusted by verifying whether mean square error (MSE) decreases. When MSE no longer decreases, the cascade layer stops growing.
- (4)
- The output layer is the augmented regression vector of the output (K-1)th layer, and the original feature vector is obtained from the multigranularity scanning as input. The final value is the weighted prediction values obtained from the T subforest models in the last layer.
5. Discussion of Results
5.1. Model Evaluation Indicators
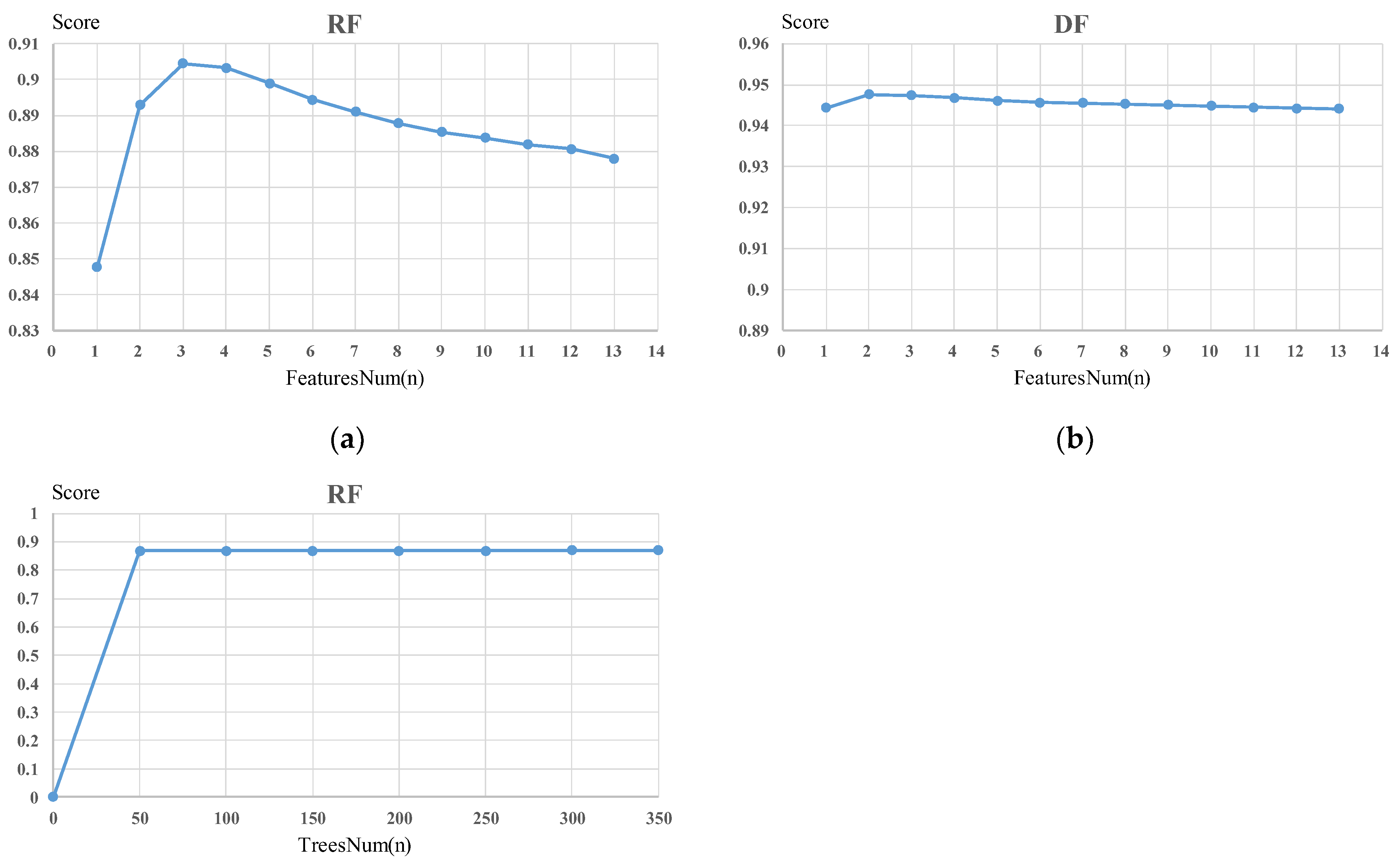
5.2. Forest Model Optimal Parameters
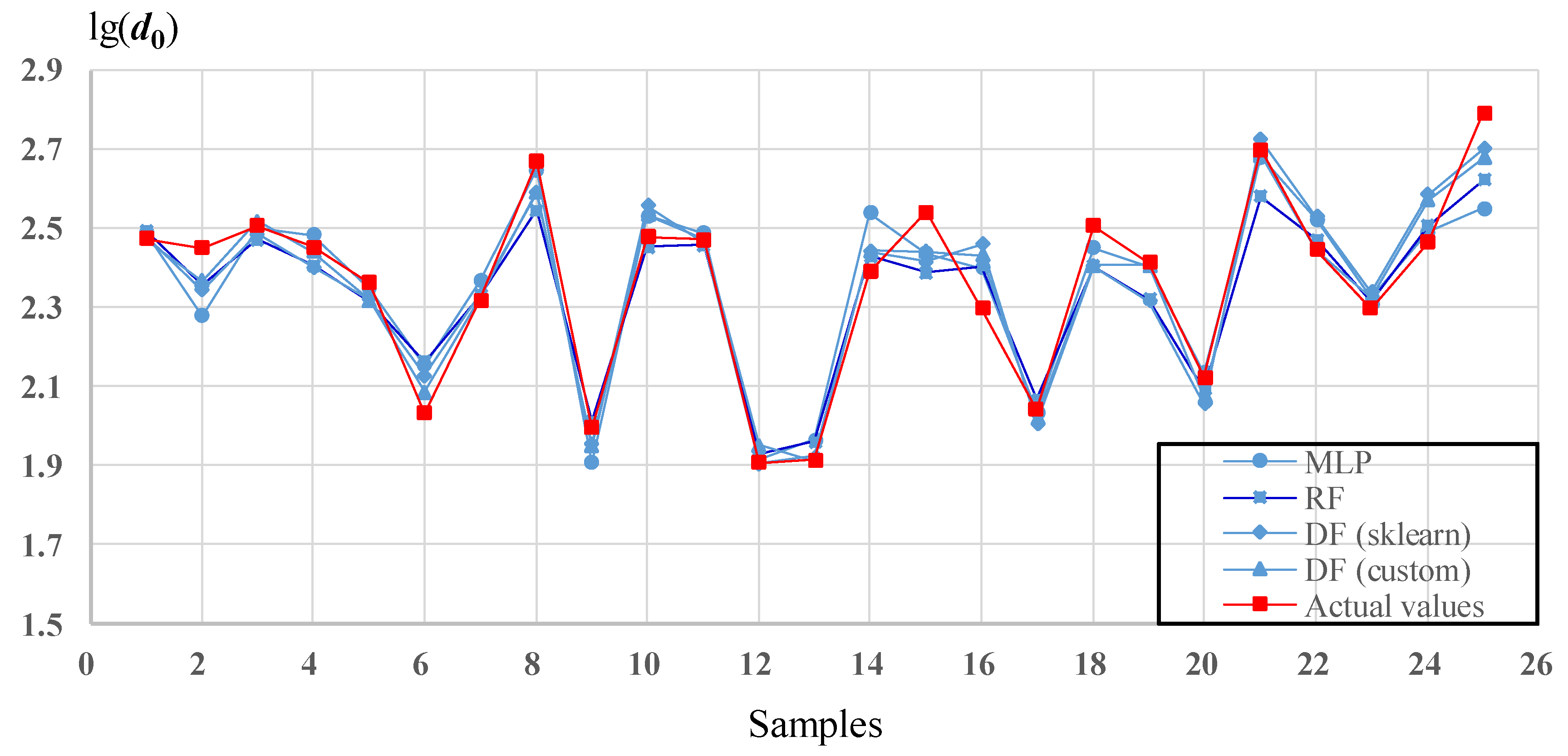
5.3. Method Comparison
- The MSE, RMSE, MAE, and R2 of DF (custom) were better than those of other models, indicating that DF could achieve higher accuracy and better stability in this study.
- The performance of DF is close to RF in learning feature characteristics, but the generalization ability is significantly better than that of RF. MLP’s performance in the training set is significantly inferior to DF and RF, but the generalization capability is good.
- Compared with the highly encapsulated DF (sklearn) model, DF (custom) has certain advantages in terms of computation time and accuracy.
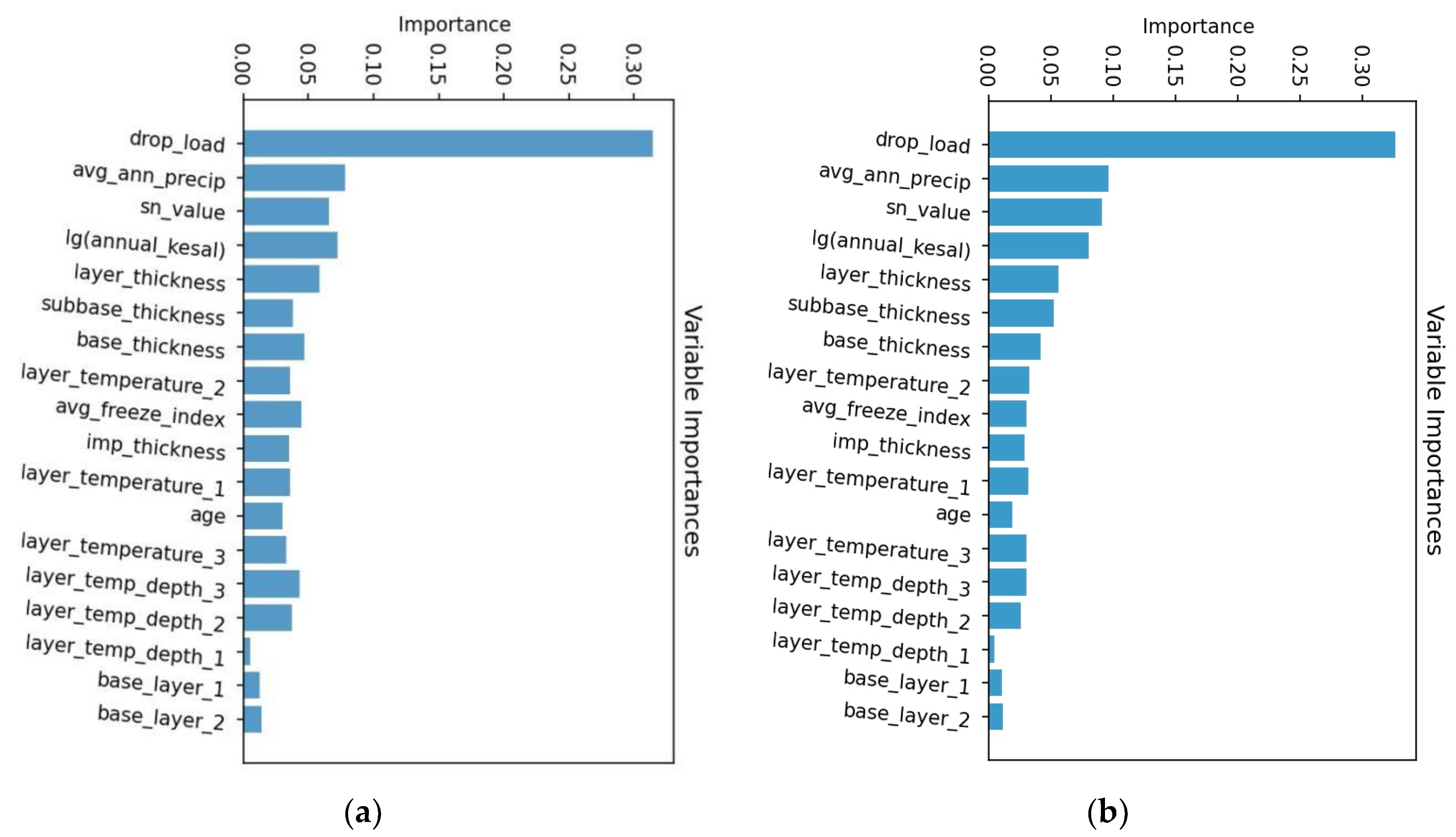
5.4. DF (sklearn) and RF Feature Importance Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mabrouk, G.M.; Elbagalati, O.S.; Dessouky, S.; Fuentes, L.; Walubita, L.F. Using ANN modeling for pavement layer moduli backcalculation as a function of traffic speed deflections. Constr. Build. Mater. 2021, 315, 125736. [Google Scholar] [CrossRef]
- Han, C.; Ma, T.; Chen, S.; Fan, J. Application of a hybrid neural network structure for FWD backcalculation based on LTPP database. Int. J. Pavement Eng. 2021, 1–14. [Google Scholar] [CrossRef]
- Plati, C.; Loizos, A.; Gkyrtis, K. Integration of non-destructive testing methods to assess asphalt pavement thickness. NDT E Int. 2020, 115, 102292. [Google Scholar] [CrossRef]
- Cao, M.; Huang, W.; Zou, Y.; Liu, G. Modulus Inversion Layer by Layer of Different Asphalt Pavement Structures. Adv. Civ. Eng. 2021, 2021, 1–10. [Google Scholar] [CrossRef]
- Elshaer, M.; Ghayoomi, M.; Daniel, J.S. The role of predictive models for resilient modulus of unbound materials in pavement FWD-deflection assessment. Road Mater. Pavement Des. 2020, 21, 374–392. [Google Scholar] [CrossRef]
- Muslim, H.B.; Haider, S.W.; Chatti, K. Influence of seasonal and diurnal FWD measurements on deflection-based parameters for rigid pavements. Int. J. Pavement Eng. 2021, 1–12. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, P.; Liu, H. Correlation between pavement temperature and deflection basin form factors of asphalt pavement. Int. J. Pavement Eng. 2019, 20, 874–883. [Google Scholar] [CrossRef]
- Sollazzo, G.; Fwa, T.; Bosurgi, G. An ANN model to correlate roughness and structural performance in asphalt pavements. Constr. Build. Mater. 2017, 134, 684–693. [Google Scholar] [CrossRef]
- Gong, H.; Sun, Y.; Shu, X.; Huang, B. Use of random forests regression for predicting IRI of asphalt pavements. Constr. Build. Mater. 2018, 189, 890–897. [Google Scholar] [CrossRef]
- Gong, H.; Sun, Y.; Dong, Y.; Han, B.; Polaczyk, P.; Hu, W.; Huang, B. Improved estimation of dynamic modulus for hot mix asphalt using deep learning. Constr. Build. Mater. 2020, 263, 119912. [Google Scholar] [CrossRef]
- Karballaeezadeh, N.; Mohammadzadeh, S.D.; Moazemi, D.; Band, S.S.; Mosavi, A.; Reuter, U. Smart Structural Health Monitoring of Flexible Pavements Using Machine Learning Methods. Coatings 2020, 10, 1100. [Google Scholar] [CrossRef]
- Barua, L.; Zou, B.; Noruzoliaee, M.; Derrible, S. A gradient boosting approach to understanding airport runway and taxiway pavement deterioration. Int. J. Pavement Eng. 2021, 22, 1673–1687. [Google Scholar] [CrossRef]
- Guo, R.; Fu, D.; Sollazzo, G. An ensemble learning model for asphalt pavement performance prediction based on gradient boosting decision tree. Int. J. Pavement Eng. 2021, 1–14. [Google Scholar] [CrossRef]
- Issa, A.; Sammaneh, H.; Abaza, K. Modeling Pavement Condition Index Using Cascade Architecture: Classical and Neural Network Methods. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 46, 483–495. [Google Scholar] [CrossRef]
- Majidifard, H.; Adu-Gyamfi, Y.; Buttlar, W.G. Deep machine learning approach to develop a new asphalt pavement condition index. Constr. Build. Mater. 2020, 247, 118513. [Google Scholar] [CrossRef]
- Ziari, H.; Maghrebi, M.; Ayoubinejad, J.; Waller, T. Prediction of Pavement Performance: Application of Support Vector Regression with Different Kernels. Transp. Res. Rec. J. Transp. Res. Board 2016, 2589, 135–145. [Google Scholar] [CrossRef]
- Todkar, S.S.; Le Bastard, C.; Baltazart, V.; Ihamouten, A.; Dérobert, X. Performance assessment of SVM-based classification techniques for the detection of artificial debondings within pavement structures from stepped-frequency A-scan radar data. NDT E Int. 2019, 107, 102128. [Google Scholar] [CrossRef]
- El-Raof, H.S.A.; El-Hakim, R.A.; El-Badawy, S.M.; Afify, H.A. Simplified Closed-Form Procedure for Network-Level Determination of Pavement Layer Moduli from Falling Weight Deflectometer Data. J. Transp. Eng. Part B Pavements. 2018, 144, 04018052. [Google Scholar] [CrossRef]
- Karballaeezadeh, N.; Tehrani, H.G.; Shadmehri, D.M.; Shamshirband, S. Estimation of flexible pavement structural capacity using machine learning techniques. Front. Struct. Civ. Eng. 2020, 14, 1083–1096. [Google Scholar] [CrossRef]
- Bonissone, P.; Cadenas, J.M.; Garrido, M.C.; Díaz-Valladares, R.A. A fuzzy random forest. Int. J. Approx. Reason. 2010, 51, 729–747. [Google Scholar] [CrossRef] [Green Version]
- Guo, D.; Chen, H.; Tang, L.; Chen, Z.; Samui, P. Assessment of rockburst risk using multivariate adaptive regression splines and deep forest model. Acta Geotech. 2022, 17, 1183–1205. [Google Scholar] [CrossRef]
- Yin, L.; Sun, Z.; Gao, F.; Liu, H. Deep Forest Regression for Short-Term Load Forecasting of Power Systems. IEEE Access 2020, 8, 49090–49099. [Google Scholar] [CrossRef]
- Zhou, Z.-H.; Feng, J. Deep forest. arXiv 2017, arXiv:1702.08835. [Google Scholar]
- Zhou, Z.-H.; Feng, J. Deep forest. National Science Review 2019, 6, 74–86. [Google Scholar] [CrossRef]
- Yao, Y.; Gu, Y.; Bao, W.; Zhang, L.; Zhu, Y. Golgi Protein Prediction with Deep Forest. In International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 647–653. [Google Scholar]
- Tang, J.; Xia, H.; Zhang, J.; Qiao, J.; Yu, W. Deep forest regression based on cross-layer full connection. Neural Comput. Appl. 2021, 33, 9307–9328. [Google Scholar] [CrossRef]

| Feature | Description | Feature | Description |
|---|---|---|---|
| drop_load | Peak drop load (plate pressure) (kPa) | annual_kesal | annual kilo equivalent standard axle load. |
| avg_ann_precip | Annual average precipitation (cm) | avg_freeze_index | The negative of the sum of all average daily temperature below 0 °C in a year. |
| sn_value | Structural number for AC pavements | layer_thickness | The measured thickness of an individual layer (cm). |
| subbase_thickness | Thickness of sub-base (cm) | base_thickness | Thickness of pavement base (cm). |
| base_layer | The type of pavement base including granular base (GB) and treated base (TB) | imp_thickness | Improvement thickness (cm). |
| layer_temperature_1 | Measured layer’s temperature at specified depth layer_temp_depth_1 (°C) | layer_temp_depth_1 | Depth of the hole at measurement layer_temperature_1 (mm). |
| layer_temperature_2 | Measured layer’s temperature at specified depth layer_temp_depth_2 (°C) | layer_temp_depth_2 | Depth of the hole at measurement layer_temperature_2 (mm). |
| layer_temperature_3 | Measured layer’s temperature at specified depth layer_temp_depth_3 (deg C) | layer_temp_depth_3 | Depth of the hole at measurement layer_temperature_3 (mm). |
| age | Pavement service age |
| Models | Main Parameters | Value |
|---|---|---|
| MLP | hidden_layer_size | (92, 46) |
| solver | ‘relu’ | |
| activation | ‘adam’ | |
| RF | n_estimatores | 250 |
| max_features | 3 | |
| DF (sklearn) | n_trees | 400 |
| Max_features | 2 | |
| DF (custom) | n_trees | 400 |
| max_features | 2 |
| Model | R2 | Adjusted R2 | MAE | MSE | RMSE | Time | Layer |
| MLP | 0.939 | 0.908 | 0.062 | 0.007 | 0.082 | ||
| RF | 0.988 | 0.917 | 0.060 | 0.006 | 0.079 | ||
| DF (sklearn) | 0.992 | 0.935 | 0.049 | 0.005 | 0.070 | 4 min 25 s | 2 |
| DF (custom) | 0.990 | 0.963 | 0.038 | 0.003 | 0.052 | 54.3 s | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Chen, X.; Jiang, D. Deflection Prediction of Rehabilitation Asphalt Pavements through Deep Forest. Coatings 2022, 12, 1057. https://doi.org/10.3390/coatings12081057
Wu Y, Chen X, Jiang D. Deflection Prediction of Rehabilitation Asphalt Pavements through Deep Forest. Coatings. 2022; 12(8):1057. https://doi.org/10.3390/coatings12081057
Chicago/Turabian StyleWu, Yi, Xueqin Chen, and Dongqi Jiang. 2022. "Deflection Prediction of Rehabilitation Asphalt Pavements through Deep Forest" Coatings 12, no. 8: 1057. https://doi.org/10.3390/coatings12081057
APA StyleWu, Y., Chen, X., & Jiang, D. (2022). Deflection Prediction of Rehabilitation Asphalt Pavements through Deep Forest. Coatings, 12(8), 1057. https://doi.org/10.3390/coatings12081057






