Mechanical Properties of σ-Phase and Its Effect on the Mechanical Properties of Austenitic Stainless Steel

Abstract

In this present paper, the mechanical properties of σ-phase and its effect on the mechanical properties of 304H austenitic stainless steel after servicing for about 8 years at 680–720 °C were studied by nano-indentation test, uniaxial tensile test, and impact test. The results showed that the nano-hardness (H), Young’s modulus (E), strain hardening exponent (n), and yield strength (σ_y) of σ-phase were 14.95 GPa, 263 GPa, 0.78, and 2.42 GPa, respectively. The presence of σ-phase increased the hardness, yield strength, and tensile strength, but greatly reduced the elongation and impact toughness of the material.

1. Introduction

Since σ-phase was first reported by Treitschke in 1907, about one century has passed. The structure and formation of σ-phase and its effects on material properties have been extensively studied and reported. σ-phase is basically an intermetallic phase that has a characteristic complex tetragonal unit cell structure [1]. The typical unit cell of σ-phase has 30 atoms, and these atoms are distributed in five inequivalent lattice sites [2,3]. A study also showed that the five inequivalent lattice sites of the σ-phase display a specific site-occupation sequence with the increase in element composition [4]. After exposure to an elevated temperature, σ-phase can be present in many stainless steels such as ferritic [5,6], austenitic [7,8], and duplex stainless steels [9,10]. The nucleation and growth of σ-phase are controlled by the thermodynamic driving forces and diffusion. σ-phase always has a high content of substitutional elements such as Cr, Mo, V, and so on. The partitioning of these elements is crucial, because their mobility and richness determine the precipitation position of σ-phase. For example, in duplex stainless steel, Cr and Mo elements are higher in the ferrite than in the austenite. Accordingly, σ-phase predominantly occurs in the ferrite–ferrite and ferrite–austenite grain boundaries. The nuclei then grow into the adjacent ferrite grains. As the precipitation continues, the ferrite-forming elements Cr and Mo diffuse from the ferrite to the σ-phase [11,12,13,14].

σ-phase is hard and brittle. Bain and Griffiths [15] have reported a hardness of ≈68 HRC for (Fe-Cr) σ-phase, and they found that specimens often fractured during hardness testing. You et al. [16] found that the nano-hardness of σ-phase in high entropy alloy was 12.2–14.7 GPa, which was ≈3 times higher than the base matrix. Because of the high hardness, the σ-phase was brittle, and they observed the preferential presence of micro-cracks at the σ/σ interfaces. It is known that the precipitation of σ-phase affects the material strength [17], elongation [18], toughness [19], creep property [20,21], creep-fatigue property [22], corrosion resistance [23,24], and weldability [25].

Because the size of σ-phase is too small, it is difficult to obtain the true mechanical properties of σ-phase directly. So, except for several articles on the hardness of σ-phase [17,26,27,28], there are no reports on other mechanical properties of σ-phase (such as Young’s modulus, yield strength, and so on). However, these mechanical properties of σ-phase itself are valuable for further understanding the mechanical properties’ degradation due to σ-phase precipitation. Therefore, it is necessary to study the mechanical properties of σ-phase.

In addition, most of these reported studies on σ-phase are determined through short-term annealing in the laboratory. A comprehensive study of the properties of σ-phase requires not only research in the laboratory, but also research under actual industrial conditions. In this paper, the hardness, Young’s modulus, yield strength, and hardening index of the σ-phase in a 304H austenitic stainless steel wing valve of rotary separator in catalytic regenerator after servicing for 8 years at 680–720 °C were investigated. The effect of the presence of σ-phase on the mechanical properties of this 304H austenitic stainless steel was also studied.

2. Experimental Details

2.1. Material and Metallographic Structure

The material used in this study is Ø 220 mm × 11 mm ASME A213 304H austenitic stainless steel tube (C 0.04, Cr 19.09, Ni 8.29, Si 0.31, Mn 1.36, P 0.03, S 0.007, and balance Fe (wt. %)), which is cut from an 8-year-old wing valve of the rotary separator in the catalytic regenerator. The cyclone separator is an important process equipment used to separate catalyst and flue gas in the catalytic cracking unit. The wing valve is located at the end part of the feed leg in the separator. When the catalyst particles accumulate to a certain weight in the feed leg, the wing valve will be opened by the dead weight of catalyst, and the catalyst will fall to the bottom of separator and be recycled. The servicing temperature of the wing valve is 680–720 °C and pressure is 0.289 MPa.

The metallographic specimens were mounted and wet abraded using progressive grits of sandpaper from 100 up to 2000 grit, and then polished with 3.5 μm synthetic diamond grinding paste. The σ-phase was revealed by electrolytic etching method (ASTM A923 standard solution of 40% NaOH, 2 V, 10 s, 25 °C). The metallographic structure was observed by optical microscopy (OM, ZEISS AXIO Imager A1m, Göttingen, Germany). The Image pro plus software (version 6.0) was used to analyse the proportion of the σ-phase. The elements’ detection was performed by scanning electron microscope (SEM, FEI quanta 250, Hillsboro, OR, USA) equipped with EDS (energy dispersive X-ray spectroscopy, Hillsboro, OR, USA).

2.2. Microhardness Test

The microhardness test specimen was mounted and wet abraded using progressive grits of sandpaper from 100 to 1000 grit, and then polished successively with 3.5 μm synthetic diamond grinding paste. Vickers hardness (HV) was measured by HVS-1000Z digital micro hardness tester with a load of 200 g (Huayin, Laizhou, China). The average value of the five measurements is taken as the final result.

2.3. Mechanical Properties Tests

According to ASTM A370 [29], standard flat ‘dog bone’ uniaxial tension test specimens (gauge length: 50 mm, width: 12.5 mm, thickness: 9 mm) and full size Charpy impact test specimens were sampled along the axial direction of the tube. Three impact and tensile specimens were processed for repeated experiments and averaged values were used for analysis. Uniaxial tension tests were performed using an electromechanical machine (INSTRON5869, Darmstadt, Germany) under total strain rate control mode with a constant strain rate of 0.002/s. The impact test was carried out on an automatic metal pendulum impact test machine (PIT-452D, Melbourne, Australia). The test machine can provide a maximum impact energy of 450 J. The test parameters are as follows: pendulum pre-lift angle: 150° and impact velocity: 5.24 m/s. After the uniaxial tension test and impact test, the fracture surfaces were observed by SEM.

2.4. Nano-Indentation Tests

The nano-indentation specimens were mounted and wet abraded using progressive grits of sandpaper from 100 to 2000 grit, and then polished successively with 3.5 μm and 0.5 μm synthetic diamond grinding paste. Nano-indentation tests were performed on Hysitron Triboindenter TI-Premier with a Berkovich indenter (Hysitron Inc., Minneapolis, MN, USA). The nanoindentation instrument is shown in Figure 1. Maximum indentation loads of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12 mN were employed. Ten nano-indentation tests were performed under each loading condition and averaged values were used for analysis. The measurement mode of loading–holding–unloading (with time as 5/2/5 s) was adopted [30]. Surface morphologies under the maximum indentation load (12 mN) were scanned by in situ scanning probe microscopy (SPM).

3. Results

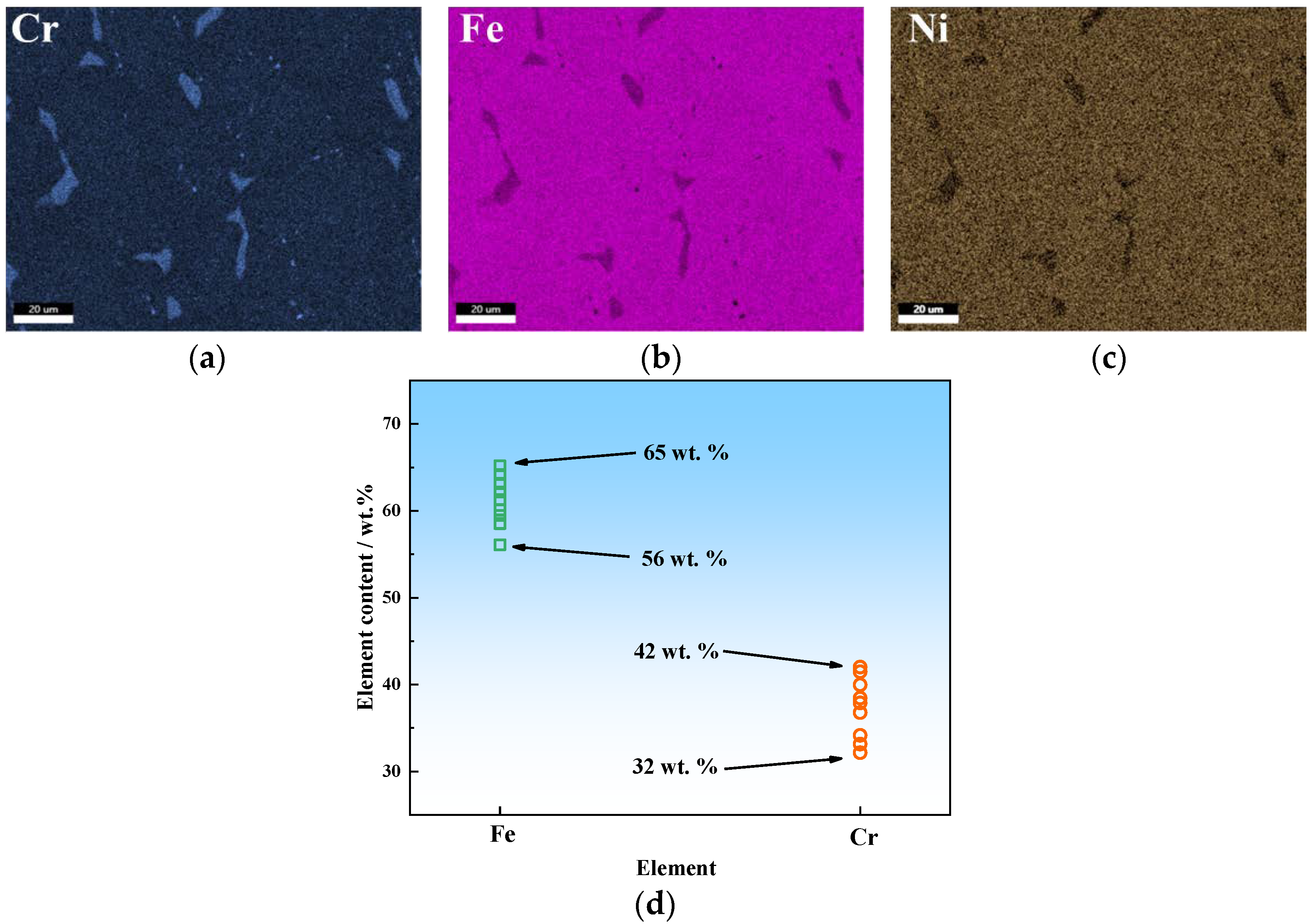
3.1. Metallographic Structure

Figure 2 shows the microstructure of serviced 304H austenitic stainless steel. After being electrolyzed in 40% NaOH solution, σ-phase exhibits an orange-brown color, and no obvious retained ferrite (which should be in a light brown color) or other phases (such as MnS in dark gray color) are observed. The Image pro plus software calculates that the σ-phase proportion is ≈3.5%. The composition of nine randomly selected independent orange-brown precipitated phases was analyzed by EDS. As shown in Figure 3, these phases displayed typical Cr-rich and Ni-depleted profiles. The Cr and Fe element content of σ-phase is not constant, but varies from ≈32 to 42 wt. % and ≈56 to 65 wt. %, respectively, which is consistent with the ratio of the Cr elements in the Fe-Cr σ-phase [1].

3.2. Room Temperature Mechanical Properties

The average value of room temperature mechanical properties of serviced 304H are listed in

Table 1. Mechanical properties of 304H.

Material	Yield Strength (σ0.2)/MPa	Tensile Strength (σs)/MPa	Elongation (δ)/%	Young’s Modulus (E) GPa	Impact Energy (Akv)/J	Hardness (HV200)
Average	320 ± 5	710 ± 8	39 ± 2	160 ± 10	25 ± 3	245 ± 12
Data on warranty	280	620	59	-	258	190 (HB180)
ASME A213 standard	≥220	≥520	≥35	-	-	≤200

, meeting the standard requirements, although the elongation is reduced. It shows that, after servicing for about 8 years at a high temperature, the strengths and elongation of the material meet the standard requirements. By comparing with the warranty data, the strength and hardness increased, while the elongation reduced from 59% for the new material to 39% after service. However, the impact energy declined greatly from 258 J to only 25 J.

The most part of the fracture surface of the tensile test specimen shows a typical ductile fracture character with dimples. Brittle cracks in σ-phase are also observed, as shown by red arrows in Figure 4. Fortunately, these brittle cracks are all located in the σ-phase and do not extend into the austenite through the σ/γ phase boundary. This is an important reason for why the material still retains the elongation of 39%. Separation along the interface between the σ/γ phases is also observed on the fracture surface (shown by the small blue arrows in Figure 4). This indicates that the cross-sectional bonding of the two phases is weak and separation will occur during deformation. Cracking characters on the side of tensile specimen are shown in Figure 4b.

It also shows that the cracks only occurred in the σ-phase and the interface of σ/γ. Cracks did not extend into the austenite phase.

Figure 5 shows the fracture surface character of the impact test specimen. On the fracture surface, a large number of banded fracture zones are distributed along the impact crack propagation direction (Figure 5a). After magnification, it can be seen that brittle fracture particles are distributed in strips on these fracture surfaces (Figure 5b). The results of energy spectrum analysis show that these small particles are σ-phase. Although the austenite zone still shows the dimple characteristic of ductile fracture, the dimple is very shallow, which is consistent with the low impact energy.

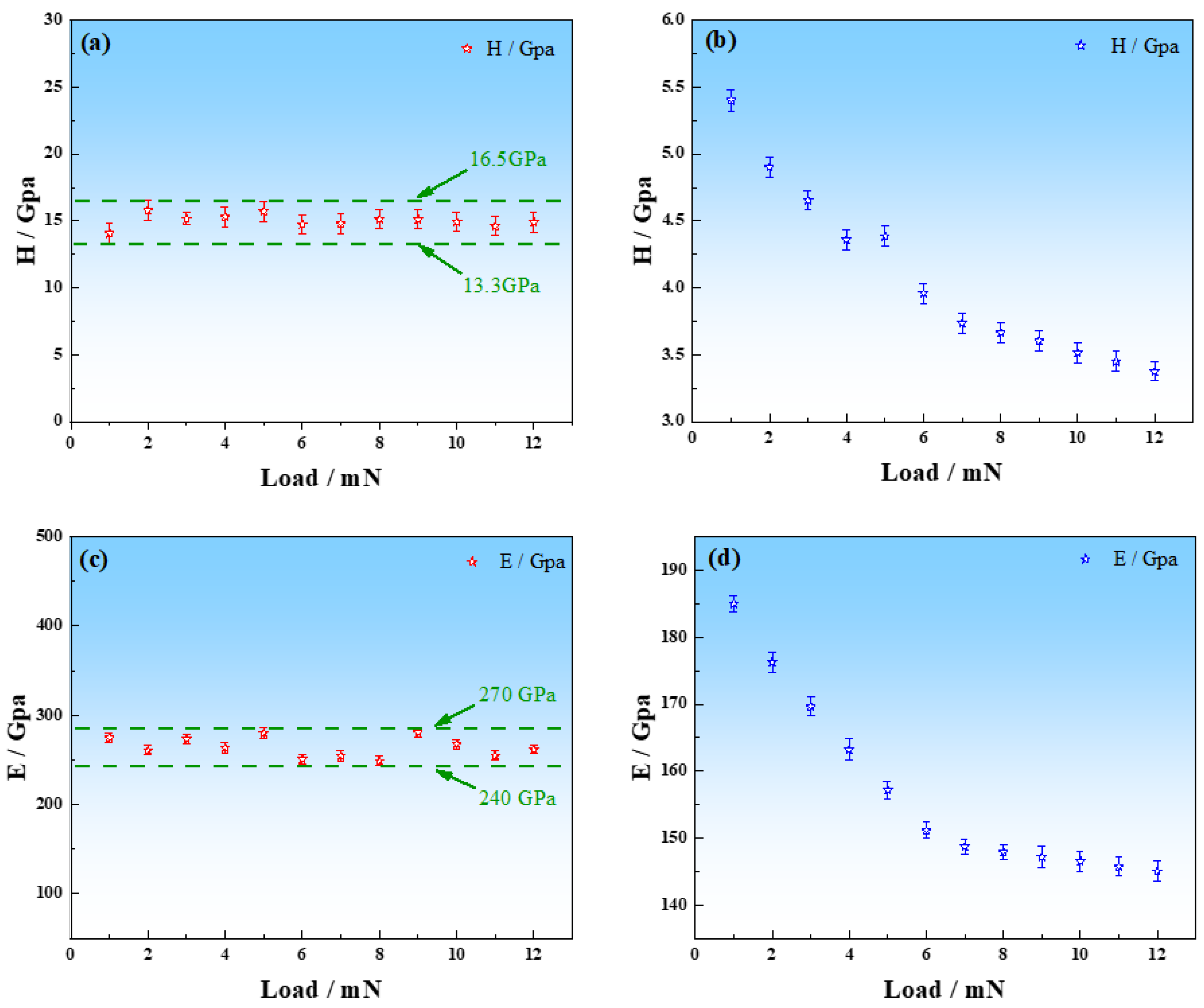
3.3. Nano-Indentation Test Results

Figure 6 shows the load–displacement curves for the σ-phase and austenitic matrix. Owing to the dependence of indentation displacement on the square root of the applied load for the Berkovich indenter, the loading part under different peak loads overlapped each other at the same depth. Figure 7 shows the typical impression in situ scanning probe microscopy (SPM) images in different micro-domains. It is clear that the indentation size of austenite is much larger than σ-phase.

The Young’s modulus E and the hardness H can be calculated from the load–displacement curves (Figure 6) using the Oliver and Pharr model [31,32] as Equations (1)–(6).

$$H=\frac{P_{max}}{A_c}$$

(1)

$$A_c=D_0{h}_c^2+D_1{h}_c+D_2{h}_c^{1/2}+D_3{h}_c^{1/4}+\cdots \dots +D_8{h}_c^{1/128}$$

(2)

$$h_c=h_{max}-\epsilon \frac{P_{max}}{S}$$

(3)

$$S=\frac{dP}{dh}{|}_{h=h_{max}}$$

(4)

$$E_r=\frac{S}{2\beta }\frac{\sqrt{\pi }}{\sqrt{A_c}}$$

(5)

$$\frac{1}{E_r}=\frac{1-v^2}{E}+\frac{1-v_{in}^2}{E_{in}}$$

(6)

where P_max is the maximum indentation load, P is the load, h is displacement, A_c is the projected contact area, D_i coefficients are the Oliver and Pharr model parameters (with D₀ = 24.56), h_c is the contact depth, and ε is a constant related to the shape of the indenter. For Berkovich indenter, ε = 0.75. S is material stiffness, which can be determined from the slope of the unloading part of the load–displacement curve. E_r is the reduced modulus, β (=1.034) is the Berkovich tip, ν (=0.3) is the Poisson’s ratio of the test material, E_in (=1140 GPa) is the modulus of the indenter, and ν_in (=0.07) is the Poisson’s ratio of the indenter. Details can be found in the relevant literature [33].

According to Equations (1)–(6), the Young’s modulus E and hardness H can be obtained for each nano-indentation load, as shown in Figure 8. It is clear that there is a great difference between E and H of σ-phase and the austenitic matrix. For σ-phase, E and H are both relatively constant and are not affected by the increase in applied load. Thus, the average values of nano-hardness H and Young’s modulus E of σ-phase are calculated as 14.95 GPa and 262.67 GPa, respectively. However, it is different in the austenitic phase (matrix), where the E and H decrease with the increase in load. This might be caused by either the factor of sinking-in behavior or the indentation size effect [34,35]. In order to verify whether the sinking-in behavior occurs, the three-dimensional shape of the indentations at matrix austenitic phase are measured, as shown in Figure 9. It is clear that there is no obvious sinking-in behavior, which indicates that the decrease in H and E with increasing applied load was due to the indentation size effect. Nix-Gao et al. [36,37,38] found that the indentation size effect can be corrected, and the relationship between true nano-hardness H₀ and nano-hardness H, as well as between true Young’s modulus E₀ and Young’s modulus E, can be written as Equations (7) and (8):

$${\left(\frac{H}{H_0}\right)}^2=1+\frac{h_H^{\ast }}{h}\Rightarrow H^2=H_0^2+\left(H_0^2\times h_H^{\ast }\right)\times \frac{1}{h}$$

(7)

$${\left(\frac{E}{E_0}\right)}^4=1+\frac{h_E^{\ast }}{h}\Rightarrow E^4=E_0^4+\left(E_0^4\times h_E^{\ast }\right)\times \frac{1}{h}$$

(8)

where h_H^* and h_E^* are both characteristic lengths, which are constants depending on the property of tested material and the shape of the indenter.

The linear regression of nano-hardness and Young’s modulus of the austenitic phase are shown in Figure 10. The true nano-hardness H₀ = 2.51 GPa and true Young’s modulus E₀ = 135 GPa.

Using dimensional and inverse analysis methods, Ma et al. [39] give the relationship between nano-indentation test results, the yield strength (σ_y), Young’s modulus (E), hardening exponent (n), and the true yield strength σ_y0 as follows:

$$\frac{P_{max}}{E{h}^2}=\left(2.77-2.11n\right){\left(\frac{{\sigma }_y}{E}\right)}^{\left[-0.064\mathit{ln}\left(\frac{{\sigma }_y}{E}\right)-0.42n\right]}$$

(9)

$$\frac{h_c}{h}=0.70+0.55\mathit{exp}(-2.16n)\cdot \mathit{exp}\left[-40.32\left(\frac{{\sigma }_y}{E}\right)\right]$$

(10)

where $h_c=h-\kappa \left(P_{max}/S\right)$, $\kappa =0.75$, and S is material stiffness.

By Equations (9) and (10), the yield strength σ_y and hardening index n of austenite and σ-phase under different loads can be obtained as shown in

Table 2. Yield strength and hardening index of σ-phase and austenite under different loads.

σ-Phase	Pmax/μN	7000	8000	9000	10,000	11,000	12,000
	σy/MPa	2.96	2.63	2.1	2.26	2.67	1.88
	n	0.57	0.67	0.75	0.74	0.64	0.87
Austenite	Pmax/μN	7000	8000	9000	10,000	11,000	12,000
	σy/GPa	575.31	559.26	543.57	519.59	500.47	495.02
	n	0.36	0.37	0.36	0.36	0.37	0.37

.

It is obvious that, for σ-phase, the yield strength and hardening index are not affected by the increase in load. Therefore, the average value is used as the true yield strength and hardening index, which are σ_y0 = 2.42 GPa and n = 0.78, respectively. It is worth noting that the σ_y and n value of σ-phase fluctuate greatly, which will be analyzed later.

However, for the austenitic phase (matrix), although the hardening index is basically constant, the yield strength decreases with the increase in load, which shows an obvious indentation size effect. According to the study of Ma et al. [37], the indentation size effect can be eliminated using Equation (11), and the relationship between yield strength σ_y and true yield strength σ_y0 can be written as follows:

$${\sigma }_y={\sigma }_{y0}\bullet {(1+\frac{h_H^{\ast }}{h})}^{f\left(n\right)}\bullet {(1+\frac{h_E^{\ast }}{h})}^{\left[0.25-0.54\frac{1}{2\left(1-n\right)}\right]}$$

(11)

Figure 11 shows the fitted curves of yield strength σ_y and true yield strength σ_y0. The true yield strength σ_y0 and hardening index n of austenite are 0.294 GPa and 0.365, respectively.

4. Discussion

4.1. Credibility of Mechanical Properties Obtained by Nano-Indentation Test

Nano-indentation is an excellent method for measuring the mechanical properties of small areas or small precipitates [40,41,42]. However, the credibility of the nano-indentation result and its consistency with macro performance have always been of concern. In order to ensure the consistency of the measurement results obtained by nano-indentation and macro test methods, some researchers [43] used both the nano-indentation and finite element method, and others [44,45] used the method of inverse analysis, combined with data fitting. Studies [46] showed that the indentation size effect could seriously affect the results of nano-indentation measurement. In our previous studies [47,48], we found that, if we first correct the indentation size effect using nano-indentation test data under different loads, then the true hardness, elastic modulus, and yield strength of austenitic stainless steel and titanium alloy can be obtained by the inverse analysis method. The results are in good agreement with the macro mechanical property test results. In this study, the mechanical properties of the σ-phase and austenitic phase were obtained by the same method. As the mechanical properties of σ-phase have not been reported, it is difficult to directly verify whether the mechanical properties of σ-phase measured by nano-indentation are reliable. Therefore, we first verify the credibility of the test method by comparing the consistency between the austenitic phase nano-indentation measurement results and the 304H macro mechanical property measurement results. If the results obtained by these two methods agree well, then the credibility of the method is proven, and the credibility of mechanical properties of σ-phase obtained by this method could be proven indirectly. By comparing the hardness Young’s modulus and yield strength obtained by nano-indentation test (H₀ = 2.51 GPa, which is equivalent to about HV = 251 [49,50], E₀ = 135 GPa, and σ_y0 = 0.294 GPa) and macro mechanical test (HV = 245, E = 165 GPa, and σ_y = 0.32 GPa), it can be concluded that the two hardness values are in good agreement. However, the yield strength and Young’s modulus measured by uniaxial tensile test are ≈10% and 20% higher, respectively, than those measured by the nano-indentation test. This is because the nano-indentation test measures the strength of the austenitic matrix, while the uniaxial tensile test measures the overall strength of the 304H matrix strengthened by the sigma phase. Therefore, it can be determined that, if the influence of σ-phase reinforcement is ignored, the error between the yield strength of the γ-phase matrix measured by the nano-indentation test and uniaxial tensile test will not exceed 10% and 20%, respectively. This indirectly proves that the mechanical properties of σ-phase obtained by the nano-indentation test are reliable.

4.2. Mechanical Properties’ Fluctuation of σ-Phase in the Nano-Indentation Test

Figure 7a shows irregular fluctuations in the measurement results of nano hardness (≈13.3 GPa to 16.5 GPa). Accordingly, the yield strength of σ-phase also showed irregular fluctuations from the minimum value as 1.88 GPa to the maximum as 2.96 GPa (Table 2). In general, uniform and stable phases have consistent mechanical properties, but in our studies, the fluctuation amplitude of hardness and yield strength of σ-phase reaches ≈24% and 50%, respectively. This is due to the non-uniformity of σ-phase itself. Zieliński et al. [51] conducted a linear measurement of element contents across the whole σ-phase and found that the element distributions of Fe and Cr were not uniform. The Cr element content was higher at the edge of σ-phase than in the center, while the distribution of Fe element was just the opposite. In the study of Kumar [26], the concentrations of Cr and Mo for all different aging temperatures were analyzed across σ/γ phase interfaces in different positions and it was found that, in the different σ-phase, the content of Cr or Mo elements fluctuated obviously. They also found that the hardness of the σ-phase varies in the range of 13–16 GPa. This is very similar to our research results in this paper (Figure 2 and Figure 7a).

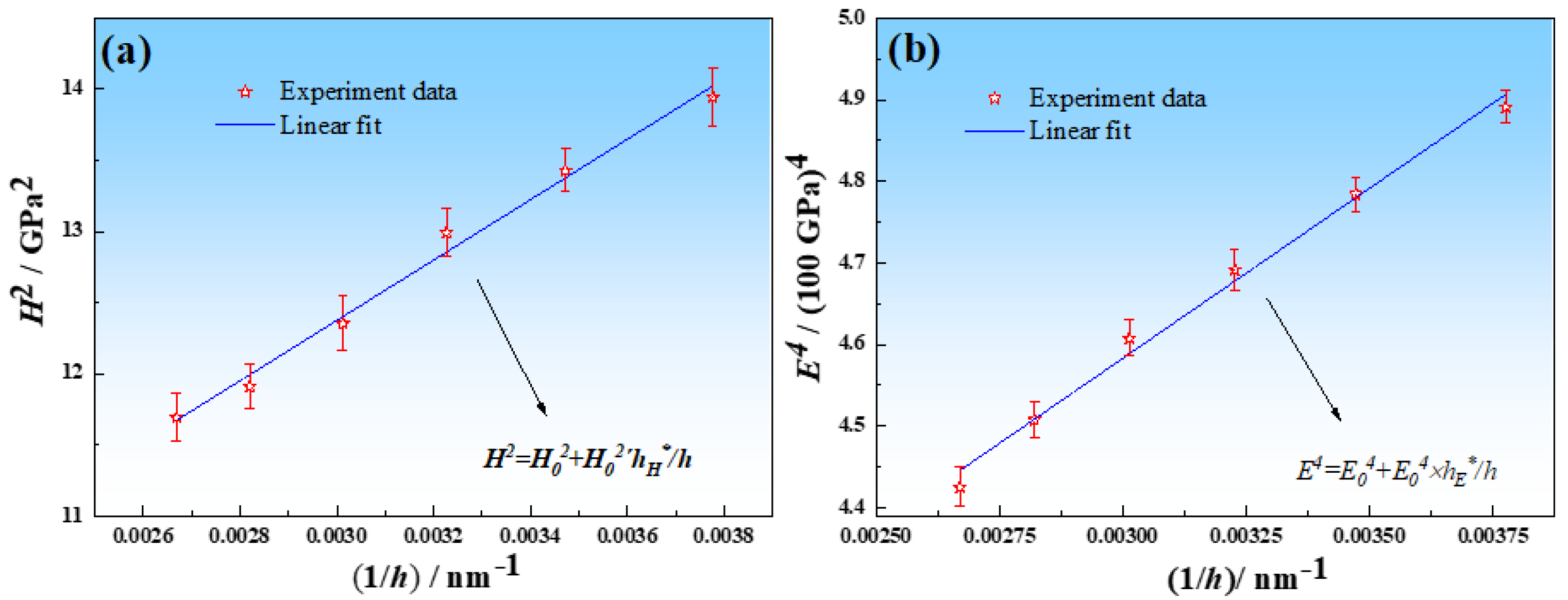
4.3. Analysis of Size Effect in Nano-Indentation

The physical description that hardness is observed to increase with the decreasing indentation size was given earlier by Stelmashenko et al. [52,53]. In 1994, Fleck et al. [54] pointed out that the indentation size effect for metals can be understood by noting that large strain gradients inherent in small indentations lead to geometrically necessary dislocations that cause enhanced hardening. In 1997, Nix and Gao [46] showed an accurate model using the concept of geometrically necessary dislocations:

$$\frac{H}{H_0}=\sqrt{1+\frac{h^{\ast }}{h}}$$

(12)

where H is the hardness for a given depth of indentation, h; H₀ is the hardness in the limit of infinite depth; and h* is a characteristic length that depends on the shape of the indenter, the shear modulus, and H₀.

$$h^{\ast }=\frac{81}{2}b{x}^{2}ta{n}^2\theta {(\frac{\mu }{H_0})}^2$$

(13)

h* is not a constant for a given material and indenter geometry. Rather, it depends on the statistically stored dislocation density through H₀. Nix and Gao also announced that this model suggests that the hardness of a material should not depend strongly on the depth of indentation if the material is intrinsically hard. Specifically, large values of H₀ would cause h* to be very small (Equation (13)), and this would cause the hardness to depend less on depth at a given depth of indentation (Equation (12)). They gave the hardness–plastic depth curve of intrinsically hard fused quartz (average hardness is 8.9 GPa), and showed that the hardness is essentially independent of the depth of indentation. In our study, the average hardness H₀ of σ-phase is 14.95 GPa, which causes the h* to be smaller. This is why no obvious size effect is observed in the nano-indentation test of σ-phase.

4.4. Effect of σ-Phase Precipitation on Mechanical Properties

Most austenitic steels have a tendency to undergo precipitation hardening. σ-phase is a hard and brittle topologically close packed (TCP) phase, and the precipitation of σ-phase particles during aging will increase the hardness of the steel [55]. This is why the hardness of 304H steel in our study increased from HV 190 to about HV 245. Hardness and strength tend to have the same trend. The tensile results show that the tensile strength of 304H austenitic stainless steel increases from 620 MPa to 710 MPa owing to the existence of σ-phase. This is because σ-phase particles, as non-shearable precipitates, can effectively prevent dislocation movement [56]. The strength and hardness show that σ-phase can be used as a strengthening phase of the material.

Similar to the results of other researchers [51,57,58], we also found that the elongation and impact toughness of the material decreased significantly owing to the precipitation of σ-phase. This is because the presence of σ-phase in the structure could serve as an obstacle to the mobility of dislocation and offer a path for brittle crack propagation, resulting in lower alloy ductility [59,60]. In austenitic stainless steel, it is widely agreed that the interfaces between the matrix and other phases, e.g., δ-ferrite, σ-phase, precipitates, and so on, are recognized as the preferential sites for crack initiation because of strain incompatibility induced by excessive dislocation pile-ups occurring at the interfaces [61,62].

About half a century ago, it was accepted that the impact toughness in steel is strongly dependent on the cracking of precipitates, inclusion, and the second phases [63]. In the particle cracking progress, the initiation sites of cracks are highly related to the distribution, size, volume fraction, and morphology of these particles [64]. In addition, according to the fracture model of the precipitated phase by Smith et al. [65], the larger the size of the precipitated phase, the lower the critical fracture stress of a precipitated phase/matrix interface. The dramatically decreased impact toughness of 304H stainless steel after long-term service should be attributed to the precipitation and coarsening of σ-phase. The dislocation pile-up at a σ/σ and σ/matrix interface thus initiate the microcrack. In Figure 4 and Figure 5, large amounts of micro-cracks are observed between the σ/σ and σ/matrix interface, which shows that these interfaces are the main source of the micro-cracks’ initiation. The easy generation of microcracks leads to a sharp decrease in the toughness of 304H studied in this paper. In addition, Pohl [66] found that the cracking strain of σ-phase is only 2.6%, which can accelerate the occurrence of fracture. They also found that the amount of σ-phases also affects the impact toughness. The impact energy of duplex stainless steels falls from 322 J to 100 J and ≈20 J when precipitated σ-phase content reached 0.5 vol.% and 5 vol.%, respectively. After analysis using Image pro plus software, the σ-phase content in this study is about 3.5%, which is why the impact energy in this study declined from 258 J to 25 J.

5. Conclusions

In this study, the mechanical properties of σ-phase and its effect on the mechanical properties of austenitic stainless steel were studied, and the following major conclusions could be made:

• σ-phase in 304H is a kind of Fe-Cr intermetallic. In different σ-phases, the Cr and Fe element content is not constant, but varies from ≈32 to 42 wt. % and ≈56 to 65 wt. %, respectively.
• Because of the high hardness of σ-phases (13.3 to 16.5 GPa), no obvious size effect is observed in the nano-indentation test of σ-phase. The average true hardness H₀, elastic modulus E₀, strain hardening exponent n, and yield strength σ_y of σ-phases are 14.95 GPa, 263 GPa, 0.78, and 2.42 GPa, respectively.
• Because of precipitation hardening effects, σ-phase leads to the improvement in Vickers hardness, yield strength, and tensile strength of 304H. However, the elongation and impact toughness of 304H are reduced greatly owing to the brittleness of σ-phase.
• According to this study, the nano-indentation test is a feasible method to study the mechanical properties of small-scale precipitates, such as σ-phase.