Marangoni Convection of Dust Particles in the Boundary Layer of Maxwell Nanofluids with Varying Surface Tension and Viscosity
Abstract
:1. Introduction
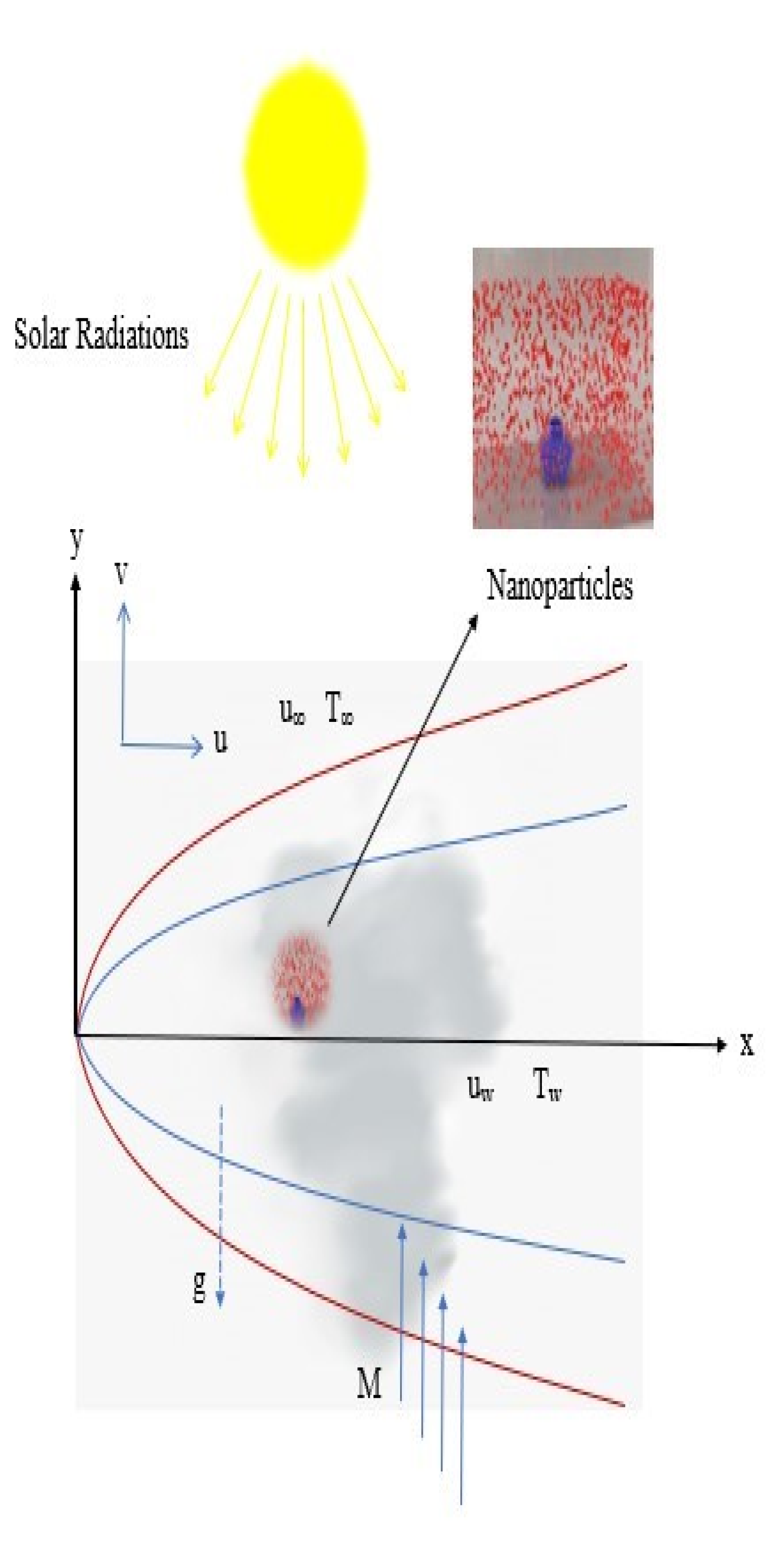
2. Mathematical Modeling
3. Numerical Techniques
4. Results and Discussions
5. Conclusions
- The results undeniably demonstrate the microconvection effects achieved by the Brownian motion of nanoparticles in these suspensions, and show that high concentrations of nanoparticles help to convincingly increase the thermal conductivity of the base fluid.
- , the mass concentration of dust particles, significantly improves the thermal conductivity of the nanofluid.
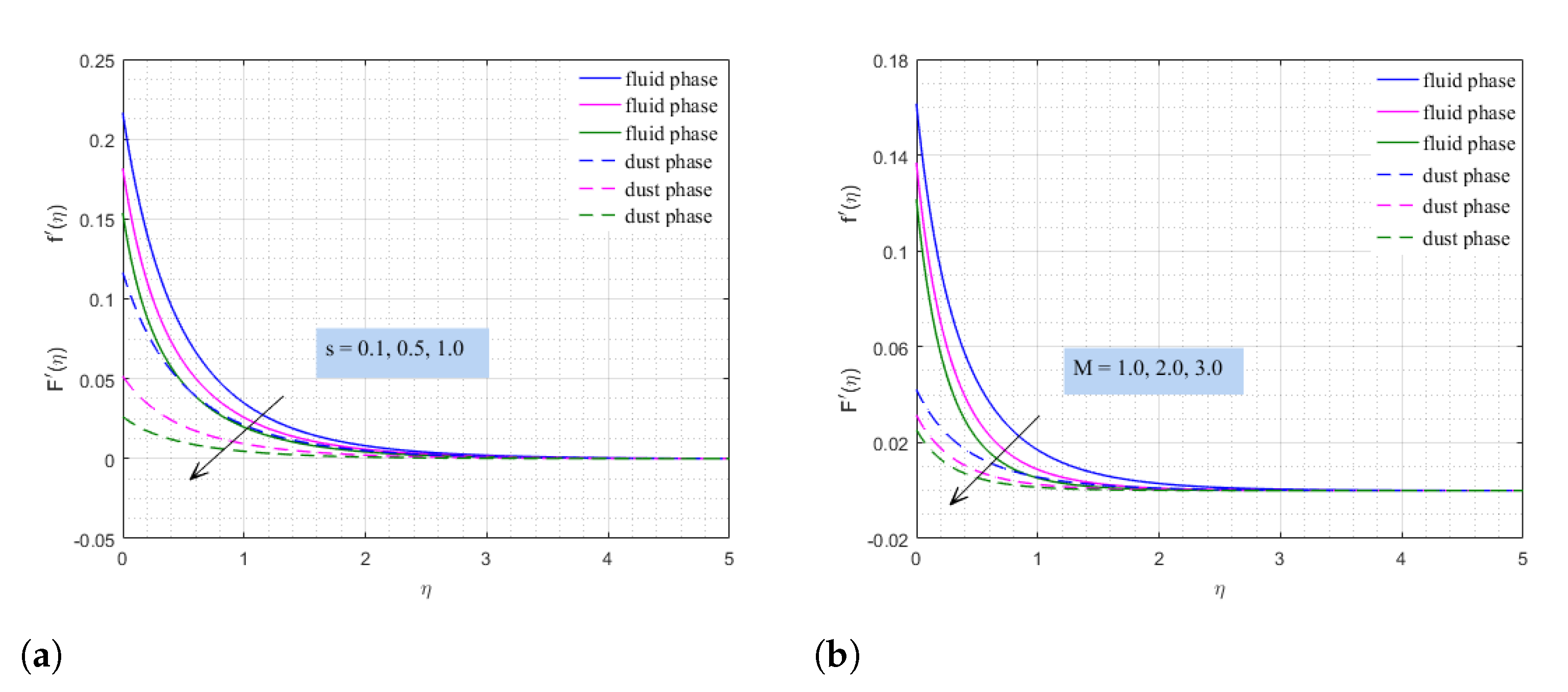
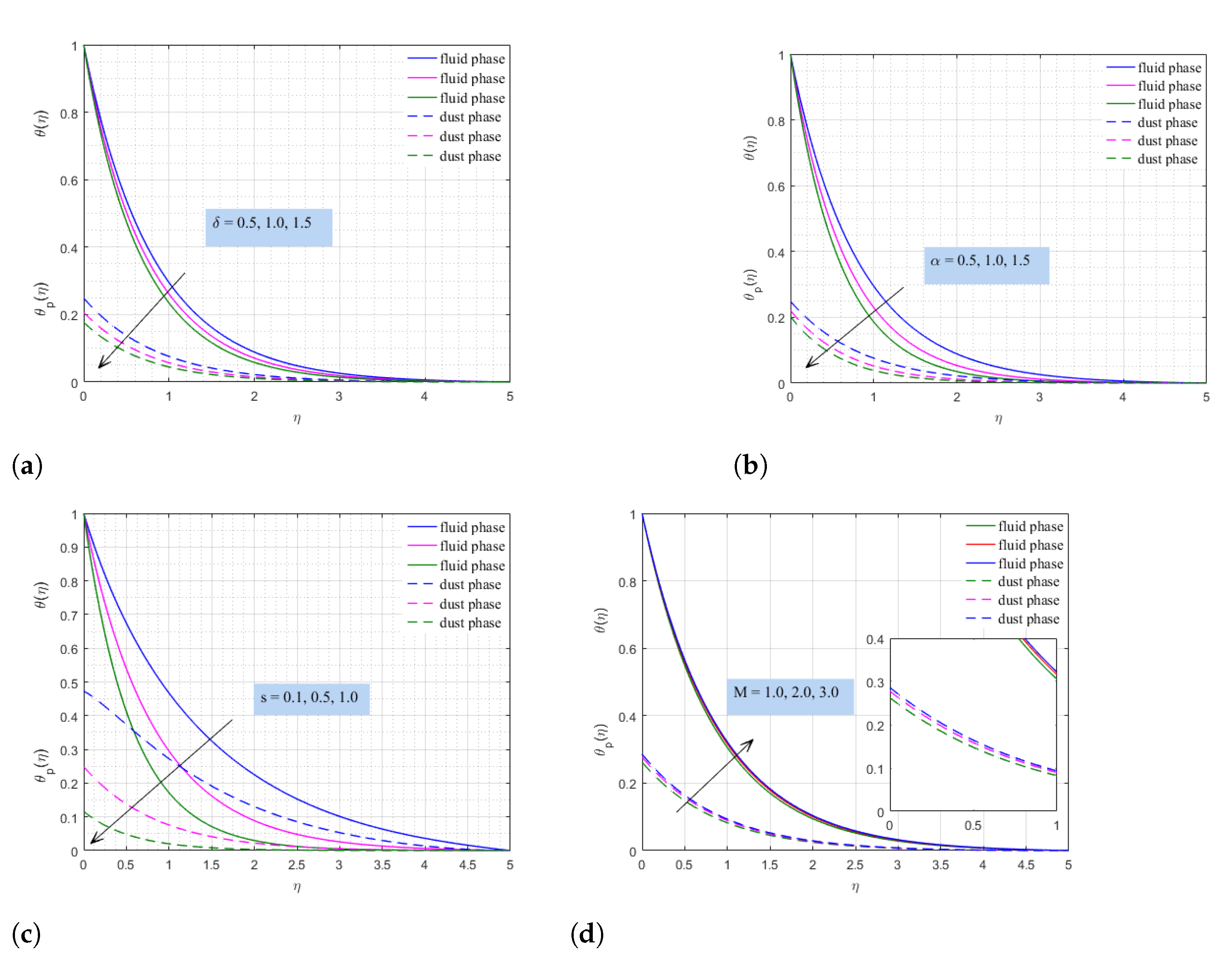
- The cooling rate in an industrial refrigeration system can be adjusted by increasing/decreasing surface suction.
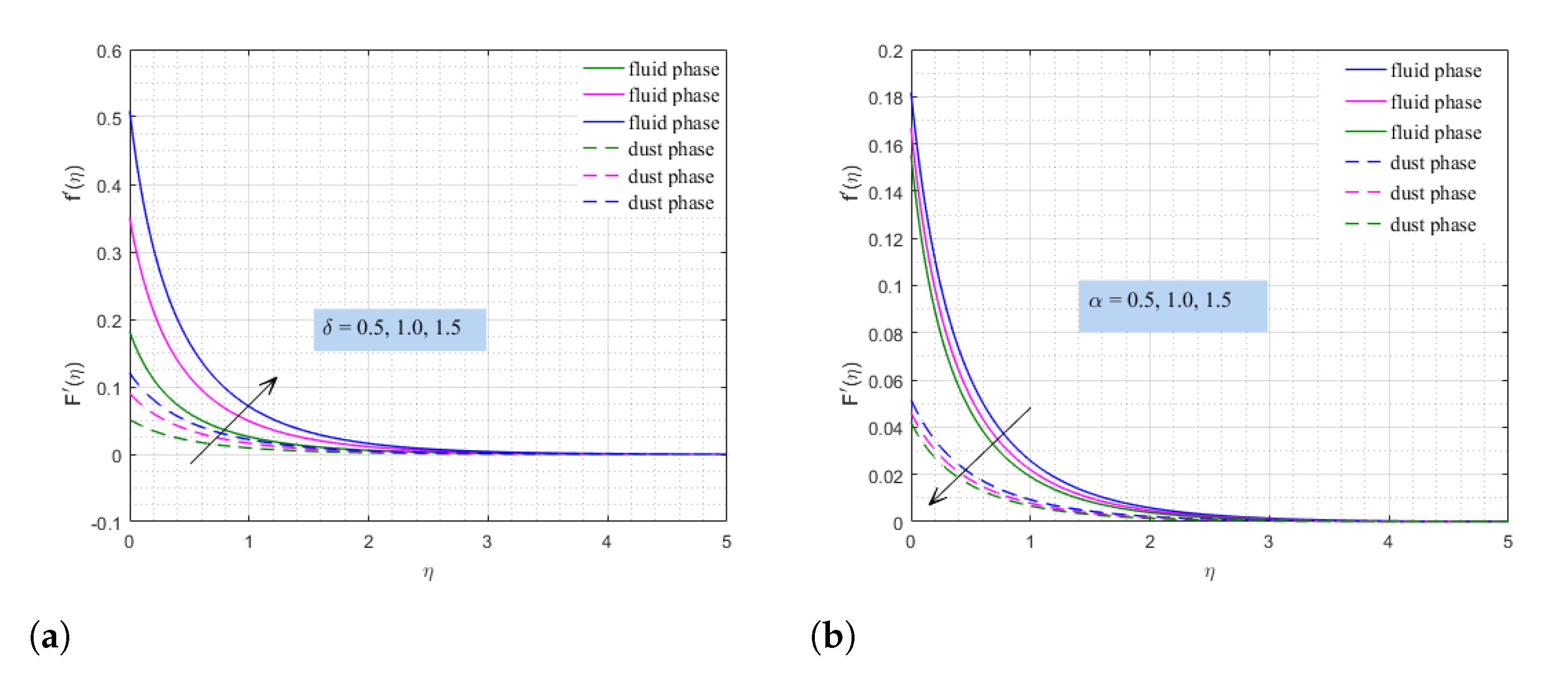
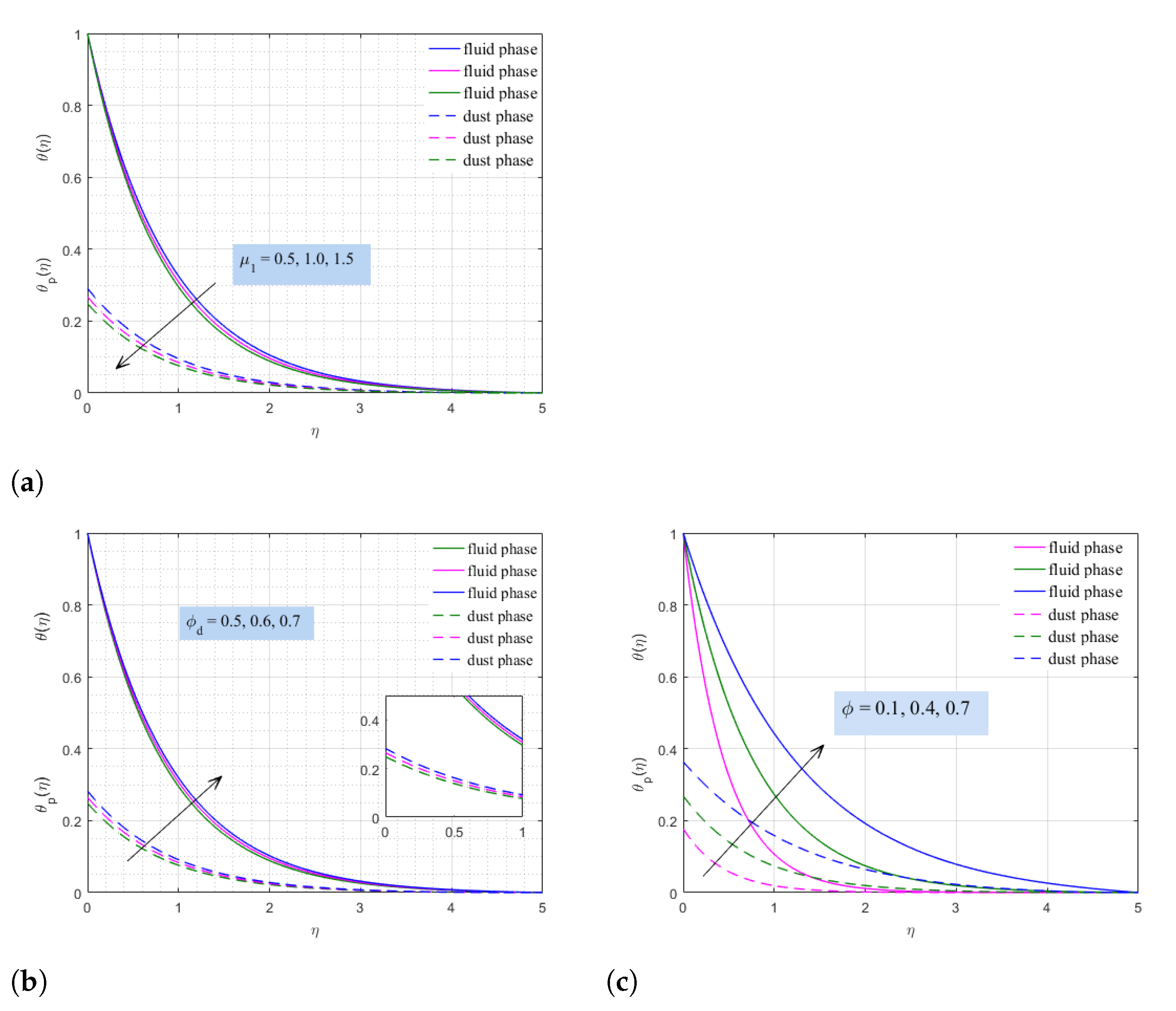
- The parameter generated by the temperature-dependent viscosity has a strong influence on the temperature profile, which indicates that this parameter tends to reduce the thermal conductivity of the base fluid.
- The variable surface tension parameter will destroy the thermal conductivity of the dusty nanofluid, and the thermal conductivity can be improved by enhancing the implanted magnetic field.
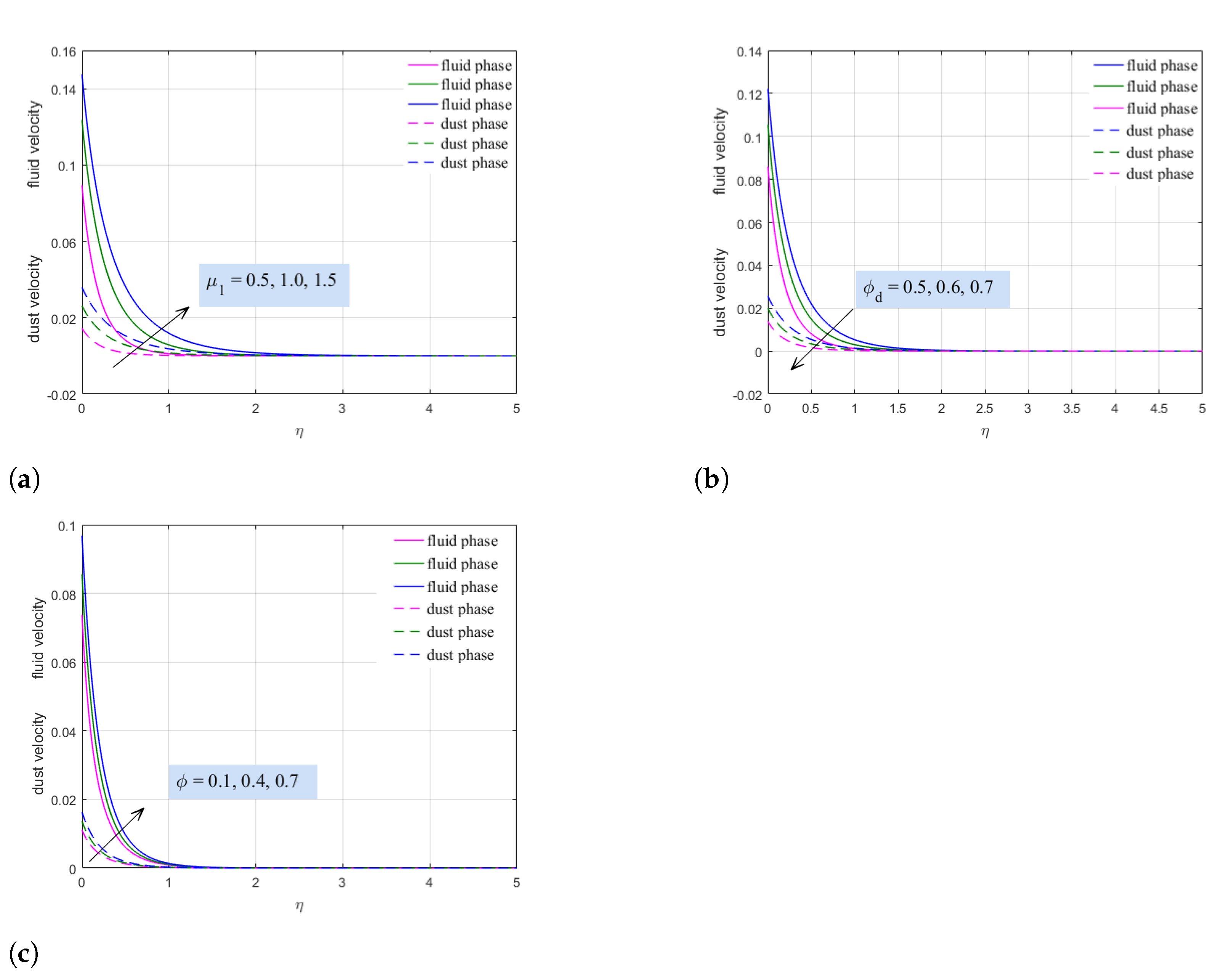
- An increase in the density of nanoparticles is inductive with an increase in the temperature distribution, but opposite to the velocity distribution. The same applies to the density of the dust particles.
- The increased interaction of the liquid with nanoparticles or dust particles is intended to improve the Nusselt number.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Description and Unit |
| x, y | Cartesian coordinates [m] |
| u | horizontal component of nanofluid velocity [m/s] |
| x component of dust particles velocity (m/s) | |
| y component of dust particles velocity (m/s) | |
| T | temperature of the nanofluid (K) |
| temperature of the dust particles (K) | |
| volume fraction of dust particles | |
| volume fraction of nanoparticles | |
| dynamic viscosity of nanofluid () | |
| density of nanofluid () | |
| K | Stokes resistance |
| N | number density of nanoparticles |
| m | mass of nanoparticles (kg) |
| specific heat capacity of the nanofluid () | |
| electrical conductivity () | |
| induced magnetic flux () | |
| thermal equilibrium time of the dust particles | |
| Relaxation time of the dust particles | |
| specific heat of the nanofluid (J/K) | |
| specific heat of the dust particles (J/K) | |
| porosity parameter |
References
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. Simulations for Maxwell fluid flow past a convectively heated exponentially stretching sheet with nanoparticles. AIP Adv. 2015, 5, 037133. [Google Scholar] [CrossRef] [Green Version]
- Jamshed, W.; Eid, M.R.; Nasir, N.A.A.M.; Nisar, K.S.; Aziz, A.; Shahzad, F.; Shukla, A. Thermal examination of renewable solar energy in parabolic trough solar collector utilizing Maxwell nanofluid: A noble case study. Case Stud. Therm. Eng. 2021, 101258. [Google Scholar] [CrossRef]
- Fetecau, C.; Vieru, D.; Abbas, T.; Ellahi, R. Analytical solutions of upper convected Maxwell fluid with exponential dependence of viscosity under the influence of pressure. Mathematics 2021, 9, 334. [Google Scholar] [CrossRef]
- Nadeem, S.; Khan, M.R.; Khan, A.U. MHD stagnation point flow of viscous nanofluid over a curved surface. Phys. Scr. 2019, 94, 115207. [Google Scholar] [CrossRef]
- Arif, M.; Kumam, P.; Khan, D.; Watthayu, W. Thermal performance of GO-MoS2/engine oil as Maxwell hybrid nanofluid flow with heat transfer in oscillating vertical cylinder. Case Stud. Therm. Eng. 2021, 101290. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F. Nonlinear dissipative slip flow of Jeffrey nanomaterial towards a curved surface with entropy generation and activation energy. Math. Comput. Simul. 2021, 185, 47–61. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F.; Hobiny, A.; Ali, Z. Modeling of Cattaneo-Christov double diffusions (CCDD) in Williamson nanomaterial slip flow subject to porous medium. J. Mater. Res. Technol. 2020, 9, 6172–6177. [Google Scholar] [CrossRef]
- Siddiqa, S.; Begum, N.; Hossain, M.A. Compressible dusty gas along a vertical wavy surface. Appl. Math. Comput. 2017, 293, 600–610. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O.K. Thermal conductivity of heterogeneous two-component systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Dey, D.; Chutia, B. Dusty nanofluid flow with bioconvection past a vertical stretching surface. J. King Saud Univ.-Eng. Sci. 2020. [Google Scholar] [CrossRef]
- Zhang, X.H.; Abidi, A.; Ahmed, A.E.S.; Khan, M.R.; El-Shorbagy, M.A.; Shutaywi, M.; Galal, A.M. MHD stagnation point flow of nanofluid over a curved stretching/shrinking surface subject to the influence of Joule heating and convective condition. Case Stud. Therm. Eng. 2021, 26, 101184. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F.; Hobiny, A.; Ali, Z. Fully developed second order velocity slip Darcy-Forchheimer flow by a variable thicked surface of disk with entropy generation. Int. Commun. Heat Mass Transf. 2020, 117, 104778. [Google Scholar] [CrossRef]
- Krishna, M.V.; Ahamad, N.A.; Chamkha, A.J. Hall and ion slip impacts on unsteady MHD convective rotating flow of heat generating/absorbing second grade fluid. Alex. Eng. J. 2021, 60, 845–858. [Google Scholar] [CrossRef]
- Li, Y.X.; Waqas, H.; Al-Khaled, K.; Khan, S.A.; Khan, M.I.; Khan, S.U.; Chu, Y.M. Simultaneous features of Wu’s slip, nonlinear thermal radiation and activation energy in unsteady bio-convective flow of Maxwell nanofluid configured by a stretching cylinder. Chin. J. Phys. 2021. [Google Scholar] [CrossRef]
- Mohammadein, S.A.; Raslan, K.; Abdel-Wahed, M.S.; Abedel-Aal, E.M. KKL-model of MHD CuO-nanofluid flow over a stagnation point stretching sheet with nonlinear thermal radiation and suction/injection. Results Phys. 2018, 10, 194–199. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD mixed convection stagnation point flow of a hybrid nanofluid past a vertical flat plate with convective boundary condition. Chin. J. Phys. 2020, 66, 630–644. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, U.S.; Li, S.; Thompson, L.J.; Lee, S. Enhanced thermal conductivity through the development of nanofluids. Mrs Online Proc. Libr. (OPL) 1996, 457, 3–11. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.R.; Pan, K.; Khan, A.U.; Ullah, N. Comparative study on heat transfer in CNTs-water nanofluid over a curved surface. Int. Commun. Heat Mass Transf. 2020, 116, 104707. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Dual solutions in mixed convection boundary layer flow of micropolar fluids. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1324–1333. [Google Scholar] [CrossRef]
- Ghosh, N.C.; Ghosh, B.C.; Gorla, R.S.R. Hydromagnetic flow of a dusty viscoelastic Maxwell fluid through a rectangular channel. Int. J. Fluid Mech. Res. 2007, 34. [Google Scholar] [CrossRef]
- Ahmed, S.F.; Hafez, M.G.; Chu, Y.M. Conversion of energy equation for fiber suspensions in dusty fluid turbulent flow. Results Phys. 2020, 19, 103341. [Google Scholar] [CrossRef]
- Damseh, R.A. Thermal boundary layer on an exponentially stretching continous surface in the presence of magnetic field effect. Int. J. Appl. Mech. Eng. 2006, 11, 289–299. [Google Scholar]
- Naramgari, S.; Sulochana, C. MHD flow of dusty nanofluid over a stretching surface with volume fraction of dust particles. Ain Shams Eng. J. 2016, 7, 709–716. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharyya, K.; Pop, I. MHD boundary layer flow due to an exponentially shrinking sheet. Magnetohydrodynamics 2011, 47, 337–344. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hassan, M. Particle shape effects on Marangoni convection boundary layer flow of a nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2160–2174. [Google Scholar] [CrossRef]
- Saidu, I.; Waziri, M.M.; Roko, A.; Musa, H. MHD effects on convective flow of dusty viscous fluid with volume fraction of dust particles. J. Eng. Appl. Sci. 2010, 5, 86–91. [Google Scholar]
- Akbar, N.S.; Nadeem, S.; Haq, R.U.; Khan, Z.H. Numerical solutions of magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet. Indian J. Phys. 2013, 87, 1121–1124. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S.; Pop, I. Marangoni hybrid nanofluid flow over a permeable infinite disk embedded in a porous medium. Int. Commun. Heat Mass Transf. 2021, 126, 105421. [Google Scholar] [CrossRef]
- Hossain, M.A.; Roy, N.C.; Siddiqa, S. Unsteady mixed convection dusty fluid flow past a vertical wedge due to small fluctuation in free stream and surface temperature. Appl. Math. Comput. 2017, 293, 480–492. [Google Scholar] [CrossRef]
- Sandeep, N.; Sugunamma, V.; Mohankrishna, P. Effects of radiation on an unsteady natural convective flow of a EG-Nimonic 80a nanofluid past an infinite vertical plate. Adv. Phys. Theor. Appl. 2013, 23, 36–43. [Google Scholar] [CrossRef]
- Mandal, S.; Shit, G.C. Entropy analysis on unsteady MHD biviscosity nanofluid flow with convective heat transfer in a permeable radiative stretchable rotating disk. Chin. J. Phys. 2021. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Thermal radiation on unsteady electrical MHD flow of nanofluid over stretching sheet with chemical reaction. J. King Saud Univ.-Sci. 2019, 31, 804–812. [Google Scholar] [CrossRef]
- Ghasemi, S.E.; Hatami, M. Solar radiation effects on MHD stagnation point flow and heat transfer of a nanofluid over a stretching sheet. Case Stud. Therm. Eng. 2021, 25, 100898. [Google Scholar] [CrossRef]
- Sandeep, N.; Saleem, S. MHD flow and heat transfer of a dusty nanofluid over a stretching surface in a porous medium. Jordan J. Civ. Eng. 2017, 11, 149–164. [Google Scholar]
- Sheikholeslami, M.; Rokni, H.B. Nanofluid two phase model analysis in existence of induced magnetic field. Int. J. Heat Mass Transf. 2017, 107, 288–299. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transfer 2006, 240–250. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 2009, 52, 5792–5795. [Google Scholar] [CrossRef]
- Batchelor, C.K.; Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ling, J.X.; Dybbs, A. Forced Convection over a Flat Plate Submersed in a Porous Medium: Variable Viscosity Case (No. CONF-871234-); American Society of Mechanical Engineers: New York, NY, USA, 1987. [Google Scholar]
- McTaggart, C.L. Convection driven by concentration-and temperature-dependent surface tension. J. Fluid Mech. 1983, 134, 301–310. [Google Scholar] [CrossRef]
- Mishra, S.R.; Sun, T.C.; Rout, B.C.; Khan, M.I.; Alaoui, M.K.; Khan, S.U. Control of dusty nanofluid due to the interaction on dust particles in a conducting medium: Numerical investigation. Alex. Eng. J. 2021. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J.; PrasannaKumara, B.C.; Shashikumar, N.S. Marangoni convection radiative flow of dusty nanoliquid with exponential space dependent heat source. Nucl. Eng. Technol. 2017, 49, 1660–1668. [Google Scholar] [CrossRef]
- Kannan, A.S.; Mark, A.; Maggiolo, D.; Sardina, G.; Sasic, S.; Ström, H. A hydrodynamic basis for off-axis Brownian diffusion under intermediate confinements in micro-channels. Int. J. Multiph. Flow 2021, 103772. [Google Scholar] [CrossRef]
- Gabbasov, R.; Yurenya, A.; Nikitin, A.; Cherepanov, V.; Polikarpov, M.; Chuev, M.; Panchenko, V. Study of Brownian motion of magnetic nanoparticles in viscous media by Mössbauer spectroscopy. J. Magn. Magn. Mater. 2019, 475, 146–151. [Google Scholar] [CrossRef]
- Heyse, A.; Kraume, M.; Drews, A. The impact of lipases on the rheological behavior of colloidal silica nanoparticle stabilized Pickering emulsions for biocatalytical applications. Colloids Surf. Biointerfaces 2020, 185, 110580. [Google Scholar] [CrossRef]
- Riedl, J.C.; Sarkar, M.; Fiuza, T.; Cousin, F.; Depeyrot, J.; DUBOIS, E.; Peyre, V. Design of long-term stable concentrated colloidal dispersions in ionic liquids up to 473 K. J. Colloid Interface Sci. 2021. [Google Scholar] [CrossRef]
- Salamon, P.; Geng, Y.; Eremin, A.; Stannarius, R.; Klein, S.; Börzsönyi, T. Rheological and flow birefringence studies of rod-shaped pigment nanoparticle dispersions. J. Mol. Liq. 2020, 313, 113401. [Google Scholar] [CrossRef]
- Ma, M.Y.; Zhai, Y.L.; Li, Z.H.; Yao, P.T.; Wang, H. Particle size-dependent rheological behavior and mechanism of Al2O3-Cu/W hybrid nanofluids. J. Mol. Liq. 2021, 335, 116297. [Google Scholar] [CrossRef]
| Pr | Current Results | Mishra [41] | Mahanthesh [42] |
|---|---|---|---|
| 0.72 | 1.088575 | 1.088562 | 1.0884 |
| 1.00 | 1.333348 | 1.333333 | 1.3333 |
| 10.0 | 4.796831 | 4.796819 | 4.7968 |
| s | M | (0) | (0) | |||||
|---|---|---|---|---|---|---|---|---|
| 0.5 | −0.5000 | 1.7312 | ||||||
| 1.0 | −0.5000 | 1.8261 | ||||||
| 1.5 | −0.5000 | 1.8999 | ||||||
| 0.5 | −0.5000 | 1.7312 | ||||||
| 0.6 | −0.5000 | 1.7048 | ||||||
| 0.7 | −0.5000 | 1.6774 | ||||||
| 0.5 | −0.5000 | 1.7312 | ||||||
| 1.0 | −0.5000 | 0.80908 | ||||||
| 1.5 | −0.5000 | 0.35507 | ||||||
| 0.5 | −0.5000 | 1.7312 | ||||||
| 1.0 | −1.0000 | 1.8443 | ||||||
| 1.5 | −1.5000 | 1.9497 | ||||||
| 0.5 | −0.5000 | 1.7312 | ||||||
| 1.0 | −0.5000 | 2.1256 | ||||||
| 1.5 | −0.5000 | 2.4530 | ||||||
| 0.5 | −0.5000 | 0.93695 | ||||||
| 1.0 | −0.5000 | 1.7312 | ||||||
| 1.5 | −0.5000 | 2.5361 | ||||||
| 0.5 | −0.5000 | 1.7312 | ||||||
| 1.0 | −0.5000 | 1.7066 | ||||||
| 1.5 | −0.5000 | 1.6908 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlQdah, K.S.; Khan, N.M.; Bacha, H.B.; Chung, J.-D.; Shah, N.A. Marangoni Convection of Dust Particles in the Boundary Layer of Maxwell Nanofluids with Varying Surface Tension and Viscosity. Coatings 2021, 11, 1072. https://doi.org/10.3390/coatings11091072
AlQdah KS, Khan NM, Bacha HB, Chung J-D, Shah NA. Marangoni Convection of Dust Particles in the Boundary Layer of Maxwell Nanofluids with Varying Surface Tension and Viscosity. Coatings. 2021; 11(9):1072. https://doi.org/10.3390/coatings11091072
Chicago/Turabian StyleAlQdah, Khaled S., Naseer M. Khan, Habib Ben Bacha, Jae-Dong Chung, and Nehad Ali Shah. 2021. "Marangoni Convection of Dust Particles in the Boundary Layer of Maxwell Nanofluids with Varying Surface Tension and Viscosity" Coatings 11, no. 9: 1072. https://doi.org/10.3390/coatings11091072
APA StyleAlQdah, K. S., Khan, N. M., Bacha, H. B., Chung, J.-D., & Shah, N. A. (2021). Marangoni Convection of Dust Particles in the Boundary Layer of Maxwell Nanofluids with Varying Surface Tension and Viscosity. Coatings, 11(9), 1072. https://doi.org/10.3390/coatings11091072








