Kinetics of the Boride Layers Obtained on AISI 1018 Steel by Considering the Amount of Matter Involved
Abstract
1. Introduction
- Experimental procedure: information about the cylindrical samples, materials used, heat treatment, and characterization techniques and a brief description of the growth kinetics is provided.
- Results and discussion: microstructure studies and layer characterization are presented. Likewise, a discussion about the kinetics of boride layer growth and activation energy is given. Finally, in this section, the use of non-linear regression analysis is detailed in order to divulge the advantages of this statistical technique.
- Conclusions: details about the importance of studying the amount of matter, temperature, and exposure time in the boride layer growth study are given.
2. Experimental Procedure
2.1. Boriding Treatment
2.2. Characterization
2.3. Kinetics of Growth
2.4. Activation Energy and Invested Energy Calculation
2.5. Regression Analysis
3. Results and Discussion
3.1. Microstructure
3.2. Characterization
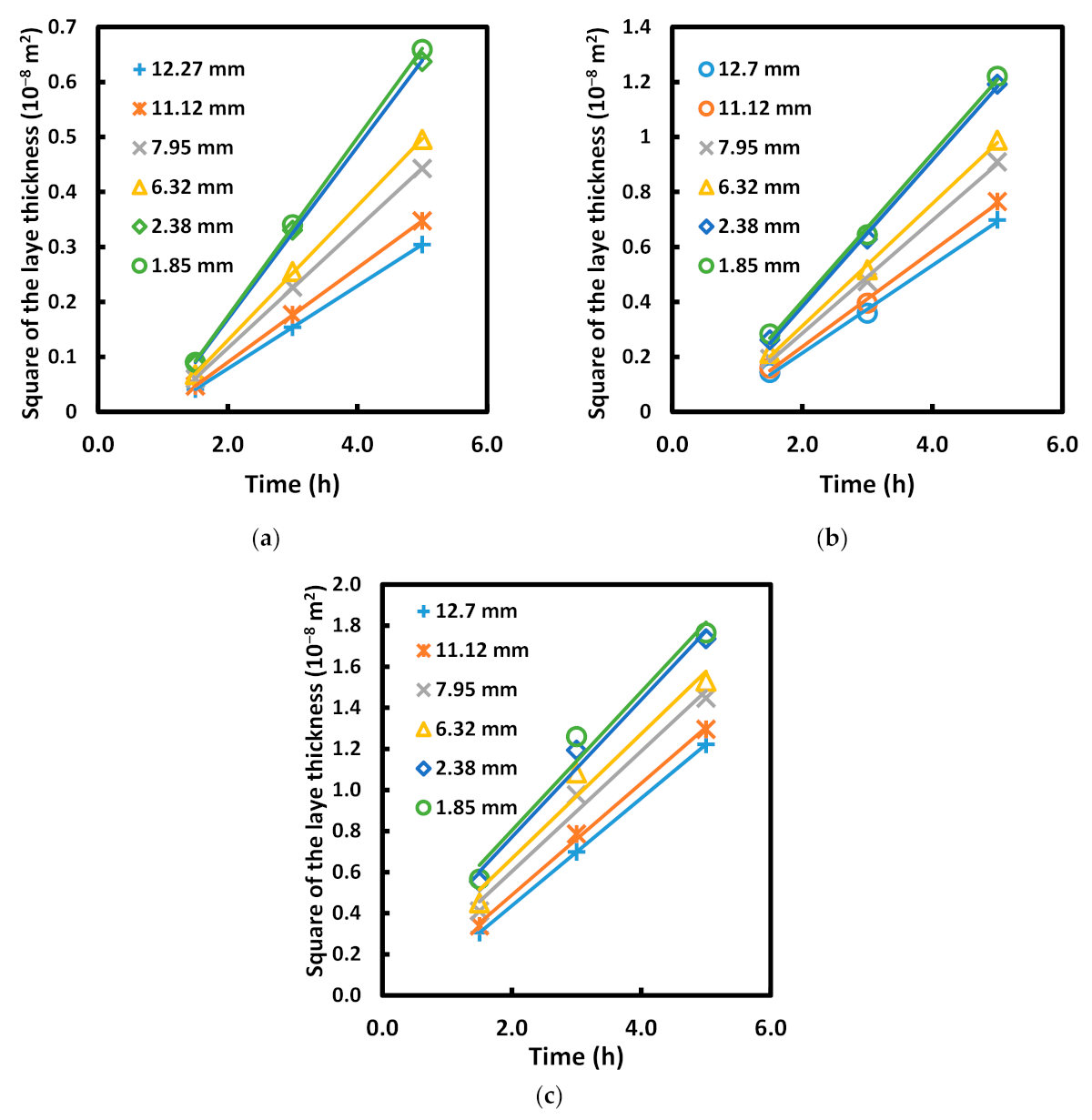
3.3. Kinetics of Growth
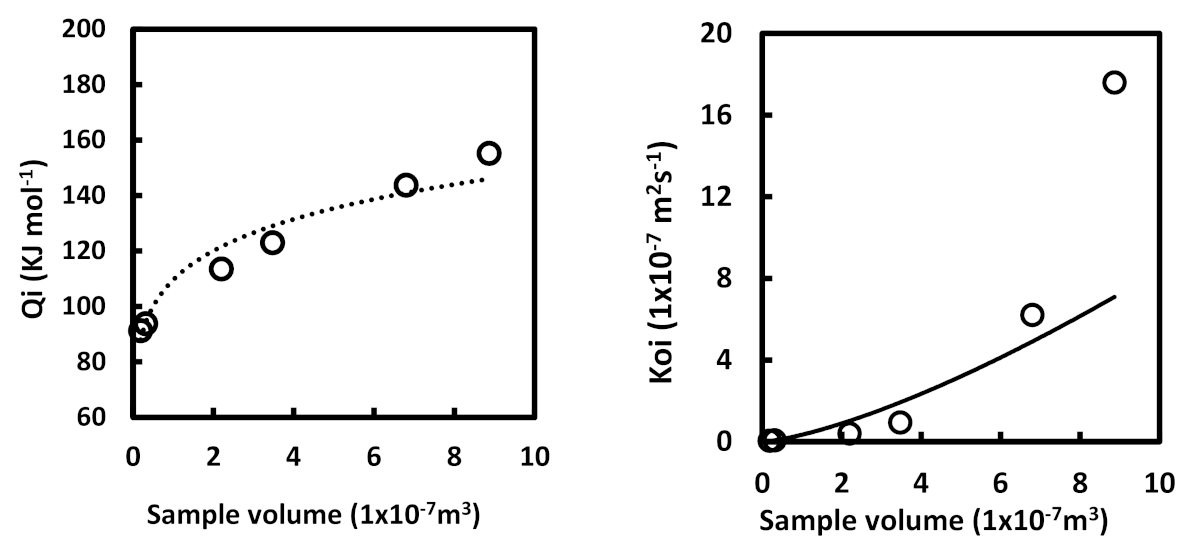
3.4. Activation Energy and Invested Energy Calculation
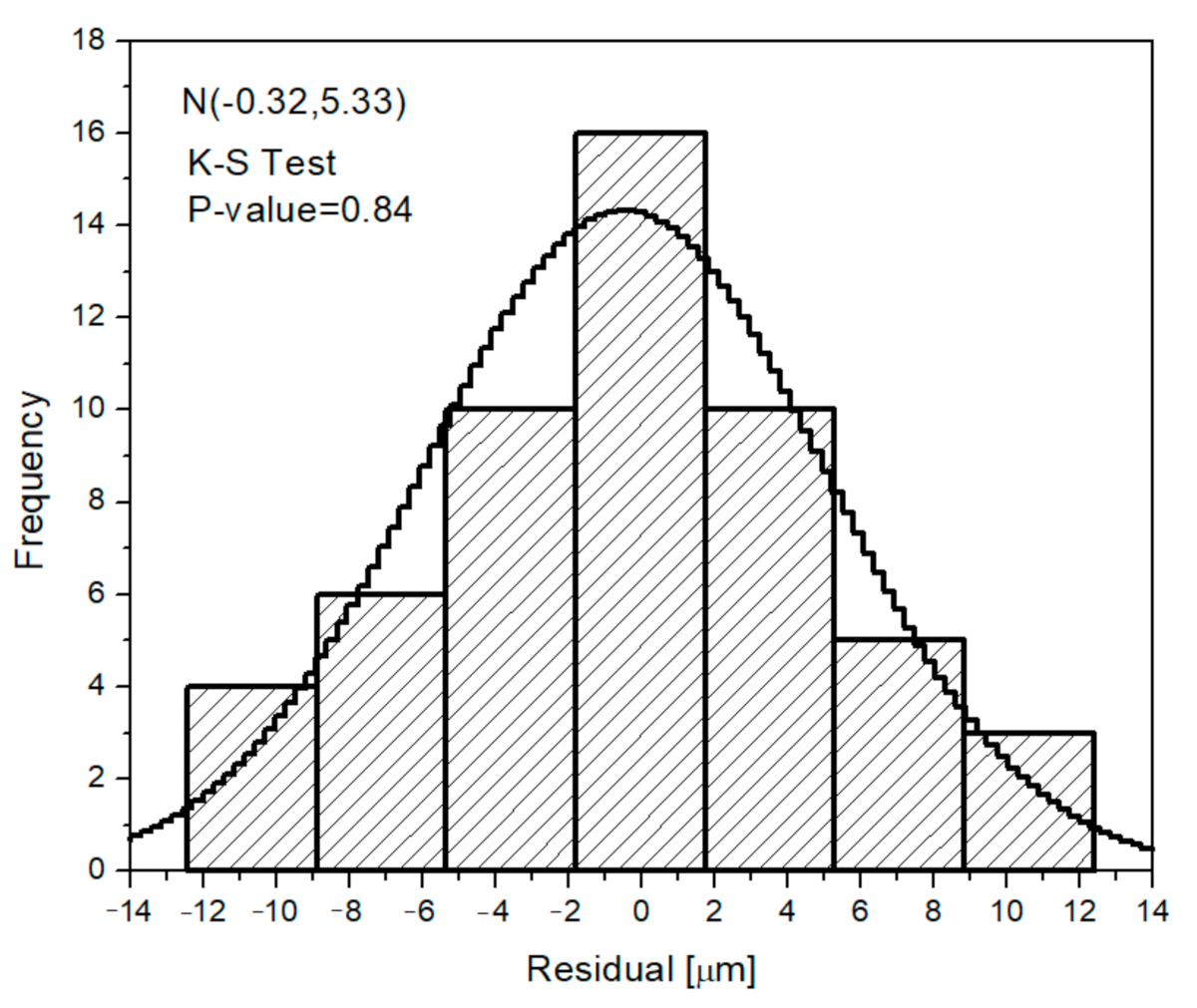
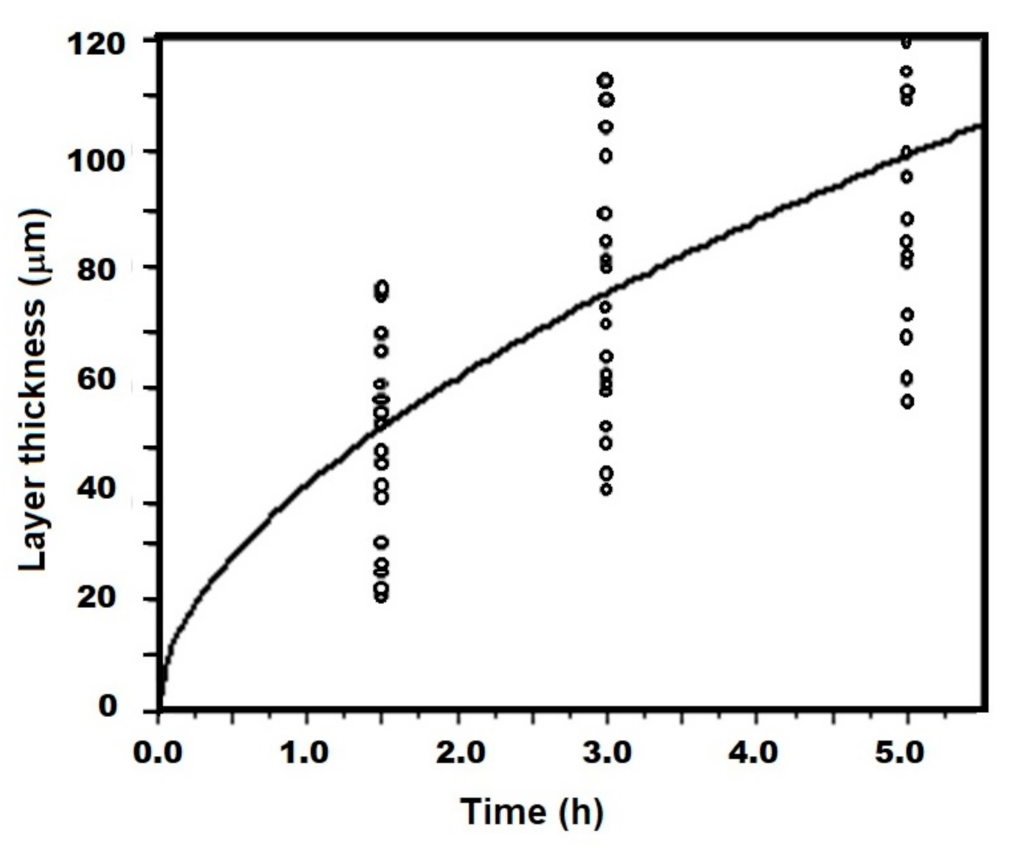
3.5. Regression Analysis
4. Conclusions
- The layers obtained from the application of the boriding process to AISI 1018 were extremely jagged because of the low content of carbon and alloyed elements.
- The values of the parabolic growth constant increased not only as a function of the temperature but also as a function of the sample size (Table 5), which indicates that the rate of layer growth is highly dependent on the experimental parameters and the size of the sample involved in the process.
- The estimated activation energy was 148.3 KJ mol–1, which seems low compared with values reported in the literature; however, this indicates that as the size of the sample decreases, the amount of energy required to make the process occur is also lower.
- According to the exhibited results, the size of the samples involved during a boriding process has to be considered to obtain better layer thickness results.
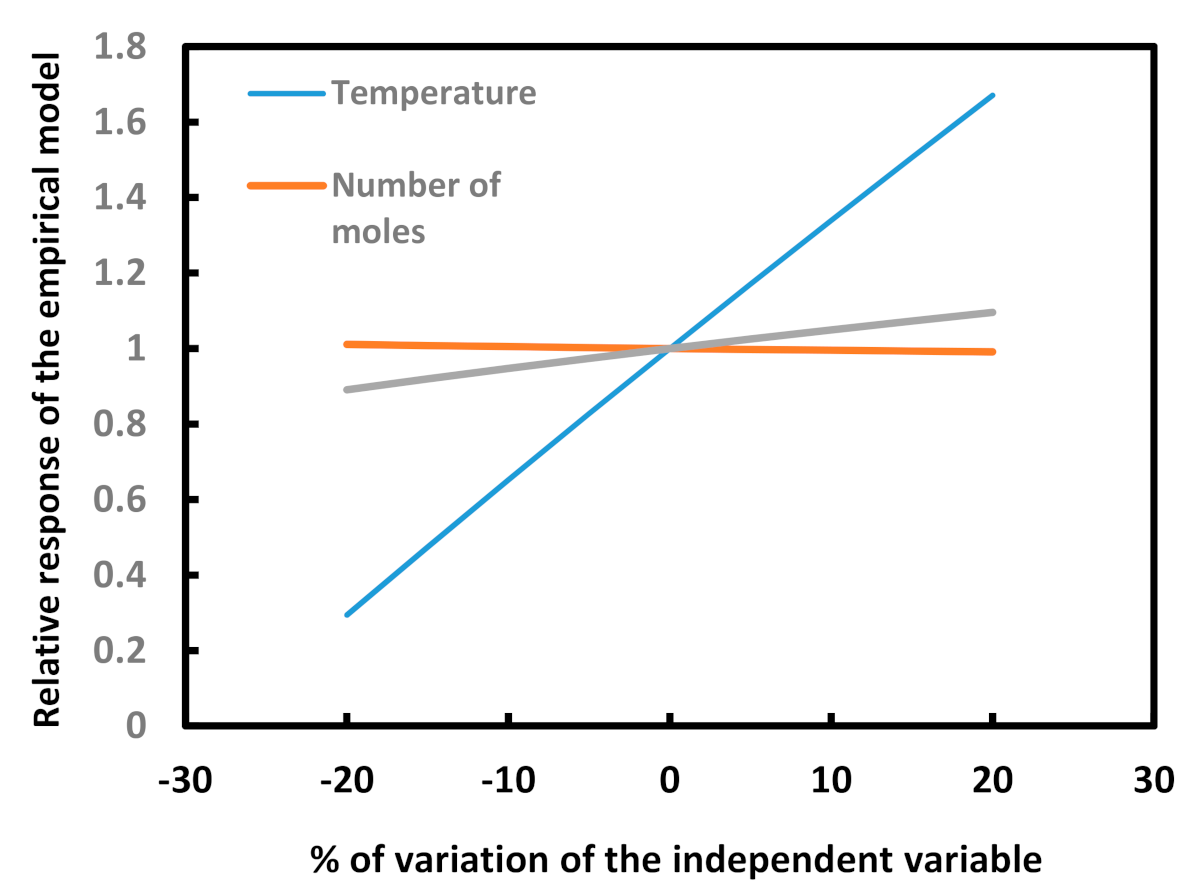
- Using regression analysis, it is possible to construct an empirical model that estimates layer growth in a boriding process by taking the three main independent variables—temperature, exposure time, and the amount of substance—into consideration. After this study, we can confirm that temperature is the variable that exerts the greatest influence on layer growth, followed by exposure time and number of moles, in that order.
- Finally, although many authors have reported that the layer thickness is independent of the sample shape and only depends on features such as the treatment conditions, the chemical composition of the substrate and the boron potential supplied during the boriding process, according to the results achieved in the present study the kinetic of growth and, by consequence, the layer thickness also depend on the number of moles of substance exposed to boriding, represented by the volume of the sample.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allaoui, O.; Bouaouadja, N.; Saindernan, G. Characterization of boronized layers on a XC38 steel. Surf. Coat. Tech. 2006, 201, 3475–3482. [Google Scholar] [CrossRef]
- Keddam, M.; Chentouf, S.M. A diffusion model for describing the bilayer growth (FeB/Fe2B) during the iron pow-der-pack boriding. Appl. Surf. Sci. 2005, 252, 393–399. [Google Scholar] [CrossRef]
- Hernández-Sánchez, E.; Domínguez-Galicia, Y.M.; Orozco-Álvarez, C.; Carrera-Espinoza, R.; Herrera-Hernández, H.; Ve-lázquez, J.C. A Study on the Effect of the Boron Potential on the Mechanical Properties of the Borided Layers Obtained by Boron Diffusion at the Surface of AISI 316L Steel. Adv. Mater. Sci. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Hernández-Sanchez, E.; Velázquez, J.C. Kinetcis of growth of iron boride layers on a low-carbon steel surface. In Laborato-ry Unit Operations and Experimental Methods in Chemical Engineering, 1st ed.; Basha, O.M., Morsi, B.I., Eds.; InTechOpen: London, UK, 2018; pp. 37–55. [Google Scholar]
- Bodycote. The Leading Provider of Heat Treatment and Specialist Thermal Processing Services Worldwide. Available online: http://hef.mx/wp-content/uploads/2017/06/Catalogo-de-sales-HEF-Durferrit.pdf (accessed on 1 November 2020).
- Keddam, M.; Ortiz-Domíguez, M.; Campos-Silva, I.; Martínez-Trinidad, J. A simple model for the growth kinetics of Fe2B iron boride on pure iron substrate. Appl. Surf. Sci. 2010, 256, 3128–3132. [Google Scholar] [CrossRef]
- Matuschka, A.; Von Graf, A. Boronizing, 1st ed.; Hanser Publisher: Wemding, Germany, 1980; pp. 31–60. [Google Scholar]
- Jain, V.; Sundararajan, G. Influence of the pack thickness of the boronizing mixture on the boriding of steel. Surf. Coat. Tech. 2002, 149, 21–26. [Google Scholar] [CrossRef]
- Campos, I.; Bautista, O.; Ramírez, G.; Islas, M.; De La Parra, J.; Zuñiga, L. Effect of boron paste thickness on the growth kinetics of Fe2B boride layers during the boriding process. Appl. Surf. Sci. 2005, 243, 429–436. [Google Scholar] [CrossRef]
- Trautmann, F. Borideing with Duferrit DURBORIT. Technical Information. H.E.F. Group. Available online: http://hef.mx/wp-content/uploads/2017/06/Catalogo-de-sales-HEF-Durferrit.pdf (accessed on 1 November 2020).
- Genel, K.; Ozbek, I.; Bindal, C. Kinetics of boriding of AISI W1 steel. Matls. Sci. Eng. A. 2003, 347, 311–314. [Google Scholar] [CrossRef]
- Sen, S.; Sen, U.; Bindal, C. The growth kinetics of borides formed on boronized AISI 4140 steel. Vacuum 2005, 77, 195–202. [Google Scholar] [CrossRef]
- Sen, S.; Sen, U.; Bindal, C. An approach of kinetic study of borided steels. Surf. Coat. Technol. 2005, 191, 274–285. [Google Scholar] [CrossRef]
- Ozbek, I.; Bindal, C. Kinetics of borided AISI M2 high speed Steel. Vacuum 2011, 86, 391–397. [Google Scholar] [CrossRef]
- Sen, S.; Ozbek, I.; Sen, U.; Bindal, C. Mechanical Behavior of Borides Formed on Borided Cold Work Tool Steel. Surf. Coat. Technol. 2001, 135, 173–177. [Google Scholar] [CrossRef]
- Velázquez, J.C.; Cruz-Ramirez, J.C.; Valor, A.; Venegas, V.; Caleyo, F.; Hallen, J.M. Modeling localized corrosion of pipeline steels in oilfield produced water environments. Eng. Fail. Anal. 2017, 79, 216–231. [Google Scholar] [CrossRef]
- Velázquez, J.C.; Valor, A.; Caleyo, F.; Venegas, V.; Espina-Hernandez, J.H.; Hallen, J.M.; Lopez, M.R. Pitting corrosion models improve integrity management, reliability. Oil Gas J. 2009, 107, 52–62. [Google Scholar]
- Velázquez, J.C.; Valor, A.; Caleyo, F.; Venegas, V.; Espina-Hernandez, J.H.; Hallen, J.M.; Lopez, M.R. Study helps model buried pipeline pitting corrosion. Oil Gas J. 2009, 107, 64–73. [Google Scholar]
- Velázquez, J.C.; Van Der Weide, J.A.M.; Hernández-Sanchez, E.; Herrera-Hernández, H. Statistical modelling of pitting corro-sion: Extrapolation of the maximum pit depth-growth. Int. J. Electrochem. Sci. 2014, 9, 4129–4143. [Google Scholar]
- Terán, G.; Capula-Colindres, S.; Angeles-Herrera, D.; Velázquez, J.C.; Fernández-Cueto, M.J. Estimation of fracture toughness K IC from Charpy impact test data in T-welded connections repaired by grinding and wet welding. Eng. Fract. Mech. 2016, 153, 351–359. [Google Scholar] [CrossRef]
- Hernández-Sanchez, E.; Rodriguez-Castro, G.; Meneses-Amador, A.; Bravo-Bárcenas, D.; Arzate-Vazquez, I.; Mar-tínez-Gutiérrez, H.; Romero-Romo, M.; Campos-Silva, I. Effect of the anisotropic growth on the fracture toughness meas-urements obtained in the Fe2B layer. Surf. Coat. Tech. 2013, 237, 292–298. [Google Scholar] [CrossRef]
- Brakman, C.M.; Gommers, A.W.J.; Mittemeijer, E.J. Boriding of Fe and Fe–C, Fe–Cr, and Fe–Ni alloys; Boride-layer growth kinetics. J. Mater. Res. 1989, 4, 1354–1370. [Google Scholar] [CrossRef]
- Dybkov, V.I.; Siderko, R.; Goncharuk, L.V.; Khoruzha, V.G.; Samelyuk, A.V. Microstructure, Growth Kinetics, and Abrasive Wear Resistance of Boride Layers on Fe–30% Cr Alloy. Powder Metall. Met. Ceram. 2013, 51, 518–530. [Google Scholar]
- Velázquez, J.C.; Caleyo, F.; Valor, A.; Hallen, J.M. Predictive model for pitting corrosion in buried oil and gas pipelines. Co-rrosion 2009, 65, 332–342. [Google Scholar] [CrossRef]
- Energía de Activación Para la Difusión del Boro Durante la Borurización de un Acero de Bajo Carbono. Available online: http://www.reibci.org/publicados/2016/dic/2000116.pdf (accessed on 20 December 2020).
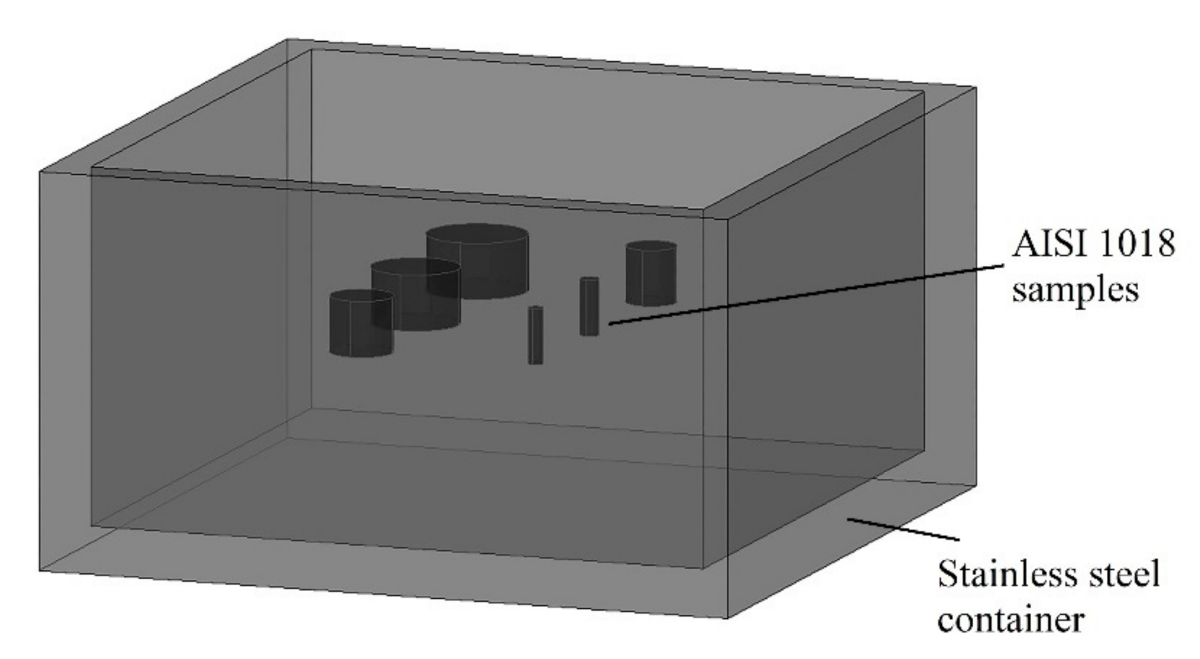
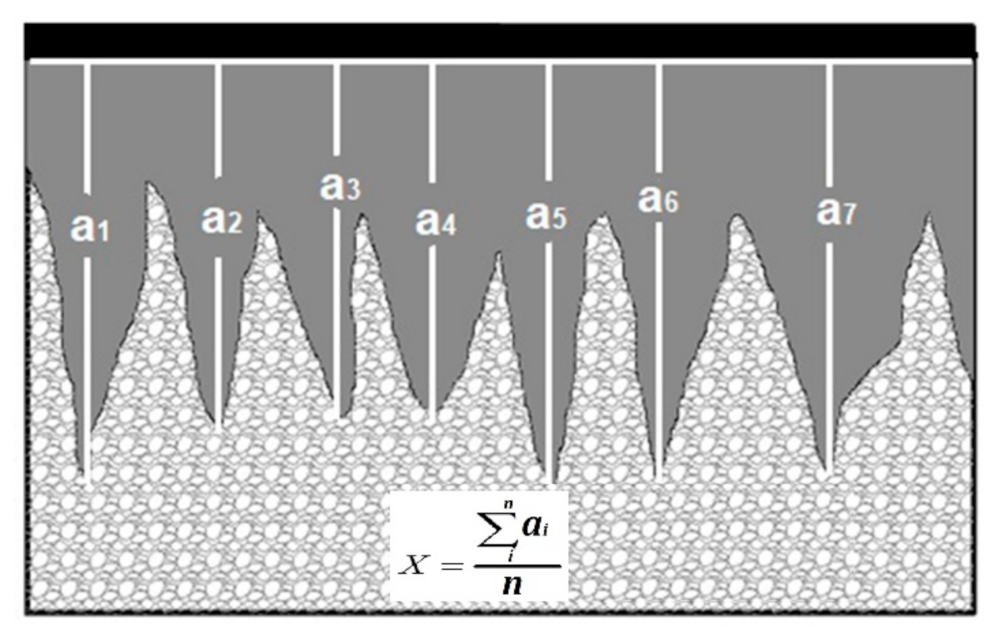

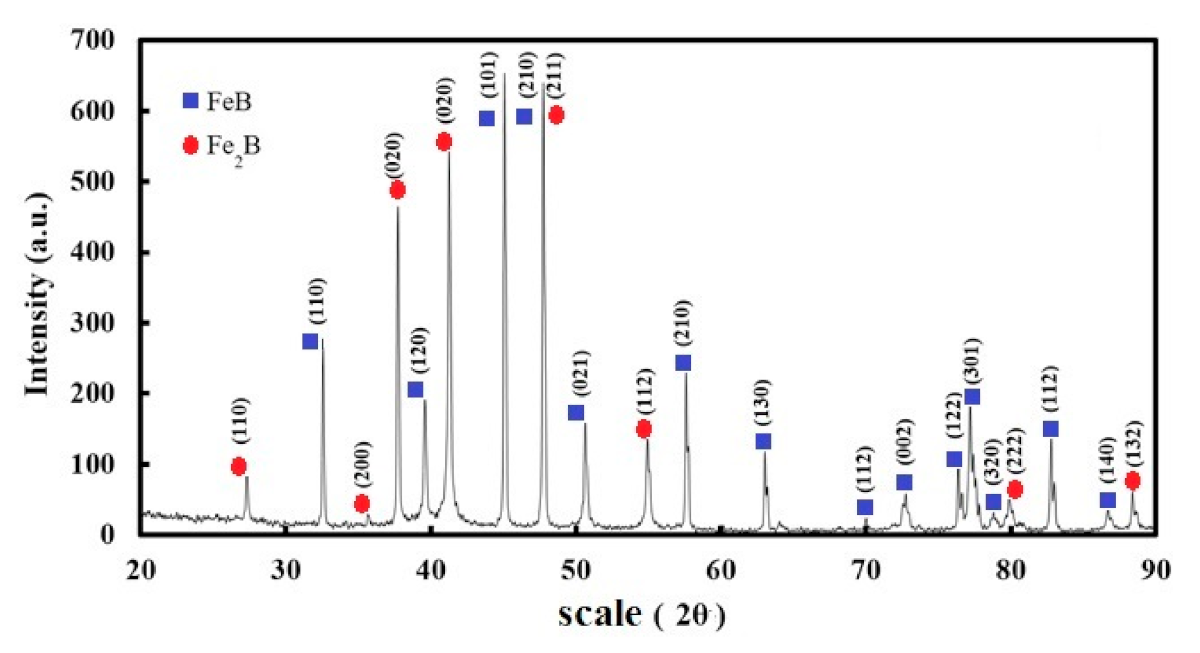
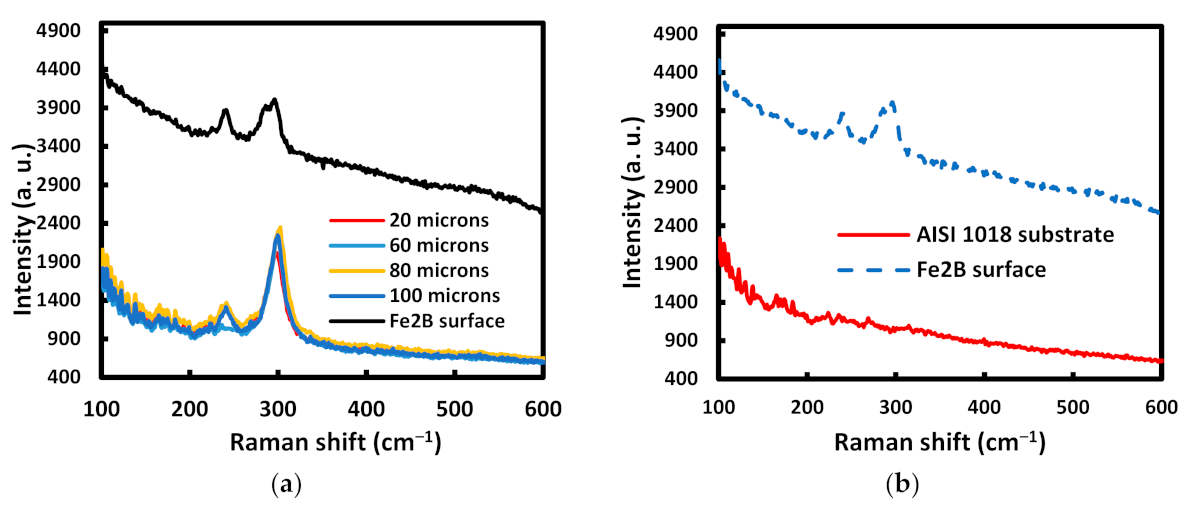


| C | Mn | Si | P max. | S max. | Fe |
|---|---|---|---|---|---|
| 0.15–0.20 | 0.60–0.90 | 0.15–0.30 | 0.04 | 0.05 | Balance |
| Diameter (mm) | Treatment Time (h) | ||
|---|---|---|---|
| 1.5 | 3 | 5 | |
| Layer thickness (µm) | |||
| 12.7 | 20.75 ± 5.25 | 39.22 ± 6.03 | 55.16 ± 7.16 |
| 11.12 | 21.69 ± 4.28 | 42.02 ± 7.23 | 58.93 ± 9.25 |
| 7.95 | 24.6 ± 5.45 | 47.62 ± 7.27 | 66.51 ± 8.36 |
| 6.32 | 26.02 ± 4.12 | 50.51 ± 8.12 | 70.39 ± 8.15 |
| 2.38 | 29.54 ± 4.18 | 67.48 ± 9.32 | 79.81 ± 9.69 |
| 1.85 | 30.02 ± 7.34 | 58.33 ± 7.27 | 81.92 ± 10.54 |
| Diameter (mm) | Treatment Time (h) | ||
|---|---|---|---|
| 1.5 | 3 | 5 | |
| Layer Thickness (µm) | |||
| 12.7 | 37.84 ± 4.23 | 59.92 ± 6.03 | 83.56 ± 8.85 |
| 11.12 | 39.88 ± 5.11 | 62.89 ± 7.43 | 87.48 ± 9.17 |
| 7.95 | 43.98 ± 5.94 | 68.83 ± 5.94 | 95.35 ± 9.42 |
| 6.32 | 46.09 ± 7.63 | 71.88 ± 7.13 | 99.43 ± 7.17 |
| 2.38 | 51.18 ± 5.23 | 79.27 ± 8.12 | 109.17 ± 9.34 |
| 1.85 | 53.25 ± 7.82 | 80.26 ± 8.37 | 110.48 ± 10.12 |
| Diameter (mm) | Treatment Time (h) | ||
|---|---|---|---|
| 1.5 | 3 | 5 | |
| Layer Thickness (µm) | |||
| 12.7 | 55.27 ± 5.30 | 83.56 ± 9.59 | 110.54 ± 11.89 |
| 11.12 | 58.19 ± 4.25 | 88.63 ± 6.67 | 113.79 ± 10.01 |
| 7.95 | 64.07 ± 4.54 | 98.81 ± 8.89 | 120.31 ± 12.67 |
| 6.32 | 67.09 ± 6.83 | 104.03 ± 8.11 | 123.66 ± 11.63 |
| 2.38 | 74.38 ± 6.28 | 109.25 ± 6.66 | 131.67 ± 14.58 |
| 1.85 | 75.25 ± 6.82 | 112.25 ± 8.42 | 132.86 ± 11.48 |
| Diameter (mm) | Ki (m2·s−1) | Qi (KJ mol−1) | ||
|---|---|---|---|---|
| 900 °C | 950 °C | 1000 °C | ||
| 12.7 | 2.09 × 10−13 | 4.42 × 10−13 | 7.27 × 10−13 | 155.22 |
| 11.12 | 2.38 × 10−13 | 4.83 × 10−13 | 7.56 × 10−13 | 143.76 |
| 7.95 | 3.03 × 10−13 | 5.70 × 10−13 | 8.14 × 10−13 | 123.04 |
| 6.32 | 3.39 × 10−13 | 6.18 × 10−13 | 8.44 × 10−13 | 113.55 |
| 2.38 | 4.36 × 10−13 | 7.40 × 10−13 | 9.2 × 10−13 | 93.8 |
| 1.85 | 4.5 × 10−13 | 7.47 × 10−13 | 9.4 × 10−13 | 91.20 |
| Di (m) | Vi | mi (kg) | Ni (Moles) | Ei (J) |
|---|---|---|---|---|
| (m3) | ||||
| 0.0127 | 8.86 × 10−7 | 6.92 × 10−3 | 1.24 × 10−1 | 19225.689 |
| 0.01112 | 6.79 × 10−7 | 5.30 × 10−3 | 9.50 × 10−2 | 13650.855 |
| 0.00795 | 3.47 × 10−7 | 2.71 × 10−3 | 4.85 × 10−2 | 5971.280 |
| 0.00632 | 2.19 × 10−7 | 1.71 × 10−3 | 3.07 × 10−2 | 3482.729 |
| 0.00238 | 3.11 × 10−8 | 2.43 × 10−4 | 4.35 × 10−3 | 408.009 |
| 0.00185 | 1.88 × 10−8 | 1.47 × 10−4 | 2.63 × 10−3 | 238.133 |
| Material | Method | Layer Morphology | Activation Energy (KJ·mol–1) | Reference |
|---|---|---|---|---|
| AISI W1 | Solid media | Flat front | 171.2 | [11] |
| AISI 4140 | Molten salt | Saw-toothed | 218.4 | [12] |
| AISI D2 | Molten salt | Saw-toothed | 170.0 | [13] |
| AISI 1018 | B4C paste | Saw-toothed | 161.8 | [15] |
| AISI 1005 | Solid media | Saw-toothed | 133.8 | [25] |
| Armco iron | Gaseous | Saw-toothed | 120.6 | [25] |
| AISI 1018 | Solid media | Saw-toothed | 148.3 | present |
| Coefficient | ||||||
|---|---|---|---|---|---|---|
| R2 | ||||||
| 0.97 | 0.07 | –216.71 | 0.67 | –0.77 | 1.16 | 0.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Trabolsi, P.A.; Velázquez, J.C.; Orozco-Álvarez, C.; Carrera-Espinoza, R.; Yescas-Hernández, J.A.; González-Arévalo, N.E.; Hernández-Sánchez, E. Kinetics of the Boride Layers Obtained on AISI 1018 Steel by Considering the Amount of Matter Involved. Coatings 2021, 11, 259. https://doi.org/10.3390/coatings11020259
Ruiz-Trabolsi PA, Velázquez JC, Orozco-Álvarez C, Carrera-Espinoza R, Yescas-Hernández JA, González-Arévalo NE, Hernández-Sánchez E. Kinetics of the Boride Layers Obtained on AISI 1018 Steel by Considering the Amount of Matter Involved. Coatings. 2021; 11(2):259. https://doi.org/10.3390/coatings11020259
Chicago/Turabian StyleRuiz-Trabolsi, Pablo A., Julio Cesar Velázquez, Carlos Orozco-Álvarez, Rafael Carrera-Espinoza, Jorge A. Yescas-Hernández, Noé Eliseo González-Arévalo, and Enrique Hernández-Sánchez. 2021. "Kinetics of the Boride Layers Obtained on AISI 1018 Steel by Considering the Amount of Matter Involved" Coatings 11, no. 2: 259. https://doi.org/10.3390/coatings11020259
APA StyleRuiz-Trabolsi, P. A., Velázquez, J. C., Orozco-Álvarez, C., Carrera-Espinoza, R., Yescas-Hernández, J. A., González-Arévalo, N. E., & Hernández-Sánchez, E. (2021). Kinetics of the Boride Layers Obtained on AISI 1018 Steel by Considering the Amount of Matter Involved. Coatings, 11(2), 259. https://doi.org/10.3390/coatings11020259





