Entropy Analysis of an MHD Synthetic Cilia Assisted Transport in a Microchannel Enclosure with Velocity and Thermal Slippage Effects
Abstract
1. Introduction
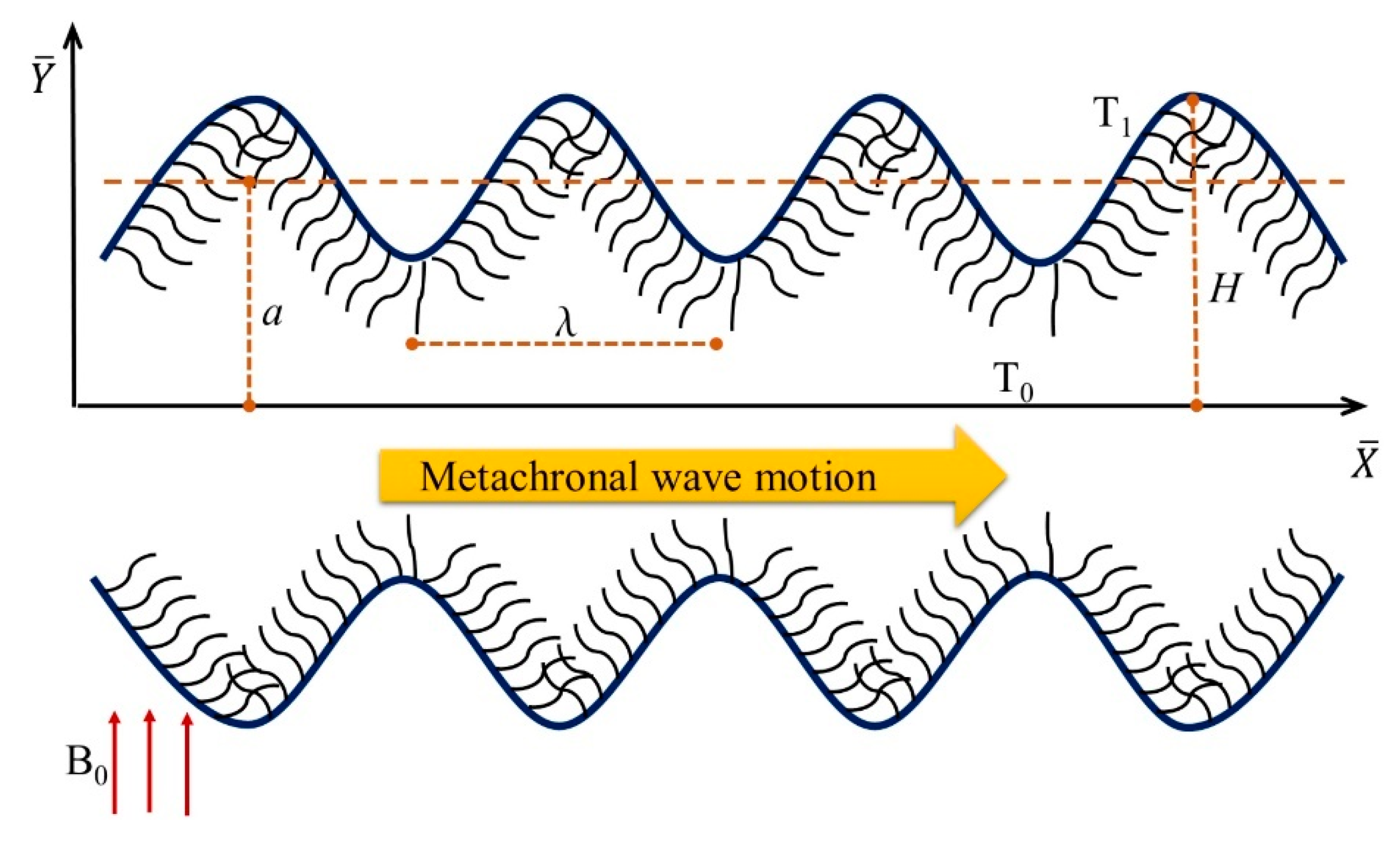
2. Mathematical Formulation
3. Perturbation Solution
3.1. Zeroth Order System
3.2. First Order System
4. Entropy Analysis
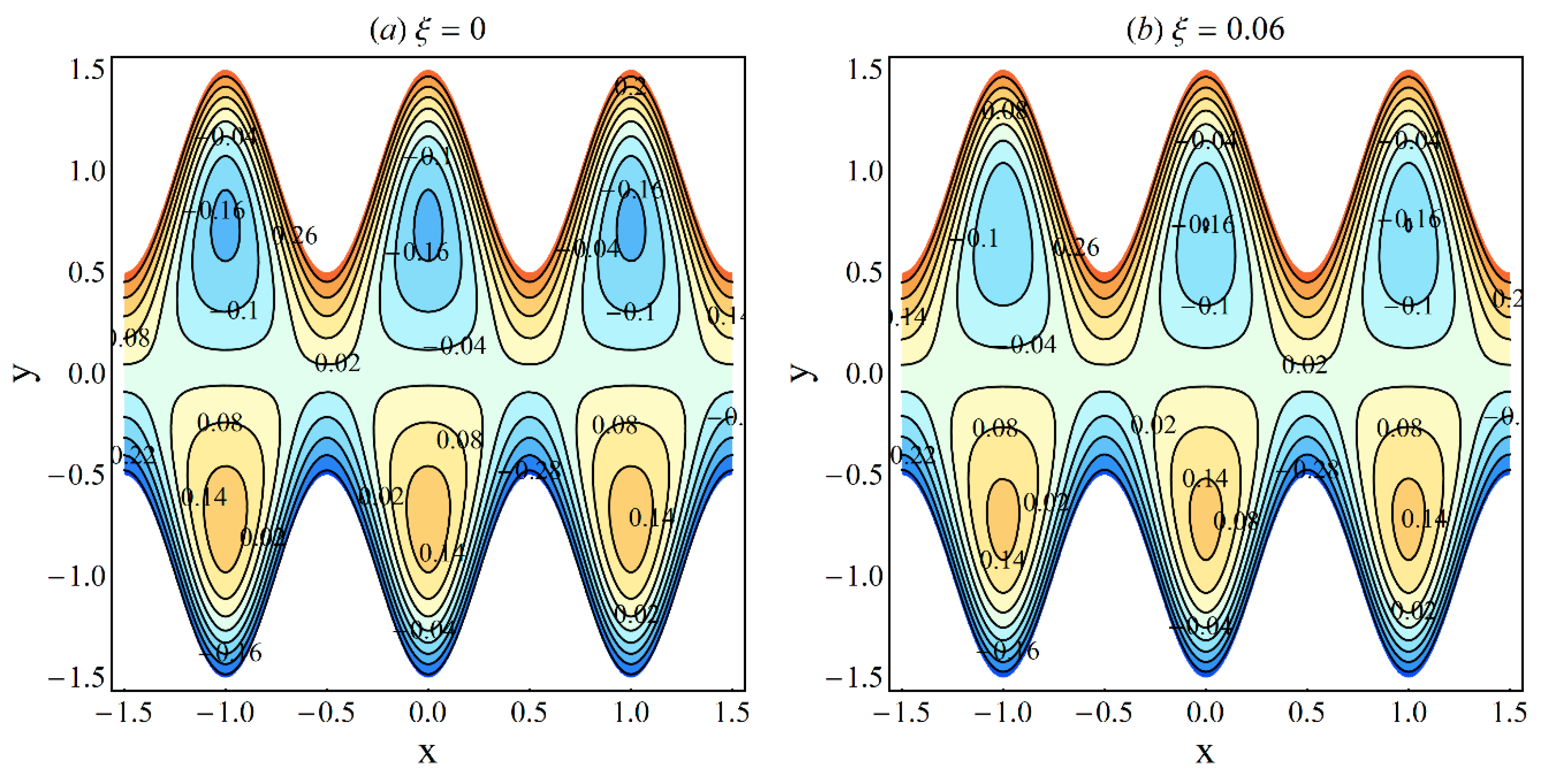
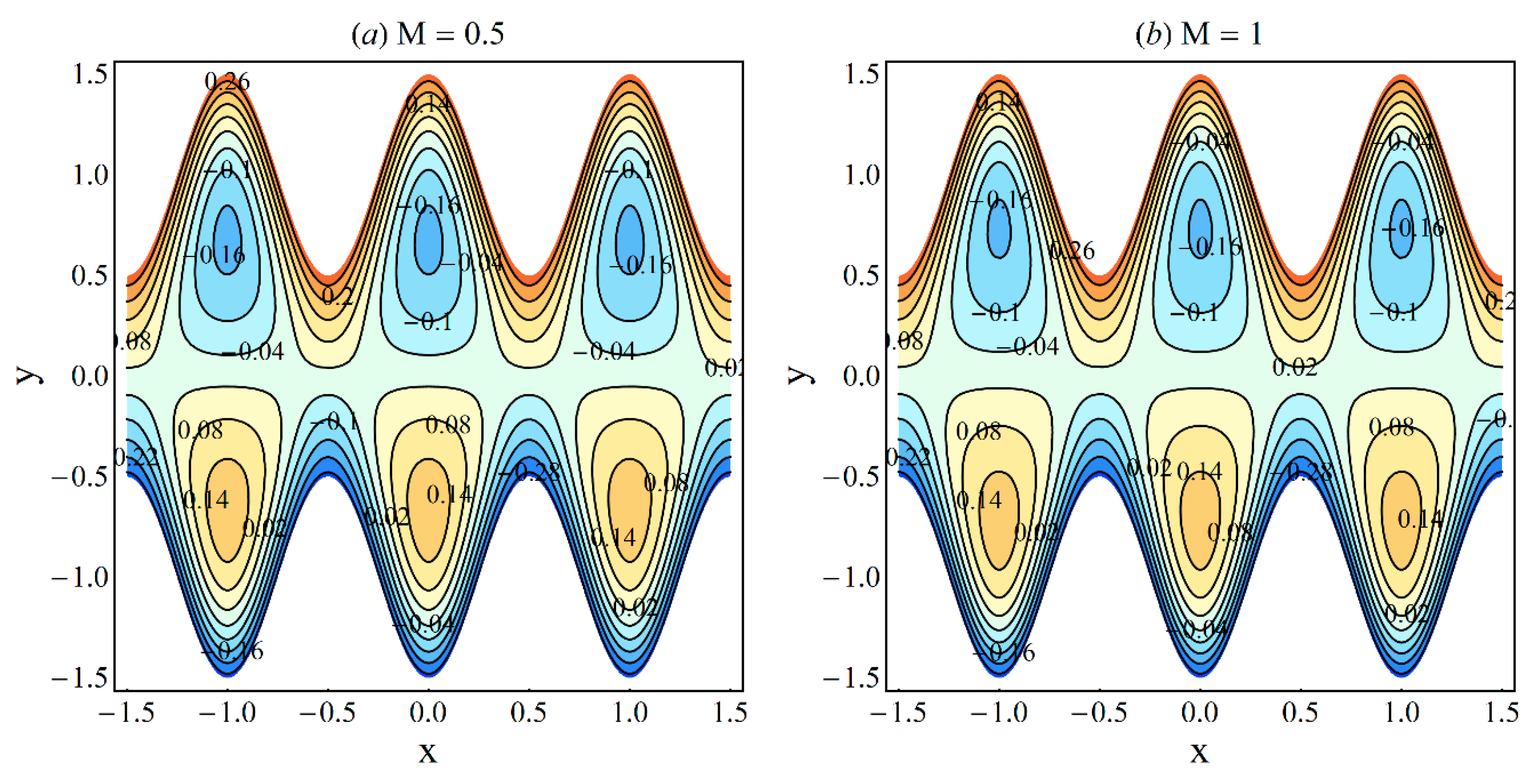
5. Results and Discussion
6. Conclusions
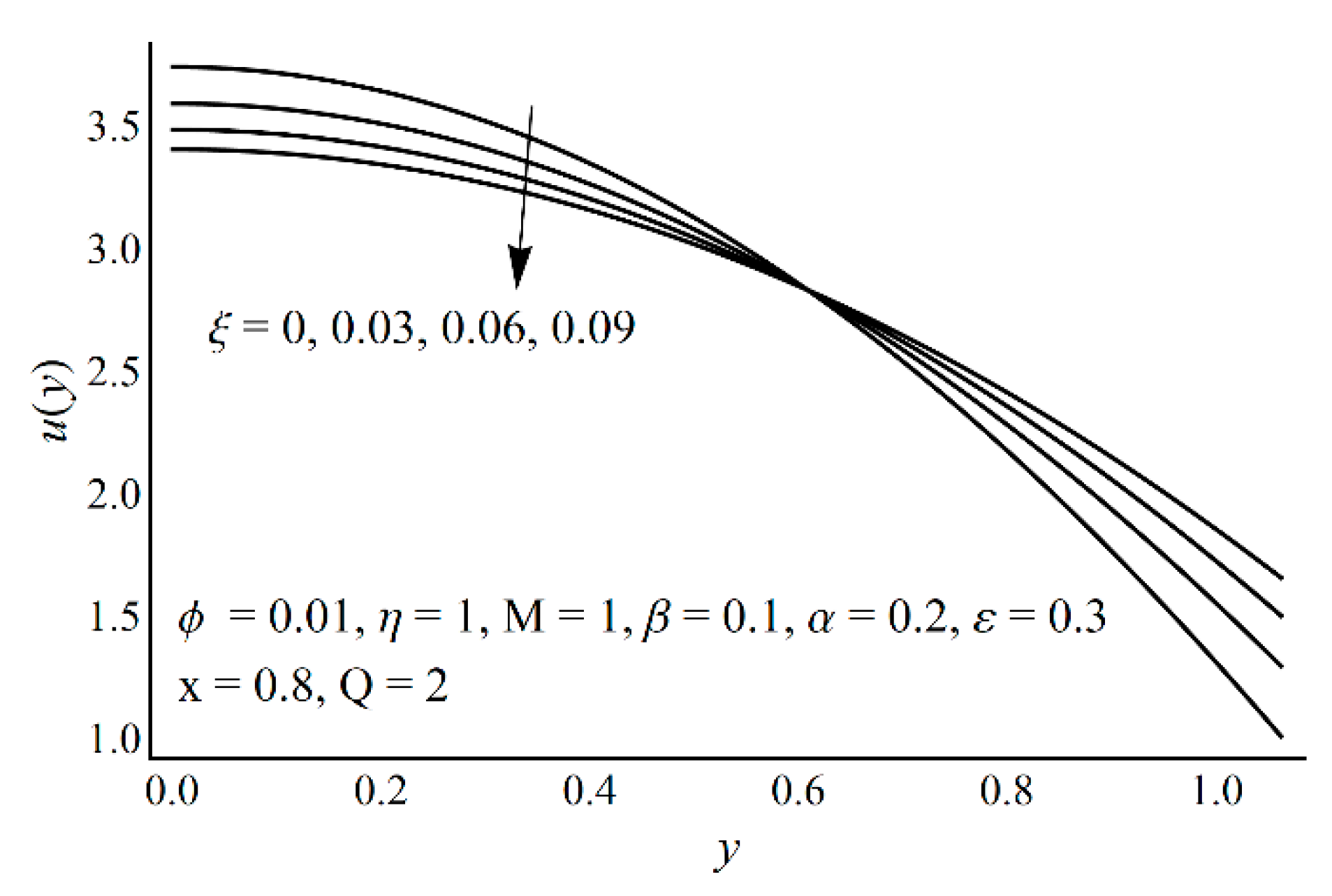
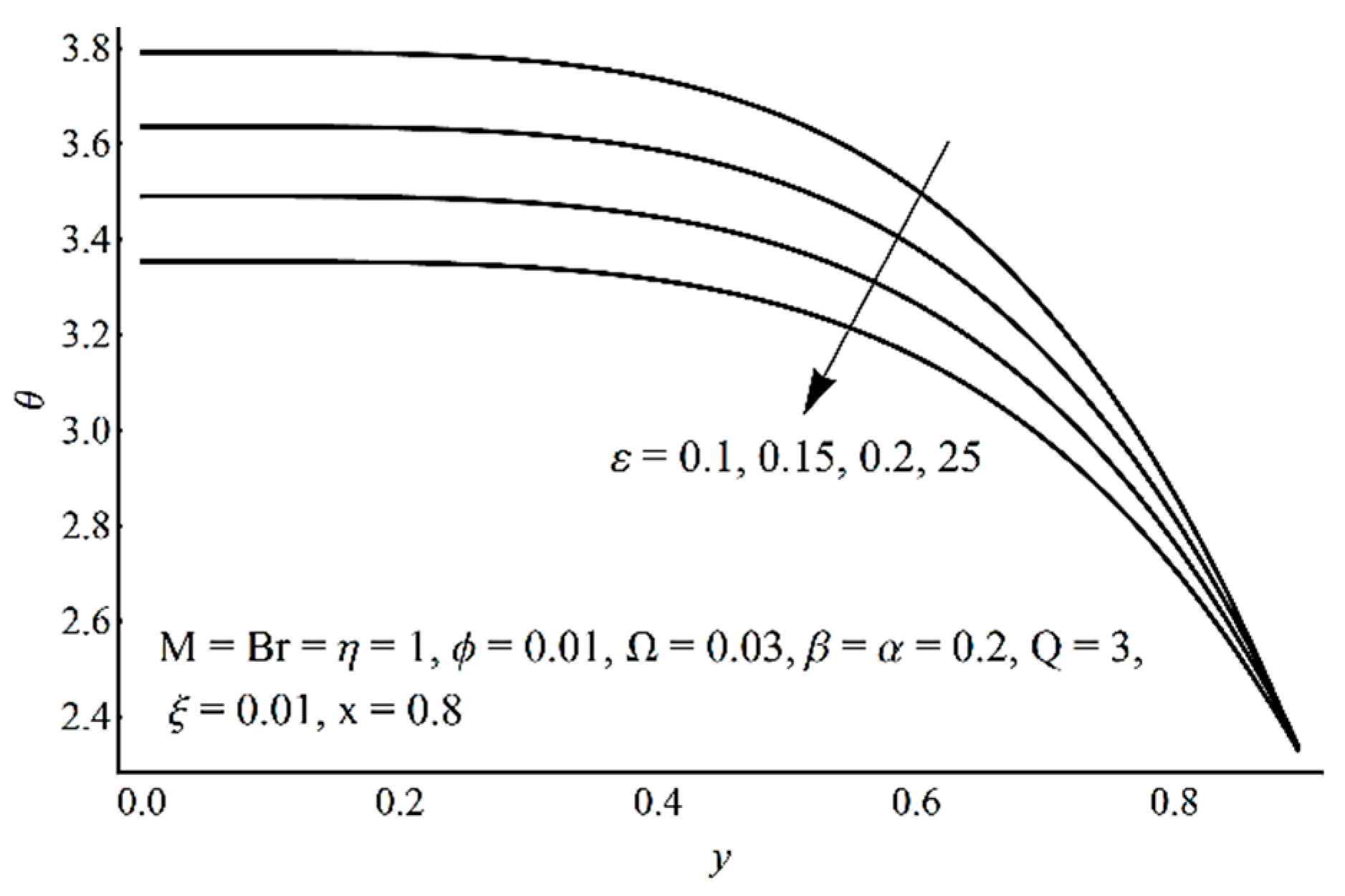
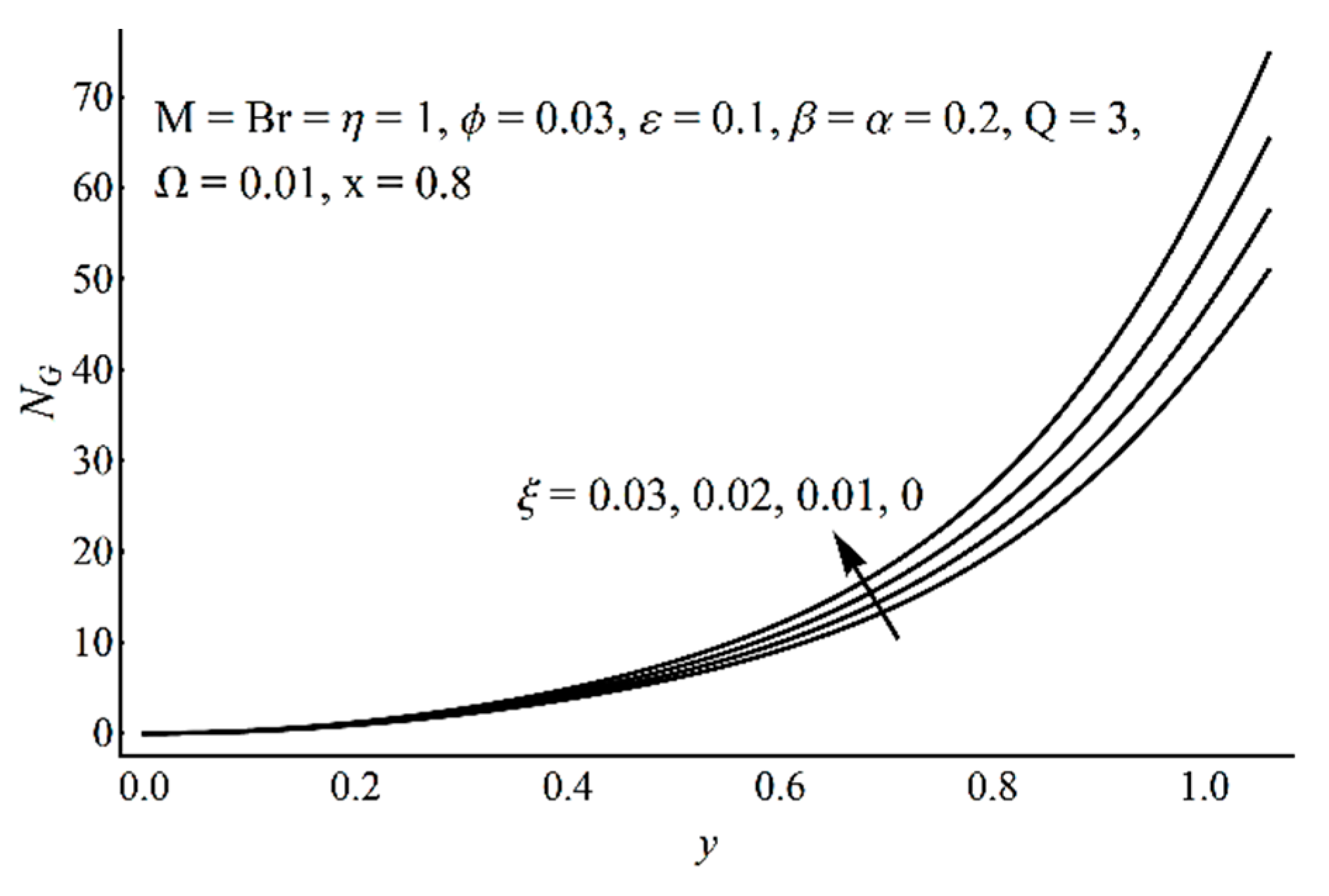
- As the cilia length increases, the temperature profile and the entropy production decrease, while the velocity profile shows the opposite effect near the boundary and demonstrates decreasing effects near the center;
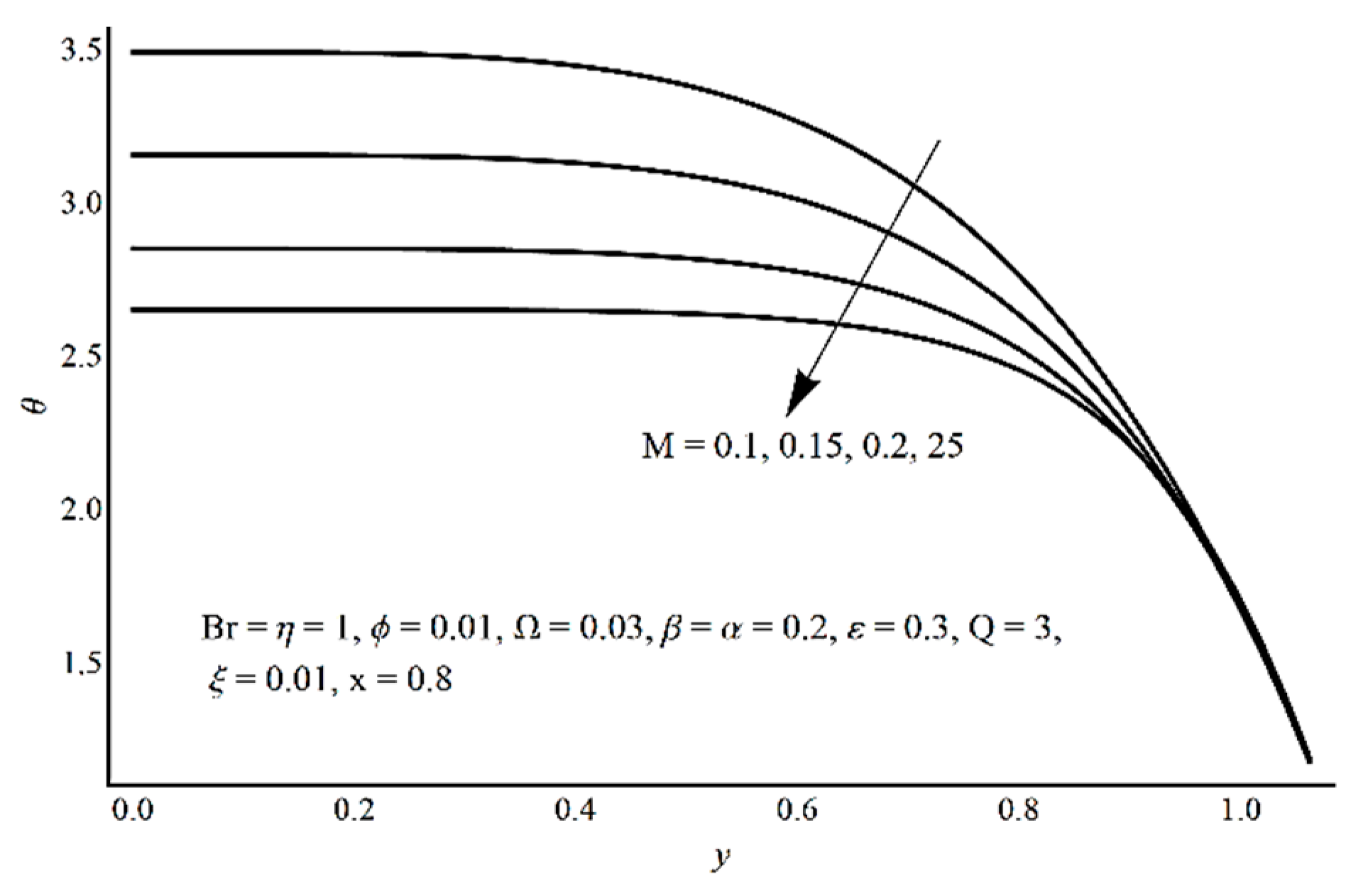
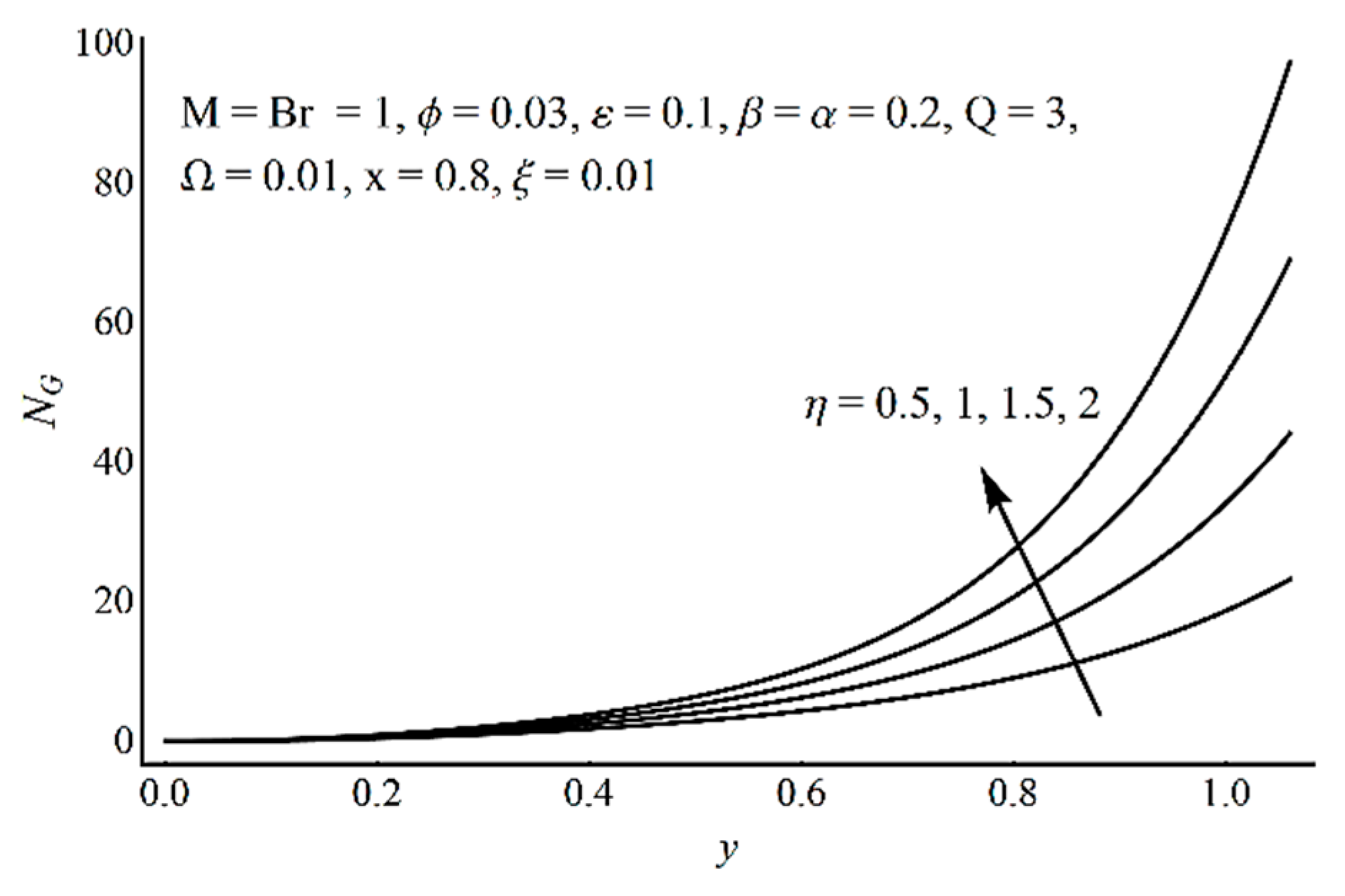
- The Prandtl fluid material parameter η has increasing effects on the velocity and entropy production near the boundary;
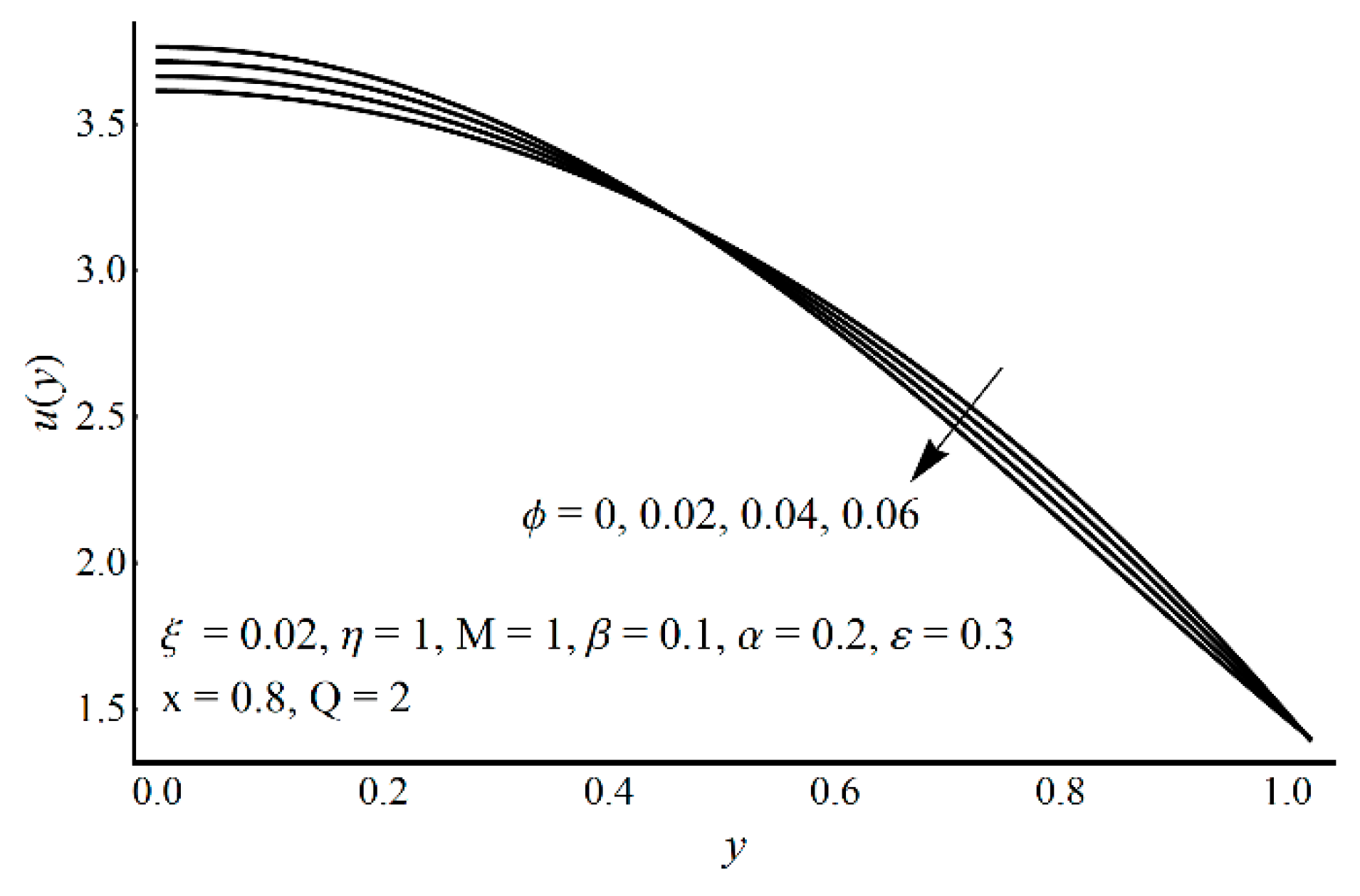
- Due to wall slip, the velocity increases, while temperature and the entropy production decrease;
- The temperature jump brought an increasing change in the temperature profile;
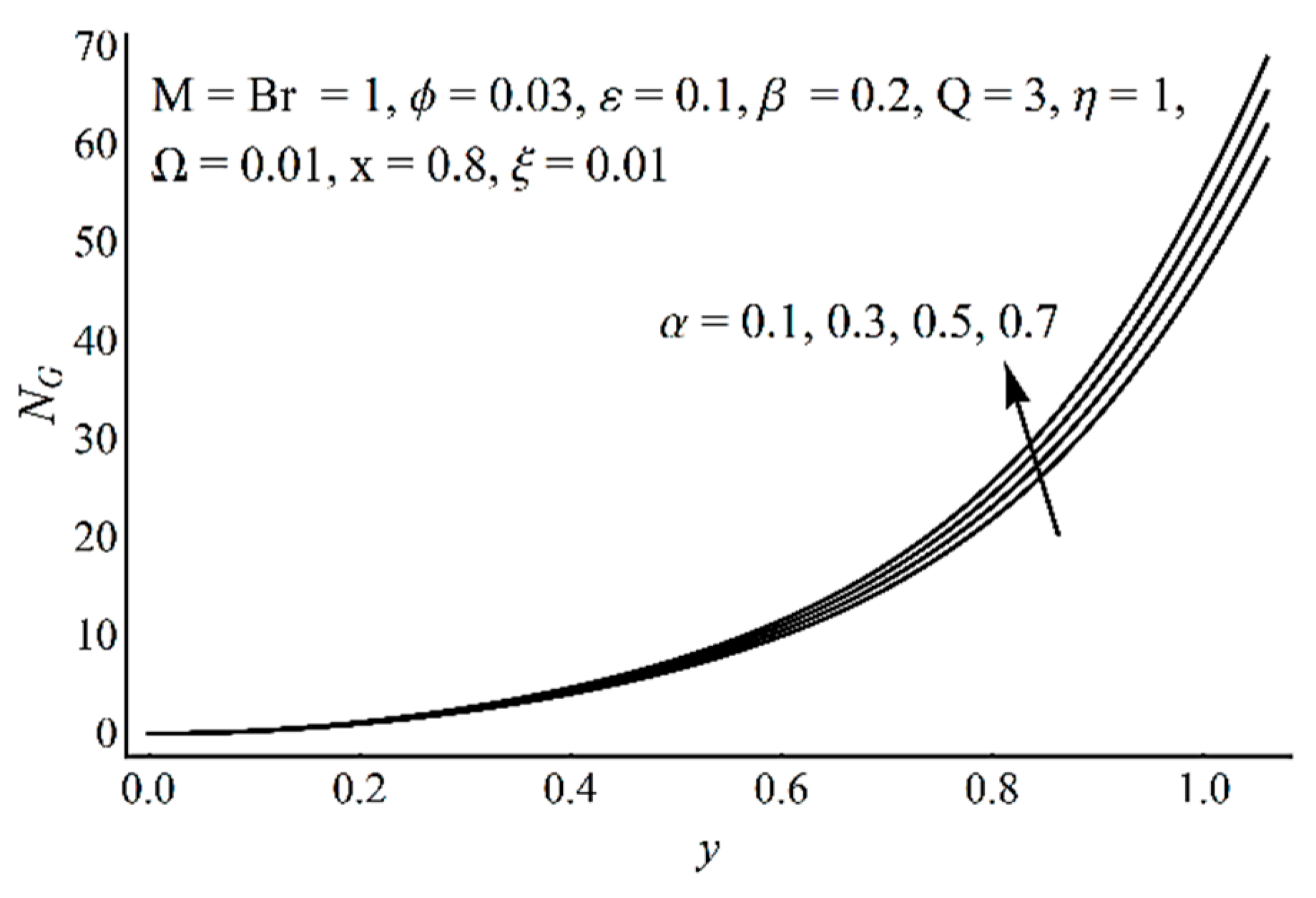
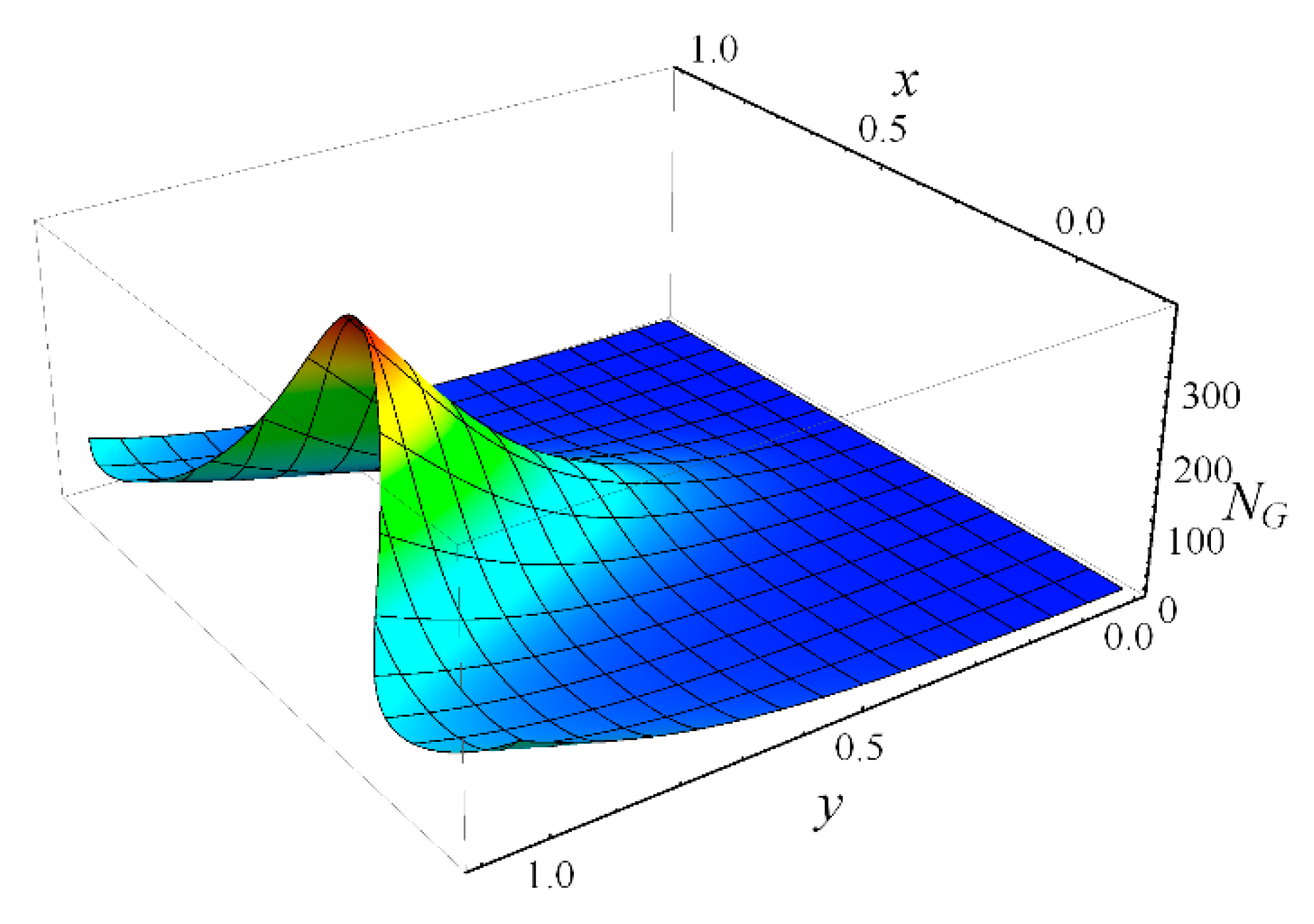
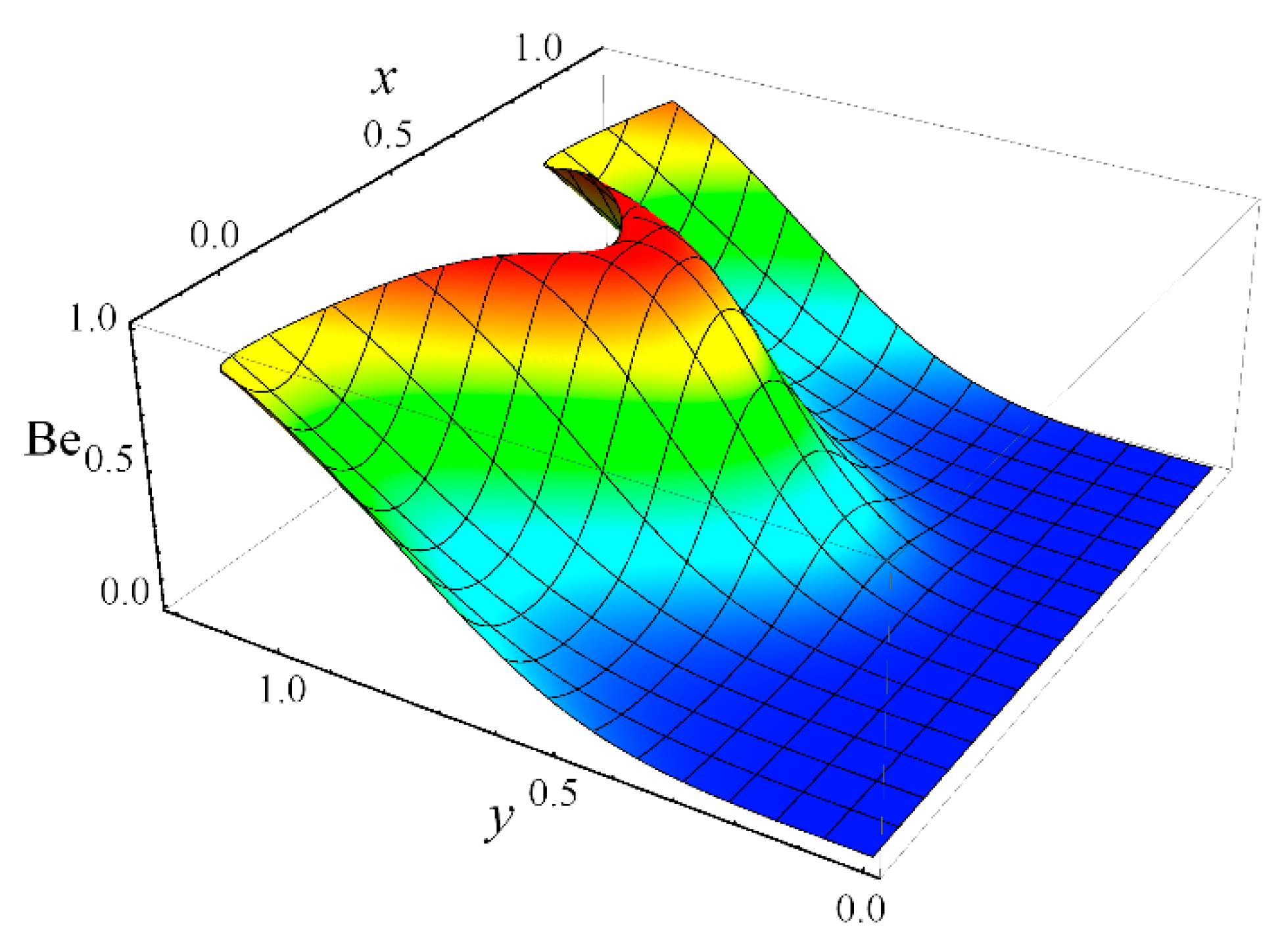
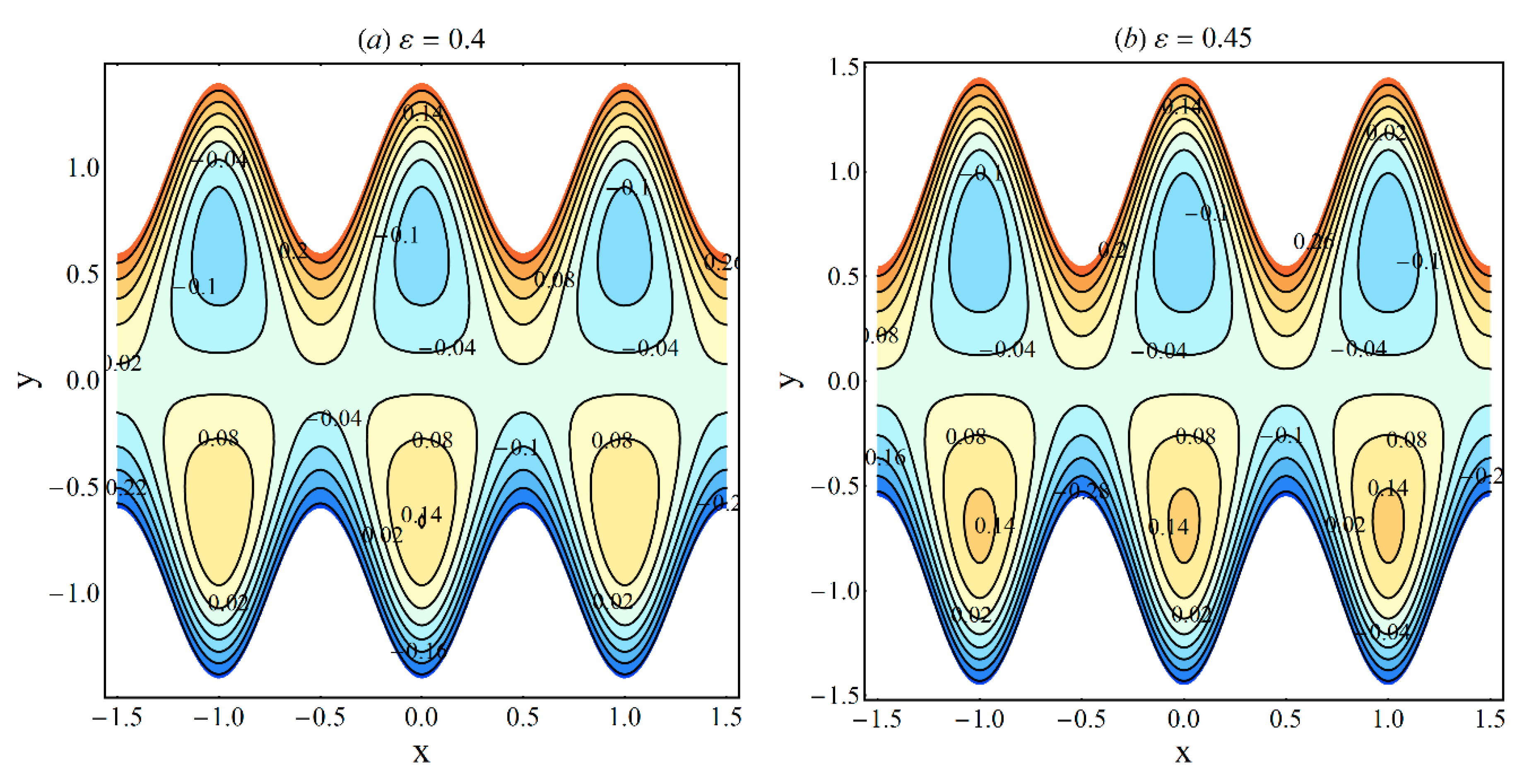
- Near the channel center, fluid friction irreversibility is dominant, whereas near the heated ciliated wall, the effect of heat transfer irreversibility is noticeable;
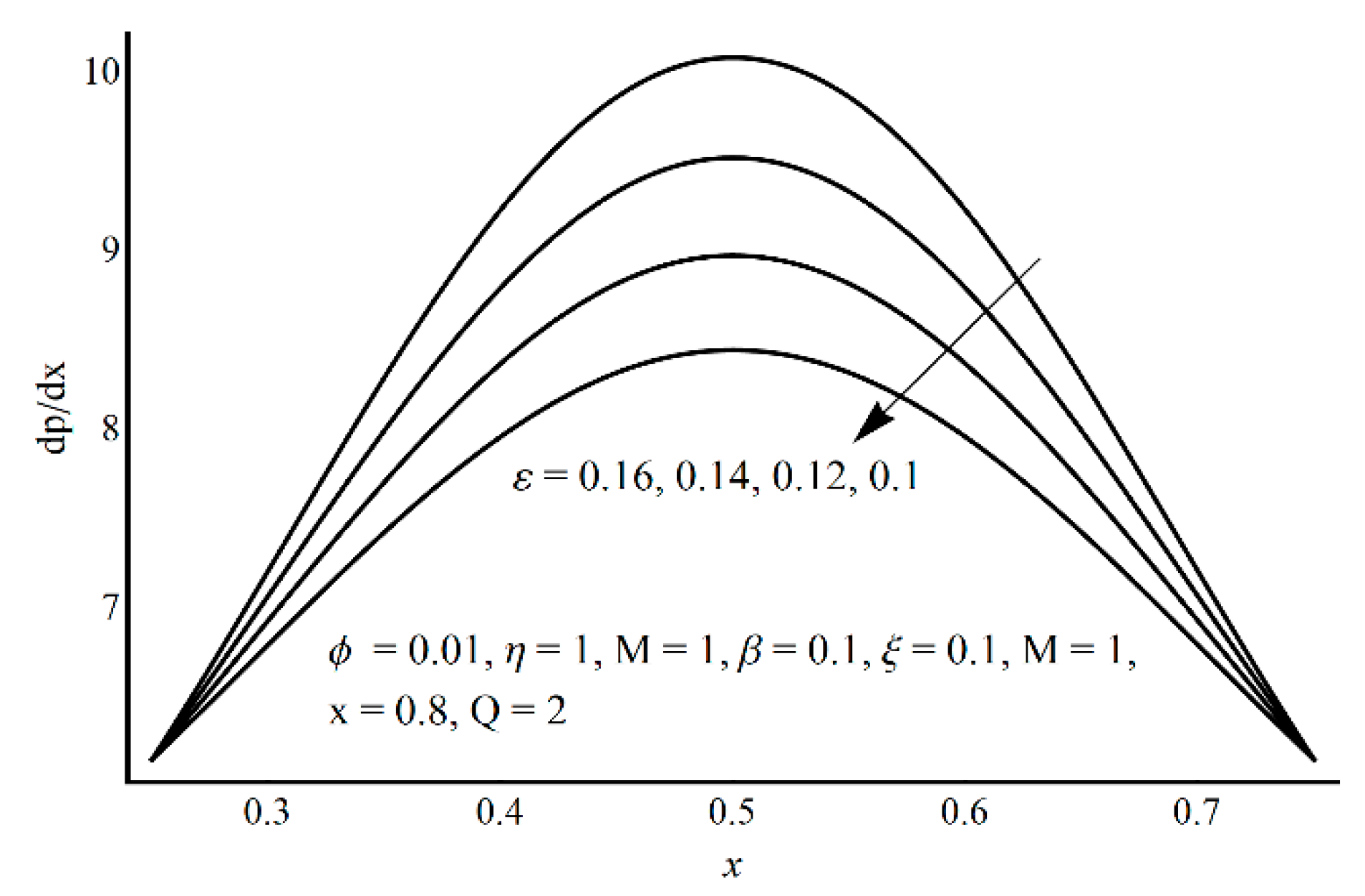
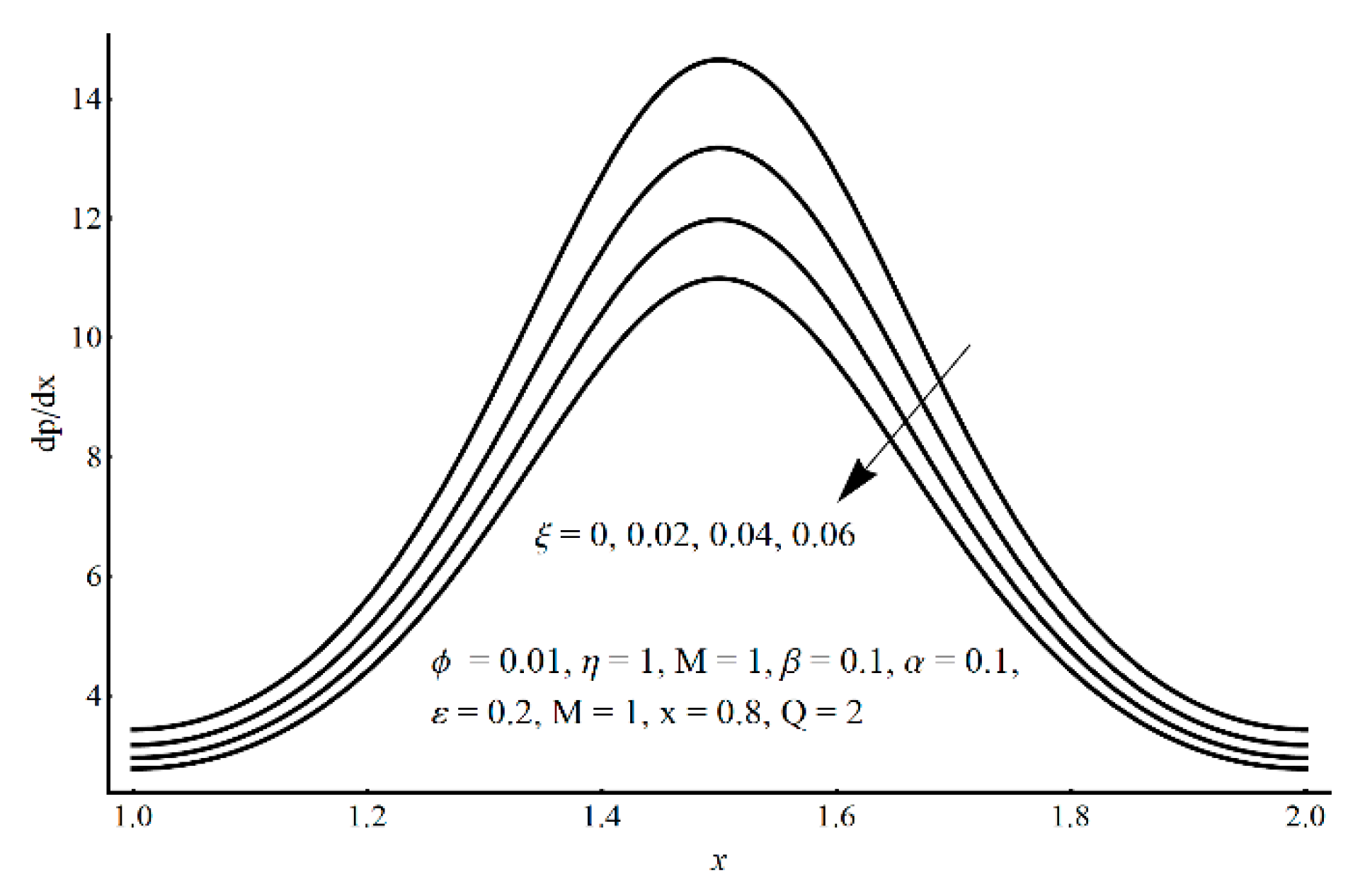
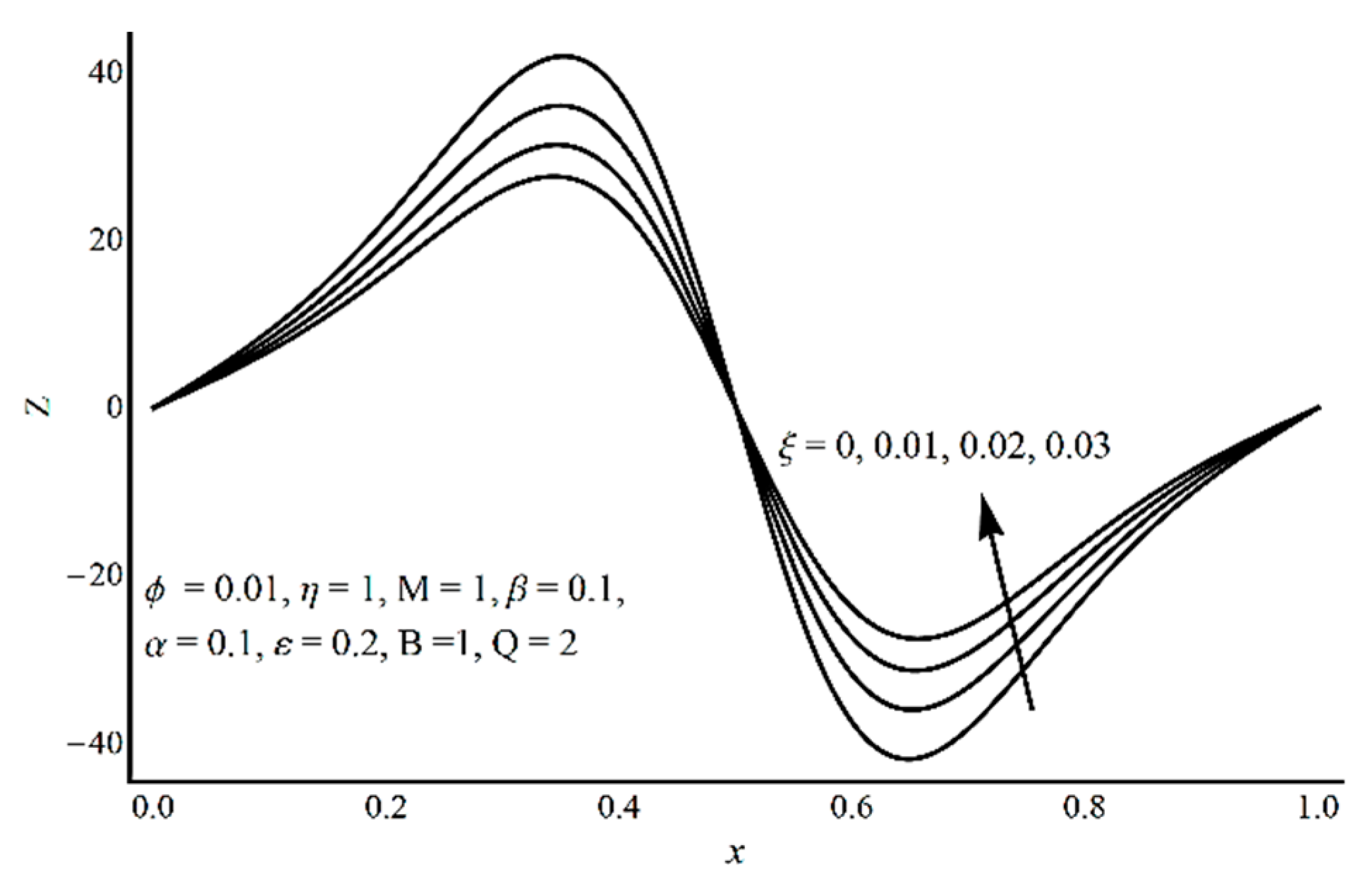
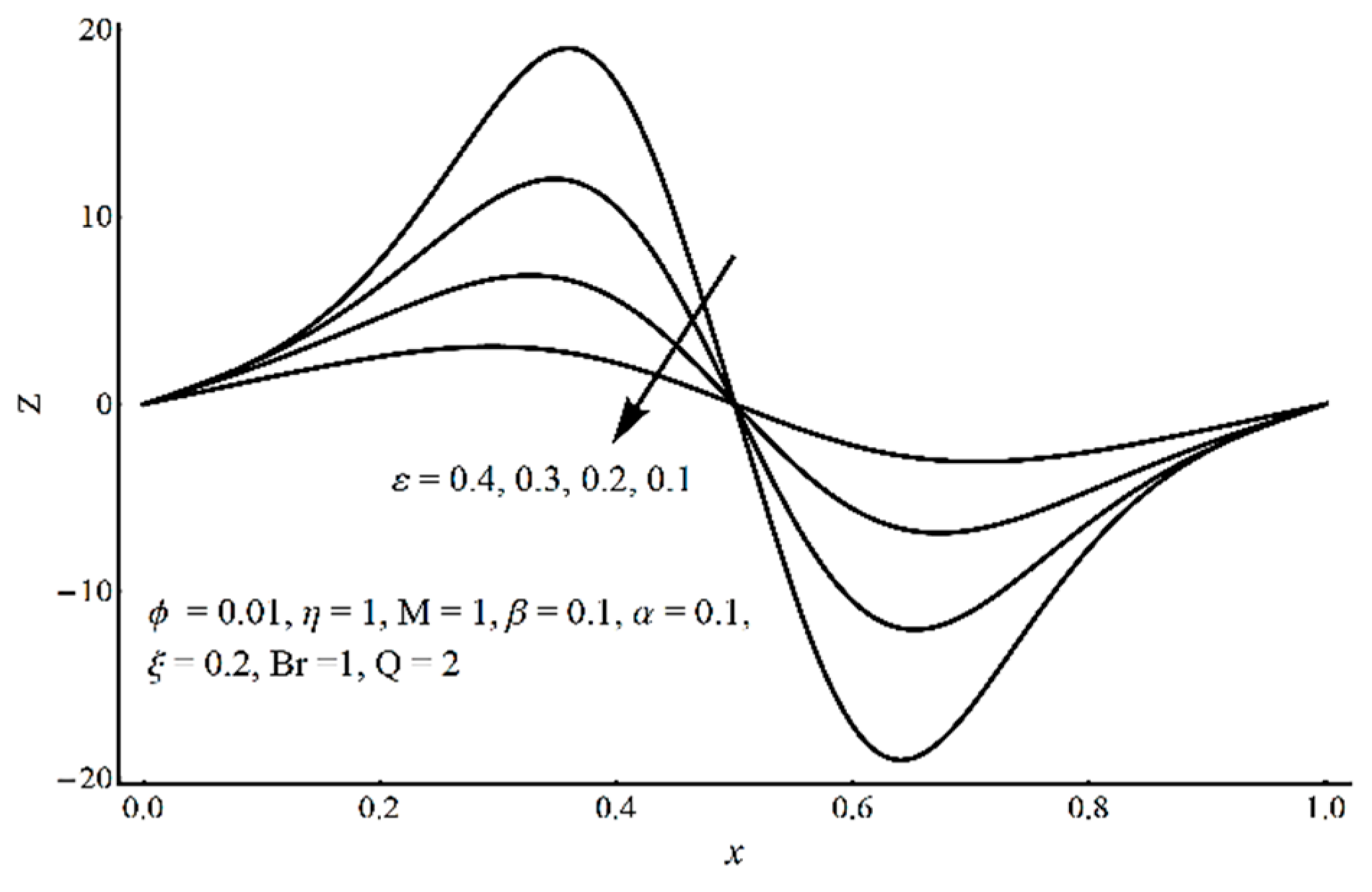
- In the contracted part, a significant elevation in pressure gradient is achieved for small values of ξ and high values of ε and η;
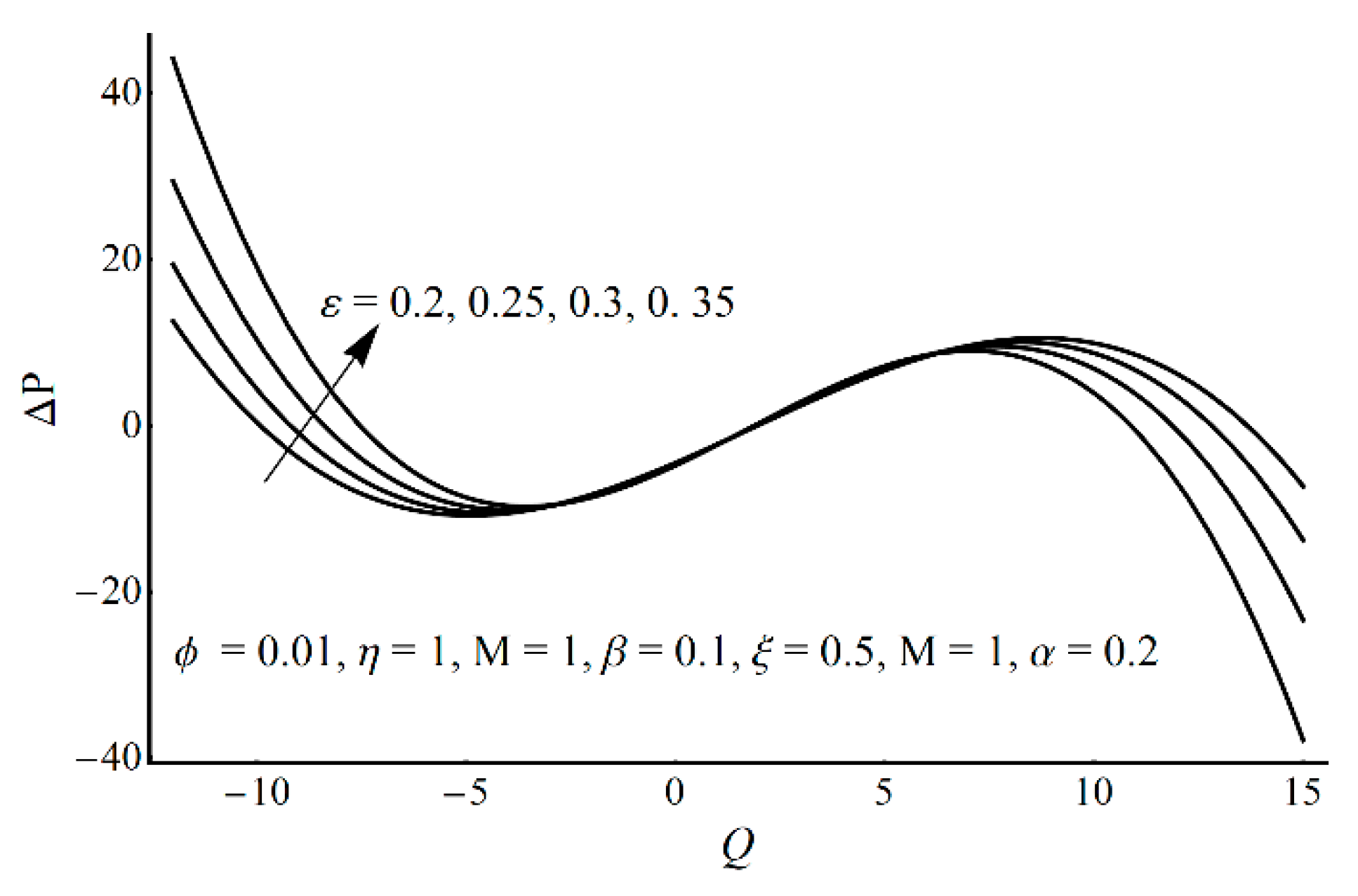
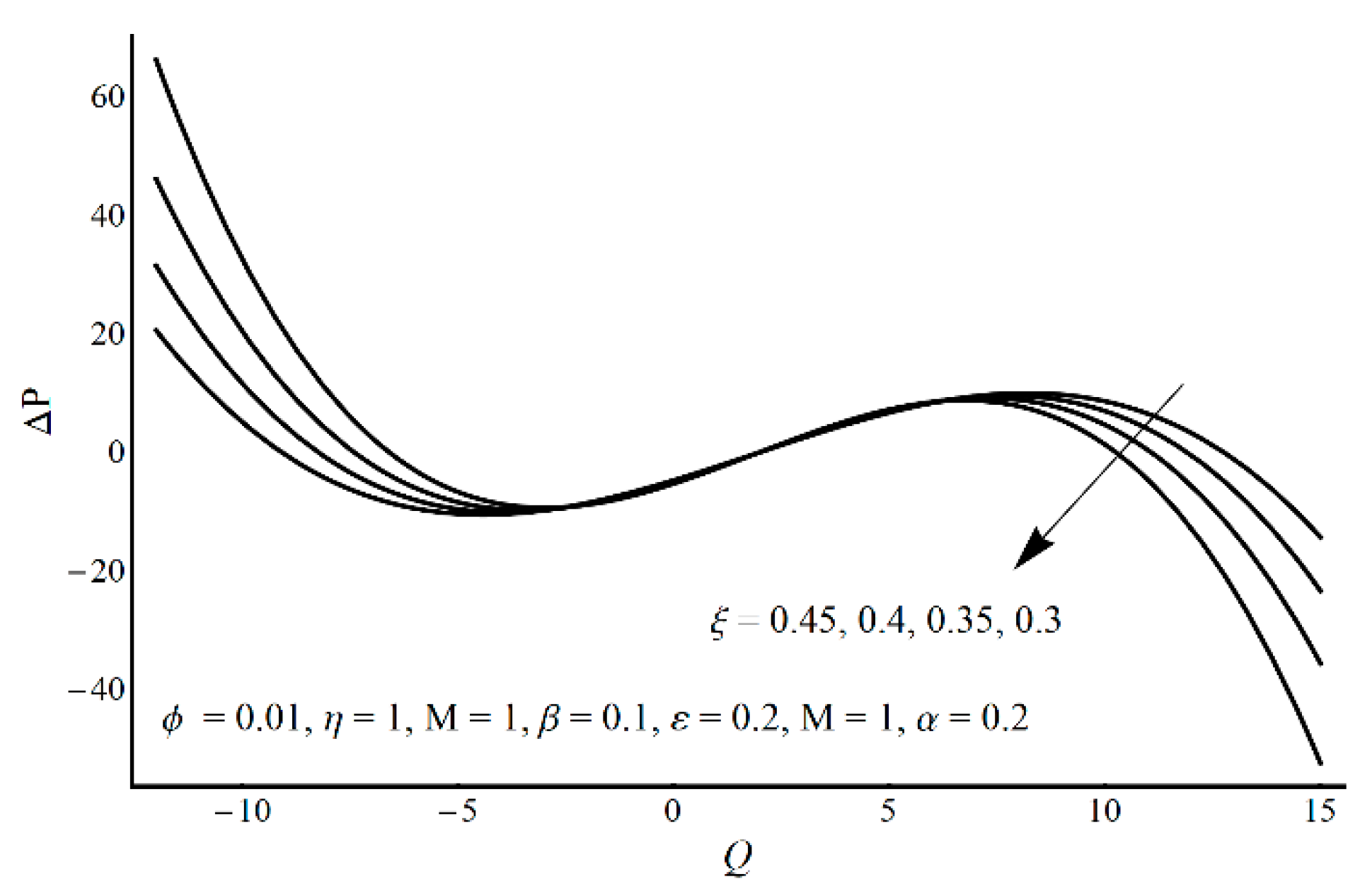
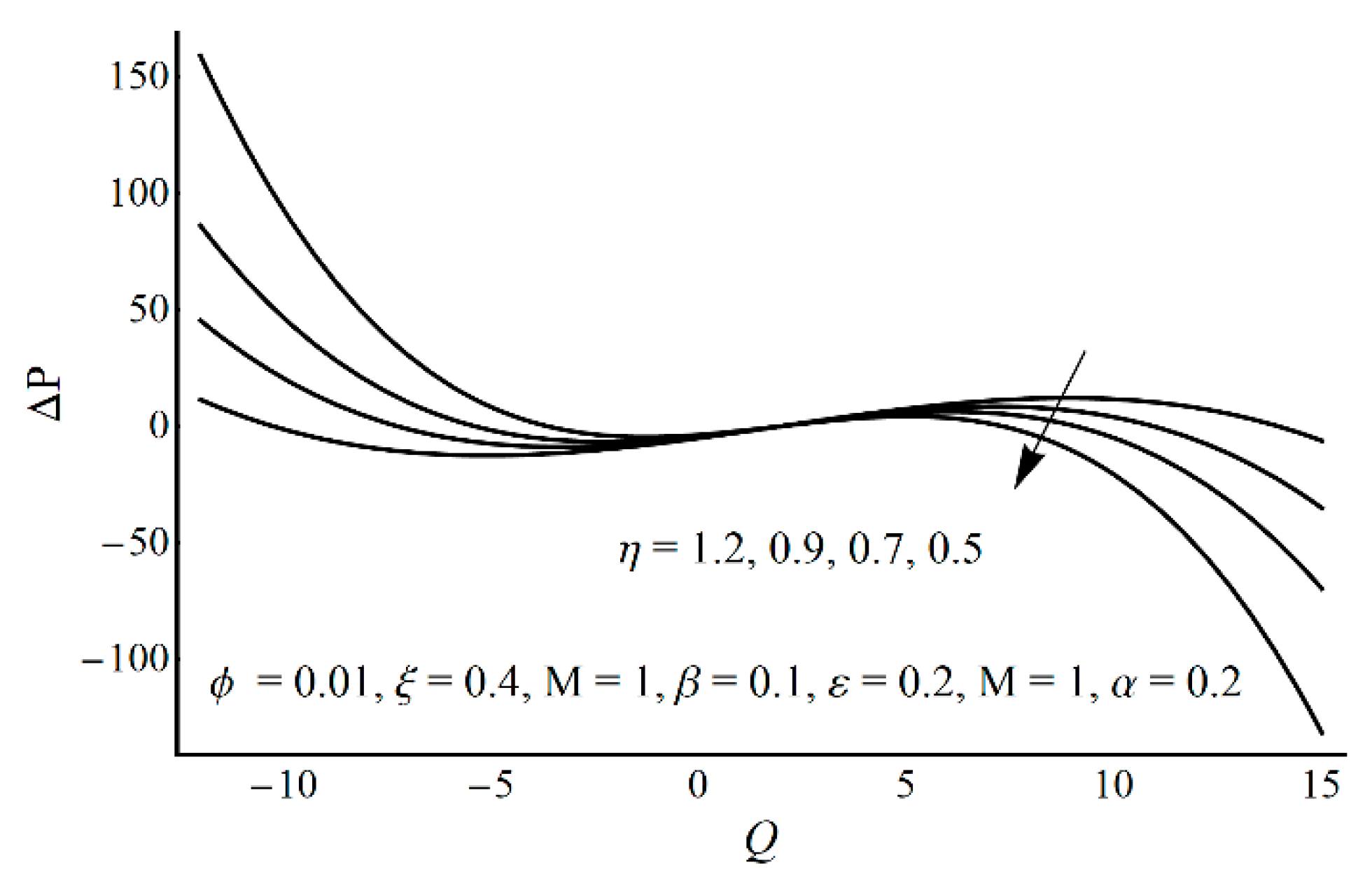
- Pressure-rise per wavelength increases as ε increases and shows a decreasing trend as ξ and η increase in the pumping part and completely reverse conduct in the augmented pumping part;
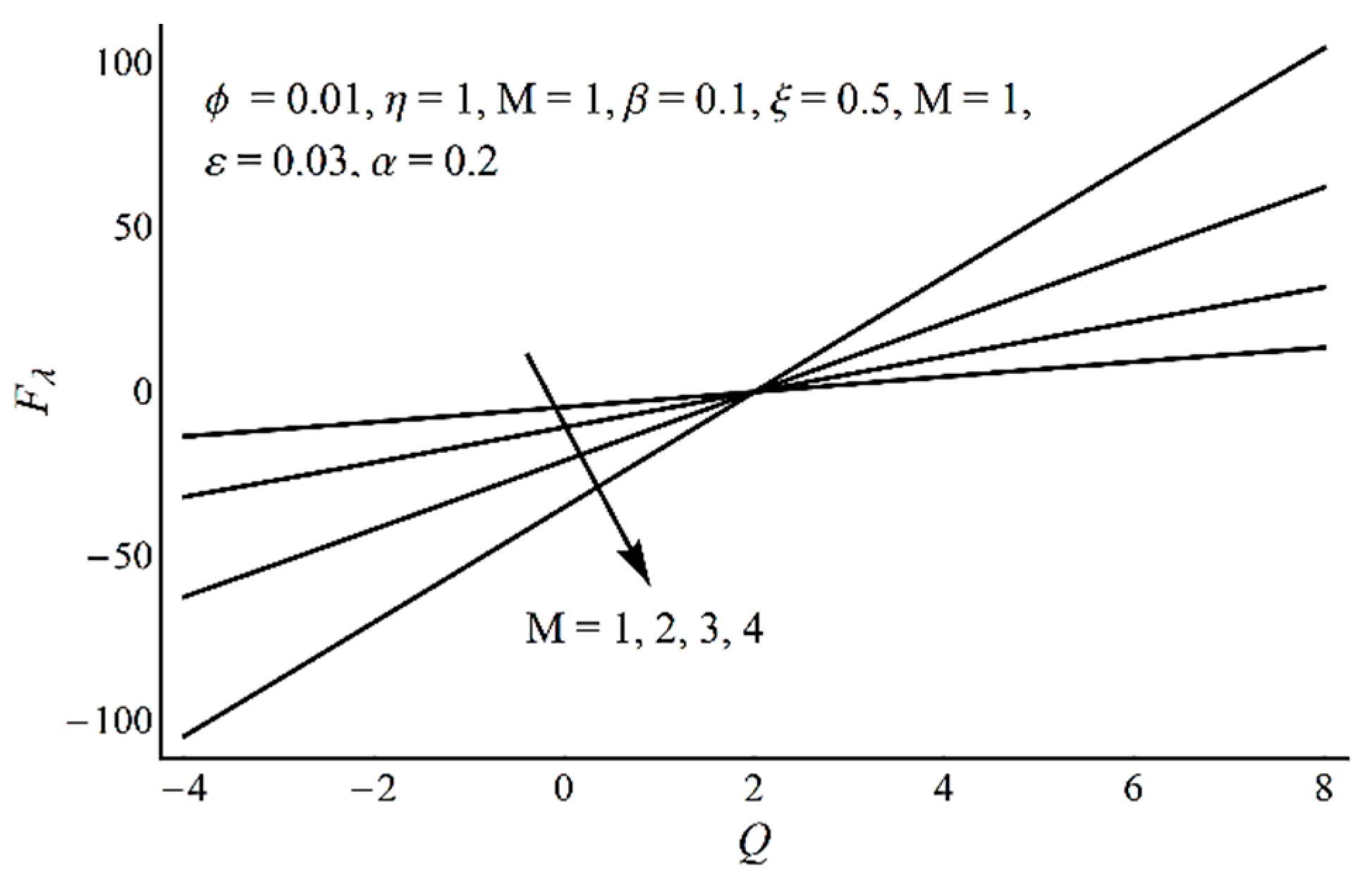
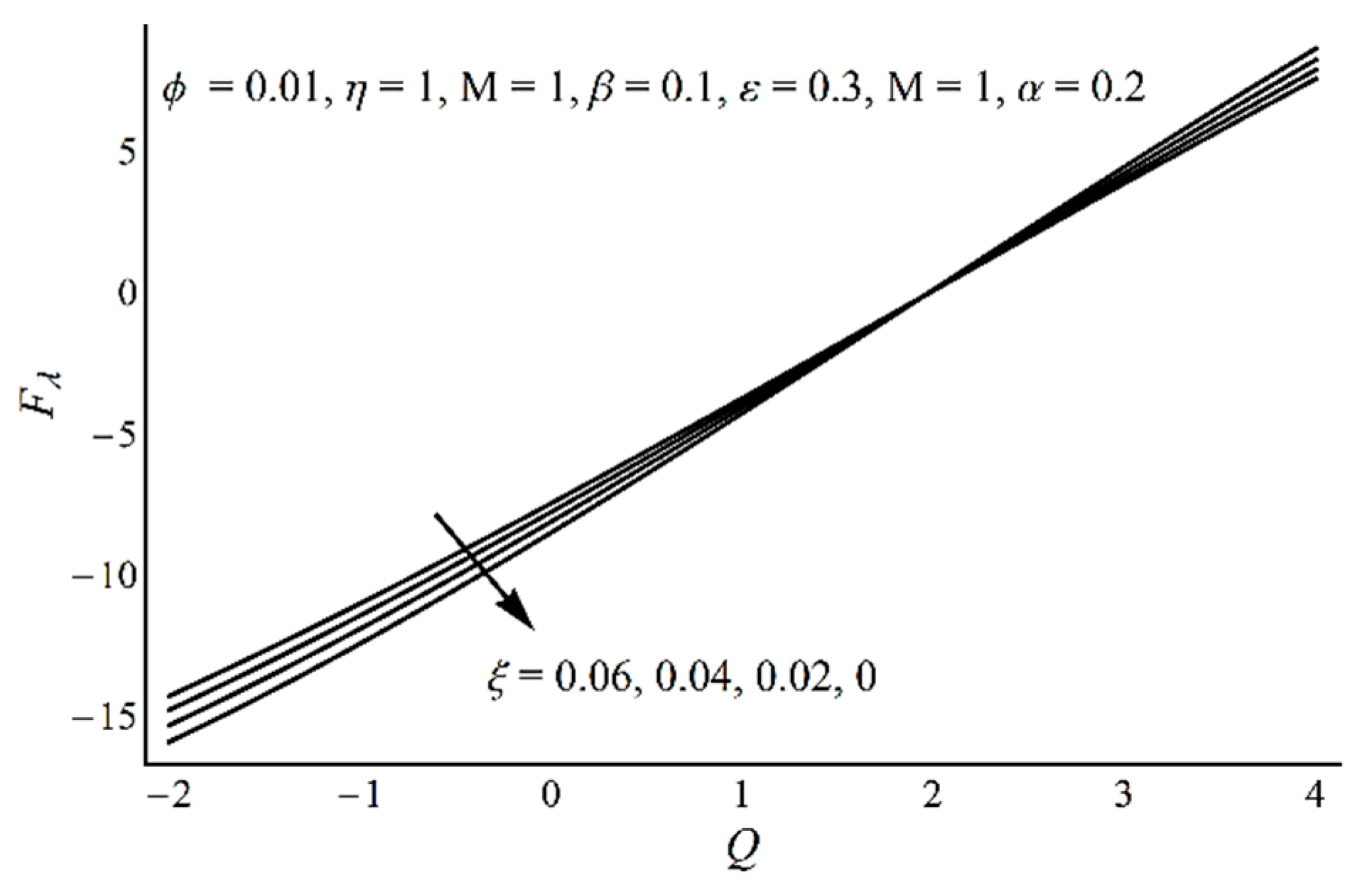
- Frictional force at the wavy wall explains a direct proportionality with mean flow rate.
Author Contributions
Funding
Conflicts of Interest
References
- Bustamante-Marin, X.M.; Ostrowski, L.E. Cilia and mucociliary clearance. Cold Spring Harb Perspect Biol. 2017, 4, a028241. [Google Scholar] [CrossRef]
- Knowles, M.R.; Boucher, R.C. Mucus clearance as a primary innate defense mechanism for mammalian airways. J. Clin. Investig. 2002, 109, 571–577. [Google Scholar] [CrossRef]
- Pablo, J.L.; DeCaen, P.G.; Clapham, D.E. Progress in ciliary ion channel physiology. J. Gen. Physiol. 2016, 1, 37–41. [Google Scholar] [CrossRef]
- Ghazal, S.; Makarov, J.K.; de Jonge, C.J. Egg transport and fertilization. Glob. Libr. Women Med. 2014, 2014. [Google Scholar] [CrossRef]
- Eddy, C.A.; Pauerstein, C.J. Anatomy and physiology of the fallopian tube. Clin. Obstet. Gynecol. 1980, 4, 1177–1193. [Google Scholar] [CrossRef]
- Lehti, M.S.; Sironen, A. Formation and function of sperm tail structures in association with sperm motility defects. Biol. Reprod. 2017, 97, 522–536. [Google Scholar] [CrossRef]
- Mills, Z.; Aziz, B.; Alexeev, A. Beating synthetic cilia enhance heat transport in microfluidic channels. Soft Matter 2012, 45, 11508–11513. [Google Scholar] [CrossRef]
- Drummond, I.A. Cilia functions in development. Curr. Opin. Cell Biol. 2012, 1, 24–30. [Google Scholar] [CrossRef]
- Agrawal, H.L. Anawaruddin. Cilia transport of bio-fluid wih variable viscosity. Indian J. Pure Appl. Math. 1984, 15, 1128–1139. [Google Scholar]
- Qiu, T.; Lee, T.; Mark, A.G.; Morozov, K.I.; Münster, R.; Mierka, O.; Turek, S.; Leshansky, A.M.; Fischer, P. Swimming by reciprocal motion at low Reynolds number. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef]
- Brennen, C. Oscillating-boundary layer theory for ciliary propulsion. J. Fluid Mech. 1974, 65, 799–824. [Google Scholar] [CrossRef]
- Wu, A.; Abbas, S.Z.; Asghar, Z.; Sun, H.; Waqas, M.; Khan, W.A. A shear-rate-dependent flow generated via magnetically controlled metachronal motion of artificial cilia. Biomech. Model. Mechanobiol. 2020. [Google Scholar] [CrossRef]
- Farooq, A.A.; Siddiqui, A.M. Mathematical model for the ciliary-induced transport of seminal liquids through the ductuli efferentes. Int. J. Biomath. 2017, 10, 1750031. [Google Scholar] [CrossRef]
- Farooq, A.A.; Tripathi, D.; Elnaqeeb, T. On the propulsion of micropolar fluid inside a channel due to ciliary induced metachronal wave. Appl. Math. Comput. 2019, 347, 225–235. [Google Scholar] [CrossRef]
- Stud, V.K.; Sephon, G.S.; Mishra, R.K. Pumping action on blood flow by a magnetic field. Bull. Math. Biol. 1977, 39, 385–390. [Google Scholar]
- Mekheimer, K.S. Peristaltic transport of a couple stress fluid in a uniform and non-uniform channels. Biorheology 2002, 39, 755–765. [Google Scholar]
- Hatzikonstantinou, P.M.; Vafeas, P. A general theoretical model for the magnetohydrodynamic flow of micropolar magnetic fluids. Application to Stokes flow. Math. Methods Appl. Sci. 2010, 33, 233–248. [Google Scholar] [CrossRef]
- Tripathi, D.; Jhorar, R.; Beg, O.A. A KadirElectro-magneto-hydrodynamic peristaltic pumping of couple stress biofluids through a complex wavy micro-channel. J. Mol. Liq. 2017, 236, 358–367. [Google Scholar] [CrossRef]
- Akram, S.; Afzal, F.; Imran, M. Influence of metachronal wave on hyperbolic tangent fluid model with inclined magnetic field. Int. J. Geom. Methods. Mod. Phys. 2019, 16, 1950139. [Google Scholar] [CrossRef]
- Mekheimer, K.S.; Mohamed, M.S. Interaction of pulsatile flow on the peristaltic motion of a magneto-micropolar fluid through porous medium in a flexible channel: Blood flow model. Int. J. Pure Appl. Math. 2014, 94, 323–339. [Google Scholar] [CrossRef]
- Saleem, N.; Hayat, T.; Alsaedi, A. A hydromagnetic mathematical model for blood flow of Carreau fluid. Int. J. Biomath. 2014, 7, 1–14. [Google Scholar] [CrossRef]
- Papadopoulos, P.K.; Vafeas, P.; Hatzikonstantinou, P.M. Ferrofluid pipe flow under the influence of the magnetic field of a cylindrical coil. Phys. Fluids 2012, 24, 1–13. [Google Scholar] [CrossRef]
- Taherali, F.; Varum, F.; Basit, A.W. A slippery slope: On the origin, role and physiology of mucus. Adv. Drug Deliv. Rev. 2018, 124, 16–33. [Google Scholar] [CrossRef]
- Tripathi, D.; Beg, O.A.; Curiel-Sosa, J.L. Homotopy semi-numerical simulation of peristaltic flow of generalised Oldroyd-B fluids with slip effects. Comput. Method. Biomec. 2014, 17, 433–442. [Google Scholar] [CrossRef]
- Makinde, O.D.; Reddy, M.G.; Reddy, K.V. Effects of thermal radiation on MHD peristaltic motion of walters-B fluid with heat source and slip conditions. J. Appl. Fluid Mech. 2017, 10, 1105–1112. [Google Scholar] [CrossRef]
- Akram, S. Effects of slip and heat transfer on a peristaltic flow of a Carreau fluid in a vertical asymmetric channel. Comp. Math. Math. Phys. 2014, 54, 1886–1902. [Google Scholar] [CrossRef]
- Akbar, N.; Nadeem, S. Thermal and velocity slip effects on the peristaltic flow of a six constant Jeffrey’s fluid model. Int. J. Heat Mass Tran. 2012, 55, 3964–3970. [Google Scholar] [CrossRef]
- Makinde, O.D. Entropy analysis for MHD boundary layer flow and heat transfer over a flat plate with a convective surface boundary condition. Int. J. Exergy 2012, 10, 142–154. [Google Scholar] [CrossRef]
- Adesanya, S.O.; Makinde, O.D. Thermodynamic analysis for a third-grade fluid through a vertical channel with internal heat generation. J. Hydrodyn. 2015, 27, 264–272. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Selimefendigil, F. MHD free convection and entropy generation in a corrugated cavity filled with a porous medium saturated with nanofluids. Entropy 2018, 20, 846. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A.; Munawar, S. Slip effects on entropy generation in MHD flow over a stretching surface in the presence of thermal radiation. Int. J. Exergy. 2013, 13, 1–20. [Google Scholar] [CrossRef]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Bejan, A. Second-law analysis in heat transfer and thermal design. Adv. Heat Transf. 1982, 15, 1–58. [Google Scholar]
- Souidi, F.; Ayachi, K.; Benyahia, N. Entropy generation rate for a peristaltic pump. J. Non-Equilib. Thermodyn. 2009, 34, 171–194. [Google Scholar] [CrossRef]
- Akbar, N.S. Entropy generation and energy conversion rate for the peristaltic flow in a tube with magnetic field. Energy 2015, 82, 23–30. [Google Scholar] [CrossRef]
- Saleem, N. Entropy production in peristaltic flow of a space dependent viscosity fluid in asymmetric channel. Therm. Sci. 2018, 22, 2909–2918. [Google Scholar] [CrossRef]
- Munawar, S.; Saleem, N.; Aboura, K. Second law analysis in the peristaltic flow of variable viscosity fluid. Int. J. Exergy 2016, 20, 170–185. [Google Scholar]
- Saleem, N.; Munawar, S. Entropy analysis in cilia driven pumping flow of hyperbolic tangent fluid with magnetic field effects. Fluid Dyn. Res. 2020, 52, 2. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Farooq, A.A.; Rana, M.A. Hydromagnetic flow of Newtonian fluid due to ciliary motion in a channel. Magnetohydrodynamics 2014, 50, 109–122. [Google Scholar]
- Ramesh, K.; Tripathi, D.; Beg, O.A. Cilia-assisted hydromagnetic pumping of biorheological couple stress fluids. J. Propul. Power 2019, 8, 221–233. [Google Scholar] [CrossRef]
- Alsaedi, A.; Batool, N.; Yasmin, H.; Hayat, T. Convective heat transfer analysis on prandtl fluid model with peristalsis. Appl. Bionic. Biomech. 2013, 10, 197–208. [Google Scholar] [CrossRef]
- Patel, M.; Timol, M.G. The stress strain relationship for viscous-inelastic non-Newtonian fluids. Int. J. Appl. Math. Mech. 2010, 6, 79–93. [Google Scholar]
- Hayat, T.; Saleem, N.; Ali, N. Peristaltic flow of a Carreau fluid in a channel with different wave forms. Numer. Meth. Part. Differ. Equ. 2010, 26, 519–534. [Google Scholar] [CrossRef]
- Tripathi, D. A mathematical model for the peristaltic flow of chyme movement in small intestine. Math. Biosci. 2011, 233, 90–97. [Google Scholar] [CrossRef]
- Mehmood, O.U.; Mustapha, N.; Shafie, S. Heat transfer on peristaltic flow of fourth grade fluid in inclined asymmetric channel with partial slip. Appl. Math. Mech. 2012, 33, 1313–1328. [Google Scholar] [CrossRef]
- Jothi, S.; Prasad, A.R.; Reddy, M.V.S. Peristaltic flow of a Prandtl fluid in a symmetric channel under the effect of a magnetic field. Adv. Appl. Sci. Res. 2012, 3, 2108–2119. [Google Scholar]
- Bejan, A. Second law analysis in heat transfer. Energy 1980, 5, 720–732. [Google Scholar] [CrossRef]
- Munawar, S.; Saleem, N. Second law analysis of ciliary pumping transport in an inclined channel coated with carreau fluid under a magnetic field. Coatings 2020, 10, 240. [Google Scholar] [CrossRef]










© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munawar, S.; Saleem, N. Entropy Analysis of an MHD Synthetic Cilia Assisted Transport in a Microchannel Enclosure with Velocity and Thermal Slippage Effects. Coatings 2020, 10, 414. https://doi.org/10.3390/coatings10040414
Munawar S, Saleem N. Entropy Analysis of an MHD Synthetic Cilia Assisted Transport in a Microchannel Enclosure with Velocity and Thermal Slippage Effects. Coatings. 2020; 10(4):414. https://doi.org/10.3390/coatings10040414
Chicago/Turabian StyleMunawar, Sufian, and Najma Saleem. 2020. "Entropy Analysis of an MHD Synthetic Cilia Assisted Transport in a Microchannel Enclosure with Velocity and Thermal Slippage Effects" Coatings 10, no. 4: 414. https://doi.org/10.3390/coatings10040414
APA StyleMunawar, S., & Saleem, N. (2020). Entropy Analysis of an MHD Synthetic Cilia Assisted Transport in a Microchannel Enclosure with Velocity and Thermal Slippage Effects. Coatings, 10(4), 414. https://doi.org/10.3390/coatings10040414





