Differences Between Flash Glucose Monitor and Fingerprick Measurements
Abstract
:1. Introduction
2. Method
2.1. Data Collection
2.2. Data Analysis
3. Results
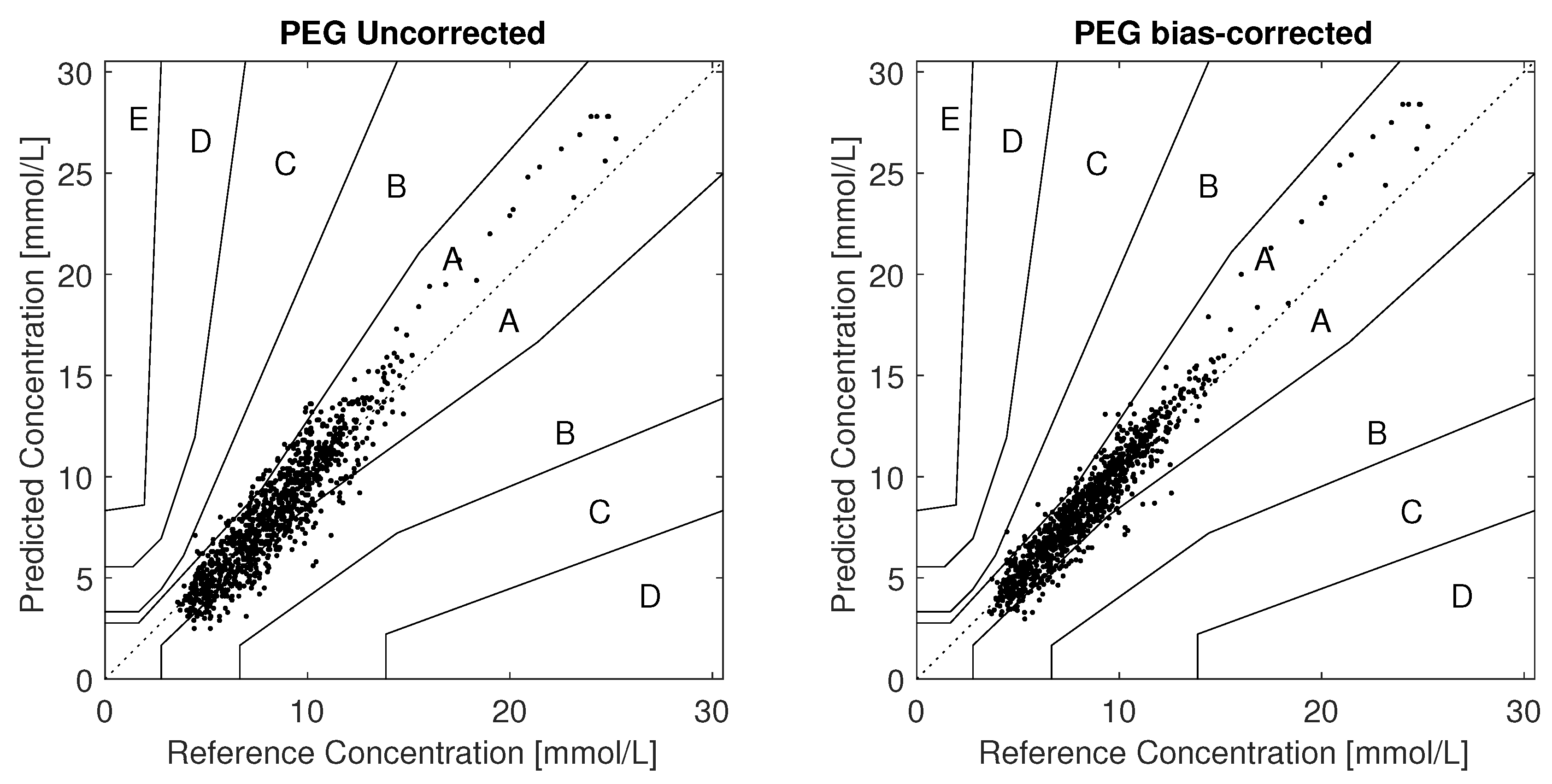
3.1. Overall MARD Analysis in Day 1 Data
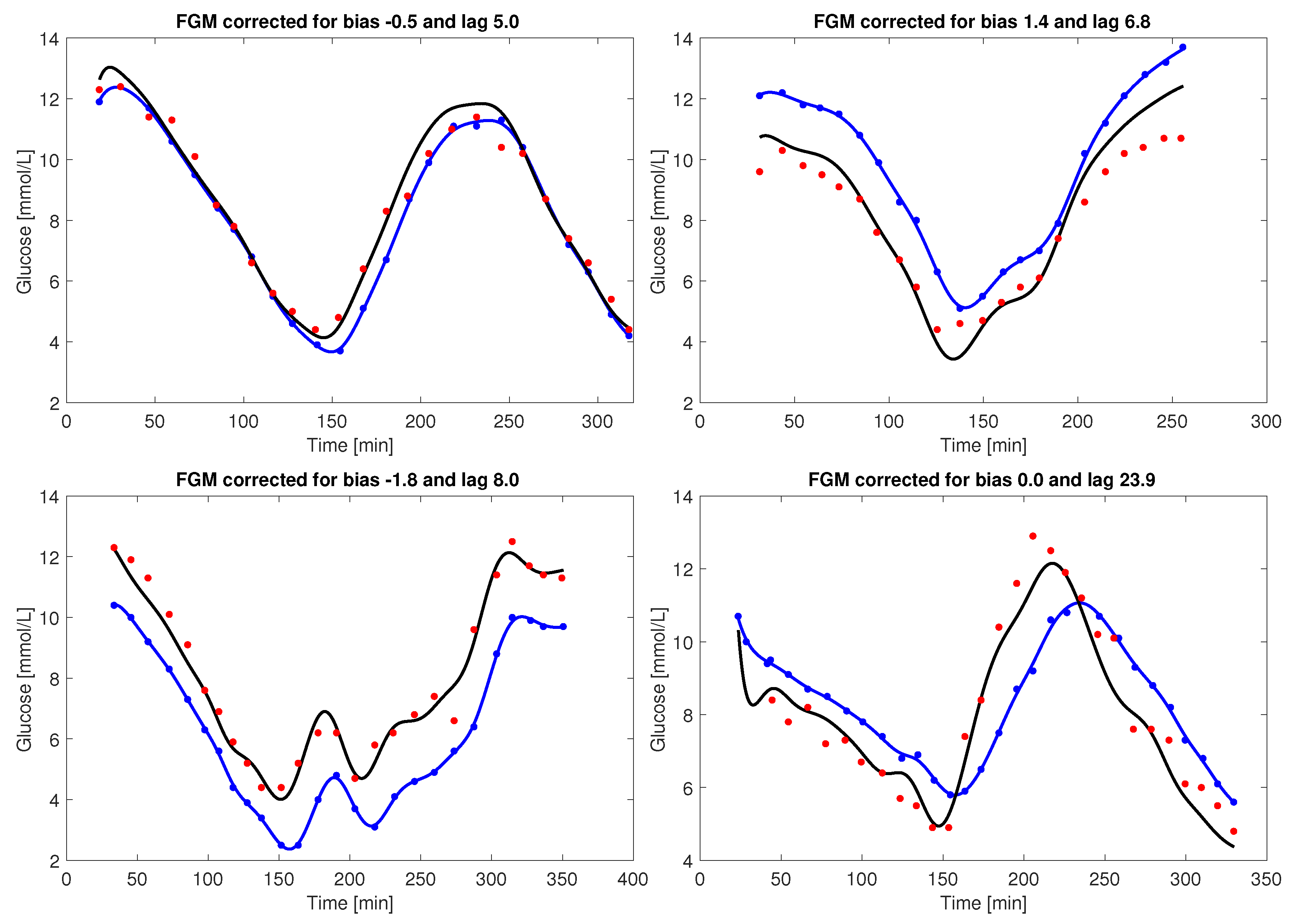
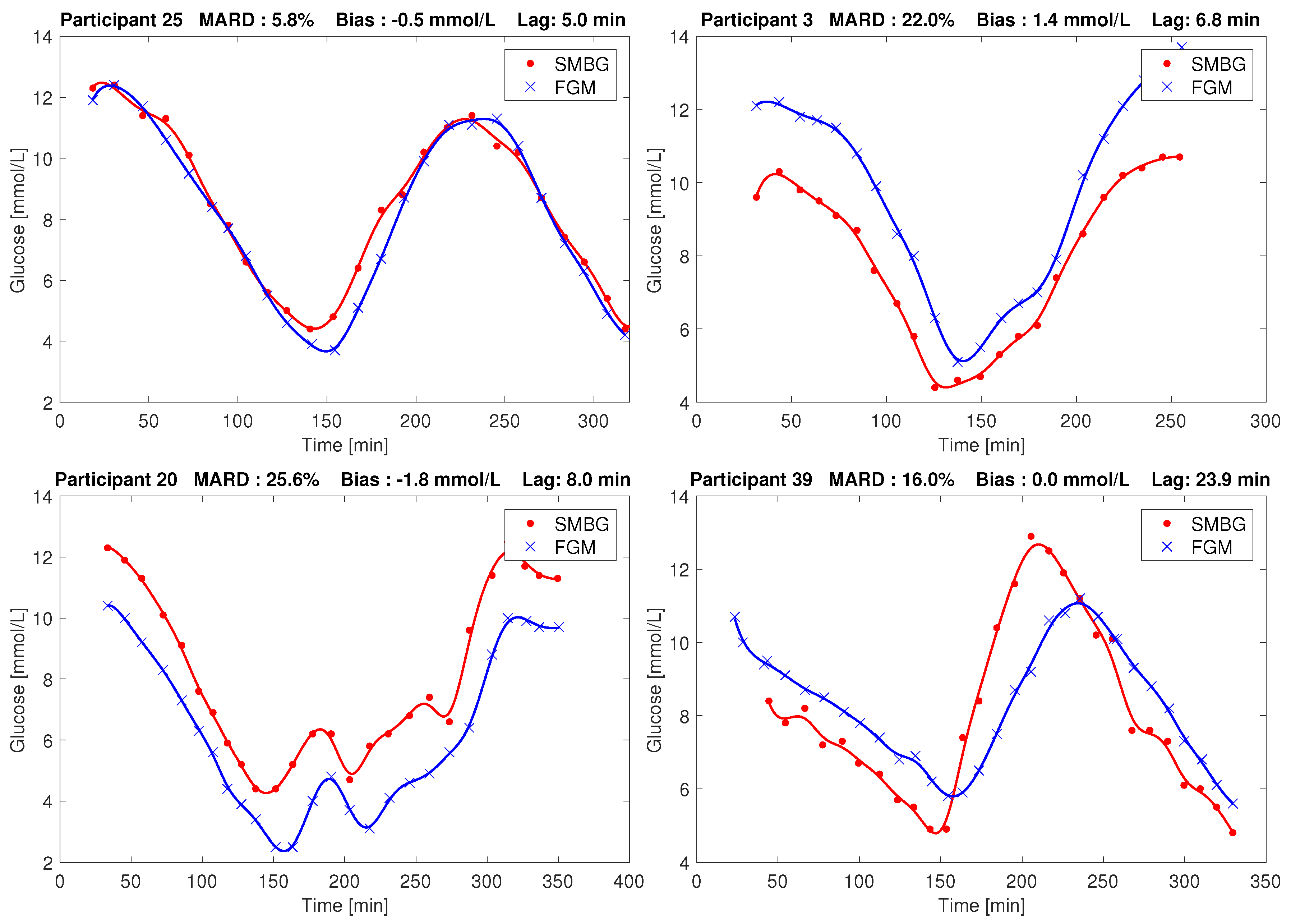
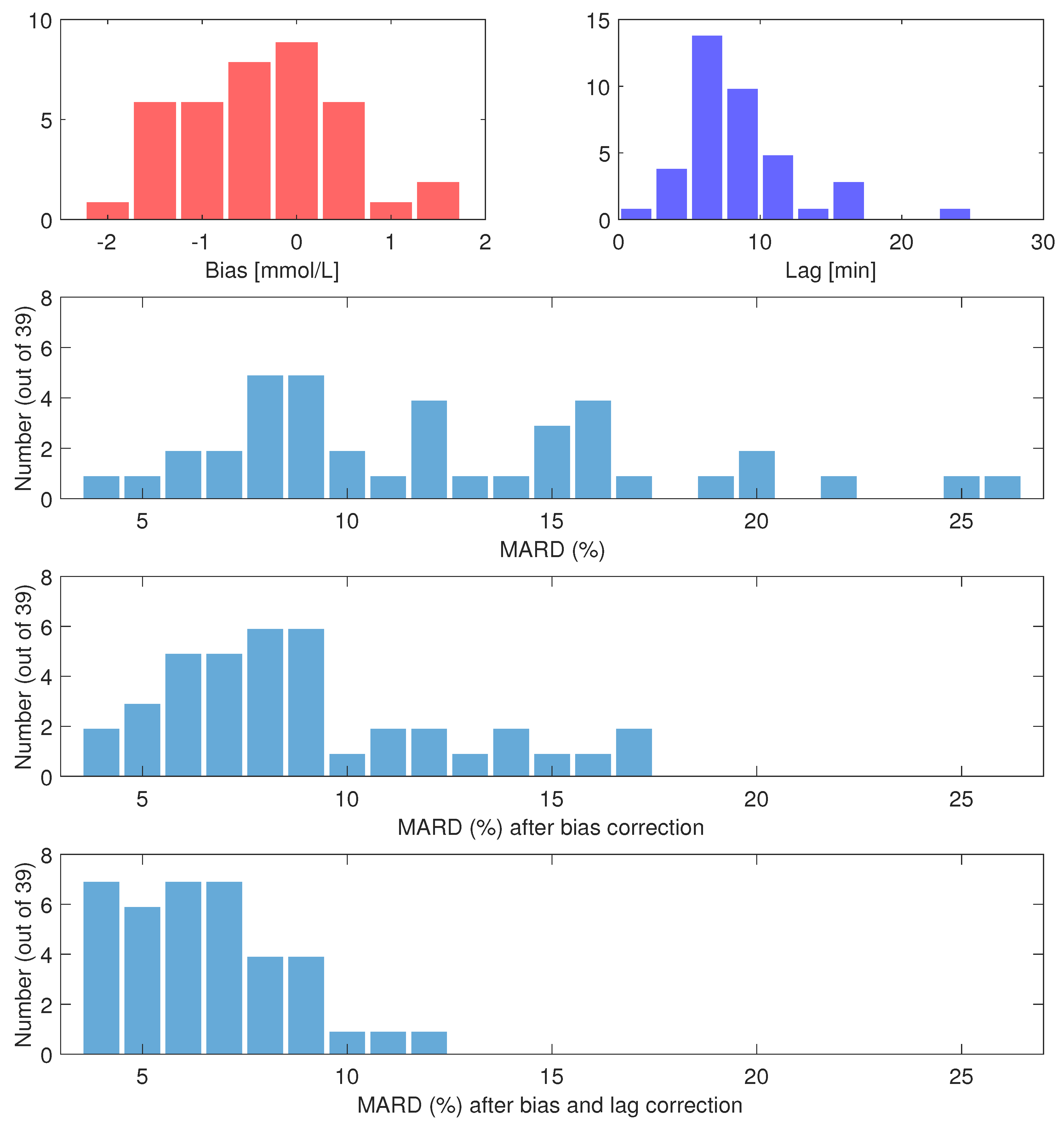
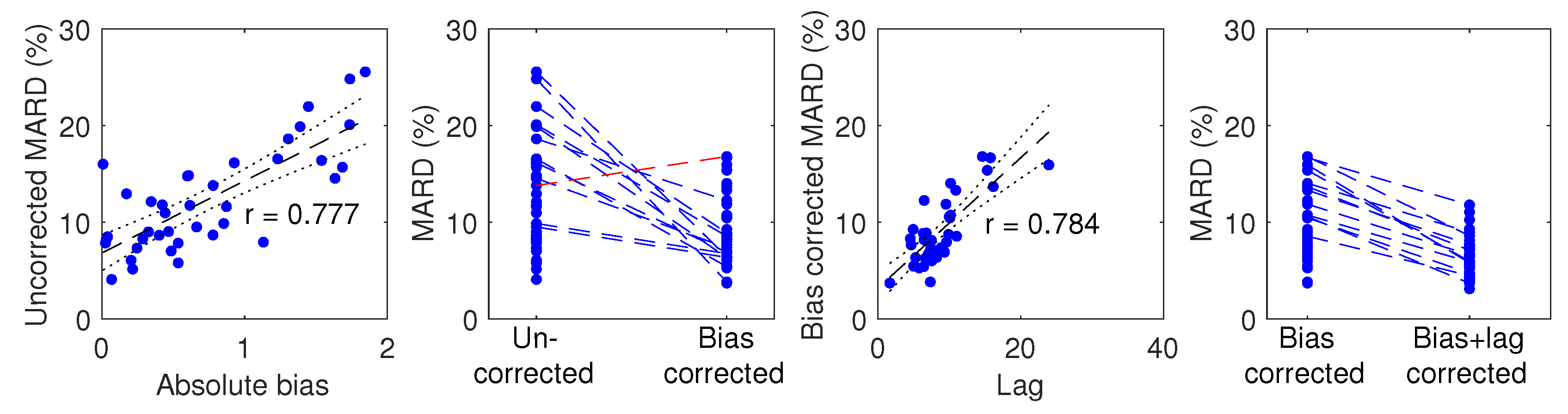
3.2. Day 1 Individual Participant MARD, Bias and Lag Analysis
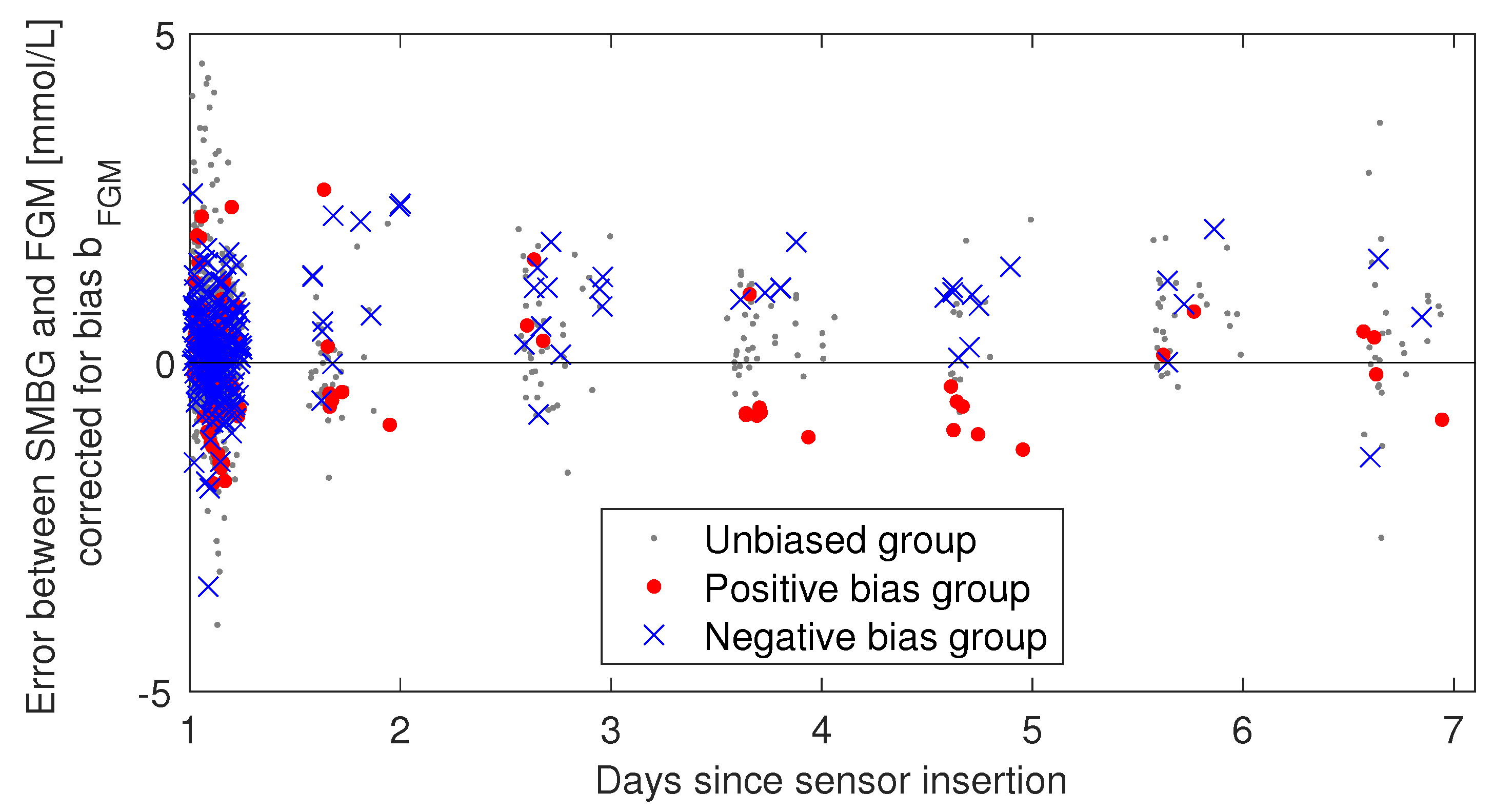
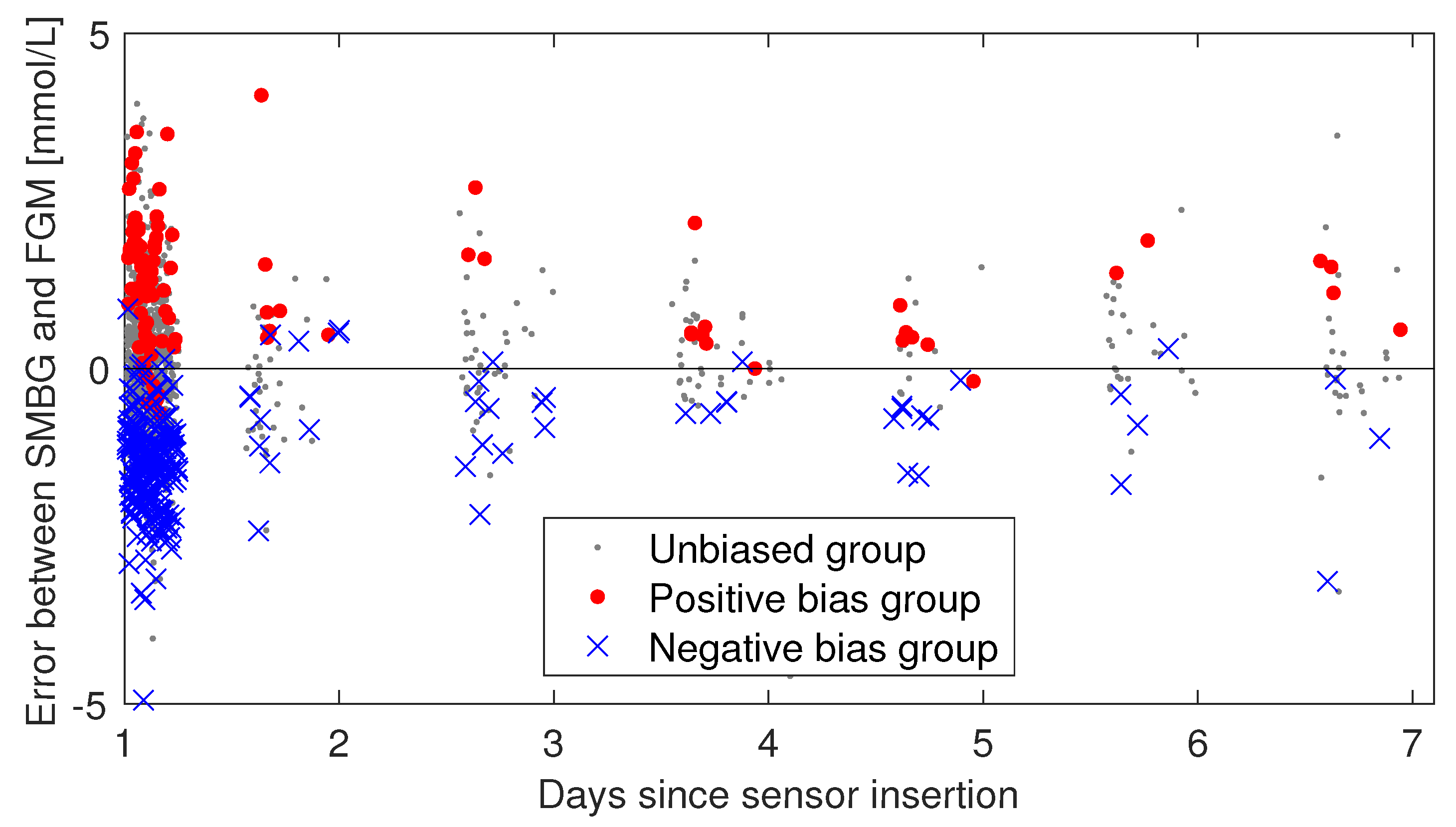
3.3. Persistence of Biases through Days 2–7
3.4. Participant Factors vs. Bias and Llag
4. Discussion
- The insertion of the sensor into the interstitial fluid introduces local trauma to and/or minor bleeds in the tissue around the sensor, altering the glucose flow, thus making the sensor less accurate in the time immediately after insertion [1].
- Biofouling of the sensor contributes to making sensor characteristic changes over the wear time likely.
- On the technical side, the electrochemical sensor may suffer from non-physiological drift in the initial period of sensor wear [9].
- Effects like Pressure Induced Sensitivity Attenuation (PISA) [35] may be present in the FGM data.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MARD | Mean Absolute Relative Difference |
| PARD | Precision Absolute Relative Difference |
| FGM | Flash Glucose Monitor |
| CGM | Continuous Glucose Monitor |
| SMBG | Self Monitoring of Blood Glucose |
| NFC | Near Field Communication |
| FL | Freestyle Libre |
| DG5 | DexCom G5 |
| CI | Confidence Interval |
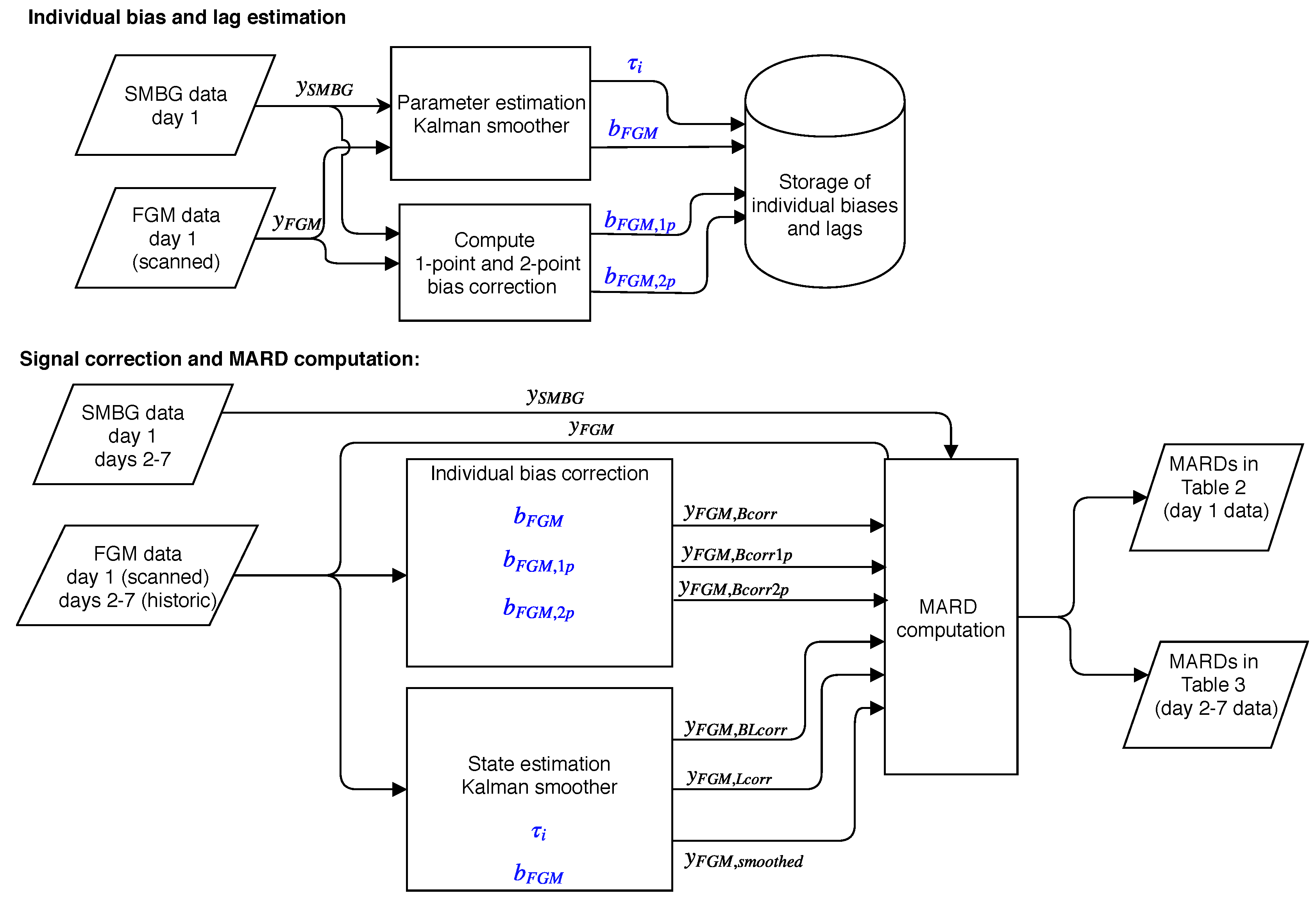
Appendix A. Kalman Smoothing to Correct for Bias and Lag
Appendix B. MARD Analysis of Day 2–7 Data Using Different Bias Correction Approaches
| Signal Processing | Symbol | MARD (%) | MAD (mmol/L) | PEG zone A/A+B (%) |
|---|---|---|---|---|
| None (FGM historic data vs SMBG) | 11.3 | 0.8 | 87.3/99.2 | |
| Bias corrected, multipoint | 12.5 | 0.8 | 89.0/97.7 | |
| Bias corrected, 1-point | 13.8 | 0.9 | 82.4/99.7 | |
| Bias corrected, 2-point | 12.2 | 0.8 | 89.2/99.7 | |
| Bias and lag corrected, multipoint | 12.7 | 0.8 | 86.7/97.5 |
References
- Schrangl, P.; Reiterer, F.; Heinemann, L.; Freckmann, G.; del Re, L. Limits to the Evaluation of the Accuracy of Continuous Glucose Monitoring Systems by Clinical Trials. Biosensors 2018, 8, 50. [Google Scholar] [CrossRef] [PubMed]
- Cengiz, E.; Tamborlane, W.V. A tale of two compartments: interstitial versus blood glucose monitoring. Diabetes Technol. Ther. 2009, 11, S11–S16. [Google Scholar] [CrossRef] [PubMed]
- Rebrin, K.; Sheppard, N.F.; Steil, G.M. Use of subcutaneous interstitial fluid glucose to estimate blood glucose: revisiting delay and sensor offset. J Diabetes Sci. Technol. 2010, 4, 1087–1098. [Google Scholar] [CrossRef] [PubMed]
- Facchinetti, A.; Del Favero, S.; Sparacino, G.; Castle, J.R.; Ward, W.K.; Cobelli, C. Modeling the glucose sensor error. IEEE Trans. Biomed. Eng. 2014, 61, 620–629. [Google Scholar] [CrossRef] [PubMed]
- Schmelzeisen-Redeker, G.; Schoemaker, M.; Kirchsteiger, H.; Freckmann, G.; Heinemann, L.; Del Re, L. Time delay of CGM sensors: Relevance, causes, and countermeasures. J. Diabetes Sci. Technol. 2015, 9, 1006–1015. [Google Scholar] [CrossRef] [PubMed]
- Shah, V.N.; Laffel, L.M.; Wadwa, R.P.; Garg, S.K. Performance of a Factory-Calibrated Real-Time Continuous Glucose Monitoring System Utilizing an Automated Sensor Applicator. Diabetes Technol. Therapeutics 2018, 20, 428–433. [Google Scholar] [CrossRef] [PubMed]
- Bailey, T.; Bode, B.W.; Christiansen, M.P.; Klaff, L.J.; Alva, S. The performance and usability of a factory- calibrated Flash Glucose Monitoring system. Diabetes Technol. Ther. 2015, 17, 787–794. [Google Scholar] [CrossRef] [PubMed]
- FreeStyle Libre | FreeStyle Blood Glucose Meters. Available online: https://abbottdiabetescare.co.uk/our-products/freestyle-libre (accessed on 20 December 2015).
- Acciaroli, G.; Vettoretti, M.; Facchinetti, A.; Sparacino, G. Calibration of minimally invasive continuous glucose monitoring sensors: state-of-the-art and current perspectives. Biosensors 2018, 8, 24. [Google Scholar] [CrossRef] [PubMed]
- Facchinetti, A.; Sparacino, G.; Cobelli, C. Modeling the error of continuous glucose monitoring sensor data: critical aspects discussed through simulation studies. J. Diabetes Sci. Technol. 2010, 4, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Pleus, S.; Heinemann, L.; Freckmann, G. Blood Glucose Monitoring Data Should Be Reported in Detail When Studies About Efficacy of Continuous Glucose Monitoring Systems Are Published. J. Diabetes Sci. Technol. 2018, 12, 1061–1063. [Google Scholar] [CrossRef] [PubMed]
- Staal, O.M.; Sælid, S.; Fougner, A.L.; Stavdahl, Ø. Kalman smoothing for objective and automatic preprocessing of glucose data. IEEE J. Biomed. Health Inform. 2018. [Google Scholar] [CrossRef] [PubMed]
- Parkes, J.L.; Slatin, S.L.; Pardo, S.; Ginsberg, B.H. A new consensus error grid to evaluate the clinical significance of inaccuracies in the measurement of blood glucose. Diabetes Care 2000, 23, 1143–1148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rauch, H.E.; Striebel, C.; Tung, F. Maximum likelihood estimates of linear dynamic systems. AIAA J. 1965, 3, 1445–1450. [Google Scholar] [CrossRef]
- Gustafsson, F. Statistical Sensor Fusion; Studentlitteratur AB: Lund, Sweden, 2010; pp. 178–179. [Google Scholar]
- Stavdahl, Ø.; Fougner, A.L.; Kölle, K.; Christiansen, S.C.; Ellingsen, R.; Carlsen, S.M. The artificial pancreas: A dynamic challenge. IFAC-PapersOnLine 2016, 49. [Google Scholar] [CrossRef]
- Del Favero, S.; Facchinetti, A.; Sparacino, G.; Cobelli, C. Improving accuracy and precision of glucose sensor profiles: Retrospective fitting by constrained deconvolution. IEEE Trans. Biomed. Eng. 2014, 61, 1044–1053. [Google Scholar] [CrossRef] [PubMed]
- Guerra, S.; Facchinetti, A.; Sparacino, G.; Nicolao, G.D.; Cobelli, C. Enhancing the accuracy of subcutaneous glucose sensors: A real-time deconvolution-based approach. IEEE Trans. Biomed. Eng. 2012, 59, 1658–1669. [Google Scholar] [CrossRef] [PubMed]
- Pleus, S.; Kamecke, U.; Link, M.; Haug, C.; Freckmann, G. Flash Glucose Monitoring: Differences Between Intermittently Scanned and Continuously Stored Data. J. Diabetes Sci. Technol. 2018, 12, 397–400. [Google Scholar] [CrossRef] [PubMed]
- Fokkert, M.J.; van Dijk, P.R.; Edens, M.A.; Abbes, S.; de Jong, D.; Slingerland, R.J.; Bilo, H.J. Performance of the FreeStyle Libre Flash glucose monitoring system in patients with type 1 and 2 diabetes mellitus. BMJ Open Diabetes Res. Care 2017, 5, 1. [Google Scholar] [CrossRef] [PubMed]
- Ólafsdóttir, A.F.; Attvall, S.; Sandgren, U.; Dahlqvist, S.; Pivodic, A.; Skrtic, S.; Theodorsson, E.; Lind, M. A clinical trial of the accuracy and treatment experience of the flash glucose monitor FreeStyle Libre in adults with type 1 diabetes. Diabetes Technol. Ther. 2017, 19, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Sekido, K.; Sekido, T.; Kaneko, A.; Hosokawa, M.; Sato, A.; Sato, Y.; Yamazaki, M.; Komatsu, M. Careful readings for a flash glucose monitoring system in nondiabetic Japanese subjects: individual differences and discrepancy in glucose concentrarion after glucose loading [Rapid Communication]. Endocr. J. 2017, 64, 827–832. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ancona, P.; Eastwood, G.M.; Lucchetta, L.; Ekinci, E.I.; Bellomo, R.; Martensson, J. The performance of flash glucose monitoring in critically ill patients with diabetes. Crit Care Resusc 2017, 19, 167–174. [Google Scholar] [PubMed]
- Alsaffar, H.; Turner, L.; Yung, Z.; Didi, M.; Senniappan, S. Continuous Flash Glucose Monitoring in children with Congenital Hyperinsulinism; first report on accuracy and patient experience. Int. J. Pediatr. Endocrin. 2018, 2018, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boscari, F.; Galasso, S.; Facchinetti, A.; Marescotti, M.C.; Vallone, V.; Amato, A.M.L.; Avogaro, A.; Bruttomesso, D. FreeStyle Libre and Dexcom G4 Platinum sensors: Accuracy comparisons during two weeks of home use and use during experimentally induced glucose excursions. Nutr. Metab. Cardiovasc Dis. 2018, 28, 180–186. [Google Scholar] [CrossRef] [PubMed]
- Scott, E.M.; Bilous, R.W.; Kautzky-Willer, A. Accuracy, user acceptability, and safety evaluation for the FreeStyle Libre Flash glucose monitoring system when used by pregnant women with diabetes. Diabetes Technol. Ther. 2018, 20, 180–188. [Google Scholar] [CrossRef] [PubMed]
- Bonora, B.; Maran, A.; Ciciliot, S.; Avogaro, A.; Fadini, G. Head-to-head comparison between flash and continuous glucose monitoring systems in outpatients with type 1 diabetes. J. Endocrinol. Invest. 2016, 39, 1391–1399. [Google Scholar] [CrossRef] [PubMed]
- Aberer, F.; Hajnsek, M.; Rumpler, M.; Zenz, S.; Baumann, P.M.; Elsayed, H.; Puffing, A.; Treiber, G.; Pieber, T.R.; Sourij, H.; et al. Evaluation of subcutaneous glucose monitoring systems under routine environmental conditions in patients with type 1 diabetes. Diabetes Obes Metab. 2017, 19, 1051–1055. [Google Scholar] [CrossRef] [PubMed]
- Freckmann, G.; Link, M.; Pleus, S.; Westhoff, A.; Kamecke, U.; Haug, C. Measurement Performance of Two Continuous Tissue Glucose Monitoring Systems Intended for Replacement of Blood Glucose Monitoring. Diabetes Technol. Ther. 2018, 20, 541–549. [Google Scholar] [CrossRef] [PubMed]
- Bösch, P.C.; Åm, M.K.; Stavdahl, Ø.; Fougner, A.L.; Ellingsen, S.M.C.R.; Hjelme, D.R. Setup and procedure for intraperitoneal glucose monitoring in anaesthetised animals. Poster Presentation at Advanced Technologies & Treatments for Diabetes (ATTD), Paris, France, 2017. [Google Scholar]
- Hoss, U.; Budiman, E.S. Factory-calibrated continuous glucose sensors: the science behind the technology. Diabetes Technol. Ther. 2017, 19, S44–S50. [Google Scholar] [CrossRef] [PubMed]
- Vettoretti, M.; Facchinetti, A.; Sparacino, G.; Cobelli, C. A model of self-monitoring blood glucose measurement error. J. Diabetes Sci. Technol. 2017, 11, 724–735. [Google Scholar] [CrossRef] [PubMed]
- Link, M.; Schmid, C.; Pleus, S.; Baumstark, A.; Rittmeyer, D.; Haug, C.; Freckmann, G. System accuracy evaluation of four systems for self-monitoring of blood glucose following ISO 15197 using a glucose oxidase and a hexokinase-based comparison method. J. Diabetes Sci. Technol. 2015, 9, 1041–1050. [Google Scholar] [CrossRef] [PubMed]
- Freckmann, G.; Baumstark, A.; Schmid, C.; Pleus, S.; Link, M.; Haug, C. Evaluation of 12 blood glucose monitoring systems for self-testing: system accuracy and measurement reproducibility. Diabetes Technol. Ther. 2014, 16, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Baysal, N.; Cameron, F.; Buckingham, B.A.; Wilson, D.M.; Chase, H.P.; Maahs, D.M.; Bequette, B.W.; Buckingham, B.A.; Wilson, D.M.; Aye, T.; et al. A novel method to detect pressure-induced sensor attenuations (PISA) in an artificial pancreas. J. Diabetes Sci. Technol. 2014, 8, 1091–1096. [Google Scholar] [CrossRef] [PubMed]
| Sex | 14 female, 25 male |
| Age | 42 (18–72) |
| Duration of diabetes | 23 (3–45) |
| Body Mass Index (BMI) | 27 (21–38) / |
| Signal Processing | Symbol | MARD (%) | MAD (mmol/L) | PEG zone A/A+B (%) |
|---|---|---|---|---|
| None (raw FGM scans vs SMBG) | 12.3 | 1.0 | 81.7/100 | |
| Bias corrected, multipoint | 9.2 | 0.8 | 91.2/100 | |
| Bias corrected, 1-point | 11.4 | 0.9 | 83.0/100 | |
| Bias corrected, 2-point | 9.7 | 0.7 | 87.7/100 | |
| Bias and lag corrected, multipoint | 6.6 | 0.5 | 97/100 | |
| Only lag corrected, multipoint | 11.7 | 0.9 | 81.5/100 | |
| Only smoothed, multipoint | 11.9 | 1.0 | 82.2/100 |
| Group | Number of Participants | Mean ± SD (N) Day 1 | Mean ± SD (N) Days 2–7 |
|---|---|---|---|
| Positive bias | 3 | (96) | (35) * |
| Unbiased | 28 | (755) | (270) |
| Negative bias | 8 | (202) | (51) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staal, O.M.; Hansen, H.M.U.; Christiansen, S.C.; Fougner, A.L.; Carlsen, S.M.; Stavdahl, Ø. Differences Between Flash Glucose Monitor and Fingerprick Measurements. Biosensors 2018, 8, 93. https://doi.org/10.3390/bios8040093
Staal OM, Hansen HMU, Christiansen SC, Fougner AL, Carlsen SM, Stavdahl Ø. Differences Between Flash Glucose Monitor and Fingerprick Measurements. Biosensors. 2018; 8(4):93. https://doi.org/10.3390/bios8040093
Chicago/Turabian StyleStaal, Odd Martin, Heidi Marie Umbach Hansen, Sverre Christian Christiansen, Anders Lyngvi Fougner, Sven Magnus Carlsen, and Øyvind Stavdahl. 2018. "Differences Between Flash Glucose Monitor and Fingerprick Measurements" Biosensors 8, no. 4: 93. https://doi.org/10.3390/bios8040093
APA StyleStaal, O. M., Hansen, H. M. U., Christiansen, S. C., Fougner, A. L., Carlsen, S. M., & Stavdahl, Ø. (2018). Differences Between Flash Glucose Monitor and Fingerprick Measurements. Biosensors, 8(4), 93. https://doi.org/10.3390/bios8040093





