Limits to the Evaluation of the Accuracy of Continuous Glucose Monitoring Systems by Clinical Trials
Abstract
:1. Introduction
1.1. Background
1.2. Challenges of the Performance Assessment of CGM Systems
1.3. Structure and Operation of a CGM Sensor
2. Materials and Methods
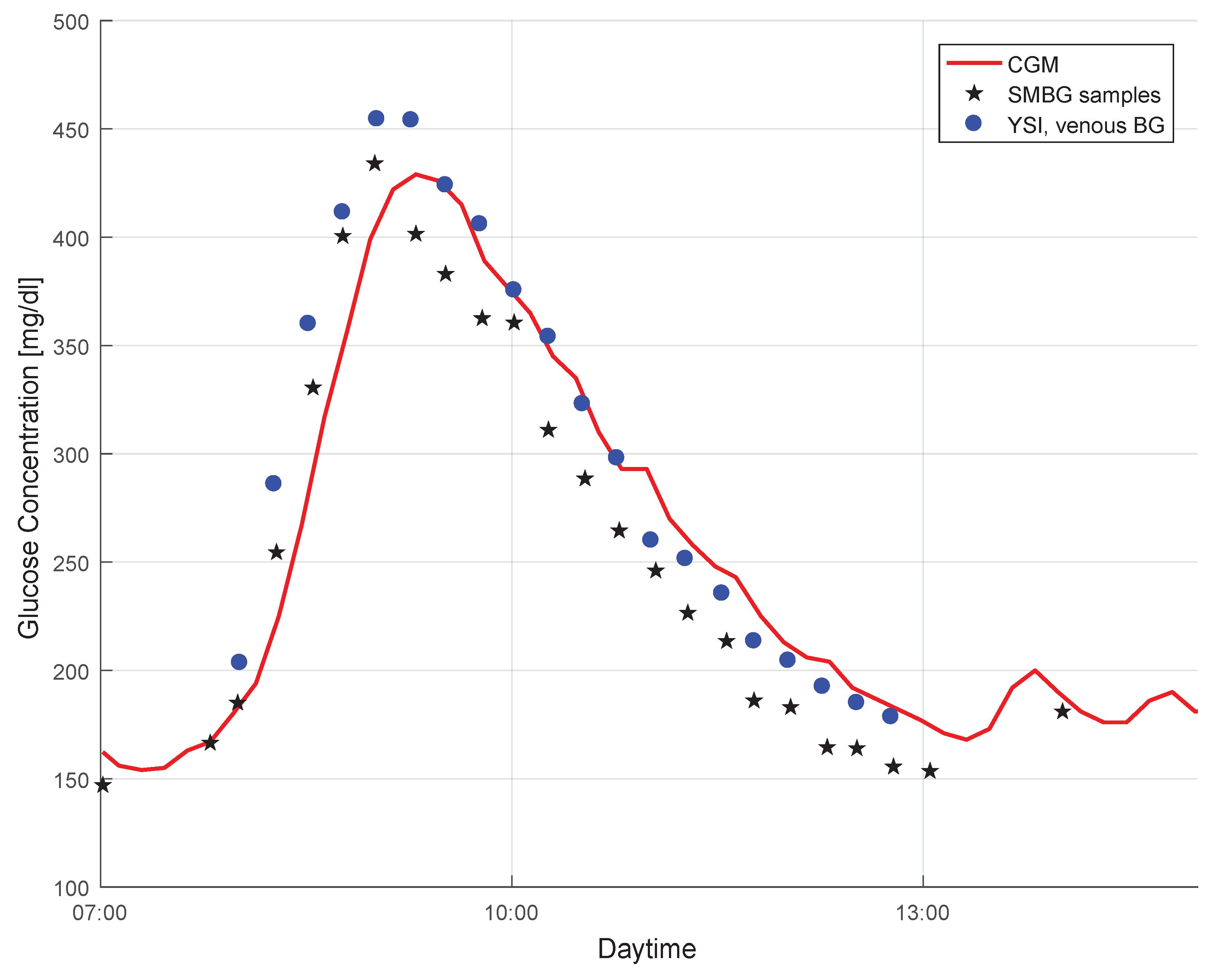
2.1. Study Data
2.2. Problem Statement
2.3. Problem Analysis
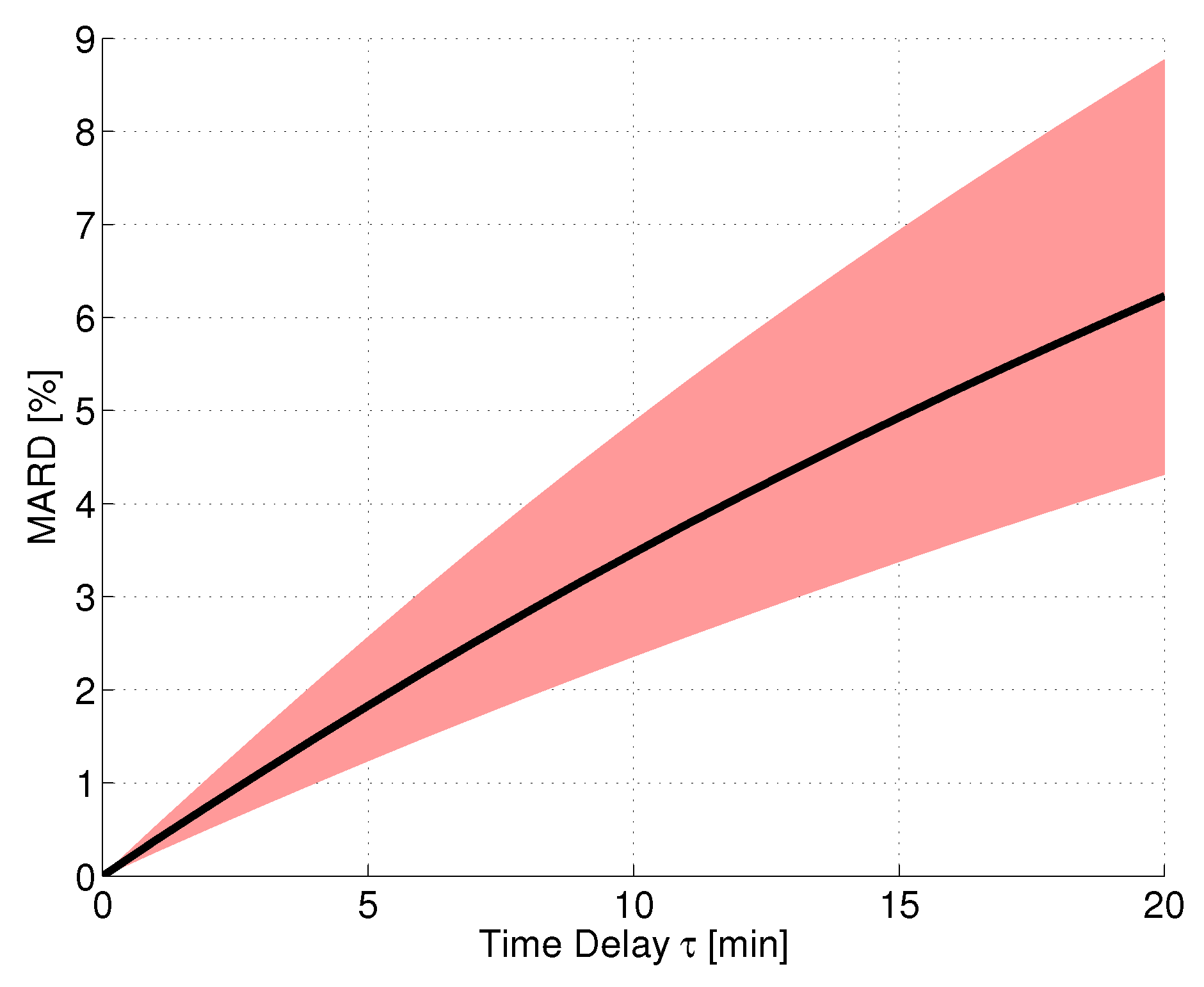
2.3.1. Time Delay
2.3.2. Choice of the Reference Method for Glucose Measurement
2.3.3. Number of Samples
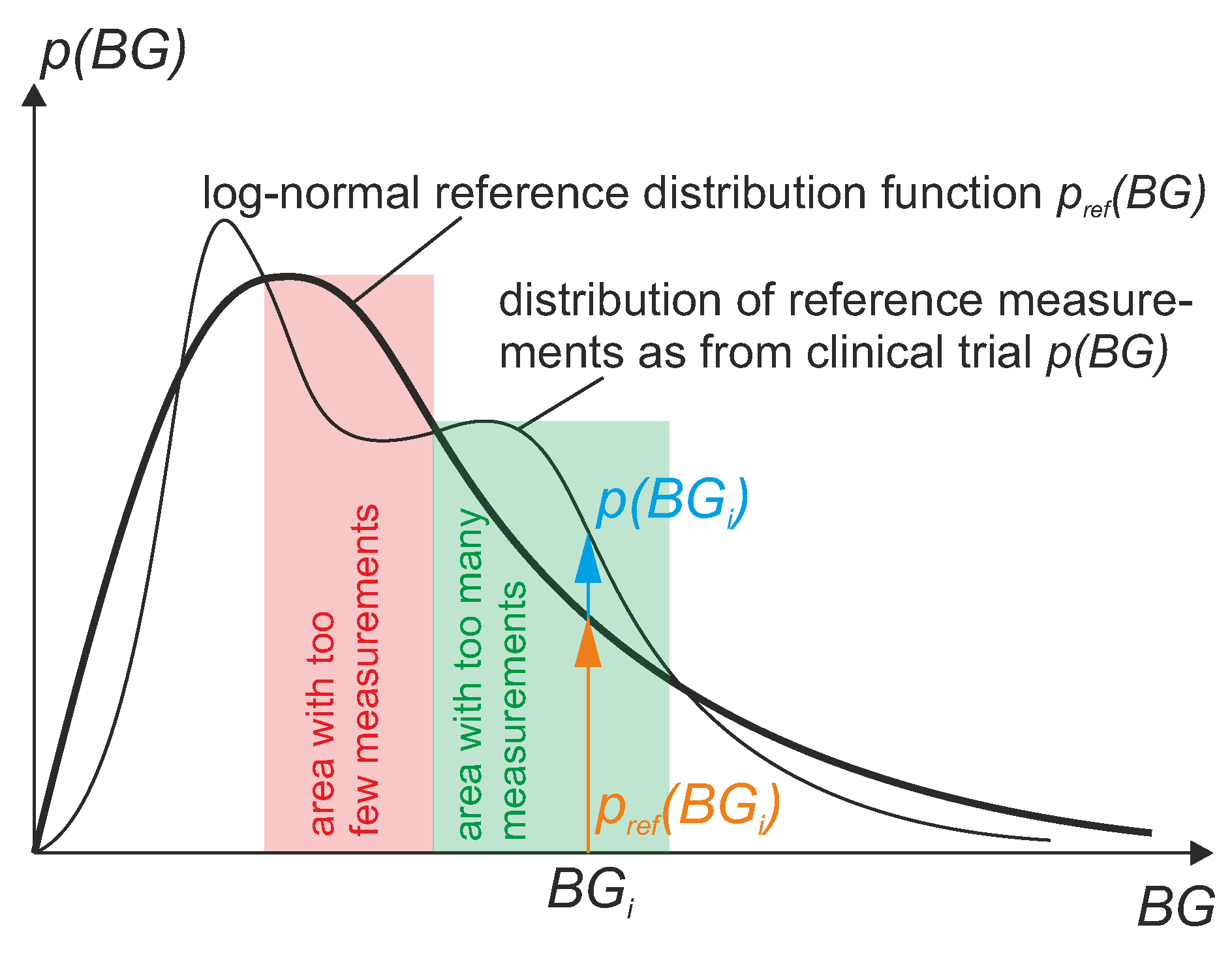
2.3.4. Distribution of Paired Measurement Points
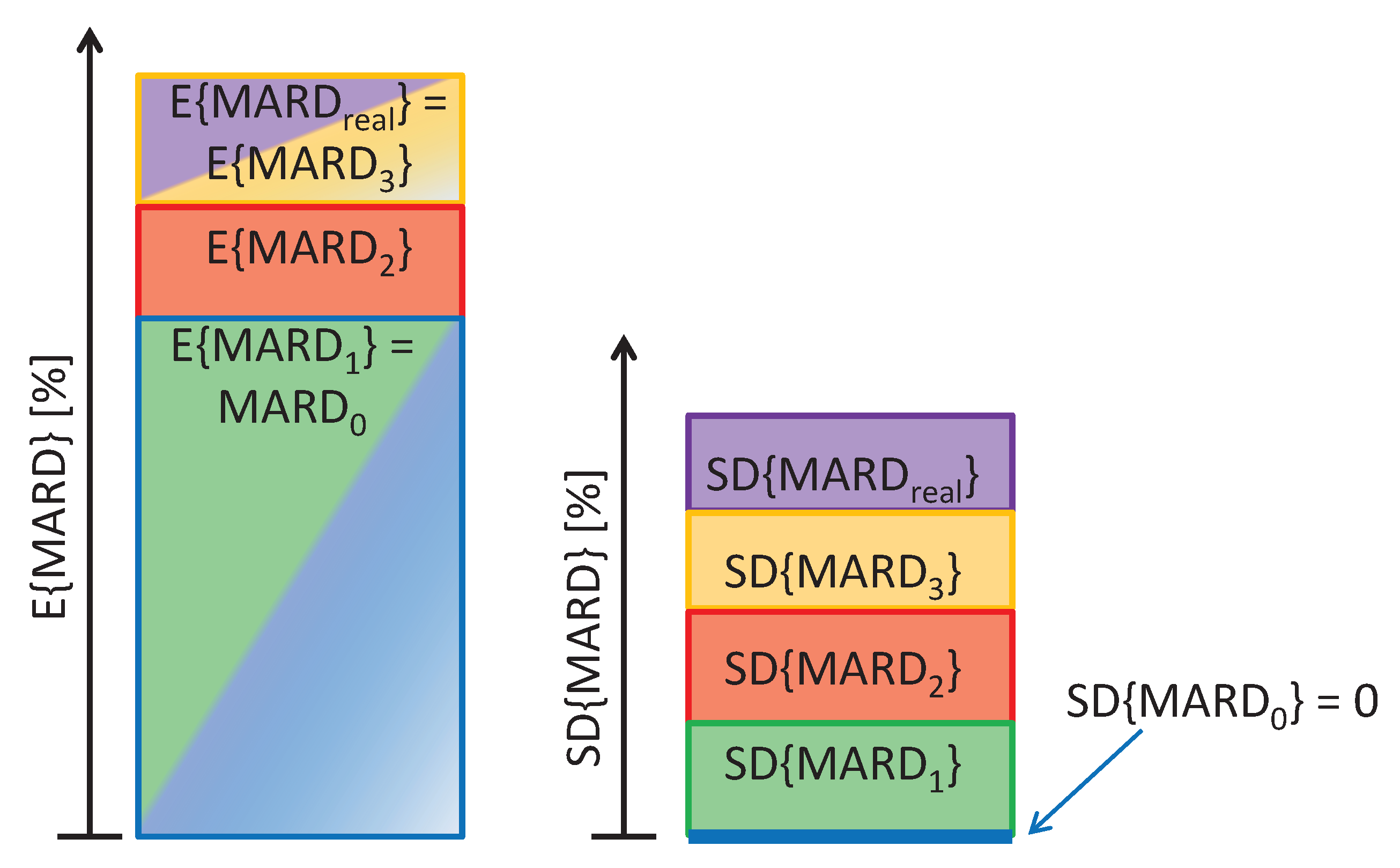
2.4. Composition of the Total MARD Error
3. Results and Discussion
3.1. Limits of the Perfect Glucose Sensor: Estimation of the Target Value under Perfect Conditions
3.2. Testing CGM Sensors under Real Conditions
3.2.1. Impact of Statistical Errors
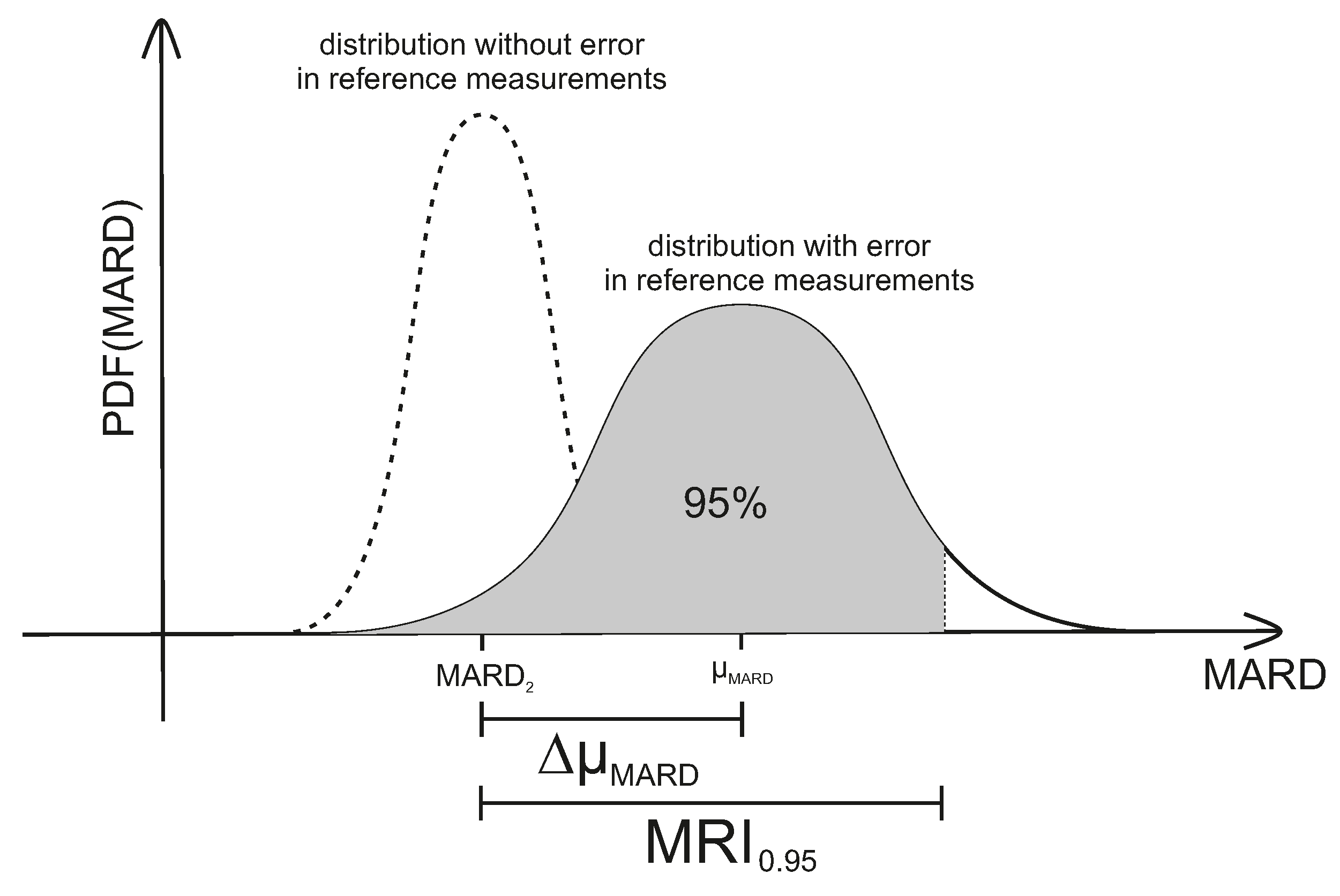
Effects in Terms of Confidence
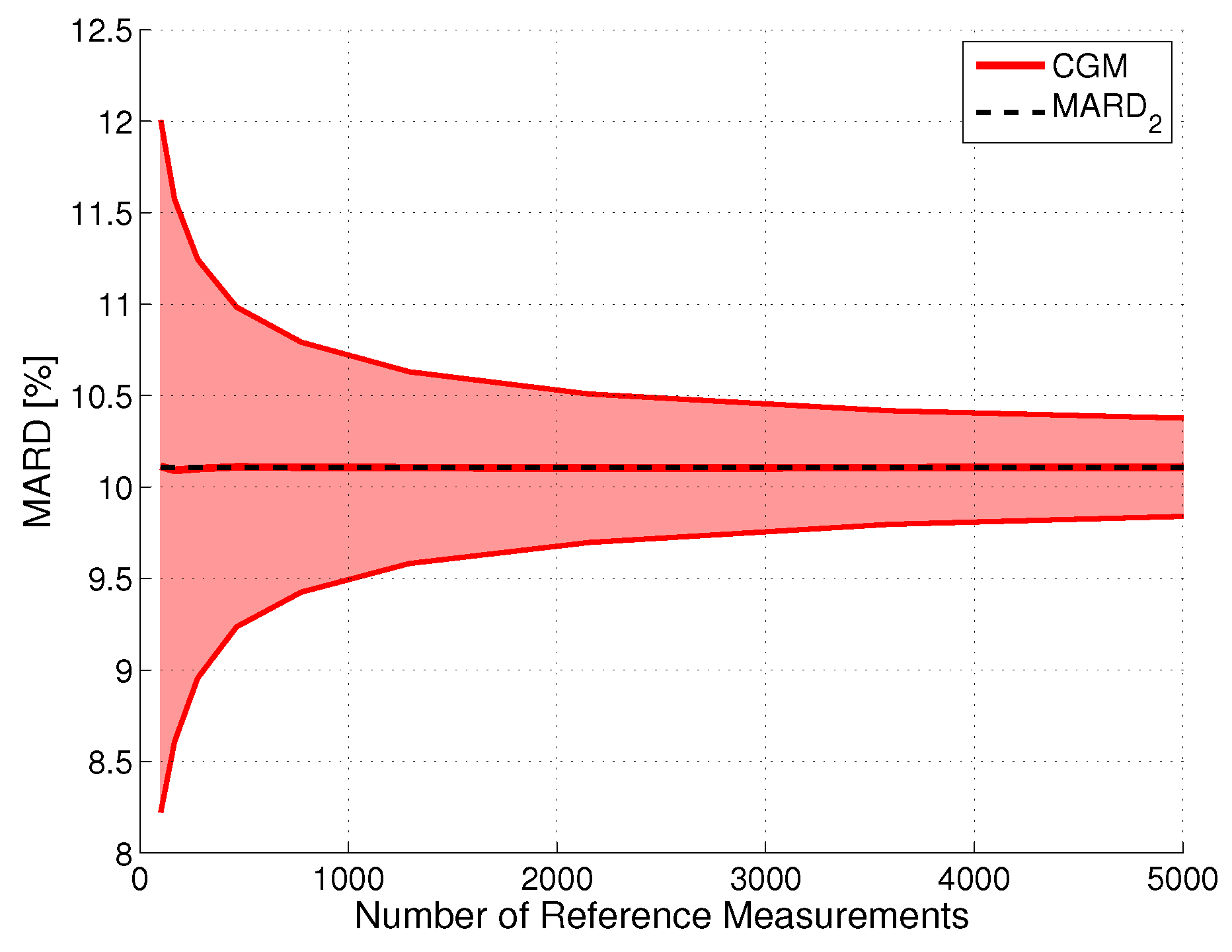
Effect of Number of Paired Measurements ()
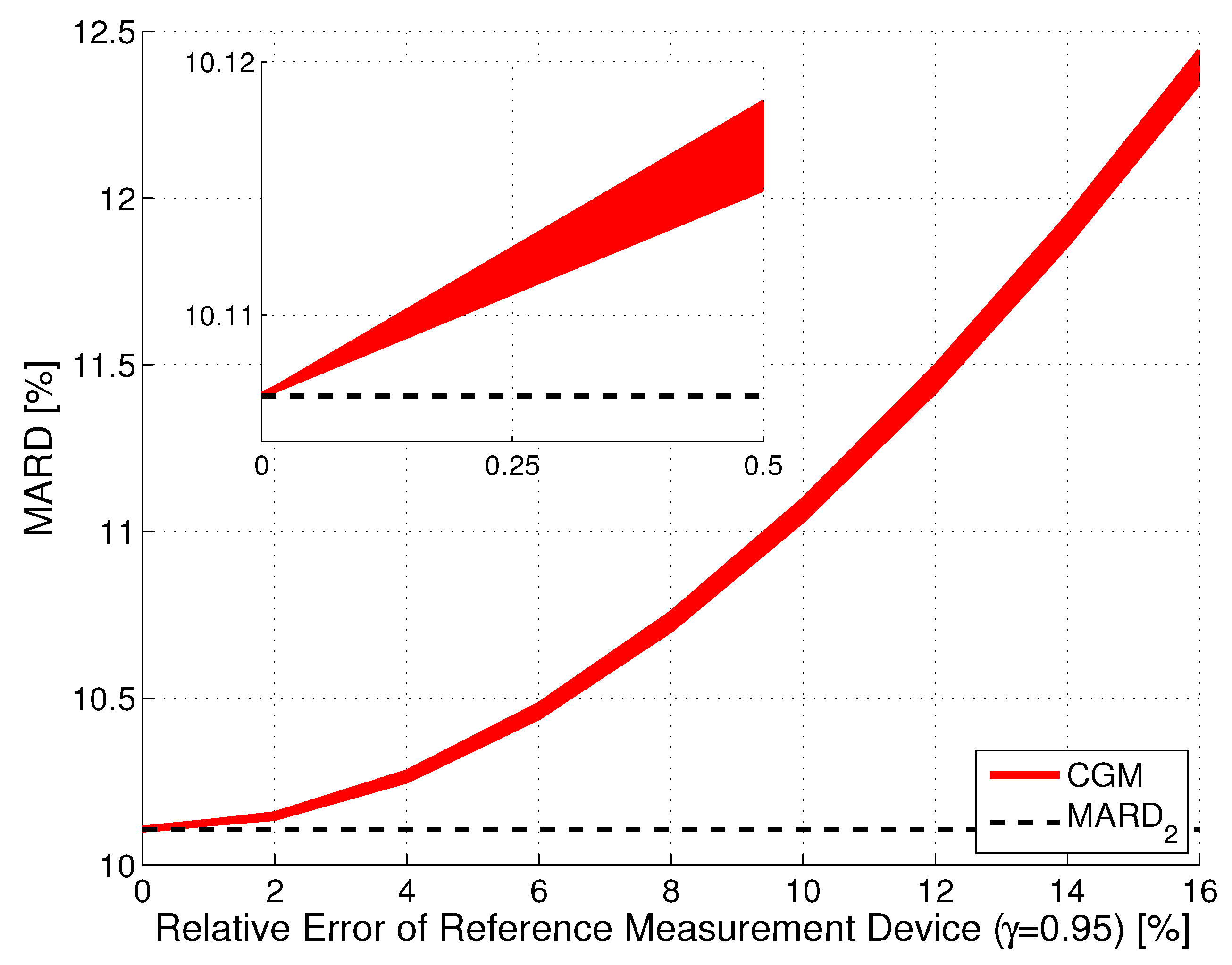
Effect of Errors in Reference Measurements ()
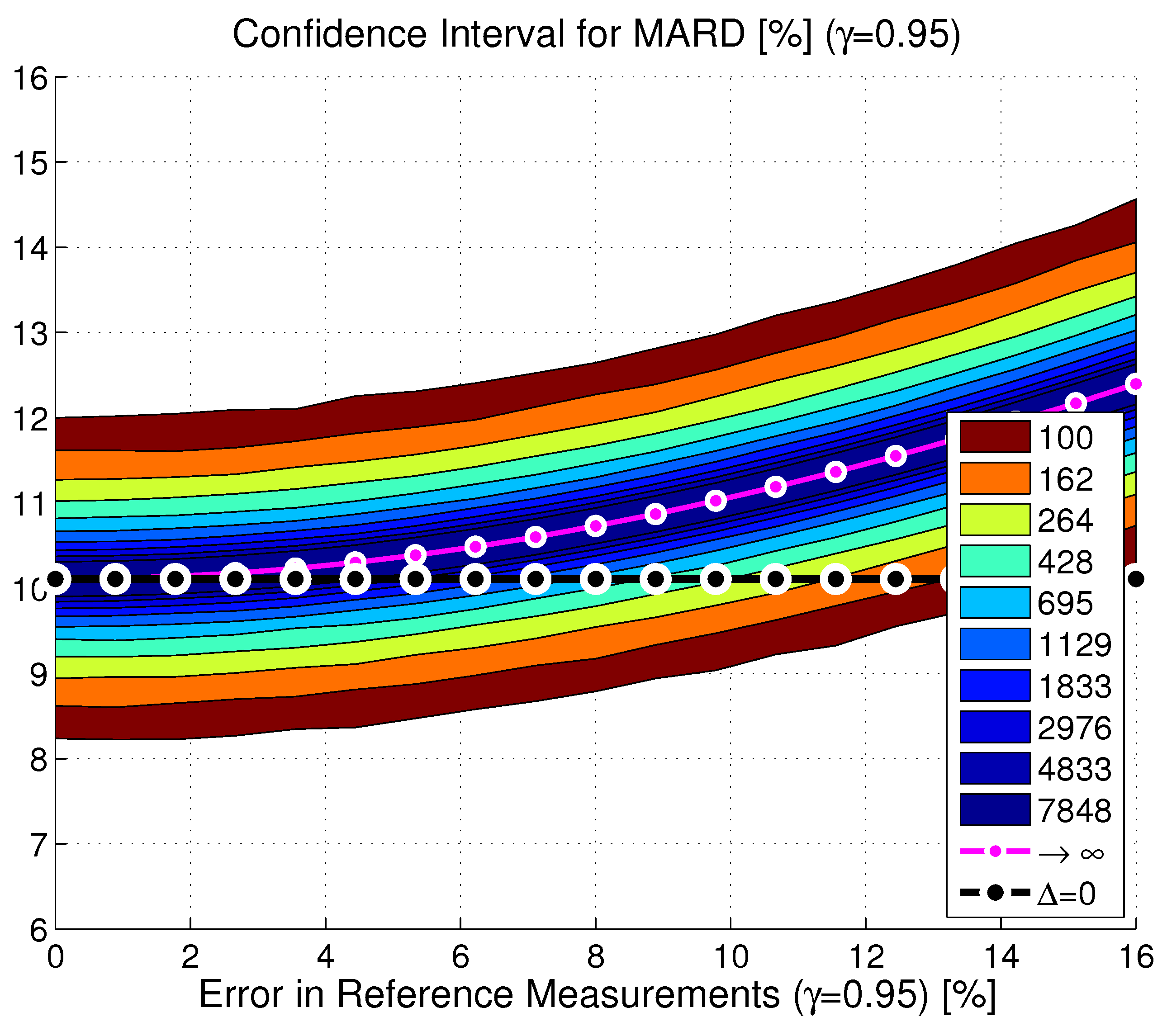
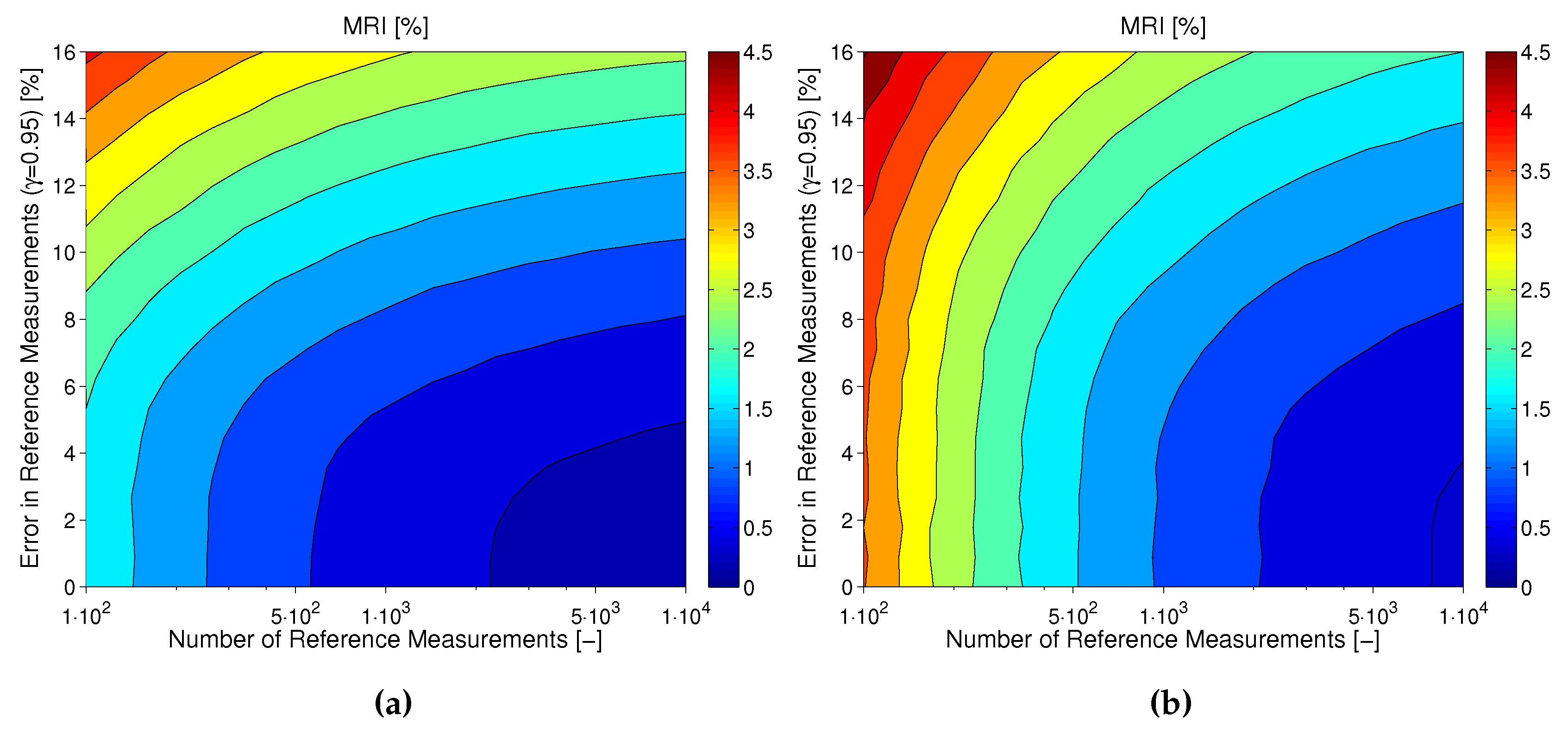
Combined Effect of Number and Uncertainty of Reference Measurements ( and )
Tackling MARD Uncertainty: Giving Bounds for MARD
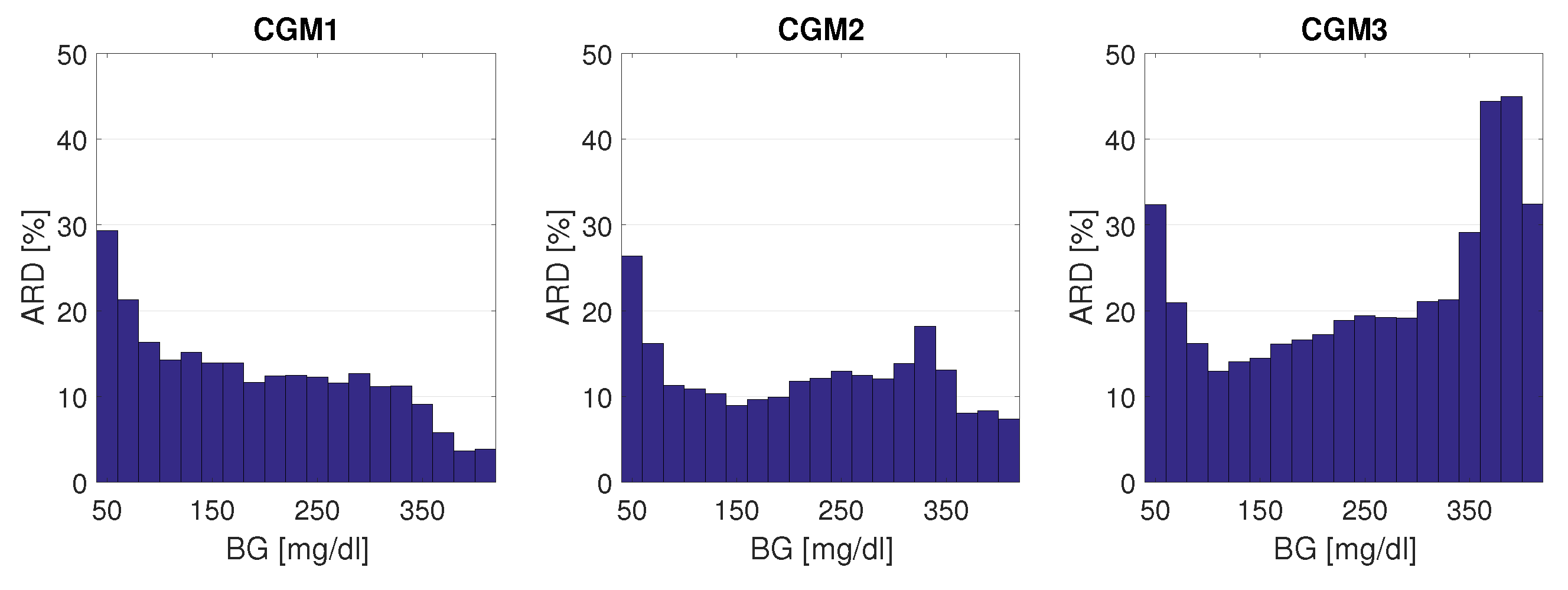
3.2.2. CGM System Performance and BG Range
CGM System Performance Differs between BG Ranges
Correcting for the Distribution of Points
- histogram-based estimation, and
- kernel density estimation.
- The bin size needs to be chosen wisely (according to number of data points).
- The histogram shape is substantially dependent on the position of the bin centers.
- use of normally-distributed (Gaussian) kernel functions.
- bandwidth (standard deviation) of .
- Between 70 mg/dL and 350 mg/dL in the measurement data of the reference sensor:
- -
- no gap larger than 10 mg/dL should exist in the data between 70 mg/dL and 200 mg/dL.
- -
- no gap larger than 20 mg/dL should exist in the data between 200 mg/dL and 350 mg/dL.
- more than 1% (and at least two points) of the data points exist in the hypoglycemic region below 70 mg/dL.
- more than 0.5% (and at least two points) of the data points exist in the hyperglycemic region above 350 mg/dL.
- The complete data set (N data pairs) of all sensors was used to select a subset with data points randomly within a Monte Carlo experiment (with 5000 repetitions).
- In each experiment, the MARD and WMARD were computed using the subset. The simulation was carried out for two cases:
- -
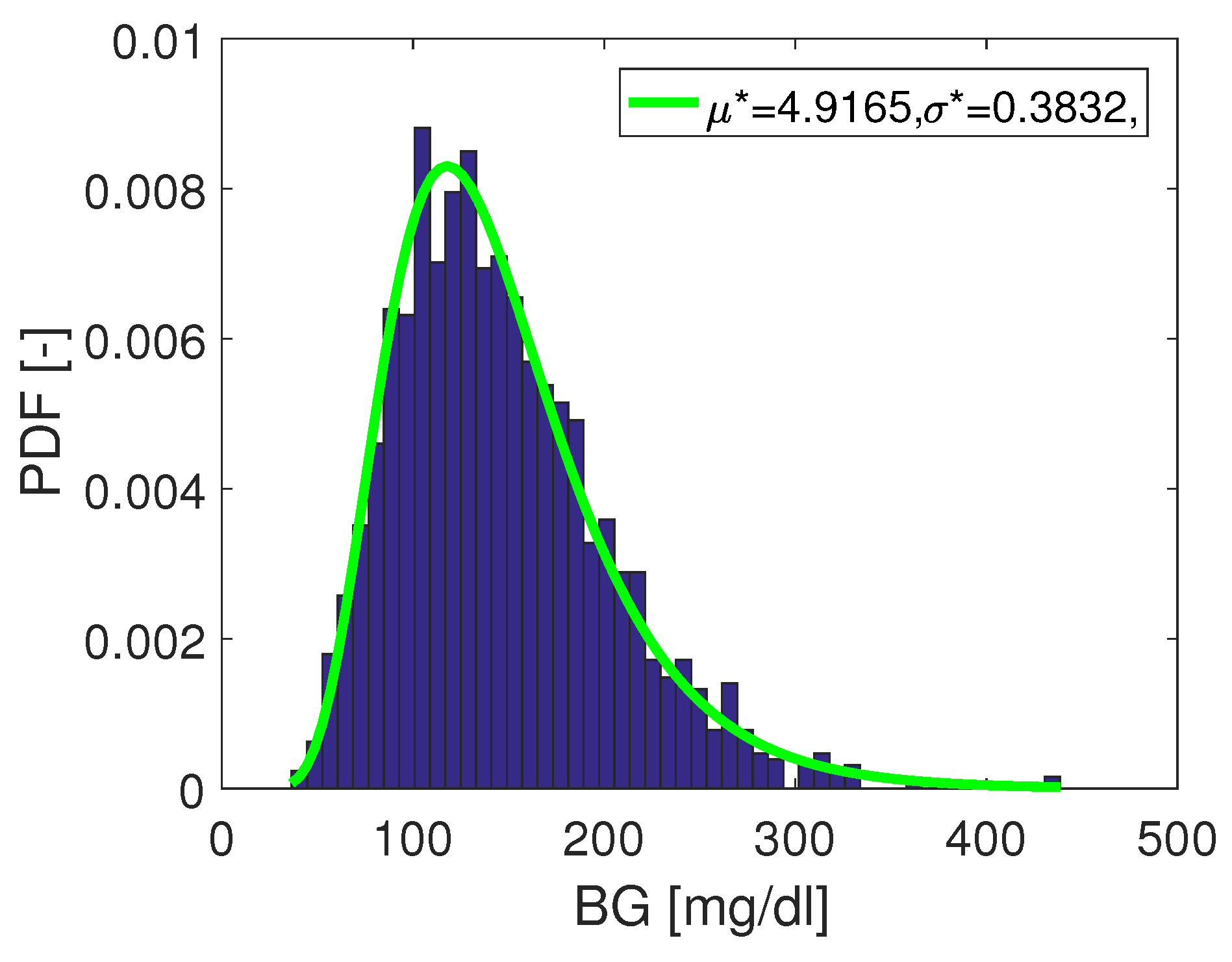
- the subset was selected in such a way that the reference data had a log-normal distribution, and
- -
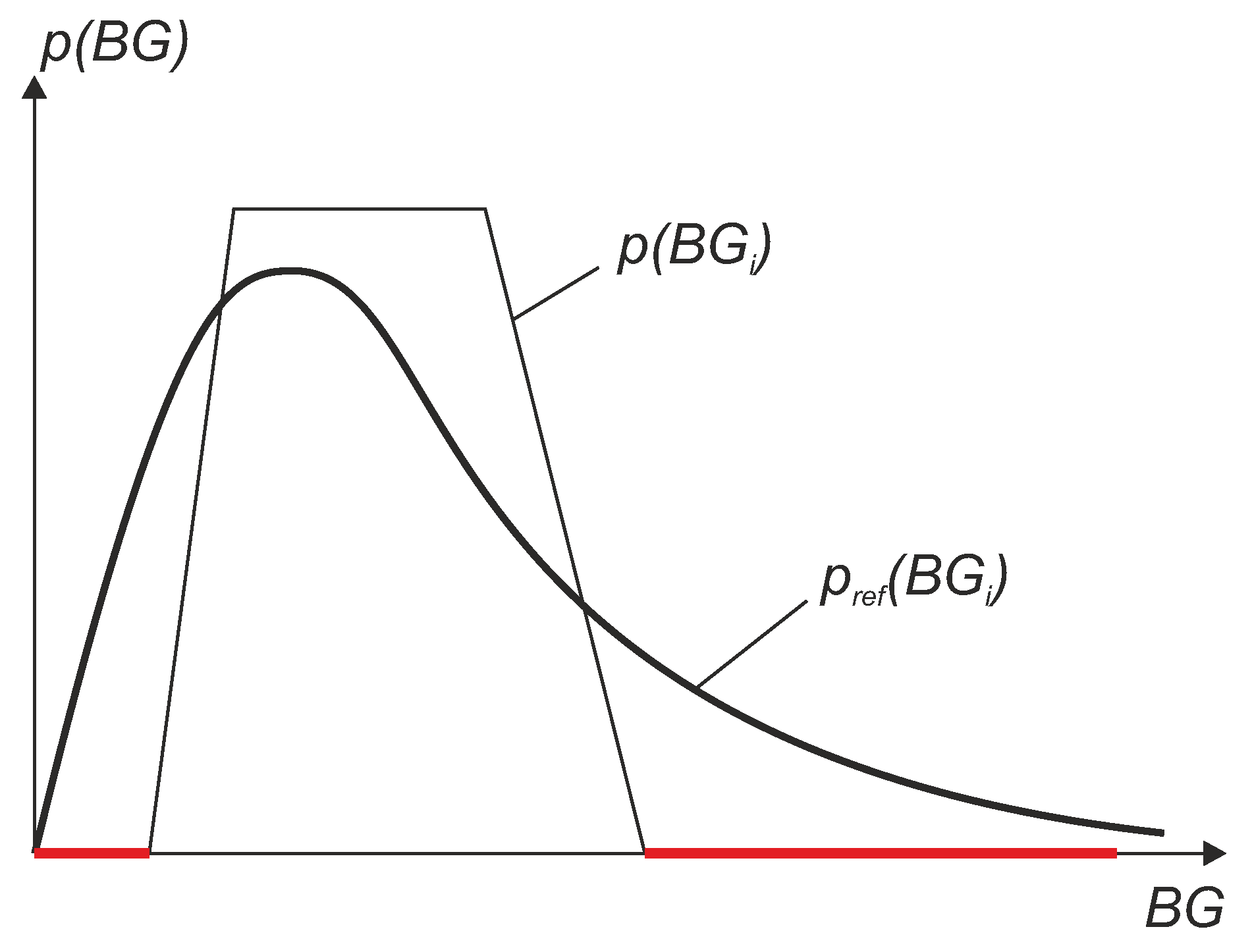
- the subset was selected in such a way that the reference sensor data had a uniform-like distribution.
- The “true” MARD value (denoted ) was computed using the complete data set with N data pairs and this resulted in the value . It can be seen from the results that WMARD was hardly affected by the distribution of the paired points, whereas for the standard MARD, significant differences occurred for the different distribution functions.
4. Conclusions
- The number of paired measurements should be appropriately high in order to reduce the uncertainty in the average results.
- The accuracy of the reference measurement device should be significantly higher than the accuracy of the CGM system. This can be done by using either highly accurate laboratory glucose analyzers for the assessment of venous BG or a high-quality BG meter for assessing the capillary BG concentration. Since modern BG meters are factory calibrated in order display a value that is indicative of venous BG, it should not actually matter whether venous or capillary BG is used as reference quantity (in the case of a comparable accuracy, of course). However, it must be considered that BG meters might have a poor measurement performance in the case of, for example, hypoxemia or anemia. This should be taken into account in the inclusion and exclusion criteria when recruiting the study population for the clinical trial.
- The same reference measurement device should be used for both calibrating the CGM system and drawing the reference BG measurements.
- An overall MARD should never be the only source for interpretation of CGM accuracy. Instead, an overall MARD should be analyzed together with additional information, such as MARD values for different glucose ranges, as well as for different days of sensor use, distribution of MARD values over all analyzed CGM systems in the trial, percentage of large measurement errors, etc.
- If the performance of two CGM systems of different manufacturers have to be compared, this should ideally be done based on data from a head-to-head assessment. In case such data is not available, it would at least be recommendable to compare WMARD values from different studies and to take the MRI into account as well.
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| AP | artificial pancreas |
| ARD | absolute relative difference |
| BG | blood glucose |
| CG-EGA | continuous glucose error grid analysis |
| CGM | continuous glucose monitoring |
| CI | confidence interval |
| IG | interstitial glucose |
| KDE | kernel density estimation |
| MARD | mean absolute relative deviation |
| MD | medical doctor |
| MRI | MARD Reliability Index |
| PARD | precision absolute relative deviation |
| probability density function | |
| ROC | rate-of-change |
| SMBG | self monitoring of blood glucose |
| t1d | type 1 diabetes |
| t2d | type 2 diabetes |
| WMARD | weighted MARD |
References
- Kirchsteiger, H.; Jørgensen, J.B.; Renard, E.; del Re, L. (Eds.) Prediction Methods for Blood Glucose Concentration: Design, Use and Evaluation; Springer International Publishing Switzerland: Cham, Switzerland, 2016. [Google Scholar]
- Freckmann, G.; Schmid, C.; Ruhland, K.; Baumstark, A.; Haug, C. System Accuracy Evaluation of 43 Blood Glucose Monitoring Systems for Self-Monitoring of Blood Glucose according to DIN EN ISO 15197. J. Diabetes Sci. Technol. 2012, 6, 1060–1075. [Google Scholar] [CrossRef] [PubMed]
- Basu, A.; Dube, S.; Veettil, S.; Slama, M.; Kudva, Y.C.; Peyser, T.; Carter, R.E.; Cobelli, C.; Basu, R. Time Lag of Glucose From Intravascular to Interstitial Compartment in Type 1 Diabetes. J. Diabetes Sci. Technol. 2015, 9, 63–68. [Google Scholar] [CrossRef] [PubMed]
- Feldman, B.; Brazg, R.; Schwartz, S.; Weinstein, R. A continuous glucose sensor based on Wired EnzymeTM technology-Results from a 3-day trial in patients with type 1 diabetes. Diabetes Technol. Ther. 2003, 5, 769–779. [Google Scholar] [CrossRef] [PubMed]
- Zschornack, E.; Schmid, C.; Pleus, S.; Link, M.; Klötzer, H.M.; Obermaier, K.; Schoemaker, M.; Strasser, M.; Frisch, G.; Schmelzeisen-Redeker, G.; Haug, C.; Freckmann, G. Evaluation of the Performance of a Novel System for Continuous Glucose Monitoring. J. Diabetes Sci. Technol. 2013, 7, 815–823. [Google Scholar] [CrossRef] [PubMed]
- Obermaier, K.; Schmelzeisen-Redeker, G.; Schoemaker, M.; Klötzer, H.M.; Kirchsteiger, H.; Eikmeier, H.; del Re, L. Performance Evaluations of Continuous Glucose Monitoring Systems: Precision Absolute Relative Deviation is Part of the Assessment. J. Diabetes Sci. Technol. 2013, 7, 824–832. [Google Scholar] [CrossRef] [PubMed]
- Kovatchev, B.; Cox, D.J.; Gonder-Frederick, L.A.; Clarke, W.L. Evaluating the Accuracy of Continuous Glucose-Monitoring Sensors. Diabetes Care 2004, 27, 1922–1928. [Google Scholar] [CrossRef] [PubMed]
- Clarke, W.L.; Cox, D.; Gonder-Frederick, L.A.; Carter, W.; Pohl, S.L. Evaluating Clinical Accuracy of Systems for Self-Monitoring of Blood Glucose. Diabetes Care 1987, 10, 622–628. [Google Scholar] [CrossRef] [PubMed]
- Parkes, J.L.; Slatin, S.L.; Pardo, S.; Ginsberg, B.H. A new consensus error grid to evaluate the clinical significance of inaccuracies in the measurement of blood glucose. Diabetes Care 2000, 23, 1143–1148. [Google Scholar] [CrossRef] [PubMed]
- Weinstein, R.L.; Schwartz, S.L.; Brazg, R.L.; Bugler, J.R.; Peyser, T.A.; McGarraugh, G.V. Accuracy of the 5-day FreeStyle navigator continuous glucose monitoring system. Diabetes Care 2007, 30, 1125–1130. [Google Scholar] [CrossRef] [PubMed]
- Kovatchev, B.; Anderson, S.; Heinemann, L.; Clarke, W. Comparison of the Numerical and Clinical Accuracy of Four Continuous Glucose Monitors. Diabetes Care 2008, 31, 1160–1164. [Google Scholar] [CrossRef] [PubMed]
- Garg, S.K.; Smith, J.; Beatson, C.; Lopez-Baca, B.; Voelmle, M.; Gottlieb, P.A. Comparison of accuracy and safety of the SEVEN and the Navigator continuous glucose monitoring systems. Diabetes Technol. Ther. 2009, 11, 65–72. [Google Scholar] [CrossRef] [PubMed]
- Luijf, Y.M.; Avogaro, A.; Benesch, C.; Bruttomesso, D.; Cobelli, C.; Ellmerer, M.; Heinemann, L.; Mader, J.K.; DeVries, J.H. Continuous glucose monitoring accuracy results vary between assessment at home and assessment at the clinical research center. J. Diabetes Sci. Technol. 2012, 6, 1103–1106. [Google Scholar] [CrossRef] [PubMed]
- Luijf, Y.M.; Mader, J.K.; Doll, W.; Pieber, T.; Farret, A.; Place, J.; Renard, E.; Bruttomesso, D.; Filippi, A.; Avogaro, A.; et al. Accuracy and reliability of continuous glucose monitoring systems: A head-to-head comparison. Diabetes Technol. Ther. 2013, 15, 721–726. [Google Scholar] [CrossRef] [PubMed]
- Freckmann, G.; Pleus, S.; Link, M.; Zschornack, E.; Klötzer, H.M.; Haug, C. Performance Evaluation of Three Continuous Glucose Monitoring Systems: Comparison of Six Sensors per Subject in Parallel. J. Diabetes Sci. Technol. 2013, 7, 842–853. [Google Scholar] [CrossRef] [PubMed]
- Leelarathna, L.; Nodale, M.; Allen, J.M.; Elleri, D.; Kumareswaran, K.; Haidar, A.; Caldwell, K.; Wilinska, M.E.; Acerini, C.L.; Evans, M.L.; et al. Evaluating the accuracy and large inaccuracy of two continuous glucose monitoring systems. Diabetes Technol. Ther. 2013, 15, 143–149. [Google Scholar] [CrossRef] [PubMed]
- Pleus, S.; Schmid, C.; Link, M.; Zschornack, E.; Klötzer, H.M.; Haug, C.; Freckmann, G. Performance evaluation of a continuous glucose monitoring system under conditions similar to daily life. J. Diabetes Sci. Technol. 2013, 7, 833–841. [Google Scholar] [CrossRef] [PubMed]
- Damiano, E.R.; El-Khatib, F.H.; Zheng, H.; Nathan, D.M.; Russell, S.J. A comparative effectiveness analysis of three continuous glucose monitors. Diabetes Care 2013, 36, 251–259. [Google Scholar] [CrossRef] [PubMed]
- Damiano, E.R.; McKeon, K.; El-Khatib, F.H.; Zheng, H.; Nathan, D.M.; Russell, S.J. A comparative effectiveness analysis of three continuous glucose monitors: The Navigator, G4 Platinum, and Enlite. J. Diabetes Sci. Technol. 2014, 8, 699–708. [Google Scholar] [CrossRef] [PubMed]
- Bailey, T.S.; Ahmann, A.; Brazg, R.; Christiansen, M.; Garg, S.; Watkins, E.; Welsh, J.B.; Lee, S.W. Accuracy and acceptability of the 6-day Enlite continuous subcutaneous glucose sensor. Diabetes Technol. Ther. 2014, 16, 277–283. [Google Scholar] [CrossRef] [PubMed]
- Bailey, T.; Bode, B.W.; Christiansen, M.P.; Klaff, L.J.; Alva, S. The performance and usability of a factory-calibrated flash glucose monitoring system. Diabetes Technol. Ther. 2015, 17, 787–794. [Google Scholar] [CrossRef] [PubMed]
- Kropff, J.; Bruttomesso, D.; Doll, W.; Farret, A.; Galasso, S.; Luijf, Y.M.; Mader, J.K.; Place, J.; Boscari, F.; Pieber, T.; et al. Accuracy of two continuous glucose monitoring systems: A head-to-head comparison under clinical research centre and daily life conditions. Diabetes Obes. Metab. 2015, 17, 343–349. [Google Scholar] [CrossRef] [PubMed]
- Bonora, B.; Maran, A.; Ciciliot, S.; Avogaro, A.; Fadini, G. Head-to-head comparison between flash and continuous glucose monitoring systems in outpatients with type 1 diabetes. J. Endocrinol. Investig. 2016, 39, 1391–1399. [Google Scholar] [CrossRef] [PubMed]
- Laffel, L. Improved accuracy of continuous glucose monitoring systems in pediatric patients with diabetes mellitus: results from two studies. Diabetes Technol. Ther. 2016, 18, S2–23. [Google Scholar] [CrossRef] [PubMed]
- Aberer, F.; Hajnsek, M.; Rumpler, M.; Zenz, S.; Baumann, P.M.; Elsayed, H.; Puffing, A.; Treiber, G.; Pieber, T.R.; Sourij, H.; et al. Evaluation of subcutaneous glucose monitoring systems under routine environmental conditions in patients with type 1 diabetes. Diabetes Obes. Metab. 2017, 19, 1051–1055. [Google Scholar] [CrossRef] [PubMed]
- Kropff, J.; Choudhary, P.; Neupane, S.; Barnard, K.; Bain, S.C.; Kapitza, C.; Forst, T.; Link, M.; Dehennis, A.; DeVries, J.H. Accuracy and longevity of an implantable continuous glucose sensor in the PRECISE study: A 180-day, prospective, multicenter, pivotal trial. Diabetes Care 2017, 40, 63–68. [Google Scholar] [CrossRef] [PubMed]
- Kirchsteiger, H.; Heinemann, L.; Freckmann, G.; Lodwig, V.; Schmelzeisen-Redeker, G.; Schoemaker, M.; del Re, L. Performance comparison of CGM systems: MARD values are not always a reliable indicator of CGM system accuracy. J. Diabetes Sci. Technol. 2015, 9, 1030–1040. [Google Scholar] [CrossRef] [PubMed]
- Reiterer, F.; Polterauer, P.; Schoemaker, M.; Schmelzeisen-Redecker, G.; Freckmann, G.; Heinemann, L.; del Re, L. Significance and Reliability of MARD for the Accuracy of CGM Systems. J. Diabetes Sci. Technol. 2017, 11, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Ajjan, R.A.; Cummings, M.H.; Jennings, P.; Leelarathna, L.; Rayman, G.; Wilmot, E.G. Accuracy of flash glucose monitoring and continuous glucose monitoring technologies: Implications for clinical practice. Diabetes Vasc. Dis. Res. 2018, 15, 175–184. [Google Scholar] [CrossRef] [PubMed]
- Oliver, N.; Toumazou, C.; Cass, A.; Johnston, D. Glucose sensors: A review of current and emerging technology. Diabet. Med. 2009, 26, 197–210. [Google Scholar] [CrossRef] [PubMed]
- Vaddiraju, S.; Burgess, D.J.; Tomazos, I.; Jain, F.C.; Papadimitrakopoulos, F. Technologies for continuous glucose monitoring: Current problems and future promises. J. Diabetes Sci. Technol. 2010, 4, 1540–1562. [Google Scholar] [CrossRef] [PubMed]
- Zarkogianni, K.; Litsa, E.; Mitsis, K.; Wu, P.Y.; Kaddi, C.D.; Cheng, C.W.; Wang, M.D.; Nikita, K.S. A review of emerging technologies for the management of diabetes mellitus. IEEE Trans. Biomed. Eng. 2015, 62, 2735–2749. [Google Scholar] [CrossRef] [PubMed]
- Lodwig, V.; Heinemann, L. Continuous glucose monitoring with glucose sensors: Calibration and assessment criteria. Diabetes Technol. Ther. 2003, 5, 572–586. [Google Scholar] [CrossRef] [PubMed]
- Bequette, B.W. Continuous Glucose Monitoring: Real-Time Algorithms for Calibration, Filtering, and Alarms. J. Diabete 2010, 4, 404–418. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.B.; Dassau, E.; Doyle, F.J. A Run-to-Run Approach to Enhance Continuous Glucose Monitor Accuracy Based on Continuous Wear. In Proceedings of the 9th IFAC Symposium on Biological and Medical Systems (BMS), Berlin, Germany, 31 August–2 September 2015; pp. 237–242. [Google Scholar]
- Barcelo-Rico, F.; Diez, J.L.; Rossetti, P.; Vehi, J.; Bondia, J. Adaptive calibration algorithm for plasma glucose estimation in continuous glucose monitoring. IEEE J. Biomed. Health Inform. 2013, 17, 530–538. [Google Scholar] [CrossRef] [PubMed]
- Facchinetti, A.; Sparacino, G.; Guerra, S.; Luijf, Y.M.; DeVries, J.H.; Mader, J.K.; Ellmerer, M.; Benesch, C.; Heinemann, L.; Bruttomesso, D.; et al. Real-time improvement of continuous glucose monitoring accuracy. Diabetes Care 2013, 36, 793–800. [Google Scholar] [CrossRef] [PubMed]
- Mahmoudi, Z.; Dencker Johansen, M.; Christiansen, J.S.; Hejlesen, O.K. A multistep algorithm for processing and calibration of microdialysis continuous glucose monitoring data. Diabetes Technol. Ther. 2013, 15, 825–835. [Google Scholar] [CrossRef] [PubMed]
- Kirchsteiger, H.; Zaccarian, L.; Renard, E.; del Re, L. LMI-based approaches for the calibration of continuous glucose measurement sensors. IEEE J. Biomed. Health Inform. 2015, 19, 1697–1706. [Google Scholar] [CrossRef] [PubMed]
- Vettoretti, M.; Facchinetti, A.; Del Favero, S.; Sparacino, G.; Cobelli, C. Online calibration of glucose sensors from the measured current by a time-varying calibration function and Bayesian priors. IEEE Trans. Biomed. Eng. 2016, 8, 1631–1641. [Google Scholar] [CrossRef] [PubMed]
- Acciaroli, G.; Vettoretti, M.; Facchinetti, A.; Sparacino, G.; Cobelli, C. Reduction of Blood Glucose Measurements to Calibrate Subcutaneous Glucose Sensors: A Bayesian Multiday Framework. IEEE Trans. Biomed. Eng. 2018, 65, 587–595. [Google Scholar] [CrossRef] [PubMed]
- Twomey, P. Plasma glucose measurement with the Yellow Springs Glucose 2300 STAT and the Olympus AU640. J. Clin. Pathol. 2004, 57, 752–754. [Google Scholar] [CrossRef] [PubMed]
- Clinical and Laboratory Standards Institute. Performance Metrics for Continuous Interstitial Glucose Monitoring; Approved Guideline. CLSI Document POCT05-A; Clinical and Laboratory Standards Institute: Wayne, PA, USA, 2008. [Google Scholar]
- Del Favero, S.; Facchinetti, A.; Sparacino, G.; Cobelli, C. Improving Accuracy and Precision of Glucose Sensor Profiles: Retrospective Fitting by Constrained Deconvolution. IEEE Trans. Biomed. Eng. 2014, 61, 1044–1053. [Google Scholar] [CrossRef] [PubMed]
- Rebrin, K.; Steil, G.; Van Antwerp, W.; Mastrototaro, J. Subcutaneous glucose predicts plasma glucose independent of insulin: implications for continuous monitoring. Am. J. Physiol. Endocrinol. Metab. 1999, 277, E561–E571. [Google Scholar] [CrossRef]
- Schiavon, M.; Dalla Man, C.; Dube, S.; Slama, M.; Kudva, Y.C.; Peyser, T.; Basu, A.; Basu, R.; Cobelli, C. Modeling plasma-to-interstitium glucose kinetics from multitracer plasma and microdialysis data. Diabetes Technol. Ther. 2015, 17, 825–831. [Google Scholar] [CrossRef] [PubMed]
- Huyett, L.M.; Dassau, E.; Zisser, H.C.; Doyle, F.J. The impact of glucose sensing dynamics on the closed-loop artificial pancreas. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 5116–5121. [Google Scholar]
- Guerra, S.; Facchinetti, A.; Sparacino, G.; De Nicolao, G.; Cobelli, C. Enhancing the Accuracy of Subcutaneous Glucose Sensors: A Real-Time Deconvolution-Based Approach. IEEE Trans. Biomed. Eng. 2012, 59, 1658–1669. [Google Scholar] [CrossRef] [PubMed]
- Schmelzeisen-Redeker, G.; Schoemaker, M.; Kirchsteiger, H.; Freckmann, G.; Heinemann, L.; del Re, L. Time delay of CGM sensors: Relevance, causes, and countermeasures. J. Diabetes Sci. Technol. 2015, 9, 1006–1015. [Google Scholar] [CrossRef] [PubMed]
- Schmelzeisen-Redeker, G.; Staib, A.; Strasser, M.; Müller, U.; Schoemaker, M. Overview of a Novel Sensor for Continuous Glucose Monitoring. J. Diabetes Sci. Technol. 2013, 7, 808–814. [Google Scholar] [CrossRef] [PubMed]
- Campos-Náñez, E.; Breton, M.D. Effect of BGM Accuracy on the Clinical Performance of CGM: An In-Silico Study. J. Diabetes Sci. Technol. 2017, 11, 1196–1206. [Google Scholar] [CrossRef] [PubMed]
- Banauch, D.; Brümmer, W.; Ebeling, W.; Metz, H.; Rindfrey, H.; Lang, H.; Leybold, K.; Rick, W. Eine glucose-dehydrogenase für die glucose-bestimmung in körperflüssigkeiten. Clin. Chem. Lab. Med. 1975, 13, 101–108. [Google Scholar] [CrossRef]
- Andelin, M.; Kropff, J.; Matuleviciene, V.; Joseph, J.I.; Attvall, S.; Theodorsson, E.; Hirsch, I.B.; Imberg, H.; Dahlqvist, S.; Klonoff, D.; et al. Assessing the accuracy of continuous glucose monitoring (CGM) calibrated with capillary values using capillary or venous glucose levels as a reference. J. Diabetes Sci. Technol. 2016, 10, 876–884. [Google Scholar] [CrossRef] [PubMed]
- Rodbard, D. Characterizing accuracy and precision of glucose sensors and meters. J. Diabetes Sci. Technol. 2014, 8, 980–985. [Google Scholar] [CrossRef] [PubMed]
- Vettoretti, M.; Facchinetti, A.; Sparacino, G.; Cobelli, C. A Model of Self-Monitoring Blood Glucose Measurement Error. J. Diabetes Sci. Technol. 2017, 11, 724–735. [Google Scholar] [CrossRef] [PubMed]
- Facchinetti, A.; Del Favero, S.; Sparacino, G.; Castle, J.; Ward, W.; Cobelli, C. Modeling the Glucose Sensor Error. IEEE Trans. Biomed. Eng. 2014, 61, 620–629. [Google Scholar] [CrossRef] [PubMed]
- Facchinetti, A.; Favero, S.D.; Sparacino, G.; Cobelli, C. Model of glucose sensor error components: Identification and assessment for new Dexcom G4 generation devices. Med. Biol. Eng. Comput. 2015, 53, 1259–1269. [Google Scholar] [CrossRef] [PubMed]
- Reiterer, F.; Polterauer, P.; Freckmann, G.; del Re, L. Identification of CGM Time Delays and Implications for BG Control in T1DM. In Proceedings of the XIV Mediterranean Conference on Medical and Biological Engineering and Computing (Medicon 2016), Paphos, Cyprus, 31 March–2 April 2016; pp. 190–195. [Google Scholar]
- Pleus, S.; Schoemaker, M.; Morgenstern, K.; Schmelzeisen-Redeker, G.; Haug, C.; Link, M.; Zschornack, E.; Freckmann, G. Rate-of-change dependence of the performance of two CGM systems during induced glucose swings. J. Diabetes Sci. Technol. 2015, 9, 801–807. [Google Scholar] [CrossRef] [PubMed]
- Meeker, W.Q.; Hahn, G.J.; Escobar, L.A. Statistical Intervals: A Guide for Practitioners and Researchers; John Wiley & Sons: Hoboken, NJ, USA, 2017; Volume 541. [Google Scholar]
- Johnson, R.; Wichern, D. Applied Multivariate Statistical Analysis; Applied Multivariate Statistical Analysis; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Hoffman, K. Banach Spaces of Analytic Functions; Courier Corporation: North Chelmsford, MA, USA, 2007. [Google Scholar]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Silverman, B. Density Estimation for Statistics and Data Analysis; Chapman & Hall/CRC Monographs on Statistics & Applied Probability; Taylor & Francis/CRC Press: Boca Raton, FL, USA, 1986. [Google Scholar]
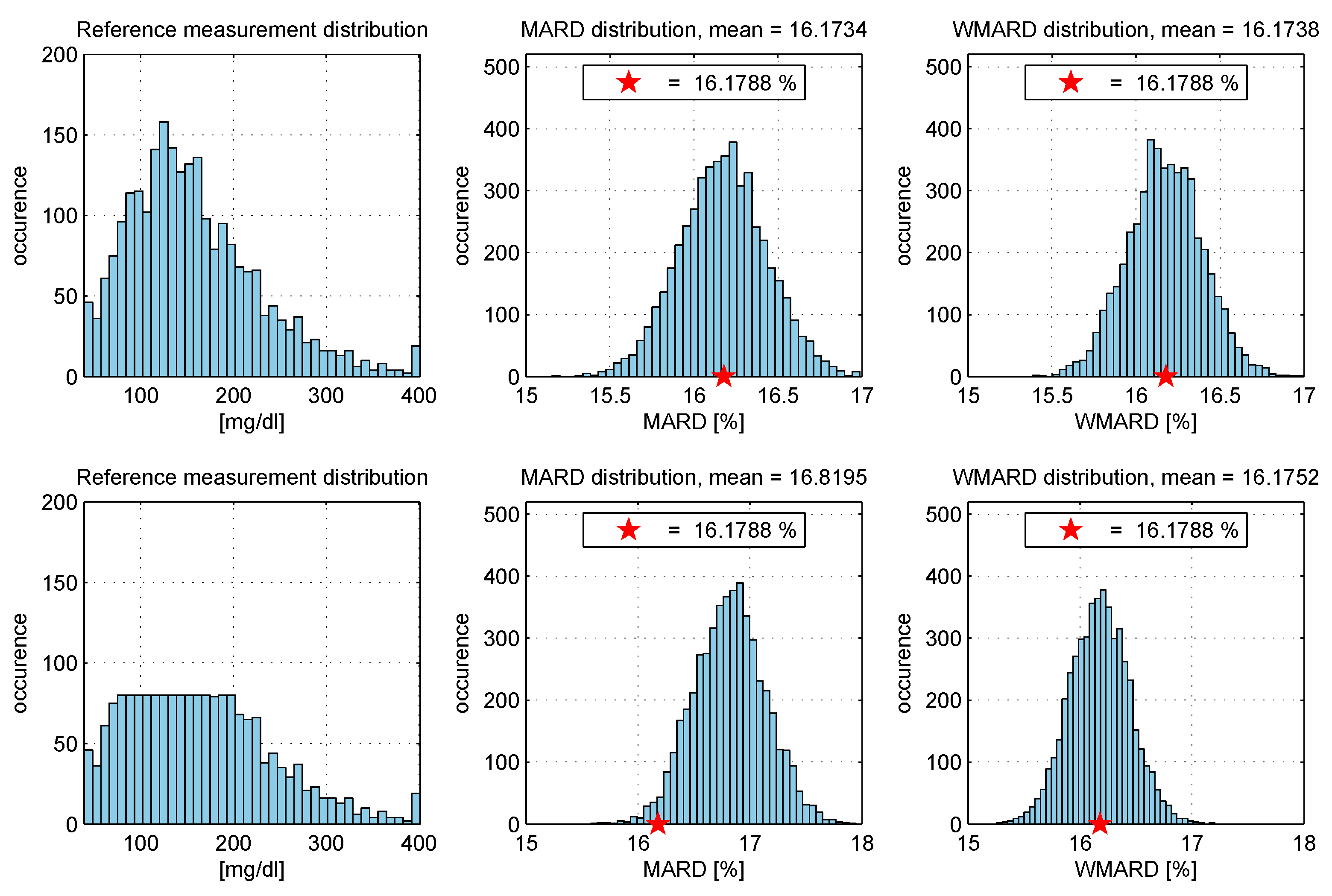
| Distribution | Mean Value of | |
|---|---|---|
| MARD | WMARD | |
| Log-normal | 16.1734% | 16.1738% |
| Uniform-like | 16.8195% | 16.1752% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schrangl, P.; Reiterer, F.; Heinemann, L.; Freckmann, G.; Del Re, L. Limits to the Evaluation of the Accuracy of Continuous Glucose Monitoring Systems by Clinical Trials. Biosensors 2018, 8, 50. https://doi.org/10.3390/bios8020050
Schrangl P, Reiterer F, Heinemann L, Freckmann G, Del Re L. Limits to the Evaluation of the Accuracy of Continuous Glucose Monitoring Systems by Clinical Trials. Biosensors. 2018; 8(2):50. https://doi.org/10.3390/bios8020050
Chicago/Turabian StyleSchrangl, Patrick, Florian Reiterer, Lutz Heinemann, Guido Freckmann, and Luigi Del Re. 2018. "Limits to the Evaluation of the Accuracy of Continuous Glucose Monitoring Systems by Clinical Trials" Biosensors 8, no. 2: 50. https://doi.org/10.3390/bios8020050
APA StyleSchrangl, P., Reiterer, F., Heinemann, L., Freckmann, G., & Del Re, L. (2018). Limits to the Evaluation of the Accuracy of Continuous Glucose Monitoring Systems by Clinical Trials. Biosensors, 8(2), 50. https://doi.org/10.3390/bios8020050






