Towards a Uniform Metrological Assessment of Grating-Based Optical Fiber Sensors: From Refractometers to Biosensors
Abstract
:1. Introduction
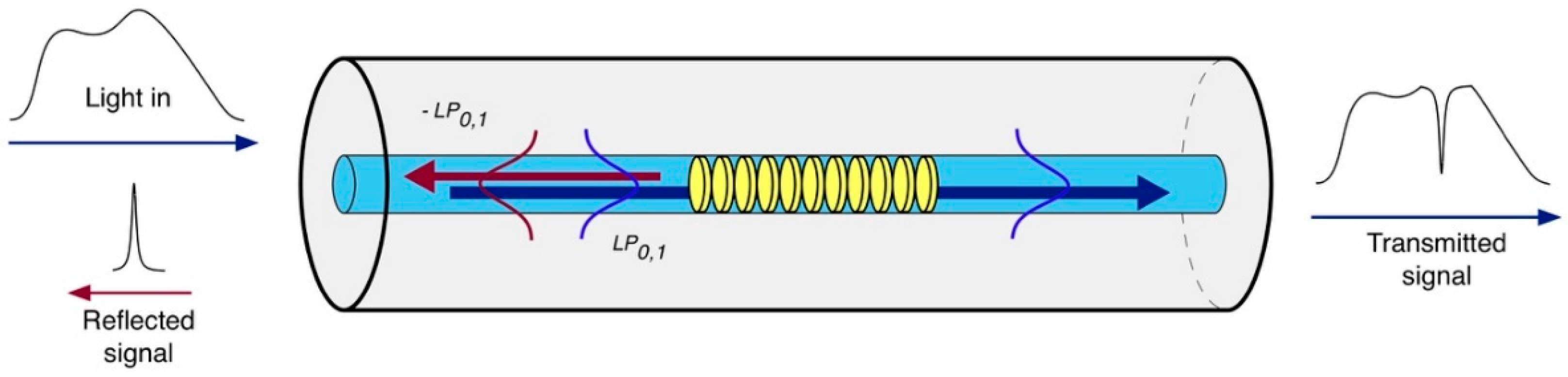
2. Fundamentals of Optical Fiber Gratings
Refractive Index Sensing in Optical Fiber Gratings
3. Metrological Parameters for Assessing Sensor Performance
3.1. Parameters of Generic Interest
3.1.1. Uncertainty
3.1.2. Accuracy and Precision
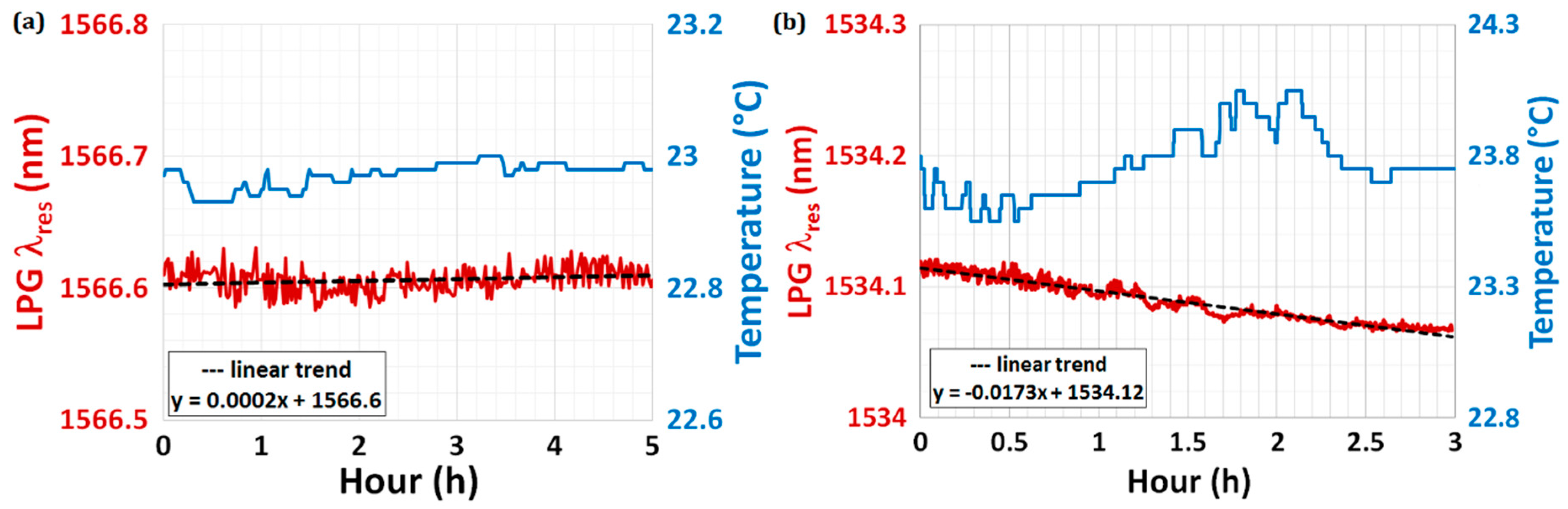
3.1.3. Sensor Drift and Fluctuations
3.1.4. Repeatability
3.1.5. Reproducibility
3.1.6. Response Time
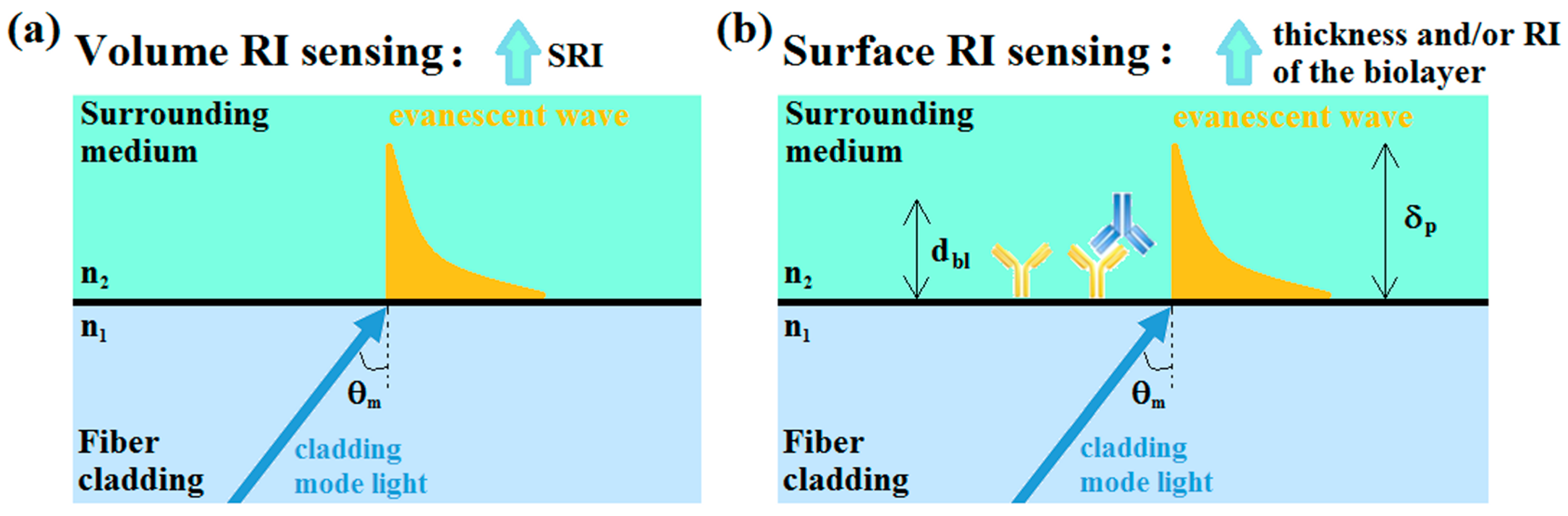
3.2. Parameters Specifically Related to Volume RI Sensing
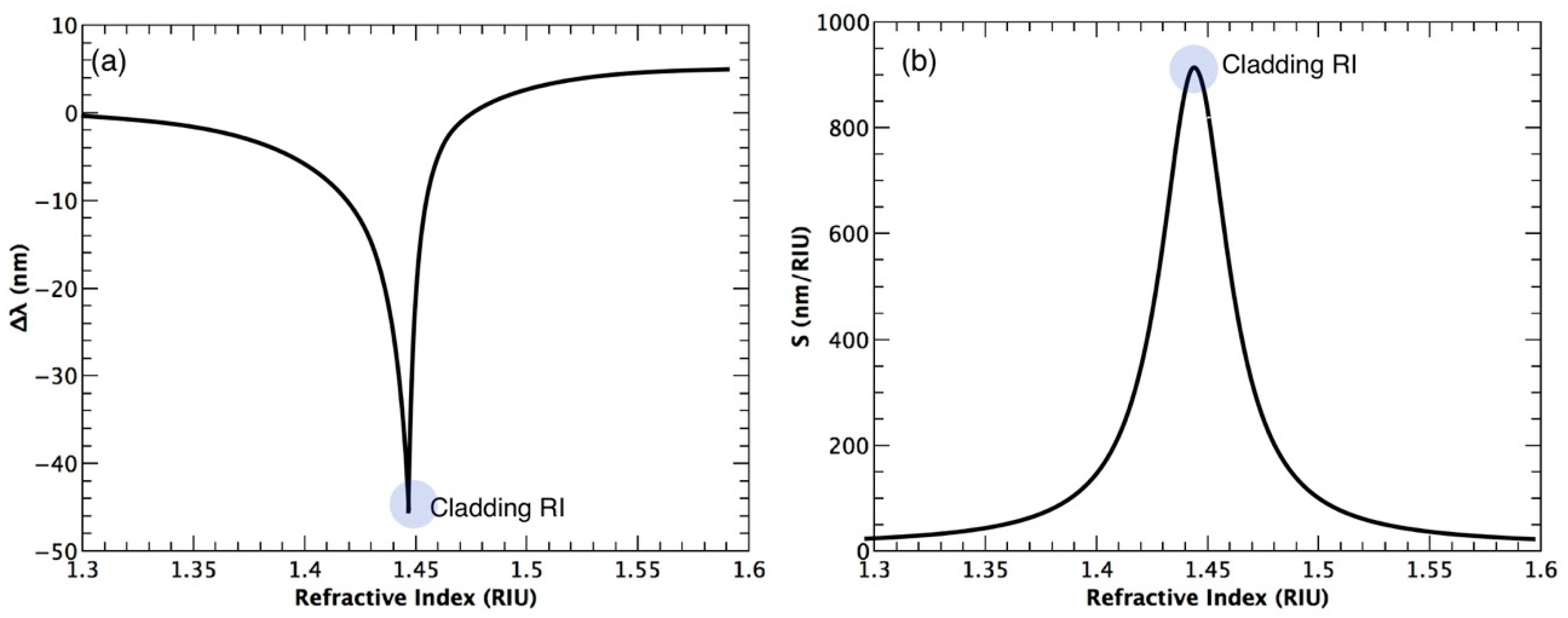
3.2.1. Response Curve and Refractive Index Sensitivity
3.2.2. Resolution
3.3. Parameters Specifically Related to Surface RI Sensing
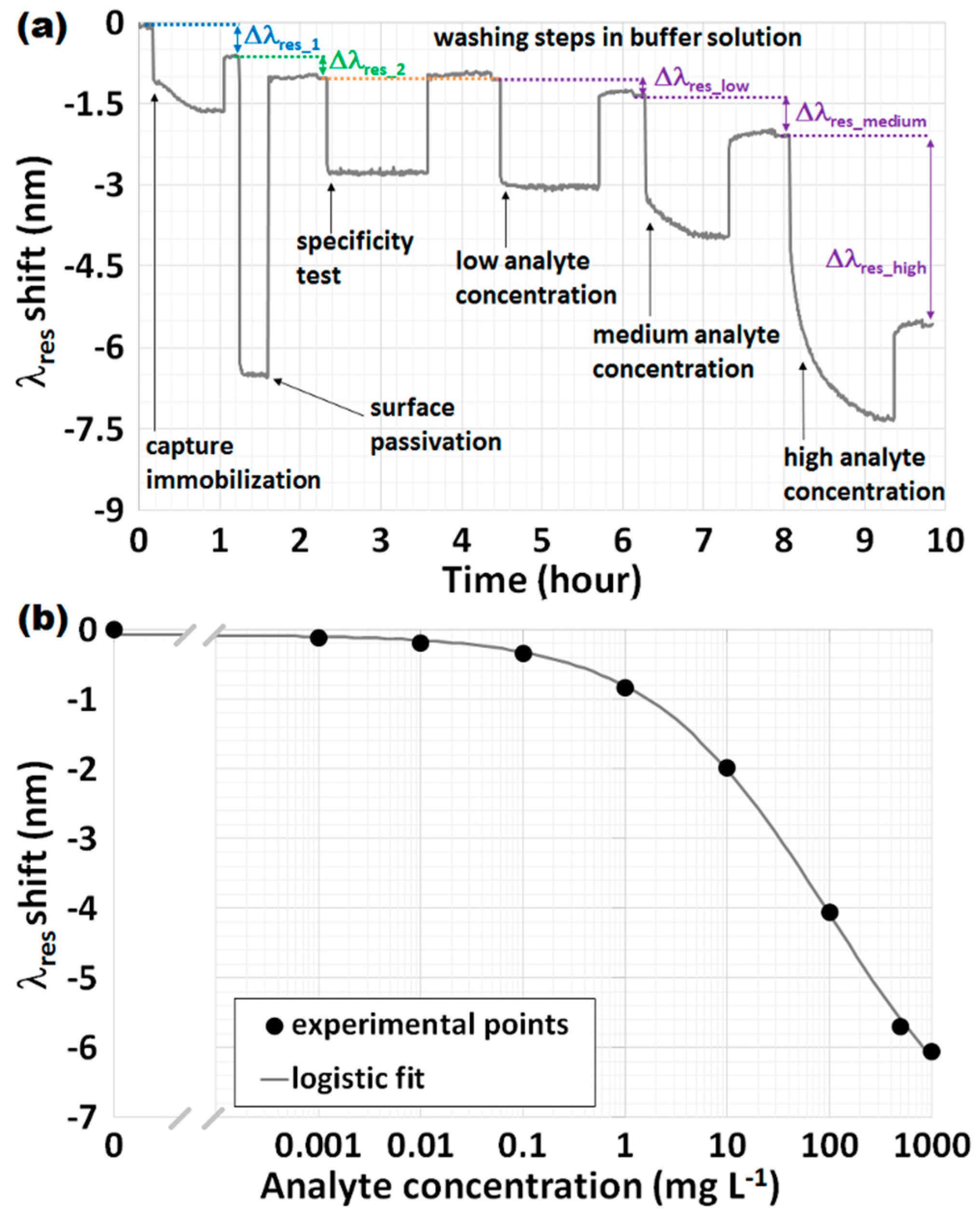
3.3.1. Sensorgram and Calibration Curve
3.3.2. Limit of Detection
3.3.3. Specificity (or Selectivity)
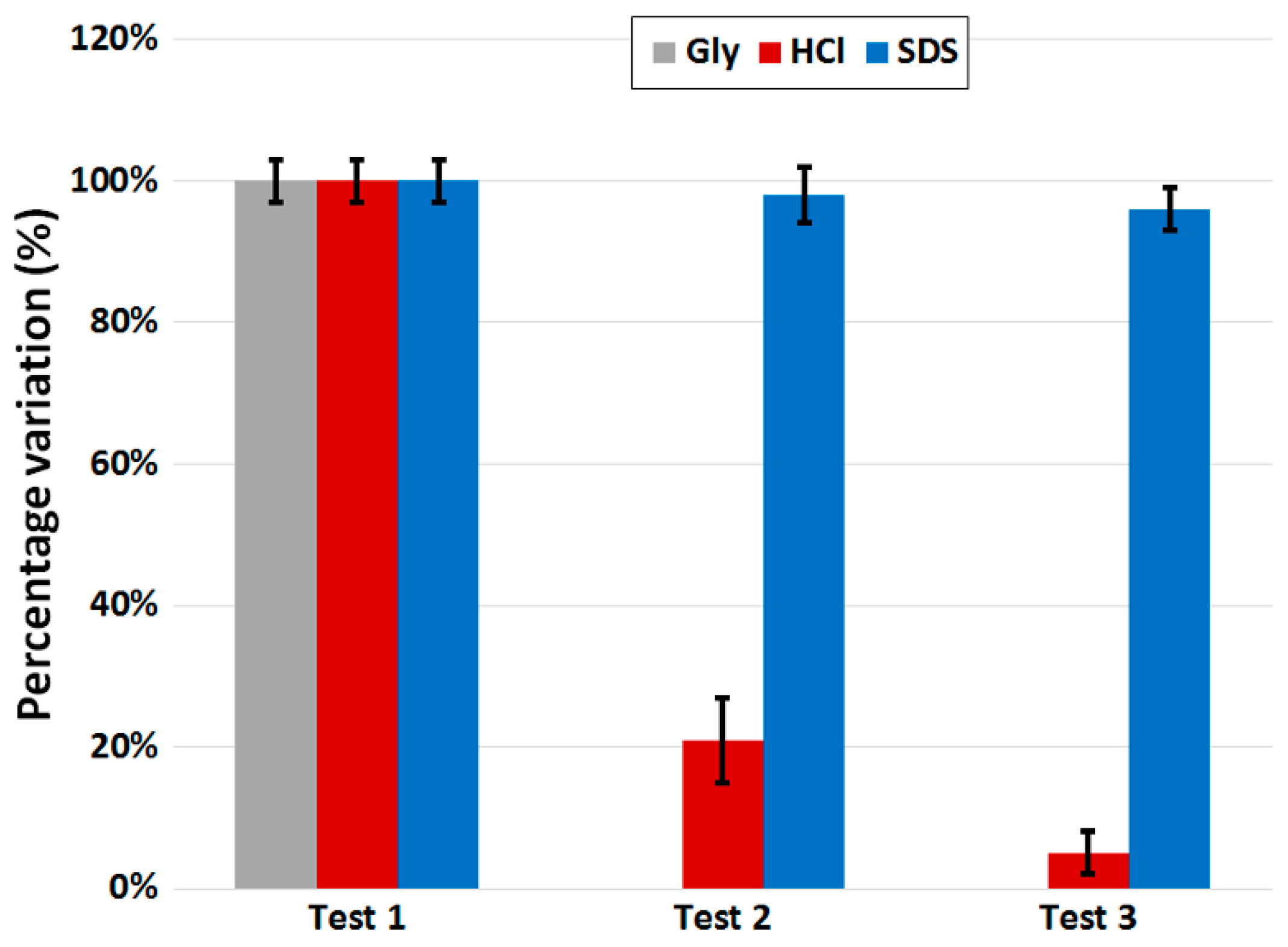
3.3.4. Regeneration (or Reusability)
3.4. Parameters More Specific to Grating-Based Sensors
3.4.1. Peak Visibility and Bandwidth
3.4.2. Influence of the λres Determination on RI Sensitivity and Resolution
4. Refractometers
4.1. Fiber Bragg Gratings
4.2. Long Period Gratings
5. Biosensors
5.1. Fiber Bragg Gratings
5.2. Long Period Gratings
6. Some Common Mistakes and an Attempt to Bring Uniformity to Performance Evaluation
- Volume Sensitivity (S) expressed as nm·RIU−1 (wavelength interrogation) or as dB·RIU−1 (intensity interrogation) and as shown in Section 3.2.1;
- Resolution (R) expressed as RIU and as fully discussed in Section 3.2.2;
- Accuracy expressed as RIU and as described in Section 3.1.2.
- Response Time, expressed in seconds or in minutes, which can be derived from the sensorgram for each concentration of the target analyte as well as from the binding kinetics;
- Limit of Detection (LOD), expressed in terms of concentration C (g·L−1 or M), which can be obtained from the calibration curve, as fully discussed in Section 3.3.2;
- Specificity, which can be tested by using a complex matrix or by performing a negative control during the assay implementation, as discussed in Section 3.3.3;
- Reusability, expressed in terms of percentage, which can be evaluated by performing at least three cycles of regeneration tests with the same sensor, as shown in Section 3.3.4;
- Surface Sensitivity, expressed as the RI change divided by the surface density concentration of the target analyte. This is not mandatory but it could provide additional information, as discussed in Section 3.3.2.
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
- RI sensitivity (nm·RIU−1), the derivative (the slope) of the response curve, in the particular RI range when the sensor response is not linear. Specifically, this value should be reported around the RI of water with a view to an application as a biosensor.
- Resolution (RIU), the smallest variation in the surrounding RI that the sensing device is able to resolve or the lowest change in the surrounding RI that produces a measurable change, in the particular RI range when the sensor response is not linear. Specifically, the influence of the noise sources and their contributions should be addressed when the “real” resolution is provided. Otherwise, one should talk about the maximum theoretical resolution attainable from the sensor by considering the instrument resolution. Clearly, in an evaluation of the resolution, certain considerations related to the visibility (i.e., shape and intensity) and bandwidth of the resonance have to come out. Therefore, the resolution is also indirectly related to the figure of merit (Q-factor for instance) of the resonance, which should be detailed.
- Accuracy (RIU), the deviation between the mean value achievable from a series of measurements (i.e., the data set) and the true value of the measurand assumed as the reference value, in the particular RI range when the sensor response is not linear. Specifically, this parameter guarantees that the device has been tested with repeated measurements, thus providing an idea of repeatability and reproducibility.
- Limit of detection (M, g·L−1 or g·mm−2), three times the standard deviation of the blank measurement from the biosensor calibration curve obtained with repeated measurements (k). Alternatively, another approach has been proposed: three times the maximum standard deviation obtained among all the experimental points of the calibration curve that usually corresponds to the maximum deviation from the fitting function. This latter approach represents a valuable option for evaluating the LOD within a certain degree of reliability and repeatability, with k < 3 as well. LOD can also be expressed in terms of surface density concentration of an analyte at saturation (g·mm−2), a condition typical of SPR-based optical platforms. Otherwise, one should talk about the minimum detectable concentration, the minimum value of the analyte concentration that the biosensor is able to detect reliably. This parameter, by not implying the utilization of the full calibration curve of the biosensor, requires only a few experimental points plus the reference point at 0 analyte concentration (i.e., blank measurement).
- Specificity or selectivity, the sensor’s ability to be sensitive to a specific or a selective measurand (or target analyte, in the particular case of biosensors), instead of to all the other interfering measurands. As a general rule, one should first develop an experimental setup with controlled environmental conditions, both mechanical and thermal. After that, during the implementation of the bioassay, two options exist for performing the specificity test: (i) simple negative control, by injecting a solution containing (one or more) analytes different from the one under investigation; (ii) by spiking the analyte under investigation into a more real and complex solution that also containing other analytes (i.e., serum, plasma, blood, etc.). If the change in the sensor is within the sensor noise or, even so, lower than the change produced by the minimum detectable concentration, the specificity test is passed; otherwise, it has to be taken it into account.
- Regeneration or reusability (percentage variation, %), a sensor’s ability to obtain the specific biolayer available for a new interaction in consecutive assay cycles, instead of for a single usage. The second kind of regeneration involves the restoration of the entire sensing layer, thus removing not only the bound analyte but also the immobilized bioreceptor and the functional layer. Clearly, for real applications, the first kind is the feasible one. To sum up, the steps of the regeneration test are the following: (i) choice of the best regeneration solution as a function of the analyte/bioreceptor pair used (each bioassay is usually regenerated by a specific regeneration solution); (ii) repetition (at least three times) of the measurement of the same analyte concentration after the respective cycle of regeneration.
References
- D’Amico, A.; Di Natale, C. A contribution on some basic definitions of sensors properties. IEEE Sens. J. 2001, 1, 183–190. [Google Scholar] [CrossRef]
- White, I.M.; Fan, X. On the performance quantification of resonant refractive index sensors. Opt. Express 2008, 16, 1020–1028. [Google Scholar] [CrossRef] [PubMed]
- Janiga, I.; Mocak, J.; Garaj, I. Comparison of minimum detectable concentration with the iupac detection limit. Meas. Sci. Rev. 2008, 8, 108–110. [Google Scholar] [CrossRef]
- Hu, J.; Sun, X.; Agarwal, A.; Kimerling, L.C. Design guidelines for optical resonator biochemical sensors. J. Opt. Soc. Am. B Opt. Phys. 2009, 26, 1032–1041. [Google Scholar] [CrossRef]
- Loock, H.P.; Wentzell, P.D. Detection limits of chemical sensors: Applications and misapplications. Sens. Actuators B Chem. 2012, 173, 157–163. [Google Scholar] [CrossRef]
- William, E.; Gordon, G.E.; Phillips, W.F.; Pojasek, R.B.; Sievers, R.E.; Amore, F.J.; Phillips, F. Guidelines for data acquisition and data quality evaluation in environmental chemistry. Anal. Chem. 1980, 52, 2242–2249. [Google Scholar]
- Possetti, G.R.C.; Kamikawachi, R.C.; Muller, M.; Fabris, J.L. Metrological evaluation of optical fiber grating-based sensors: An approach towards the standardization. J. Lightwave Technol. 2012, 30, 1042–1052. [Google Scholar] [CrossRef]
- Squires, T.M.; Messinger, R.J.; Manalis, S.R. Making it stick: Convection, reaction and diffusion in surface-based biosensors. Nat. Biotechnol. 2008, 26, 417–426. [Google Scholar] [CrossRef] [PubMed]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.; Askins, C.; Putnam, M.; Friebele, E.J. Fiber grating sensors. J. Lightwave Technol. 1997, 15, 1442–1463. [Google Scholar] [CrossRef]
- Asseh, A.; Sandgren, S.; Ahlfeldt, H.; Sahlgren, B.; Stubbe, R.; Edwall, G. Fiber optical Bragg grating refractometer. Fiber Integr. Opt. 1998, 17, 51–62. [Google Scholar]
- Schroeder, K.; Ecke, W.; Mueller, R.; Willsch, R.; Andreev, A. A fibre bragg grating refractometer. Meas. Sci. Technol. 2001, 12, 757–764. [Google Scholar] [CrossRef]
- Liu, Y.; Meng, C.; Zhang, A.P.; Xiao, Y.; Yu, H.; Tong, L. Compact microfiber bragg gratings with high-index contrast. Opt. Lett. 2011, 36, 3115–3117. [Google Scholar] [CrossRef] [PubMed]
- Laffont, G.; Ferdinand, P. Tilted short-period fibre-bragg-grating-induced coupling to cladding modes for accurate refractometry. Meas. Sci. Technol. 2001, 12, 765–770. [Google Scholar] [CrossRef]
- Zhou, K.; Zhang, L.; Chen, X.; Bennion, I. Optic sensors of high refractive-index responsivity and low thermal cross sensitivity that use fiber bragg gratings of> 80 tilted structures. Opt. Lett. 2006, 31, 1193–1195. [Google Scholar] [CrossRef] [PubMed]
- Chan, C.-F.; Chen, C.; Jafari, A.; Laronche, A.; Thomson, D.J.; Albert, J. Optical fiber refractometer using narrowband cladding-mode resonance shifts. Appl. Opt. 2007, 46, 1142–1149. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, V.; Vengsarkar, A.M. Optical fiber long-period grating sensors. Opt. Lett. 1996, 21, 692–694. [Google Scholar] [CrossRef] [PubMed]
- Vengsarkar, A.M.; Lemaire, P.J.; Judkins, J.B.; Bhatia, V.; Erdogan, T.; Sipe, J.E. Long-period fiber gratings as band-rejection filters. J. Lightwave Technol. 1996, 14, 58–65. [Google Scholar] [CrossRef]
- Pilla, P.; Trono, C.; Baldini, F.; Chiavaioli, F.; Giordano, M.; Cusano, A. Giant sensitivity of long period gratings in transition mode near the dispersion turning point: An integrated design approach. Opt. Lett. 2012, 37, 4152–4154. [Google Scholar] [CrossRef] [PubMed]
- Maguis, S.; Laffont, G.; Ferdinand, P.; Carbonnier, B.; Kham, K.; Mekhalif, T.; Millot, M.-C. Biofunctionalized tilted fiber bragg gratings for label-free immunosensing. Opt. Express 2008, 16, 19049. [Google Scholar] [CrossRef] [PubMed]
- Stewart, G.; Jin, W.; Culshaw, B. Prospects for fibre-optic evanescent-field gas sensors using absorption in the near-infrared. Sens. Actuators B Chem. 1997, 38, 42–47. [Google Scholar] [CrossRef]
- Baldini, F.; Brenci, M.; Chiavaioli, F.; Giannetti, A.; Trono, C. Optical fibre gratings as tools for chemical and biochemical sensing. Anal. Bioanal. Chem. 2011, 402, 109–116. [Google Scholar] [CrossRef] [PubMed]
- Patrick, H.J.; Kersey, A.D.; Bucholtz, F. Analysis of the response of long period fiber gratings to external index of refraction. J. Lightwave Technol. 1998, 16, 1606–1612. [Google Scholar] [CrossRef]
- Sinibaldi, A.; Danz, N.; Anopchenko, A.; Munzert, P.; Schmieder, S.; Chandrawati, R.; Rizzo, R.; Rana, S.; Sonntag, F.; Occhicone, A. Label-free detection of tumor angiogenesis biomarker angiopoietin 2 using bloch surface waves on one dimensional photonic crystals. J. Lightwave Technol. 2015, 33, 3385–3393. [Google Scholar] [CrossRef]
- Saerens, D.; Huang, L.; Bonroy, K.; Muyldermans, S. Antibody fragments as probe in biosensor development. Sensors 2008, 8, 4669–4686. [Google Scholar] [CrossRef] [PubMed]
- Reth, M. Matching cellular dimensions with molecular sizes. Nat. Immunol. 2013, 14, 765–767. [Google Scholar] [CrossRef] [PubMed]
- Del Villar, I.; Matías, I.R.; Arregui, F.J.; Lalanne, P. Optimization of sensitivity in long period fiber gratings with overlay deposition. Opt. Express 2005, 13, 56–69. [Google Scholar] [CrossRef] [PubMed]
- Pilla, P.; Manzillo, P.F.; Malachovska, V.; Buosciolo, A.; Campopiano, S.; Cutolo, A.; Ambrosio, L.; Giordano, M.; Cusano, A. Long period grating working in transition mode as promising technological platform for label-free biosensing. Opt. Express 2009, 17, 20039–20050. [Google Scholar] [CrossRef] [PubMed]
- Chiavaioli, F.; Biswas, P.; Trono, C.; Jana, S.; Bandyopadhyay, S.; Basumallick, N.; Giannetti, A.; Tombelli, S.; Bera, S.; Mallick, A. Sol–gel-based titania–silica thin film overlay for long period fiber grating-based biosensors. Anal. Chem. 2015, 87, 12024–12031. [Google Scholar] [CrossRef] [PubMed]
- Renoirt, J.-M.; Zhang, C.; Debliquy, M.; Olivier, M.-G.; Megret, P.; Caucheteur, C. High-refractive-index transparent coatings enhance the optical fiber cladding modes refractometric sensitivity. Opt. Express 2013, 21, 29073–29082. [Google Scholar] [CrossRef] [PubMed]
- Shu, X.; Zhang, L.; Bennion, I. Sensitivity characteristics of long-period fiber gratings. J. Lightwave Technol. 2002, 20, 255–266. [Google Scholar]
- Wang, Z.; Ramachandran, S. Ultrasensitive long-period fiber gratings for broadband modulators and sensors. Opt. Lett. 2003, 28, 2458–2460. [Google Scholar] [CrossRef] [PubMed]
- Del Villar, I. Ultrahigh-sensitivity sensors based on thin-film coated long period gratings with reduced diameter, in transition mode and near the dispersion turning point. Opt. Express 2015, 23, 8389–8398. [Google Scholar] [CrossRef] [PubMed]
- Smietana, M.; Koba, M.; Mikulic, P.; Bock, W.J. Combined plasma-based fiber etching and diamond-like carbon nano-overlay deposition for enhancing sensitivity of long-period gratings. J. Lightwave Technol. 2016, 34, 4615–4619. [Google Scholar] [CrossRef]
- Homola, J.; Yee, S.S.; Gauglitz, G. Surface plasmon resonance sensors: Review. Sens. Actuators B Chem. 1999, 54, 3–15. [Google Scholar] [CrossRef]
- Shevchenko, Y.Y.; Albert, J. Plasmon resonances in gold-coated tilted fiber bragg gratings. Opt. Lett. 2007, 32, 211–213. [Google Scholar] [CrossRef] [PubMed]
- Schuster, T.; Herschel, R.; Neumann, N.; Schäffer, C.G. Miniaturized long-period fiber grating assisted surface plasmon resonance sensor. J. Lightwave Technol. 2012, 30, 1003–1008. [Google Scholar] [CrossRef]
- Rindorf, L.; Jensen, J.B.; Dufva, M.; Pedersen, L.H.; Bang, O. Photonic crystal fiber long-period gratings for biochemical sensing. Opt. Express 2006, 14, 8224–8231. [Google Scholar] [CrossRef] [PubMed]
- Huy, M.C.P.; Laffont, G.; Dewynter, V.; Ferdinand, P.; Labonté, L.; Pagnoux, D.; Roy, P.; Blanc, W.; Dussardier, B. Tilted fiber bragg grating photowritten in microstructured optical fiber for improved refractive index measurement. Opt. Express 2006, 14, 10359–10370. [Google Scholar]
- Huy, M.C.P.; Laffont, G.; Dewynter, V.; Ferdinand, P.; Roy, P.; Auguste, J.-L.; Pagnoux, D.; Blanc, W.; Dussardier, B. Three-hole microstructured optical fiber for efficient fiber bragg grating refractometer. Opt. Lett. 2007, 32, 2390–2392. [Google Scholar]
- Calcerrada, M.; García-Ruiz, C.; González-Herráez, M. Chemical and biochemical sensing applications of microstructured optical fiber-based systems. Laser Photonics Rev. 2015, 9, 604–627. [Google Scholar] [CrossRef]
- IUPAC Compendium of Chemical Terminology, Gold Book Version 2.3.3; International Union of Pure and Applied Chemistry: Zürich, Switzerland, 2014; pp. 1301–1302.
- Homola, J. Present and future of surface plasmon resonance biosensors. Anal. Bioanal. Chem. 2003, 377, 528–539. [Google Scholar] [CrossRef] [PubMed]
- MacCraith, B.; McDonagh, C.; O’Keeffe, G.; McEvoy, A.; Butler, T.; Sheridan, F. Sol-gel coatings for optical chemical sensors and biosensors. Sens. Actuators B Chem. 1995, 29, 51–57. [Google Scholar] [CrossRef]
- DeLisa, M.P.; Zhang, Z.; Shiloach, M.; Pilevar, S.; Davis, C.C.; Sirkis, J.S.; Bentley, W.E. Evanescent wave long-period fiber bragg grating as an immobilized antibody biosensor. Anal. Chem. 2000, 72, 2895–2900. [Google Scholar] [CrossRef] [PubMed]
- Norman, P.; Davis, C. An Intensity-Based Demodulation Approach for the Measurement of Strains Induced by Structural Vibrations Using Bragg Gratings; DSTO-TR-2370 (Technical Report); The DSpace Foundation: Port Melbourne, Australia, 2011. [Google Scholar]
- Gouveia, C.; Zibaii, M.; Latifi, H.; Marques, M.J.; Baptista, J.; Jorge, P.A. High resolution temperature independent refractive index measurement using differential white light interferometry. Sens. Actuators B Chem. 2013, 188, 1212–1217. [Google Scholar] [CrossRef]
- Shu, X.; Allsop, T.; Gwandu, B.; Zhang, L.; Bennion, I. High-temperature sensitivity of long-period gratings in b-ge codoped fiber. IEEE Photonics Technol. Lett. 2001, 13, 818–820. [Google Scholar]
- Trono, C.; Baldini, F.; Brenci, M.; Chiavaioli, F.; Mugnaini, M. Flow cell for strain-and temperature-compensated refractive index measurements by means of cascaded optical fibre long period and bragg gratings. Meas. Sci. Technol. 2011, 22, 075204. [Google Scholar] [CrossRef]
- Chryssis, A.N.; Lee, S.M.; Lee, S.B.; Saini, S.S.; Dagenais, M. High sensitivity evanescent field fiber bragg grating sensor. IEEE Photonics Technol. Lett. 2005, 17, 1253–1255. [Google Scholar] [CrossRef]
- Iadicicco, A.; Campopiano, S.; Cutolo, A.; Giordano, M.; Cusano, A. Nonuniform thinned fiber bragg gratings for simultaneous refractive index and temperature measurements. IEEE Photonics Technol. Lett. 2005, 17, 1495–1497. [Google Scholar] [CrossRef]
- Liang, W.; Huang, Y.; Xu, Y.; Lee, R.K.; Yariv, A. Highly sensitive fiber bragg grating refractive index sensors. Appl. Phys. Lett. 2005, 86, 151122. [Google Scholar] [CrossRef]
- Renoirt, J.-M.; Debliquy, M.; Albert, J.; Ianoul, A.; Caucheteur, C. Surface plasmon resonances in oriented silver nanowire coatings on optical fibers. J. Phys. Chem. C 2014, 118, 11035–11042. [Google Scholar] [CrossRef]
- Smietana, M.; Koba, M.; Brzozowska, E.; Krogulski, K.; Nakonieczny, J.; Wachnicki, L.; Mikulic, P.; Godlewski, M.; Bock, W.J. Label-free sensitivity of long-period gratings enhanced by atomic layer deposited TiO2 nano-overlays. Opt. Express 2015, 23, 8441–8453. [Google Scholar] [CrossRef] [PubMed]
- Rego, G. A review of refractometric sensors based on long period fibre gratings. Sci. World J. 2013, 2013, 913418. [Google Scholar] [CrossRef] [PubMed]
- Debowska, A.K.; Smietana, M.; Mikulic, P.; Bock, W.J. High temperature nano-coated electric-arc-induced long-period gratings working at the dispersion turning point for refractive index sensing. Jpn. J. Appl. Phys. 2014, 53, 8S2. [Google Scholar] [CrossRef]
- He, Z.; Zhu, Y.; Du, H. Long-period gratings inscribed in air-and water-filled photonic crystal fiber for refractometric sensing of aqueous solution. Appl. Phys. Lett. 2008, 92, 044105. [Google Scholar] [CrossRef]
- Allsop, T.; Reeves, R.; Webb, D.J.; Bennion, I.; Neal, R. A high sensitivity refractometer based upon a long period grating mach–zehnder interferometer. Rev. Sci. Instrum. 2002, 73, 1702–1705. [Google Scholar] [CrossRef]
- Mosquera, L.; Sáez-Rodriguez, D.; Cruz, J.L.; Andrés, M.V. In-fiber fabry-perot refractometer assisted by a long-period grating. Opt. Lett. 2010, 35, 613–615. [Google Scholar] [CrossRef] [PubMed]
- Chryssis, A.N.; Saini, S.S.; Lee, S.M.; Yi, H. Detecting hybridization of DNA by highly sensitive evanescent field etched core fiber bragg grating sensors. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 864–872. [Google Scholar] [CrossRef]
- Sun, D.; Guo, T.; Ran, Y.; Huang, Y.; Guan, B.-O. In-situ DNA hybridization detection with a reflective microfiber grating biosensor. Biosens. Bioelectron. 2014, 61, 541–546. [Google Scholar] [CrossRef] [PubMed]
- Candiani, A.; Bertucci, A.; Giannetti, S.; Konstantaki, M.; Manicardi, A.; Pissadakis, S.; Cucinotta, A.; Corradini, R.; Selleri, S. Label-free DNA biosensor based on a peptide nucleic acid-functionalized microstructured optical fiber-bragg grating. J. Biomed. Opt. 2013, 18, 57004. [Google Scholar] [CrossRef] [PubMed]
- Lépinay, S.; Staff, A.; Ianoul, A.; Albert, J. Improved detection limits of protein optical fiber biosensors coated with gold nanoparticles. Biosens. Bioelectron. 2014, 52, 337–344. [Google Scholar] [CrossRef] [PubMed]
- Luo, B.; Yan, Z.; Sun, Z.; Li, J.; Zhang, L. Novel glucose sensor based on enzyme-immobilized 81° tilted fiber grating. Opt. Express 2014, 22, 30571–30578. [Google Scholar] [CrossRef] [PubMed]
- Shevchenko, Y.; Francis, T.J.; Blair, D.A.D.; Walsh, R.; DeRosa, M.C.; Albert, J. In situ biosensing with a surface plasmon resonance fiber grating aptasensor. Anal. Chem. 2011, 83, 7027–7034. [Google Scholar] [CrossRef] [PubMed]
- Shevchenko, Y.; Camci-Unal, G.; Cuttica, D.F.; Dokmeci, M.R.; Albert, J.; Khademhosseini, A. Surface plasmon resonance fiber sensor for real-time and label-free monitoring of cellular behavior. Biosens. Bioelectron. 2014, 56, 359–367. [Google Scholar] [CrossRef] [PubMed]
- Malachovská, V.; Ribaut, C.; Voisin, V.; Surin, M.; Leclère, P.; Wattiez, R.; Caucheteur, C. Fiber-optic spr immunosensors tailored to target epithelial cells through membrane receptors. Anal. Chem. 2015, 87, 5957–5965. [Google Scholar] [CrossRef] [PubMed]
- Shibru, H.; Zhang, Y.; Cooper, K.L.; Pickrell, G.R.; Wang, A. Optimization of layer-by-layer electrostatic self-assembly processing parameters for optical biosensing. Opt. Eng. 2006, 45, 024401. [Google Scholar] [CrossRef]
- Wang, D.Y.; Wang, Y.; Han, M.; Gong, J.; Wang, A. Fully distributed fiber-optic biological sensing. IEEE Photonics Technol. Lett. 2010, 22, 1553–1555. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, L.; Zhou, K.; Davies, E.; Sugden, K.; Bennion, I.; Hughes, M.; Hine, A. Real-time detection of DNA interactions with long-period fiber-grating-based biosensor. Opt. Lett. 2007, 32, 2541–2543. [Google Scholar] [CrossRef] [PubMed]
- Pilla, P.; Sandomenico, A.; Malachovská, V.; Borriello, A.; Giordano, M.; Cutolo, A.; Ruvo, M.; Cusano, A. A protein-based biointerfacing route toward label-free immunoassays with long period gratings in transition mode. Biosens. Bioelectron. 2012, 31, 486–491. [Google Scholar] [CrossRef] [PubMed]
- Pilla, P.P.; Malachovská, V.; Borriello, A.; Buosciolo, A.; Giordano, M.; Ambrosio, L.; Cutolo, A.; Cusano, A. Transition mode long period grating biosensor with functional multilayer coatings. Opt. Express 2011, 19, 512–526. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.W.; Zhang, Y.; Cooper, K.L.; Wang, A. Fibre-optic interferometric immuno-sensor using long period grating. Electron. Lett. 2006, 42, 324–325. [Google Scholar] [CrossRef]
- Yang, J.; Sandhu, P.; Liang, W.; Xu, C.Q.; Li, Y. Label-free fiber optic biosensors with enhanced sensitivity. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 1691–1696. [Google Scholar] [CrossRef]
- He, Z.; Tian, F.; Zhu, Y.; Lavlinskaia, N.; Du, H. Long-period gratings in photonic crystal fiber as an optofluidic label-free biosensor. Biosens. Bioelectron. 2011, 26, 4774–4778. [Google Scholar] [CrossRef] [PubMed]
- Cooper, K.L.; Bandara, A.B.; Wang, Y.; Wang, A.; Inzana, T.J. Photonic biosensor assays to detect and distinguish subspecies of francisella tularensis. Sensors 2011, 11, 3004–3019. [Google Scholar] [CrossRef] [PubMed]
- Chiavaioli, F.; Trono, C.; Giannetti, A.; Brenci, M.; Baldini, F. Characterisation of a label-free biosensor based on long period grating. J. Biophotonics 2014, 7, 312–322. [Google Scholar] [CrossRef] [PubMed]
- Chiavaioli, F.; Biswas, P.; Trono, C.; Bandyopadhyay, S.; Giannetti, A.; Tombelli, S.; Basumallick, N.; Dasgupta, K.; Baldini, F. Towards sensitive label-free immunosensing by means of turn-around point long period fiber gratings. Biosens. Bioelectron. 2014, 60, 305–310. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Liu, C.; Hughes, M.D.; Nagel, D.A.; Hine, A.V.; Zhang, L. Edc-mediated oligonucleotide immobilization on a long period grating optical biosensor. J. Biosens. Bioelectron. 2015, 6, 1000173. [Google Scholar] [CrossRef]
- Jang, H.S.; Park, K.N.; Kim, J.P.; Sim, S.J.; Kwon, O.J.; Han, Y.G.; Lee, K.S. Sensitive DNA biosensor based on a long-period grating formed on the side-polished fiber surface. Opt. Express 2009, 17, 3855–3860. [Google Scholar] [CrossRef] [PubMed]
- Hine, A.V.; Chen, X.; Hughes, M.D.; Zhou, K.; Davies, E.; Sugden, K.; Bennion, I.; Zhang, L. Optical fibre-based detection of DNA hybridization. Biochem. Soc. Trans. 2009, 37, 445–449. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, H.M.R.; Moreira, L.; Pereira, L.; Jorge, P.; Gouveia, C.; Martins-Lopes, P.; Fernandes, J.R.A. Biosensor for label-free DNA quantification based on functionalized LPGs. Biosens. Bioelectron. 2016, 84, 30–36. [Google Scholar] [CrossRef] [PubMed]
- Carrasquilla, C.; Xiao, Y.; Xu, C.Q.; Li, Y.; Brennan, J.D. Enhancing sensitivity and selectivity of long-period grating sensors using structure-switching aptamers bound to gold-doped macroporous silica coatings. Anal. Chem. 2011, 83, 7984–7991. [Google Scholar] [CrossRef] [PubMed]
- Queirós, R.B.; Gouveia, C.; Fernandes, J.R.A.; Jorge, P.A.S. Evanescent wave DNA-aptamer biosensor based on long period gratings for the specific recognition of e. Coli outer membrane proteins. Biosens. Bioelectron. 2014, 62, 227–233. [Google Scholar] [CrossRef] [PubMed]
- Smietana, M.; Bock, W.J.; Mikulic, P.; Ng, A.; Chinnappan, R.; Zourob, M. Detection of bacteria using bacteriophages as recognition elements immobilized on long-period fiber gratings. Opt. Express 2011, 19, 7971–7978. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, S.M.; Bock, W.J.; Mikulic, P.; Chinnappan, R.; Ng, A.; Tolba, M.; Zourob, M. Long period grating based biosensor for the detection of escherichia coli bacteria. Biosens. Bioelectron. 2012, 35, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Brzozowska, E.; Śmietana, M.; Koba, M.; Górska, S.; Pawlik, K.; Gamian, A.; Bock, W.J. Recognition of bacterial lipopolysaccharide using bacteriophage-adhesin-coated long-period gratings. Biosens. Bioelectron. 2015, 67, 93–99. [Google Scholar] [CrossRef] [PubMed]
- Deep, A.; Tiwari, U.; Kumar, P.; Mishra, V.; Jain, S.C.; Singh, N.; Kapur, P.; Bharadwaj, L.M. Immobilization of enzyme on long period grating fibers for sensitive glucose detection. Biosens. Bioelectron. 2012, 33, 190–195. [Google Scholar] [CrossRef] [PubMed]
- Baliyan, A.; Sital, S.; Tiwari, U.; Gupta, R.; Sharma, E.K. Long period fiber grating based sensor for the detection of triacylglycerides. Biosens. Bioelectron. 2016, 79, 693–700. [Google Scholar] [CrossRef] [PubMed]


| Type of Sensing Structure | RI Range (RIU) | Sensitivity (nm·RIU−1) | Resolution (RIU) | Ref. |
|---|---|---|---|---|
| EFBG | ~1.46 | 1394 | 7.2 × 10−6 † | [49] |
| Microfiber FBG | ~1.38 | 660 | - | [12] |
| 81° TFBG | ~1.33 | 340 | - | [14] |
| HRI coated TFBG | ~1.33 | 210 | 10−5 † | [29] |
| SPR-based TFBG | ~1.33 | 650 | - | [52] |
| Fabry-Pérot cavity-based FBG | ~1.33 | 71.2 | 1.4 × 10−5 | [51] |
| FBG in MOF | ~1.33 | 210 | 3 × 10−5 † | [39] |
| TAP LPG | 1.33–1.36 | 1481 | - | [30] |
| HRI coated TAP LPG | ~1.35 | 9100 | - | [18] |
| HRI coated LPG | ~1.33 | 7075 | 4.6 × 10−6 | [28] |
| LPG in MOF | 1.33–1.35 | 2991 | 3.3 × 10−7 † | [56] |
| Mach-Zehnder-based LPG | 1.37–1.40 | - | 1.8 × 10−6 | [57] |
| Type of Sensing Structure | Biosensing Interaction | Detection Range | LOD | Ref. |
|---|---|---|---|---|
| Microfiber FBG | DNA hybridization | 0.5–20 μM | 0.5 μM † | [60] |
| TFBG | BSA/anti-BSA | 1–100 mg·L−1 | 0.086 mg·L−1 ‡ | [19] |
| TFBG with gold nanospheres and nanocages | Avidin/Biotin | 10 pM–100·μM | 8 pM | [62] |
| 81° TFBG | Glucose | 0–3 g·L−1 | 0.1 g·L−1 † | [63] |
| SPR-based TFBG | Aptamer/Thrombin | 0.1–5 μM | 22.6 nM | [64] |
| SPR-based TFBG | Single cell and membrane proteins | 0.5−5 × 106 cells·mL−1 | 2 × 106 cells·mL−1 † | [66] |
| LPG | IgG/anti-IgG | 2–50 mg·L−1 | 2 mg·L−1 † | [44] |
| TAP LPG | Biotin/Streptavidin | 0–100 mg·L−1 | 12.5 mg·L−1 † | [68] |
| LPG | IgG/anti-IgG | 0.1–500 mg·L−1 | 0.5 mL−1/3.33 nM (buffer) | [75] |
| TAP LPG | IgG/anti-IgG | 0.001–100 mg·L−1 | 70 μg L−1/460 pM (serum) | [77] |
| HRI coated LPG | IgG/anti-IgG | 0.001–100 mg·L−1 | 8 μg L−1/53 pM (serum) | [28] |
| TAP LPG | DNA hybridization | 0–5 μM | 4 nM | [78] |
| LPG | DNA hybridization | - | 62 nM § | [81] |
| Michelson-based LPG | Aptamer/Adenosine triphosphate | 0–2.5 mM | 400 μM | [82] |
| LPG | Aptamer/E. coli outer proteins | 0.1–30 nM | 1 nM | [83] |
| LPG | Bacteriophages/E. coli | 0–109 cfu·mL−1 | 103 cfu·mL−1 † | [84] |
| LPG | Glucose/enzymatic | 0.1–3 g L−1 | - | [87] |
| LPG | Triacylglyceride/enzymatic | 0–7 mM | 0.5 mM † | [88] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiavaioli, F.; Gouveia, C.A.J.; Jorge, P.A.S.; Baldini, F. Towards a Uniform Metrological Assessment of Grating-Based Optical Fiber Sensors: From Refractometers to Biosensors. Biosensors 2017, 7, 23. https://doi.org/10.3390/bios7020023
Chiavaioli F, Gouveia CAJ, Jorge PAS, Baldini F. Towards a Uniform Metrological Assessment of Grating-Based Optical Fiber Sensors: From Refractometers to Biosensors. Biosensors. 2017; 7(2):23. https://doi.org/10.3390/bios7020023
Chicago/Turabian StyleChiavaioli, Francesco, Carlos A. J. Gouveia, Pedro A. S. Jorge, and Francesco Baldini. 2017. "Towards a Uniform Metrological Assessment of Grating-Based Optical Fiber Sensors: From Refractometers to Biosensors" Biosensors 7, no. 2: 23. https://doi.org/10.3390/bios7020023
APA StyleChiavaioli, F., Gouveia, C. A. J., Jorge, P. A. S., & Baldini, F. (2017). Towards a Uniform Metrological Assessment of Grating-Based Optical Fiber Sensors: From Refractometers to Biosensors. Biosensors, 7(2), 23. https://doi.org/10.3390/bios7020023