Utilizing Circadian Heart Rate Variability Features and Machine Learning for Estimating Left Ventricular Ejection Fraction Levels in Hypertensive Patients: A Composite Multiscale Entropy Analysis
Abstract
1. Introduction
2. Method
2.1. Dataset
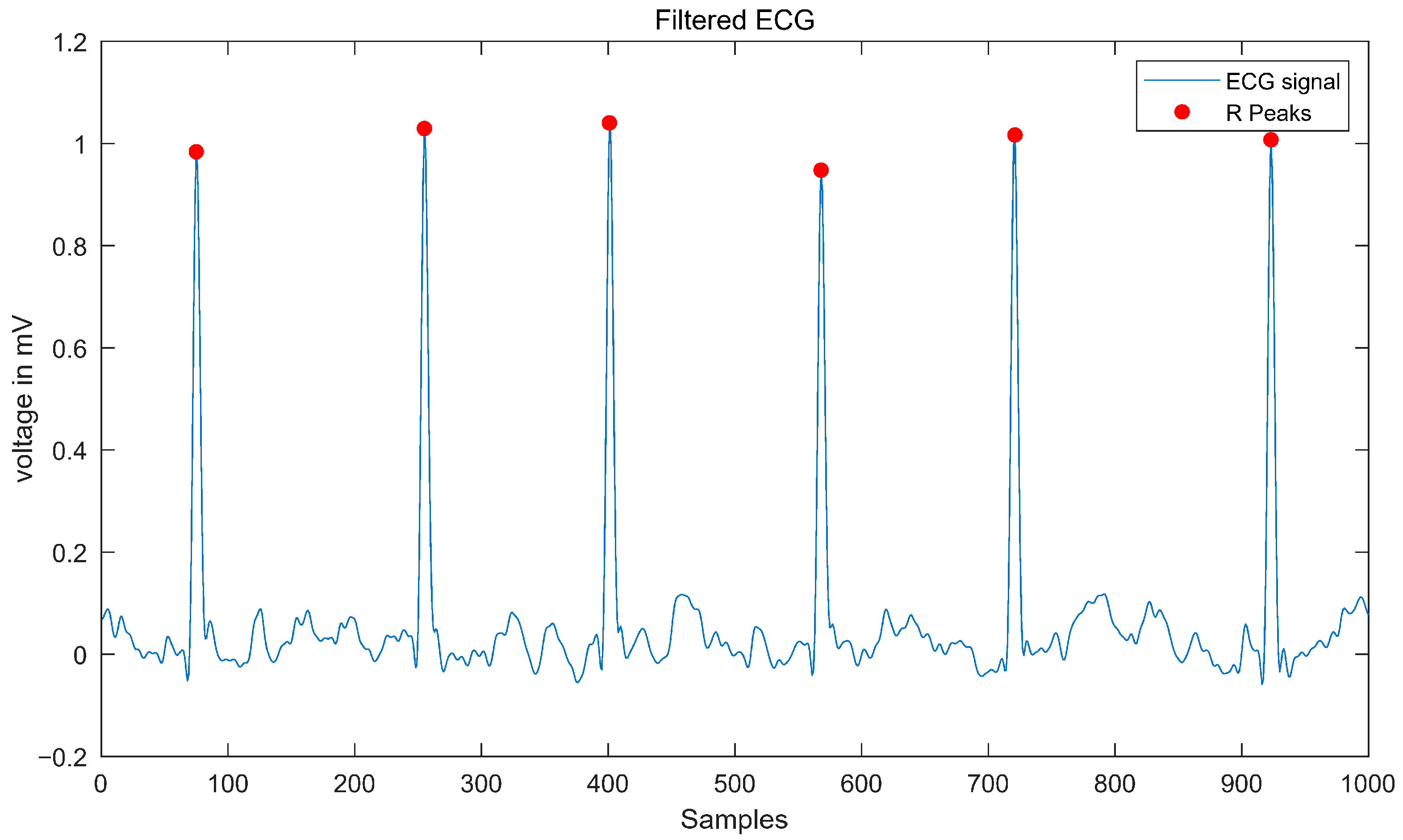
2.2. Data Processing
2.3. HRV Features
- The value of entropy at scale 1.
- The value of entropy at scale 5.
- Slope 1–5: The linear-fitted slope between scales 1 and 5.
- The area under the curve between scales 1 and 5 (Area 1–5), which serves as a measure of complexity across short timescales, also known as the short-term Complexity Index (CI).
- The area under the curve between scales 6 and 20 (Area 6–20), which serves as a measure of complexity across long timescales, also known as the long-term CI.
2.4. Machine Learning Framework
2.5. Explainability and Visualization
3. Results
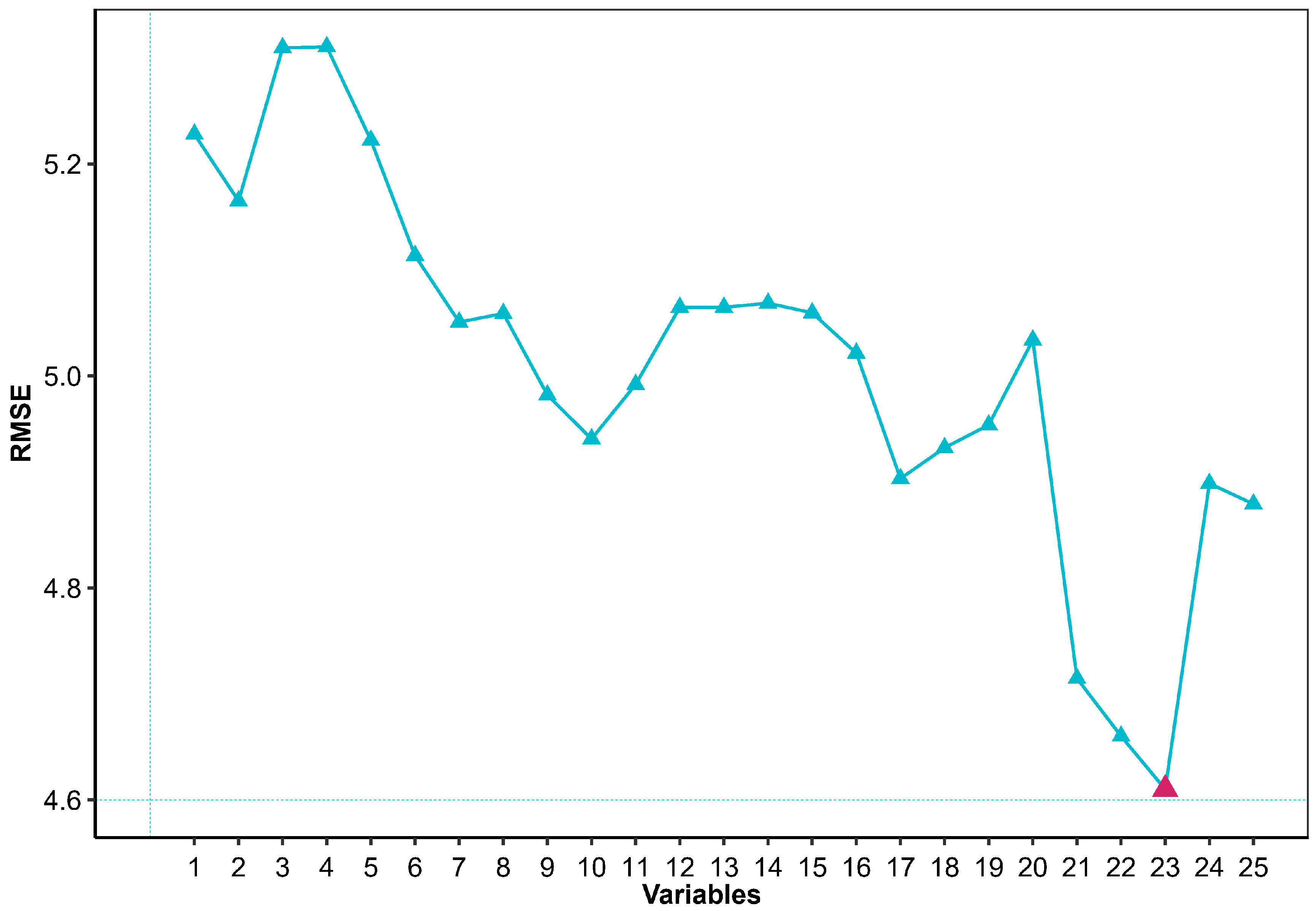
3.1. Recursive Feature Elimination
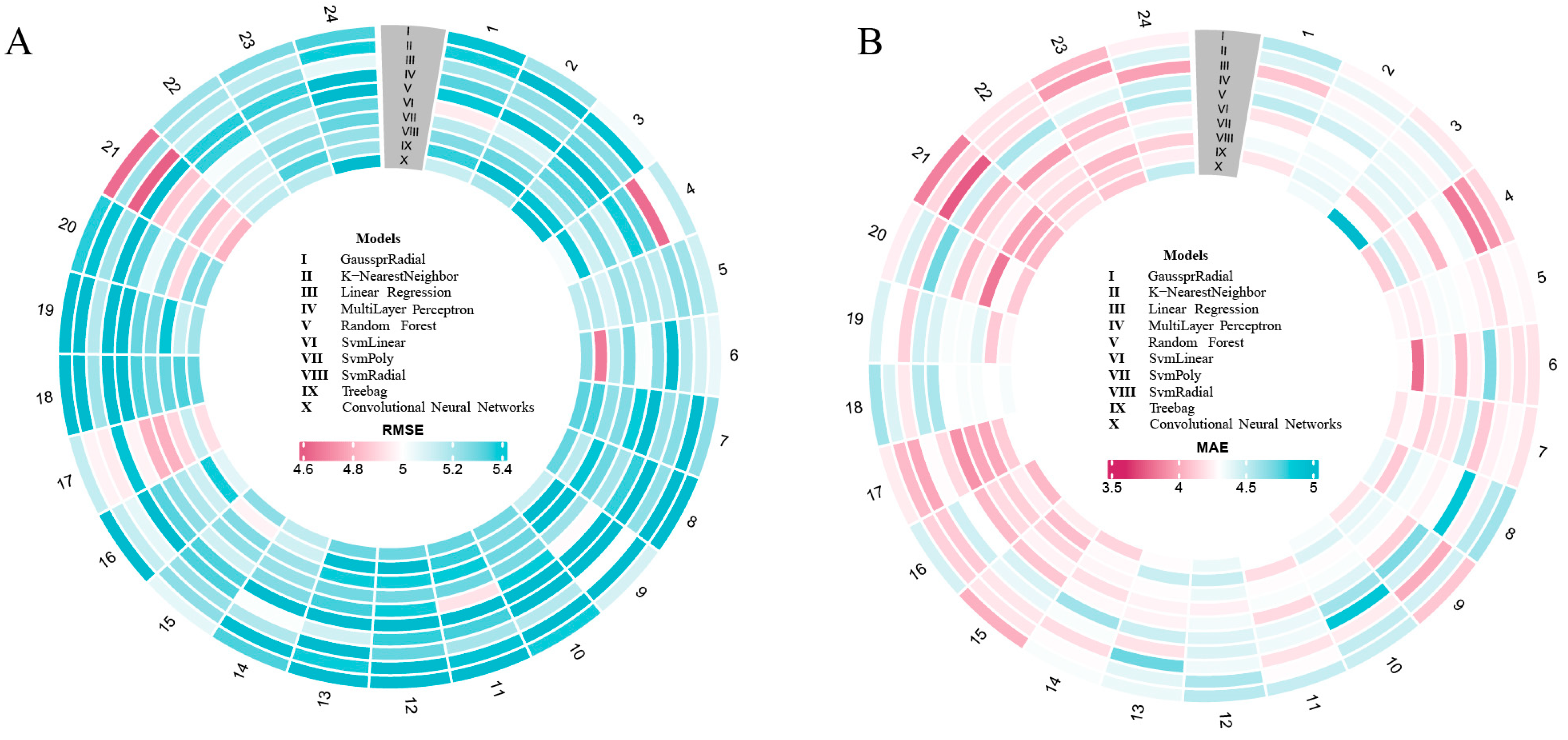
3.2. Model Performance
3.3. Bland–Altman Analysis
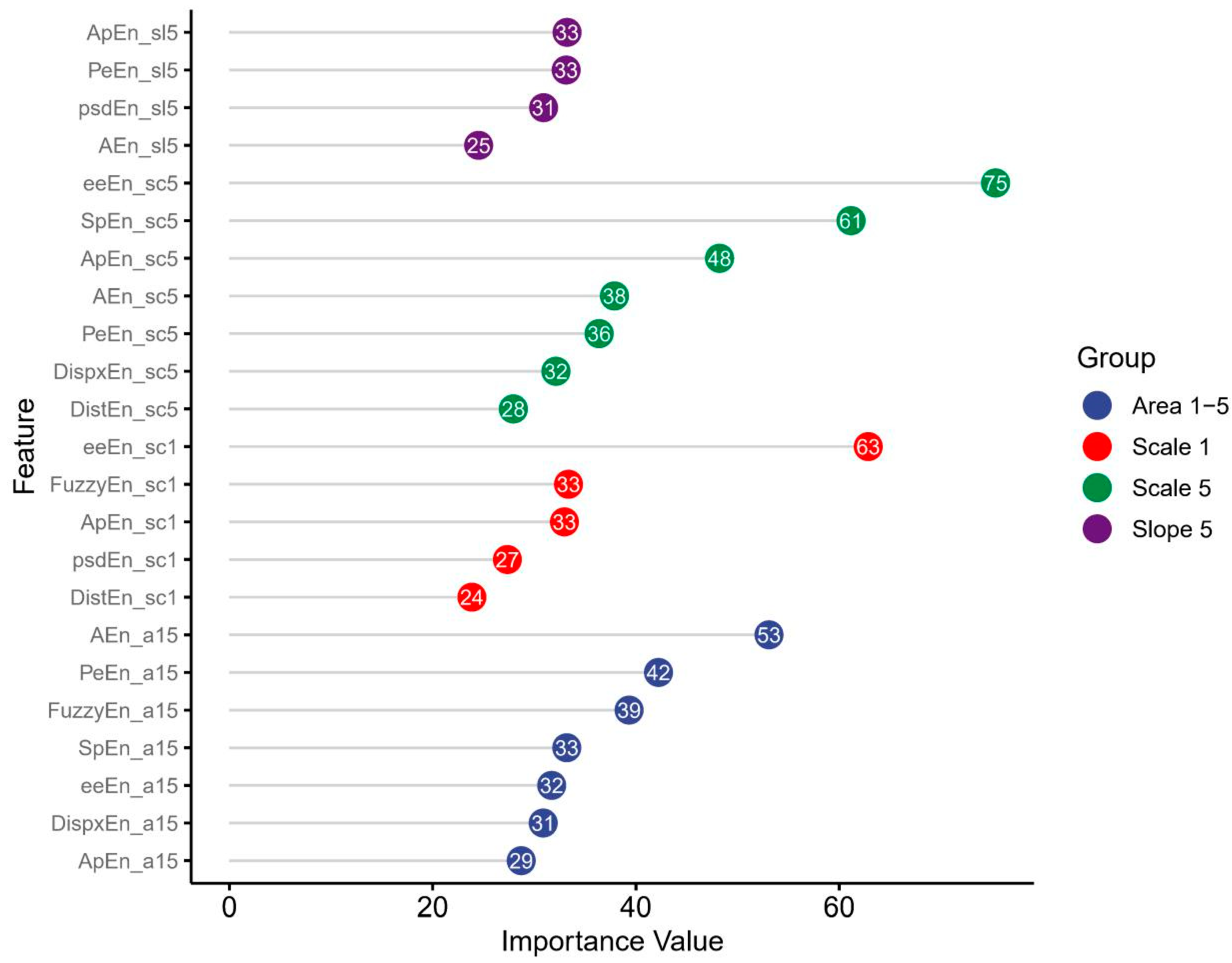
3.4. Feature Importance
4. Discussion
5. Limitations
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martin, S.S.; Aday, A.W.; Almarzooq, Z.I.; Anderson, C.A.M.; Arora, P.; Avery, C.L.; Baker-Smith, C.M.; Barone Gibbs, B.; Beaton, A.Z.; Boehme, A.K.; et al. 2024 Heart Disease and Stroke Statistics: A Report of US and Global Data from the American Heart Association. Circulation 2024, 149, e347–e913. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.W.; Whelton, P.K.; Allen, N.; Clark, D.; Gidding, S.S.; Muntner, P.; Nesbitt, S.; Mitchell, N.S.; Townsend, R.; Falkner, B.; et al. Management of Stage 1 Hypertension in Adults with a Low 10-Year Risk for Cardiovascular Disease: Filling a Guidance Gap: A Scientific Statement from the American Heart Association. Hypertension 2021, 77, e58–e67. [Google Scholar] [CrossRef] [PubMed]
- Williams, S.S. Advances in Genetic Hypertension. Curr. Opin. Pediatr. 2007, 19, 192–198. [Google Scholar] [CrossRef]
- Cohn, J.N.; Ferrari, R.; Sharpe, N. Cardiac Remodeling—Concepts and Clinical Implications: A Consensus Paper from an International Forum on Cardiac Remodeling. J. Am. Coll. Cardiol. 2000, 35, 569–582. [Google Scholar] [CrossRef] [PubMed]
- Sacks, C.A.; Jarcho, J.A.; Curfman, G.D. Paradigm Shifts in Heart-Failure Therapy—A Timeline. N. Engl. J. Med. 2014, 371, 989–991. [Google Scholar] [CrossRef]
- McMurray, J.J.V.; Packer, M.; Desai, A.S.; Gong, J.; Lefkowitz, M.P.; Rizkala, A.R.; Rouleau, J.L.; Shi, V.C.; Solomon, S.D.; Swedberg, K.; et al. Angiotensin–Neprilysin Inhibition versus Enalapril in Heart Failure. N. Engl. J. Med. 2014, 371, 993–1004. [Google Scholar] [CrossRef]
- Foley, T.A.; Mankad, S.V.; Anavekar, N.S.; Bonnichsen, C.R.; Miller, M.F.; Miller, T.D.; Araoz, P.A. Measuring Left Ventricular Ejection Fraction—Techniques and Potential Pitfalls. Eur. Cardiol. Rev. 2012, 8, 108. [Google Scholar] [CrossRef]
- Breen, C.J.; Kelly, G.P.; Kernohan, W.G. ECG Interpretation Skill Acquisition: A Review of Learning, Teaching and Assessment. J. Electrocardiol. 2022, 73, 125–128. [Google Scholar] [CrossRef]
- Da Silva, S.T.; De Godoy, M.F.; Gregório, M.L.; Viana, R.L.; Batista, A.M. Analysis of Heartbeat Time Series via Machine Learning for Detection of Illnesses. Chaos Solitons Fractals 2023, 171, 113388. [Google Scholar] [CrossRef]
- Tian, X.; Zhu, Q.; Li, Y.; Wu, M. Cross-Domain Joint Dictionary Learning for ECG Inference From PPG. IEEE Internet Things J. 2023, 10, 8140–8154. [Google Scholar] [CrossRef]
- Tan, H.; Xie, S.; Liu, R.; Cheng, J.; Jing, K. Fatigue Condition Diagnosis of Rolling Bearing Based on Normalized Balanced Multiscale Sample Entropy. Int. J. Fatigue 2023, 172, 107642. [Google Scholar] [CrossRef]
- Agrawal, A.; Chauhan, A.; Shetty, M.K.; Girish, M.P.; Gupta, M.D.; Gupta, A. ECG-iCOVIDNet: Interpretable AI Model to Identify Changes in the ECG Signals of Post-COVID Subjects. Comput. Biol. Med. 2022, 146, 105540. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.-C.; Jen, H.-I.; Lin, Y.-H.; Hung, C.-S.; Jou, W.-J.; Huang, P.-W.; Shieh, J.-S.; Ho, Y.-L.; Lai, D.-M.; Wu, A.-Y.; et al. Complexity of Heart Rate Variability Predicts Outcome in Intensive Care Unit Admitted Patients with Acute Stroke. J. Neurol. Neurosurg. Psychiatry 2015, 86, 95–100. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Wang, C.-C.; Lee, K.-Y. Time Series Analysis Using Composite Multiscale Entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Vaid, A.; Johnson, K.W.; Badgeley, M.A.; Somani, S.S.; Bicak, M.; Landi, I.; Russak, A.; Zhao, S.; Levin, M.A.; Freeman, R.S.; et al. Using Deep-Learning Algorithms to Simultaneously Identify Right and Left Ventricular Dysfunction from the Electrocardiogram. JACC Cardiovasc. Imaging 2022, 15, 395–410. [Google Scholar] [CrossRef]
- Lang, R.M.; Badano, L.P.; Mor-Avi, V.; Afilalo, J.; Armstrong, A.; Ernande, L.; Flachskampf, F.A.; Foster, E.; Goldstein, S.A.; Kuznetsova, T.; et al. Recommendations for Cardiac Chamber Quantification by Echocardiography in Adults: An Update from the American Society of Echocardiography and the European Association of Cardiovascular Imaging. Eur. Heart J. Cardiovasc. Imaging 2015, 16, 233–271. [Google Scholar] [CrossRef]
- Tripathi, P.M.; Kumar, A.; Komaragiri, R.; Kumar, M. A Review on Computational Methods for Denoising and Detecting ECG Signals to Detect Cardiovascular Diseases. Arch. Comput. Methods Eng. 2022, 29, 1875–1914. [Google Scholar] [CrossRef]
- Li, Q.; Li, T.; Zhu, S.; Kambhamettu, C. Improving Medical/Biological Data Classification Performance by Wavelet Preprocessing. In Proceedings of the 2002 IEEE International Conference on Data Mining, 2002. Proceedings, Maebashi City, Japan, 9–12 December 2002; IEEE Computer Society: Washington, DC, USA, 2002; pp. 657–660. [Google Scholar]
- Pilia, N.; Nagel, C.; Lenis, G.; Becker, S.; Dössel, O.; Loewe, A. ECGdeli—An Open Source ECG Delineation Toolbox for MATLAB. SoftwareX 2021, 13, 100639. [Google Scholar] [CrossRef]
- Inouye, T.; Shinosaki, K.; Sakamoto, H.; Toi, S.; Ukai, S.; Iyama, A.; Katsuda, Y.; Hirano, M. Quantification of EEG Irregularity by Use of the Entropy of the Power Spectrum. Electroencephalogr. Clin. Neurophysiol. 1991, 79, 204–210. [Google Scholar] [CrossRef]
- Han, C.; Shi, L. Automated Interpretable Detection of Myocardial Infarction Fusing Energy Entropy and Morphological Features. Comput. Methods Programs Biomed. 2019, 175, 9–23. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate Entropy as a Measure of System Complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Yang, J.; Choudhary, G.I.; Rahardja, S.; Fränti, P. Classification of Interbeat Interval Time-Series Using Attention Entropy. IEEE Trans. Affect. Comput. 2023, 14, 321–330. [Google Scholar] [CrossRef]
- Manis, G.; Aktaruzzaman, M.; Sassi, R. Bubble Entropy: An Entropy Almost Free of Parameters. IEEE Trans. Biomed. Eng. 2017, 64, 2711–2718. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Li, P.; Liu, C.; Li, K.; Zheng, D.; Liu, C.; Hou, Y. Assessing the Complexity of Short-Term Heartbeat Interval Series by Distribution Entropy. Med. Biol. Eng. Comput. 2015, 53, 77–87. [Google Scholar] [CrossRef]
- Yan, C.; Li, P.; Liu, C.; Wang, X.; Yin, C.; Yao, L. Novel Gridded Descriptors of Poincaré Plot for Analyzing Heartbeat Interval Time-Series. Comput. Biol. Med. 2019, 109, 280–289. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Zhou, X.; Jiang, A. Appropriate Use of the Increment Entropy for Electrophysiological Time Series. Comput. Biol. Med. 2018, 95, 13–23. [Google Scholar] [CrossRef]
- Rohila, A.; Sharma, A. Phase Entropy: A New Complexity Measure for Heart Rate Variability. Physiol. Meas. 2019, 40, 105006. [Google Scholar] [CrossRef]
- Seguí Moreno, J.; Molina Picó, A. A Comprehensive Literature Review on Slope Entropy Algorithm: Bridging Past Insights with Future Directions. In Intelligent Computing; Arai, K., Ed.; Lecture Notes in Networks and Systems; Springer Nature: Cham, Switzerland, 2024; Volume 1018, pp. 134–144. ISBN 978-3-031-62268-7. [Google Scholar]
- Schulz, S.; Voss, A. Symbolic Dynamics, Poincaré Plot Analysis and Compression Entropy Estimate Complexity in Biological Time Series. In Complexity and Nonlinearity in Cardiovascular Signals; Barbieri, R., Scilingo, E.P., Valenza, G., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 45–85. ISBN 978-3-319-58708-0. [Google Scholar]
- Seeger, M. Gaussian Processes for Machine Learning. Int. J. Neur. Syst. 2004, 14, 69–106. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest Neighbor Pattern Classification. IEEE Trans. Inform. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Aspuru, J.; Ochoa-Brust, A.; Félix, R.A.; Mata-López, W.; Mena, L.J.; Ostos, R.; Martínez-Peláez, R. Segmentation of the ECG Signal by Means of a Linear Regression Algorithm. Sensors 2019, 19, 775. [Google Scholar] [CrossRef] [PubMed]
- Übeyli, E.D.; Güler, İ. Detection of Electrocardiographic Changes in Partial Epileptic Patients Using Lyapunov Exponents with Multilayer Perceptron Neural Networks. Eng. Appl. Artif. Intell. 2004, 17, 567–576. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhang, F.; O’Donnell, L.J. Support Vector Regression. In Machine Learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 123–140. ISBN 978-0-12-815739-8. [Google Scholar]
- Ghiasi, M.M.; Zendehboudi, S.; Mohsenipour, A.A. Decision Tree-Based Diagnosis of Coronary Artery Disease: CART Model. Comput. Methods Programs Biomed. 2020, 192, 105400. [Google Scholar] [CrossRef]
- Kuhn, M. Caret: Classification and Regression Training 2007, 7.0-1. Available online: https://www.google.com.sg/url?sa=t&source=web&rct=j&opi=89978449&url=https://cran.r-project.org/web/packages/caret/caret.pdf&ved=2ahUKEwjvr7GK0duNAxX7imMGHQJcI7YQFnoECBcQAQ&usg=AOvVaw3MfbIGqp54M3I8wkSBN5AY (accessed on 10 December 2024).
- Fonarow, G.C.; Hsu, J.J. Left Ventricular Ejection Fraction. JACC Heart Fail. 2016, 4, 511–513. [Google Scholar] [CrossRef]
- Kagiyama, N.; Piccirilli, M.; Yanamala, N.; Shrestha, S.; Farjo, P.D.; Casaclang-Verzosa, G.; Tarhuni, W.M.; Nezarat, N.; Budoff, M.J.; Narula, J.; et al. Machine Learning Assessment of Left Ventricular Diastolic Function Based on Electrocardiographic Features. J. Am. Coll. Cardiol. 2020, 76, 930–941. [Google Scholar] [CrossRef]
- Alkhodari, M.; Jelinek, H.F.; Werghi, N.; Hadjileontiadis, L.J.; Khandoker, A.H. Estimating Left Ventricle Ejection Fraction Levels Using Circadian Heart Rate Variability Features and Support Vector Regression Models. IEEE J. Biomed. Health Inform. 2021, 25, 746–754. [Google Scholar] [CrossRef]
- Silva, L.E.V.; Moreira, H.T.; Bernardo, M.M.M.; Schmidt, A.; Romano, M.M.D.; Salgado, H.C.; Fazan, R.; Tinós, R.; Marin-Neto, J.A. Prediction of Echocardiographic Parameters in Chagas Disease Using Heart Rate Variability and Machine Learning. Biomed. Signal Process. Control 2021, 67, 102513. [Google Scholar] [CrossRef]
- Zhu, Y.; Zou, L.; Tan, T.L. A Clustering Group Lasso Method for Quantification of Adulteration in Black Cumin Seed Oil Using Fourier Transform Infrared Spectroscopy. Chemom. Intell. Lab. Syst. 2022, 220, 104471. [Google Scholar] [CrossRef]
- Park, S.; Luk, S.H.C.; Bains, R.S.; Whittaker, D.S.; Chiem, E.; Jordan, M.C.; Roos, K.P.; Ghiani, C.A.; Colwell, C.S. Targeted Genetic Reduction of Mutant Huntingtin Lessens Cardiac Pathology in the BACHD Mouse Model of Huntington’s Disease. Front. Cardiovasc. Med. 2021, 8, 810810. [Google Scholar] [CrossRef]
- Serin, Y.; Acar Tek, N. Effect of Circadian Rhythm on Metabolic Processes and the Regulation of Energy Balance. Ann. Nutr. Metab. 2019, 74, 322–330. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Tian, L.; Li, Z.; Ren, Z.; Zha, K.; Wei, X.; Peng, C.-K. On the Variability of Heart Rate Variability—Evidence from Prospective Study of Healthy Young College Students. Entropy 2020, 22, 1302. [Google Scholar] [CrossRef]
- Malan, S.F.; Van der Walt, J.J.; Van der Schyf, C.J. Structure-Activity Relationships of Polycyclic Aromatic Amines with Calcium Channel Blocking Activity. Arch. Pharm. 2000, 333, 10–16. [Google Scholar] [CrossRef]
- Fournier, S.; Taffé, P.; Radovanovic, D.; Von Elm, E.; Morawiec, B.; Stauffer, J.-C.; Erne, P.; Beggah, A.; Monney, P.; Pascale, P.; et al. Myocardial Infarct Size and Mortality Depend on the Time of Day—A Large Multicenter Study. PLoS ONE 2015, 10, e0119157. [Google Scholar] [CrossRef]
- Shih, P.-Y.; Cheng, Y.-J.; Ho, S.-I.; Huang, H.-H.; Yeh, J.-R.; Sun, W.-Z.; Chan, K.-C. Recovery of Cardiac Electrophysiological Alterations by Heart Rate Complexity Based on Multiscale Entropy Following Liver Transplantation. Sci. Rep. 2024, 14, 7467. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-H.; Huang, P.-W.; Tang, S.-C.; Shieh, J.-S.; Lai, D.-M.; Wu, A.-Y.; Jeng, J.-S. Complexity of Heart Rate Variability Can Predict Stroke-In-Evolution in Acute Ischemic Stroke Patients. Sci. Rep. 2015, 5, 17552. [Google Scholar] [CrossRef]
- Tang, S.-Y.; Ma, H.-P.; Lin, C.; Lo, M.-T.; Lin, L.-Y.; Chen, T.-Y.; Wu, C.-K.; Chiang, J.-Y.; Lee, J.-K.; Hung, C.-S.; et al. Heart Rhythm Complexity Analysis in Patients with Inferior ST-Elevation Myocardial Infarction. Sci. Rep. 2023, 13, 20861. [Google Scholar] [CrossRef]


| Characteristics | Value |
|---|---|
| Age (years) | 59.4 ± 9.3 |
| Sex (male), n (%) | 102 (51.0) |
| Diabetes mellitus, n (%) | 157 (78.5) |
| Working type (day work), n (%) | 169 (84.5) |
| Hypertension history (years) | 7.5 ± 6.8 |
| LVEF (%) | 65 ± 7 |
| Features | Calculation Methods |
|---|---|
| Power spectral entropy | , where pi is the normalized power spectral coefficient. |
| Energy entropy | , where ei is the normalized energy coefficient. |
| Approximate entropy | , where Cm(r) is the number of m-length sequences within a tolerance r of each other. |
| Sample entropy | , where Am(r) and Bm(r) are the counts of m-length and (m + 1)-length similar sequences, respectively. |
| Fuzzy entropy | , where Nm(r) and Nm+1(r) are the counts of m-length and (m + 1)-length fuzzy similar sequences, respectively. |
| Permutation entropy | , where pi is the probabilities of the permutation pattern. |
| Attention entropy | , where ai is the attention coefficient. |
| Bubble entropy | , where bi is the normalized bubble count. |
| Dispersion entropy | , where di is the normalized dispersion coefficient. |
| Distribution entropy | , where di is the normalized distribution coefficient. |
| Gridded distribution entropy | , where gi is the normalized gridded distribution coefficient. |
| Incremental entropy | , where ii is the normalized incremental coefficient. |
| Phase entropy | , where ϕi is the normalized phase coefficient. |
| Slope entropy | , where si is the normalized slope coefficient. |
| Symbolic dynamic entropy | , where si is the probabilities of the symbolic sequence. |
| Time | GPR | KNN | LR | MLP | RF | SvmLinear | SvmPoly | SvmRadial | Treebag | CNN |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5.45 | 5.38 | 5.21 | 5.33 | 5.41 | 4.95 | 5.16 | 5.27 | 5.36 | 5.13 |
| 2 | 5.21 | 5.61 | 5.25 | 5.21 | 5.48 | 5.08 | 5.21 | 5.31 | 5.61 | 5.19 |
| 3 | 5.03 | 5.45 | 5.26 | 5.31 | 5.50 | 5.35 | 5.31 | 5.19 | 5.45 | 6.62 |
| 4 | 5.15 | 5.00 | 4.64 | 5.32 | 5.38 | 5.11 | 5.29 | 5.11 | 5.44 | 5.02 |
| 5 | 5.11 | 5.21 | 5.25 | 5.15 | 5.18 | 5.19 | 5.21 | 5.09 | 5.17 | 5.15 |
| 6 | 5.05 | 5.10 | 5.17 | 5.83 | 5.25 | 5.01 | 5.28 | 5.17 | 4.67 | 5.25 |
| 7 | 5.25 | 5.54 | 5.26 | 5.22 | 5.68 | 5.39 | 5.27 | 5.24 | 5.35 | 5.32 |
| 8 | 5.64 | 5.80 | 5.24 | 6.43 | 5.36 | 5.20 | 5.30 | 5.43 | 5.16 | 5.31 |
| 9 | 5.10 | 5.53 | 5.00 | 5.50 | 5.79 | 4.99 | 5.22 | 5.48 | 5.66 | 5.13 |
| 10 | 5.38 | 5.52 | 5.17 | 6.07 | 5.59 | 5.39 | 5.28 | 5.30 | 5.27 | 5.29 |
| 11 | 5.66 | 5.44 | 5.20 | 5.35 | 5.54 | 4.93 | 5.30 | 5.39 | 5.36 | 5.31 |
| 12 | 5.59 | 5.53 | 5.31 | 5.36 | 5.56 | 5.38 | 5.29 | 5.38 | 5.52 | 5.30 |
| 13 | 5.54 | 5.38 | 5.52 | 5.11 | 5.63 | 5.35 | 5.29 | 5.38 | 5.48 | 5.30 |
| 14 | 5.34 | 5.48 | 5.18 | 5.01 | 5.62 | 5.27 | 5.23 | 5.22 | 5.11 | 5.15 |
| 15 | 5.06 | 5.25 | 5.23 | 5.34 | 5.34 | 5.11 | 5.24 | 5.27 | 4.97 | 5.25 |
| 16 | 5.52 | 5.14 | 5.06 | 5.53 | 5.33 | 5.25 | 5.18 | 5.12 | 5.38 | 5.07 |
| 17 | 5.14 | 4.97 | 4.95 | 5.44 | 4.97 | 4.81 | 4.80 | 4.90 | 5.13 | 4.92 |
| 18 | 5.60 | 5.51 | 5.21 | 5.76 | 5.54 | 5.34 | 5.28 | 5.31 | 5.34 | 5.31 |
| 19 | 5.51 | 5.50 | 5.17 | 5.64 | 5.53 | 5.31 | 5.27 | 5.43 | 5.13 | 5.21 |
| 20 | 5.37 | 5.45 | 5.21 | 5.88 | 5.32 | 5.04 | 5.24 | 4.90 | 5.27 | 5.25 |
| 21 | 4.64 | 5.22 | 4.61 | 5.50 | 4.85 | 4.92 | 5.22 | 4.84 | 4.93 | 4.81 |
| 22 | 5.22 | 5.20 | 5.13 | 5.37 | 5.36 | 5.02 | 5.14 | 5.10 | 5.11 | 5.15 |
| 23 | 5.28 | 5.15 | 5.25 | 5.36 | 5.29 | 5.11 | 5.23 | 5.24 | 5.34 | 5.16 |
| 24 | 5.34 | 5.38 | 5.06 | 5.55 | 5.54 | 5.31 | 5.31 | 5.23 | 5.22 | 5.51 |
| Time | GPR | KNN | LR | MLP | RF | SvmLinear | SvmPoly | SvmRadial | Treebag | CNN |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.54 | 4.42 | 4.10 | 4.37 | 4.51 | 4.20 | 4.30 | 4.34 | 4.21 | 4.30 |
| 2 | 4.27 | 4.39 | 4.27 | 4.35 | 4.46 | 4.30 | 4.34 | 4.34 | 4.38 | 4.34 |
| 3 | 4.22 | 4.41 | 4.27 | 4.36 | 4.36 | 4.40 | 4.36 | 4.13 | 4.30 | 5.24 |
| 4 | 4.16 | 3.93 | 3.84 | 4.35 | 4.30 | 4.05 | 4.34 | 4.19 | 4.47 | 4.12 |
| 5 | 4.27 | 4.29 | 4.19 | 4.25 | 4.29 | 4.32 | 4.33 | 4.25 | 4.24 | 4.27 |
| 6 | 4.20 | 4.19 | 4.23 | 4.68 | 4.25 | 4.06 | 4.33 | 4.26 | 3.80 | 4.29 |
| 7 | 4.20 | 4.28 | 4.25 | 4.11 | 4.50 | 4.22 | 4.21 | 4.15 | 4.29 | 4.21 |
| 8 | 4.60 | 4.53 | 4.25 | 4.88 | 4.31 | 4.26 | 4.32 | 4.40 | 4.11 | 4.37 |
| 9 | 4.10 | 4.45 | 4.01 | 4.45 | 4.68 | 4.13 | 4.29 | 4.35 | 4.38 | 4.20 |
| 10 | 4.48 | 4.50 | 4.23 | 4.88 | 4.60 | 4.41 | 4.32 | 4.29 | 4.42 | 4.33 |
| 11 | 4.49 | 4.29 | 4.20 | 4.35 | 4.37 | 4.17 | 4.32 | 4.29 | 4.18 | 4.30 |
| 12 | 4.53 | 4.56 | 4.35 | 4.42 | 4.41 | 4.34 | 4.25 | 4.36 | 4.48 | 4.36 |
| 13 | 4.36 | 4.39 | 4.72 | 4.20 | 4.47 | 4.26 | 4.26 | 4.29 | 4.48 | 4.29 |
| 14 | 4.32 | 4.29 | 4.18 | 4.32 | 4.60 | 4.28 | 4.19 | 4.27 | 4.28 | 4.15 |
| 15 | 4.02 | 4.21 | 4.21 | 4.37 | 4.43 | 4.10 | 4.26 | 4.15 | 4.07 | 4.23 |
| 16 | 4.44 | 4.14 | 4.11 | 4.46 | 4.30 | 4.06 | 4.17 | 4.13 | 4.24 | 4.05 |
| 17 | 4.23 | 4.06 | 3.99 | 4.29 | 4.17 | 3.92 | 3.99 | 3.99 | 4.12 | 4.30 |
| 18 | 4.59 | 4.42 | 4.22 | 4.52 | 4.57 | 4.30 | 4.32 | 4.32 | 4.30 | 4.33 |
| 19 | 4.42 | 4.30 | 4.14 | 4.46 | 4.42 | 4.32 | 4.32 | 4.39 | 4.11 | 4.27 |
| 20 | 4.24 | 4.44 | 4.11 | 4.71 | 4.39 | 4.05 | 4.23 | 3.83 | 4.29 | 4.11 |
| 21 | 3.86 | 4.16 | 3.74 | 4.45 | 4.00 | 4.17 | 4.25 | 3.98 | 3.99 | 4.06 |
| 22 | 4.21 | 4.20 | 4.18 | 4.57 | 4.34 | 3.96 | 4.21 | 4.19 | 4.13 | 4.20 |
| 23 | 4.05 | 3.95 | 4.27 | 4.39 | 4.11 | 4.09 | 4.27 | 4.06 | 4.13 | 4.10 |
| 24 | 4.25 | 4.43 | 3.97 | 4.47 | 4.54 | 4.24 | 4.36 | 4.13 | 4.24 | 4.50 |
| Author | ECG Duration | Data | Features | Regression Model | RMSE (%) | Bland–Altman Mean ± 1.96 SD (%) | MAE (%) |
|---|---|---|---|---|---|---|---|
| Mohanad et al. (2021) [45] | 1 h (24 h study) | America, 92 (Heart Failure) | HRV parameters | SVM | 10.4 | 0.53 ± 20.44 | NA |
| Luiz et al. (2021) [46] | 15 min | Brazil, 63 (Chagas disease) | HRV parameters | RF/MLP/ KNN/SVM | NA | −0.48 ± 23.53 | NA |
| Akhil et al. (2022) [15] | 5 s | America, 219,437 (Normal) | ECG features | CNN | NA | NA | 6.14 |
| Current study | 1 h (24 h study) | China, 200 (Hypertension) | CMSE-based HRV features | GPR/KNN/LR/ MLP/RF/SVM/Treebag/CNN | 4.61 | 0.22 ± 10.61 | 3.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Pan, Q.; Yang, S.; Huang, L.; Yin, J.; Lin, H.; Huang, X.; Ding, C.; Zou, X.; Zheng, Y.; et al. Utilizing Circadian Heart Rate Variability Features and Machine Learning for Estimating Left Ventricular Ejection Fraction Levels in Hypertensive Patients: A Composite Multiscale Entropy Analysis. Biosensors 2025, 15, 442. https://doi.org/10.3390/bios15070442
Zhang N, Pan Q, Yang S, Huang L, Yin J, Lin H, Huang X, Ding C, Zou X, Zheng Y, et al. Utilizing Circadian Heart Rate Variability Features and Machine Learning for Estimating Left Ventricular Ejection Fraction Levels in Hypertensive Patients: A Composite Multiscale Entropy Analysis. Biosensors. 2025; 15(7):442. https://doi.org/10.3390/bios15070442
Chicago/Turabian StyleZhang, Nanxiang, Qi Pan, Shuo Yang, Leen Huang, Jianan Yin, Hai Lin, Xiang Huang, Chonglong Ding, Xinyan Zou, Yongjun Zheng, and et al. 2025. "Utilizing Circadian Heart Rate Variability Features and Machine Learning for Estimating Left Ventricular Ejection Fraction Levels in Hypertensive Patients: A Composite Multiscale Entropy Analysis" Biosensors 15, no. 7: 442. https://doi.org/10.3390/bios15070442
APA StyleZhang, N., Pan, Q., Yang, S., Huang, L., Yin, J., Lin, H., Huang, X., Ding, C., Zou, X., Zheng, Y., & Zhang, J. (2025). Utilizing Circadian Heart Rate Variability Features and Machine Learning for Estimating Left Ventricular Ejection Fraction Levels in Hypertensive Patients: A Composite Multiscale Entropy Analysis. Biosensors, 15(7), 442. https://doi.org/10.3390/bios15070442





