Automatic Calculation of Average Power in Electroencephalography Signals for Enhanced Detection of Brain Activity and Behavioral Patterns
Abstract
1. Introduction
2. Experimental Materials and Theory
2.1. Experiment and Equipment
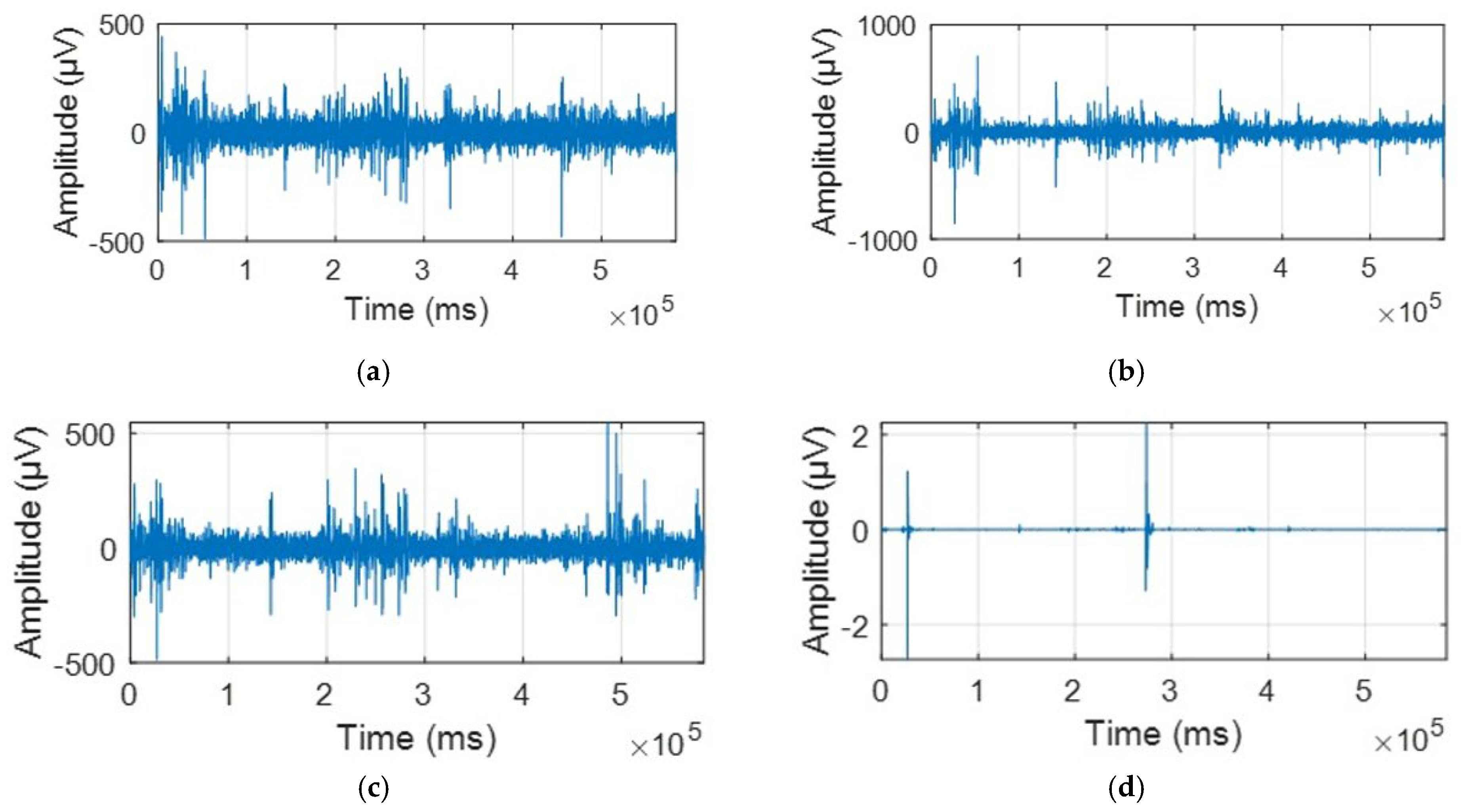
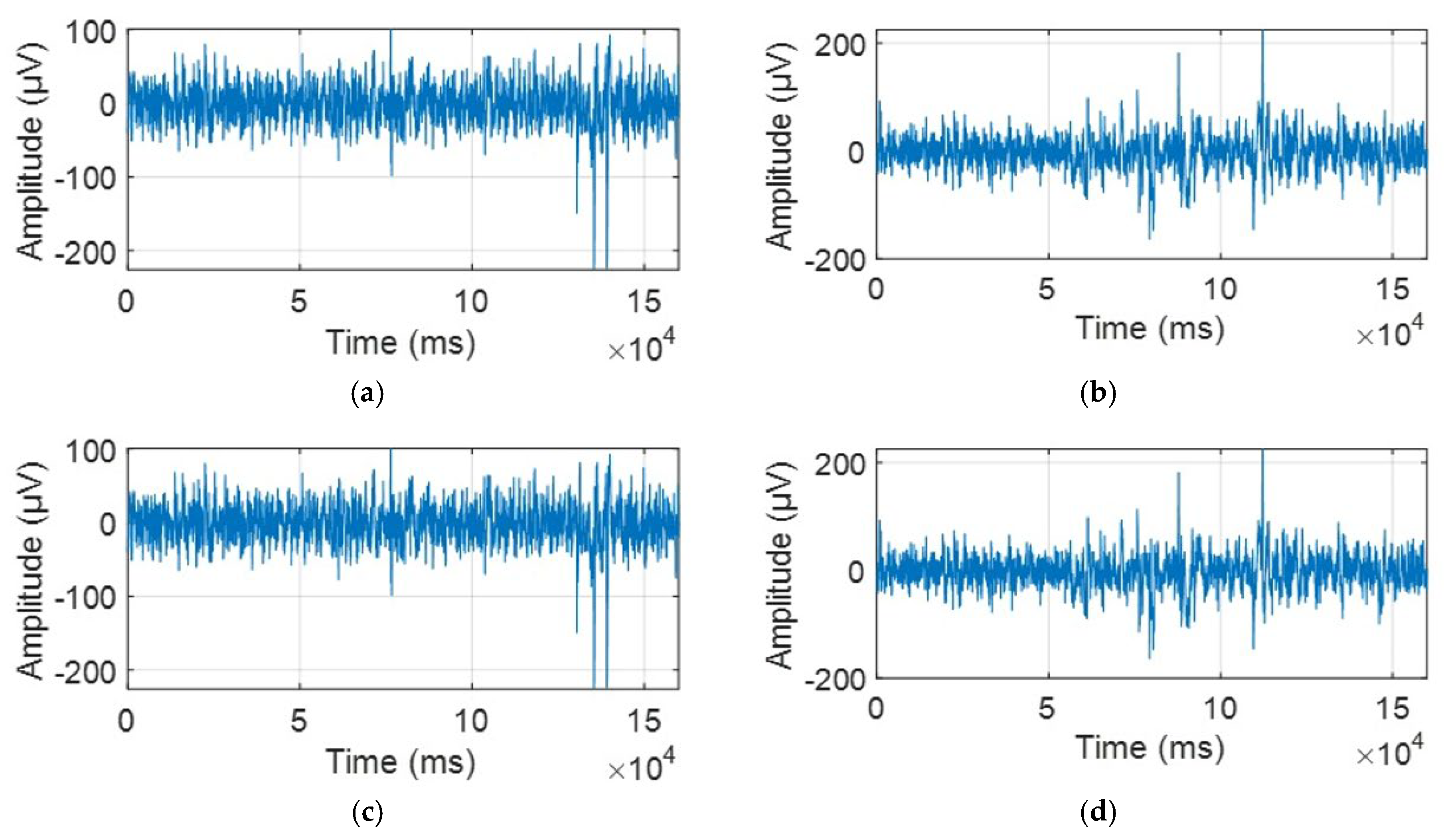
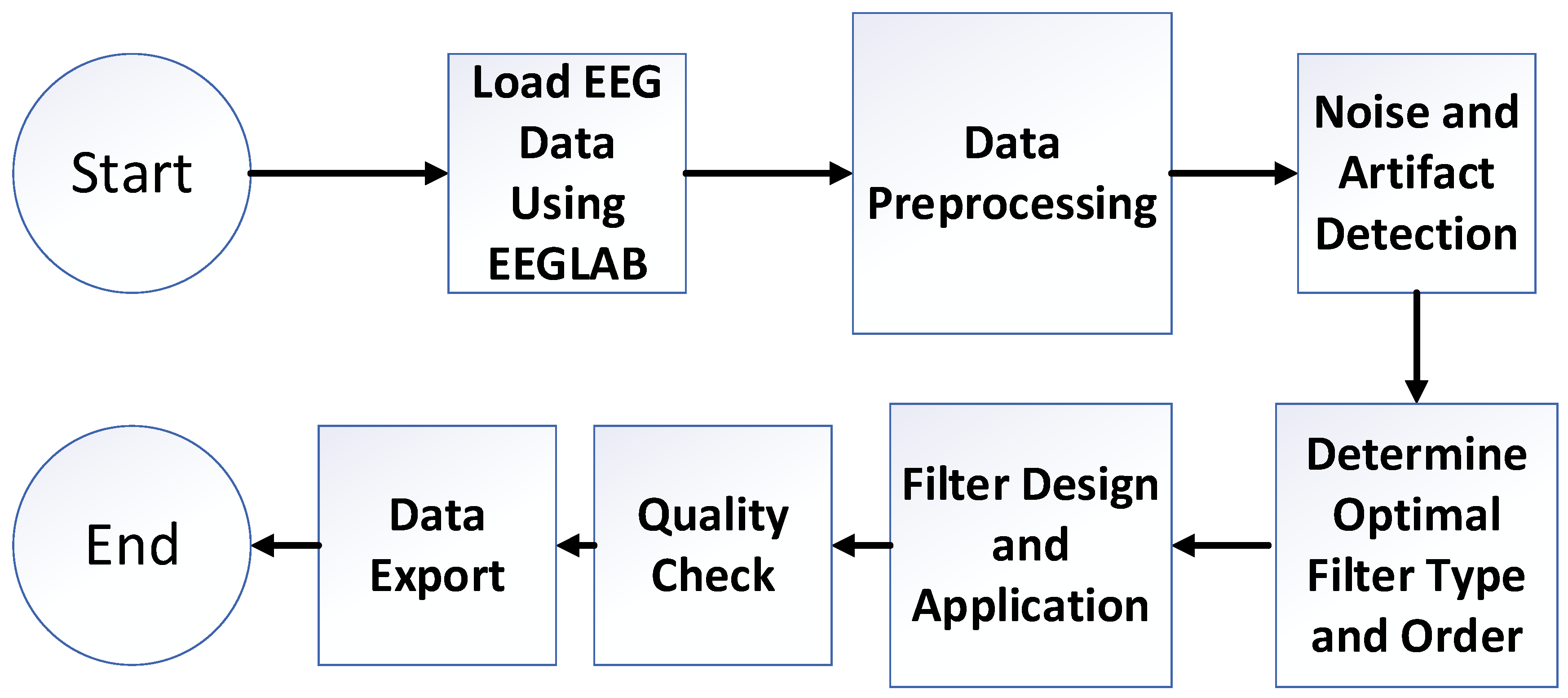
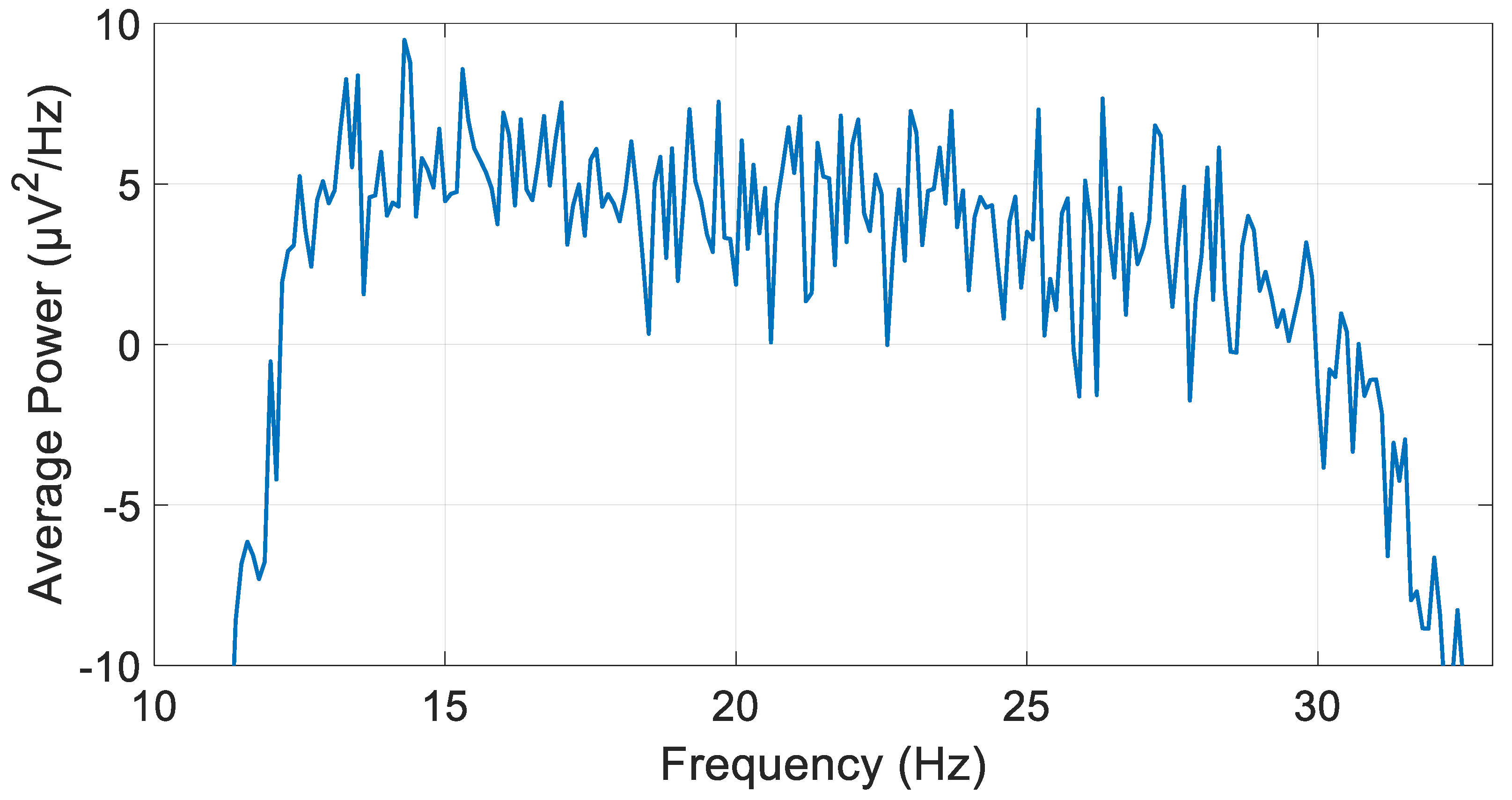
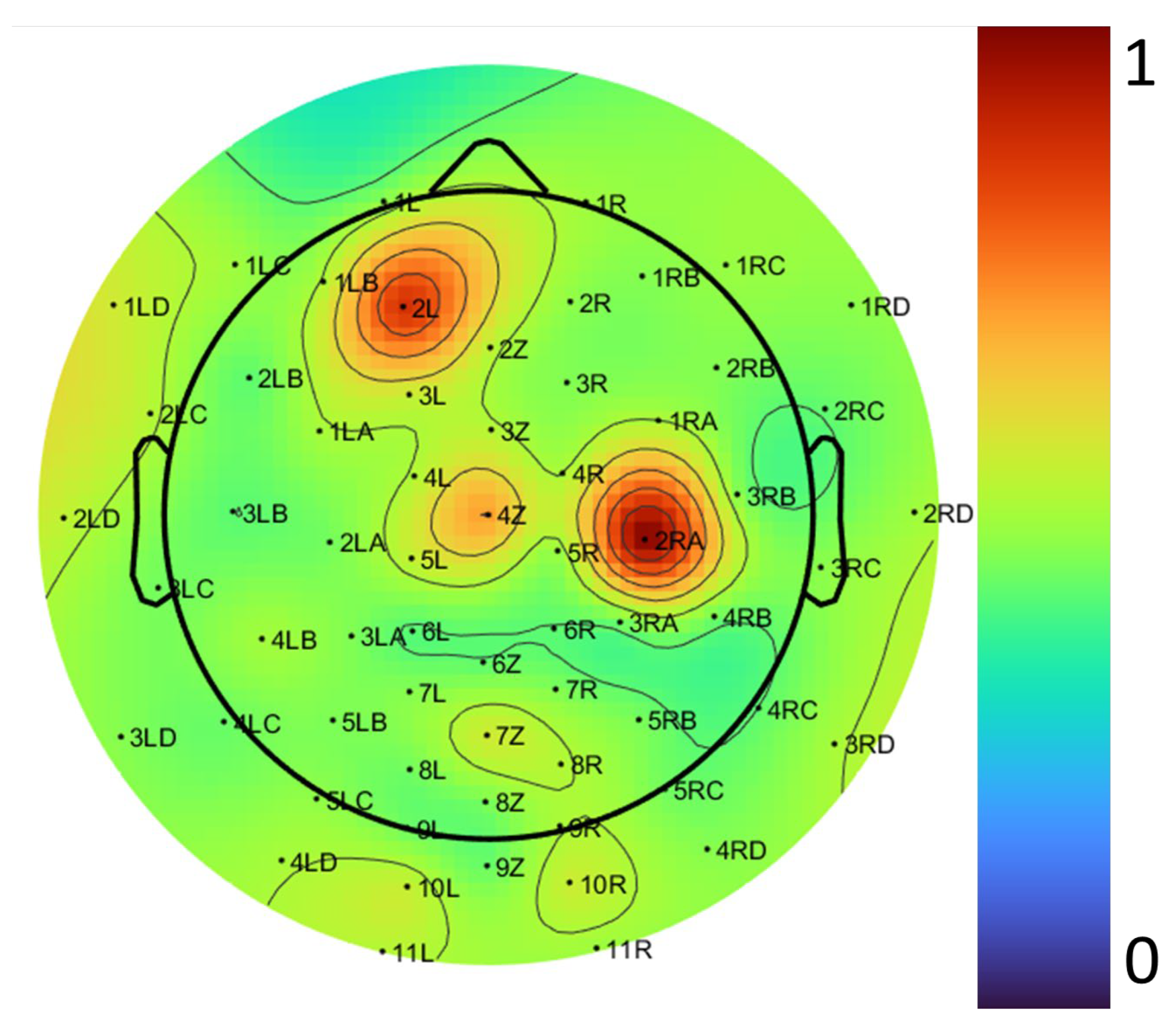
2.2. Data Acquisition and Preprocessing
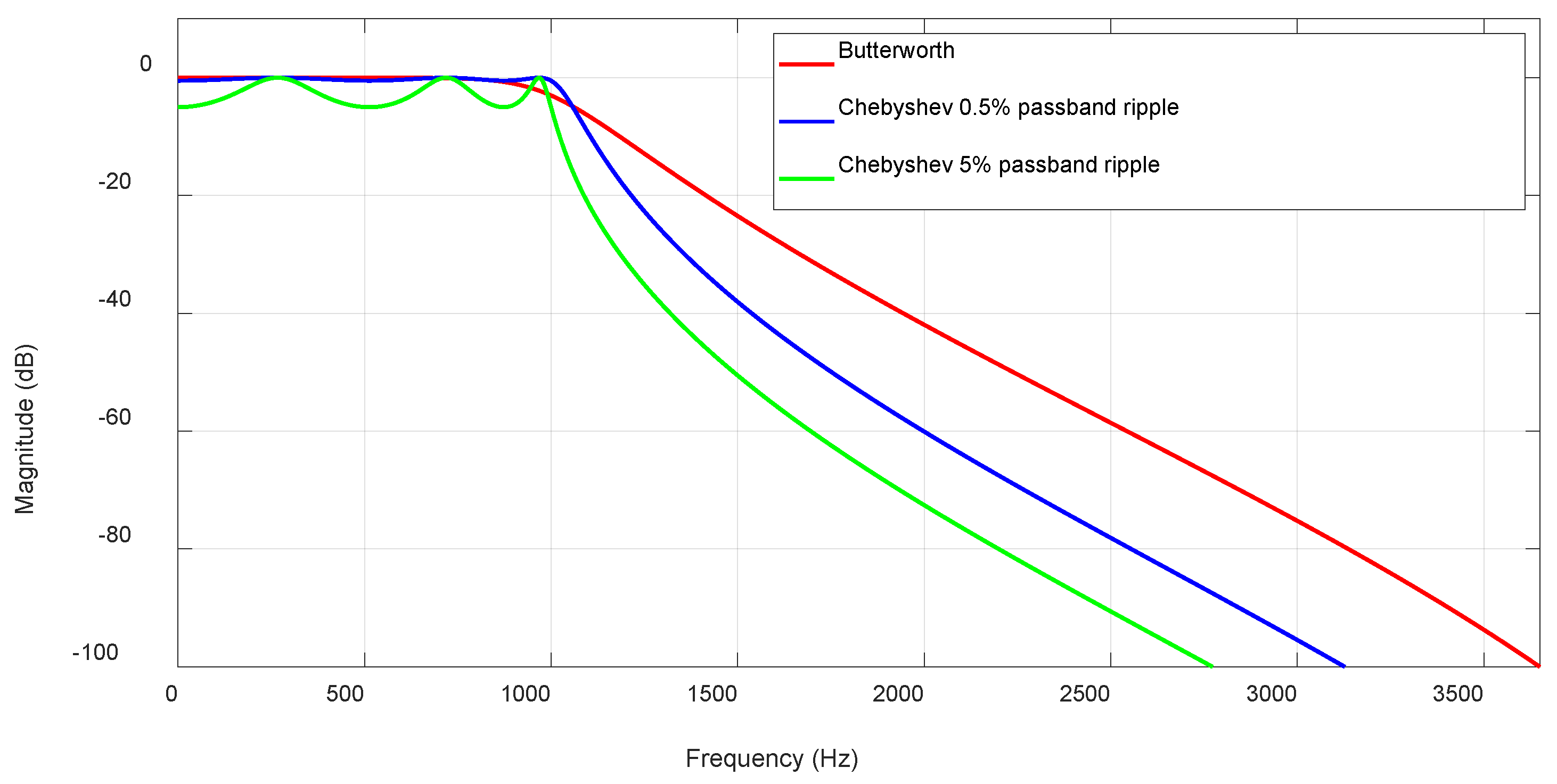
2.3. Digital Filters
2.4. Optimization Algorithm
3. Comprehensive Analysis of Optimization Algorithm Results
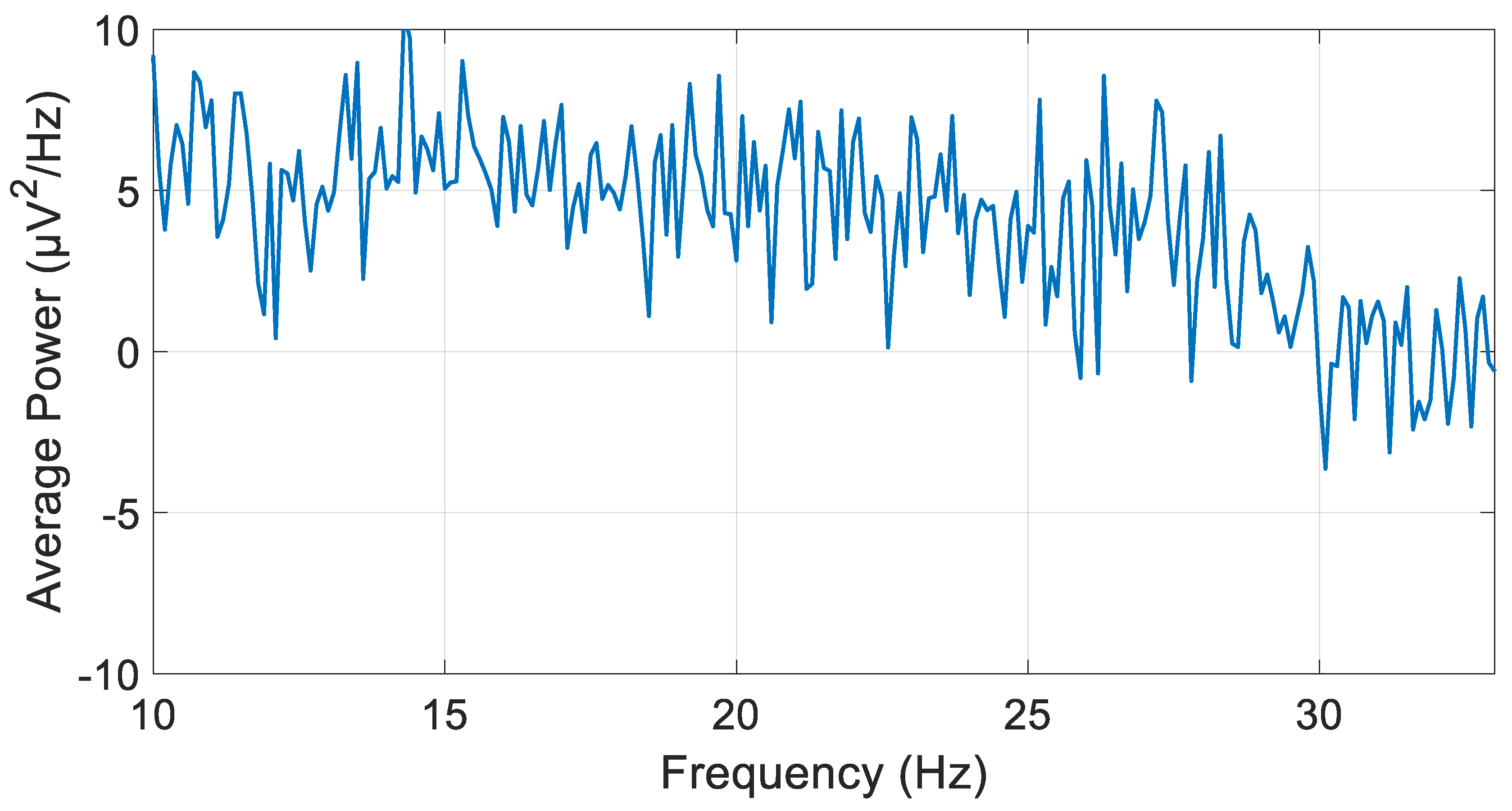
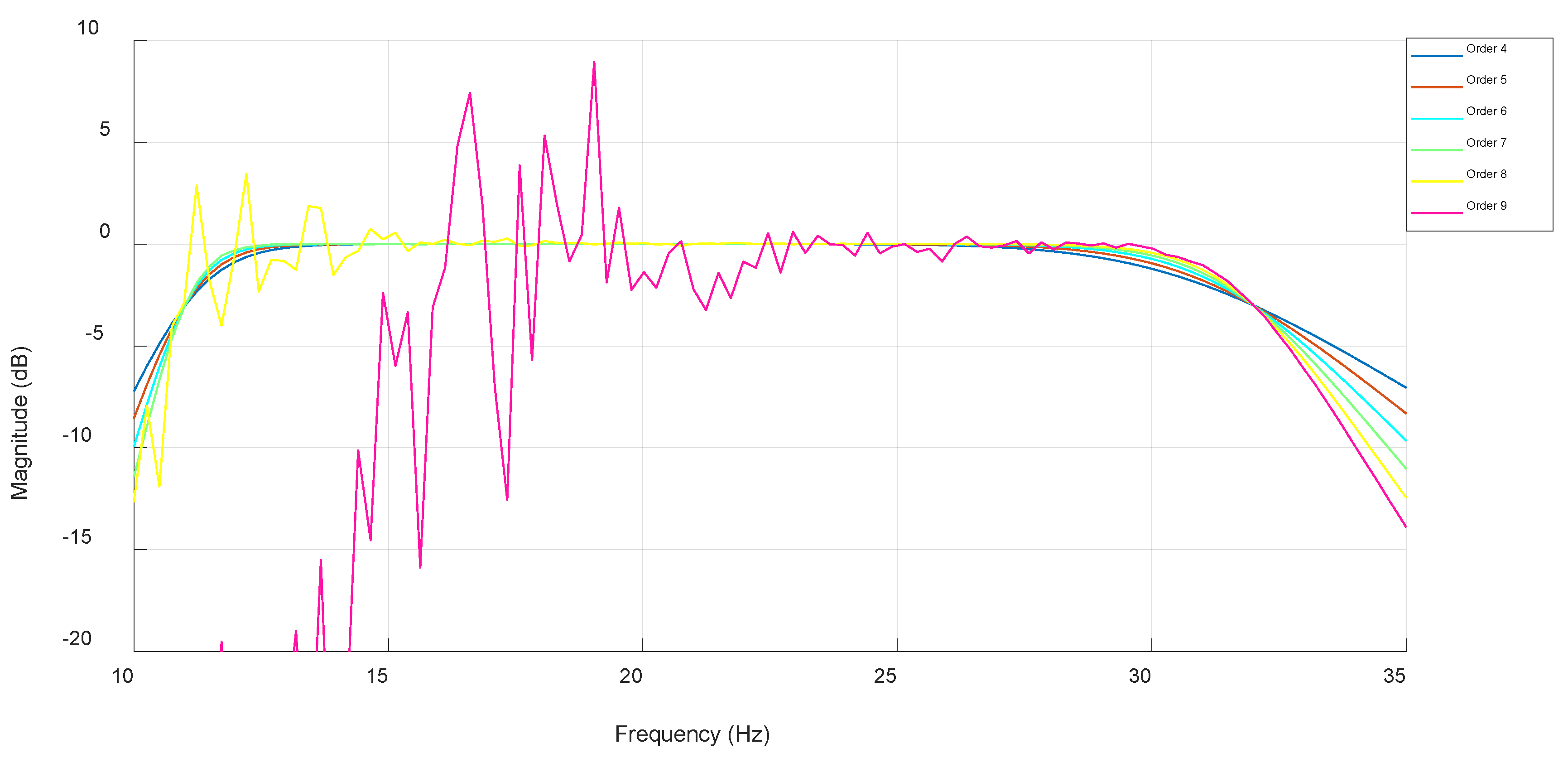
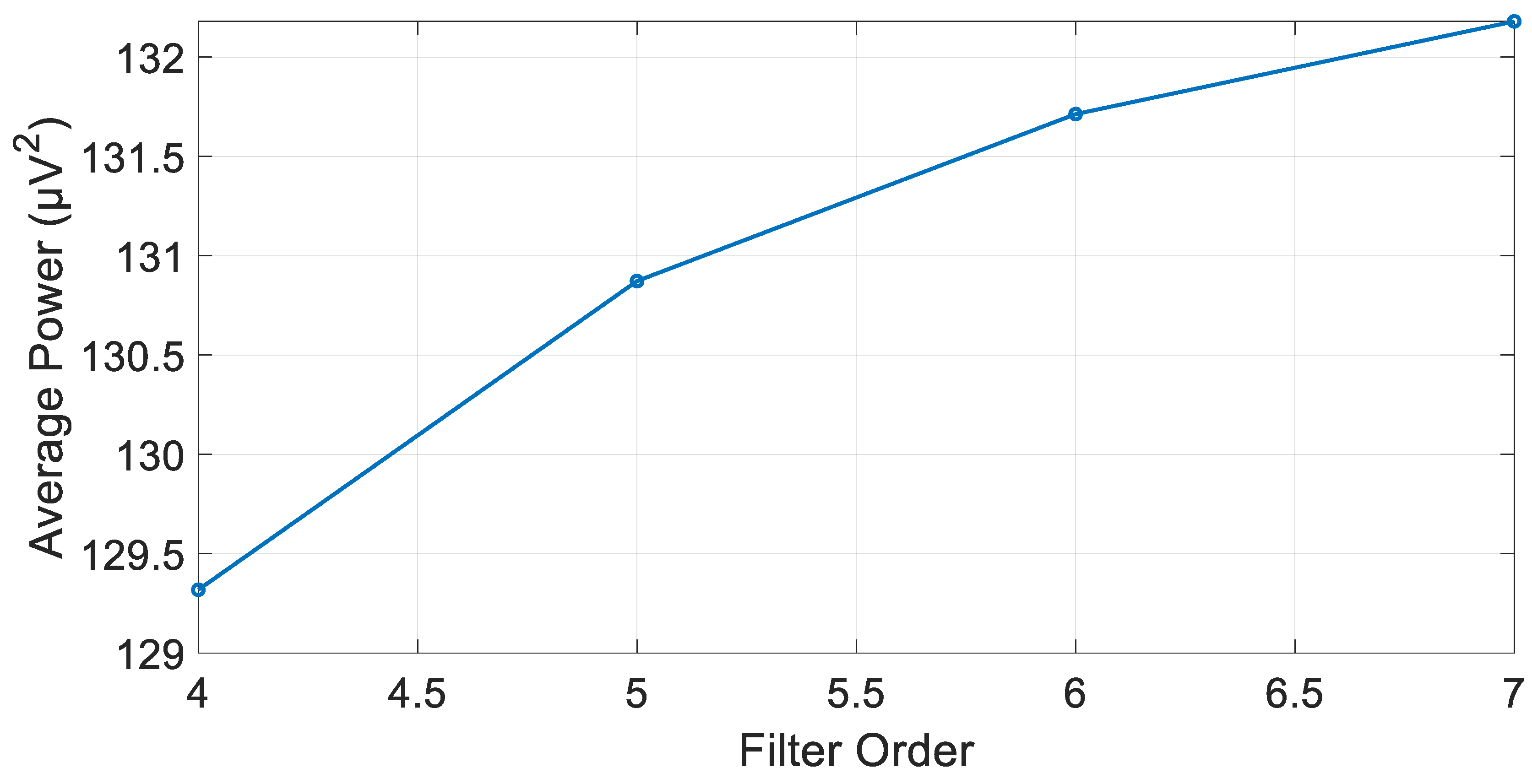
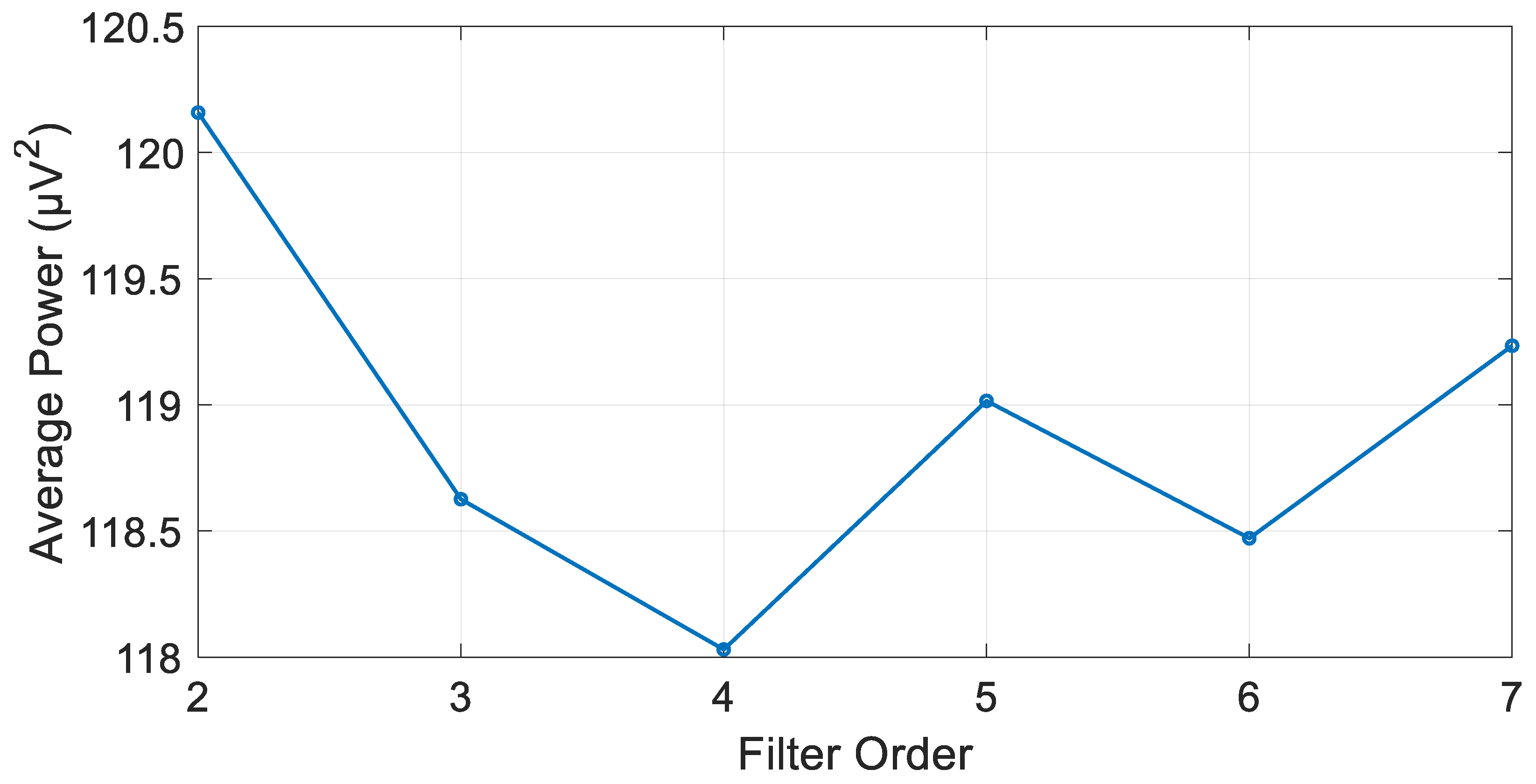
3.1. IIR Butterworth Filter
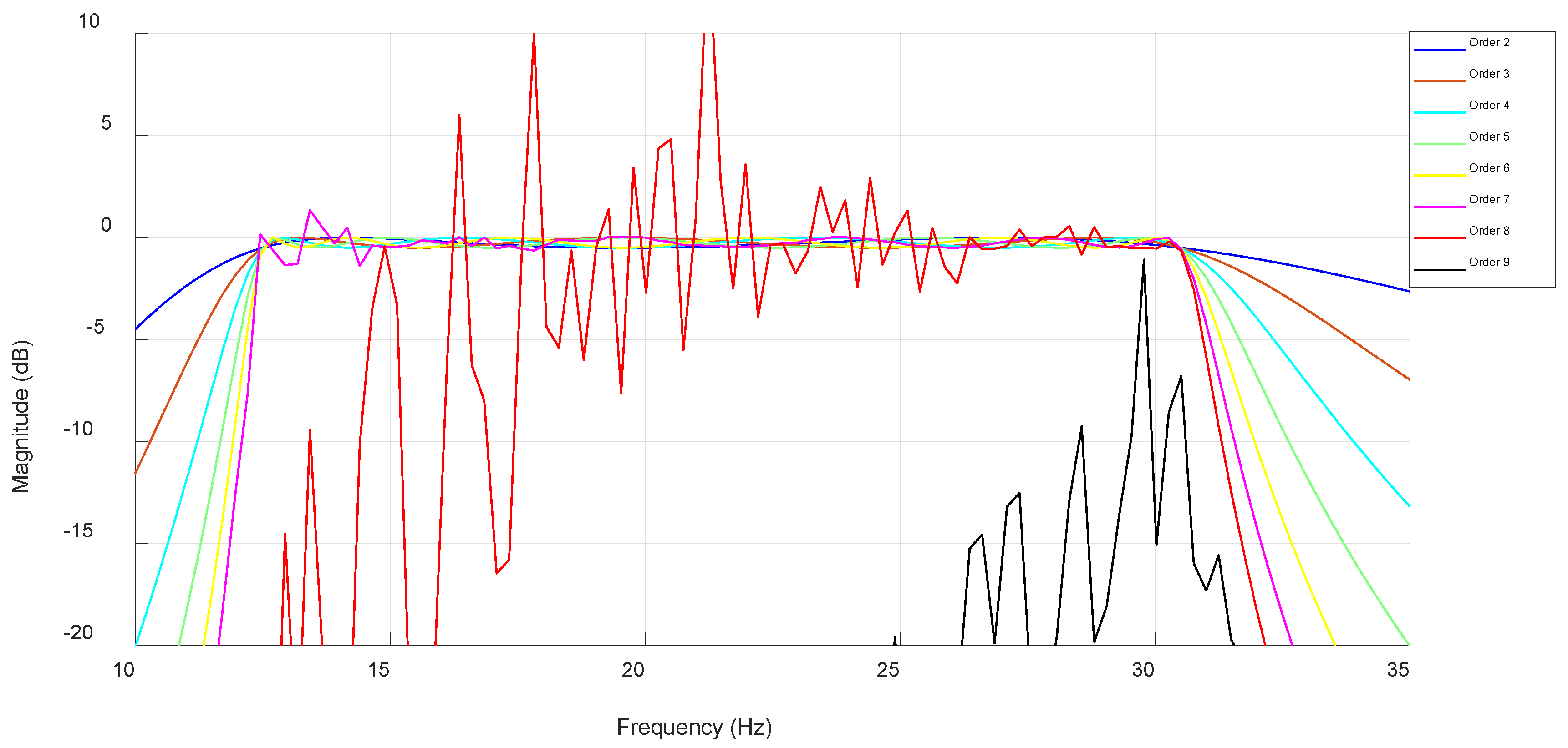
3.2. IIR Chebyshev Filter with 0.5% Passband Ripple
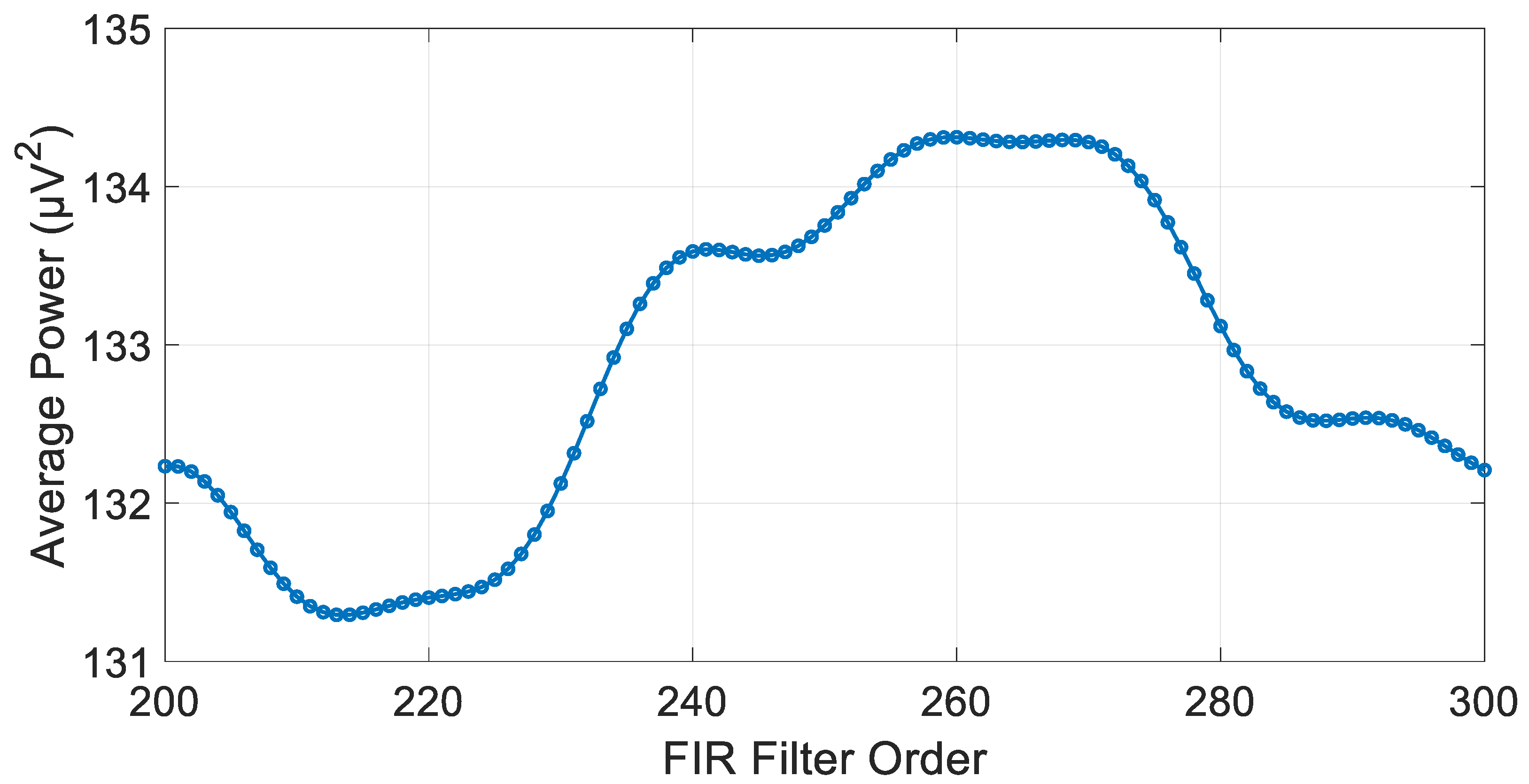
3.3. FIR Filter
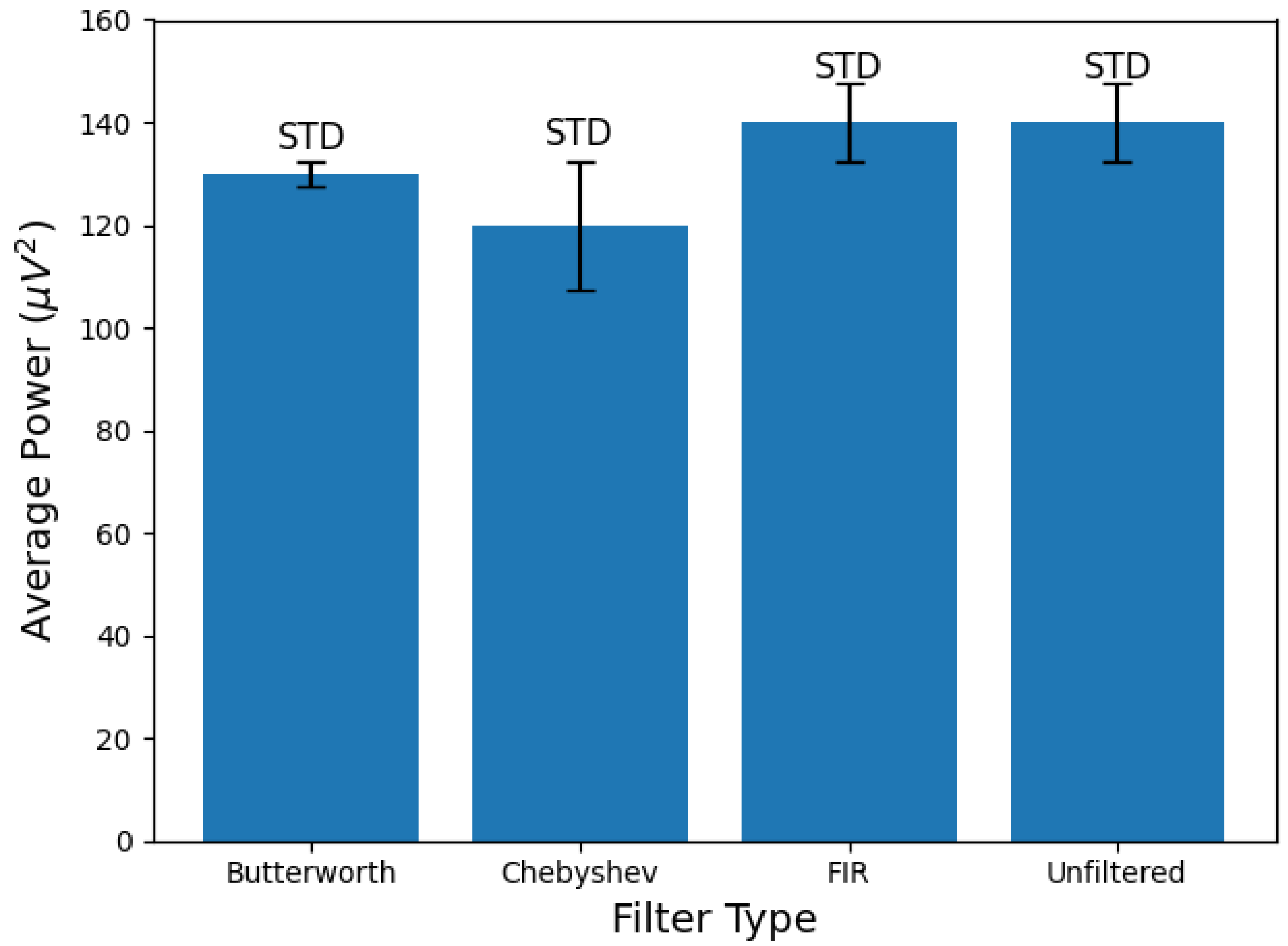
3.4. Algorithm Optimization and Comparative Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pica, A.Ș.; Olteanu, G.; Stoica, A.A. The Contribution of EEG Headsets in the Development of Brain Capacity. Sci. Bull. Electr. Eng. Fac. 2024, 23, 54–63. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, W.; Liu, X.; Wu, H.; Liu, H.; Chen, T.; Zhao, Y. A Wirelessly Powered Scattered Neural Recording Wearable System. IEEE Trans. Biomed. Circuits Syst. 2024, in press. [Google Scholar] [CrossRef]
- Soufineyestani, M.; Dowling, D.; Khan, A. Electroencephalography (EEG) Technology Applications and Available Devices. Appl. Sci. 2020, 10, 7453. [Google Scholar] [CrossRef]
- Yu, M.; Li, Y.; Tian, F. Responses of Functional Brain Networks while Watching 2D and 3D Videos: An EEG Study. Biomed. Signal Process. Control 2021, 68, 102613. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Li, T.; Wang, L.; Wang, J. The Applied Principles of EEG Analysis Methods in Neuroscience and Clinical Neurology. Mil. Med. Res. 2023, 10, 67. [Google Scholar] [CrossRef] [PubMed]
- Chaddad, A.; Boukouvalas, C.; Jubran, M.; Lu, L.; Sequeira, M.; Kazan, F. Electroencephalography Signal Processing: A Comprehensive Review and Analysis of Methods and Techniques. Sensors 2023, 23, 6434. [Google Scholar] [CrossRef]
- Lin, C.-T.; Ko, L.-W.; Chang, C.-J.; Wang, Y.-K.; Chung, C.-H.; Yang, F.-S.; Liang, S.-F. A Real-Time Wireless Brain-Computer Interface System for Drowsiness Detection. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 214–222. [Google Scholar] [CrossRef]
- Shrestha, A. Home Automation Enhancement and Music Player Control with EEG-Based Headset. Master’s Thesis, Tribhuvan University, Kathmandu, Nepal, 2018. [Google Scholar]
- Sosa, O.A.P.; Quijano, Y.; Doniz, M.; Quero, J.E.C. Development of an EEG Signal Processing Program Based on EEGLAB. In Proceedings of the 2011 Pan American Health Care Exchanges, Rio de Janeiro, Brazil, 28 March–1 April 2011. [Google Scholar]
- Delorme, A.; Makeig, S. EEGLAB: An Open Source Toolbox for Analysis of Single-Trial EEG Dynamics Including Independent Component Analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef]
- Bigdely-Shamlo, N.; Mullen, T.; Kreutz-Delgado, K.; Makeig, S. Measure Projection Analysis: A Probabilistic Approach to EEG Source Comparison and Multi-Subject Inference. NeuroImage 2013, 72, 287–303. [Google Scholar] [CrossRef]
- Klimesch, W. EEG Alpha and Theta Oscillations Reflect Cognitive and Memory Performance: A Review and Analysis. Brain Res. Rev. 1999, 29, 169–195. [Google Scholar] [CrossRef]
- Smith, S.W. The Scientist and Engineer’s Guide to Digital Signal Processing, 2nd ed.; California Technical Publishing: San Diego, CA, USA, 1997. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Mitra, S.K. Digital Signal Processing: A Computer-Based Approach, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Rangayyan, R.M. Biomedical Signal Analysis; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Koudelková, Z.; Strmiska, M.; Jašek, R. Analysis of Brain Waves According to Their Frequency. Int. J. Biol. Biomed. Eng. 2018, 12, 202–207. [Google Scholar]
- Kweon, S.H.; Park, S.-J.; Ha, S.; Lee, S.; Jeon, K.-W. A Brain Wave Research on VR (Virtual Reality) Usage: Comparison between VR and 2D Video in EEG Measurement. In Proceedings of the Advances in Human Factors and Systems Interaction: Proceedings of the AHFE 2017 International Conference on Human Factors and Systems Interaction, Los Angeles, CA, USA, 17–21 July 2017; Springer International Publishing: Cham, Switzerland, 2018; pp. 433–439. [Google Scholar]
- Langlois, D.; Chartier, S.; Gosselin, D. An Introduction to Independent Component Analysis: InfoMax and FastICA Algorithms. Tut. Quant. Methods Psychol. 2010, 6, 31–38. [Google Scholar] [CrossRef]
- Malka, D.; Cohen, M.; Zalevsky, Z.; Turkiewicz, J. Optical micro-multi-racetrack resonator filter based on SOI waveguide. Photon. Nanostruct. 2015, 16, 16–23. [Google Scholar] [CrossRef]
- Ifeachor, E.C.; Jervis, B.W. Digital Signal Processing: A Practical Approach, 2nd ed.; Pearson Education: London, UK, 2002. [Google Scholar]
- Kumar, S.; Singh, R. A Comprehensive Review and Analysis on Digital Filter Design. Int. J. Recent Technol. Eng. 2019, 8, 1023–1030. [Google Scholar]
- Jackson, L.B. Digital Filters and Signal Processing: With MATLAB® Exercises; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Gustafsson, F. Determining the Initial States in Forward-Backward Filtering. IEEE Trans. Signal Process. 1996, 44, 988–992. [Google Scholar] [CrossRef] [PubMed]
- Pfurtscheller, G.; Lopes da Silva, F.H. Event-Related EEG/MEG Synchronization and Desynchronization: Basic Principles. Clin. Neurophysiol. 1999, 110, 1842–1857. [Google Scholar] [CrossRef]
- Avital, N.; Nahum, E.; Carmel Levi, G.; Malka, D. Cognitive State Classification Using Convolutional Neural Networks on Gamma-Band EEG Signals. Appl. Sci. 2024, 14, 5223. [Google Scholar] [CrossRef]
- Avital, N.; Egel, I.; Weinstock, I.; Malka, D. Enhancing Real-Time Emotion Recognition in Classroom Environments Using Convolutional Neural Networks: A Step Towards Optical Neural Networks for Advanced Data Processing. Inventions 2024, 9, 113. [Google Scholar] [CrossRef]
- Rabinovitch, A.; Baruch, E.B.; Siton, M.; Avital, N.; Yeari, M.; Malka, D. Efficient Detection of Mind Wandering During Reading Aloud Using Blinks, Pitch Frequency, and Reading Rate. AI 2025, 6, 83. [Google Scholar] [CrossRef]
- Cai, Y.; Meng, Z.; Huang, D. DHCT-GAN: Improving EEG Signal Quality with a Dual-Branch Hybrid CNN–Transformer Network. Sensors 2025, 25, 231. [Google Scholar] [CrossRef]
- Yin, J.; Liu, A.; Li, C.; Qian, R.; Chen, X. A GAN Guided Parallel CNN and Transformer Network for EEG Denoising. IEEE J. Biomed. Health Inform. 2023, 27, 1–2. [Google Scholar] [CrossRef] [PubMed]







| Test Approach | N = 1 | N = 10 | N = 20 | |||
|---|---|---|---|---|---|---|
| Preprocessing | Classification | Preprocessing | Classification | Preprocessing | Classification | |
| EEGLAB | 18 min | 6 min | ~180 min | ~60 min | ~360 min | ~120 min |
| Automatic algorithm | 5 min | <30 s | ~50 min | <30 s | 100 min | <30 s |
| Feature | DHCT-GAN [29] and CTNet [30] | Automatic-Algorithm |
|---|---|---|
| Hardware Requirements | High (typically requires GPU acceleration) | Low (runs efficiently on standard CPUs) |
| Computational Cost | High | Low |
| Memory Consumption | High | Low |
| Energy Consumption | High | Low |
| Speed | Fast (with GPU) | Comparable to deep learning (without GPU) and maintains scalability |
| Generalizability | Can be limited by dataset-specific training | High |
| Deployment Complexity | High (complex model training and optimization) | Low (simple and straightforward) |
| Suitability | Applications with access to high-performance computing | Resource-constrained environments, real-time applications, and portable devices |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avital, N.; Shulkin, N.; Malka, D. Automatic Calculation of Average Power in Electroencephalography Signals for Enhanced Detection of Brain Activity and Behavioral Patterns. Biosensors 2025, 15, 314. https://doi.org/10.3390/bios15050314
Avital N, Shulkin N, Malka D. Automatic Calculation of Average Power in Electroencephalography Signals for Enhanced Detection of Brain Activity and Behavioral Patterns. Biosensors. 2025; 15(5):314. https://doi.org/10.3390/bios15050314
Chicago/Turabian StyleAvital, Nuphar, Nataniel Shulkin, and Dror Malka. 2025. "Automatic Calculation of Average Power in Electroencephalography Signals for Enhanced Detection of Brain Activity and Behavioral Patterns" Biosensors 15, no. 5: 314. https://doi.org/10.3390/bios15050314
APA StyleAvital, N., Shulkin, N., & Malka, D. (2025). Automatic Calculation of Average Power in Electroencephalography Signals for Enhanced Detection of Brain Activity and Behavioral Patterns. Biosensors, 15(5), 314. https://doi.org/10.3390/bios15050314





