White Light Spectroscopy Characteristics and Expansion Dynamic Behavior of Primary T-Cells: A Possibility of Online, Real-Time, and Sampling-Less CAR T-Cell Production Monitoring
Abstract
1. Introduction
1.1. Context
1.2. Commercial Methods
1.3. Alternative Techniques
1.4. T-Cell Lines Versus Primary T-Cells
1.5. Current Needs and Proposal
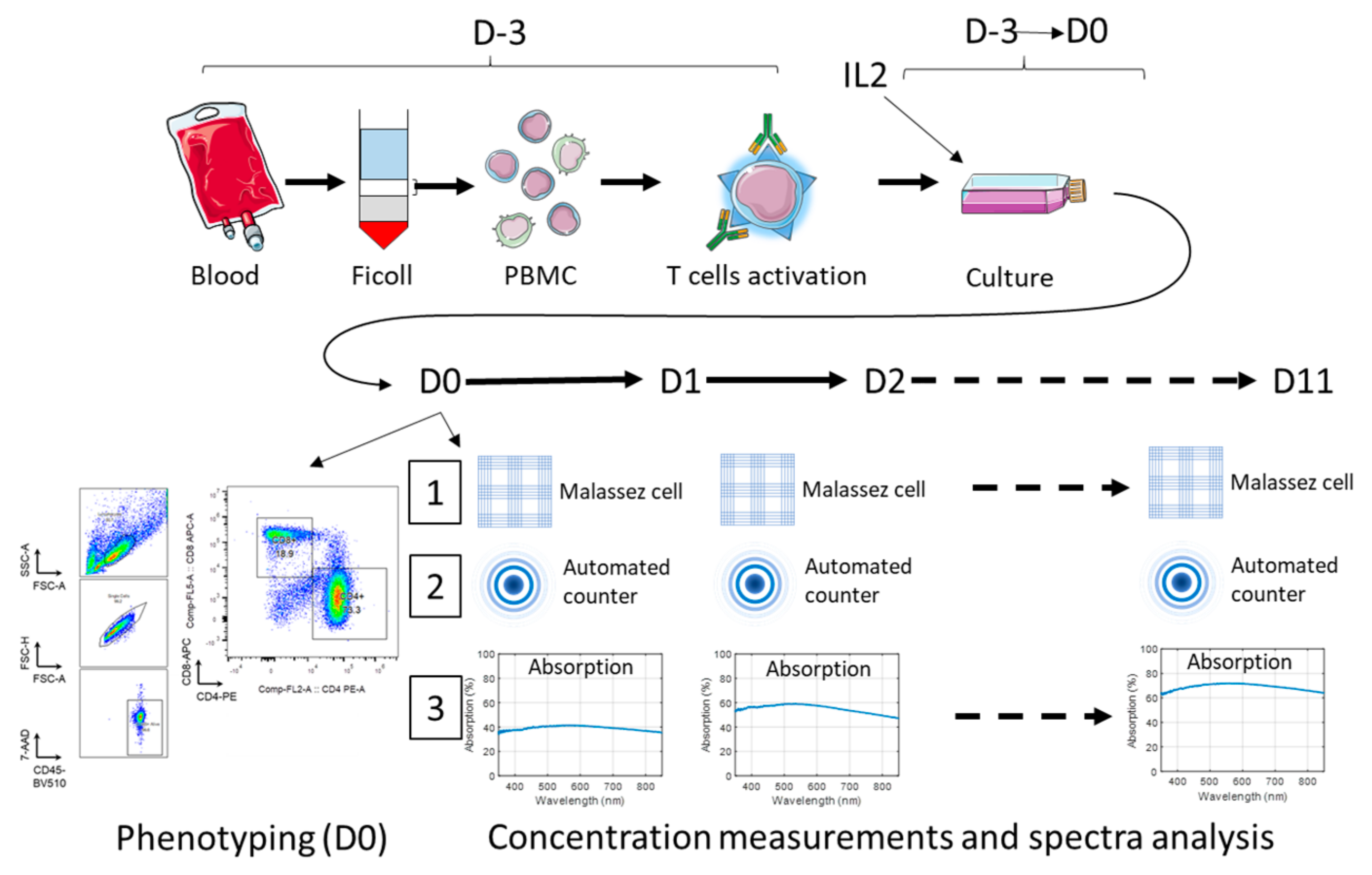
2. Materials and Methods
2.1. Peripheral Blood Mononuclear Cell (PBMC) Extraction, Platelet Removal and T-Cell Activation
2.2. T-Cell Seeding and Phenotyping at D0
2.3. Absorption Spectra Acquisitions
2.4. T-Cell Culture Experiments
2.5. Dilution Ranges
3. Results
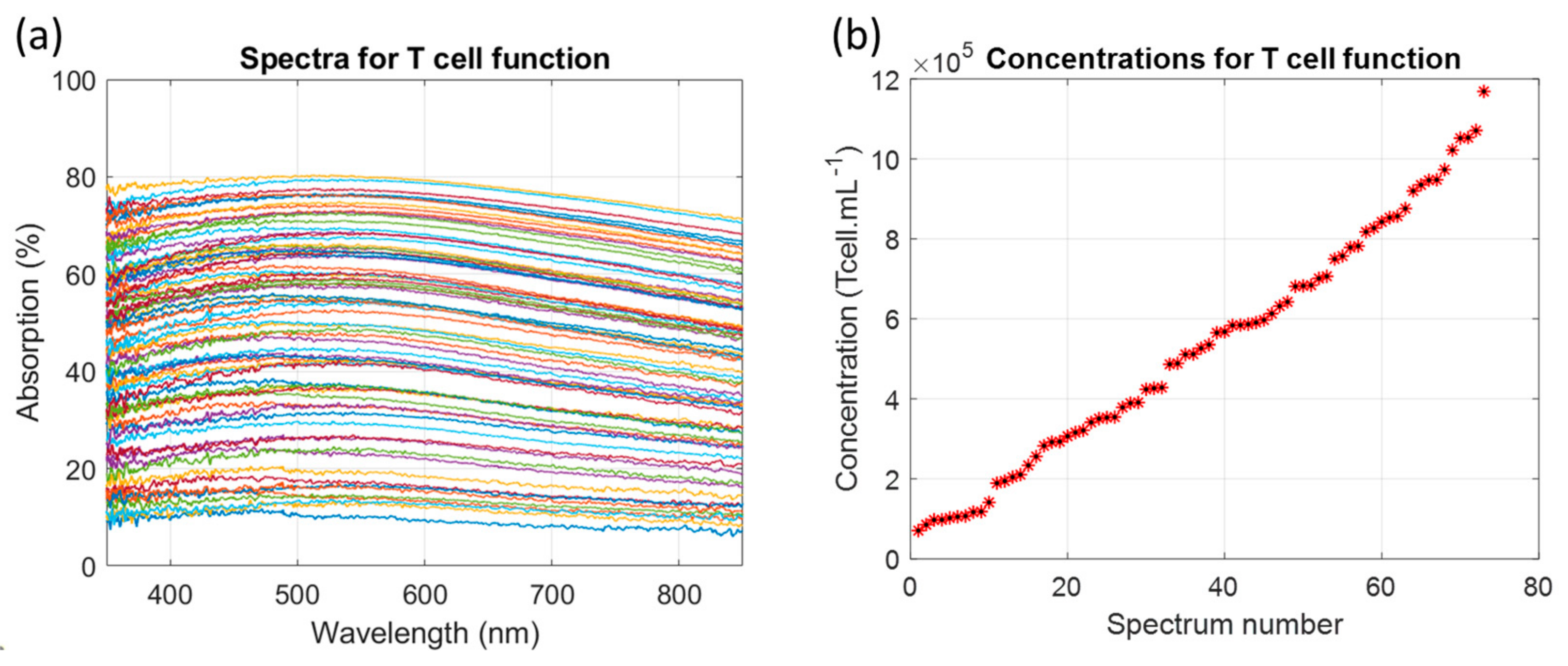
3.1. Description of the Primary T-Cell Absorption Spectra Shapes
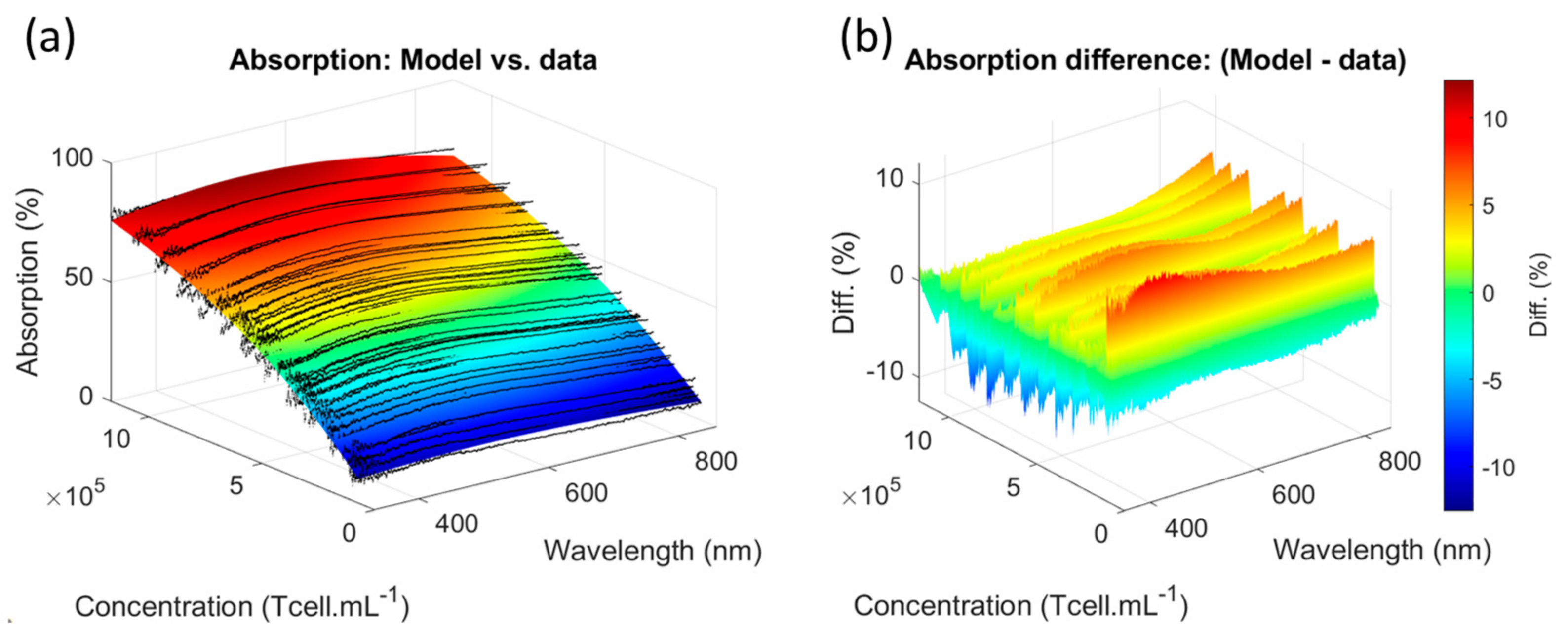
3.1.1. Determining the Primary T-Cell Absorption Spectra Shapes
3.1.2. Measuring Dilution Ranges with the T-Cell Absorption Function
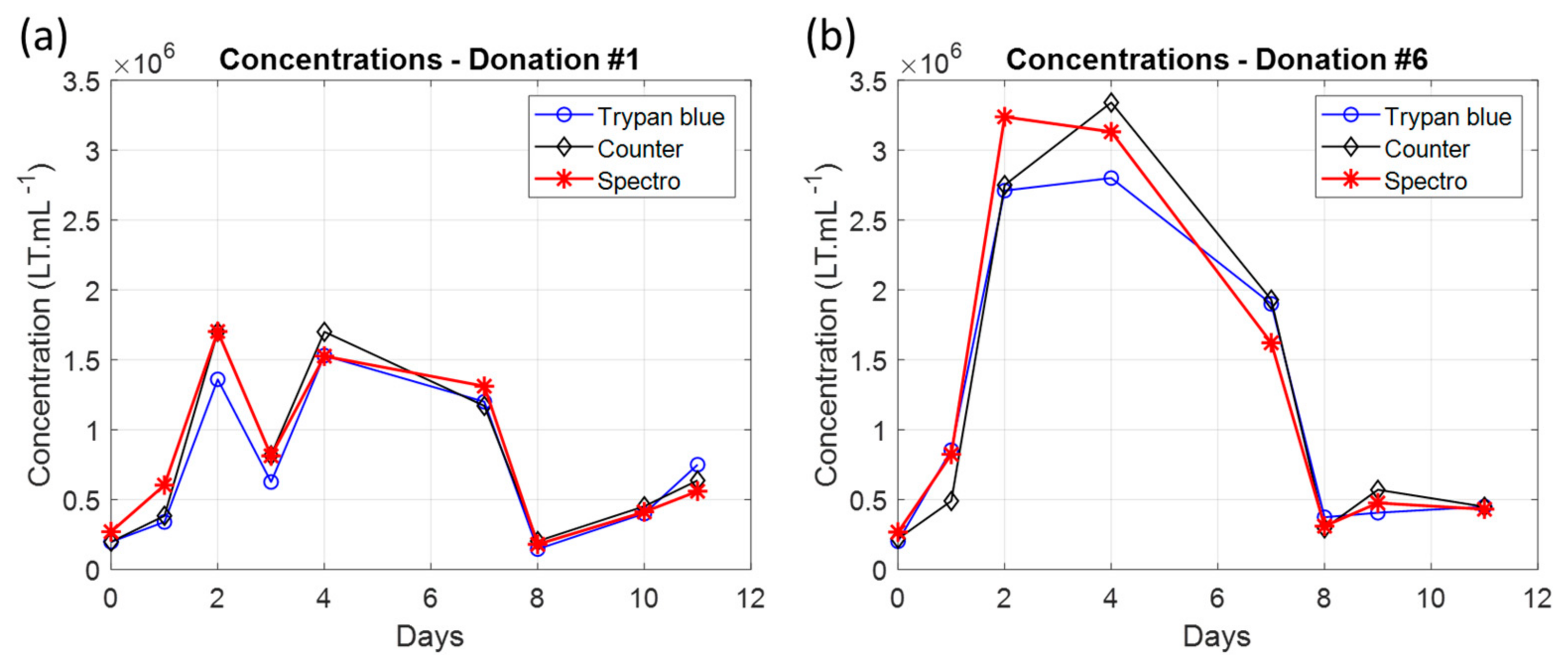
3.2. Primary T-Cell Culture Monitoring
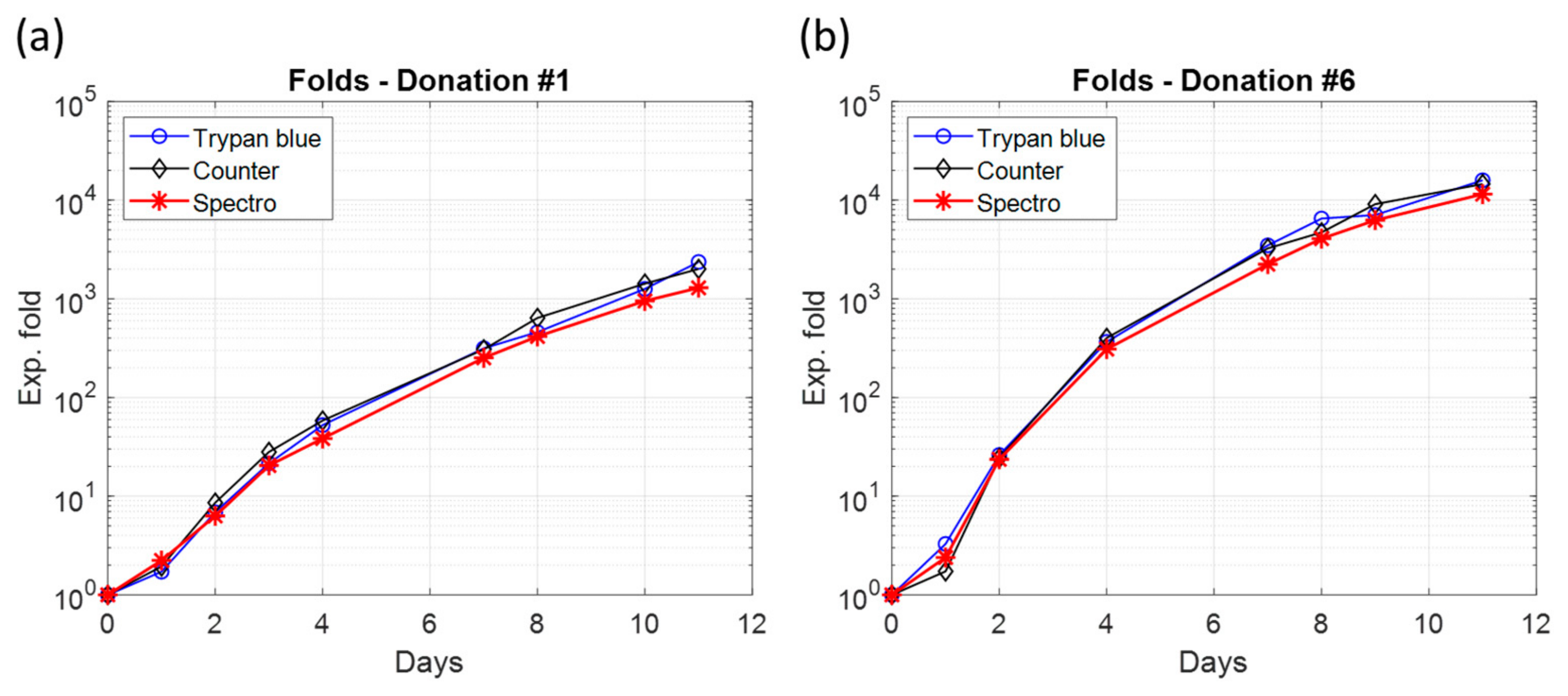
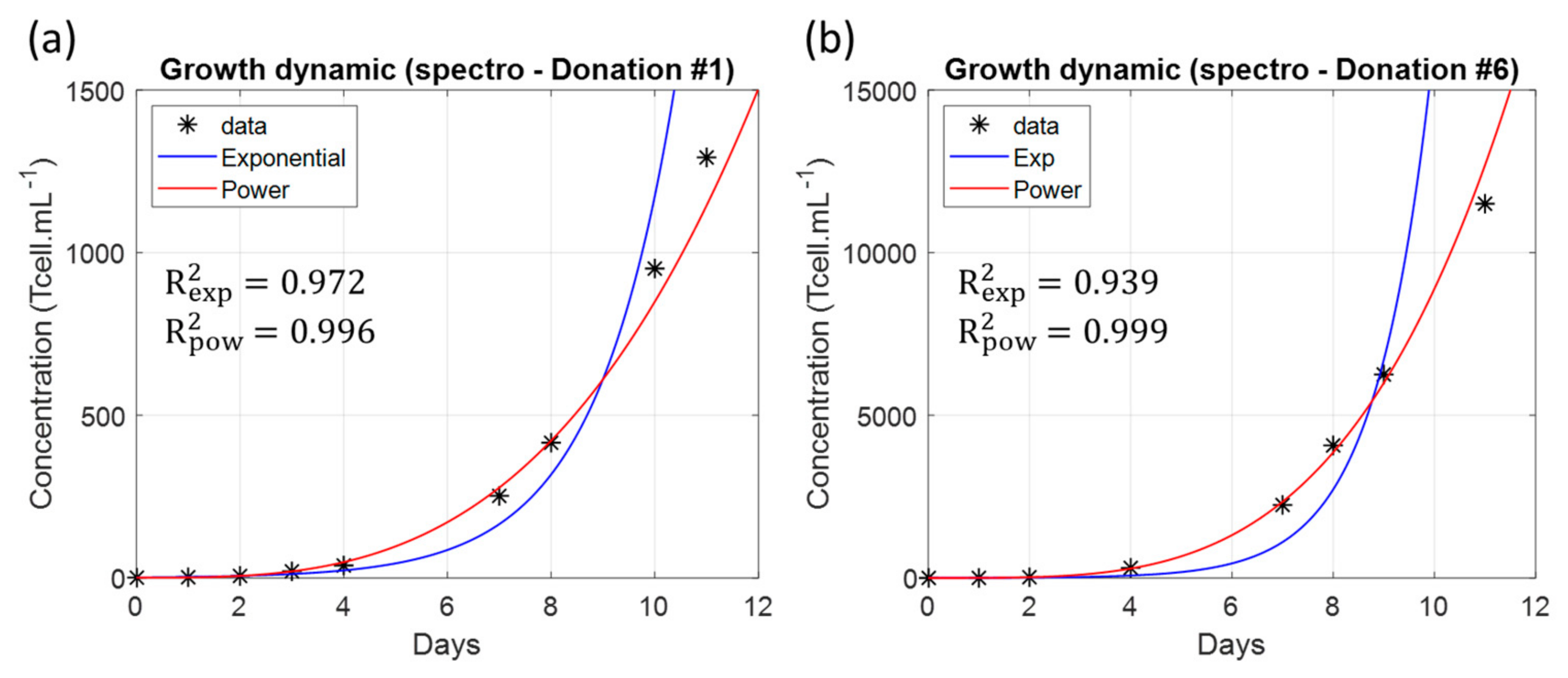
3.3. Non-Exponential T-Cell Multiplication
3.4. Proposal of an Instantaneous Generation Time (IGT)
4. Discussion
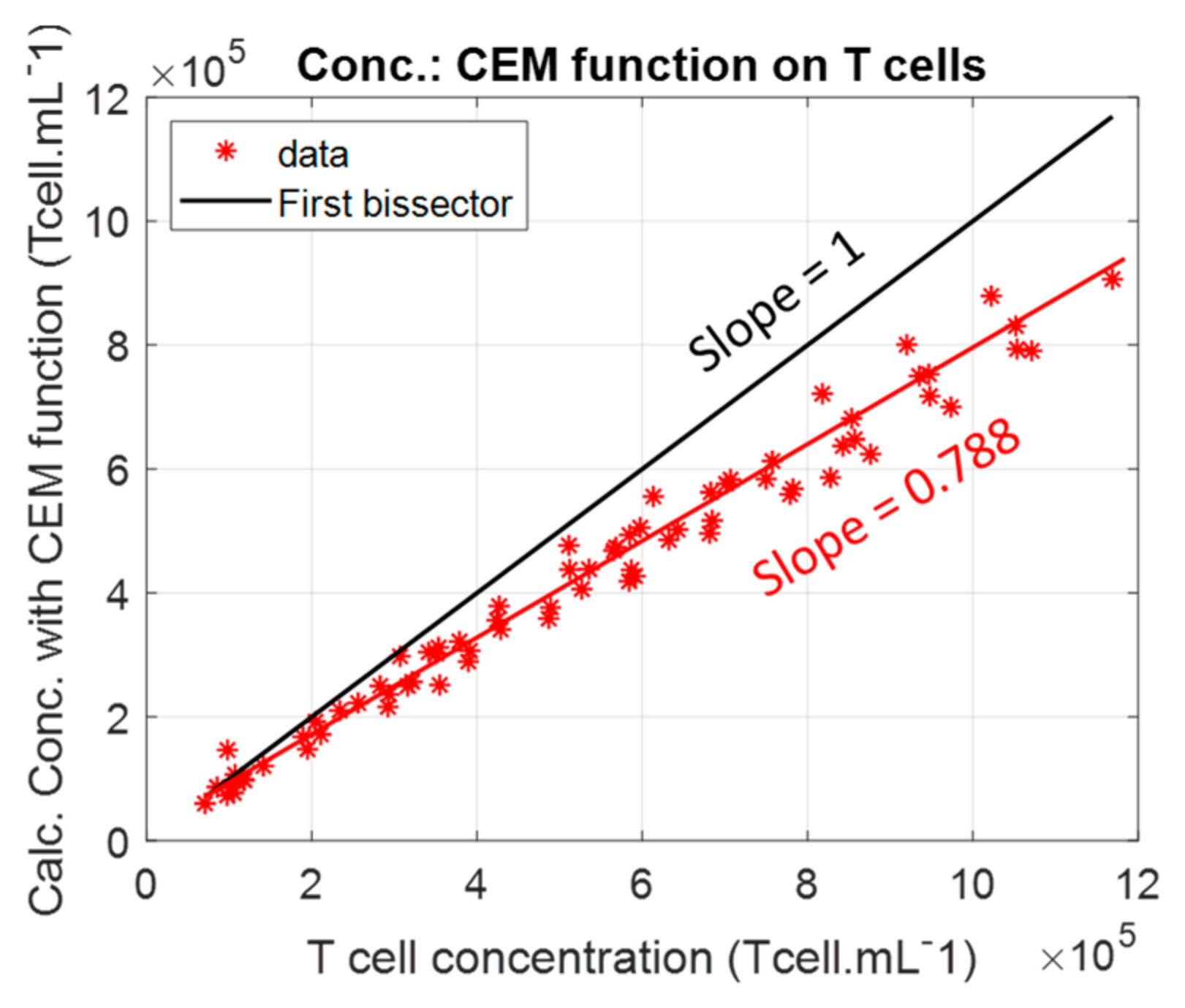
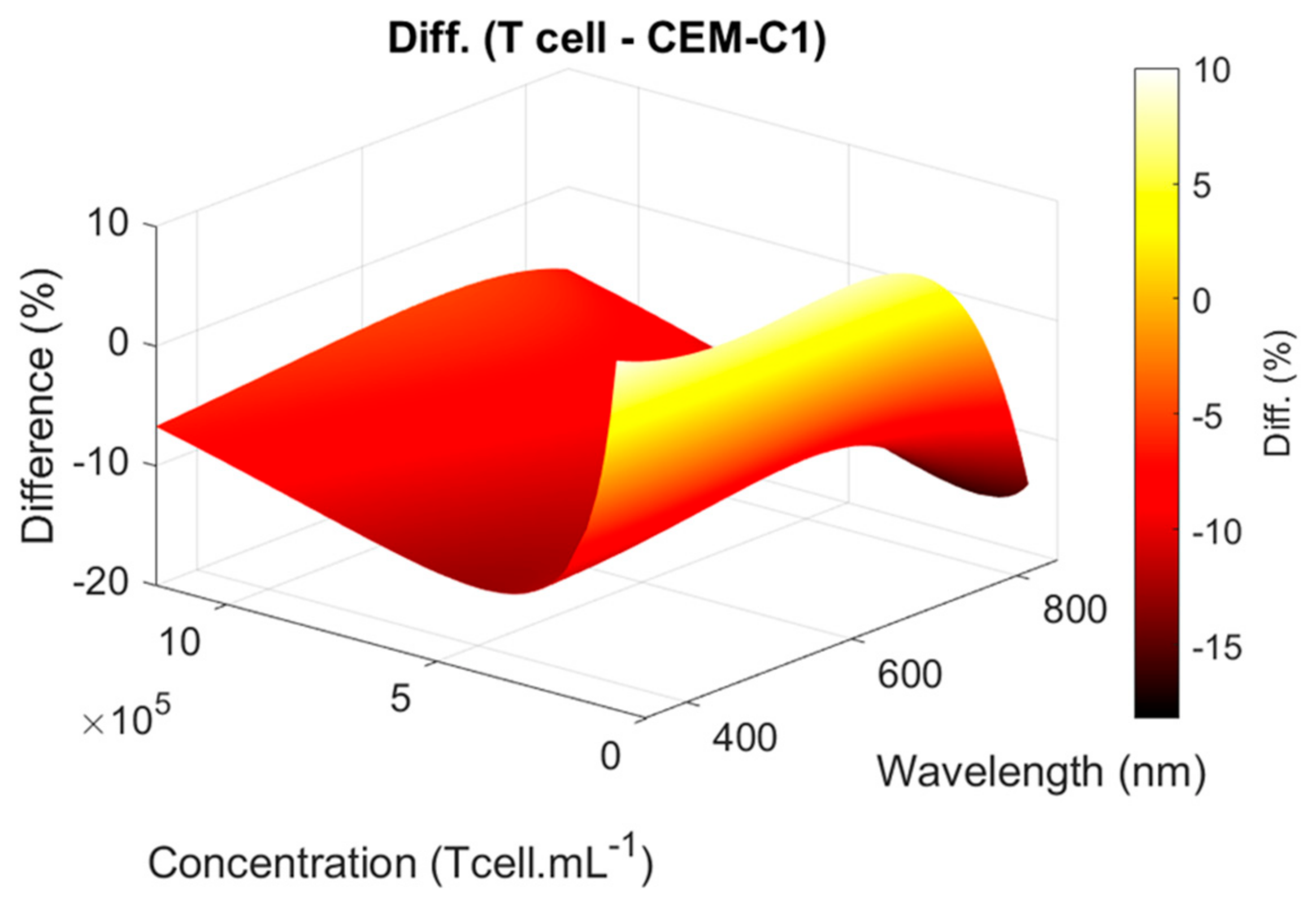
4.1. Primary T-Cell vs. CEM-C1 Optical Absorption
4.2. Concerning T-Cell Spectra Shape Function
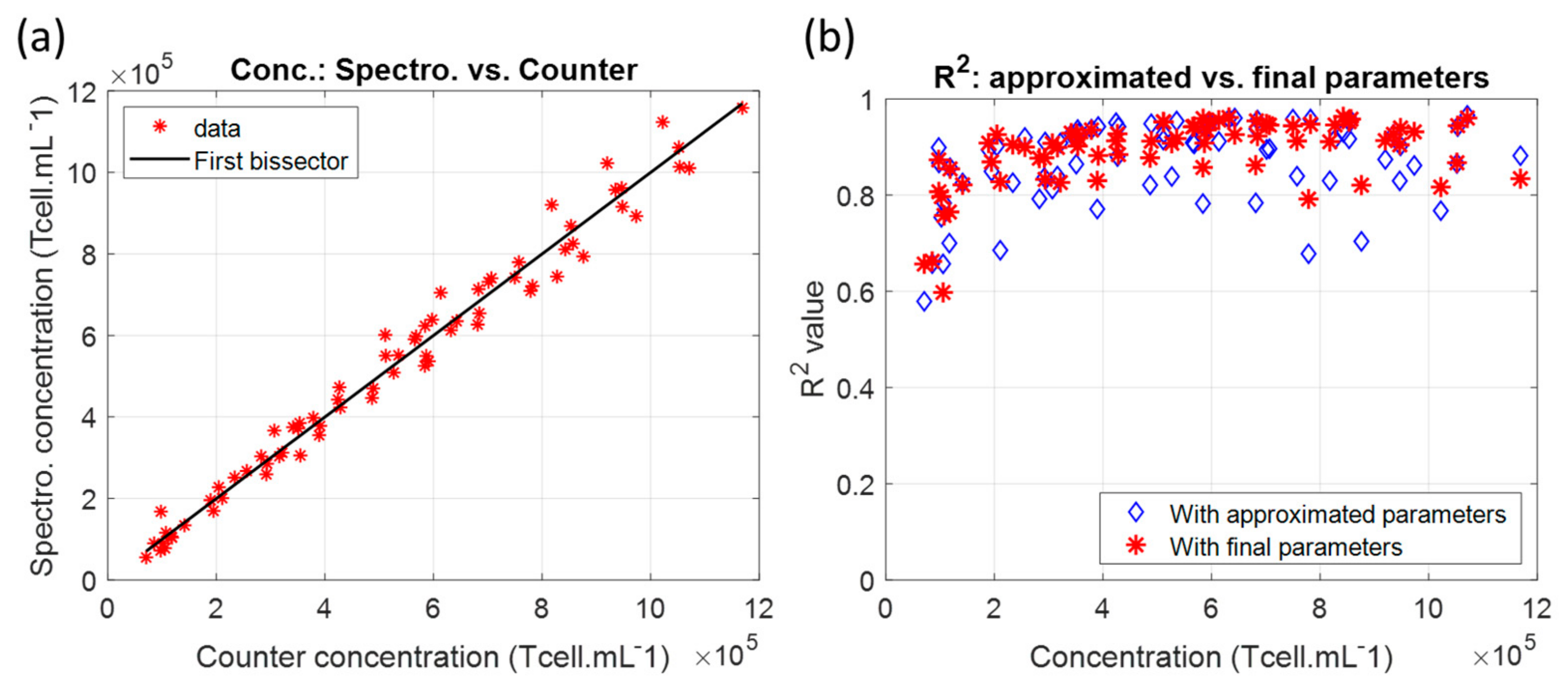
4.3. Concerning Concentration Measurements’ Accuracy
4.4. Precaution to Be Taken When Fitting Expansion Folds
4.5. Considerations About Instantaneous Generation Times
4.6. Power-Law Dynamic of Primary T-Cell Culture
4.7. Integration Possibility in a Closed-Loop, Real Time and Sampling-Less Device
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ATMP: Advanced Therapy Medicinal Product. European Medicines Agency. Available online: https://www.ema.europa.eu/en/human-regulatory-overview/advanced-therapy-medicinal-products-overview (accessed on 4 December 2024).
- Wang, X.; Rivière, I. Clinical manufacturing of CAR T-cells: Foundation of a promising therapy. Mol. Ther. Oncolytics 2016, 3, 16015. [Google Scholar] [CrossRef] [PubMed]
- Wacogne, B.; Legrand, D.; Azzopardi, C.L.; Pieralli, C.; Frelet-Barrand, A. Optical Spectroscopy Methods to Monitor Cells and Bacteria Concentrations and to Detect Contamination during Cell Culture: Application to the Fabrication of ATMPs. In Biomedical Engineering Systems and Technologies. Communications in Computer and Information Science; Ye, X., Soares, F., De Maria, E., Comez Vilda, P., Cabitza, F., Fred, A., Gamboa, H., Eds.; Springer Book Series; Springer Nature: Cham, Switzerland, 2021; Volume 1400, pp. 53–75. [Google Scholar]
- Wacogne, B.; Legrand, D.; Pieralli, C.; Frelet-Barrand, A. Optical Spectroscopy for the Quality Control of ATMP Fabrication: A New Method to Monitor Cell Expansion and to Detect Contaminations. In Proceedings of the 13th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2020)—BIODEVICES, Valletta, Malta, 24–26 February 2020; Volume 1, pp. 64–72. [Google Scholar]
- Lo, E.K.K.; Lee, P.C.; El-Nezami, H. Low dose of zearalenone elevated colon cancer cell growth through G protein-coupled estrogenic receptor. Sci. Rep. 2021, 11, 7403. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Al-Momin, S.; Vanitha, V.K.; Al-Aqeel, H.; Al-Musallam, L.; Al-Mansour, H.; Shajan, A.B. Evaluation of Various Growth Conditions for the Cultivation of Microalgae Species in the Arid Regions. J. Mech. Cont. Math. Sci. 2019, 4, 255–265. [Google Scholar] [CrossRef]
- Gauchotte, G.; Hergalant, S.; Vigouroux, C.; Casse, J.M.; Houlgatte, R.; Kaoma, T.; Helle, D.; Brochin, L.; Rech, F.; Peyre, M.; et al. Cytoplasmic overexpression of RNA-binding protein HuR is a marker of poor prognosis in meningioma, and HuR knockdown decreases meningioma cell growth and resistance to hypoxia. J. Pathol. 2017, 242, 421–434. [Google Scholar] [CrossRef]
- Available online: https://www.iprasense.com/ (accessed on 4 December 2024).
- Empower Your Research with IncuCyte® Live-Cell Analysis Systems. Available online: https://www.sartorius.com/en/products/cell-analysis/incucyte-live-cell-analysis-system (accessed on 4 December 2024).
- IncuCyte® S3 Live-Cell Analysis System. Available online: https://www.sartorius.com/en/products/live-cell-imaging-analysis/live-cell-analysis-instruments/s3-live-cell-analysis-instrument (accessed on 4 December 2024).
- Available online: https://phiab.com (accessed on 4 December 2024).
- Engvall, E.; Perlman, P. Enzyme-linked immunosorbent assay (ELISA). Quantitative assay of immunoglobulin G. Immunochemistry 1971, 8, 871–874. [Google Scholar]
- Balkian, G.K.; Flores, K.M.; Llull, R.; Ko, H.S.; Walker, K.W.; Black, K.S.; Hewitt, C.W. A rapid and sensitive cellular enzyme-linked immunoabsorbent assay (Celisa) for the detection and quantitation of antibodies against cell surface determinants II. Optimal reagent concentrations and predictive analysis. Cell Transplant. 1997, 6, 431–437. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Trinh, K.T.L.; Yoon, W.J.; Lee, N.Y.; Ju, H. Integration of a microfluidic polymerase chain reaction device and surface plasmon resonance fiber sensor into an inline all-in-one platform for pathogenic bacteria detection. Sens. Actuators B Chem. 2016, 242, 1–8. [Google Scholar] [CrossRef]
- Karlsson, R.; Stahlberg, R. Surface plasmon resonance detection and multispot sensing for direct monitoring of interactions involving low-molecular-weight analytes and for determination of low affinities. Anal. Biochem. 1995, 228, 274–280. [Google Scholar] [CrossRef]
- Tsong-Rong, Y.; Chao-Fa, L.; Hung-Che, C. QCM as Cell-Based Biosensor. In Chemical Biology; Ekinci, D., Ed.; Intechopen: London, UK, 2012; pp. 411–434. [Google Scholar]
- Wudy, F.; Multerer, M.; Stock, C.; Schmeer, G.; Gores, H.J. Rapid impedance scanning QCM for electrochemical applications based on miniaturized hardware and high-performance curve fitting. Electrochim. Acta 2008, 53, 6568–6574. [Google Scholar] [CrossRef]
- Cole, H.; Demont, A.; Marison, I. The Application of Dielectric Spectroscopy and Biocalorim-etry for the Monitoring of Biomass in Immobilized Mammalian Cell Cultures. Processes 2015, 3, 384–405. [Google Scholar] [CrossRef]
- Downey, B.J.; Graham, L.J.; Breit, J.F.; Glutting, N.K.A. Novel approach for using dielectric spectroscopy to predict viable cell volume (VCV) in early process development. Biotechnol. Prog. 2014, 30, 479–487. [Google Scholar] [CrossRef] [PubMed]
- Musmann, C.; Joeris, K.; Markert, S.; Solle, D.; Scheper, T. Spectroscopic methods and their applicability for high-throughput characterization of mammalian cell cultures in automated cell culture systems. Eng. Life Sci. 2016, 16, 405–416. [Google Scholar] [CrossRef]
- Chen, G.; Hu, J.; Qin, Y.; Zhou, W. Viable cell density on-line auto-control in perfusion cell culture aided by in-situ Raman spectroscopy. Biochem. Eng. J. 2021, 172, 108063. [Google Scholar] [CrossRef]
- Calvet, A.; Ryder, A.G. Monitoring Cell culture media degradation using surface enhanced Raman scattering (SERS) spectroscopy. Anal. Chim. Acta 2014, 840, 58–67. [Google Scholar] [CrossRef]
- Romo-Herrera, J.M.; Juarez-Moreno, K.; Guerrini, L.; Kang, Y.; Feliu, N.; Parak, W.J.; Alvarez-Pueblan, R.A. Paper-based plasmonic substrates as surface-enhanced Raman scattering spectroscopy platforms for cell culture applications. Mater. Today Bio. 2021, 11, 100125. [Google Scholar] [CrossRef]
- Esmonde-White, K.A.; Cuellar, M.; Uerpmann, C.; Lenain, B.; Lewis, I.R. Raman spectroscopy as a process analytical technology for pharmaceutical manufacturing and bioprocessing. Anal. Bio-Anal. Chem. 2017, 409, 637–649. [Google Scholar] [CrossRef]
- Yoo, S.M.; Lee, S.Y. Optical Biosensors for the Detection of Pathogenic Microorganisms. Trends Biotechnol. 2016, 34, 7–25. [Google Scholar] [CrossRef]
- Maryamchik, E.; Gallagher, K.M.; Preffer, F.I.; Kadauke, S.; Maus, M.V. New directions in chimeric antigen receptor T-cell CAR-T therapy and related flow cytometry. Cytom. Part B Clin. Cytom. 2020, 98, 299–327. [Google Scholar] [CrossRef]
- Pitoiset, F.; Cassard, L.; El Soufi, K.; Boselli, L.; Grivel, J.; Roux, A.; Klatzmann, D.; Chaput, N.; Rosenzwajg, M. Deep phenotyping of immune cell populations by optimized and standardized flow cytometry analyses. Cytom. Part A 2018, 93, 793–802. [Google Scholar] [CrossRef]
- van de Geijn, G.J.M.; van Gent, M.; van Pul-Bom, N.; Beunis, M.H.; van Tilburg, A.J.P.; Njo, T.L. A New Flow Cytometric Method for Differential Cell Counting in Ascitic Fluid. Cytom. Part B 2016, 90, 506–511. [Google Scholar] [CrossRef]
- Tahir, M.A.; Dina, N.E.; Cheng, H.; Valev, V.K.; Zhang, L. Surface-enhanced Raman spectroscopy for bioanalysis and diagnosis. Nanoscale 2021, 13, 11593–11634. [Google Scholar] [CrossRef] [PubMed]
- Melnykovych, G.; Haug, J.S.; Goldner, C.M. Growth inhibition of leukemia cell line CEM-C1 by farnesol: Effects of phosphatidylcholine and diacylglycerol. Biochem. Biophys. Res. Commun. 1992, 186, 543–548. [Google Scholar] [CrossRef] [PubMed]
- de Bardet, J.C.; Cardentey, C.R.; González, B.L.; Patrone, D.; Mulet, I.L.; Siniscalco, D.; Robinson-Agramonte, M.d.l.A. Cell Immortalization: In Vivo Molecular Bases and In Vitro Techniques for Obtention. Biotechnology 2023, 12, 14. [Google Scholar] [CrossRef] [PubMed]
- Wacogne, B.; Vaccari, N.; Koubevi, C.; Belinger-Podevin, M.; Robert-Nicoud, M.; Rouleau, A.; Frelet-Barrand, A. Absorption Spectra Description for T-Cell Concentrations Determination and Simultaneous Measurements of Species during Co-Cultures. Sensors 2022, 22, 9223. [Google Scholar] [CrossRef]
- Vaccari, N.; Wacogne, B.; Koubevi, C.; Podevin, M.; Rouleau, A.; Frelet-Barrand, A. White light spectroscopy for T-cell culture growth monitoring: Towards a real-time and sampling free device for ATMPs production. J. Transl. Sci. 2021, 7, 1–10. [Google Scholar] [CrossRef]
- Wacogne, B.; Belinger-Podevin, M.; Vaccari, N.; Koubevi, C.; Codjiova, C.; Gutierrez, E.; Bourgeois, P.; Davoine, L.; Robert-Nicoud, M.; Rouleau, A.; et al. Absorption/attenuation spectra description of ESKAPEE bacteria: Application to seeder-free culture monitoring, mammalian T-cell and bacteria mixture analysis and contamination description. Sensors 2023, 23, 4325. [Google Scholar] [CrossRef]
- Hollyman, D.; Stefanski, J.; Przybylowski, M.; Bartido, S.; Borquez-Ojeda, O.; Taylor, C.; Yeh, R.; Capacio, V.; Olszewska, M.; Hosey, J.; et al. Manufacturing validation of biologically functional T-cells targeted to CD19 antigen for autologous adoptive cell therapy. J. Immunother. 2009, 32, 169–180. [Google Scholar] [CrossRef]
- Ceppi, F.; Wilson, A.L.; Annesley, C.; Kimmerly, G.R.; Summers, C.; Brand, A.; Seidel, K.; Vicky Wu, Q.; Beebe, A.; Brown, C.; et al. Modified manufacturing process modulates CD19CAR T-cell engraftment fitness and leukemia-free survival in pediatric and young adult subjects. Concern Immunol. Res. 2022, 10, 856–870. [Google Scholar] [CrossRef]
- Nicod, C.; Neto da Rocha, M.; Warda, W.; Roussel, X.; Haderbache, R.; Seffar, E.; Trad, R.; Bouquet, L.; Goncalves, M.; Bosdure, L.; et al. CAR-T-cells targeting IL-1RAP produced in a closed semiautomatic system are ready for the first phase I clinical investigation in humans. Curr. Res. Transl. Med. 2023, 71, 103385. [Google Scholar] [CrossRef]
- Sato, K.; Kondo, M.; Sakuta, K.; Hosoi, A.; Noji, S.; Sugiura, M.; Yoshida, Y.; Kakimi, K. Impact of culture medium on the expansion of T-cells for immunotherapy. Cytotherapy 2009, 11, 936–946. [Google Scholar] [CrossRef]
- Caël, B.; Galaine, J.; Bardey, I.; Marton, C.; Fredon, M.; Biichle, S.; Poussard, M.; Godet, Y.; Angelot-Delettre, F.; Barisien, C.; et al. Umbilical Cord Blood as a Source of Less Differentiated T-cells to Produce CD123 CAR-T-cells. Cancers 2022, 14, 3168. [Google Scholar] [CrossRef] [PubMed]
- Kath, J.; Franke, F.; Drosdek, V.; Du, W.; Glaser, V.; Fuster-Garcia, C.; Stein, M.; Zittel, T.; Schulenberg, S.; Porter, C.E.; et al. Integration of ζ-deficient CARs into the CD3ζ gene conveys potent cytotoxicity in T and NK cells. Immunobiol. Immunother. 2024, 143, 25. [Google Scholar]
- Monod Equation. Available online: https://en.wikipedia.org/wiki/Monod_equation (accessed on 4 December 2024).
- Exponential and Logistic Growth. Available online: https://www.khanacademy.org/science/ap-biology/ecology-ap/population-ecology-ap/a/exponential-logistic-growth (accessed on 4 December 2024).
- Gompertz Growth Model. Available online: https://fr.wikipedia.org/wiki/Mod%C3%A8le_de_Gompertz (accessed on 4 December 2024).
- Power-Law Decay. Available online: https://en.wikipedia.org/wiki/Power_law (accessed on 4 December 2024).
- Wang, J.Y.; Wang, L. CAR-T-cell therapy: Where are we now, and where are we heading? Blood Sci. 2023, 5, 237–248. [Google Scholar] [CrossRef] [PubMed]
- Bogert, R. Improving Outcomes and Mitigating Costs Associated With CAR T-Cell Therapy. Suppl. Am. J. Manag. Care 2021, 27, S253–S261. [Google Scholar]
- Yujileds. Available online: https://store.yujiintl.com/products/yujileds-hyperspectral-350nm-1000nm-0-4w-led-smd-2835 (accessed on 4 December 2024).
- Hamamatsu. Available online: https://www.hamamatsu.com/eu/en/product/optical-sensors/spectrometers/mini-spectrometer.html (accessed on 4 December 2024).
- Miltenyi Biotec. Available online: https://www.miltenyibiotec.com/DE-en/applications/by-technology/clinimacs-prodigy-applications.html (accessed on 20 March 2025).
- Avantes. Available online: https://www.avantes.com/products/fiber-optics/transmission-probes/transmission-dip-probes/ (accessed on 20 March 2025).


| Reagent | Supplier (Country) | Reference |
|---|---|---|
| T-cell TransActTM Human | Miltenyi (Bergisch Gladbach, Germany, supplier France) | 130-111-160 |
| RPMI | Corning (Glendale, AZ, USA, supplier France) | 98-1507-LT |
| Human Serum (HS) | Internal product from French Blood Agency (France) | Batch: #2 du 2022-12-16 |
| Penicillin/Streptomycin (PS) | EUROBIO (Les Ulis, France) | CABPES01-0U |
| IL2 (interleukin 2) | Clinigen (Yardley, PA, USA, supplier France) | 03400956215867 |
| Brilliant Violet 510TM Anti-human CD45 | SONY Biotechnology (San Jose, CA, supplier France) | 2120180 |
| PE Mouse anti human CD4 | Becton Dickinson (Franklin Lakes, NJ, USA, supplier France) | 555347 |
| APC Mouse anti human CD8 | Becton Dickinson (Franklin Lakes, NJ, USA, supplier France) | 555369 |
| 7-AAD Viability Staining Solution | SONY Biotechnology (San Jose, CA, USA, supplier France) | 2702020 |
| Equipment | Supplier (country) | Reference |
| 6-well plate | Corning (Glendale, AZ, USA, supplier France) | 351146 |
| T75 flask | Corning (Glendale, AZ, USA, supplier France) | 353136 |
| Malassez cell | NanoEntek (Seoul, Republic of Korea, supplier France) | DHC-M01 2M18222 |
| Automated Cell Counter | Anvajo (Dresde, Germany, supplier France) | FluidLab R-300 |
| Heraeus Cryofuge Centrifuge | Thermo Scientific (Waltham, MA, USA, supplier France) | 5500i |
| Centrifuge | Eppendorf (Wesseling-Berzdorf, Germany, supplier France) | 5702 R |
| Cytometer | Becton Dickinson (Franklin Lakes, NJ, USA, supplier France) | FACS Fortessa Flow Cytometer |
| Cytometer | Miltenyi (Bergisch Gladbach, Germany, supplier France) | Analyzer 16 |
| White light source | Avantes (Apeldoorn, The Netherlands, supplier France) | Avalight-DH-S-BAL |
| Cuvette holder | Avantes (Apeldoorn, The Netherlands, supplier France) | CUV_UV/VIS |
| Spectrometer | Ocean Optics (Orlando, FL, USA, supplier France) | USB 4000 UV-VIS-ES |
| OceanView software | Ocean Optics (USA, supplier France) | N° 2.0.15 |
| Calculation Software | MathWorks (Natick, MA, USA, supplier France) | MatlabTM R2020b |
| D0 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 | D11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #1 | X | X | X | X | X | X | X | X | X | |||
| #2 | X | X | X | X | X | X | X | X | X | |||
| #3 | X | X | X | X | X | X | X | X | X | |||
| #4 | X | X | X | X | X | X | X | X | X | |||
| #5 | X | X | X | X | X | X | X | X | X | |||
| #6 | X | X | X | X | X | X | X | X |
| Final Parameters | p1a1 | b1 | p1c1 | p2c1 | a2 | b2 | c2 |
|---|---|---|---|---|---|---|---|
| Value | 5.59 × 10−7 | 535.93 | 39.49 | 0.21 | 3.48 | 274.01 | 1281.6 |
| Day | D0 | D1 | D2 | D3 | D4 | D7 | D8 | D9 | D11 |
|---|---|---|---|---|---|---|---|---|---|
| #1 | 1 | 1 | 1 | 6.8 | 1 | 7.6 | 12 | 1 | 1 |
| #2 | 1 | 1 | 1 | 6.45 | 1 | 7.45 | 20.5 | 1 | 1 |
| #3 | 1 | 1 | 1 | 5.6 | 1 | 9.5 | 14.5 | 1 | 1.325 |
| #4 | 1 | 1 | 1 | 7.05 | 1 | 9.95 | 5.75 | 1 | 1 |
| #5 | 1 | 1 | 1 | 6.05 | 1 | 8.45 | 4.83 | 1 | 1 |
| #6 | 1 | 1 | 2.5 | - | 13.5 | 14 | 9.5 | 1 | 2.03 |
| Donation | #1 | #2 | #3 | #4 | #5 | #6 |
|---|---|---|---|---|---|---|
| Final fold value | 1889 | 2301 | 4279 | 740 | 544 | 13,994 |
| Donation | #1 | #2 | #3 | #4 | #5 | #6 |
|---|---|---|---|---|---|---|
| (day−1) | 0.91 | 0.2 | 0.35 | 0.56 | 1.05 | 1.62 |
| (no unit) | 3.14 | 3.81 | 3.71 | 2.97 | 2.49 | 3.74 |
| R2 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.997 |
| Donation | #1 | #2 | #3 | #4 | #5 | #6 |
|---|---|---|---|---|---|---|
| Slope (h.day−1) | 6.5 | 5.8 | 5.8 | 7.3 | 8.5 | 5.4 |
| Donation | #1 | #2 | #3 | #4 | #5 | #6 |
|---|---|---|---|---|---|---|
| Without | 0.94 | 0.94 | 0.89 | 0.94 | 0.81 | 0.96 |
| With | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.997 |
| Donation | #1 | #2 | #3 | #4 | #5 | #6 |
|---|---|---|---|---|---|---|
| Initial value (h) | 24.7 | 36.6 | 31.8 | 29.2 | 23.5 | 21.1 |
| Min. time (h) | 26.7 | 42.7 | 37.3 | 32 | 21.3 | 24 |
| Donation | #1 | #2 | #3 | #4 | #5 | #6 |
|---|---|---|---|---|---|---|
| C(2) | 1.7 | 1.55 | 1.39 | 1.74 | 1.6 | 3.23 |
| Slope | 6.5 | 5.8 | 5.8 | 7.3 | 8.5 | 5.4 |
| Q | 0.2615 | 0.2672 | 0.2397 | 0.2384 | 0.1882 | 0.5981 |
| Final fold value | 1889 | 2301 | 4279 | 740 | 544 | 13,994 |
| % diff. at D11 | 11 | 8 | 28 | −5 | −15 | −10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wacogne, B.; Brito, M.; Gamonet, C.; Rouleau, A.; Frelet-Barrand, A. White Light Spectroscopy Characteristics and Expansion Dynamic Behavior of Primary T-Cells: A Possibility of Online, Real-Time, and Sampling-Less CAR T-Cell Production Monitoring. Biosensors 2025, 15, 251. https://doi.org/10.3390/bios15040251
Wacogne B, Brito M, Gamonet C, Rouleau A, Frelet-Barrand A. White Light Spectroscopy Characteristics and Expansion Dynamic Behavior of Primary T-Cells: A Possibility of Online, Real-Time, and Sampling-Less CAR T-Cell Production Monitoring. Biosensors. 2025; 15(4):251. https://doi.org/10.3390/bios15040251
Chicago/Turabian StyleWacogne, Bruno, Maxime Brito, Clémentine Gamonet, Alain Rouleau, and Annie Frelet-Barrand. 2025. "White Light Spectroscopy Characteristics and Expansion Dynamic Behavior of Primary T-Cells: A Possibility of Online, Real-Time, and Sampling-Less CAR T-Cell Production Monitoring" Biosensors 15, no. 4: 251. https://doi.org/10.3390/bios15040251
APA StyleWacogne, B., Brito, M., Gamonet, C., Rouleau, A., & Frelet-Barrand, A. (2025). White Light Spectroscopy Characteristics and Expansion Dynamic Behavior of Primary T-Cells: A Possibility of Online, Real-Time, and Sampling-Less CAR T-Cell Production Monitoring. Biosensors, 15(4), 251. https://doi.org/10.3390/bios15040251






