Evaluating the Performance of Hyperspectral Imaging Endoscopes: Mitigating Parameters Affecting Spectral Accuracy
Abstract
1. Introduction
2. Methodology
2.1. Experimental Setup and Design
2.2. Data Analysis Methods
2.3. Parameters Affecting Spectral Accuracy
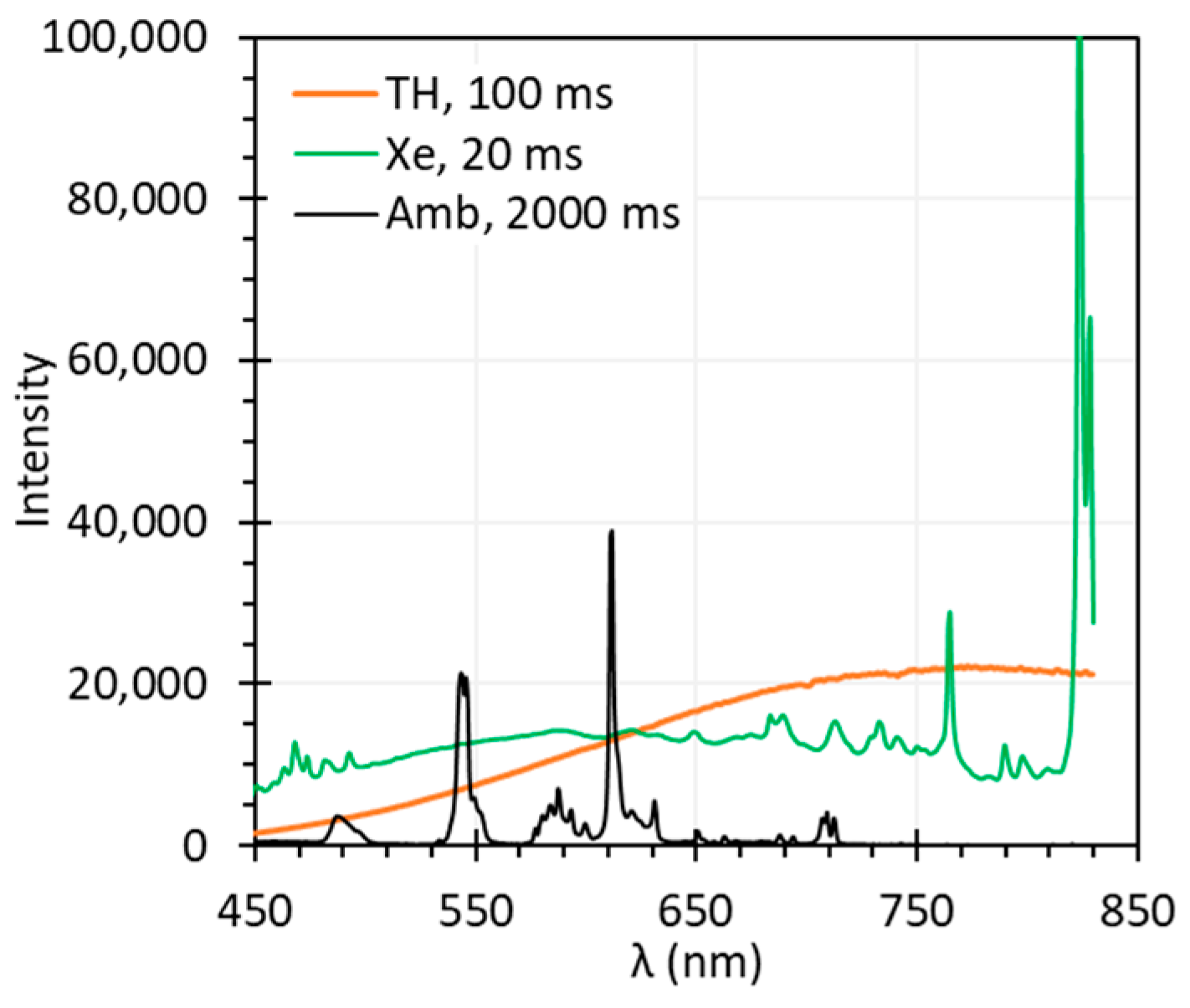
2.3.1. Ambient Light
2.3.2. Exposure Time
2.3.3. Camera Warm-Up Time
2.3.4. Spatial and Temporal Averaging
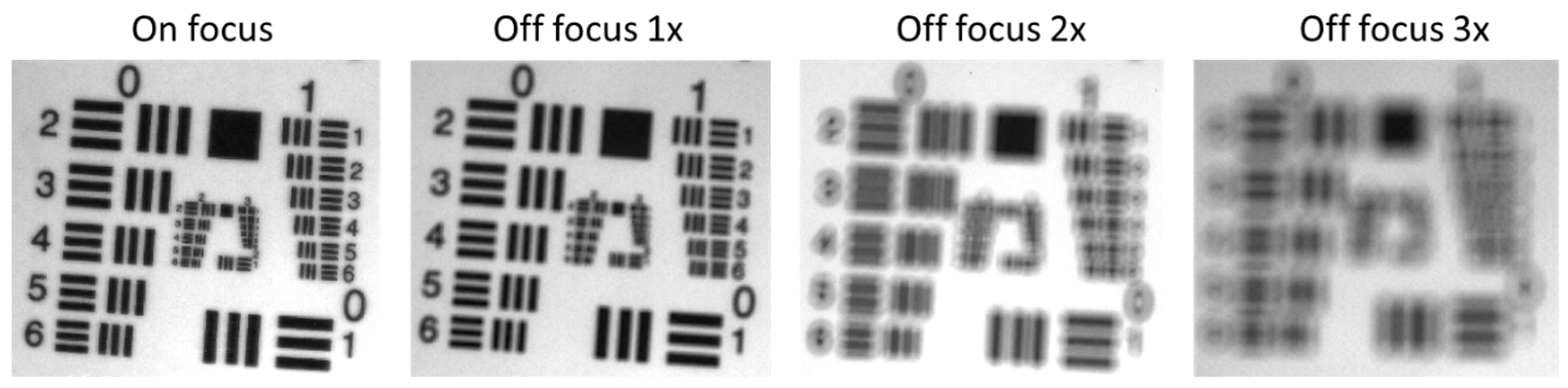
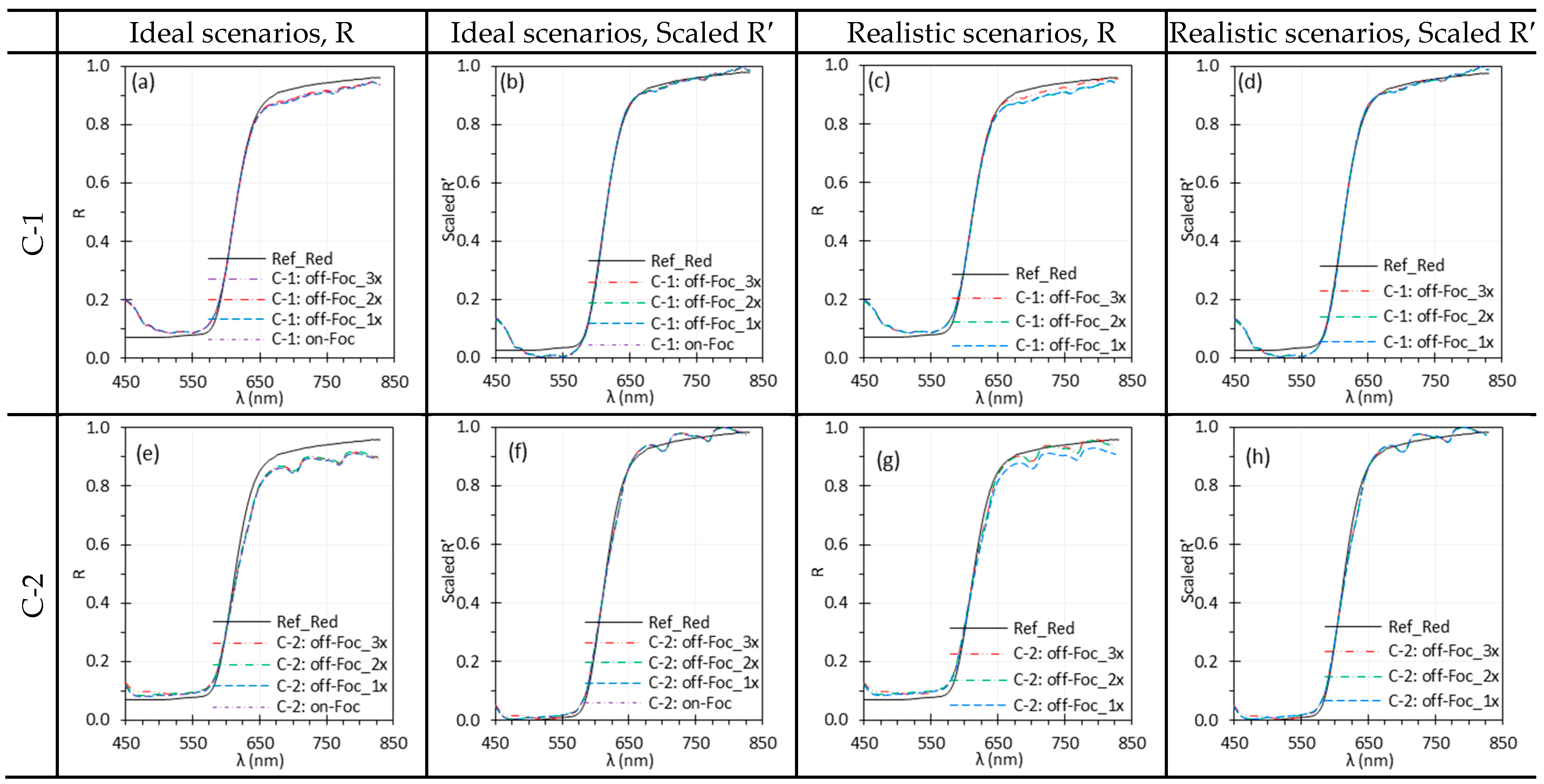
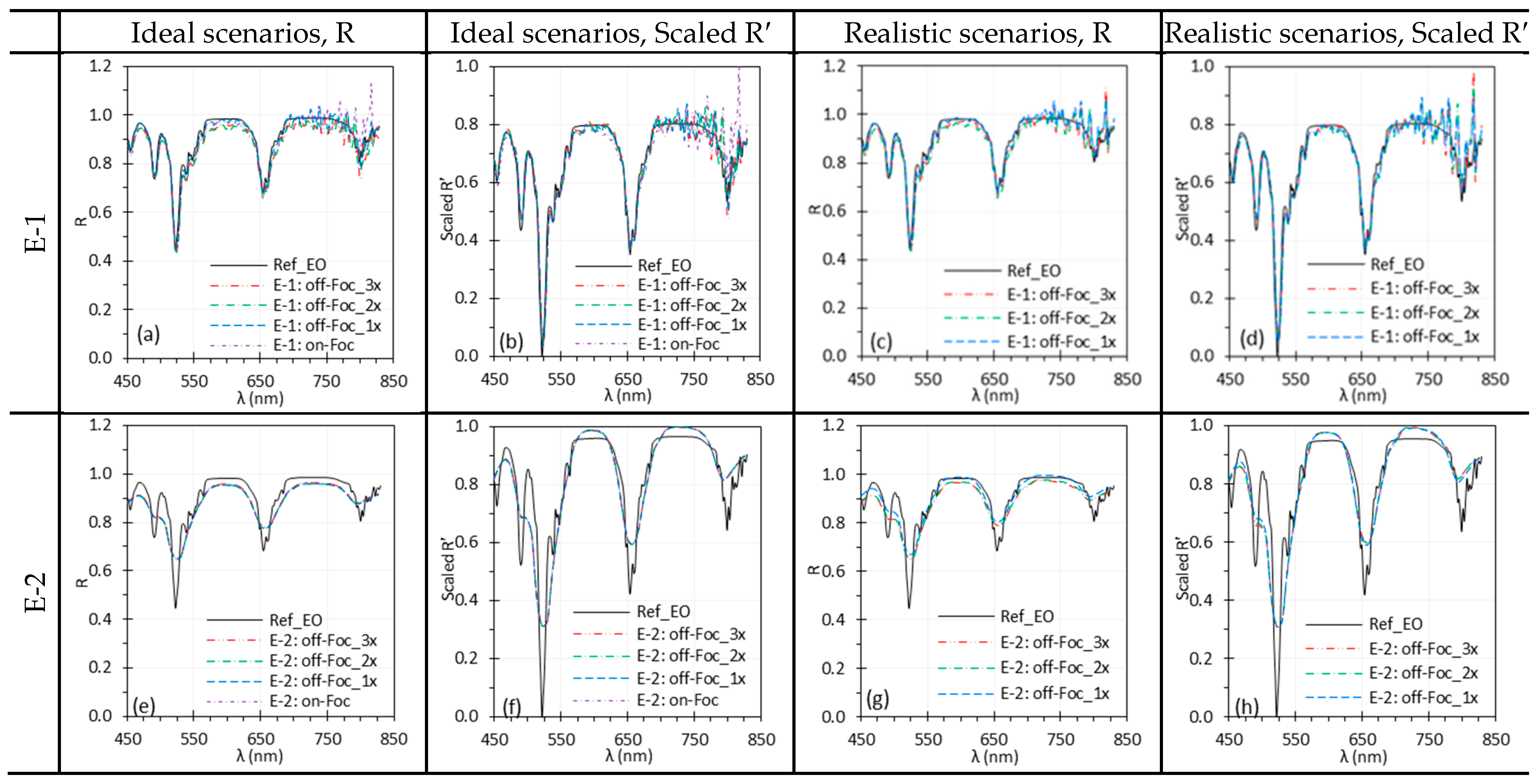
2.3.5. Camera Focus
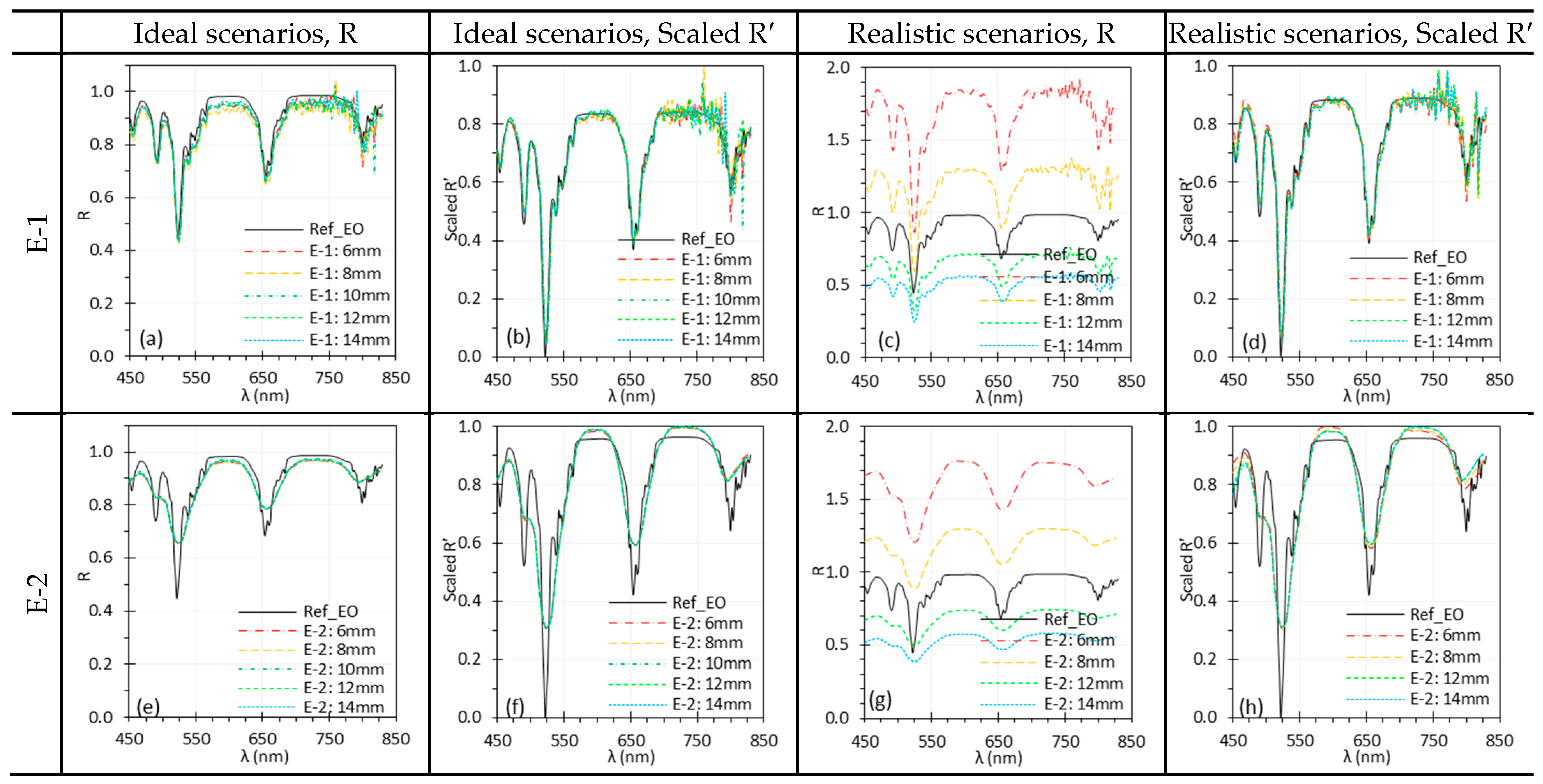
2.3.6. Working Distance (WD)
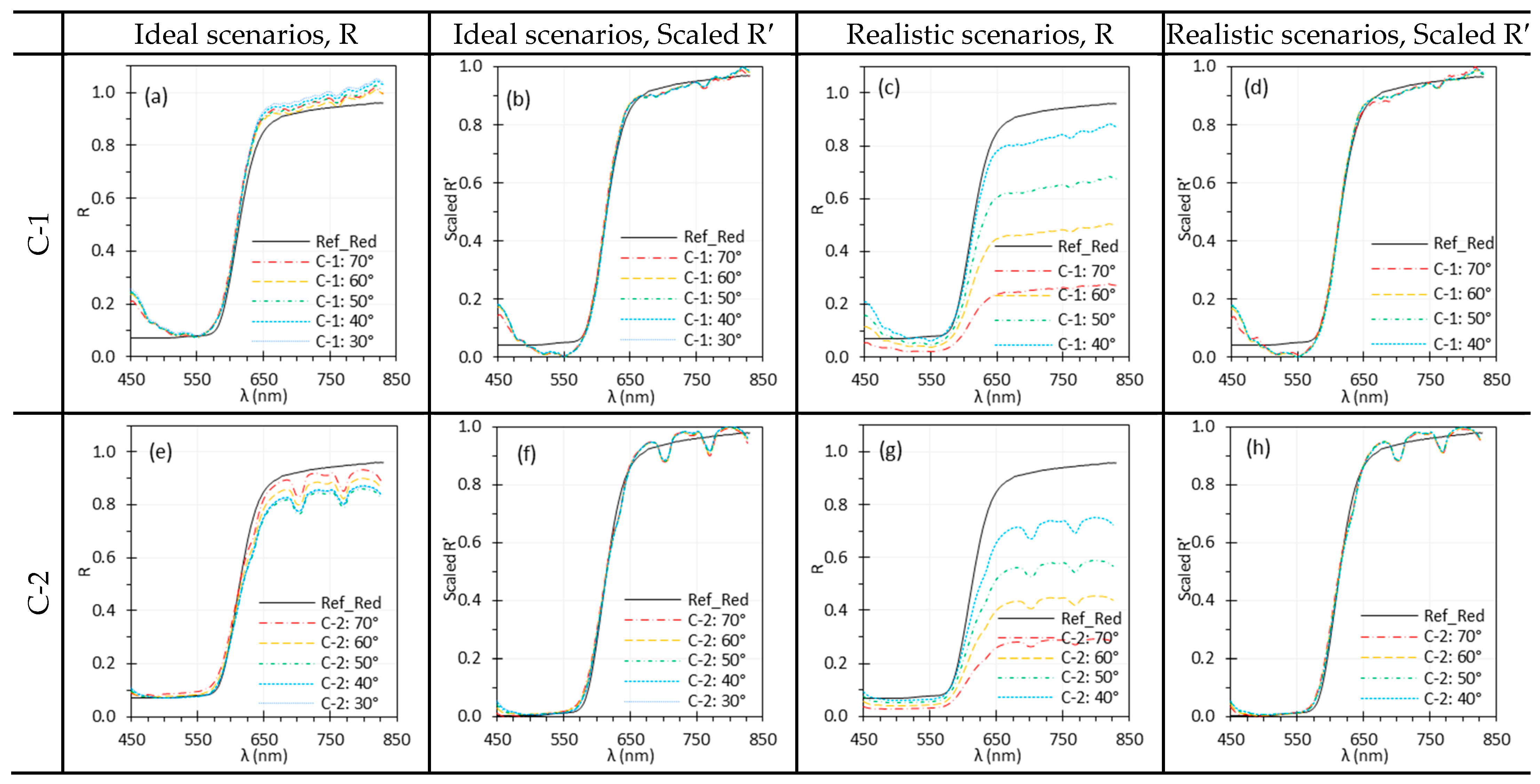
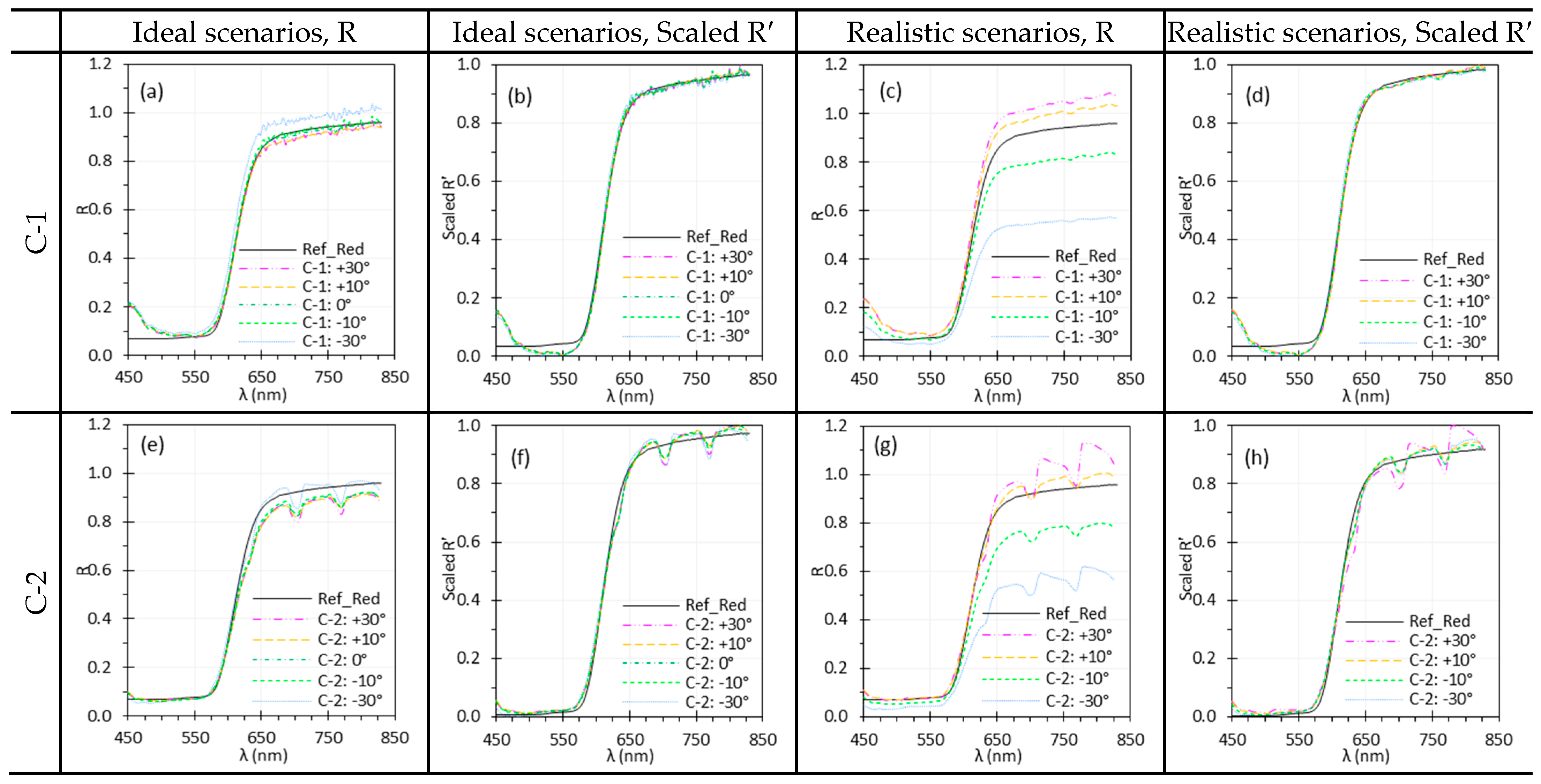
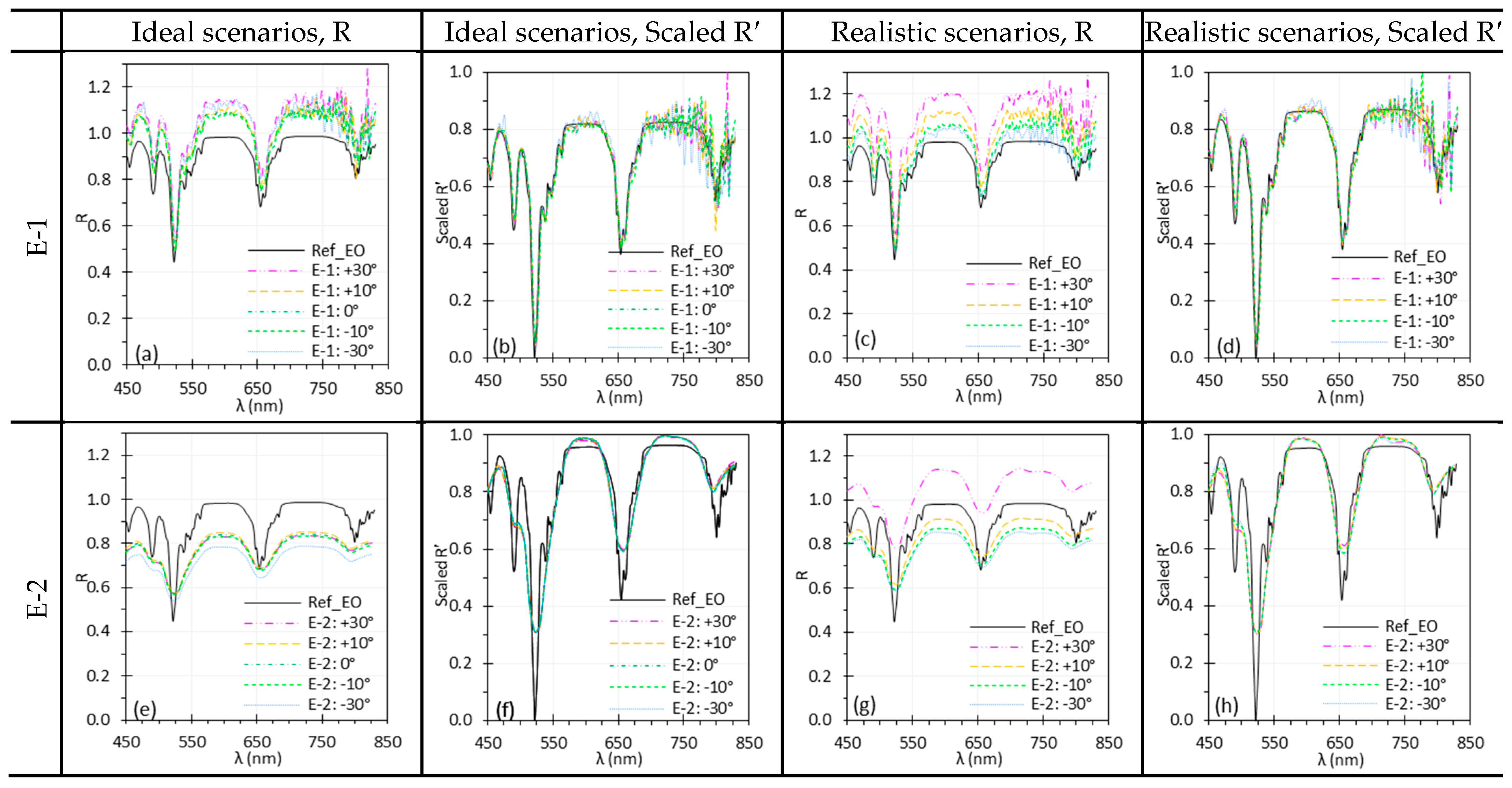
2.3.7. Illumination Angle ()
2.3.8. Target Angle ()
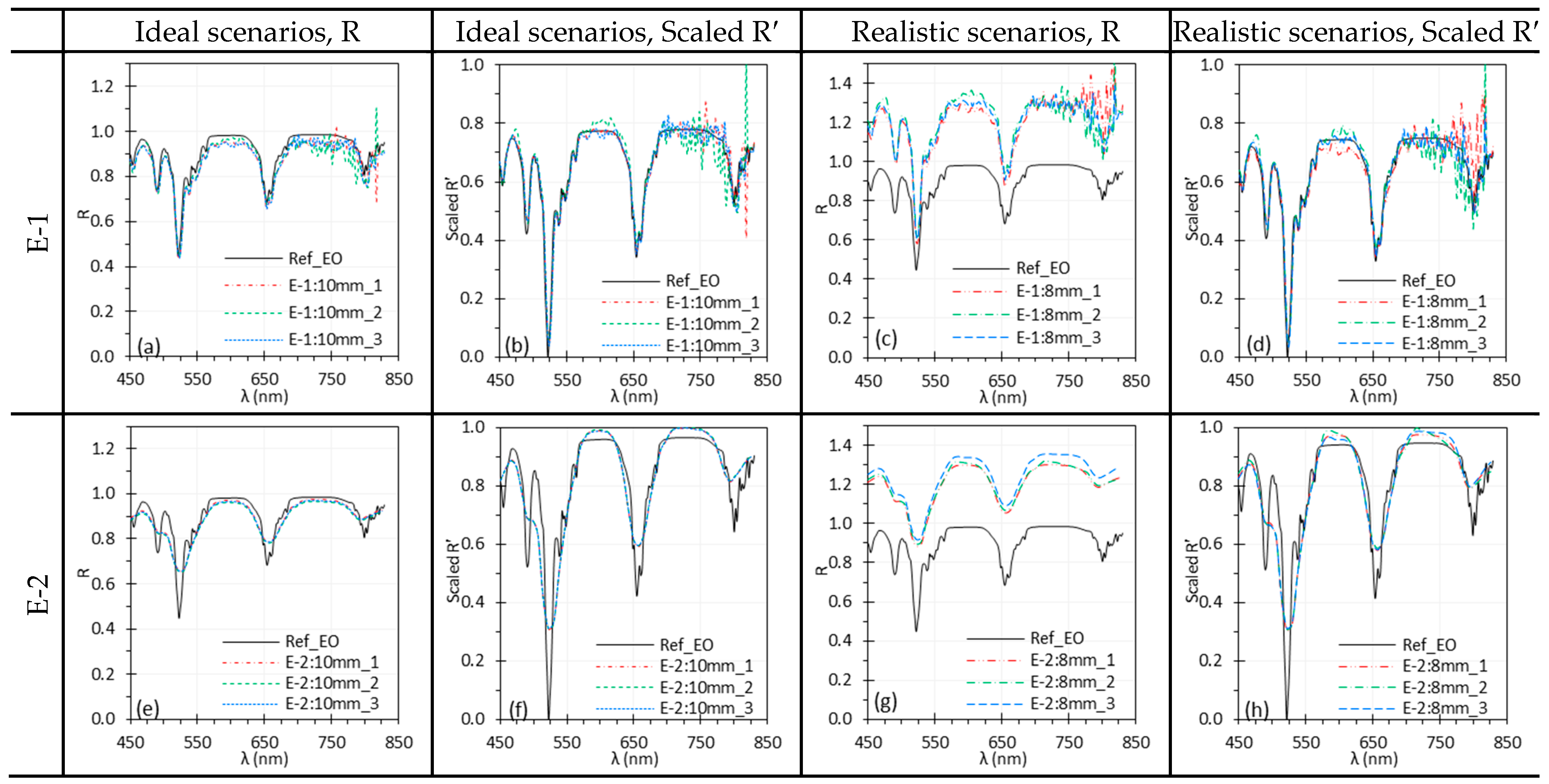
2.3.9. Measurement Repeatability
3. Results
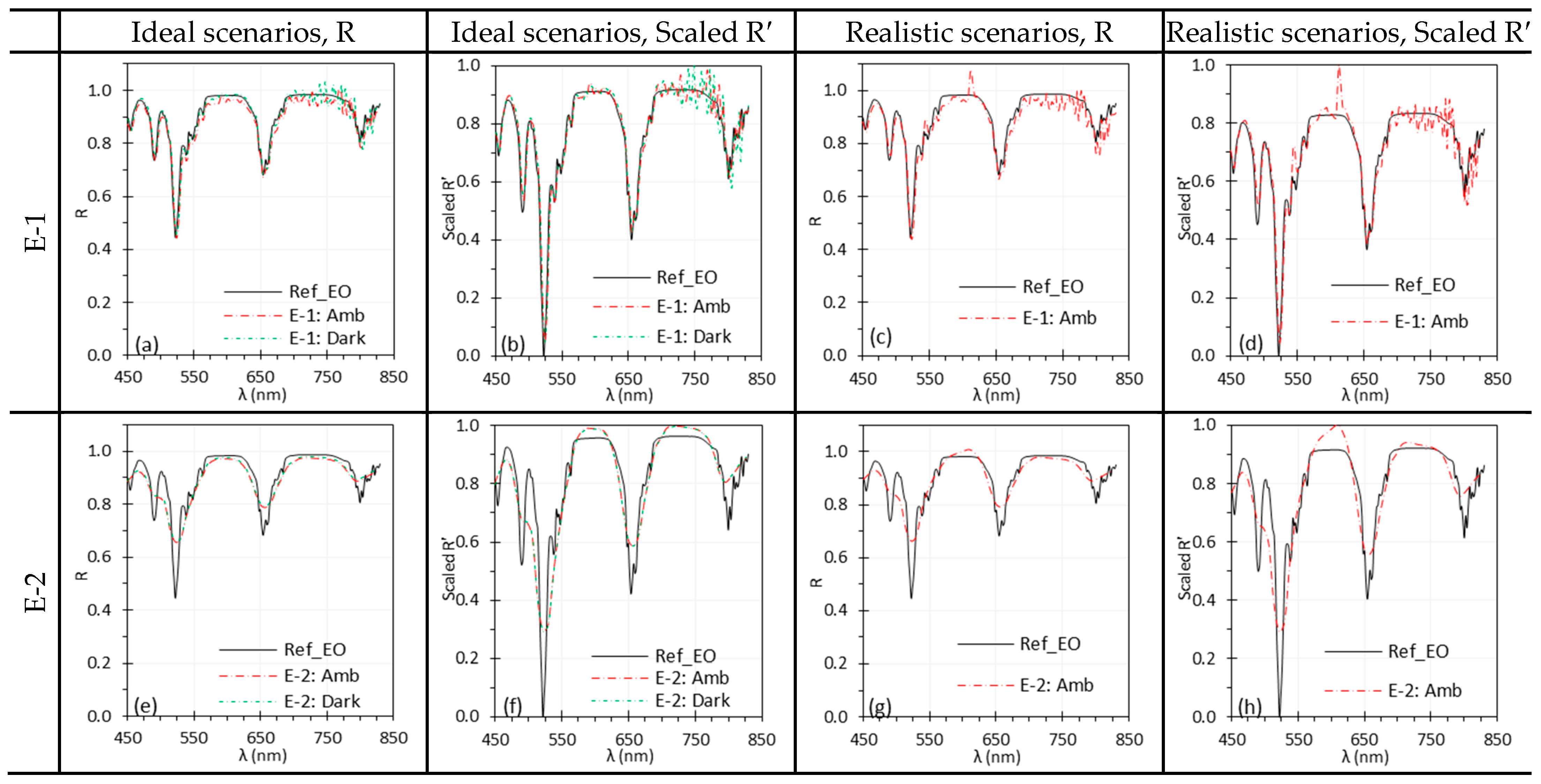
3.1. Ambient Light
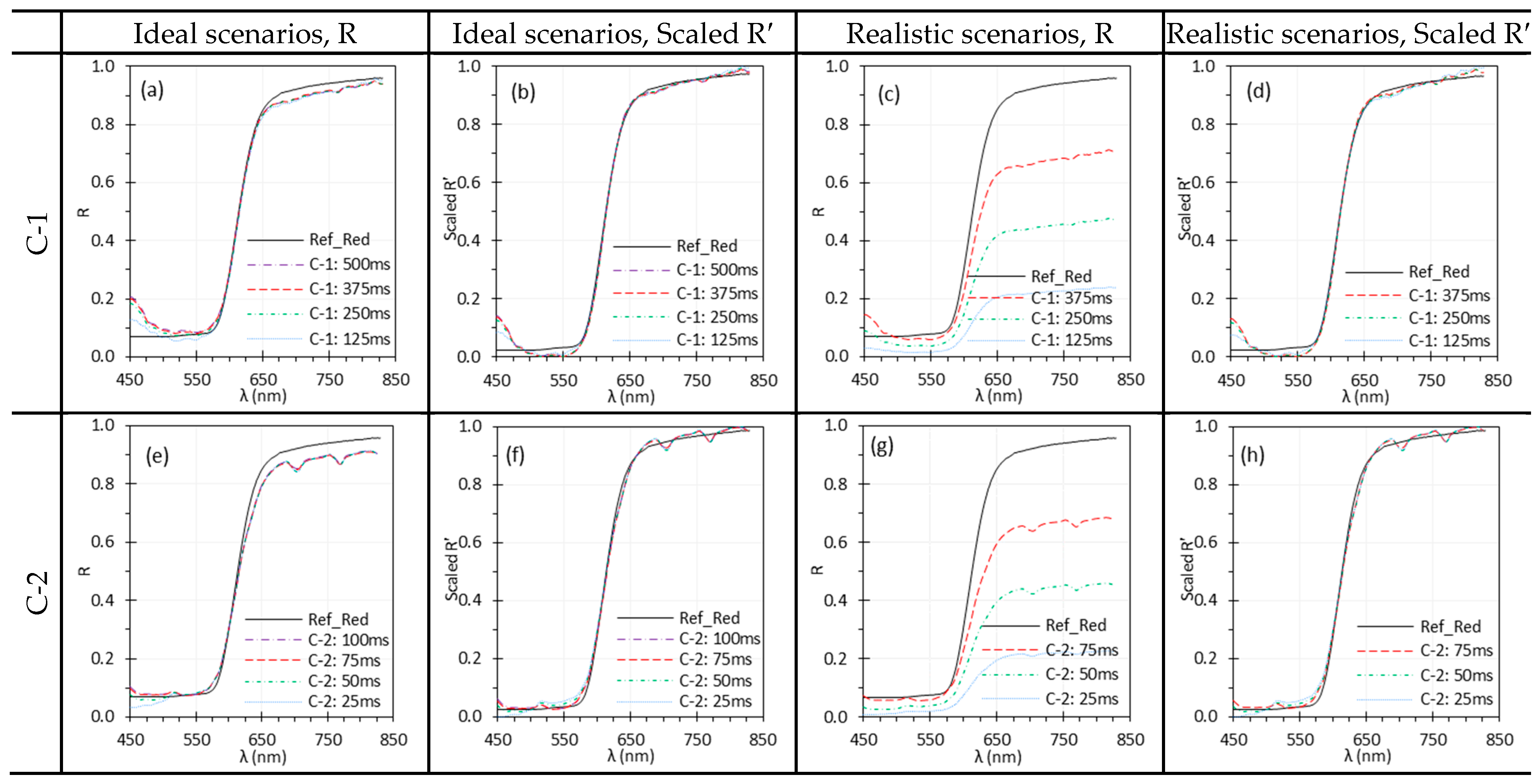
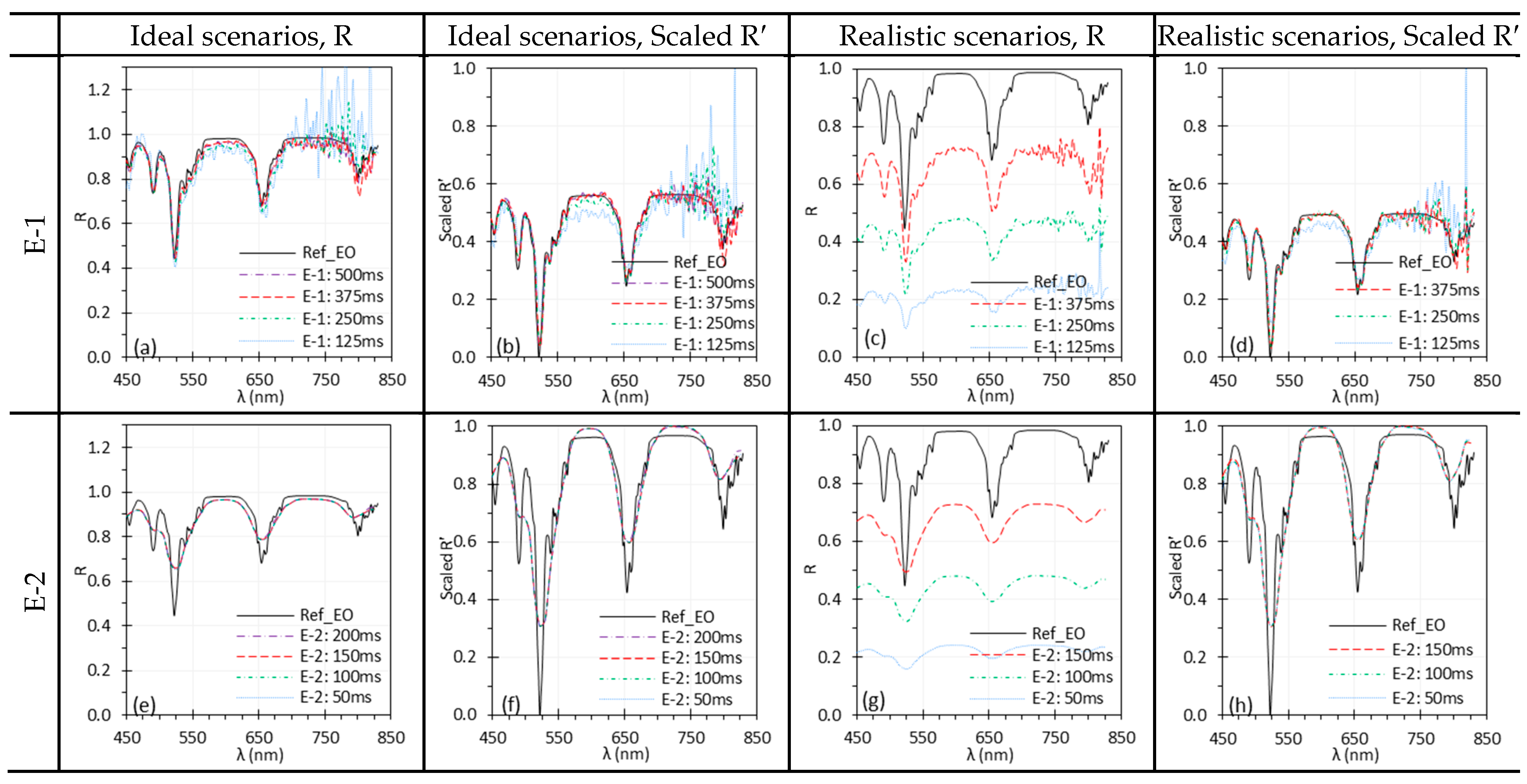
3.2. Exposure Time
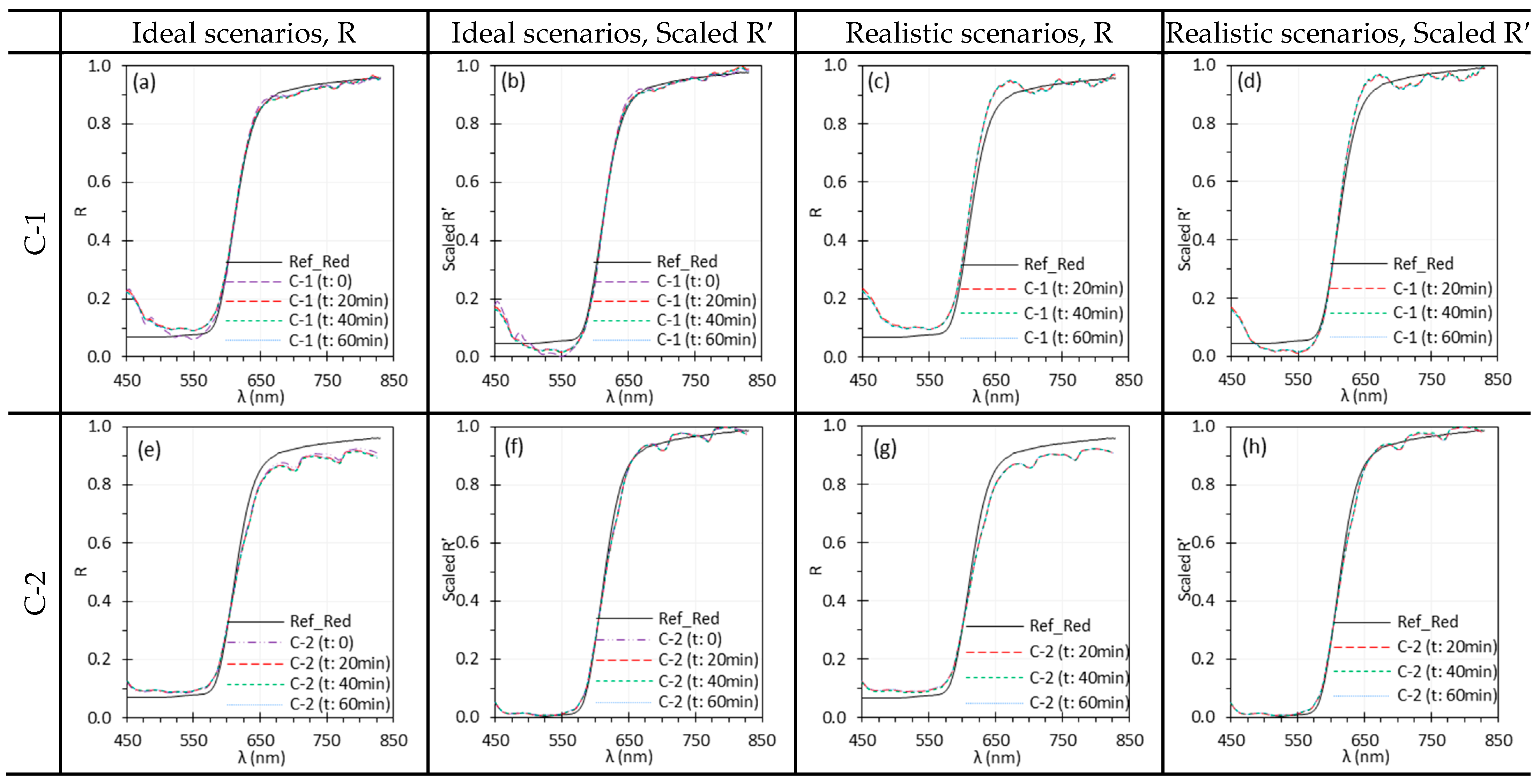
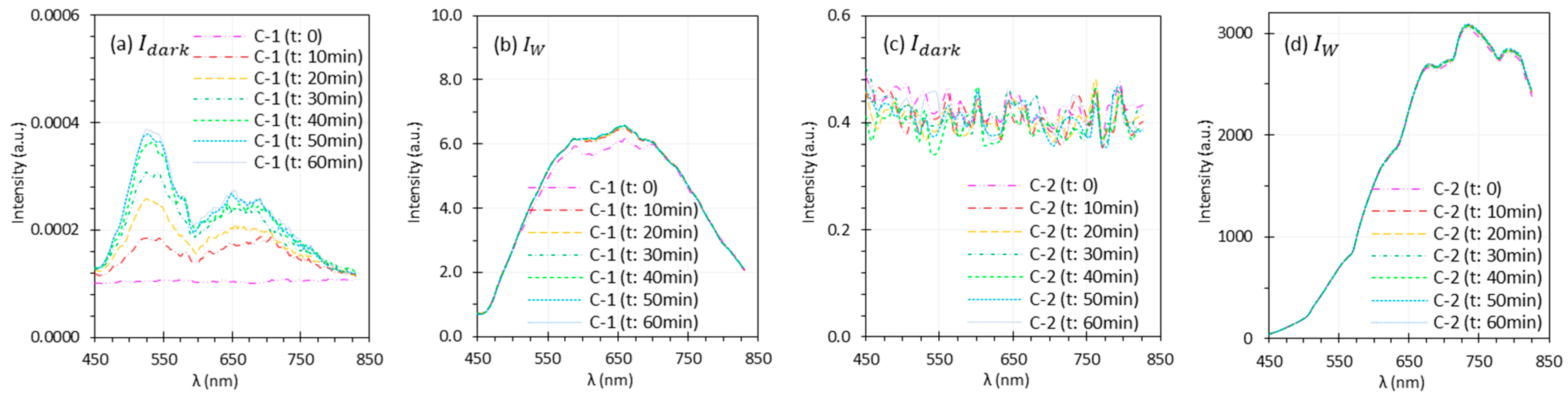
3.3. Camera Warm-Up Time
3.4. Spatial and Temporal Averaging
3.5. Camera Focus
3.6. Working Distance
3.7. Illumination Angle
3.8. Target Angle
3.9. Measurement Repeatability
4. Discussion
4.1. HSI Technologies
4.2. Illumination Spectra
4.3. Spectral Noise
4.4. Focus and Working Distance
4.5. Illumination and Target Angles
4.6. Normalization Methods
4.7. Study Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Characteristics | C-1 | C-2 | |
|---|---|---|---|
| Spectral | Spectral range (nm) | 400–1000 | 450–850 |
| Number of spectral bands/channels | Up to 301 | 51 | |
| Spectral sampling interval (nm) | 2–50 * | 8 | |
| Spectral response function (SRF) peak width | ~4 nm | 26 nm @ 532 nm | |
| Spectral accuracy | ±0.6 nm RMSE | - | |
| Spatial | Number of output pixels per band | 1936 × 1216 | 290 × 275 |
| Field of view | 15° | 15° | |
| Temporal | Exposure time (ms) | 0.1–1000 | 0.1–60,000 |
| Hypercube rate | One hypercube/~2.5 min (500 ms exposure, 301 bands) ** | Maximum 15 Hz | |
| Other | Bit depth (bits) | 8 or 16 | 12 |
| Dimensions (mm) | 78 × 81 × 198 | 29 × 29 × 107 | |
| Weight (g) | 1247 | 176 | |
| Operating temperature (°C) | 15–40 | - | |
| Pixel size (µm) | 5.86 | 3.45 |
| Parameters | Exposure Time (ms) | WD (mm) | ||||||
|---|---|---|---|---|---|---|---|---|
| C-1 | E-1 | C-2 | E-2 | C-1 | E-1 | C-2 | E-2 | |
| Ambient light | 375 | 500 | 85 | 100 | 150 | 10 | 88 | 10 |
| Exposure time | 125, 250, 375, 500 | 125, 250, 375, 500 | 25, 50, 75, 100 | 50, 100, 150,200 | 150 | 10 | 100 | 10 |
| Camera warm-up time | 600 | - | 85 | - | 150 | - | 87 | - |
| Spatial and temporal averaging | - | 500 | - | 200 | - | 10 | - | 10 |
| Camera focus | 375 | 500 | 85 | 200 | 150 | 10 | 88 | 10 |
| WD | 375 | 500 | 70 | 200 | 150 ± 15 | 10 ± 4 | 90 ± 15 | 10 ± 4 |
| 500 | - | 200 | - | 140 | - | 92 | - | |
| 350 | 500 | 85 | 100 | 161 | 15 | 85 | 13 | |
References
- Fu, Z.; Jin, Z.; Zhang, C.; He, Z.; Zha, Z.; Hu, C.; Gan, T.; Yan, Q.; Wang, P.; Ye, X. The future of endoscopic navigation: A review of advanced endoscopic vision technology. IEEE Access 2021, 9, 41144–41167. [Google Scholar] [CrossRef]
- Boese, A.; Wex, C.; Croner, R.; Liehr, U.B.; Wendler, J.J.; Weigt, J.; Walles, T.; Vorwerk, U.; Lohmann, C.H.; Friebe, M.; et al. Endoscopic Imaging Technology Today. Diagnostics 2022, 12, 1262. [Google Scholar] [CrossRef]
- Bedard, N.; Pierce, M.; El-Naggar, A.; Anandasabapathy, S.; Gillenwater, A.; Richards-Kortum, R. Emerging roles for multimodal optical imaging in early cancer detection: A global challenge. Technol. Cancer Res. Treat. 2010, 9, 211–217. [Google Scholar] [CrossRef] [PubMed]
- Le, V.N.D.; Wang, Q.; Gould, T.; Ramella-Roman, J.C.; Pfefer, T.J. Vascular contrast in narrow-band and white light imaging. Appl. Opt. 2014, 53, 4061–4071. [Google Scholar] [CrossRef]
- Fang, Y.-J.; Huang, C.-W.; Karmakar, R.; Mukundan, A.; Tsao, Y.-M.; Yang, K.-Y.; Wang, H.-C. Assessment of Narrow-Band Imaging Algorithm for Video Capsule Endoscopy Based on Decorrelated Color Space for Esophageal Cancer: Part II, Detection and Classification of Esophageal Cancer. Cancers 2024, 16, 572. [Google Scholar] [CrossRef]
- Frimberger, D.; Zaak, D.; Stepp, H.; Knuchel, R.; Baumgartner, R.; Schneede, P.; Schmeller, N.; Hofstetter, A. Autofluorescence imaging to optimize 5-ALA-induced fluorescence endoscopy of bladder carcinoma. Urology 2001, 58, 372–375. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.M.; Cable, M.L.; Hook, S.J.; Green, R.O.; Ustin, S.L.; Mandl, D.J.; Middleton, E.M. An introduction to the NASA Hyperspectral InfraRed Imager (HyspIRI) mission and preparatory activities. Remote Sens. Environ. 2015, 167, 6–19. [Google Scholar] [CrossRef]
- Özdoğan, G.; Lin, X.; Sun, D.-W. Rapid and noninvasive sensory analyses of food products by hyperspectral imaging: Recent application developments. Trends Food Sci. Technol. 2021, 111, 151–165. [Google Scholar] [CrossRef]
- Li, Q.; He, X.; Wang, Y.; Liu, H.; Xu, D.; Guo, F. Review of spectral imaging technology in biomedical engineering: Achievements and challenges. J. Biomed. Opt. 2013, 18, 100901. [Google Scholar] [CrossRef]
- Abdlaty, R.; Sahli, S.; Hayward, J.; Fang, Q. Hyperspectral imaging: Comparison of acousto-optic and liquid crystal tunable filters. Proc. SPIE 2018, 10537, 105732P. [Google Scholar] [CrossRef]
- Hernández, G. Fabry-Perot Interferometers; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Mehta, N.; Shaik, S.; Devireddy, R.; Gartia, M.R. Single-Cell Analysis Using Hyperspectral Imaging Modalities. J. Biomech. Eng. 2018, 140, 0208021–02080216. [Google Scholar] [CrossRef]
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 010901. [Google Scholar] [CrossRef]
- Collins, T.; Bencteux, V.; Benedicenti, S.; Moretti, V.; Mita, M.T.; Barbieri, V.; Rubichi, F.; Altamura, A.; Giaracuni, G.; Marescaux, J. Automatic optical biopsy for colorectal cancer using hyperspectral imaging and artificial neural networks. Surg. Endosc. 2022, 36, 8549–8559. [Google Scholar] [CrossRef] [PubMed]
- Hadoux, X.; Hui, F.; Lim, J.K.; Masters, C.L.; Pébay, A.; Chevalier, S.; Ha, J.; Loi, S.; Fowler, C.J.; Rowe, C. Non-invasive in vivo hyperspectral imaging of the retina for potential biomarker use in Alzheimer’s disease. Nat. Commun. 2019, 10, 4227. [Google Scholar] [CrossRef] [PubMed]
- Saiko, G.; Lombardi, P.; Au, Y.; Queen, D.; Armstrong, D.; Harding, K. Hyperspectral imaging in wound care: A systematic review. Int. Wound J. 2020, 17, 1840–1856. [Google Scholar] [CrossRef]
- Barberio, M.; Benedicenti, S.; Pizzicannella, M.; Felli, E.; Collins, T.; Jansen-Winkeln, B.; Marescaux, J.; Viola, M.G.; Diana, M. Intraoperative guidance using hyperspectral imaging: A review for surgeons. Diagnostics 2021, 11, 2066. [Google Scholar] [CrossRef]
- Yoon, J. Hyperspectral imaging for clinical applications. BioChip J. 2022, 16, 1–12. [Google Scholar] [CrossRef]
- Mun, N.E.; Tran, T.K.C.; Park, D.H.; Im, J.H.; Park, J.I.; Le, T.D.; Moon, Y.J.; Kwon, S.-Y.; Yoo, S.W. Endoscopic Hyperspectral Imaging System to Discriminate Tissue Characteristics in Tissue Phantom and Orthotopic Mouse Pancreatic Tumor Model. Bioengineering 2024, 11, 208. [Google Scholar] [CrossRef]
- Stergar, J.; Hren, R.; Milanič, M. Design and validation of a custom-made laboratory hyperspectral imaging system for biomedical applications using a broadband LED light source. Sensors 2022, 22, 6274. [Google Scholar] [CrossRef]
- Qiu, K.; Chen, W.; Zhou, H.; Wang, C.; Cui, Z. Evaluation of the color measurement based on a microscopic hyperspectral imaging system. Color Res. Appl. 2021, 46, 1205–1217. [Google Scholar] [CrossRef]
- Gebhart, S.C.; Thompson, R.C.; Mahadevan-Jansen, A. Liquid-crystal tunable filter spectral imaging for brain tumor demarcation. Appl. Opt. 2007, 46, 1896–1910. [Google Scholar] [CrossRef] [PubMed]
- Lodhi, V.; Chakravarty, D.; Mitra, P. Hyperspectral Imaging System: Development Aspects and Recent Trends. Sens. Imaging 2019, 20, 35. [Google Scholar] [CrossRef]
- Zahavi, A.; Palshin, A.; Liyanage, D.C.; Tamre, M. Influence of Illumination Sources on Hyperspectral Imaging. In Proceedings of the 2019 20th International Conference on Research and Education in Mechatronics (REM), Wels, Austria, 23–24 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Mazdeyasna, S.; Arefin, M.S.; Fales, A.; Leavesley, S.J.; Pfefer, T.J.; Wang, Q. Evaluating Normalization Methods for Robust Spectral Performance Assessments of Hyperspectral Imaging Cameras. Biosensors 2025, 15, 20. [Google Scholar] [CrossRef]
- Genangeli, A.; Avola, G.; Bindi, M.; Cantini, C.; Cellini, F.; Riggi, E.; Gioli, B. A Novel Correction Methodology to Improve the Performance of a Low-Cost Hyperspectral Portable Snapshot Camera. Sensor 2023, 23, 9685. [Google Scholar] [CrossRef]
- Gómez Manzanares, Á.; Vázquez Moliní, D.; Alvarez Fernandez-Balbuena, A.; Mayorga Pinilla, S.; Martínez Antón, J.C. Measuring high dynamic range spectral reflectance of artworks through an image capture matrix hyperspectral camera. Sensors 2022, 22, 4664. [Google Scholar] [CrossRef]
- Rahkonen, S.; Lind, L.; Raita-Hakola, A.-M.; Kiiskinen, S.; Pölönen, I. Reflectance measurement method based on sensor fusion of frame-based hyperspectral imager and time-of-flight depth camera. Sensors 2022, 22, 8668. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Yoon, J. Assessment of angle-dependent spectral distortion to develop accurate hyperspectral endoscopy. Sci. Rep. 2022, 12, 11892. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37–R61. [Google Scholar] [CrossRef]
- Yoon, J.; Grigoroiu, A.; Bohndiek, S.E. A background correction method to compensate illumination variation in hyperspectral imaging. PLoS ONE 2020, 15, e0229502. [Google Scholar] [CrossRef]
- Pan, B.; Zhang, X.; Lv, Y.; Yu, L. Automatic optimal camera exposure time control for digital image correlation. Meas. Sci. Technol. 2022, 33, 105205. [Google Scholar] [CrossRef]
- Mazdeyasna, S.; Huang, C.; Zhao, M.; Agochukwu, N.B.; Bahrani, A.A.; Wong, L.; Yu, G. Noncontact speckle contrast diffuse correlation tomography of blood flow distributions in tissues with arbitrary geometries. J. Biomed. Opt. 2018, 23, 096005. [Google Scholar] [CrossRef] [PubMed]
- Taylor, B.N.; Kuyatt, C.E. NIST Technical Note 1297: Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1994.
- IEEE P4001; Draft Standard for Characterization and Calibration of Ultraviolet through Shortwave Infrared (250 nm to 2500 nm) Hyperspectral Imaging Devices. Institute of Electrical and Electronics Engineers: New York, NY, USA, 2025.
- Paulus, S.; Mahlein, A.-K. Technical workflows for hyperspectral plant image assessment and processing on the greenhouse and laboratory scale. GigaScience 2020, 9, giaa090. [Google Scholar] [CrossRef]
- IEC 62471; Photobiological Safety of Lamps and Lamp Systems. International Electrotechnical Commission: Geneva, Switzerland, 2006.
- IEC 60825-1; Safety of Laser Products—Part 1: Equipment Classification and Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2014.
- ANSI Z136.1; American National Standard for Safe Use of Lasers. Laser Institute of America: Orlando, FL, USA, 2022.
- Abel, E.W.; Fotiadis, N.; White, P.S. Light intensity distribution in images from rigid endoscopes used in minimal access sinus surgery. Laryngoscope Investig. Otolaryngol. 2021, 6, 1283–1288. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, W.-C.; Suresh, N.; Hua, H. Development of the local magnification method for quantitative evaluation of endoscope geometric distortion. J. Biomed. Opt. 2016, 21, 056003. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Tran, C.; Burns, P.; Namazi, N.M. Best Practices for Measuring the Modulation Transfer Function of Video Endoscopes. Sensors 2024, 24, 5075. [Google Scholar] [CrossRef] [PubMed]
- Waterhouse, D.J.; Borsetto, D.; Santarius, T.; Tysome, J.R.; Bohndiek, S.E. First-in-human pilot study of snapshot multispectral endoscopy for delineation of pituitary adenoma. J. Biomed. Opt. 2025, 30, 056002. [Google Scholar] [CrossRef]
- Ghassemi, P.; Wang, J.; Melchiorri, A.J.; Ramella-Roman, J.C.; Mathews, S.A.; Coburn, J.C.; Sorg, B.S.; Chen, Y.; Pfefer, T.J. Rapid prototyping of biomimetic vascular phantoms for hyperspectral reflectance imaging. J. Biomed. Opt. 2015, 20, 121312. [Google Scholar] [CrossRef] [PubMed]
- Rinnan, Å.; Berg, F.v.d.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Janesick, J.R. CCD transfer method: Standard for absolute performance of CCDs and digital CCD camera systems. Proc. SPIE 1997, 3019, 70–102. [Google Scholar] [CrossRef]
- Weigert, M.; Schmidt, U.; Boothe, T.; Muller, A.; Dibrov, A.; Jain, A.; Wilhelm, B.; Schmidt, D.; Broaddus, C.; Culley, S.; et al. Content-aware image restoration: Pushing the limits of fluorescence microscopy. Nat. Methods 2018, 15, 1090–1097. [Google Scholar] [CrossRef]
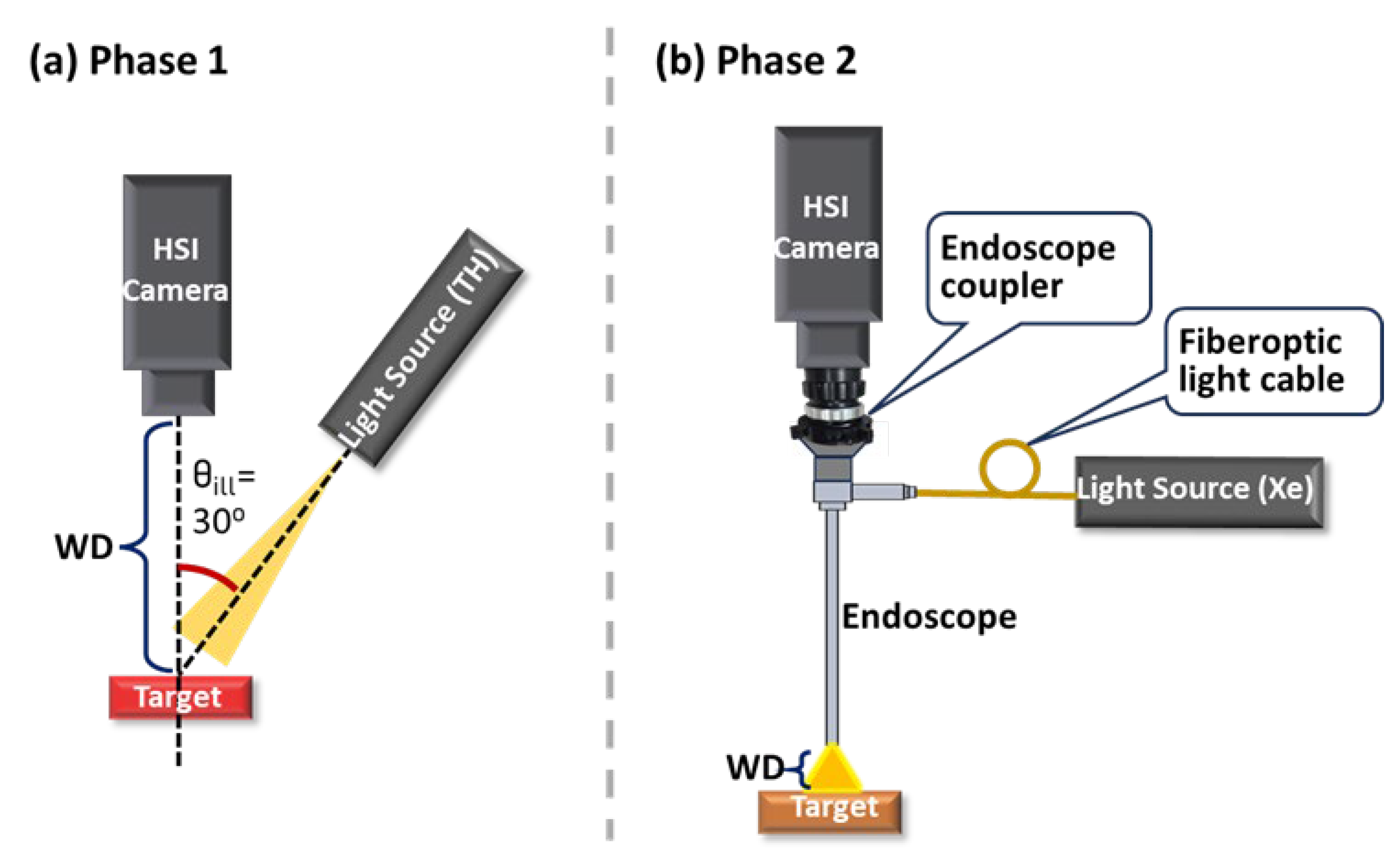
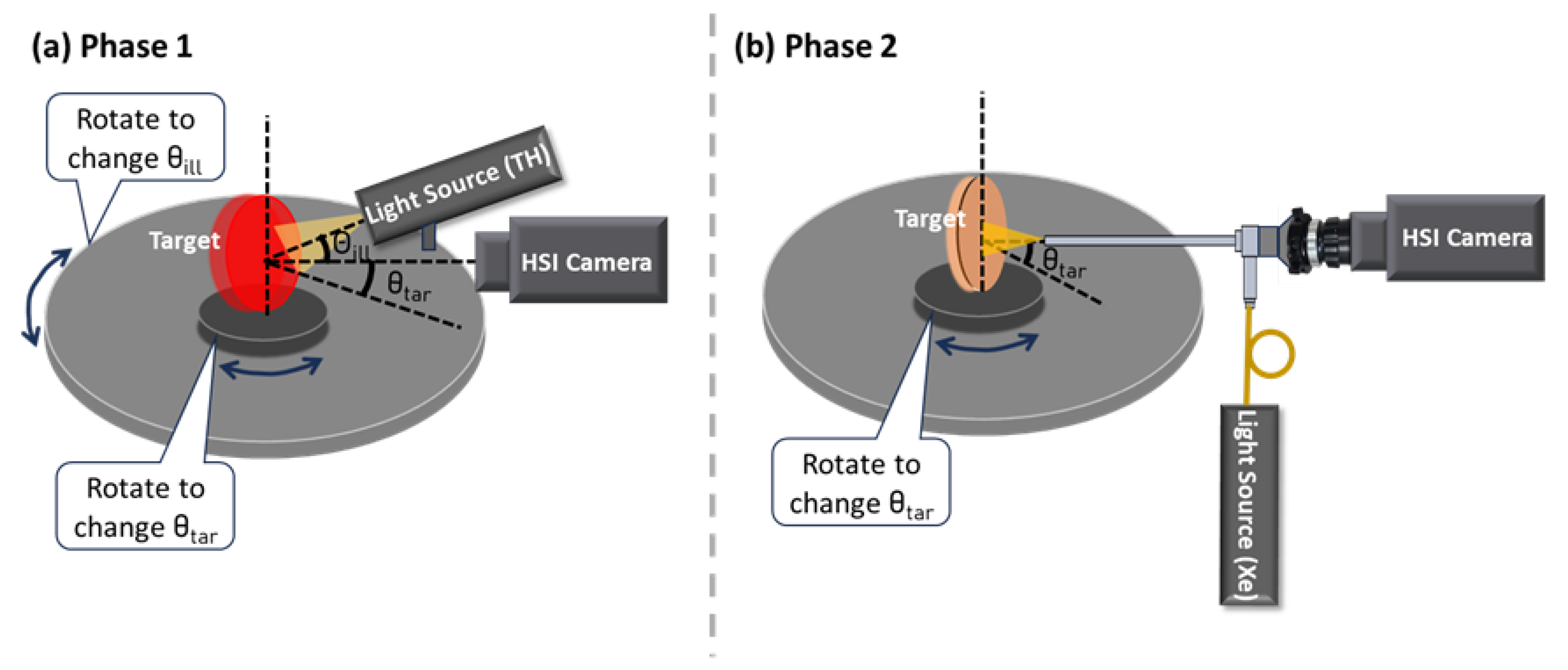



| Components | Abbreviation | Models | Functions and Specifications |
|---|---|---|---|
| HSI cameras (HSICs) | C-1 | 4250 VNIR | Spectral scanning with a Fabry–Perot Interferometer (FPI), coupled with a customized manual zoom lens |
| C-2 | Ultris SR5 | Snapshot imaging, using a linear variable filter (LVF), coupled with a customized manual zoom Lens. | |
| Rigid endoscope | - | 502-537-010 | The main component of an HSIE. Designed for fluorescence imaging, with good transmission within near-infrared range. |
| Endoscope coupler | - | 8020I | 22.5–50 mm parfocal zoom, connecting C-1 or C-2 to the rigid endoscope. |
| Light sources | Xe | Dyonics 300XL | Xenon light source coupled to E-1 and E-2 by default. |
| TH | SLS201 | Tungsten halogen light source for C-1 and C-2 by default. | |
| HSI endoscopes (HSIEs) | E-1 | - | Combination of C-1, the rigid endoscope, the endoscope coupler, and the Xe. |
| E-2 | - | Combination of C-2, the rigid endoscope, the endoscope coupler, and the Xe. | |
| Targets | White | SRT-99-100 | White Spectralon® diffuse reflectance target (99% reflectance across a wide spectral range). To measure in Equation (1). |
| Red | SCS-RD-010 | Red Spectralon® diffuse reflectance target, for C-1 and C-2 by default. To measure in Equation (1). | |
| EO | WCS-EO-010 | Spectralon® wavelength calibration target with erbium oxide (EO), for E-1 and E-2 by default. To measure in Equation (1). |
| Parameters | Ambient Light | Exposure Time | Camera Warm-Up Time | Spatial & Temporal Averaging | Camera Focus | WD | Measurement Repeatability | ||
|---|---|---|---|---|---|---|---|---|---|
| Phase 1: C-1 and C-2 | √ | √ | √ | - | √ | √ | √ | √ | - |
| Phase 2: E-1 and E-2 | √ | √ | - | √ | √ | √ | - | √ | √ |
| ROI Size (Pixels) | E-1, Single | E-1, Average | E-2, Single | E-2, Average |
|---|---|---|---|---|
| 2 × 2 | 0.089 | 0.084 | 0.090 | 0.086 |
| E-1:200 × 200/E-2:80 × 80 | 0.048 | 0.035 | 0.083 | 0.082 |
| Parameters | Effects | Considerations |
|---|---|---|
| Illumination spectrum (light source + ambient light) | Illumination spectrum can significantly impact spectral accuracy, especially for HSI systems with high spectral resolution. TH light sources offer smooth but weak light at short wavelengths, while Xe light sources provide stronger light with sharp peaks that can introduce artifacts. Ambient light with spectral peaks, though dimmer, can also distort spectra. | An ideal light source for HSI exhibits spectrally uniform output with sufficient intensity. Reduce or eliminate ambient light and assure the source does not contain sharp spectral peaks. and should be acquired under illumination whose spectra overlap after normalization. |
| Exposure time | Insufficient exposure, which may result from low scene radiance or short exposure time, can lead to elevated noise levels due to low SNR. This issue is particularly pertinent in HSI systems with high spectral resolution (e.g., E-1). While normalization can reduce spectral differences across exposure settings, it cannot compensate for the increased noise under low exposure conditions. | Illuminate the target with sufficient intensity and use an adequate exposure time without saturation to capture high-quality reflectance spectra; apply normalization to mitigate low exposure effects. |
| Camera warm-up time | C-1 showed significant and changes during warm-up, with sensor temperature rising from 30.5 °C to 54.3 °C, causing artifacts in reflectance spectra. In contrast, C-2 had minimal temperature change (39 °C to 42 °C) and relatively stable performance. | Sufficient warm-up time is critical for stable spectral performance, especially for HSI systems with large thermal drift. The required warm-up time may vary by system. Validate for each system to ensure accurate reflectance measurements. |
| Spatial and temporal averaging | Spatial averaging using a large ROI significantly reduced spectral noise, particularly for C-1 and E-1, but may compromise spatial resolution. Temporal averaging offered only modest noise reduction and can reduce scanning speed. | Match the ROI size to the feature size in realistic scenarios. Use a large ROI only if the target is mostly homogenous and lacks fine spatial detail. Avoid temporal averaging in bench tests if the realistic applications involve dynamic targets/tissue. |
| Camera focus | Slight defocus had little impact on reflectance spectra and can even slightly reduce noise for a uniform target. However, defocus compromises spatial resolution. Small discrepancies can be mitigated by normalization. | Proper focus is important for preserving spatial resolution. In clinical imaging, precise focus is needed for fine structures, while slight defocus may be acceptable for larger, uniform areas. Apply normalization to mitigate defocus effects. |
| WD | For HSI systems without autofocus feature, WD changes affect both spatial resolution and illumination intensity. Under realistic conditions, WD changes significantly affected spectra across all tested systems, though normalization largely mitigated the differences, preserving peak locations. | Maintain a relatively consistent WD if possible. Apply normalization to mitigate the effects of WD change. |
| and | Changes in and affect irradiance uniformity and scene radiance depending on the target’s BRDF, leading to spectral variations. Normalization can mitigate the spectral difference due to angle change. | Care is needed when imaging surfaces with variable BRDFs or uneven textures. Minimize oblique angles that may cause glare, shadows, or shading artifacts for accurate spectral measurements. Apply normalization to mitigate angle-induced variations. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazdeyasna, S.; Arefin, M.S.; Fales, A.; Leavesley, S.J.; Pfefer, T.J.; Wang, Q. Evaluating the Performance of Hyperspectral Imaging Endoscopes: Mitigating Parameters Affecting Spectral Accuracy. Biosensors 2025, 15, 738. https://doi.org/10.3390/bios15110738
Mazdeyasna S, Arefin MS, Fales A, Leavesley SJ, Pfefer TJ, Wang Q. Evaluating the Performance of Hyperspectral Imaging Endoscopes: Mitigating Parameters Affecting Spectral Accuracy. Biosensors. 2025; 15(11):738. https://doi.org/10.3390/bios15110738
Chicago/Turabian StyleMazdeyasna, Siavash, Mohammed Shahriar Arefin, Andrew Fales, Silas J. Leavesley, T. Joshua Pfefer, and Quanzeng Wang. 2025. "Evaluating the Performance of Hyperspectral Imaging Endoscopes: Mitigating Parameters Affecting Spectral Accuracy" Biosensors 15, no. 11: 738. https://doi.org/10.3390/bios15110738
APA StyleMazdeyasna, S., Arefin, M. S., Fales, A., Leavesley, S. J., Pfefer, T. J., & Wang, Q. (2025). Evaluating the Performance of Hyperspectral Imaging Endoscopes: Mitigating Parameters Affecting Spectral Accuracy. Biosensors, 15(11), 738. https://doi.org/10.3390/bios15110738





