A Novel Approach to Monitor the Concentration of Phosphate Buffers in the Range of 1 M to 0.1 M Using a Silicon-Based Impedance Sensor
Abstract
:1. Introduction
2. Materials and Methods
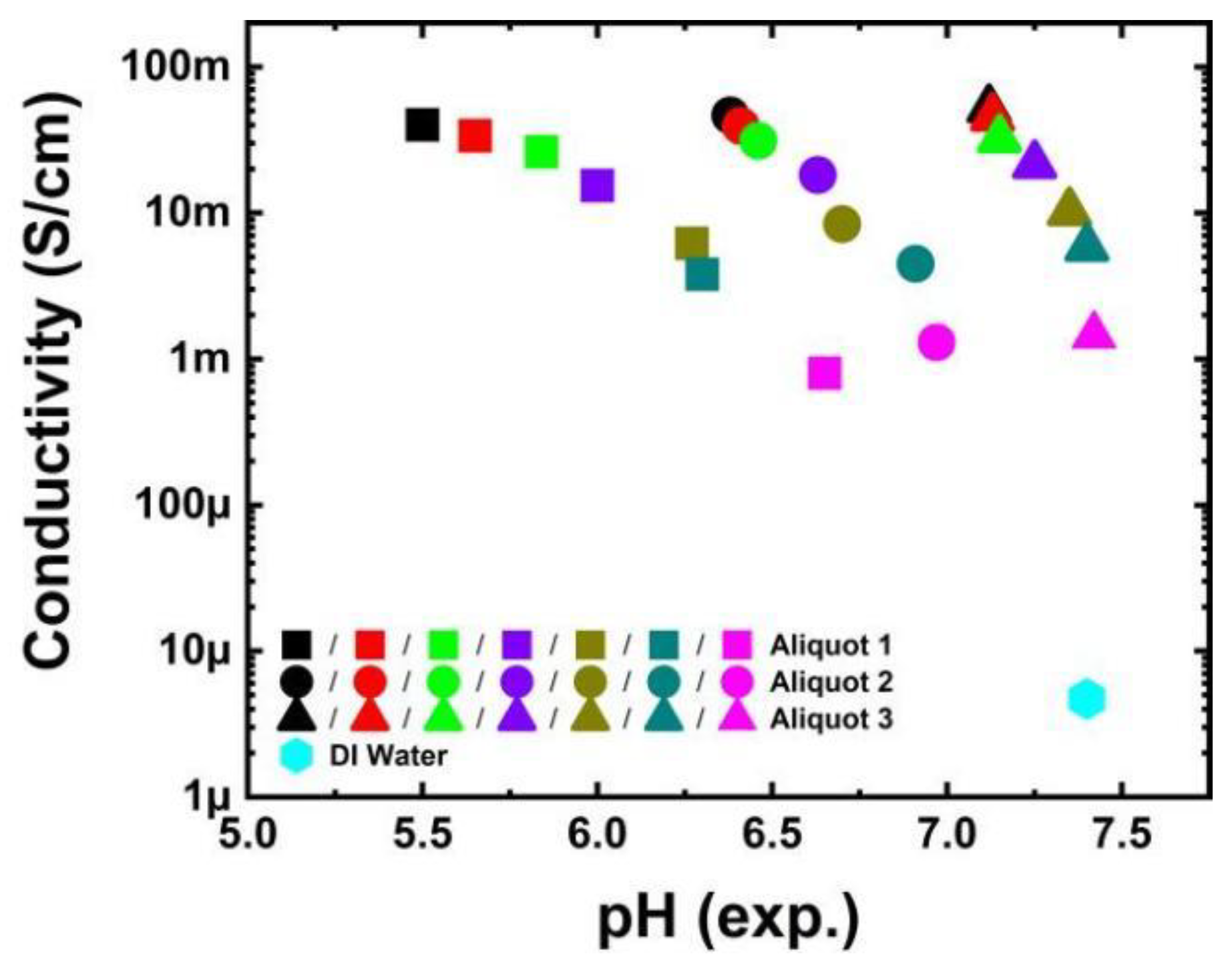
2.1. Sodium Phosphate Buffer Preparation and Characterization
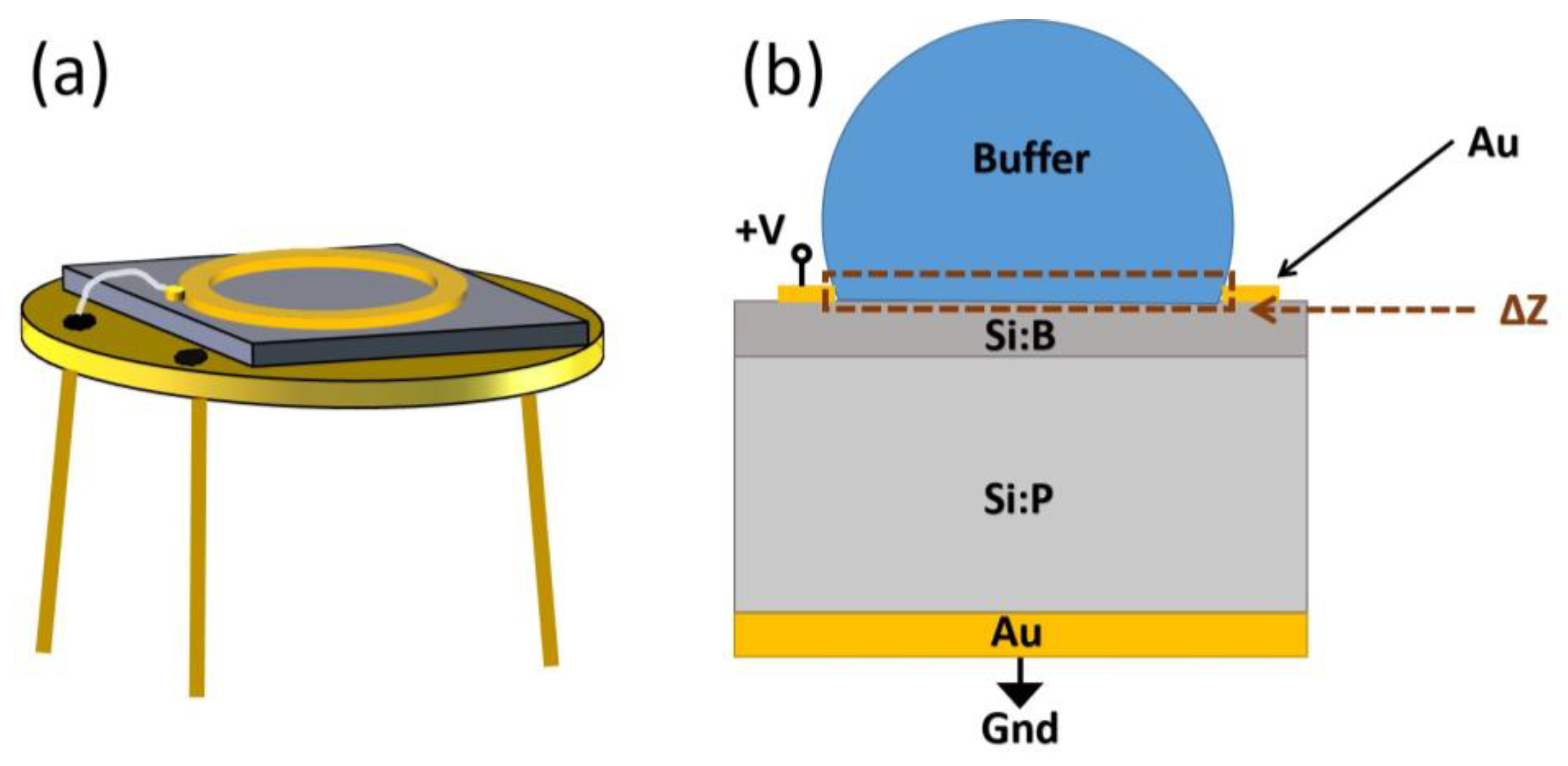
2.2. Silicon-Based Impedance Sensor
2.3. Impedance Spectroscopy
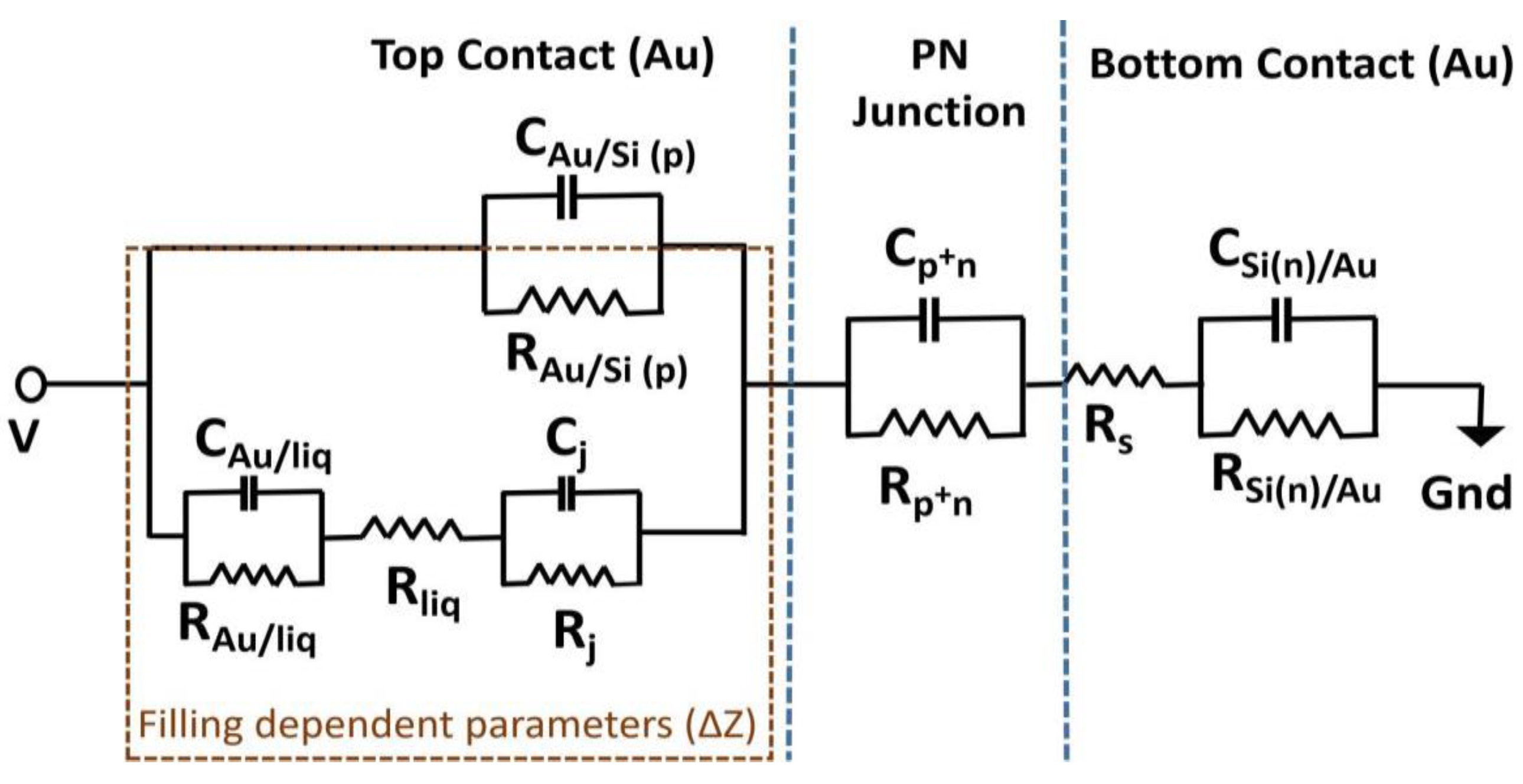
2.4. Impedance Modeling
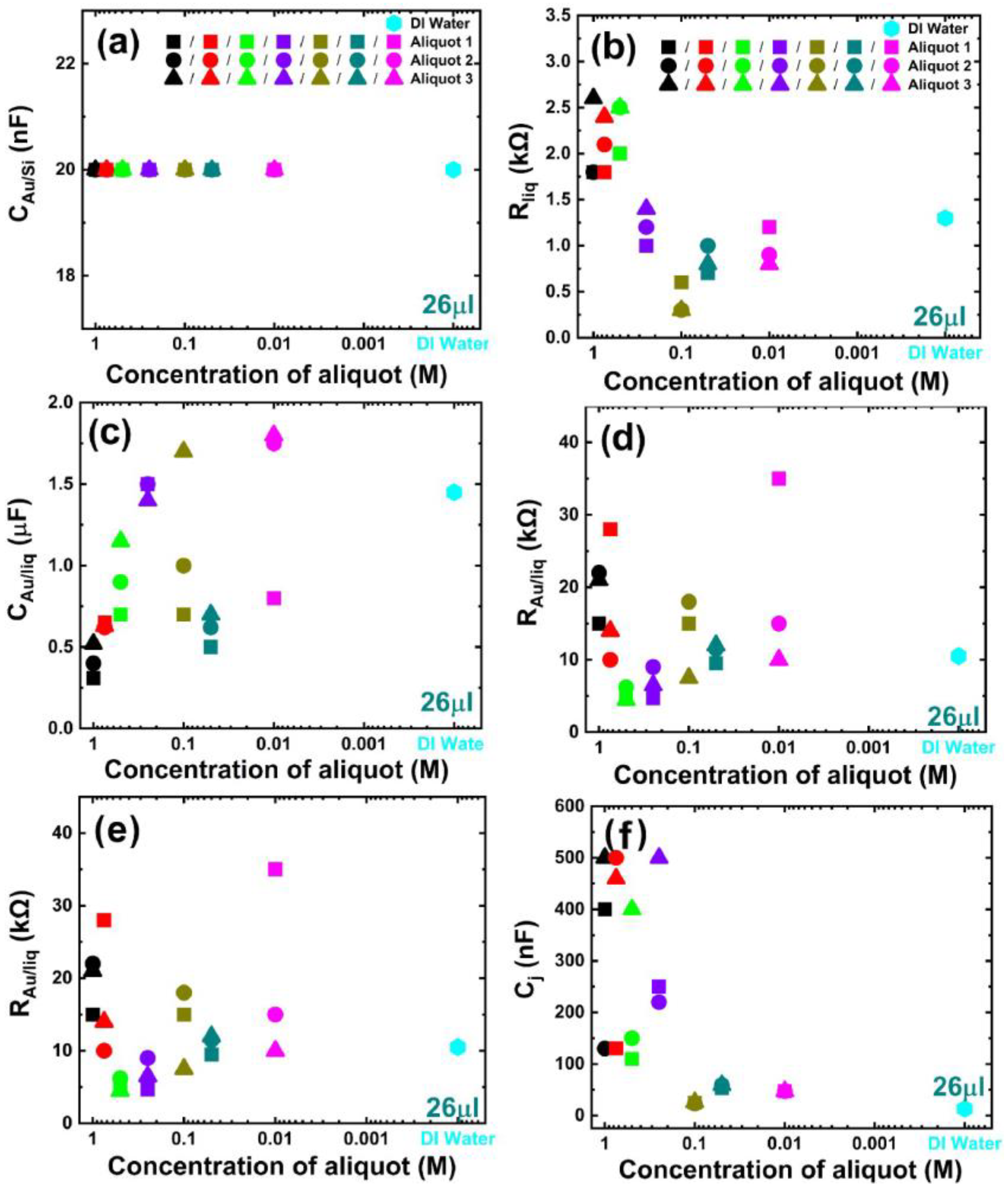
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
| 26 μL | Top Contact | p+n Junction | Bottom Contact | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CAu/liq (μF) | RAu/liq (kΩ) | Cj (nF) | Rj (kΩ) | Rliq (kΩ) | CAu/Si(p+) (nF) | RAu/Si(p+) (kΩ) | Cp+n (nF) | Rp+n (kΩ) | Rs (Ω) | CSi(n)/Au (nF) | RSi(n)/Au (Ω) | |
| Aliquot 1 | ||||||||||||
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 25.70 | 7.00 | 17.00 | 14.00 |
| 1.00 M | 0.31 | 15.00 | 400.00 | 2.20 | 1.80 | 20.00 | 12.00 | 8.00 | 27.30 | 8.00 | 17.00 | 26.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 25.70 | 7.00 | 17.00 | 14.00 |
| 0.75 M | 0.65 | 28.00 | 130.00 | 10.50 | 1.80 | 20.00 | 14.00 | 9.00 | 24.80 | 8.00 | 15.00 | 29.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 28.00 | 7.00 | 17.00 | 14.00 |
| 0.50 M | 0.70 | 5.20 | 110.00 | 7.50 | 2.00 | 20.00 | 17.00 | 6.70 | 27.80 | 8.00 | 16.00 | 29.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 8.00 | 5.80 | 23.40 | 6.00 | 16.00 | 15.00 |
| 0.25 M | 1.50 | 4.70 | 250.00 | 6.00 | 1.00 | 20.00 | 21.00 | 8.70 | 25.40 | 8.00 | 10.00 | 53.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 25.70 | 7.00 | 17.00 | 14.00 |
| 0.10 M | 0.70 | 15.00 | 25.00 | 2.80 | 0.60 | 20.00 | 25.00 | 12.00 | 25.80 | 9.00 | 8.00 | 55.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 15.55 | 7.00 | 17.00 | 14.00 |
| 0.05 M | 0.50 | 9.50 | 53.00 | 8.80 | 0.70 | 20.00 | 26.00 | 10.20 | 16.90 | 7.00 | 11.00 | 80.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 18.00 | 7.00 | 17.00 | 14.00 |
| 0.01 M | 0.80 | 35.0 | 47.00 | 11.80 | 1.20 | 20.00 | 26.00 | 12.00 | 19.00 | 7.00 | 11.00 | 80.00 |
| 26 μL | Top Contact | p+n Junction | Bottom Contact | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CAu/liq (μF) | RAu/liq (kΩ) | Cj (nF) | Rj (kΩ) | Rliq (kΩ) | CAu/Si(p+) (nF) | RAu/Si(p+) (kΩ) | Cp+n (nF) | Rp+n (kΩ) | Rs (Ω) | CSi(n)/Au (nF) | RSi(n)/Au (Ω) | |
| Aliquot 2 | ||||||||||||
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 25.60 | 7.00 | 17.00 | 14.00 |
| 1.00 M | 0.40 | 22.00 | 130.00 | 10.20 | 1.80 | 20.00 | 12.00 | 8.00 | 24.60 | 8.00 | 21.00 | 28.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 25.60 | 7.00 | 17.00 | 14.00 |
| 0.75 M | 0.62 | 10.00 | 500.00 | 3.50 | 2.10 | 20.00 | 14.00 | 9.20 | 27.10 | 9.00 | 15.00 | 23.00 |
| Empty | 20.00 | 0.30 | 170.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 25.60 | 7.00 | 17.00 | 14.00 |
| 0.50 M | 0.90 | 6.20 | 150.00 | 6.50 | 2.50 | 20.00 | 17.00 | 8.20 | 26.30 | 8.00 | 16.00 | 29.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.30 | 16.00 | 8.00 | 5.90 | 22.90 | 6.00 | 16.00 | 15.00 |
| 0.25 M | 1.50 | 9.00 | 220.00 | 6.50 | 1.20 | 20.00 | 21.00 | 9.50 | 24.20 | 8.00 | 10.00 | 33.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 25.70 | 7.00 | 17.00 | 14.00 |
| 0.10 M | 1.00 | 18.00 | 23.00 | 2.80 | 0.30 | 20.00 | 25.00 | 12.00 | 26.90 | 9.00 | 10.00 | 35.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 15.55 | 7.00 | 17.00 | 14.00 |
| 0.05 M | 0.60 | 11.50 | 59.00 | 5.20 | 1.00 | 20.00 | 25.00 | 12.10 | 16.00 | 7.00 | 8.00 | 50.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 18.00 | 7.00 | 17.00 | 14.00 |
| 0.01 M | 1.75 | 15.00 | 47.00 | 11.50 | 0.90 | 20.00 | 26.00 | 12.50 | 18.60 | 7.00 | 13.00 | 52.00 |
| 26 μL | Top Contact | p+n Junction | Bottom Contact | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CAu/liq (μF) | RAu/liq (kΩ) | Cj (nF) | Rj (kΩ) | Rliq (kΩ) | CAu/Si(p+) (nF) | RAu/Si(p+) (kΩ) | Cp+n (nF) | Rp+n (kΩ) | Rs (Ω) | CSi(n)/Au (nF) | RSi(n)/Au (Ω) | |
| Aliquot 3 | ||||||||||||
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 24.40 | 7.00 | 17.00 | 14.00 |
| 1.00 M | 0.52 | 21.00 | 500.00 | 6.50 | 2.60 | 20.00 | 12.00 | 10.60 | 24.80 | 9.00 | 17.00 | 18.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 24.40 | 7.00 | 17.00 | 14.00 |
| 0.75 M | 0.63 | 14.00 | 460.00 | 3.90 | 2.40 | 20.00 | 14.00 | 10.30 | 25.20 | 8.00 | 15.00 | 33.00 |
| Empty | 20.00 | 0.30 | 170.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 25.40 | 7.00 | 17.00 | 14.00 |
| 0.50 M | 1.15 | 4.50 | 400.00 | 4.80 | 2.50 | 20.00 | 17.00 | 9.60 | 26.30 | 8.00 | 16.00 | 48.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.30 | 16.00 | 8.00 | 5.90 | 22.70 | 6.00 | 16.00 | 15.00 |
| 0.25 M | 1.40 | 6.50 | 500.00 | 5.00 | 1.40 | 20.00 | 21.00 | 10.50 | 23.60 | 8.00 | 12.00 | 34.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 25.70 | 7.00 | 17.00 | 14.00 |
| 0.10 M | 1.70 | 7.50 | 26.00 | 2.80 | 0.30 | 20.00 | 25.00 | 12.30 | 26.60 | 9.00 | 10.00 | 50.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 15.55 | 7.00 | 17.00 | 14.00 |
| 0.05 M | 0.70 | 12.00 | 59.00 | 5.20 | 0.80 | 20.00 | 25.00 | 11.80 | 17.00 | 7.00 | 8.00 | 80.00 |
| Empty | 20.00 | 0.30 | 160.00 | 2.80 | 2.25 | 16.00 | 11.00 | 5.90 | 18.00 | 7.00 | 17.00 | 14.00 |
| 0.01 M | 1.80 | 10.00 | 47.00 | 11.80 | 0.80 | 20.00 | 26.00 | 12.00 | 20.10 | 7.00 | 12.00 | 40.00 |
Appendix C
References
- Kim, N.A.; An, I.B.; Lim, D.G.; Lim, J.Y.; Lee, S.Y.; Shim, W.S.; Kang, N.G.; Jeong, S.H. Effects of pH and buffer concentration on the thermal stability of etanercept using DSC and DLS. Biol. Pharm. Bull. 2014, 37, 808–816. [Google Scholar] [CrossRef] [PubMed]
- Pavani, P.; Kumar, K.; Rani, A.; Venkatesu, P.; Lee, M.J. The influence of sodium phosphate buffer on the stability of various proteins: Insights into protein-buffer interactions. J. Mol. Liq. 2021, 331, 115753. [Google Scholar] [CrossRef]
- Uddin, M.; Mamun, A.; Kabir, M.D.; Setu, J.; Zaman, S.; Begum, Y.; Amran, M. Quality control tests for ophthalmic pharmaceuticals: Pharmacopoeial standards and specifications. J. Adv. Med. Pharm. Sci. 2017, 14, 1–17. [Google Scholar] [CrossRef]
- Keller, V.D.; Williams, R.J.; Lofthouse, C.; Johnson, A.C. Worldwide estimation of river concentrations of any chemical originating from sewage-treatment plants using dilution factors. Environ. Toxicol. Chem. 2014, 33, 447–452. [Google Scholar] [CrossRef] [PubMed]
- Link, M.; von der Ohe, P.C.; Voß, K.; Schäfer, R.B. Comparison of dilution factors for German wastewater treatment plant effluents in receiving streams to the fixed dilution factor from chemical risk assessment. Sci. Total. Environ. 2017, 598, 805–813. [Google Scholar] [CrossRef] [PubMed]
- Phibunwatthanawong, T.; Riddech, N. Liquid organic fertilizer production for growing vegetables under hydroponic condition. Int. J. Recycl. Org. Waste Agric. 2019, 8, 369–380. [Google Scholar] [CrossRef]
- Wen, H.; Jung, H.; Li, X. Drug delivery approaches in addressing clinical pharmacology-related issues: Opportunities and challenges. AAPS J. 2015, 17, 1327–1340. [Google Scholar] [CrossRef] [PubMed]
- Kowalska-Krochmal, B.; Dudek-Wicher, R. The minimum inhibitory concentration of antibiotics: Methods, interpretation, clinical relevance. Pathogens 2021, 10, 165. [Google Scholar] [CrossRef] [PubMed]
- Mantle, T.J.; Harris, D.A. Spectrophotometric assays. In Spectrophotometry and Spectrofluorimetry: A Practical Approach, Online ed.; Oxford University Press: Oxford, UK, 2000; pp. 183–208. [Google Scholar]
- Kozak, J.; Townshend, A. Titrimetry|Overview. In Encyclopedia of Analytical Science, 3rd ed.; Worsfold, P., Poole, C., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 111–120. [Google Scholar]
- Zachary, Y.; Rufus, L. The dilution method and concentration difference spectrophotometry: New designs for an old method. In Methods in Enzymology; Academic Press: Cambridge, MA, USA, 1979; Volume 61, pp. 65–96. [Google Scholar]
- De Caro, C.A.; Claudia, H. UV/VIS Spectrophotometry—Fundamentals and Applications; No. ME-30256131; Mettler-Toledo Publication: Schwerzenbach, Switzerland, 2015. [Google Scholar]
- Reule, A.G. Errors in spectrophotometry and calibration procedures to avoid them. J. Res. Natl. Bur. Standards. Sect. A Phys. Chem. 1976, 80, 609. [Google Scholar] [CrossRef]
- Jessica, G. Selecting the Right Volume to Measure Your Samples. Available online: www.biocompare.com/Bench-Tips/175408-Selecting-the-Right-Volume-to-Measure-Your-Samples/ (accessed on 24 June 2023).
- Hillerich, J.; Jürgen, P. Xylem Analytics Titration Handbook—Basics, Methods and Applications of Titration. 2018 Xylem Analytics, Germany. Available online: https://www.domagroup.eu/en/n/xylem-analytics-titration-handbook---basics-methods-and-applications-of-titration (accessed on 24 June 2023).
- Patterson, B.J. Automated in-line dilution—A QbD manufacturing method. J. GXP Compliance 2008, 12, 20–34. [Google Scholar]
- Kiani, M.; Du, N.; Vogel, M.; Raff, J.; Hübner, U.; Skorupa, I.; Bürger, D.; Schulz, S.E.; Schmidt, O.G.; Schmidt, H. PN junction-based Si biochips with ring electrodes for novel biosensing applications. Biosensors 2019, 9, 120. [Google Scholar] [CrossRef] [PubMed]
- Bhat, V.J.; Vegesna, S.V.; Kiani, M.; Zhao, X.; Blaschke, D.; Du, N.; Vogel, M.; Kluge, S.; Raff, J.; Hübner, U.; et al. Detecting Bacterial Cell Viability in Few µL Solutions from Impedance Measurements on Silicon-Based Biochips. Int. J. Mol. Sci. 2021, 22, 3541. [Google Scholar] [CrossRef] [PubMed]
- Poltorak, L.; Verheijden, M.L.; Bosma, D.; Jonkheijm, P.; De Smet, L.C.; Sudhölter, E.J. Lipid bilayers cushioned with polyelectrolyte-based films on doped silicon surfaces. Biochim. Biophys. Acta (BBA)-Biomembr. 2018, 1860, 2669–2680. [Google Scholar] [CrossRef] [PubMed]
- James, C.D.; Reuel, N.; Lee, E.S.; Davalos, R.V.; Mani, S.S.; Carroll-Portillo, A.; Rebeil, R.; Martino, A.; Apblett, C.A. Impedimetric and optical interrogation of single cells in a microfluidic device for real-time viability and chemical response assessment. Biosens. Bioelectron. 2008, 23, 845–851. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wong, C.C.; Pui, T.S.; Nadipalli, R.; Weerasekera, R.; Chandran, J.; Yu, H.; Rahman, A.R.A. CMOS high density electrical impedance biosensor array for tumor cell detection. Sens. Actuator B Chem. 2012, 173, 903–907. [Google Scholar] [CrossRef]
- Chaparro, C.V.; Herrera, L.V.; Meléndez, A.M.; Miranda, D.A. Considerations on electrical impedance measurements of electrolyte solutions in a four-electrode cell. J. Phys. Conf. Ser. 2016, 687, 012101. [Google Scholar] [CrossRef]


| 1 M NaH2PO4 (mL) | 1 M Na2HPO4 (mL) | pH (Experiment) |
|---|---|---|
| 80 | 20 | 5.50 (Aliquot 1) |
| 50 | 50 | 6.38 (Aliquot 2) |
| 20 | 80 | 7.12 (Aliquot 3) |
| Aliquot | Concentration of Aliquot (M) | pH (Experiment) DI Water pH 7.45 | pH (Experiment) DI Water pH 5.56 |
|---|---|---|---|
| Aliquot 1 | 1.00 | 5.50 | 5.67 |
| 0.75 | 5.65 | 5.76 | |
| 0.50 | 5.84 | 5.91 | |
| 0.25 | 6.00 | 6.10 | |
| 0.10 | 6.27 | 6.30 | |
| 0.05 | 6.30 | 6.40 | |
| 0.01 | 6.65 | 6.55 | |
| Aliquot 2 | 1.00 | 6.38 | 6.42 |
| 0.75 | 6.41 | 6.53 | |
| 0.50 | 6.46 | 6.61 | |
| 0.25 | 6.63 | 6.71 | |
| 0.10 | 6.70 | 6.89 | |
| 0.05 | 6.93 | 6.96 | |
| 0.01 | 6.97 | 7.15 | |
| Aliquot 3 | 1.00 | 7.12 | 7.18 |
| 0.75 | 7.13 | 7.31 | |
| 0.50 | 7.15 | 7.32 | |
| 0.25 | 7.25 | 7.40 | |
| 0.10 | 7.35 | 7.52 | |
| 0.05 | 7.40 | 7.59 | |
| 0.01 | 7.38 | 7.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhat, V.J.; Blaschke, D.; Müller, E.; Ehricht, R.; Schmidt, H. A Novel Approach to Monitor the Concentration of Phosphate Buffers in the Range of 1 M to 0.1 M Using a Silicon-Based Impedance Sensor. Biosensors 2023, 13, 841. https://doi.org/10.3390/bios13090841
Bhat VJ, Blaschke D, Müller E, Ehricht R, Schmidt H. A Novel Approach to Monitor the Concentration of Phosphate Buffers in the Range of 1 M to 0.1 M Using a Silicon-Based Impedance Sensor. Biosensors. 2023; 13(9):841. https://doi.org/10.3390/bios13090841
Chicago/Turabian StyleBhat, Vinayak J., Daniel Blaschke, Elke Müller, Ralf Ehricht, and Heidemarie Schmidt. 2023. "A Novel Approach to Monitor the Concentration of Phosphate Buffers in the Range of 1 M to 0.1 M Using a Silicon-Based Impedance Sensor" Biosensors 13, no. 9: 841. https://doi.org/10.3390/bios13090841
APA StyleBhat, V. J., Blaschke, D., Müller, E., Ehricht, R., & Schmidt, H. (2023). A Novel Approach to Monitor the Concentration of Phosphate Buffers in the Range of 1 M to 0.1 M Using a Silicon-Based Impedance Sensor. Biosensors, 13(9), 841. https://doi.org/10.3390/bios13090841





