An ML-Based Approach to Reconstruct Heart Rate from PPG in Presence of Motion Artifacts
Abstract
1. Introduction
Background
2. Materials and Methods
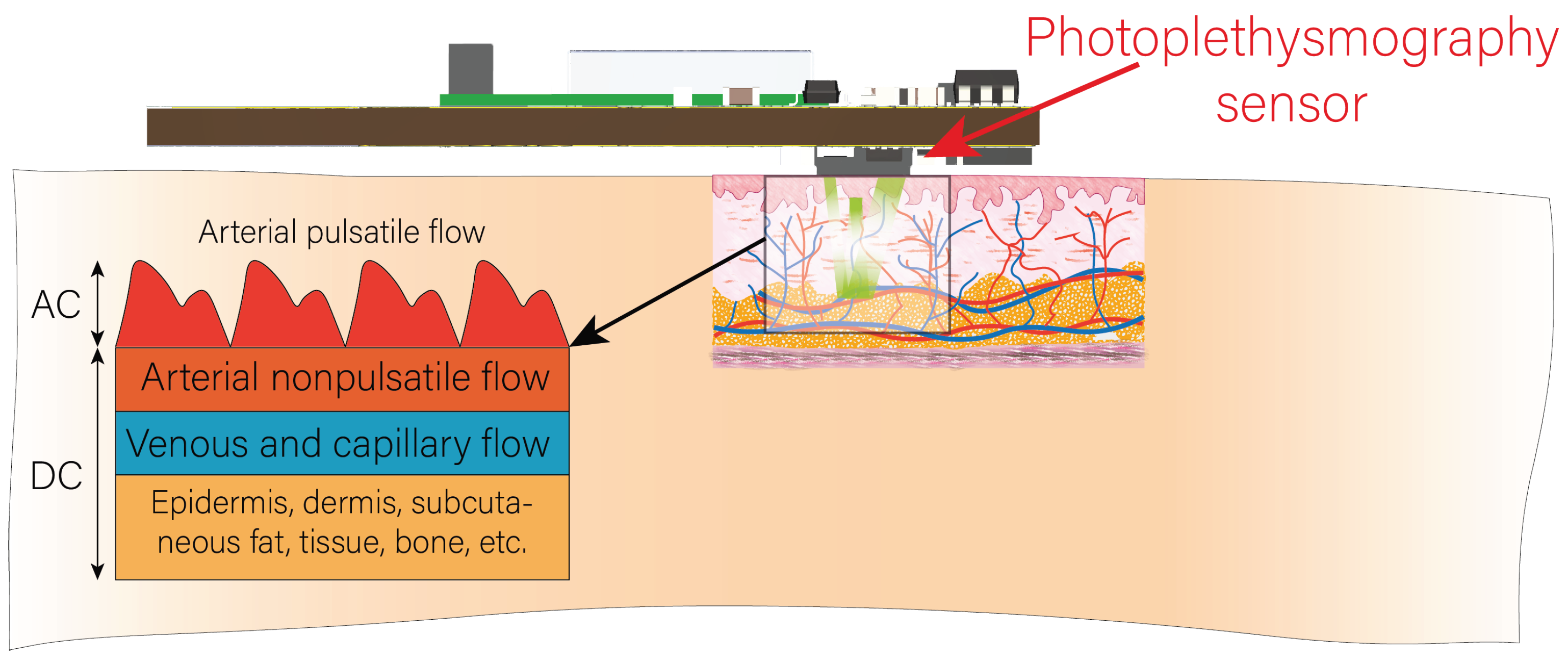
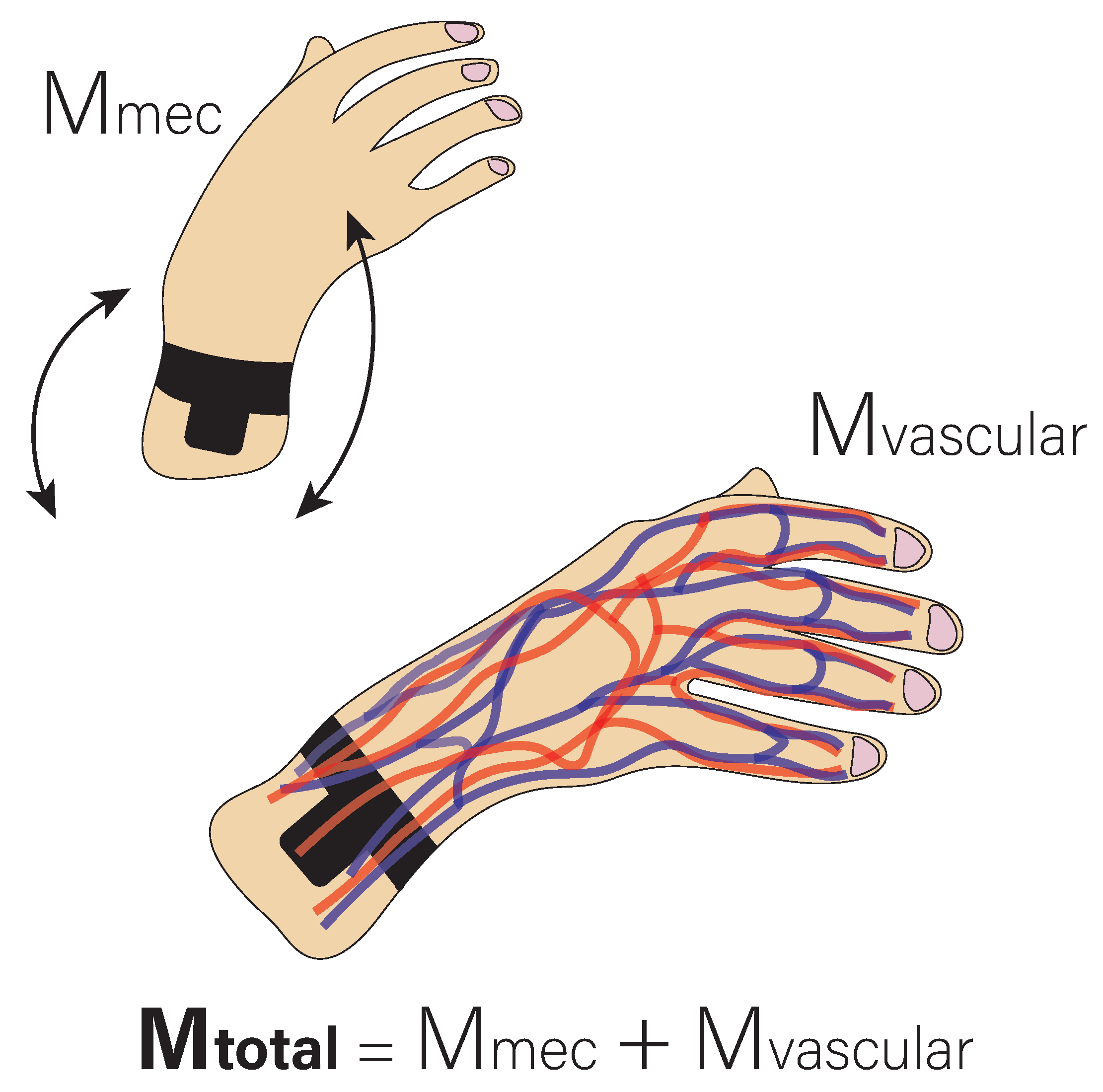
2.1. Experimental Setup
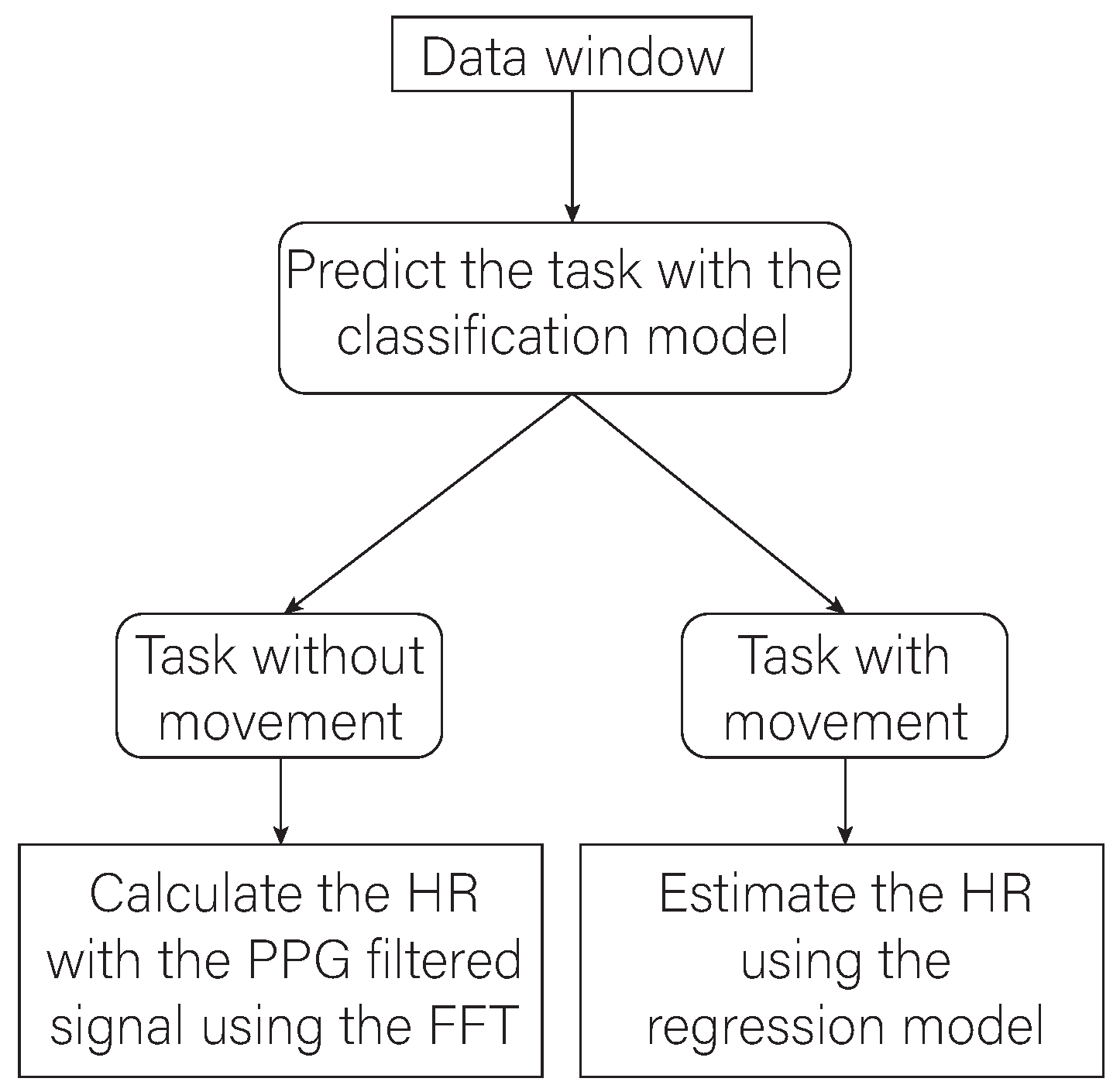
2.2. Proposed Algorithm
2.3. Signal Acquisition and Processing
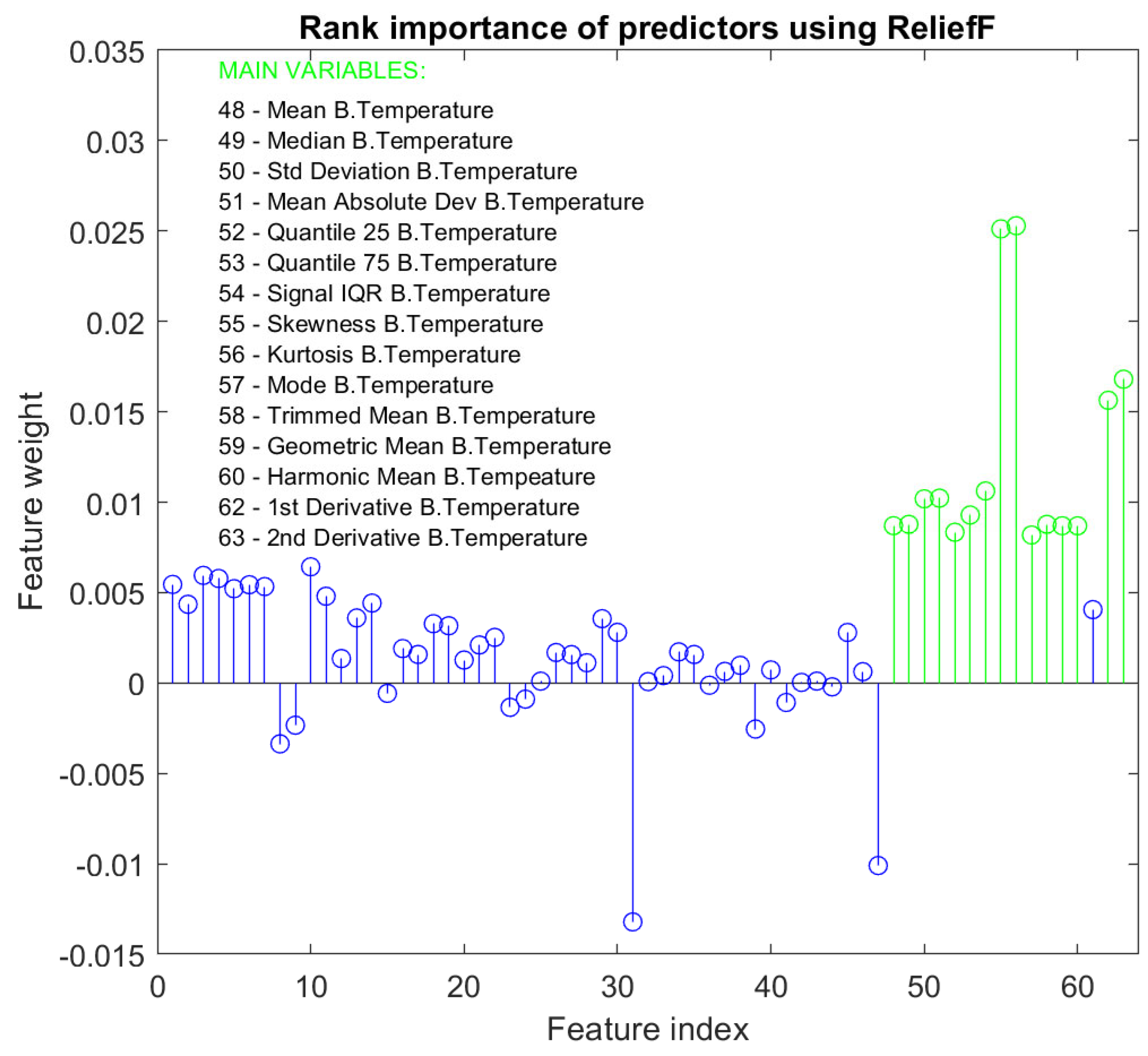
2.4. Training of an Activity Classification Model
2.5. Training of a Heart Rate Estimation Model
- Gaussian Process Regression Model
- Bagged Trees Model
2.6. Final Architecture of the Proposed Algorithm
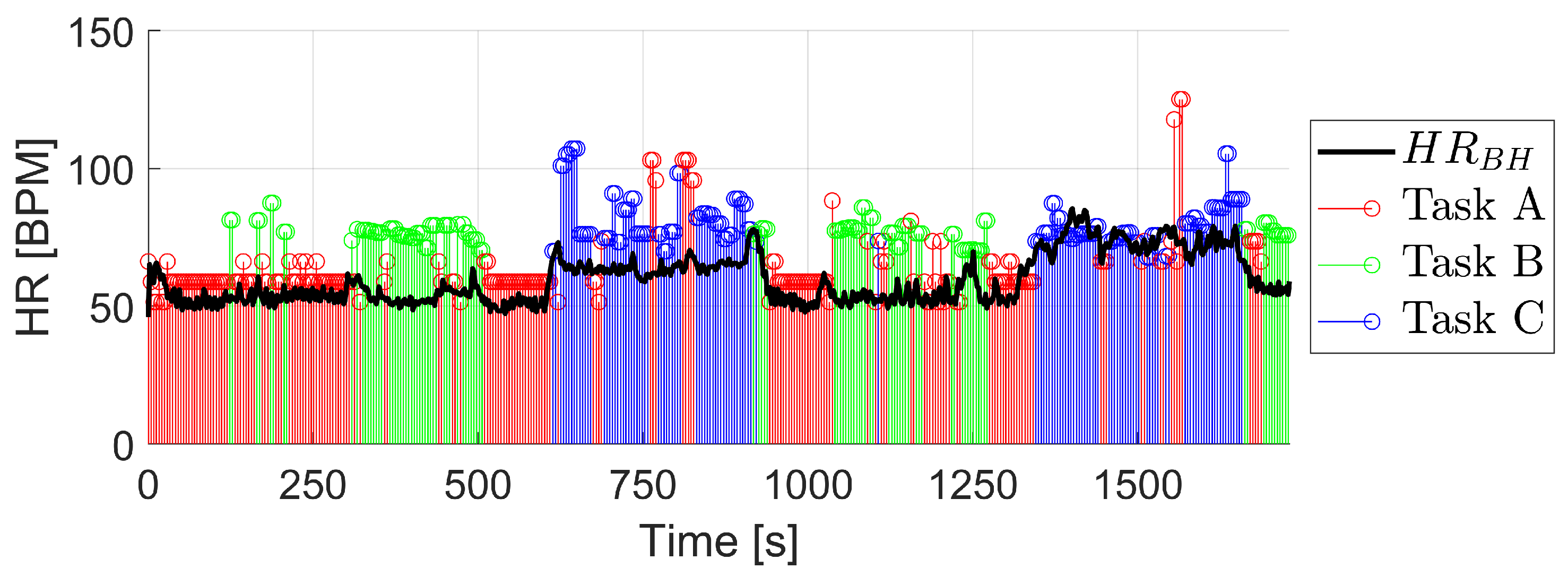
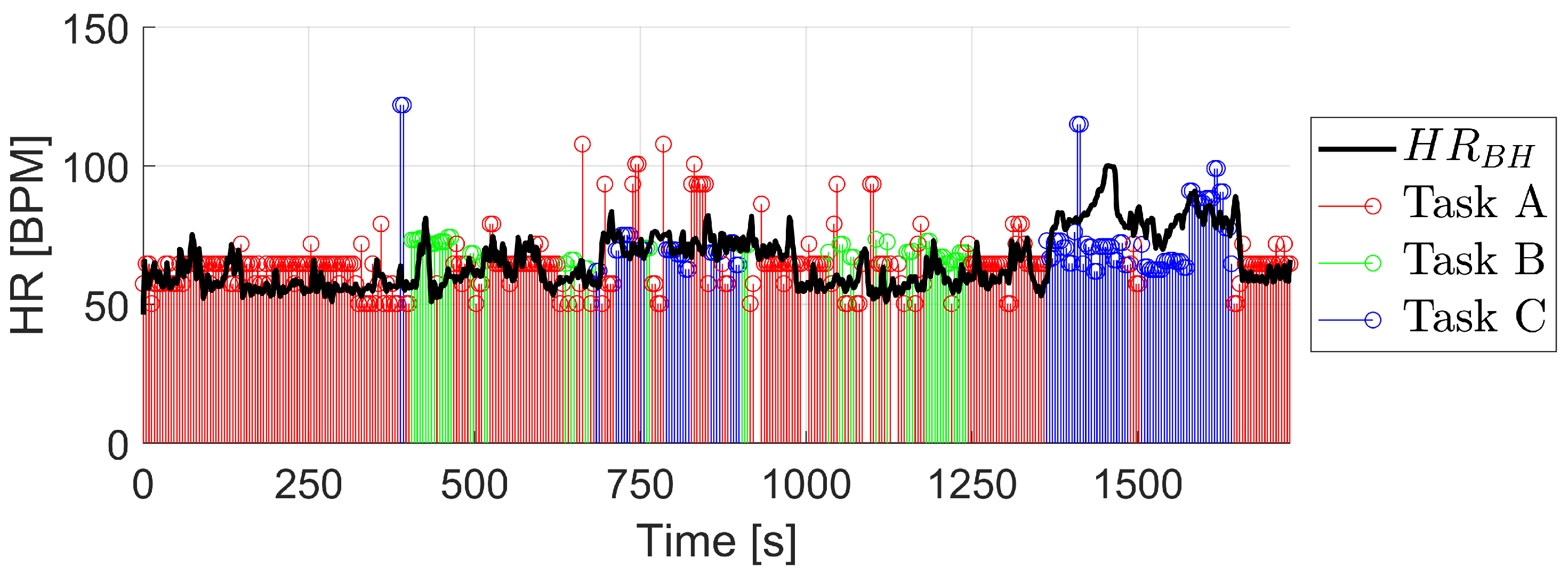
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wilkinson, I.B.; MacCallum, H.; Flint, L.; Cockcroft, J.R.; Newby, D.E.; Webb, D.J. The influence of heart rate on augmentation index and central arterial pressure in humans. J. Physiol. 2000, 525, 263–270. [Google Scholar] [CrossRef]
- Mulder, L. Measurement and analysis methods of heart rate and respiration for use in applied environments. Biol. Psychol. 1992, 34, 205–236. [Google Scholar] [CrossRef]
- Fox, K.; Borer, J.S.; Camm, A.J.; Danchin, N.; Ferrari, R.; Lopez Sendon, J.L.; Steg, P.G.; Tardif, J.C.; Tavazzi, L.; Tendera, M. Resting Heart Rate in Cardiovascular Disease. J. Am. Coll. Cardiol. 2007, 50, 823–830. [Google Scholar] [CrossRef] [PubMed]
- Challoner, A.V.; Ramsay, C.A. A photoelectric plethysmograph for the measurement of cutaneous blood flow. Phys. Med. Biol. 1974, 19, 317–328. [Google Scholar] [CrossRef]
- Elgendi, M.; Fletcher, R.; Liang, Y.; Howard, N.; Lovell, N.H.; Abbott, D.; Lim, K.; Ward, R. The use of photoplethysmography for assessing hypertension. npj Digit. Med. 2019, 2, 60. [Google Scholar] [CrossRef]
- Anderson, R.R.; Parrish, J.A. The Optics of Human Skin. J. Investig. Dermatol. 1981, 77, 13–19. [Google Scholar] [CrossRef]
- Cui, W.; Ostrander, L.; Lee, B. In Vivo reflectance of blood and tissue as a function of light wavelength. IEEE Trans. Biomed. Eng. 1990, 37, 632–639. [Google Scholar] [CrossRef]
- Jones, D.P. Medical electro-optics: Measurements in the human microcirculation. Phys. Technol. 1987, 18, 79–85. [Google Scholar] [CrossRef]
- Murray, A.; Marjanovic, D. Optical assessment of recovery of tissue blood supply after removal of externally applied pressure. Med. Biol. Eng. Comput. 1997, 35, 425–427. [Google Scholar] [CrossRef] [PubMed]
- Jänig, W.; Häbler, H.J. Chapter 25—Specificity in the organization of the autonomic nervous system: A basis for precise neural regulation of homeostatic and protective body functions. In The Biological Basis for Mind Body Interactions; Mayer, E., Saper, C., Eds.; Progress in Brain Research; Elsevier: Amsterdam, The Netherlands, 2000; Volume 122, pp. 351–367. [Google Scholar] [CrossRef]
- Kreibig, S.D. Autonomic nervous system activity in emotion: A review. Biol. Psychol. 2010, 84, 394–421. [Google Scholar] [CrossRef]
- Uijtdehaage, S.H.; Thayer, J.F. Accentuated antagonism in the control of human heart rate. Clin. Auton. Res. 2000, 10, 107–110. [Google Scholar] [CrossRef]
- Massin, M.M.; Maeyns, K.; Withofs, N.; Ravet, F.; Gérard, P. Circadian rhythm of heart rate and heart rate variability. Arch. Dis. Child. 2000, 83, 179–182. [Google Scholar] [CrossRef]
- Badesa, F.J.; Diez, J.A.; Catalan, J.M.; Trigili, E.; Cordella, F.; Nann, M.; Crea, S.; Soekadar, S.R.; Zollo, L.; Vitiello, N.; et al. Physiological responses during hybrid BNCI control of an upper-limb exoskeleton. Sensors 2019, 19, 4931. [Google Scholar] [CrossRef]
- Baker, A.E.; Lane, A.; Angley, M.T.; Young, R.L. The relationship between sensory processing patterns and behavioural responsiveness in autistic disorder: A pilot study. J. Autism Dev. Disord. 2008, 38, 867–875. [Google Scholar] [CrossRef]
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1. [Google Scholar] [CrossRef]
- Bent, B.; Goldstein, B.A.; Kibbe, W.A.; Dunn, J.P. Investigating sources of inaccuracy in wearable optical heart rate sensors. npj Digit. Med. 2020, 3, 18. [Google Scholar] [CrossRef]
- Swinehart, D.F. The Beer-Lambert law. J. Chem. Educ. 1962, 39, 333–335. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, S.; Vullings, R.; Biswas, D.; Simões-Capela, N.; Van Helleputte, N.; Van Hoof, C.; Groenendaal, W. Motion artifact reduction for wrist-worn photoplethysmograph sensors based on different wavelengths. Sensors 2019, 19, 673. [Google Scholar] [CrossRef]
- Lee, J.; Kim, M.; Park, H.K.; Kim, I.Y. Motion artifact reduction in wearable photoplethysmography based on multi-channel sensors with multiple wavelengths. Sensors 2020, 20, 1493. [Google Scholar] [CrossRef]
- Wang, M.; Li, Z.; Zhang, Q.; Wang, G. Removal of motion artifacts in photoplethysmograph sensors during intensive exercise for accurate heart rate calculation based on frequency estimation and notch filtering. Sensors 2019, 19, 3312. [Google Scholar] [CrossRef]
- Zhu, L.; Kan, C.; Du, Y.; Du, D. Heart Rate Monitoring during Physical Exercise from Photoplethysmography Using Neural Network. IEEE Sensors Lett. 2019, 3, 7100904. [Google Scholar] [CrossRef]
- Essalat, M.; Mashhadi, M.B.; Marvasti, F. supervized heart rate tracking using wrist-type photoplethysmographic (PPG) signals during physical exercise without simultaneous acceleration signals. In Proceedings of the 2016 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Washington, DC, USA, 7–9 December 2016; IEEE: Piscataway, NJ, USA, 2017; pp. 1166–1170. [Google Scholar] [CrossRef]
- Biswas, D.; Everson, L.; Liu, M.; Panwar, M.; Verhoef, B.E.; Patki, S.; Kim, C.H.; Acharyya, A.; Van Hoof, C.; Konijnenburg, M.; et al. CorNET: Deep Learning Framework for PPG-Based Heart Rate Estimation and Biometric Identification in Ambulant Environment. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 282–291. [Google Scholar] [CrossRef]
- Vicente-Samper, J.M.; Ávila Navarro, E.; Sabater-Navarro, J.M. Data Acquisition Devices Towards a System for Monitoring Sensory Processing Disorders. IEEE Access 2020, 8, 183596–183605. [Google Scholar] [CrossRef]
- Vicente-Samper, J.M.; Avila-Navarro, E.; Esteve, V.; Sabater-Navarro, J.M. Intelligent Monitoring Platform to Evaluate the Overall State of People with Neurological Disorders. Appl. Sci. 2021, 11, 2789. [Google Scholar] [CrossRef]
- Maxim Integrated. MAX86160 Integrated Heart-Rate Sensor for In-Ear Applications. Available online: https://datasheets.maximintegrated.com/en/ds/MAX86160.pdf (accessed on 15 July 2021).
- Medtronic. Zephyr Performance Systems. Available online: https://www.zephyranywhere.com/ (accessed on 15 July 2022).
- Johnstone, J.A.; Ford, P.A.; Hughes, G.; Watson, T.; Mitchell, A.C.; Garrett, A.T. Field based reliability and validity of the bioharness™ multivariable monitoring device. J. Sport. Sci. Med. 2012, 11, 643. [Google Scholar]
- Nazari, G.; Bobos, P.; MacDermid, J.C.; Sinden, K.E.; Richardson, J.; Tang, A. Psychometric properties of the Zephyr bioharness device: A systematic review. BMC Sport. Sci. Med. Rehabil. 2018, 10, 6. [Google Scholar] [CrossRef]
- Fariha, M.; Ikeura, R.; Hayakawa, S.; Tsutsumi, S. Analysis of Pan-Tompkins algorithm performance with noisy ECG signals. J. Phys. Conf. Ser. 2020, 1532, 012022. [Google Scholar] [CrossRef]
- Bidargaddi, N.; Sarela, A.; Klingbeil, L.; Karunanithi, M. Detecting walking activity in cardiac rehabilitation by using accelerometer. In Proceedings of the 2007 3rd International Conference on Intelligent Sensors, Sensor Networks and Information, Melbourne, Australia, 3–6 December 2007; pp. 555–560. [Google Scholar]
- Tamantini, C.; Rondoni, C.; Cordella, F.; Guglielmelli, E.; Zollo, L. A classification method for workers’ physical risk. Sensors 2023, 23, 1575. [Google Scholar] [CrossRef]
- Foroozan, F.; Mohan, M.; Wu, J.S. Robust Beat-To-Beat Detection Algorithm for Pulse Rate Variability Analysis from Wrist Photoplethysmography Signals. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2136–2140. [Google Scholar] [CrossRef]
- Cittadini, R.; Tamantini, C.; Scotto di Luzio, F.; Lauretti, C.; Zollo, L.; Cordella, F. Affective state estimation based on Russell’s model and physiological measurements. Sci. Rep. 2023, 13, 9786. [Google Scholar] [CrossRef]
- Chen, X.w.; Jeong, J.C. Enhanced recursive feature elimination. In Proceedings of the Sixth International Conference on Machine Learning and Applications (ICMLA 2007), Cincinnati, OH, USA, 13–15 December 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 429–435. [Google Scholar]
- Novak, D.; Mihelj, M.; Munih, M. A survey of methods for data fusion and system adaptation using autonomic nervous system responses in physiological computing. Interact. Comput. 2012, 24, 154–172. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L.A. A Practical Approach to Feature Selection. In Machine Learning Proceedings 1992; Sleeman, D., Edwards, P., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1992; pp. 249–256. [Google Scholar] [CrossRef]







| Activity | Time (min) |
|---|---|
| Rest (A) | 5 |
| Read (B) | 3 |
| Rest (A) | 2 |
| Walk slow (D) | 5 |
| Rest (A) | 2 |
| Write/Draw (C) | 3 |
| Rest (A) | 2 |
| Walk fast (E) | 5 |
| Rest (A) | 2 |
| TOTAL | ∼30 |
| Algorithm | Accuracy (9 Features) | Accuracy (63 Features) |
|---|---|---|
| Decission Tree | 94.3% | 92.9% |
| KNN | 96.1% | 96.2% |
| SVM | 91.3% | 73.0% |
| Ensemble: Bagged Trees | 96.9% | 96.5% |
| Naive Bayes | 76.8% | 74.1% |
| Algorithm | RMSE (15 Features) | RMSE (22 Features) |
|---|---|---|
| Decission Tree | 5.08 | 6.93 |
| Gaussian Process Regression | 5.07 | 9.68 |
| Support Vector Machine (SVM) | 6.89 | 12.47 |
| Ensemble: Bagged Trees | 4.95 | 5.44 |
| Linear Regression | 16.4 | 18.43 |
| Task Classification | HR Calculation | ||||
|---|---|---|---|---|---|
| Task | Precision | Recall | F1-Score | Task | RMSE (BPM) |
| 1 | 0.79 | 0.86 | 0.83 | 1 | 13.06 |
| 2 | 0.75 | 0.76 | 0.76 | 2 | 7.95 |
| 3 | 0.98 | 0.85 | 0.91 | 3 | 13.82 |
| Accuracy | 83.3% | Total | 12.20 | ||
| Task Classification | HR Calculation | ||||
|---|---|---|---|---|---|
| Task | Precision | Recall | F1-Score | Task | RMSE (BPM) |
| 1 | 0.71 | 0.86 | 0.78 | 1 | 12.08 |
| 2 | 0.73 | 0.70 | 0.71 | 2 | 22.91 |
| 3 | 0.98 | 0.81 | 0.89 | 3 | 16.49 |
| Accuracy | 80.0% | Total | 16.64 | ||
| Task Classification | HR Calculation | ||||
|---|---|---|---|---|---|
| Task | Precision | Recall | F1-Score | Task | RMSE (BPM) |
| 1 | 0.76 | 0.96 | 0.85 | 1 | 13.22 |
| 2 | 0.72 | 0.58 | 0.64 | 2 | 10.80 |
| 3 | 0.97 | 0.67 | 0.79 | 3 | 15.17 |
| Accuracy | 80.6% | Total | 13.03 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vicente-Samper, J.M.; Tamantini, C.; Ávila-Navarro, E.; De La Casa-Lillo, M.Á.; Zollo, L.; Sabater-Navarro, J.M.; Cordella, F. An ML-Based Approach to Reconstruct Heart Rate from PPG in Presence of Motion Artifacts. Biosensors 2023, 13, 718. https://doi.org/10.3390/bios13070718
Vicente-Samper JM, Tamantini C, Ávila-Navarro E, De La Casa-Lillo MÁ, Zollo L, Sabater-Navarro JM, Cordella F. An ML-Based Approach to Reconstruct Heart Rate from PPG in Presence of Motion Artifacts. Biosensors. 2023; 13(7):718. https://doi.org/10.3390/bios13070718
Chicago/Turabian StyleVicente-Samper, José María, Christian Tamantini, Ernesto Ávila-Navarro, Miguel Ángel De La Casa-Lillo, Loredana Zollo, José María Sabater-Navarro, and Francesca Cordella. 2023. "An ML-Based Approach to Reconstruct Heart Rate from PPG in Presence of Motion Artifacts" Biosensors 13, no. 7: 718. https://doi.org/10.3390/bios13070718
APA StyleVicente-Samper, J. M., Tamantini, C., Ávila-Navarro, E., De La Casa-Lillo, M. Á., Zollo, L., Sabater-Navarro, J. M., & Cordella, F. (2023). An ML-Based Approach to Reconstruct Heart Rate from PPG in Presence of Motion Artifacts. Biosensors, 13(7), 718. https://doi.org/10.3390/bios13070718










