Recent Advances in Nanomechanical Membrane-Type Surface Stress Sensors towards Artificial Olfaction
Abstract
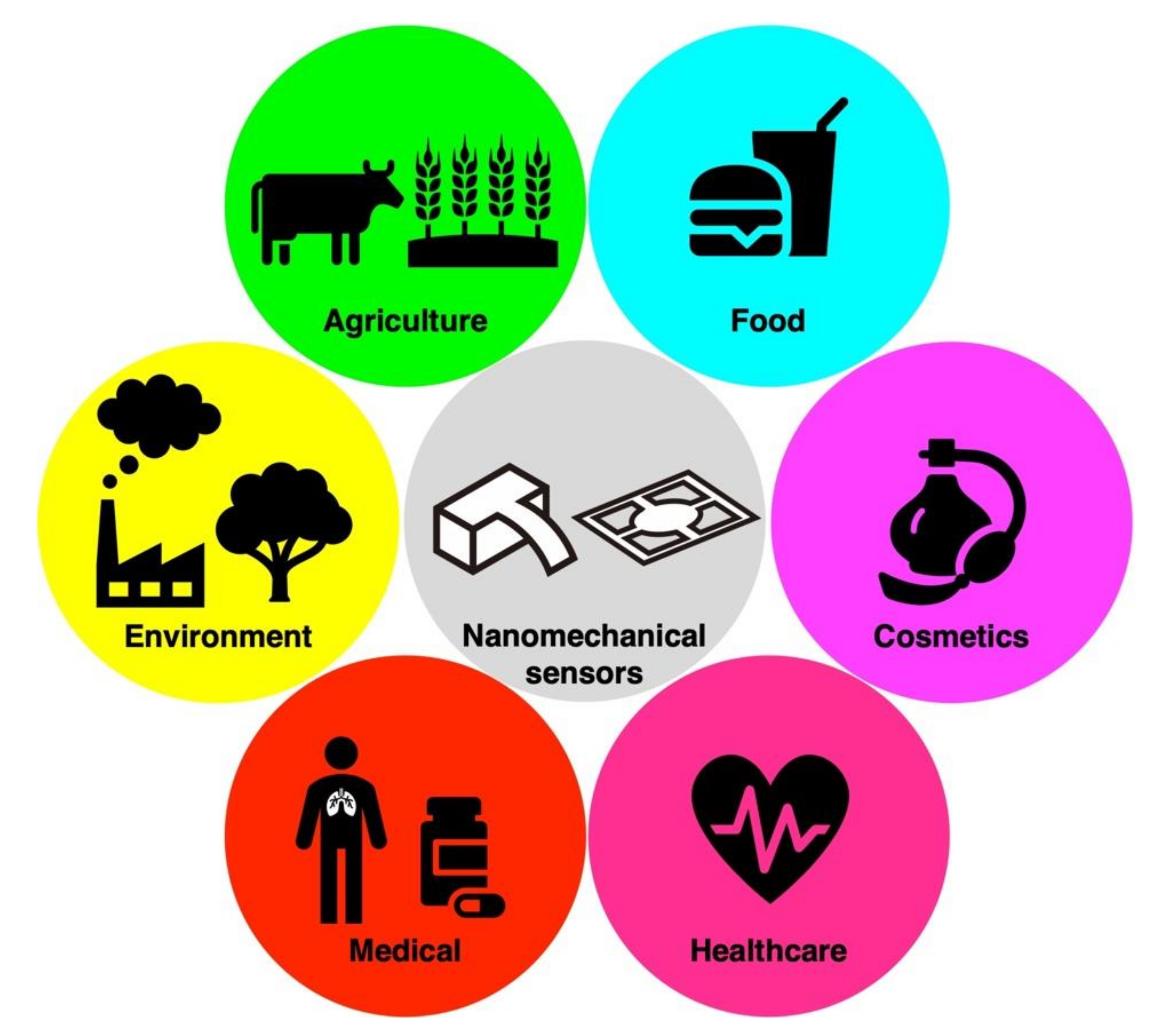
1. Introduction
2. Nanomechanical Sensors
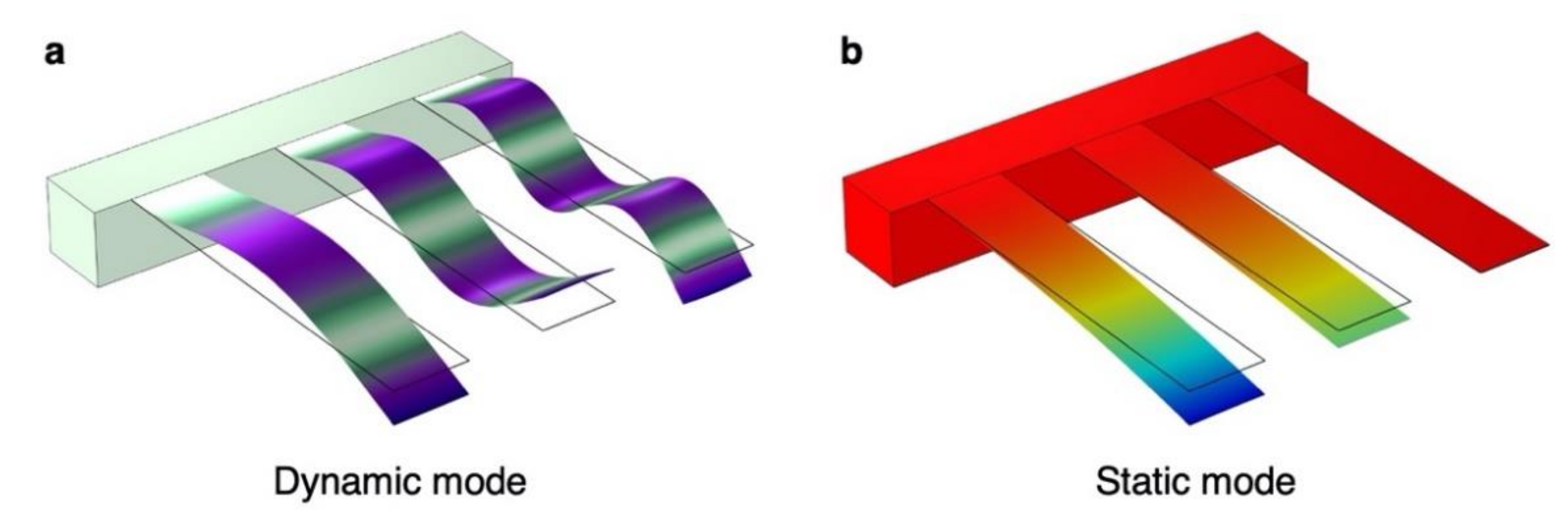
2.1. Static and Dynamic Mode
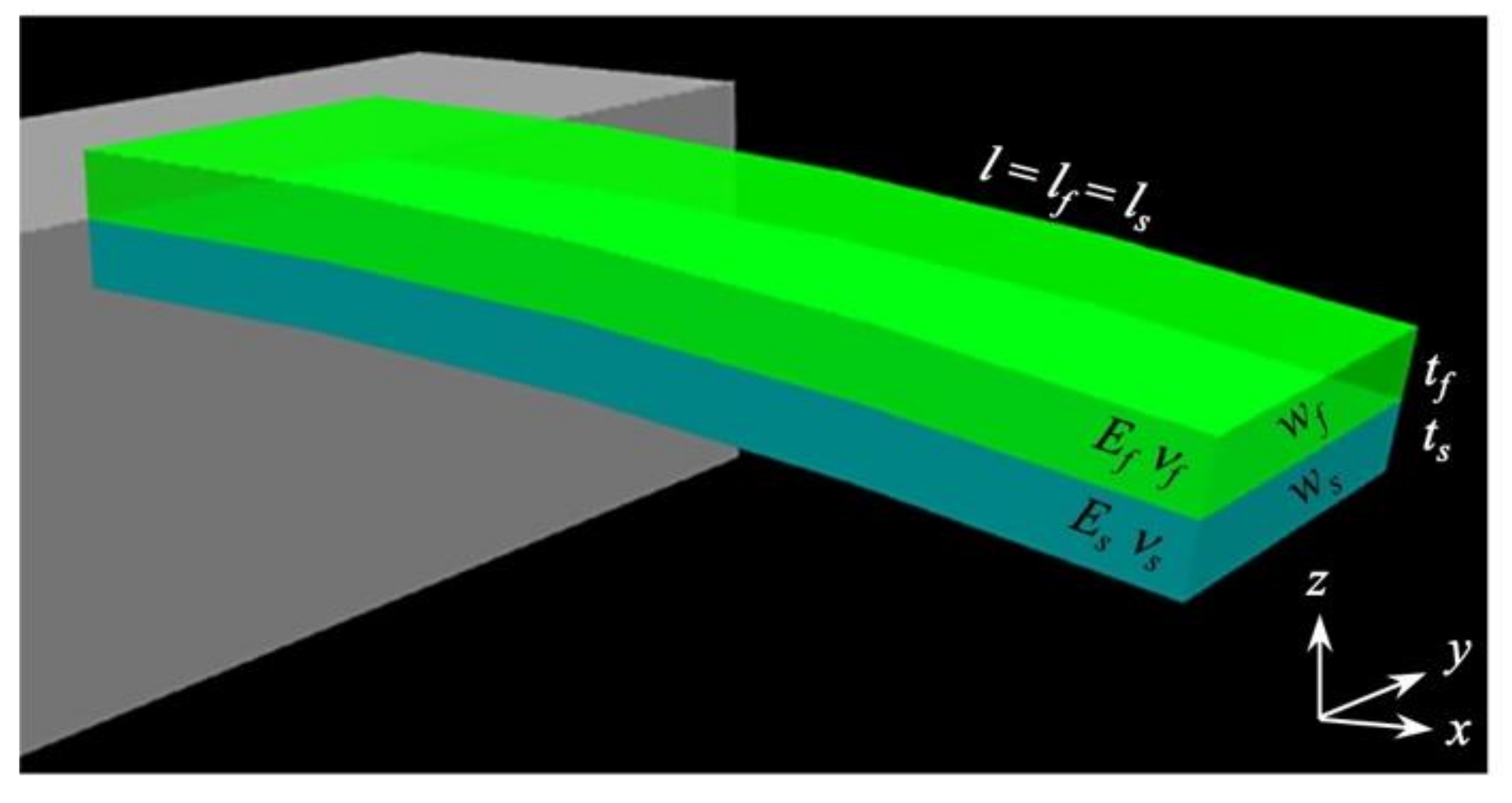
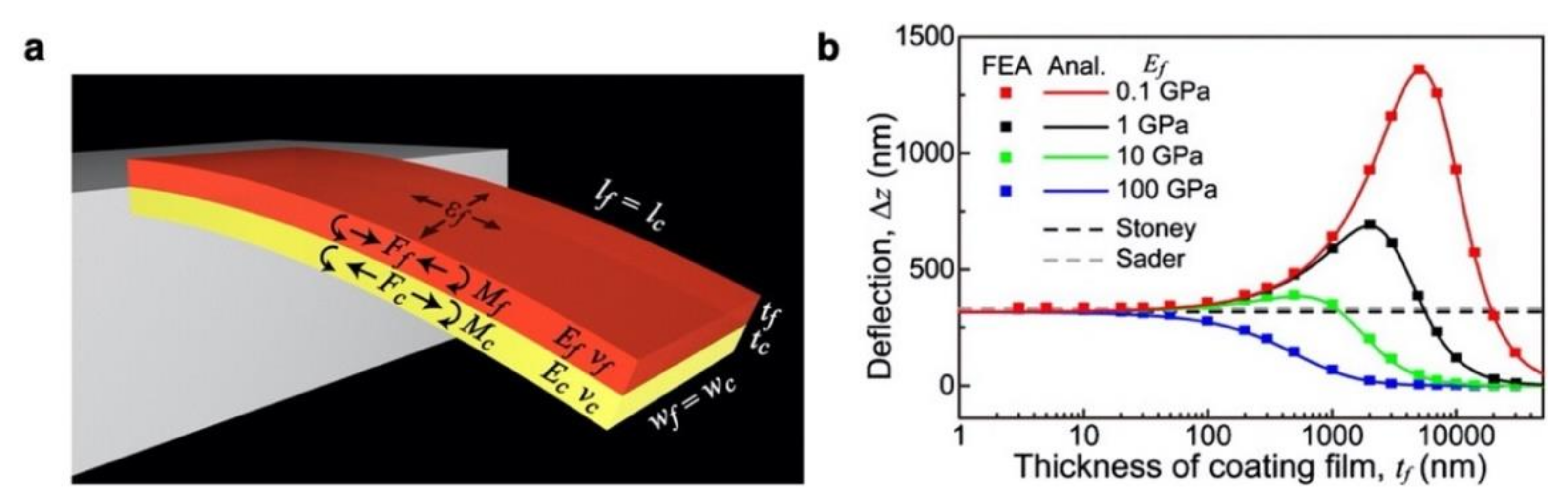
2.2. Effects of Surface Stress in Static Mode
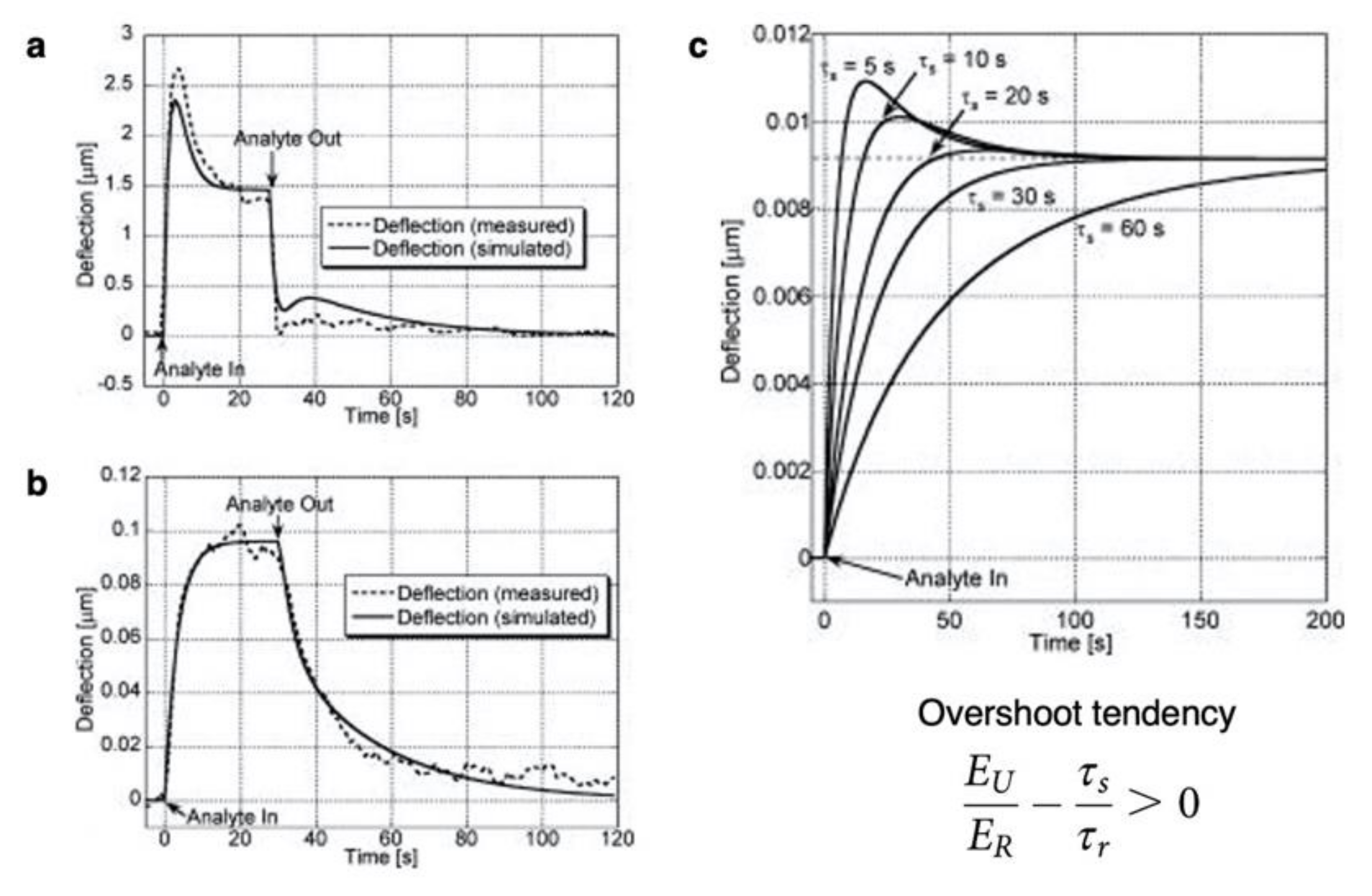
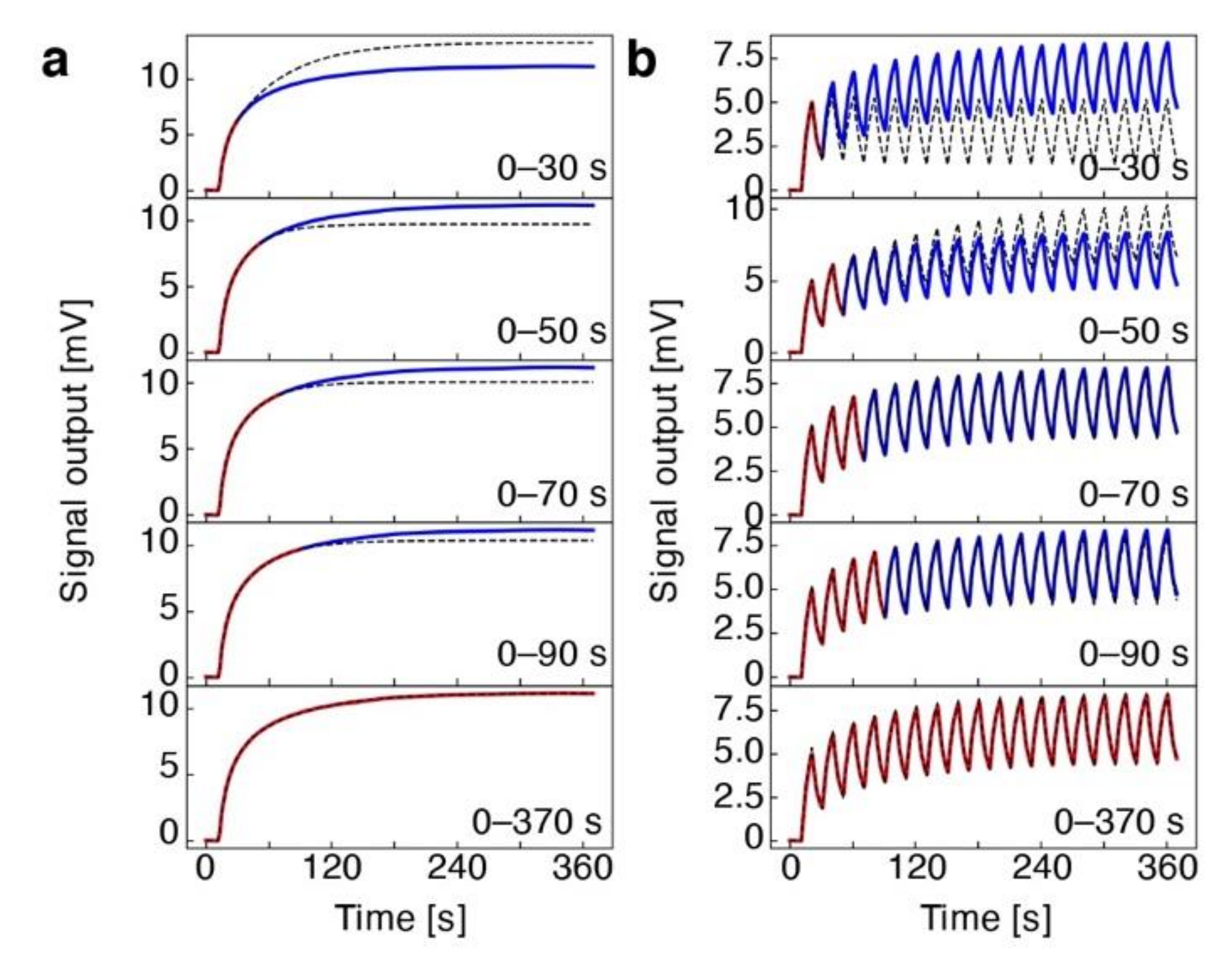
2.3. Sorption Kinetics and Viscoelastic Behaviors of Receptor Materials in Static Mode
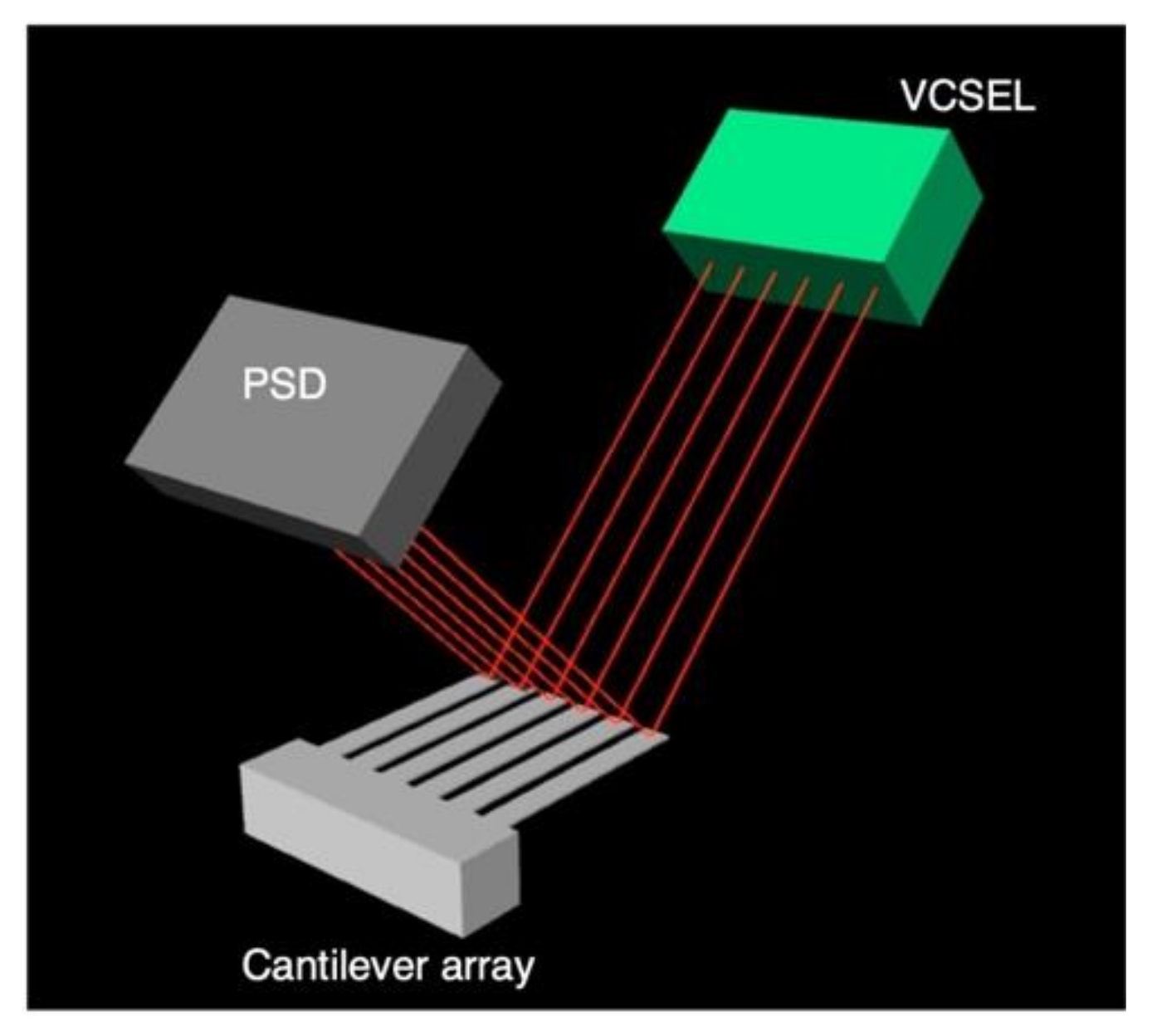
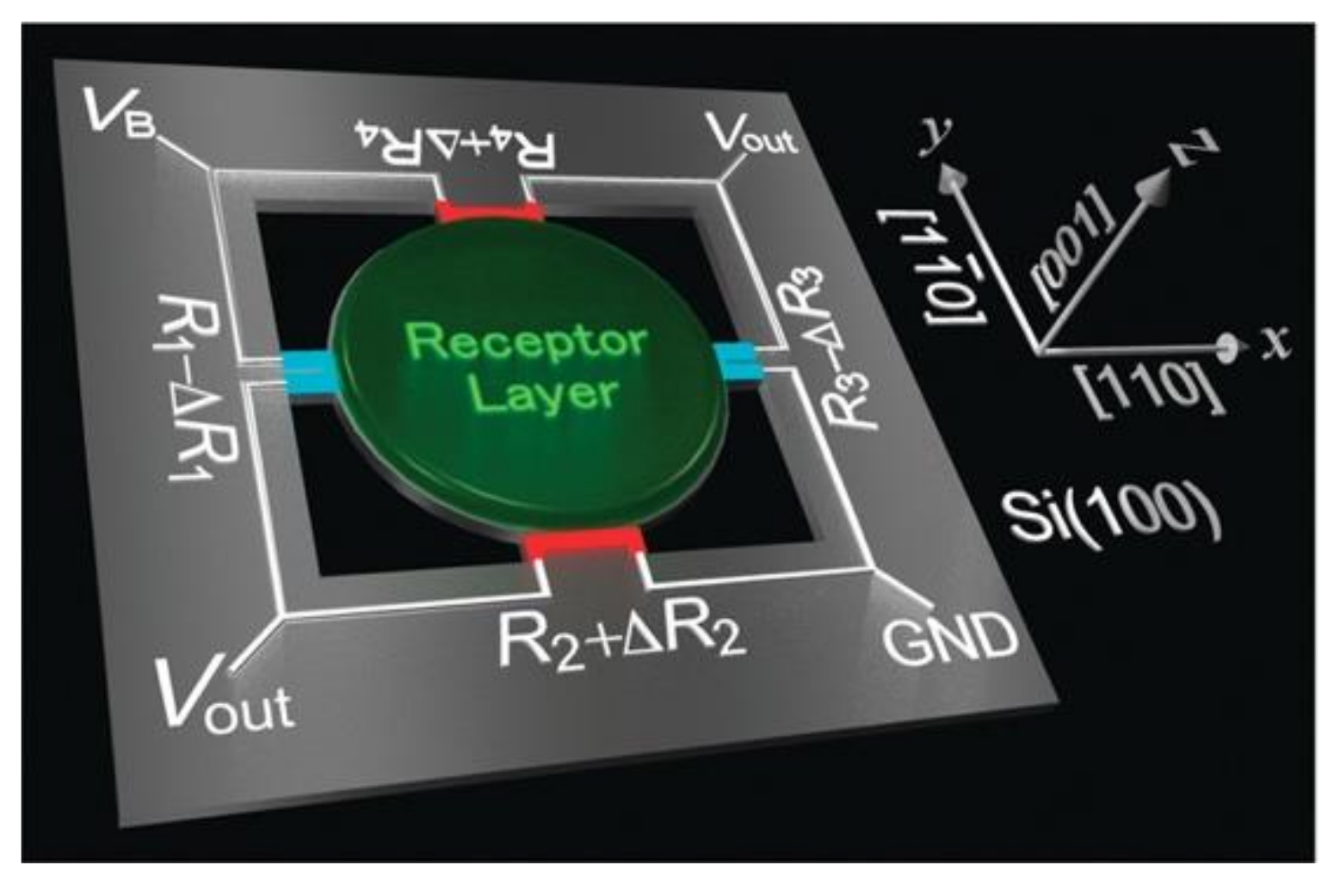
2.4. Membrane-Type Surface Stress Sensor (MSS)
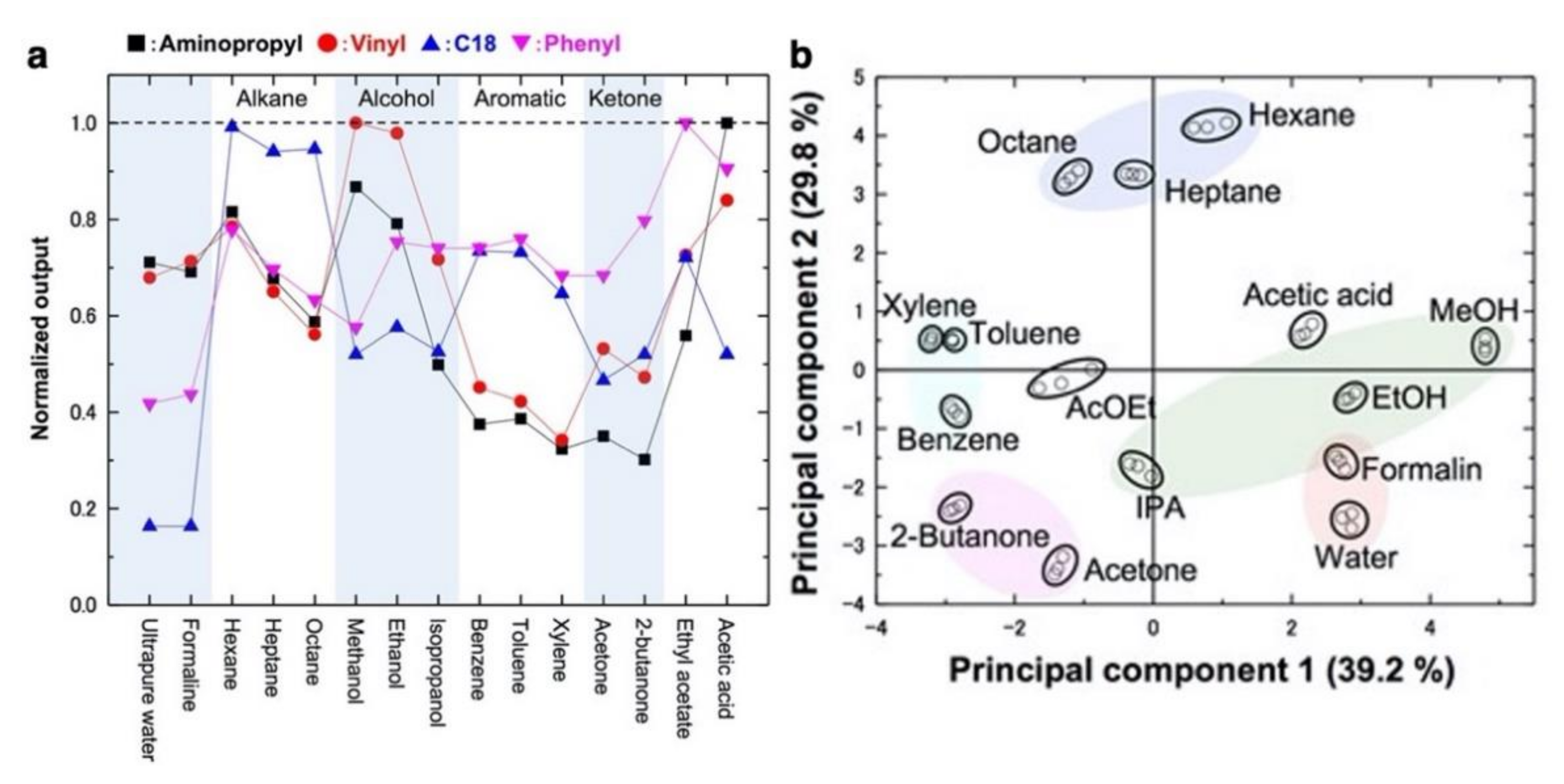
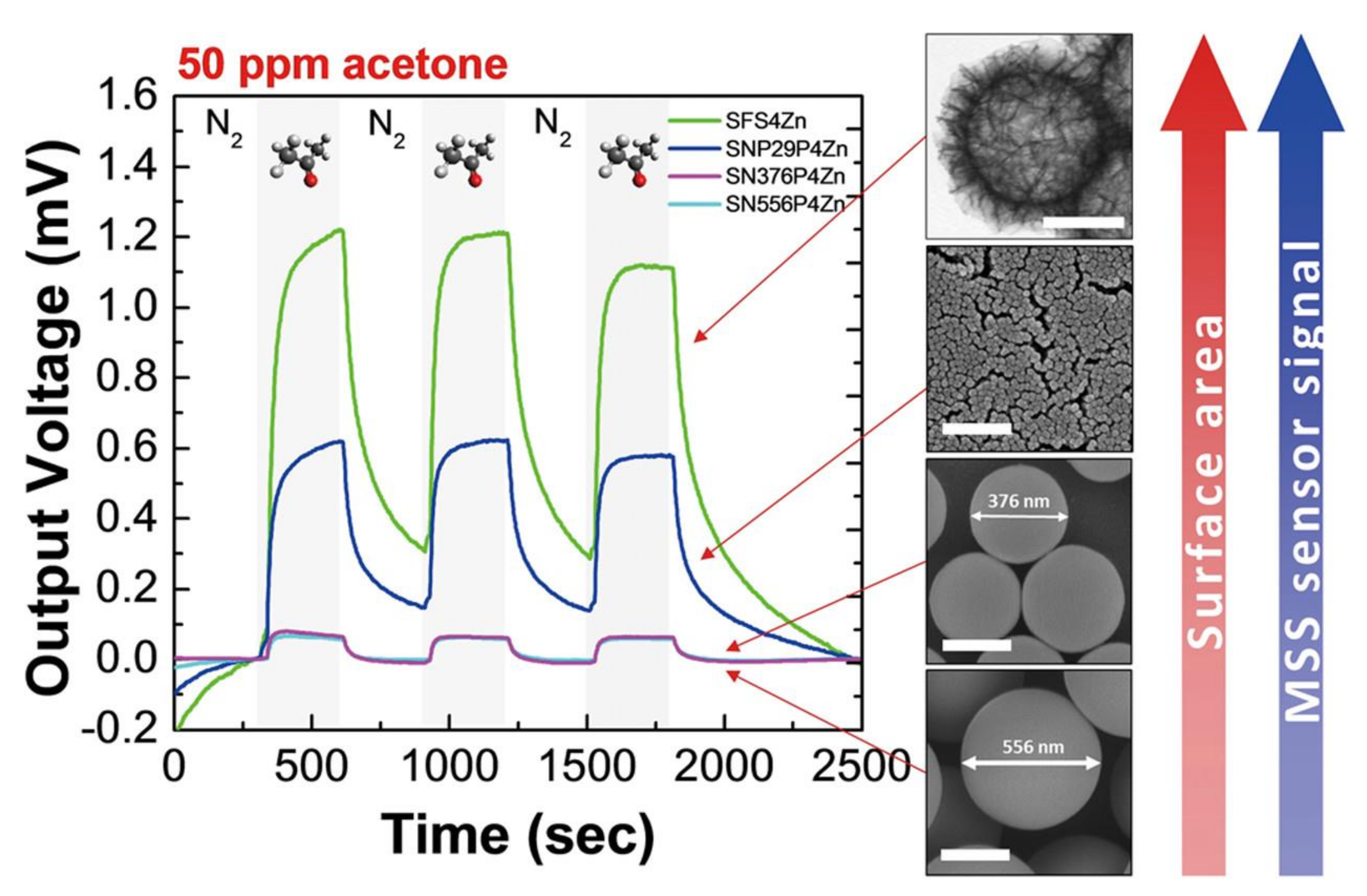
3. Design of Receptor Materials for Nanomechanical Sensors
4. Applications for Artificial Olfaction Using MSS
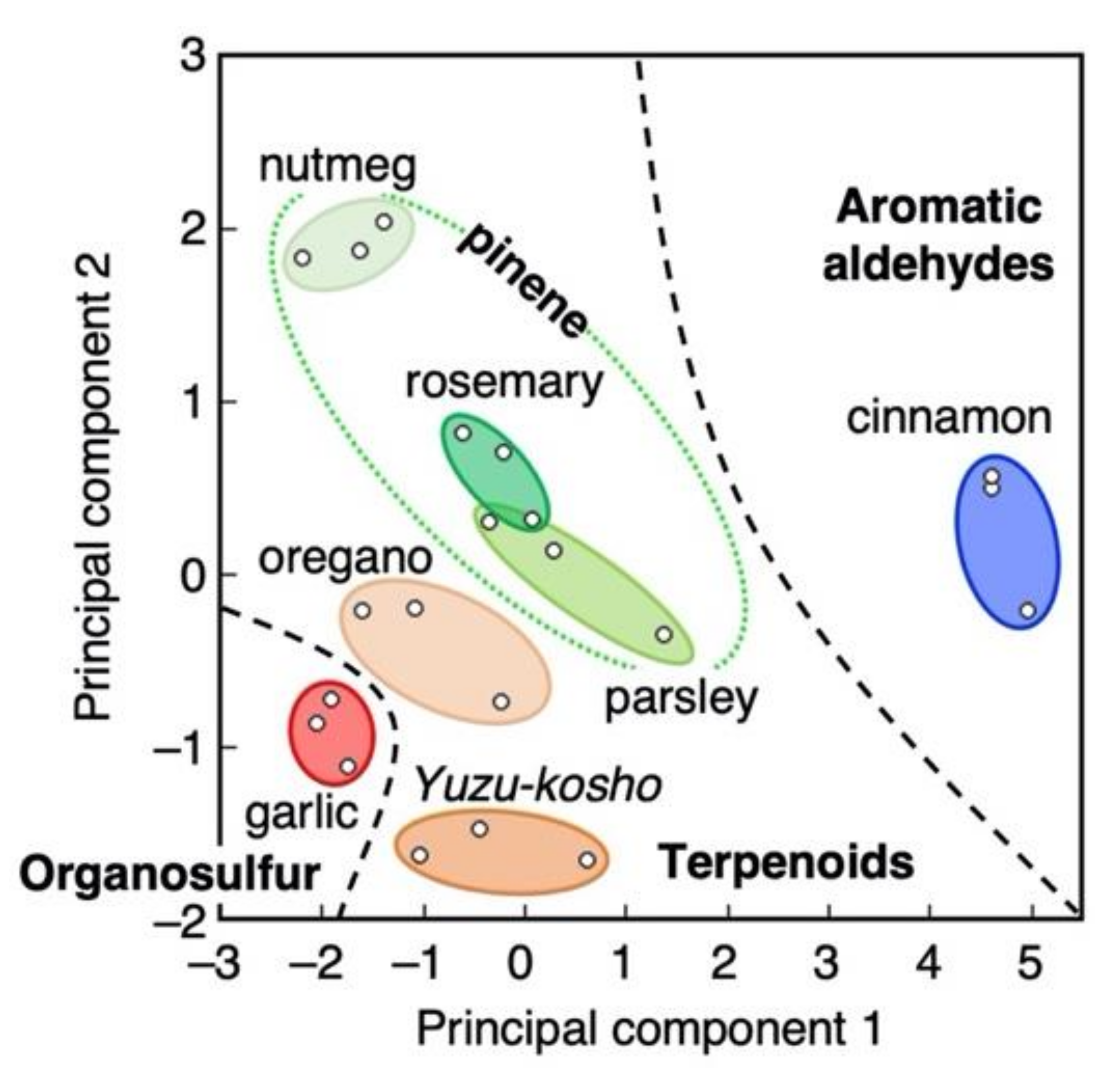
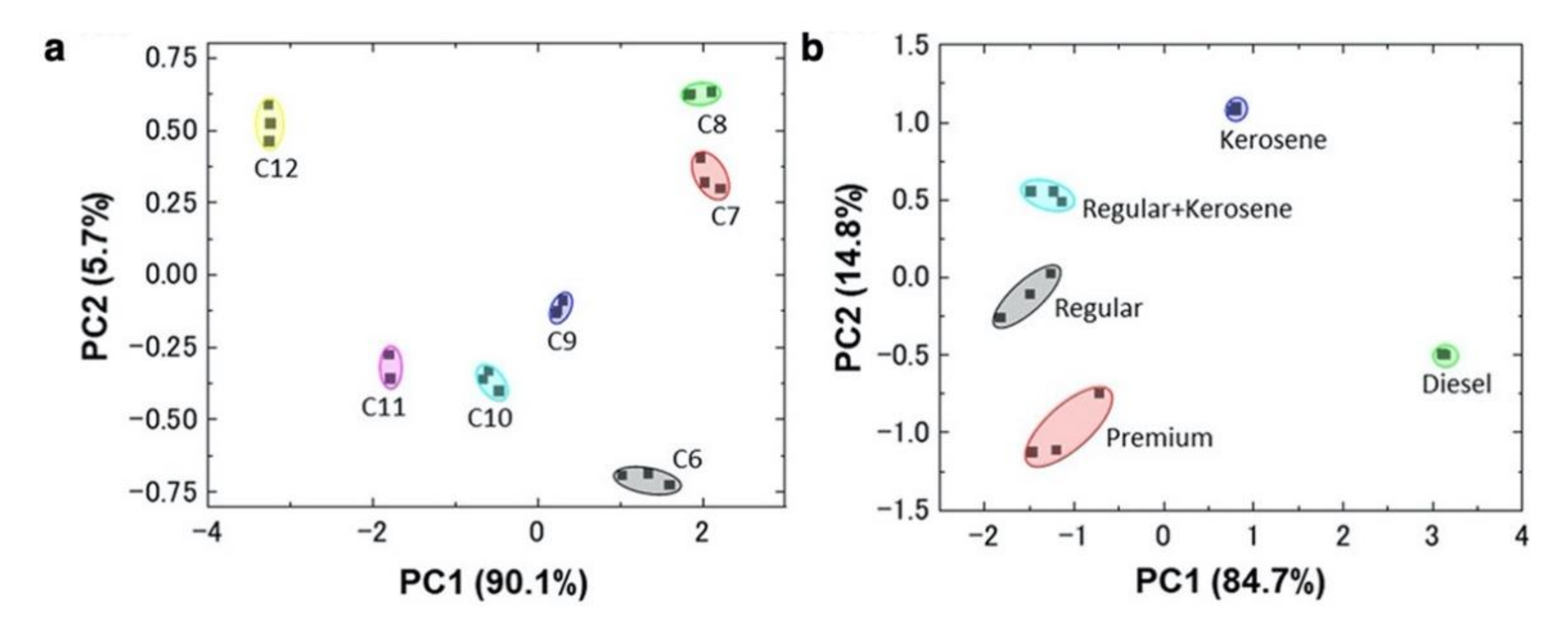
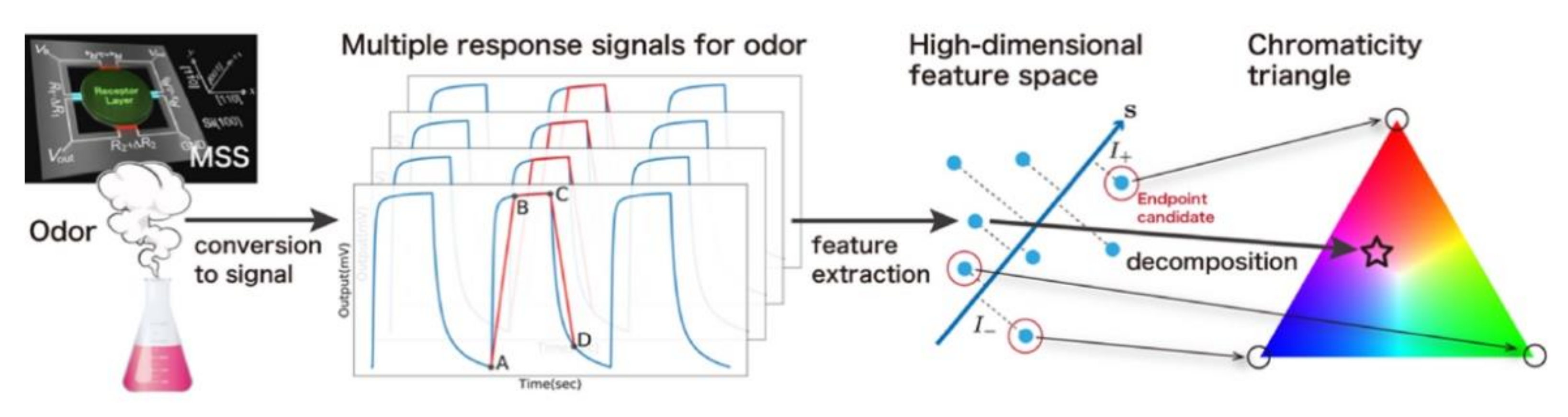
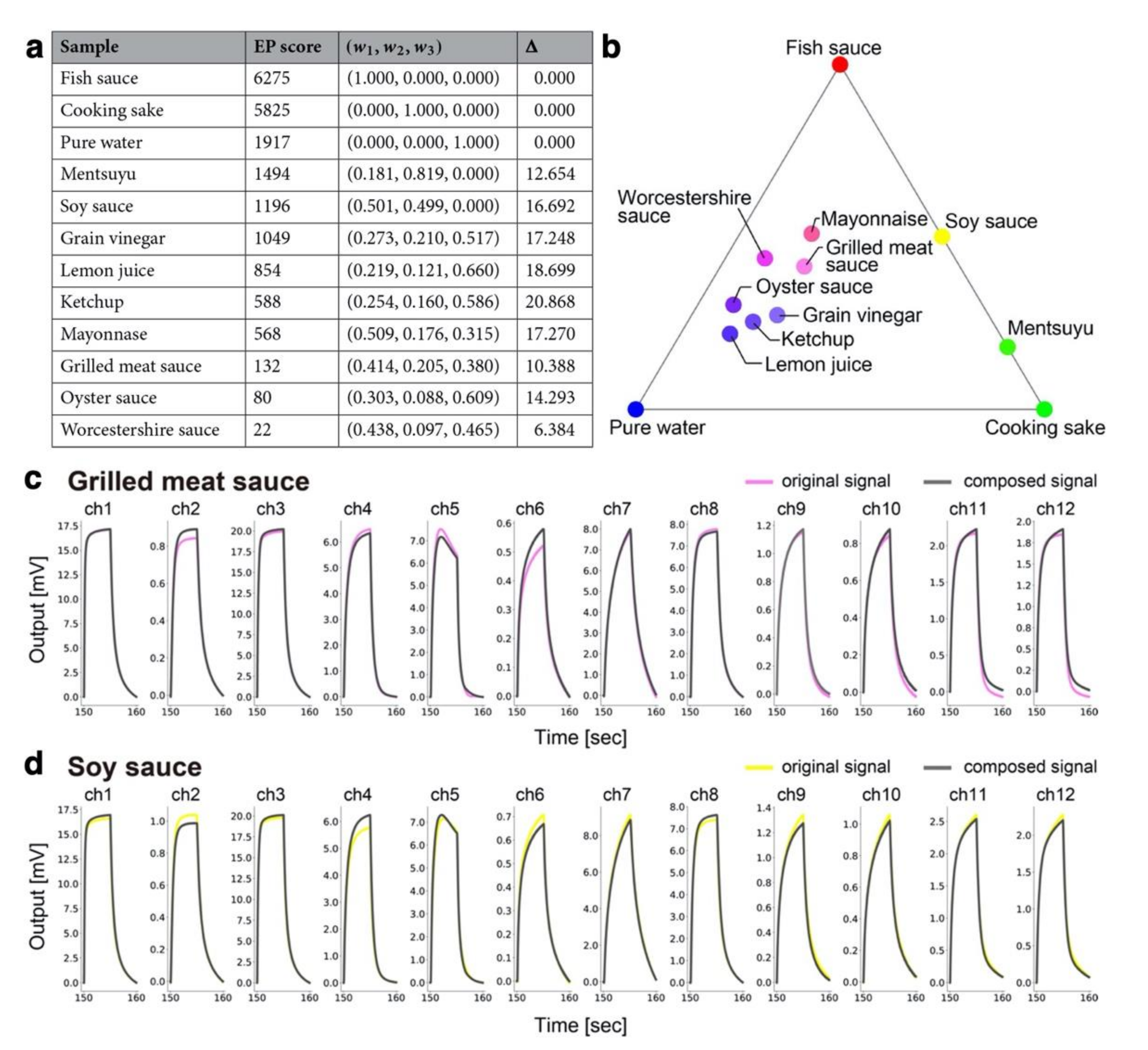
4.1. Smell Identification
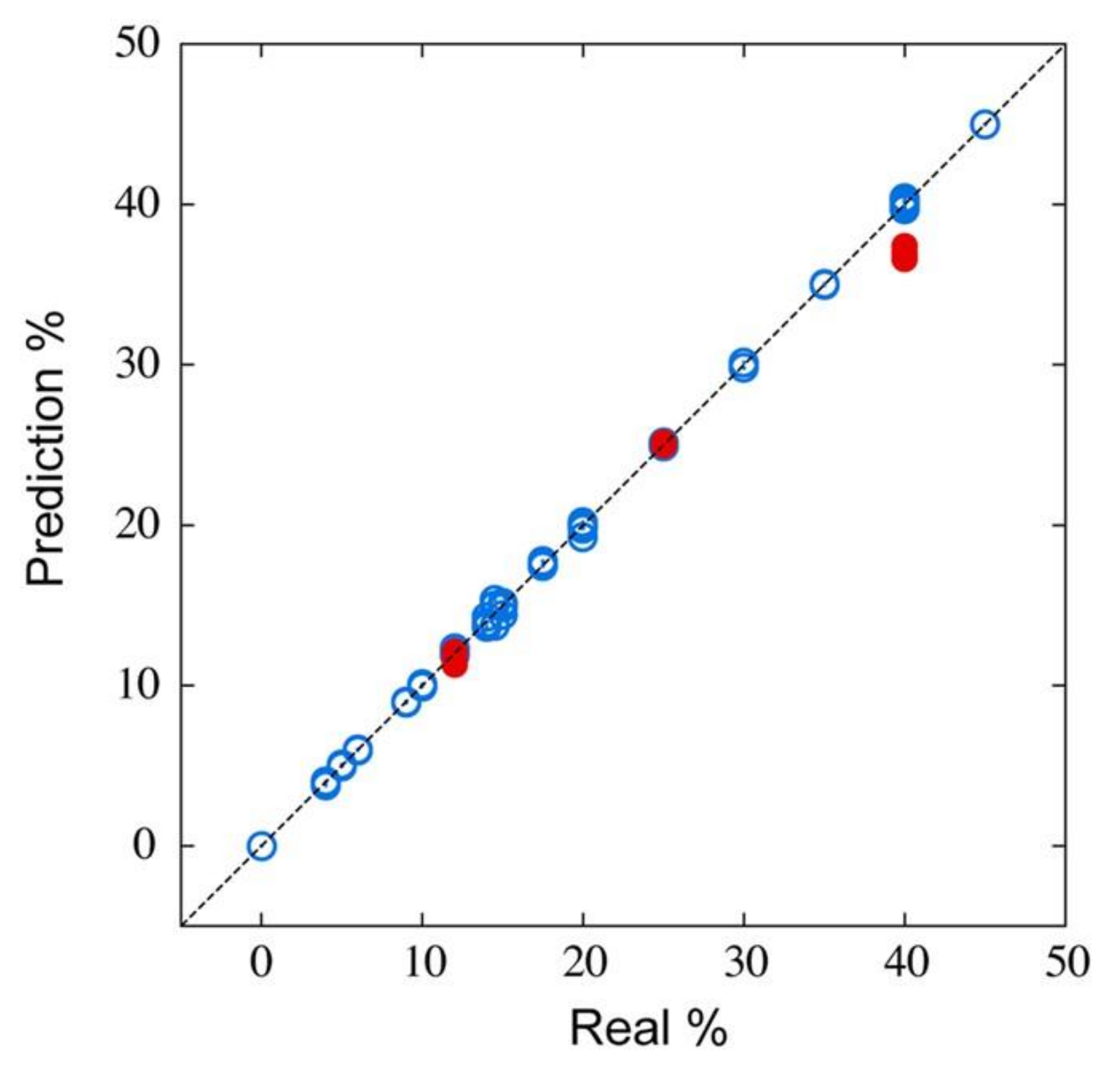
4.2. Quantification of Gas Components
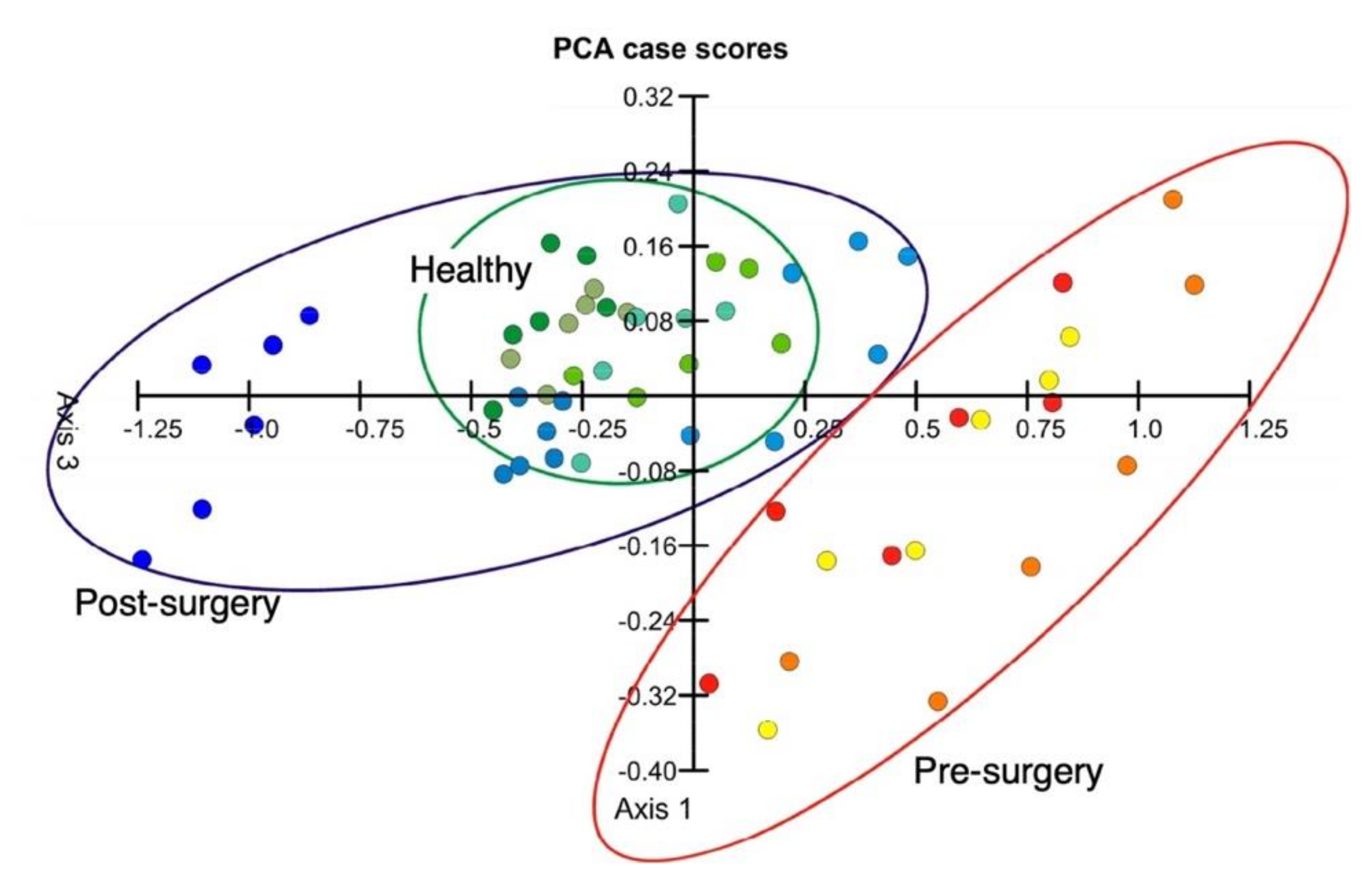
4.3. Exhaled Breath Diagnosis
4.4. Olfactory Sensors without Any Flow Controls
5. Conclusions and Perspective
| Receptor Materials | MSS (Static) | Cantilever (Static) | Cantilever (Dynamic) |
|---|---|---|---|
| Small molecules | |||
| Calix[n]arene | — | [178] | — |
| Cu complex | [179] | — | — |
| Cyclodextrin | — | [178] | — |
| Metallo-phthalocyanine | — | [178] | — |
| Metallo-porphyrins | [139,180] | — | — |
| Porphyrins | [139,180] | — | — |
| Squalene | — | [178] | |
| Polymers 1 | |||
| CAB | [42,154] | — | — |
| CMC | [154,156] | — | [181] |
| Dextran | [154,182] | [182] | — |
| Gelatin | — | — | [183,184] |
| HPC | [156] | — | — |
| Tenax | [157] | — | — |
| P4MS | [96,157,173,185] | — | — |
| PAA-AA | [156] | — | — |
| PAH | [144,145] | [118] | [181] |
| PCL | [8,96,173,185,186] | — | — |
| PDPP | — | [178] | — |
| PECh | [174] | [178] | — |
| PEG/PEO | [99,156] | [187] | [181] |
| PEG-MEMA | [156] | — | — |
| PEI | [38,156] | [118] | [181] |
| PEMA | — | [188] | — |
| PHEMA | — | [189] | [189] |
| PIB | [156] | [178] | — |
| PLL | — | [190] | — |
| PMMA | [10,92,99,144,145] | [35,36,37,188,191] | [36,157,174,181,192] |
| PS | [37,96,185,186] | [189] | [189] |
| PS-AA | [174] | — | — |
| PSS | [39,89,154] | — | [181] |
| PSU | [8,173] | — | — |
| PU | — | [37] | — |
| PVA | — | [118] | [181] |
| PVC | [99] | — | — |
| PVF | [173,185] | — | — |
| PVP | [89,144,193] | [118] | — |
| PVPh | [174] | — | — |
| PVPy | [154,156] | [37] | [181] |
| Inorganic nanomaterials | |||
| Copper nanorods | — | — | [194] |
| Gold NPs | [195] | [196] | [197,198,199] |
| Silica NPs | [9,10,139,173] | — | [200,201] |
| Nanostructured silica NPs | [139,202] | — | — |
| Silica-Titania hybrid NPs | [8,9,10,96,143,145,173,203] | — | — |
| TiO2@MnO2 nanorods | — | — | [204] |
| ZnO@Si nanorods | — | — | [205,206] |
| 2D materials | |||
| Graphenes | [207,208,209] | [190,210] | [43,197,198] |
| MoS2 | [208] | — | — |
| WS2 | [208] | — | — |
| Self-assembled monolayer | |||
| Alkanethiols | — | [45,181,211] | [212,213,214] |
| Carboxylated thiols | [133] | [35,36,181,215,216] | — |
| Aminated silane | — | [217] | [206] |
| DNA | — | [46,47,48,102,117,218,219] | [220] |
| Proteins | — | [103,133,215,216,221,222,223,224,225,226] | [223] |
| Metal films | |||
| Au | — | [35,36] | [41,44,63] |
| Cr | — | [227] | — |
| SiN | — | — | [192] |
| Pd | [20] | — | — |
| PdCuSi | [21] | — | — |
| Pt | — | [36,40] | — |
| Other materials | |||
| Carbon nanotubes | — | [190] | — |
| MOFs 2 | [228] | — | [229] |
| Zeolites | [193] | — | — |
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sarafoleanu, C.; Mella, C.; Georgescu, M.; Perederco, C. The importance of the olfactory sense in the human behavior and evolution. J. Med. Life 2009, 2, 196–198. [Google Scholar] [PubMed]
- Gottfried, J.A. Function follows form: Ecological constraints on odor codes and olfactory percepts. Curr. Opin. Neurobiol. 2009, 19, 422–429. [Google Scholar] [CrossRef] [PubMed]
- Persaud, K.; Dodd, G. Analysis of discrimination mechanisms in the mammalian olfactory system using a model nose. Nature 1982, 299, 352–355. [Google Scholar] [CrossRef]
- Gardner, J.W.; Bartlett, P.N. A brief history of electronic noses. Sens. Actuators B Chem. 1994, 18, 210–211. [Google Scholar] [CrossRef]
- Manzini, I.; Schild, D.; Di Natale, C. Principles of odor coding in vertebrates and artificial chemosensory systems. Physiol. Rev. 2022, 102, 61–154. [Google Scholar] [CrossRef]
- Kim, C.; Raja, I.S.; Lee, J.M.; Lee, J.H.; Kang, M.S.; Lee, S.H.; Oh, J.W.; Han, D.W. Recent Trends in Exhaled Breath Diagnosis Using an Artificial Olfactory System. Biosensors 2021, 11, 337. [Google Scholar] [CrossRef]
- Archibald, R.; Datskos, P.; Devault, G.; Lamberti, V.; Lavrik, N.; Noid, D.; Sepaniak, M.; Dutta, P. Independent component analysis of nanomechanical responses of cantilever arrays. Anal. Chim. Acta 2007, 584, 101–105. [Google Scholar] [CrossRef]
- Shiba, K.; Tamura, R.; Imamura, G.; Yoshikawa, G. Data-driven nanomechanical sensing: Specific information extraction from a complex system. Sci. Rep. 2017, 7, 3661. [Google Scholar] [CrossRef]
- Shiba, K.; Tamura, R.; Sugiyama, T.; Kameyama, Y.; Koda, K.; Sakon, E.; Minami, K.; Ngo, H.T.; Imamura, G.; Tsuda, K.; et al. Functional Nanoparticles-Coated Nanomechanical Sensor Arrays for Machine Learning-Based Quantitative Odor Analysis. ACS Sens. 2018, 3, 1592–1600. [Google Scholar] [CrossRef]
- Xu, H.; Kitai, K.; Minami, K.; Nakatsu, M.; Yoshikawa, G.; Tsuda, K.; Shiba, K.; Tamura, R. Determination of quasi-primary odors by endpoint detection. Sci. Rep. 2021, 11, 12070. [Google Scholar] [CrossRef]
- Albert, K.J.; Lewis, N.S.; Schauer, C.L.; Sotzing, G.A.; Stitzel, S.E.; Vaid, T.P.; Walt, D.R. Cross-reactive chemical sensor arrays. Chem. Rev. 2000, 100, 2595–2626. [Google Scholar] [CrossRef] [PubMed]
- Baldwin, E.A.; Bai, J.; Plotto, A.; Dea, S. Electronic noses and tongues: Applications for the food and pharmaceutical industries. Sensors 2011, 11, 4744–4766. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.D. Review of Electronic-nose Technologies and Algorithms to Detect Hazardous Chemicals in the Environment. Proc. Technol. 2012, 1, 453–463. [Google Scholar] [CrossRef]
- Konvalina, G.; Haick, H. Sensors for breath testing: From nanomaterials to comprehensive disease detection. Acc. Chem. Res. 2014, 47, 66–76. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez, J.; Horrillo, M.C. Advances in artificial olfaction: Sensors and applications. Talanta 2014, 124, 95–105. [Google Scholar] [CrossRef]
- Potyrailo, R.A. Multivariable Sensors for Ubiquitous Monitoring of Gases in the Era of Internet of Things and Industrial Internet. Chem. Rev. 2016, 116, 11877–11923. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.-W.; Lee, J.-H. Toward breath analysis on a chip for disease diagnosis using semiconductor-based chemiresistors: Recent progress and future perspectives. Lab Chip 2017, 17, 3537–3557. [Google Scholar] [CrossRef]
- Kou, L.; Zhang, D.; Liu, D. A Novel Medical E-Nose Signal Analysis System. Sensors 2017, 17, 402. [Google Scholar] [CrossRef]
- Sysoev, V.V.; Goschnick, J.; Schneider, T.; Strelcov, E.; Kolmakov, A. A gradient microarray electronic nose based on percolating SnO2 nanowire sensing elements. Nano Lett. 2007, 7, 3182–3188. [Google Scholar] [CrossRef]
- Yakabe, T.; Imamura, G.; Yoshikawa, G.; Kitajima, M.; Itakura, A.N. Hydrogen detection using membrane-type surface stress sensor. J. Phys. Commun. 2020, 4, 025005. [Google Scholar] [CrossRef]
- Yakabe, T.; Imamura, G.; Yoshikawa, G.; Miyauchi, N.; Kitajima, M.; Itakura, A.N. 2-step reaction kinetics for hydrogen absorption into bulk material via dissociative adsorption on the surface. Sci. Rep. 2021, 11, 18836. [Google Scholar] [CrossRef] [PubMed]
- Rinaldi, A. The scent of life. The exquisite complexity of the sense of smell in animals and humans. EMBO Rep. 2007, 8, 629–633. [Google Scholar] [CrossRef] [PubMed]
- Zak, J.D.; Reddy, G.; Vergassola, M.; Murthy, V.N. Antagonistic odor interactions in olfactory sensory neurons are widespread in freely breathing mice. Nat. Commun. 2020, 11, 3350. [Google Scholar] [CrossRef]
- Goeders, K.M.; Colton, J.S.; Bottomley, L.A. Microcantilevers: Sensing chemical interactions via mechanical motion. Chem. Rev. 2008, 108, 522–542. [Google Scholar] [CrossRef] [PubMed]
- Arlett, J.L.; Myers, E.B.; Roukes, M.L. Comparative advantages of mechanical biosensors. Nat. Nanotechnol. 2011, 6, 203–215. [Google Scholar] [CrossRef]
- Hanay, M.S.; Kelber, S.; Naik, A.K.; Chi, D.; Hentz, S.; Bullard, E.C.; Colinet, E.; Duraffourg, L.; Roukes, M.L. Single-protein nanomechanical mass spectrometry in real time. Nat. Nanotechnol. 2012, 7, 602–608. [Google Scholar] [CrossRef]
- Kosaka, P.M.; Pini, V.; Ruz, J.J.; da Silva, R.A.; Gonzalez, M.U.; Ramos, D.; Calleja, M.; Tamayo, J. Detection of cancer biomarkers in serum using a hybrid mechanical and optoplasmonic nanosensor. Nat. Nanotechnol. 2014, 9, 1047–1053. [Google Scholar] [CrossRef]
- Malvar, O.; Ruz, J.J.; Kosaka, P.M.; Dominguez, C.M.; Gil-Santos, E.; Calleja, M.; Tamayo, J. Mass and stiffness spectrometry of nanoparticles and whole intact bacteria by multimode nanomechanical resonators. Nat. Commun. 2016, 7, 13452. [Google Scholar] [CrossRef]
- Chien, M.H.; Brameshuber, M.; Rossboth, B.K.; Schutz, G.J.; Schmid, S. Single-molecule optical absorption imaging by nanomechanical photothermal sensing. Proc. Natl. Acad. Sci. USA 2018, 115, 11150–11155. [Google Scholar] [CrossRef]
- Garcia, R. Nanomechanical mapping of soft materials with the atomic force microscope: Methods, theory and applications. Chem. Soc. Rev. 2020, 49, 5850–5884. [Google Scholar] [CrossRef]
- Pujol-Vila, F.; Villa, R.; Alvarez, M. Nanomechanical Sensors as a Tool for Bacteria Detection and Antibiotic Susceptibility Testing. Front. Mech. Eng. 2020, 6, 44. [Google Scholar] [CrossRef]
- Ruz, J.J.; Malvar, O.; Gil-Santos, E.; Ramos, D.; Calleja, M.; Tamayo, J. A Review on Theory and Modelling of Nanomechanical Sensors for Biological Applications. Processes 2021, 9, 164. [Google Scholar] [CrossRef]
- Minami, K. Nanomechanical Sensors for Gas Detection towards Artificial Olfaction. Biosensors 2022, 12, 256. [Google Scholar] [CrossRef]
- Young, J.M.; Shykind, B.M.; Lane, R.P.; Tonnes-Priddy, L.; Ross, J.A.; Walker, M.; Williams, E.M.; Trask, B.J. Odorant receptor expressed sequence tags demonstrate olfactory expression of over 400 genes, extensive alternate splicing and unequal expression levels. Genome Biol. 2003, 4, R71. [Google Scholar] [CrossRef]
- Lang, H.P.; Battiston, F.M.; Baller, M.K.; Berger, R.; Ramseyer, J.-P.; Fornaro, P.; Meyer, E.; Güntherodt, H.-J.; Andreoli, C.; Brugger, J.; et al. An Electronic Nose Based on A Micromechanical Cantilever Array. Micro Total Anal. Syst. 1998, 98, 57–60. [Google Scholar] [CrossRef]
- Lang, H.P.; Baller, M.K.; Berger, R.; Gerber, C.; Gimzewski, J.K.; Battiston, F.M.; Fornaro, P.; Ramseyer, J.P.; Meyer, E.; Güntherodt, H.J. An artificial nose based on a micromechanical cantilever array. Anal. Chim. Acta 1999, 393, 59–65. [Google Scholar] [CrossRef]
- Baller, M.K.; Lang, H.P.; Fritz, J.; Gerber, C.; Gimzewski, J.K.; Drechsler, U.; Rothuizen, H.; Despont, M.; Vettiger, P.; Battiston, F.M.; et al. A cantilever array-based artificial nose. Ultramicroscopy 2000, 82, 1–9. [Google Scholar] [CrossRef]
- Yoshikawa, G.; Akiyama, T.; Gautsch, S.; Vettiger, P.; Rohrer, H. Nanomechanical membrane-type surface stress sensor. Nano Lett. 2011, 11, 1044–1048. [Google Scholar] [CrossRef]
- Yoshikawa, G.; Akiyama, T.; Loizeau, F.; Shiba, K.; Gautsch, S.; Nakayama, T.; Vettiger, P.; de Rooij, N.F.; Aono, M. Two dimensional array of piezoresistive nanomechanical Membrane-type Surface Stress Sensor (MSS) with improved sensitivity. Sensors 2012, 12, 15873–15887. [Google Scholar] [CrossRef]
- Gimzewski, J.K.; Gerber, C.; Meyer, E.; Schlittler, R.R. Observation of a chemical reaction using a micromechanical sensor. Chem. Phys. Lett. 1994, 217, 589–594. [Google Scholar] [CrossRef]
- Thundat, T.; Warmack, R.J.; Chen, G.Y.; Allison, D.P. Thermal and ambient-induced deflections of scanning force microscope cantilevers. Appl. Phys. Lett. 1994, 64, 2894–2896. [Google Scholar] [CrossRef]
- Loizeau, F.; Akiyama, T.; Gautsch, S.; Vettiger, P.; Yoshikawa, G.; de Rooij, N. Membrane-Type Surface Stress Sensor with Piezoresistive Readout. Proc. Eng. 2012, 47, 1085–1088. [Google Scholar] [CrossRef]
- Yaqoob, U.; Jaber, N.; Alcheikh, N.; Younis, M.I. Selective multiple analyte detection using multi-mode excitation of a MEMS resonator. Sci. Rep. 2022, 12, 5297. [Google Scholar] [CrossRef]
- Thundat, T.; Wachter, E.A.; Sharp, S.L.; Warmack, R.J. Detection of mercury vapor using resonating microcantilevers. Appl. Phys. Lett. 1995, 66, 1695–1697. [Google Scholar] [CrossRef]
- Berger, R.d.; Delamarche, E.; Lang, H.P.; Gerber, C.; Gimzewski, J.K.; Meyer, E.; Güntherodt, H.-J. Surface Stress in the Self-Assembly of Alkanethiols on Gold. Science 1997, 276, 2021–2024. [Google Scholar] [CrossRef]
- Fritz, J.; Baller, M.K.; Lang, H.P.; Rothuizen, H.; Vettiger, P.; Meyer, E.; Guntherodt, H.; Gerber, C.; Gimzewski, J.K. Translating biomolecular recognition into nanomechanics. Science 2000, 288, 316–318. [Google Scholar] [CrossRef] [PubMed]
- Mertens, J.; Rogero, C.; Calleja, M.; Ramos, D.; Martin-Gago, J.A.; Briones, C.; Tamayo, J. Label-free detection of DNA hybridization based on hydration-induced tension in nucleic acid films. Nat. Nanotechnol. 2008, 3, 301–307. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, C.M.; Ramos, D.; Mendieta-Moreno, J.I.; Fierro, J.L.G.; Mendieta, J.; Tamayo, J.; Calleja, M. Effect of water-DNA interactions on elastic properties of DNA self-assembled monolayers. Sci. Rep. 2017, 7, 536. [Google Scholar] [CrossRef]
- Rugar, D.; Budakian, R.; Mamin, H.J.; Chui, B.W. Single spin detection by magnetic resonance force microscopy. Nature 2004, 430, 329–332. [Google Scholar] [CrossRef]
- Barson, M.S.; Peddibhotla, P.; Ovartchaiyapong, P.; Ganesan, K.; Taylor, R.L.; Gebert, M.; Mielens, Z.; Koslowski, B.; Simpson, D.A.; McGuinness, L.P.; et al. Nanomechanical Sensing Using Spins in Diamond. Nano Lett. 2017, 17, 1496–1503. [Google Scholar] [CrossRef]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.; Alegre, T.P.; Safavi-Naeini, A.H.; Hill, J.T.; Krause, A.; Groblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 2011, 478, 89–92. [Google Scholar] [CrossRef] [PubMed]
- Waggoner, P.S.; Craighead, H.G. Micro- and nanomechanical sensors for environmental, chemical, and biological detection. Lab Chip 2007, 7, 1238–1255. [Google Scholar] [CrossRef]
- Boisen, A.; Dohn, S.; Keller, S.S.; Schmid, S.; Tenje, M. Cantilever-like micromechanical sensors. Rep. Prog. Phys. 2011, 74, 036101. [Google Scholar] [CrossRef]
- Yoshikawa, G. Nanomechanical Sensors and Membrane-type Surface Stress Sensor (MSS) for Medical, Security and Environmental Applications. In Manipulation of Nanoscale Materials: An Introduction to Nanoarchitectonics; Ariga, K., Ed.; RSC: London, UK, 2012; pp. 428–448. [Google Scholar] [CrossRef]
- Tamayo, J.; Kosaka, P.M.; Ruz, J.J.; San Paulo, A.; Calleja, M. Biosensors based on nanomechanical systems. Chem. Soc. Rev. 2013, 42, 1287–1311. [Google Scholar] [CrossRef]
- Shiba, K.; Imamura, G.; Yoshikawa, G. Nanomechanical Sensors. In Biomaterials Nanoarchitectonics; Ebara, M., Ed.; Elsevier: Oxford, UK, 2016; pp. 177–196. [Google Scholar] [CrossRef]
- Ngo, H.T.; Minami, K.; Shiba, K.; Yoshikawa, G. Advanced Nanomechanical Sensor for Artificial Olfactory System: Membrane-Type Surface Stress Sensor (MSS). In System-Materials Nanoarchitectonics; Wakayama, Y., Ariga, K., Eds.; Springer: Tokyo, Japan, 2022; pp. 169–180. [Google Scholar] [CrossRef]
- Gil-Santos, E.; Ramos, D.; Martinez, J.; Fernandez-Regulez, M.; Garcia, R.; San Paulo, A.; Calleja, M.; Tamayo, J. Nanomechanical mass sensing and stiffness spectrometry based on two-dimensional vibrations of resonant nanowires. Nat. Nanotechnol. 2010, 5, 641–645. [Google Scholar] [CrossRef] [PubMed]
- Malvar, O.; Gil-Santos, E.; Ruz, J.J.; Ramos, D.; Pini, V.; Fernandez-Regulez, M.; Calleja, M.; Tamayo, J.; San Paulo, A. Tapered silicon nanowires for enhanced nanomechanical sensing. Appl. Phys. Lett. 2013, 103, 033101. [Google Scholar] [CrossRef]
- Dominguez-Medina, S.; Fostner, S.; Defoort, M.; Sansa, M.; Stark, A.K.; Halim, M.A.; Vernhes, E.; Gely, M.; Jourdan, G.; Alava, T.; et al. Neutral mass spectrometry of virus capsids above 100 megadaltons with nanomechanical resonators. Science 2018, 362, 918–922. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.T.; Callegari, C.; Feng, X.L.; Ekinci, K.L.; Roukes, M.L. Zeptogram-scale nanomechanical mass sensing. Nano Lett. 2006, 6, 583–586. [Google Scholar] [CrossRef]
- Li, M.; Tang, H.X.; Roukes, M.L. Ultra-sensitive NEMS-based cantilevers for sensing, scanned probe and very high-frequency applications. Nat. Nanotechnol. 2007, 2, 114–120. [Google Scholar] [CrossRef]
- Naik, A.K.; Hanay, M.S.; Hiebert, W.K.; Feng, X.L.; Roukes, M.L. Towards single-molecule nanomechanical mass spectrometry. Nat. Nanotechnol. 2009, 4, 445–450. [Google Scholar] [CrossRef] [PubMed]
- Hanay, M.S.; Kelber, S.I.; O’Connell, C.D.; Mulvaney, P.; Sader, J.E.; Roukes, M.L. Inertial imaging with nanomechanical systems. Nat. Nanotechnol. 2015, 10, 339–344. [Google Scholar] [CrossRef] [PubMed]
- Sage, E.; Brenac, A.; Alava, T.; Morel, R.; Dupre, C.; Hanay, M.S.; Roukes, M.L.; Duraffourg, L.; Masselon, C.; Hentz, S. Neutral particle mass spectrometry with nanomechanical systems. Nat. Commun. 2015, 6, 6482. [Google Scholar] [CrossRef] [PubMed]
- Ramos, D.; Malvar, O.; Davis, Z.J.; Tamayo, J.; Calleja, M. Nanomechanical Plasmon Spectroscopy of Single Gold Nanoparticles. Nano Lett. 2018, 18, 7165–7170. [Google Scholar] [CrossRef] [PubMed]
- Demir, A. Adaptive Time-Resolved Mass Spectrometry With Nanomechanical Resonant Sensors. IEEE Sens. J. 2021, 21, 27582–27589. [Google Scholar] [CrossRef]
- Martin-Perez, A.; Ramos, D.; Tamayo, J.; Calleja, M. Nanomechanical Molecular Mass Sensing Using Suspended Microchannel Resonators. Sensors 2021, 21, 3337. [Google Scholar] [CrossRef]
- Hajjaj, A.Z.; Jaber, N.; Alcheikh, N.; Younis, M.I. A Resonant Gas Sensor Based on Multimode Excitation of a Buckled Microbeam. IEEE Sens. J. 2020, 20, 1778–1785. [Google Scholar] [CrossRef]
- Tsumune, K.; Warisawa, S.i.; Kometani, R. Highly sensitive vibration measurement method of nanomechanical resonators using a convolutional neural network. Jpn. J. Appl. Phys. 2022, 61, Sd1038. [Google Scholar] [CrossRef]
- Stachiv, I.; Machů, Z.; Ševeček, O.; Tuhovcak, O.; Kotoul, M.; Jeng, Y.-R. Resolving measurement of large (~ GDa) chemical/biomolecule complexes with multimode nanomechanical resonators. Sens. Actuators B Chem. 2022, 353, 131062. [Google Scholar] [CrossRef]
- Stoney, G.G. The Tension of Metallic Films Deposited by Electrolysis. Proc. R. Soc. London Ser. A 1909, 82, 172–175. [Google Scholar] [CrossRef]
- Chu, W.-H.; Mehregany, M.; Mullen, R.L. Analysis of tip deflection and force of a bimetallic cantilever microactuator. J. Micromech. Microeng. 1993, 3, 4–7. [Google Scholar] [CrossRef]
- Minami, K.; Yoshikawa, G. Effects of partial attachment at the interface between receptor and substrate on nanomechanical cantilever sensing. Sens. Actuators A Phys. 2021, 319, 112533. [Google Scholar] [CrossRef]
- Zeng, X.; Deng, J.; Luo, X. Deflection of a cantilever rectangular plate induced by surface stress with applications to surface stress measurement. J. Appl. Phys. 2012, 111, 083531. [Google Scholar] [CrossRef]
- Sader, J.E. Surface stress induced deflections of cantilever plates with applications to the atomic force microscope: Rectangular plates. J. Appl. Phys. 2001, 89, 2911–2921. [Google Scholar] [CrossRef]
- Tamayo, J.; Ruz, J.J.; Pini, V.; Kosaka, P.; Calleja, M. Quantification of the surface stress in microcantilever biosensors: Revisiting Stoney’s equation. Nanotechnology 2012, 23, 475702. [Google Scholar] [CrossRef]
- Timoshenko, S. Analysis of Bi-Metal Thermostats. J. Opt. Soc. Am. 1925, 11, 233. [Google Scholar] [CrossRef]
- Yoshikawa, G. Mechanical analysis and optimization of a microcantilever sensor coated with a solid receptor film. Appl. Phys. Lett. 2011, 98, 173502. [Google Scholar] [CrossRef]
- Sader, J.E. Surface stress induced deflections of cantilever plates with applications to the atomic force microscope: V-shaped plates. J. Appl. Phys. 2002, 91, 9354–9361. [Google Scholar] [CrossRef]
- Lachut, M.J.; Sader, J.E. Effect of surface stress on the stiffness of cantilever plates. Phys. Rev. Lett. 2007, 99, 206102. [Google Scholar] [CrossRef]
- Lachut, M.J.; Sader, J.E. Effect of surface stress on the stiffness of thin elastic plates and beams. Phys. Rev. B 2012, 85, 085440. [Google Scholar] [CrossRef]
- Klein, C.A. How accurate are Stoney’s equation and recent modifications. J. Appl. Phys. 2000, 88, 5487–5489. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.-p. Applicability range of Stoney’s formula and modified formulas for a film/substrate bilayer. J. Appl. Phys. 2006, 99, 053513. [Google Scholar] [CrossRef]
- Zhang, Y. Extended Stoney’s formula for a film-substrate bilayer with the effect of interfacial slip. J. Appl. Mech. 2008, 75, 011008. [Google Scholar] [CrossRef]
- Chou, T.-L.; Yang, S.-Y.; Chiang, K.-N. Overview and applicability of residual stress estimation of film–substrate structure. Thin Solid Films 2011, 519, 7883–7894. [Google Scholar] [CrossRef]
- Liu, H.; Dai, M.; Tian, X.; Chen, S.; Dong, F.; Lu, L. Modified Stoney formula for determining stress within thin films on large-deformation isotropic circular plates. AIP Adv. 2021, 11, 125009. [Google Scholar] [CrossRef]
- Yoshikawa, G.; Loizeau, F.; Lee, C.J.Y.; Akiyama, T.; Shiba, K.; Gautsch, S.; Nakayama, T.; Vettiger, P.; de Rooij, N.F.; Aono, M. Double-side-coated nanomechanical membrane-type surface stress sensor (MSS) for one-chip-one-channel setup. Langmuir 2013, 29, 7551–7556. [Google Scholar] [CrossRef]
- Imamura, G.; Shiba, K.; Yoshikawa, G. Finite Element Analysis on Nanomechanical Detection of Small Particles: Toward Virus Detection. Front. Microbiol. 2016, 7, 488. [Google Scholar] [CrossRef]
- Imamura, G.; Shiba, K.; Yoshikawa, G. Finite Element Analysis on Nanomechanical Sensing of Cellular Forces. Anal. Sci. 2016, 32, 1189–1194. [Google Scholar] [CrossRef]
- Minami, K.; Yoshikawa, G. Finite Element Analysis of Interface Dependence on Nanomechanical Sensing. Sensors 2020, 20, 1518. [Google Scholar] [CrossRef]
- Hu, Z.; Thundat, T.; Warmack, R.J. Investigation of adsorption and absorption-induced stresses using microcantilever sensors. J. Appl. Phys. 2001, 90, 427–431. [Google Scholar] [CrossRef]
- Dareing, D.W.; Thundat, T. Simulation of adsorption-induced stress of a microcantilever sensor. J. Appl. Phys. 2005, 97, 043526. [Google Scholar] [CrossRef]
- Wenzel, M.J.; Josse, F.; Heinrich, S.M.; Yaz, E.; Datskos, P.G. Sorption-induced static bending of microcantilevers coated with viscoelastic material. J. Appl. Phys. 2008, 103, 064913. [Google Scholar] [CrossRef]
- Minami, K.; Shiba, K.; Yoshikawa, G. Sorption-induced static mode nanomechanical sensing with viscoelastic receptor layers for multistep injection-purge cycles. J. Appl. Phys. 2021, 129, 124503. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: New York, NY, USA, 1980; p. 608. [Google Scholar]
- Flügge, W. Viscoelasticity, 2nd ed.; Springer: New York, NY, USA, 1975. [Google Scholar]
- Imamura, G.; Shiba, K.; Yoshikawa, G.; Washio, T. Analysis of nanomechanical sensing signals; physical parameter estimation for gas identification. AIP Adv. 2018, 8, 075007. [Google Scholar] [CrossRef]
- Minami, K.; Shiba, K.; Imamura, G.; Yoshikawa, G. Identification of gas species and their concentrations by using sorption kinetics of viscoelastic film. In Proceedings of the 2022 IEEE International Symposium on Olfaction and Electronic Nose (ISOEN), Aveiro, Portugal, 29 May–1 June 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Barnes, J.R.; Stephenson, R.J.; Welland, M.E.; Gerber, C.; Gimzewski, J.K. Photothermal spectroscopy with femtojoule sensitivity using a micromechanical device. Nature 1994, 372, 79–81. [Google Scholar] [CrossRef]
- McKendry, R.; Zhang, J.; Arntz, Y.; Strunz, T.; Hegner, M.; Lang, H.P.; Baller, M.K.; Certa, U.; Meyer, E.; Guntherodt, H.J.; et al. Multiple label-free biodetection and quantitative DNA-binding assays on a nanomechanical cantilever array. Proc. Natl. Acad. Sci. USA 2002, 99, 9783–9788. [Google Scholar] [CrossRef] [PubMed]
- Backmann, N.; Zahnd, C.; Huber, F.; Bietsch, A.; Plückthun, A.; Lang, H.-P.; Güntherodt, H.-J.; Hegner, M.; Gerber, C. A label-free immunosensor array using single-chain antibody fragments. Proc. Natl. Acad. Sci. USA 2005, 102, 14587–14592. [Google Scholar] [CrossRef]
- Zhang, J.; Lang, H.P.; Huber, F.; Bietsch, A.; Grange, W.; Certa, U.; McKendry, R.; Guntherodt, H.J.; Hegner, M.; Gerber, C. Rapid and label-free nanomechanical detection of biomarker transcripts in human RNA. Nat. Nanotechnol. 2006, 1, 214–220. [Google Scholar] [CrossRef]
- Watari, M.; Galbraith, J.; Lang, H.P.; Sousa, M.; Hegner, M.; Gerber, C.; Horton, M.A.; McKendry, R.A. Investigating the molecular mechanisms of in-plane mechanochemistry on cantilever arrays. J. Am. Chem. Soc. 2007, 129, 601–609. [Google Scholar] [CrossRef]
- Ndieyira, J.W.; Watari, M.; Barrera, A.D.; Zhou, D.; Vogtli, M.; Batchelor, M.; Cooper, M.A.; Strunz, T.; Horton, M.A.; Abell, C.; et al. Nanomechanical detection of antibiotic-mucopeptide binding in a model for superbug drug resistance. Nat. Nanotechnol. 2008, 3, 691–696. [Google Scholar] [CrossRef] [PubMed]
- Raorane, D.A.; Lim, M.D.; Chen, F.F.; Craik, C.S.; Majumdar, A. Quantitative and label-free technique for measuring protease activity and inhibition using a microfluidic cantilever array. Nano Lett. 2008, 8, 2968–2974. [Google Scholar] [CrossRef] [PubMed]
- Tortonese, M.; Barrett, R.C.; Quate, C.F. Atomic resolution with an atomic force microscope using piezoresistive detection. Appl. Phys. Lett. 1993, 62, 834–836. [Google Scholar] [CrossRef]
- Lutwyche, M.; Andreoli, C.; Binnig, G.; Brugger, J.; Drechsler, U.; Häberle, W.; Rohrer, H.; Rothuizen, H.; Vettiger, P.; Yaralioglu, G.; et al. 5 × 5 2D AFM cantilever arrays a first step towards a Terabit storage device. Sens. Actuators A Phys. 1999, 73, 89–94. [Google Scholar] [CrossRef]
- Thaysen, J.; Boisen, A.; Hansen, O.; Bouwstra, S. Atomic force microscopy probe with piezoresistive read-out and a highly symmetrical Wheatstone bridge arrangement. Sens. Actuators A Phys. 2000, 83, 47–53. [Google Scholar] [CrossRef]
- Hierlemann, A.; Lange, D.; Hagleitner, C.; Kerness, N.; Koll, A.; Brand, O.; Baltes, H. Application-specific sensor systems based on CMOS chemical microsensors. Sens. Actuators B Chem. 2000, 70, 2–11. [Google Scholar] [CrossRef]
- Akiyama, T.; Gautsch, S.; de Rooij, N.F.; Staufer, U.; Niedermann, P.; Howald, L.; Müller, D.; Tonin, A.; Hidber, H.R.; Pike, W.T.; et al. Atomic force microscope for planetary applications. Sens. Actuators A Phys. 2001, 91, 321–325. [Google Scholar] [CrossRef]
- Gautsch, S.; Akiyama, T.; Imer, R.; de Rooij, N.F.; Staufer, U.; Niedermann, P.; Howald, L.; Brändlin, D.; Tonin, A.; Hidber, H.R.; et al. Measurement of quartz particles by means of an atomic force microscope for planetary exploration. Surf. Interface Anal. 2002, 33, 163–167. [Google Scholar] [CrossRef]
- Mukhopadhyay, R.; Sumbayev, V.V.; Lorentzen, M.; Kjems, J.; Andreasen, P.A.; Besenbacher, F. Cantilever sensor for nanomechanical detection of specific protein conformations. Nano Lett. 2005, 5, 2385–2388. [Google Scholar] [CrossRef]
- Aeschimann, L.; Meister, A.; Akiyama, T.; Chui, B.W.; Niedermann, P.; Heinzelmann, H.; De Rooij, N.F.; Staufer, U.; Vettiger, P. Scanning probe arrays for life sciences and nanobiology applications. Microelectron. Eng. 2006, 83, 1698–1701. [Google Scholar] [CrossRef]
- Arlett, J.L.; Maloney, J.R.; Gudlewski, B.; Muluneh, M.; Roukes, M.L. Self-Sensing Micro- and Nanocantilevers with Attonewton-Scale Force Resolution. Nano Lett. 2006, 6, 1000–1006. [Google Scholar] [CrossRef]
- Hecht, M.H.; Marshall, J.; Pike, W.T.; Staufer, U.; Blaney, D.; Braendlin, D.; Gautsch, S.; Goetz, W.; Hidber, H.R.; Keller, H.U.; et al. Microscopy capabilities of the Microscopy, Electrochemistry, and Conductivity Analyzer. J. Geophys. Res. Plants 2008, 113, E00A22. [Google Scholar] [CrossRef]
- Yoshikawa, G.; Lang, H.-P.; Akiyama, T.; Aeschimann, L.; Staufer, U.; Vettiger, P.; Aono, M.; Sakurai, T.; Gerber, C. Sub-ppm detection of vapors using piezoresistive microcantilever array sensors. Nanotechnology 2009, 20, 015501. [Google Scholar] [CrossRef] [PubMed]
- Boisen, A.; Thundat, T. Design & fabrication of cantilever array biosensors. Mater. Today 2009, 12, 32–38. [Google Scholar] [CrossRef]
- Yu, X.; Tang, Y.; Zhang, H.; Li, T.; Wang, W. Design of High-Sensitivity Cantilever and Its Monolithic Integration With CMOS Circuits. IEEE Sens. J. 2007, 7, 489–495. [Google Scholar] [CrossRef]
- Privorotskaya, N.L.; King, W.P. The mechanics of polymer swelling on microcantilever sensors. Microsys. Technol. 2008, 15, 333–340. [Google Scholar] [CrossRef]
- Goericke, F.T.; King, W.P. Modeling Piezoresistive Microcantilever Sensor Response to Surface Stress for Biochemical Sensors. IEEE Sens. J. 2008, 8, 1404–1410. [Google Scholar] [CrossRef]
- Loui, A.; Goericke, F.T.; Ratto, T.V.; Lee, J.; Hart, B.R.; King, W.P. The effect of piezoresistive microcantilever geometry on cantilever sensitivity during surface stress chemical sensing. Sens. Actuators A Phys. 2008, 147, 516–521. [Google Scholar] [CrossRef]
- Momin, M.A.; Wang, Z.; Toda, M.; Yamazaki, M.; Moorthi, K.; Kawaguchi, Y.; Ono, T. Development of Nanomechanical Multisensory Arrays for Detection of Hazardous Volatile Materials and Gases. In Proceedings of the 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS), Tokyo, Japan, 9–13 January 2022; pp. 732–734. [Google Scholar] [CrossRef]
- Pfann, W.G.; Thurston, R.N. Semiconducting Stress Transducers Utilizing the Transverse and Shear Piezoresistance Effects. J. Appl. Phys. 1961, 32, 2008–2019. [Google Scholar] [CrossRef]
- Kanda, Y. A graphical representation of the piezoresistance coefficients in silicon. IEEE Trans. Electron Devices 1982, 29, 64–70. [Google Scholar] [CrossRef]
- Kanda, Y. Piezoresistance effect of silicon. Sens. Actuators A Phys. 1991, 28, 83–91. [Google Scholar] [CrossRef]
- Rasmussen, P.A.; Hansen, O.; Boisen, A. Cantilever surface stress sensors with single-crystalline silicon piezoresistors. Appl. Phys. Lett. 2005, 86, 203502. [Google Scholar] [CrossRef]
- Tina, B.S.; Joel, Z.; Rao, R.S.S.; Seena, V. Silicon MEMS Nanomechanical Membrane Flexure Sensor With Integrated High Gauge Factor ITO. J. Microelectromech. Sys. 2021, 30, 939–949. [Google Scholar] [CrossRef]
- Miller, T.M.; Fang, H.; Magruder, R.H.; Weller, R.A. Fabrication of a micro-scale, indium-tin-oxide thin film strain-sensor by pulsed laser deposition and focused ion beam machining. Sens. Actuators A Phys. 2003, 104, 162–170. [Google Scholar] [CrossRef]
- Rasia, L.A.; Mansano, R.D.; Damiani, L.R.; Viana, C.E. Piezoresistive response of ITO films deposited at room temperature by magnetron sputtering. J. Mater. Sci. 2010, 45, 4224–4228. [Google Scholar] [CrossRef]
- Vamshi, G.P.; Tina, B.S.; Seena, V. Polymer Based Hybrid Membrane-Flexure Nanomechanical Piezoresistive Sensor. In Proceedings of the 2018 IEEE Sensors, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Yen, Y.K.; Chiu, C.Y. A CMOS MEMS-based Membrane-Bridge Nanomechanical Sensor for Small Molecule Detection. Sci. Rep. 2020, 10, 2931. [Google Scholar] [CrossRef]
- Jackman, J.A.; Cho, N.J.; Nishikawa, M.; Yoshikawa, G.; Mori, T.; Shrestha, L.K.; Ariga, K. Materials Nanoarchitectonics for Mechanical Tools in Chemical and Biological Sensing. Chem. Asian J. 2018, 13, 3366–3377. [Google Scholar] [CrossRef]
- Minami, K.; Shiba, K.; Imamura, G.; Ngo, H.T.; Yoshikawa, G. Highly Sensi tive and Selective Receptor Materials for Membrane-type Surface Stress Sensor (MSS) and their Applications as an Artificial Olfaction. J. Jpn. Assoc. Odor. Environ. 2018, 49, 297–304. [Google Scholar] [CrossRef]
- Ngo, H.T.; Minami, K.; Imamura, G.; Shiba, K.; Yoshikawa, G. Membrane-type Surface stress Sensor (MSS) for artificial olfactory system. In Chemical, Gas, and Biosensors for Internet of Things and Related Applications; Elsevier Science Publishing Co Inc.: Amsterdam, The Netherlands, 2019; pp. 27–38. [Google Scholar] [CrossRef]
- Ngo, H.T.; Minami, K.; Imamura, G.; Shiba, K.; Yoshikawa, G. Membrane-type Surface Stress Sensor (MSS) for Artificial Olfaction. In Proceedings of the 2019 IEEE International Symposium on Olfaction and Electronic Nose (ISOEN), Fukuoka, Japan, 26–29 May 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Shiba, K.; Sugiyama, T.; Takei, T.; Yoshikawa, G. Controlled growth of silica-titania hybrid functional nanoparticles through a multistep microfluidic approach. Chem. Commun. 2015, 51, 15854–15857. [Google Scholar] [CrossRef]
- Osica, I.; Imamura, G.; Shiba, K.; Ji, Q.; Shrestha, L.K.; Hill, J.P.; Kurzydłowski, K.J.; Yoshikawa, G.; Ariga, K. Highly Networked Capsular Silica-Porphyrin Hybrid Nanostructures as Efficient Materials for Acetone Vapor Sensing. ACS Appl. Mater. Interfaces 2017, 9, 9945–9954. [Google Scholar] [CrossRef]
- Ji, Q.; Guo, C.; Yu, X.; Ochs, C.J.; Hill, J.P.; Caruso, F.; Nakazawa, H.; Ariga, K. Flake-shell capsules: Adjustable inorganic structures. Small 2012, 8, 2345–2349. [Google Scholar] [CrossRef]
- Ji, Q.; Ishihara, S.; Terentyeva, T.G.; Deguchi, K.; Ohki, S.; Tansho, M.S.; Shimizu, T.; Hill, J.P.; Ariga, K. Manipulation of shell morphology of silicate spheres from structural evolution in a purely inorganic system. Chem. Asian J. 2015, 10, 1379–1386. [Google Scholar] [CrossRef] [PubMed]
- MSS Forum. Available online: https://mss-forum.com/en/ (accessed on 8 August 2022).
- Minami, K.; Shiba, K.; Yoshikawa, G. Discrimination of structurally similar odorous molecules with various concentrations by using a nanomechanical sensor. Anal. Methods 2018, 10, 3720–3726. [Google Scholar] [CrossRef]
- Imamura, G.; Shiba, K.; Yoshikawa, G. Smell identification of spices using nanomechanical membrane-type surface stress sensors. Jpn. J. Appl. Phys. 2016, 55, 1102b3. [Google Scholar] [CrossRef]
- Shiba, K.; Imamura, G.; Yoshikawa, G. Odor-Based Nanomechanical Discrimination of Fuel Oils Using a Single Type of Designed Nanoparticles with Nonlinear Viscoelasticity. ACS Omega 2021, 6, 23389–23398. [Google Scholar] [CrossRef] [PubMed]
- Vempatapu, B.P.; Kanaujia, P.K. Monitoring petroleum fuel adulteration: A review of analytical methods. Trends. Anal. Chem. 2017, 92, 1–11. [Google Scholar] [CrossRef]
- Babu, V.; Krishna, R.; Mani, N. Review on the Detection of Adulteration in Fuels through Computational Techniques. Mater. Today Proc. 2017, 4, 1723–1729. [Google Scholar] [CrossRef]
- Fullman, B. Stereochemical Theory of Olfaction. Nature 1963, 199, 912. [Google Scholar] [CrossRef]
- Amoore, J.E. Directions for preparing aqueous solutions of primary odorants to diagnose eight types of specific anosmia. Chem. Sens. 1979, 4, 153–161. [Google Scholar] [CrossRef]
- Hsieh, M.D.; Zellers, E.T. Limits of recognition for simple vapor mixtures determined with a microsensor array. Anal. Chem. 2004, 76, 1885–1895. [Google Scholar] [CrossRef]
- Yoshinogawa Co. Ltd.; Asahi Kasei Corporation; National Institute for Materials Science; Nippon Telegraph and Telephone East Corporation (Niigata Branch). Conducting a Demonstration Experiment to Visualize Alcohol Content Using “Smell” Data in the Sake Manufacturing Process [Press release]. Available online: https://www.nims.go.jp/news/press/2020/04/202004210.html (accessed on 8 August 2022).
- Das, S.; Pal, M. Review—Non-Invasive Monitoring of Human Health by Exhaled Breath Analysis: A Comprehensive Review. J. Electrochem. Soc. 2020, 167, 037562. [Google Scholar] [CrossRef]
- Cheng, W.-H.; Lee, W.-J. Technology development in breath microanalysis for clinical diagnosis. J. Lab. Clin. Med. 1999, 133, 218–228. [Google Scholar] [CrossRef]
- Loizeau, F.; Lang, H.P.; Akiyama, T.; Gautsch, S.; Vettiger, P.; Tonin, A.; Yoshikawa, G.; Gerber, C.; de Rooij, N. Piezoresistive membrane-type surface stress sensor arranged in arrays for cancer diagnosis through breath analysis. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 621–624. [Google Scholar] [CrossRef]
- Lang, H.P.; Loizeau, F.; Hiou, A.; Rivals, J.-P.; Romero, P.; Akiyama, T.; Gerber, C.; Meyer, E. Piezoresistive membrane surface stress sensors for characterization of breath samples of head and neck cancer patients. In Proceedings of the 2nd International Electronic Conference on Sensors and Applications, Online, 15–30 November 2015. [Google Scholar] [CrossRef]
- Lang, H.P.; Loizeau, F.; Hiou-Feige, A.; Rivals, J.-P.; Romero, P.; Akiyama, T.; Gerber, C.; Meyer, E. Piezoresistive Membrane Surface Stress Sensors for Characterization of Breath Samples of Head and Neck Cancer Patients. Sensors 2016, 16, 1149. [Google Scholar] [CrossRef] [PubMed]
- Inada, K.; Kojima, H.; Cho-Isoda, Y.; Tamura, R.; Imamura, G.; Minami, K.; Nemoto, T.; Yoshikawa, G. Statistical Evaluation of Total Expiratory Breath Samples Collected throughout a Year: Reproducibility and Applicability toward Olfactory Sensor-Based Breath Diagnostics. Sensors 2021, 21, 4742. [Google Scholar] [CrossRef] [PubMed]
- Hines, E.L.; Llobet, E.; Gardner, J.W. Electronic noses: A review of signal processing techniques. IEE Proc. Circuits Devices Syst. 1999, 146, 297. [Google Scholar] [CrossRef]
- Nakamura, M.; Sugimoto, I.; Kuwano, H.; Lemos, R. Chemical sensing by analysing dynamics of plasma polymer film-coated sensors. Sens. Actuators B Chem. 1994, 20, 231–237. [Google Scholar] [CrossRef]
- Nakamura, M.; Sugimoto, I.; Kuwano, K. Application of plasma-polymer-film-coated sensors to gas identification using linear filters. Sens. Actuators B Chem. 1996, 33, 122–127. [Google Scholar] [CrossRef]
- Davide, F.A.M.; Natale, C.D.; D’Amico, A.; Hierlemann, A.; Mitrovics, J.; Schweizer, M.; Weimar, U.; Göpel, W.; Marco, S.; Pardo, A. Dynamic calibration of QMB polymer-coated sensors by Wiener kernel estimation. Sens. Actuators B Chem. 1995, 27, 275–285. [Google Scholar] [CrossRef]
- Marco, S.; Pardo, A.; Davide, F.A.M.; Natale, C.D.; D’Amico, A.; Hierlemann, A.; Mitrovics, J.; Schweizer, M.; Weimar, U.; Göpel, W. Different strategies for the identification of gas sensing systems. Sens. Actuators B Chem. 1996, 34, 213–223. [Google Scholar] [CrossRef]
- Pardo, A.; Marco, S.; Samitier, J. Nonlinear inverse dynamic models of gas sensing systems based on chemical sensor arrays for quantitative measurements. IEEE Trans. Instrum. Meas. 1998, 47, 644–651. [Google Scholar] [CrossRef]
- Trincavelli, M.; Coradeschi, S.; Loutfi, A. Odour classification system for continuous monitoring applications. Sens. Actuators B Chem. 2009, 139, 265–273. [Google Scholar] [CrossRef]
- Trincavelli, M.; Loutfi, A. Feature selection for gas identification with a mobile robot. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 4–8 May 2010; pp. 2852–2857. [Google Scholar] [CrossRef]
- Trincavelli, M. Gas Discrimination for Mobile Robots. KI Künstliche Intell. 2011, 25, 351–354. [Google Scholar] [CrossRef]
- Monroy, J.G.; Lilienthal, A.J.; Blanco, J.-L.; Gonzalez-Jimenez, J.; Trincavelli, M. Probabilistic gas quantification with MOX sensors in Open Sampling Systems—A Gaussian Process approach. Sens. Actuators B Chem. 2013, 188, 298–312. [Google Scholar] [CrossRef]
- Vergara, A.; Fonollosa, J.; Mahiques, J.; Trincavelli, M.; Rulkov, N.; Huerta, R. On the performance of gas sensor arrays in open sampling systems using Inhibitory Support Vector Machines. Sens. Actuators B Chem. 2013, 185, 462–477. [Google Scholar] [CrossRef]
- Mead, M.I.; Popoola, O.A.M.; Stewart, G.B.; Landshoff, P.; Calleja, M.; Hayes, M.; Baldovi, J.J.; McLeod, M.W.; Hodgson, T.F.; Dicks, J.; et al. The use of electrochemical sensors for monitoring urban air quality in low-cost, high-density networks. Atom. Environ. 2013, 70, 186–203. [Google Scholar] [CrossRef]
- Bennetts, V.H.; Schaffernicht, E.; Sesé, V.P.; Lilienthal, A.J.; Trincavelli, M. A novel approach for gas discrimination in natural environments with Open Sampling Systems. In Proceedings of the 2014 IEEE Sensors, Valencia, Spain, 2–5 November 2014; pp. 2046–2049. [Google Scholar] [CrossRef]
- Esposito, E.; De Vito, S.; Salvato2, M.; Bright, V.; Jones, R.L.; Popoola, O. Dynamic neural network architectures for on field stochastic calibration of indicative low cost air quality sensing systems. Sens. Actuators B Chem. 2016, 231, 701–713. [Google Scholar] [CrossRef]
- Fan, H.; Bennetts, V.H.; Schaffernicht, E.; Lilienthal, A.J. A cluster analysis approach based on exploiting density peaks for gas discrimination with electronic noses in open environments. Sens. Actuators B Chem. 2018, 259, 183–203. [Google Scholar] [CrossRef]
- Imamura, G.; Shiba, K.; Yoshikawa, G.; Washio, T. Free-hand gas identification based on transfer function ratios without gas flow control. Sci. Rep. 2019, 9, 9768. [Google Scholar] [CrossRef]
- Imamura, G.; Yoshikawa, G. Development of a Mobile Device for Odor Identification and Optimization of Its Measurement Protocol Based on the Free-Hand Measurement. Sensors 2020, 20, 6190. [Google Scholar] [CrossRef]
- Yaegashi, A.; Yoshikawa, G.; Yokota, T.; Aoki, Y. Industry-academia-government joint research framework towards de factor standard for olfactory IoT sensors/systems. J. Jpn. Assoc. Odor. Environ. 2018, 49, 323–327. [Google Scholar] [CrossRef]
- National Institute for Materials Science; Kyocera Corporation; Osaka University; NEC Corporation; Sumitomo Seika Chemicals Co., Ltd.; Asahi Kasei Corporation; NanoWorld AG. MSS Alliance Launched to Set De Facto Standard for Odor-Sensing Systems [Press Release]. Available online: https://www.nims.go.jp/eng/news/press/2015/10/201510130.html (accessed on 8 August 2022).
- National Institute for Materials Science; Kyocera Corporation; Osaka University; NEC Corporation; Sumitomo Seika Chemicals Co., Ltd.; Asahi Kasei Corporation; NanoWorld AG. “MSS Forum” Launched to Promote the Establishment of a De Facto Standard for Olfactory IoT Sensing Systems [Press release]. Available online: https://www.nims.go.jp/eng/news/press/2017/201710160.html (accessed on 8 August 2022).
- Senesac, L.R.; Dutta, P.; Datskos, P.G.; Sepaniak, M.J. Analyte species and concentration identification using differentially functionalized microcantilever arrays and artificial neural networks. Anal. Chim. Acta 2006, 558, 94–101. [Google Scholar] [CrossRef]
- Nishikawa, M.; Murata, T.; Ishihara, S.; Shiba, K.; Shrestha, L.K.; Yoshikawa, G.; Minami, K.; Ariga, K. Discrimination of Methanol from Ethanol in Gasoline Using a Membrane-type Surface Stress Sensor Coated with Copper(I) Complex. Bull. Chem. Soc. Jpn. 2021, 94, 648–654. [Google Scholar] [CrossRef]
- Ngo, H.T.; Minami, K.; Imamura, G.; Shiba, K.; Yoshikawa, G. Effects of Center Metals in Porphines on Nanomechanical Gas Sensing. Sensors 2018, 18, 1640. [Google Scholar] [CrossRef] [PubMed]
- Bietsch, A.; Zhang, J.; Hegner, M.; Lang, H.P.; Gerber, C. Rapid functionalization of cantilever array sensors by inkjet printing. Nanotechnology 2004, 15, 873–880. [Google Scholar] [CrossRef]
- Loizeau, F.; Akiyama, T.; Gautsch, S.; Vettiger, P.; Yoshikawa, G.; de Rooij, N.F. Comparing membrane- and cantilever-based surface stress sensors for reproducibility. Sens. Actuators A Phys. 2015, 228, 9–15. [Google Scholar] [CrossRef]
- Chen, G.Y.; Thundat, T.; Wachter, E.A.; Warmack, R.J. Adsorption-induced surface stress and its effects on resonance frequency of microcantilevers. J. Appl. Phys. 1995, 77, 3618–3622. [Google Scholar] [CrossRef]
- Thundat, T.; Chen, G.Y.; Warmack, R.J.; Allison, D.P.; Wachter, E.A. Vapor Detection Using Resonating Microcantilevers. Anal. Chem. 2002, 67, 519–521. [Google Scholar] [CrossRef]
- Minami, K.; Imamura, G.; Nemoto, T.; Shiba, K.; Yoshikawa, G. Pattern recognition of solid materials by multiple probe gases. Mater. Horiz. 2019, 6, 580–586. [Google Scholar] [CrossRef]
- Minami, K.; Yoshikawa, G. Pattern Recognition of Solid Materials By Multiple Probe Gases. ECS Meet. Abstr. 2020, MA2020-01, 2260. [Google Scholar] [CrossRef]
- Federici, S.; Ridolfi, A.; Zendrini, A.; Radeghieri, A.; Bontempi, E.; Depero, L.; Bergese, P. Interaction of Extracellular Vesicles with Si Surface Studied by Nanomechanical Microcantilever Sensors. Appl. Sci. 2018, 8, 404. [Google Scholar] [CrossRef]
- Toda, M.; Moorthi, K.; Hokama, T.; Wang, Z.; Yamazaki, M.; Ono, T. Miniature piezoresistive sensor for detecting volatile organic components. Sens. Actuators B Chem. 2021, 333, 129524. [Google Scholar] [CrossRef]
- Del Rey, M.; da Silva, R.A.; Meneses, D.; Petri, D.F.S.; Tamayo, J.; Calleja, M.; Kosaka, P.M. Monitoring swelling and deswelling of thin polymer films by microcantilever sensors. Sens. Actuators B Chem. 2014, 204, 602–610. [Google Scholar] [CrossRef][Green Version]
- Basu, A.K.; Sah, A.N.; Pradhan, A.; Bhattacharya, S. Poly-L-Lysine functionalised MWCNT-rGO nanosheets based 3-d hybrid structure for femtomolar level cholesterol detection using cantilever based sensing platform. Sci. Rep. 2019, 9, 3686. [Google Scholar] [CrossRef] [PubMed]
- Bumbu, G.G.; Wolkenhauer, M.; Kircher, G.; Gutmann, J.S.; Berger, R. Micromechanical cantilever technique: A tool for investigating the swelling of polymer brushes. Langmuir 2007, 23, 2203–2207. [Google Scholar] [CrossRef]
- Villanueva, L.G.; Karabalin, R.B.; Matheny, M.H.; Chi, D.; Sader, J.E.; Roukes, M.L. Nonlinearity in nanomechanical cantilevers. Phys. Rev. B 2013, 87, 024304. [Google Scholar] [CrossRef]
- Shafiei, M.; Shiba, K.; Imamura, G.; Yoshikawa, G.; Mackinnon, I.D.R. Humidity and VOC Sensing Performance of a PVP and PVP/ZSM5 Composite. In Proceedings of the 2019 IEEE Sensors, Montréal, QC, Canada, 27–30 October 2019. [Google Scholar] [CrossRef]
- Schlur, L.; Hofer, M.; Ahmad, A.; Bonnot, K.; Holz, M.; Spitzer, D. Cu(OH)2 and CuO Nanorod Synthesis on Piezoresistive Cantilevers for the Selective Detection of Nitrogen Dioxide. Sensors 2018, 18, 1108. [Google Scholar] [CrossRef]
- Osica, I.; Melo, A.F.A.A.; Lima, F.C.D.A.; Shiba, K.; Imamura, G.; Crespilho, F.N.; Betlej, J.; Kurzydowski, K.J.; Yoshikawa, G.; Ariga, K. Nanomechanical Recognition and Discrimination of Volatile Molecules by Au Nanocages Deposited on Membrane-Type Surface Stress Sensors. ACS Appl. Nano Mater. 2020, 3, 4061–4068. [Google Scholar] [CrossRef]
- Zheng, F.; Wang, P.; Du, Q.; Chen, Y.; Liu, N. Simultaneous and Ultrasensitive Detection of Foodborne Bacteria by Gold Nanoparticles-Amplified Microcantilever Array Biosensor. Front. Chem. 2019, 7, 232. [Google Scholar] [CrossRef]
- Xu, P.; Yu, H.; Xia, X.; Yu, F.; Liu, M.; Li, X. Resonant cantilevers with nanoparticles-spaced functional graphene-oxide sheets for high-performance sensing to ppt-level explosive vapor. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 989–992. [Google Scholar] [CrossRef]
- Yu, H.; Xu, P.; Li, X. Functionalized gold-nanoparticles directly grown on graphene-oxide sheets to form porous-stacked sensing material for micro-gravimetric gas sensing. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 433–436. [Google Scholar] [CrossRef]
- Park, C.; Kang, J.; Baek, I.; You, J.; Jang, K.; Na, S. Highly sensitive and selective detection of single-nucleotide polymorphisms using gold nanoparticle MutS enzymes and a micro cantilever resonator. Talanta 2019, 205, 120154. [Google Scholar] [CrossRef]
- Bao, Y.; Xu, P.; Cai, S.; Yu, H.; Li, X. Detection of volatile-organic-compounds (VOCs) in solution using cantilever-based gas sensors. Talanta 2018, 182, 148–155. [Google Scholar] [CrossRef]
- Huber, C.; Pina, M.P.; Morales, J.J.; Mehdaoui, A. A Multiparameter Gas-Monitoring System Combining Functionalized and Non-Functionalized Microcantilevers. Micromachines 2020, 11, 283. [Google Scholar] [CrossRef]
- Osica, I.; Melo, A.F.A.A.; Imamura, G.; Shiba, K.; Ji, Q.; Hill, J.P.; Crespilho, F.N.; Kurzydłowski, K.J.; Yoshikawa, G.; Ariga, K. Fabrication of Silica-Protein Hierarchical Nanoarchitecture with Gas-Phase Sensing Activity. J. Nanosci. Nanotechnol. 2017, 17, 5908–5917. [Google Scholar] [CrossRef]
- Shiba, K.; Takei, T.; Yoshikawa, G.; Ogawa, M. Deposition of a titania layer on spherical porous silica particles and their nanostructure-induced vapor sensing properties. Nanoscale 2017, 9, 16791–16799. [Google Scholar] [CrossRef] [PubMed]
- Thomas, G.; Spitzer, D. 3D Core-Shell TiO2@MnO2 Nanorod Arrays on Microcantilevers for Enhancing the Detection Sensitivity of Chemical Warfare Agents. Acs Appl. Mater. Inter. 2021, 13, 47185–47197. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Setiono, A.; Bertke, M.; Strempel, K.; Markiewicz, N.; Schmidt, A.; Waag, A.; Prades, J.D.; Peiner, E. Piezoresistive Microcantilevers 3D-Patterned Using Zno-Nanorods@Silicon-Nanopillars for Room-Temperature Ethanol Detection. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (transducers & eurosensors XXXIII), Berlin, Germany, 23–27 June 2019; pp. 1211–1214. [Google Scholar] [CrossRef]
- Xu, J.; Setiono, A.; Peiner, E. Piezoresistive Microcantilever with SAM-Modified ZnO-Nanorods@Silicon-Nanopillars for Room-Temperature Parts-per-Billion NO2 Detection. ACS Appl. Nano Mater. 2020, 3, 6609–6620. [Google Scholar] [CrossRef]
- Imamura, G.; Minami, K.; Shiba, K.; Mistry, K.; Musselman, K.; Yavuz, M.; Yoshikawa, G.; Saiki, K.; Obata, S. Graphene Oxide as a Sensing Material for Gas Detection Based on Nanomechanical Sensors in the Static Mode. Chemosensors 2020, 8, 82. [Google Scholar] [CrossRef]
- Mistry, K.; Ibrahim, K.H.; Novodchuk, I.; Ngo, H.T.; Imamura, G.; Sanderson, J.; Yavuz, M.; Yoshikawa, G.; Musselman, K.P. Nanomechanical Gas Sensing with Laser Treated 2D Nanomaterials. Adv. Mater. Technol. 2020, 5, 2000704. [Google Scholar] [CrossRef]
- Yao, Y.; Chen, X.; Guo, H.; Wu, Z.; Li, X. Humidity sensing behaviors of graphene oxide-silicon bi-layer flexible structure. Sens. Actuators B: Chem. 2012, 161, 1053–1058. [Google Scholar] [CrossRef]
- Conley, H.; Lavrik, N.V.; Prasai, D.; Bolotin, K.I. Graphene bimetallic-like cantilevers: Probing graphene/substrate interactions. Nano Lett. 2011, 11, 4748–4752. [Google Scholar] [CrossRef]
- Godin, M.; Tabard-Cossa, V.; Miyahara, Y.; Monga, T.; Williams, P.J.; Beaulieu, L.Y.; Bruce Lennox, R.; Grutter, P. Cantilever-based sensing: The origin of surface stress and optimization strategies. Nanotechnology 2010, 21, 75501. [Google Scholar] [CrossRef]
- Campbell, G.A.; Mutharasan, R. Detection and quantification of proteins using self-excited PZT-glass millimeter-sized cantilever. Biosens. Bioelectron. 2005, 21, 597–607. [Google Scholar] [CrossRef]
- Campbell, G.A.; Mutharasan, R. Monitoring of the self-assembled monolayer of 1-hexadecanethiol on a gold surface at nanomolar concentration using a piezo-excited millimeter-sized cantilever sensor. Langmuir 2005, 21, 11568–11573. [Google Scholar] [CrossRef] [PubMed]
- Tamayo, J.; Ramos, D.; Mertens, J.; Calleja, M. Effect of the adsorbate stiffness on the resonance response of microcantilever sensors. Appl. Phys. Lett. 2006, 89, 224104. [Google Scholar] [CrossRef]
- Yen, Y.K.; Lai, Y.C.; Hong, W.T.; Pheanpanitporn, Y.; Chen, C.S.; Huang, L.S. Electrical detection of C-reactive protein using a single free-standing, thermally controlled piezoresistive microcantilever for highly reproducible and accurate measurements. Sensors 2013, 13, 9653–9668. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, R.; Liu, Y.; Yu, X. A Low Spring Constant Piezoresistive Microcantilever for Biological Reagent Detection. Micromachines 2020, 11, 1001. [Google Scholar] [CrossRef] [PubMed]
- Toda, M.; Joseph, Y.; Berger, R. Swelling of Composite Films at Interfaces. J. Phys. Chem. C 2010, 114, 2012–2017. [Google Scholar] [CrossRef]
- Zhang, J.; Lang, H.P.; Yoshikawa, G.; Gerber, C. Optimization of DNA hybridization efficiency by pH-driven nanomechanical bending. Langmuir 2012, 28, 6494–6501. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, T.; Mei, K.; Rao, D.; Wu, W.; Chen, Y.; Peng, Y.; Wang, J.; Wu, S.; Zhang, Q. Nanomechanical assay for ultrasensitive and rapid detection of SARS-CoV-2 based on peptide nucleic acid. Nano Res. 2022, 1–13. [Google Scholar] [CrossRef]
- Huang, Y.-J.; Huang, C.-W.; Lin, T.-H.; Lin, C.-T.; Chen, L.-G.; Hsiao, P.-Y.; Wu, B.-R.; Hsueh, H.-T.; Kuo, B.-J.; Tsai, H.-H.; et al. A CMOS Cantilever-Based Label-Free DNA SoC With Improved Sensitivity for Hepatitis B Virus Detection. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 820–831. [Google Scholar] [CrossRef]
- Ku, Y.F.; Huang, L.S.; Yen, Y.K. A Real-Time Thermal Self-Elimination Method for Static Mode Operated Freestanding Piezoresistive Microcantilever-Based Biosensors. Biosensors 2018, 8, 18. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, Y.; Wang, Y.; Xu, J.; Yu, X. A Flexible PI/Si/SiO2 Piezoresistive Microcantilever for Trace-Level Detection of Aflatoxin B1. Sensors 2021, 21, 1118. [Google Scholar] [CrossRef]
- Lei, R.; Wu, P.; Li, L.; Huang, Q.; Wang, J.; Zhang, D.; Li, M.; Chen, N.; Wang, X. Ultrasensitive isothermal detection of a plant pathogen by using a gold nanoparticle-enhanced microcantilever sensor. Sens. Actuators B Chem. 2021, 338, 129874. [Google Scholar] [CrossRef]
- Rao, D.; Mei, K.; Yan, T.; Wang, Y.; Wu, W.; Chen, Y.; Wang, J.; Zhang, Q.; Wu, S. Nanomechanical sensor for rapid and ultrasensitive detection of tumor markers in serum using nanobody. Nano Res. 2022, 15, 1003–1012. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, D.K.; Hunt, A.C.; Shekhawat, G.S.; Carter, L.; Chan, S.; Wu, K.; Cao, L.; Baker, D.; Lorenzo-Redondo, R.; Ozer, E.A.; et al. Rapid and Sensitive Detection of Antigen from SARS-CoV-2 Variants of Concern by a Multivalent Minibinder-Functionalized Nanomechanical Sensor. Anal. Chem. 2022, 94, 8105–8109. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, D.K.; Nandwana, V.; Henrich, S.E.; Josyula, V.; Thaxton, C.S.; Qi, C.; Simons, L.M.; Hultquist, J.F.; Ozer, E.A.; Shekhawat, G.S.; et al. Highly sensitive and ultra-rapid antigen-based detection of SARS-CoV-2 using nanomechanical sensor platform. Biosens. Bioelectron. 2022, 195, 113647. [Google Scholar] [CrossRef] [PubMed]
- Ramos, D.; Mertens, J.; Calleja, M.; Tamayo, J. Study of the origin of bending induced by bimetallic effect on microcantilever. Sensors 2007, 7, 1757–1765. [Google Scholar] [CrossRef]
- Yeung, H.H.-M.; Yoshikawa, G.; Minami, K.; Shiba, K. Strain-based chemical sensing using metal–organic framework nanoparticles. J. Mater. Chem. A 2020, 8, 18007–18014. [Google Scholar] [CrossRef]
- Cai, S.; Li, W.; Xu, P.; Xia, X.; Yu, H.; Zhang, S.; Li, X. In situ construction of metal-organic framework (MOF) UiO-66 film on Parylene-patterned resonant microcantilever for trace organophosphorus molecules detection. Analyst 2019, 144, 3729–3735. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minami, K.; Imamura, G.; Tamura, R.; Shiba, K.; Yoshikawa, G. Recent Advances in Nanomechanical Membrane-Type Surface Stress Sensors towards Artificial Olfaction. Biosensors 2022, 12, 762. https://doi.org/10.3390/bios12090762
Minami K, Imamura G, Tamura R, Shiba K, Yoshikawa G. Recent Advances in Nanomechanical Membrane-Type Surface Stress Sensors towards Artificial Olfaction. Biosensors. 2022; 12(9):762. https://doi.org/10.3390/bios12090762
Chicago/Turabian StyleMinami, Kosuke, Gaku Imamura, Ryo Tamura, Kota Shiba, and Genki Yoshikawa. 2022. "Recent Advances in Nanomechanical Membrane-Type Surface Stress Sensors towards Artificial Olfaction" Biosensors 12, no. 9: 762. https://doi.org/10.3390/bios12090762
APA StyleMinami, K., Imamura, G., Tamura, R., Shiba, K., & Yoshikawa, G. (2022). Recent Advances in Nanomechanical Membrane-Type Surface Stress Sensors towards Artificial Olfaction. Biosensors, 12(9), 762. https://doi.org/10.3390/bios12090762









