Information-Based Similarity of Ordinal Pattern Sequences as a Novel Descriptor in Obstructive Sleep Apnea Screening Based on Wearable Photoplethysmography Bracelets
Abstract
:1. Introduction
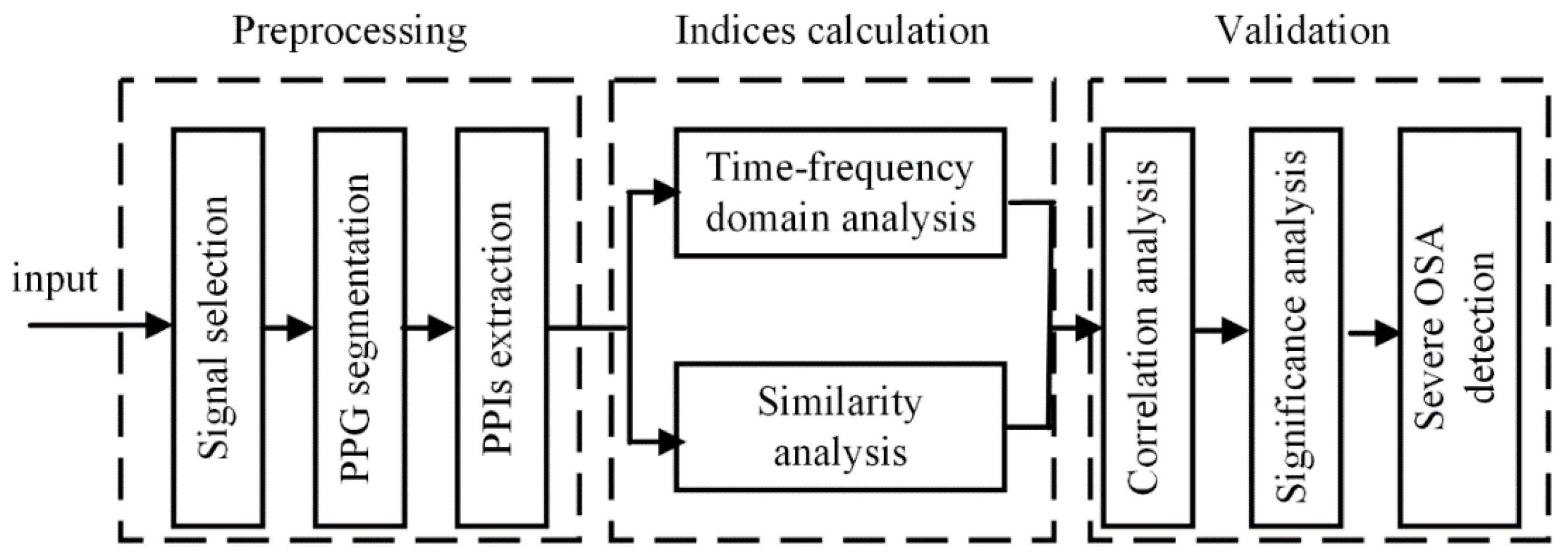
2. Materials and Methods
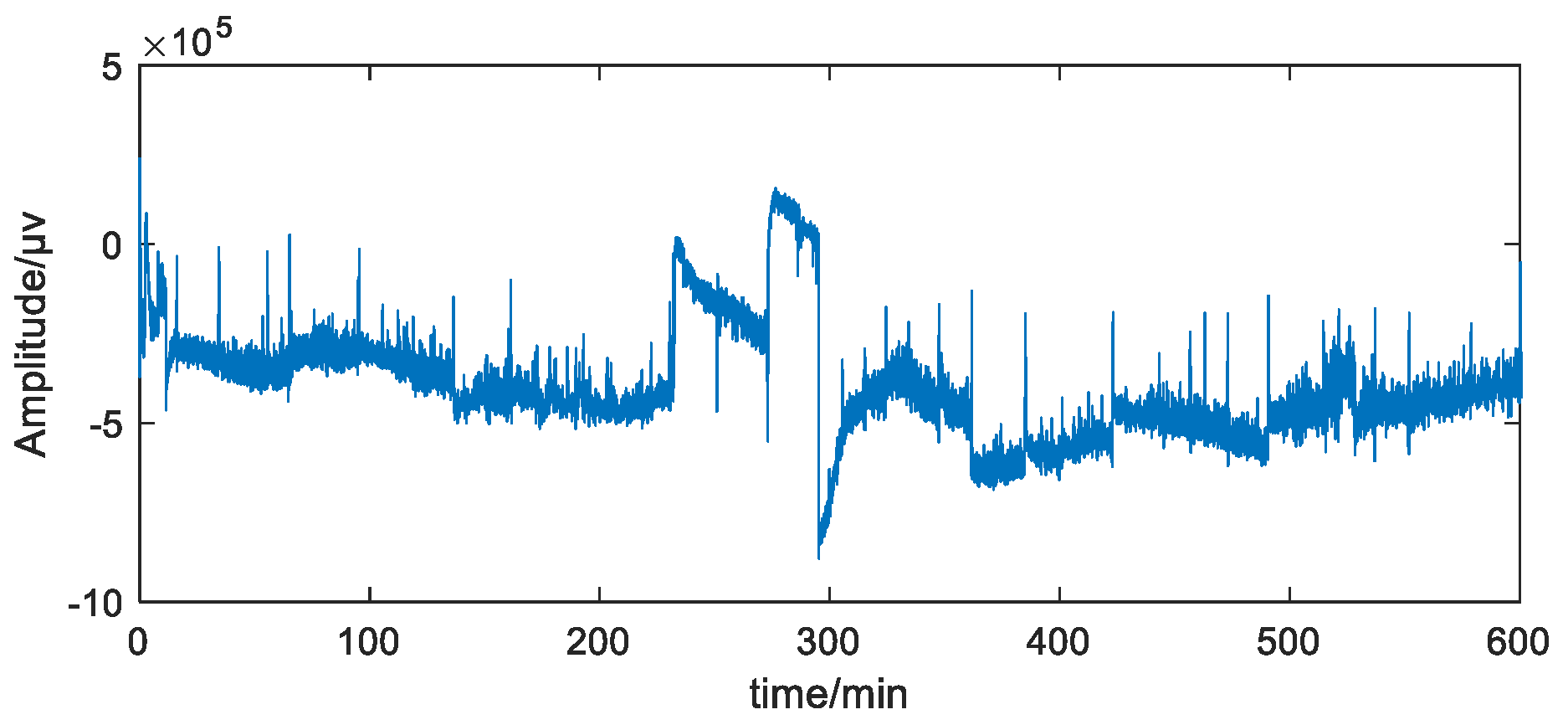
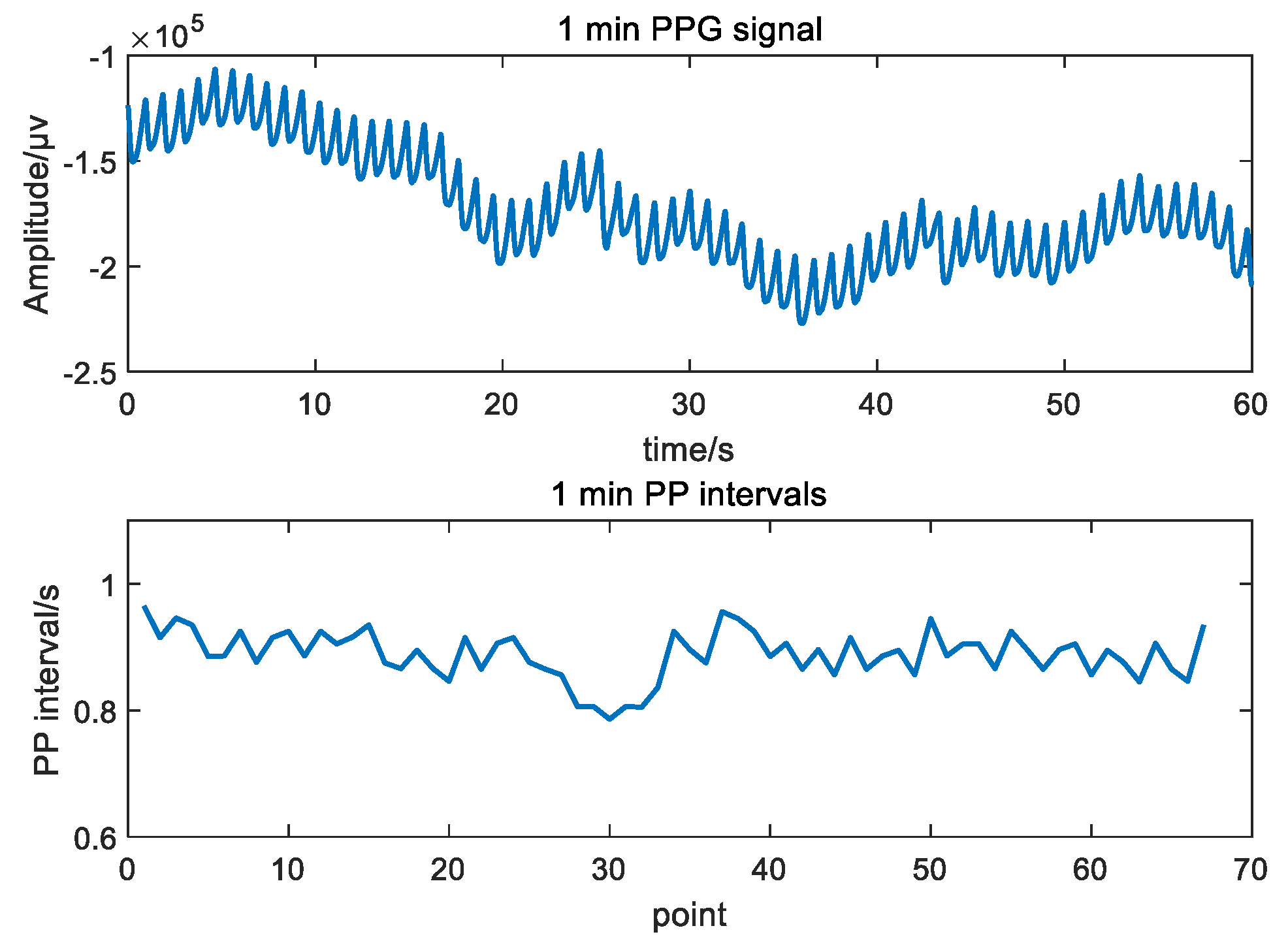
2.1. Data
2.2. Time-Domain Indices
2.3. Frequency-Domain Indices
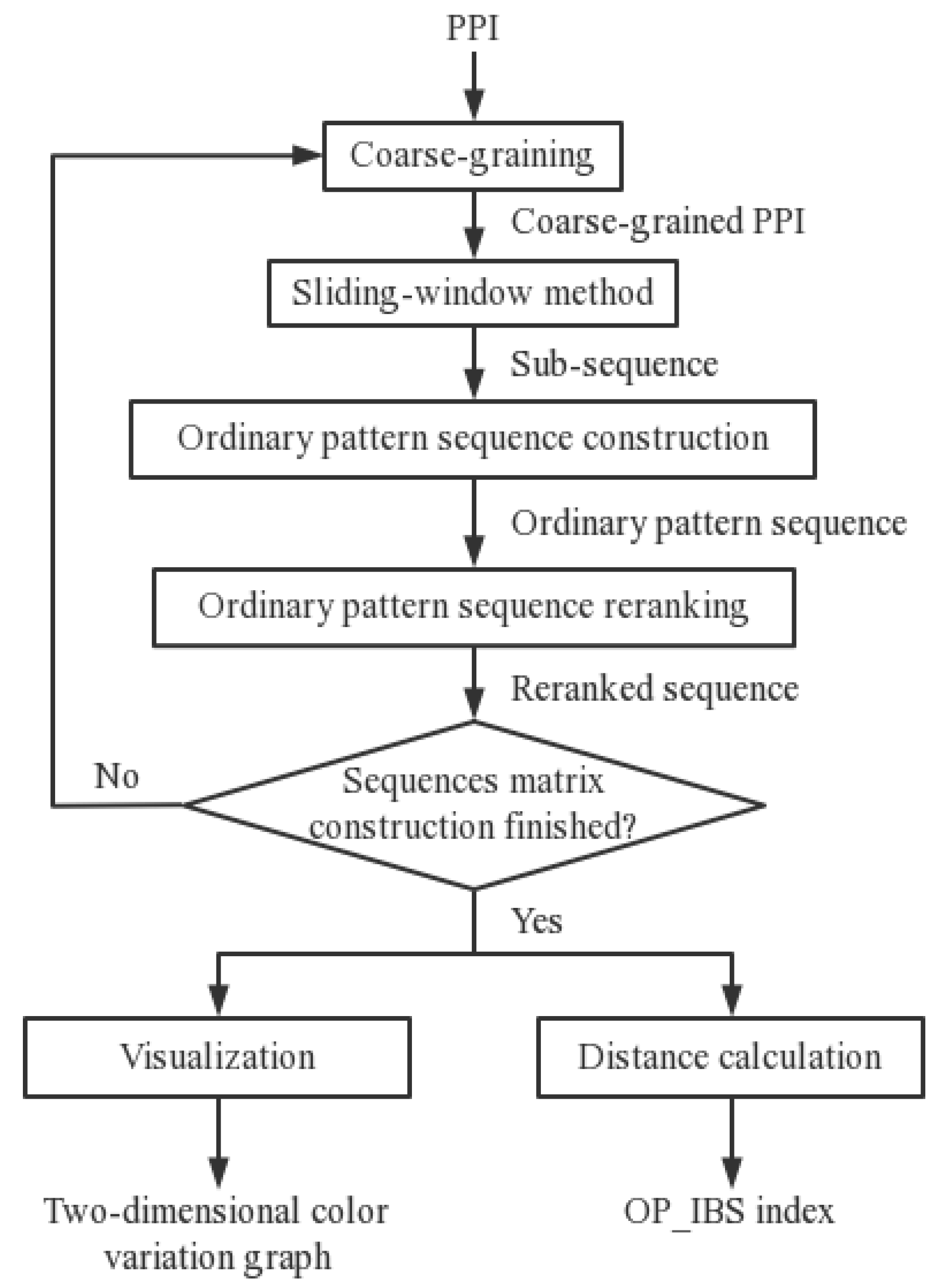
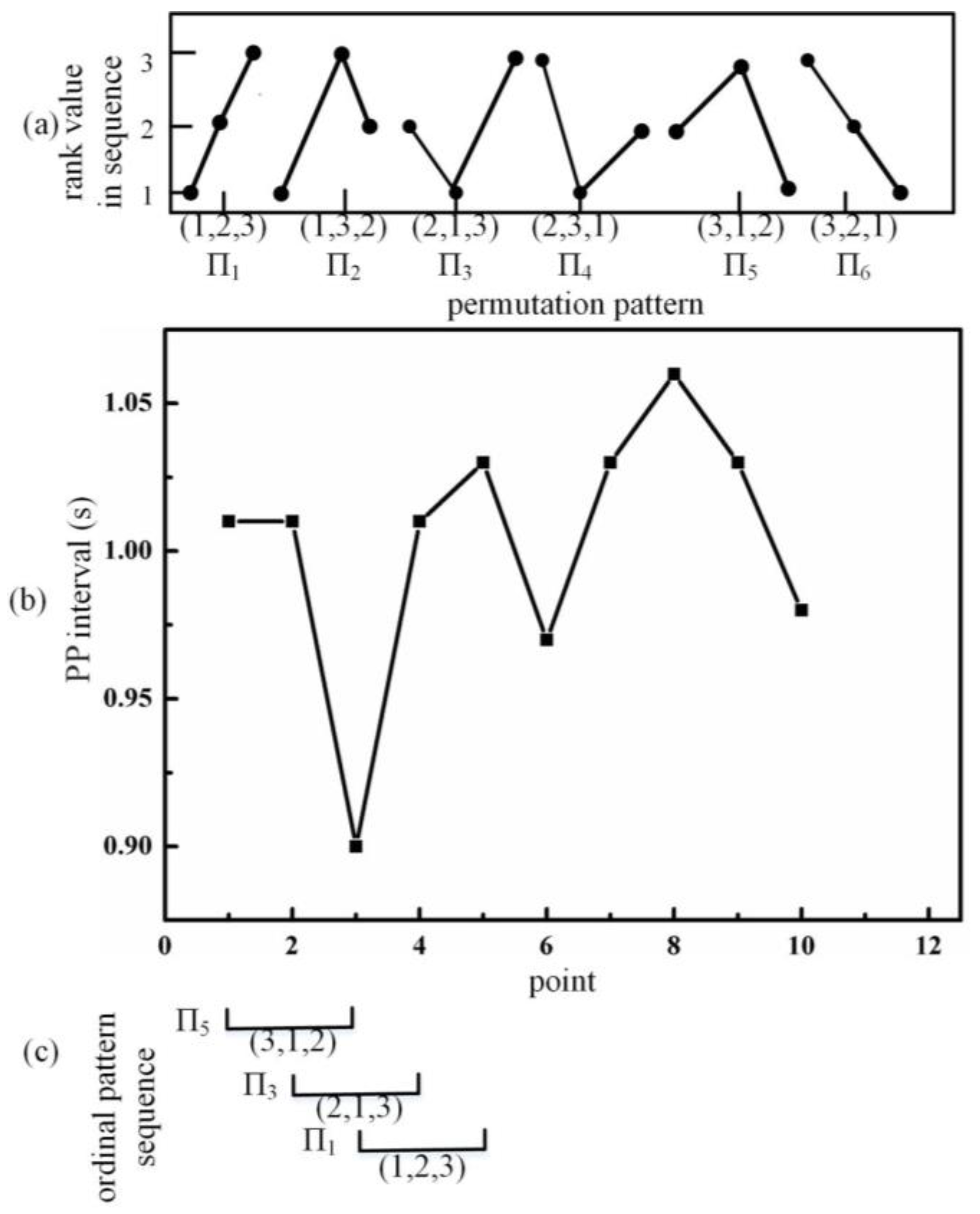
2.4. Information-Based Similarity of Ordinal Pattern Sequences (OP_IBS)
2.5. Validation
2.6. Parameter Selection for OP_IBS
2.7. OP_IBS in the Physionet Database
3. Results
3.1. Similarity in Heart Fluctuation among Normal, OSA-m and OSA-s Groups
3.2. Severe OSA Screening
4. Discussion
4.1. Comparison with Studies Using Wearable Data
4.2. Comparison with Studies on the Physionet Database
4.3. OP_IBS Method and Parameter Selection
4.4. Physiological Significance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gilman, M.P.; Floras, J.S.; Usui, K.; Kaneko, Y.; Leung, R.S.T.; Bradley, T.D. Continuous positive airway pressure increases heart rate variability in heart failure patients with obstructive sleep apnoea. Clin. Sci. 2008, 114, 243–249. [Google Scholar] [CrossRef] [PubMed]
- Benjafield, A.V.; Ayas, N.T.; Eastwood, P.R.; Heinzer, R.; Ip, M.S.M.; Morrell, M.J.; Nunez, C.M.; Patel, S.R.; Penzel, T.; Pépin, J.-L.; et al. Estimation of the global prevalence and burden of obstructive sleep apnoea: A literature-based analysis. Lancet Respir. Med. 2019, 7, 687–698. [Google Scholar] [CrossRef] [PubMed]
- Pafili, K.; Steiropoulos, P.; Papanas, N. The relationship between obstructive sleep apnoea and coronary heart disease. Curr. Opin. Cardiol. 2015, 30, 439–446. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wu, S.; Yang, Q.; Liu, G.; Ge, L. Application of the Variance Delay Fuzzy Approximate Entropy for Autonomic Nervous System Fluctuation Analysis in Obstructive Sleep Apnea Patients. Entropy 2020, 22, 915. [Google Scholar] [CrossRef]
- Angius, G.; Raffo, L. A sleep apnoea keeper in a wearable device for Continuous detection and screening during daily life. In Proceedings of the 2008 Computers in Cardiology, Bologna, Italy, 14–17 September 2008; pp. 433–436. [Google Scholar] [CrossRef]
- Pecchia, L.; Melillo, P.; Sansone, M.; Bracale, M. Discrimination power of short-term heart rate variability measures for CHF assessment. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 40–46. [Google Scholar] [CrossRef] [PubMed]
- Sequeira, V.C.C.; Bandeira, P.M.; Azevedo, J.C.M. Heart rate variability in adults with obstructive sleep apnea: A systematic review. Sleep Sci. 2019, 12, 214–221. [Google Scholar] [CrossRef] [PubMed]
- Song, M.-K.; Ha, J.H.; Ryu, S.-H.; Yu, J.; Park, D.-H. The Effect of Aging and Severity of Sleep Apnea on Heart Rate Variability Indices in Obstructive Sleep Apnea Syndrome. Psychiatry Investig. 2012, 9, 65–72. [Google Scholar] [CrossRef]
- Xie, J.; Yu, W.; Wan, Z.; Han, F.; Wang, Q.; Chen, R. Correlation Analysis between Obstructive Sleep Apnea Syndrome (OSAS) and Heart Rate Variability. Iran. J. Public Health 2017, 46, 1502–1511. [Google Scholar] [PubMed]
- Li, Y.; Pan, W.; Li, K.; Jiang, Q.; Liu, G. Sliding Trend Fuzzy Approximate Entropy as a Novel Descriptor of Heart Rate Variability in Obstructive Sleep Apnea. IEEE J. Biomed. Health Inform. 2019, 23, 175–183. [Google Scholar] [CrossRef] [PubMed]
- Bolaños, M.; Nazeran, H.; Haltiwanger, E. Comparison of Heart Rate Variability Signal Features Derived from Electrocardiography and Photoplethysmography in Healthy Individuals. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 4289–4294. [Google Scholar] [CrossRef]
- Dey, J.; Bhowmik, T.; Sahoo, S.; Tiwari, V.N. Wearable PPG sensor based alertness scoring system. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Republic of Korea, 11–15 July 2017. [Google Scholar]
- Karmakar, C.; Khandoker, A.; Penzel, T.; Schobel, C.; Palaniswami, M. Detection of Respiratory Arousals Using Photoplethysmography (PPG) Signal in Sleep Apnea Patients. IEEE J. Biomed. Health Inform. 2013, 18, 1065–1073. [Google Scholar] [CrossRef] [PubMed]
- Lázaro, J.; Gil, E.; Vergara, J.M.; Laguna, P. OSAS Detection in Children by using PPG Amplitude Fluctuation Decreases and Pulse Rate Variability. In Proceedings of the 2012 Computing in Cardiology, Krakow, Poland, 9–12 September 2012. [Google Scholar]
- Castaneda, D.; Esparza, A.; Ghamari, M.; Soltanpur, C.; Nazeran, H. A review on wearable photoplethysmography sensors and their potential future applications in health care. Int. J. Biosens. Bioelectron. 2018, 4, 195–202. [Google Scholar] [PubMed]
- Naghsh, S.; Ataei, M.; Yazdchi, M.; Hashemi, M. Chaos-based analysis of heart rate variability time series in obstructive sleep apnea subjects. J. Med. Signals Sens. 2020, 10, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; He, A.; Feng, K.; Liu, G.; Wang, Q. Empirical Mode Decomposition as a Novel Approach to Study Heart Rate Variability in Congestive Heart Failure Assessment. Entropy 2019, 21, 1169. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Parlitz, U.; Berg, S.; Luther, S.; Schirdewan, A.; Kurths, J.; Wessel, N. Classifying cardiac biosignals using ordinal pattern statistics and symbolic dynamics. Comput. Biol. Med. 2012, 42, 319–327. [Google Scholar] [CrossRef] [PubMed]
- Frank, B.; Pompe, B.; Schneider, U.; Hoyer, D. Permutation entropy improves fetal behavioural state classification based on heart rate analysis from biomagnetic recordings in near term fetuses. Med. Biol. Eng. Comput. 2006, 44, 179–187. [Google Scholar] [CrossRef] [PubMed]
- Nicolaou, N.; Georgiou, J. Detection of epileptic electroencephalogram based on Permutation Entropy and Support Vector Machines. Expert Syst. Appl. 2012, 39, 202–209. [Google Scholar] [CrossRef]
- Cui, X.; Chang, E.; Yang, W.-H.; Jiang, B.C.; Yang, A.C.; Peng, C.-K. Automated Detection of Paroxysmal Atrial Fibrillation Using an Information-Based Similarity Approach. Entropy 2017, 19, 677. [Google Scholar] [CrossRef] [Green Version]
- Baumert, M.; Czippelova, B.; Porta, A.; Javorka, M. Decoupling of QT interval variability from heart rate variability with ageing. Physiol. Meas. 2013, 34, 1435–1448. [Google Scholar] [CrossRef]
- Wu, S.; Chen, M.; Wei, K.; Liu, G. Sleep apnea screening based on Photoplethysmography data from wearable bracelets using an information-based similarity approach. Comput. Methods Programs Biomed. 2021, 211, 106442. [Google Scholar] [CrossRef]
- Shen, Q.; Yang, X.; Zou, L.; Wei, K.; Wang, C.; Liu, G. Multi-Task Multi-Attention Residual Shrinkage Convolutional Neural Network for Sleep Apnea Detection Based on Wearable Bracelet Photoplethysmography. IEEE Internet Things J. 2022, 1. [Google Scholar] [CrossRef]
- Wu, S.; Liang, D.; Yang, Q.; Liu, G. Regularity of heart rate fluctuations analysis in obstructive sleep apnea patients using information-based similarity. Biomed. Signal Process. Control 2021, 65, 102370. [Google Scholar] [CrossRef]
- Elgendi, M.; Norton, I.; Brearley, M.; Abbott, D.; Schuurmans, D. Systolic Peak Detection in Acceleration Photoplethysmograms Measured from Emergency Responders in Tropical Conditions. PLoS ONE 2013, 8, e76585. [Google Scholar] [CrossRef] [PubMed]
- Iber, C.; Ancoli-Israel, S.; Chesson, A.L.; Quan, S.F. The AASM Manual for the Scoring of Sleep and Associated Events: Rules, Terminology and Technical Specifications; American Academy of Sleep Medicine: Westchester, IL, USA, 2007. [Google Scholar]
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef] [PubMed]
- Burg, J.P. A New Analysis Technique for Time Series Data. In Proceedings of the NATO Advanced Study Institute on Signal Processing with Emphasis on Underwater Acoustics, Enschede, The Netherlands, 12–23 August 1968. [Google Scholar]
- Tran, Y.; Wijesuriya, N.; Tarvainen, M.; Karjalainen, P.; Craig, A. The Relationship Between Spectral Changes in Heart Rate Variability and Fatigue. J. Psychophysiol. 2009, 23, 143–151. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Wang, L.; Wang, Q.; Zhou, G.; Wang, Y.; Jiang, Q. A New Approach to Detect Congestive Heart Failure Using Short-Term Heart Rate Variability Measures. PLoS ONE 2014, 9, e93399. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Liu, G. The novel approach of temporal dependency complexity analysis of heart rate variability in obstructive sleep apnea. Comput. Biol. Med. 2021, 135, 104632. [Google Scholar] [CrossRef]
- Kamiński, B.; Jakubczyk, M.; Szufel, P. A framework for sensitivity analysis of decision trees. Cent. Eur. J. Oper. Res. 2018, 26, 135–159. [Google Scholar] [CrossRef]
- Venkataramanaiah, B.; Kamala, J. ECG signal processing and KNN classifier-based abnormality detection by VH-doctor for remote cardiac healthcare monitoring. Soft Comput. 2020, 24, 17457–17466. [Google Scholar] [CrossRef]
- Lazazzera, R.; Deviaene, M.; Varon, C.; Buyse, B.; Testelmans, D.; Laguna, P.; Gil, E.; Carrault, G. Detection and Classification of Sleep Apnea and Hypopnea Using PPG and SpO2 Signals. IEEE Trans. Biomed. Eng. 2020, 68, 1496–1506. [Google Scholar] [CrossRef] [PubMed]
- Feng, K.; Qin, H.; Wu, S.; Pan, W.; Liu, G. A Sleep Apnea Detection Method Based on Unsupervised Feature Learning and Single-Lead Electrocardiogram. IEEE Trans. Instrum. Meas. 2020, 70, 1–12. [Google Scholar] [CrossRef]
- Costa, M.D.; Peng, C.-K.; Goldberger, A.L. Multiscale Analysis of Heart Rate Dynamics: Entropy and Time Irreversibility Measures. Cardiovasc. Eng. 2008, 8, 88–93. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Ivanov, K.; Omisore, O.M.; Igbe, T.; Liu, Q.; Nie, Z.; Wang, L. Gait Rhythm Dynamics for Neuro-Degenerative Disease Classification via Persistence Landscape- Based Topological Representation. Sensors 2020, 20, 2006. [Google Scholar] [CrossRef]
- Penzel, T.; Moody, G.B.; Mark, R.G.; Goldberger, A.L.; Peter, J.H. The apnea-ECG database. In Proceedings of the Computers in Cardiology 2000, Cambridge, MA, USA, 24–27 September 2000. [Google Scholar]
- Malliani, A.; Pagani, M.; Lombardi, F.; Cerutti, S. Cardiovascular neural regulation explored in the frequency domain. Circulation 1991, 84, 482–492. [Google Scholar] [CrossRef]
- Lombardi, F.; Tarricone, D.; Tundo, F.; Colombo, F.; Belletti, S.; Fiorentini, C. Autonomic nervous system and paroxysmal atrial fibrillation: A study based on the analysis of RR interval changes before, during and after paroxysmal atrial fibrillation. Eur. Heart J. 2004, 25, 1242–1248. [Google Scholar] [CrossRef]
- Jarchi, D.; Casson, A.J. Towards Photoplethysmography-Based Estimation of Instantaneous Heart Rate During Physical Activity. IEEE Trans. Biomed. Eng. 2017, 64, 2042–2053. [Google Scholar] [CrossRef]
- Hsu, Y.-S.; Chen, T.-Y.; Wu, D.; Lin, C.-M.; Juang, J.-N.; Liu, W.-T. Screening of obstructive sleep apnea in patients who snore using a patch-type device with electrocardiogram and 3-axis accelerometer. J. Clin. Sleep Med. 2020, 16, 1149–1160. [Google Scholar] [CrossRef]
- Baty, F.; Boesch, M.; Widmer, S.; Annaheim, S.; Fontana, P.; Camenzind, M.; Rossi, R.M.; Schoch, O.D.; Brutsche, M.H. Classification of Sleep Apnea Severity by Electrocardiogram Monitoring Using a Novel Wearable Device. Sensors 2020, 20, 286. [Google Scholar] [CrossRef]
- Hayano, J.; Yamamoto, H.; Nonaka, I.; Komazawa, M.; Itao, K.; Ueda, N.; Tanaka, H.; Yuda, E. Quantitative detection of sleep apnea with wearable watch device. PLoS ONE 2020, 15, e0237279. [Google Scholar] [CrossRef]
- Papini, G.B.; Fonseca, P.; Van Gilst, M.M.; Bergmans, J.W.M.; Vullings, R.; Overeem, S. Wearable monitoring of sleep-disordered breathing: Estimation of the apnea–hypopnea index using wrist-worn reflective photoplethysmography. Sci. Rep. 2020, 10, 13512. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Yang, X.; Wang, G.; Ma, J.; Liu, Y.; Peng, C.-K.; Zhang, J.; Fang, J. HHT based cardiopulmonary coupling analysis for sleep apnea detection. Sleep Med. 2012, 13, 503–509. [Google Scholar] [CrossRef]
- Pietrzak, A.; Cybulski, G. New indices for sleep apnea detection from long-time ECG recordings. In Proceedings of the 2015 Computing in Cardiology Conference (CinC), Nice, France, 6–9 September 2015. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, X.; Song, C. An Automatic Screening Approach for Obstructive Sleep Apnea Diagnosis Based on Single-Lead Electrocardiogram. IEEE Trans. Autom. Sci. Eng. 2015, 12, 106–115. [Google Scholar] [CrossRef]
- Esco, M.R.; Flatt, A.A. Ultra-Short-Term Heart Rate Variability Indexes at Rest and Post-Exercise in Athletes: Evaluating the Agreement with Accepted Recommendations. J. Sports Sci. Med. 2014, 13, 535–541. [Google Scholar] [PubMed]
- Singh, J.; Sharma, R.K.; Gupta, A.K. A method of REM-NREM sleep distinction using ECG signal for unobtrusive personal monitoring. Comput. Biol. Med. 2016, 78, 138–143. [Google Scholar] [CrossRef]
- Galal, I. Nocturnal heart rate variability analysis as a screening tool for obstructive sleep apnea syndrome. Egypt. J. Chest Dis. Tuberc. 2012, 61, 187–195. [Google Scholar] [CrossRef]
- Iyengar, N.; Peng, C.-K.; Morin, R.; Goldberger, A.L.; Lipsitz, L.A. Age-related alterations in the fractal scaling of cardiac interbeat interval dynamics. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1996, 271, R1078–R1084. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.-K.; Hausdorff, J.M.; Havlin, S.; Mietus, J.E.; Stanley, H.E.; Goldberger, A.L. Multiple-time scales analysis of physiological time series under neural control. Phys. A Stat. Mech. Its Appl. 1998, 249, 491–500. [Google Scholar] [CrossRef]
- Trimer, R.; Cabidu, R.; Sampaio, L.; Stirbulov, R.; Poiares, D.; Guizilini, S.; Bianchi, A.; Costa, F.; Mendes, R.; Delfino, A.; et al. Heart rate variability and cardiorespiratory coupling in obstructive sleep apnea: Elderly compared with young. Sleep Med. 2014, 15, 1324–1331. [Google Scholar] [CrossRef]
- Peng, C.-K.; Yang, A.C.-C.; Goldberger, A.L. Statistical physics approach to categorize biologic signals: From heart rate dynamics to DNA sequences. Chaos 2007, 17, 015115. [Google Scholar] [CrossRef]
- Shen, Q.; Qin, H.; Wei, K.; Liu, G. Multiscale Deep Neural Network for Obstructive Sleep Apnea Detection Using RR Interval from Single-lead ECG Signal. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Pan, W.-Y.; Su, M.-C.; Wu, H.-T.; Lin, M.-C.; Tsai, I.-T.; Sun, C.-K. Multiscale Entropy Analysis of Heart Rate Variability for Assessing the Severity of Sleep Disordered Breathing. Entropy 2015, 17, 231–243. [Google Scholar] [CrossRef]
- Blomster, H.; Tuomilehto, H.; Laitinen, T.P.; Lyyra-Laitinen, T.; Randell, J.; Kokkarinen, J.; Gylling, H.; Sahlman, J.; Seppä, J.; Hartikainen, J.E.; et al. Mild obstructive sleep apnea does not modulate baroreflex sensitivity in adult patients. Nat. Sci. Sleep 2015, 7, 73–80. [Google Scholar] [CrossRef] [PubMed]
- Walker-Engström, M.-L.; Ringqvist, I.; Vestling, O.; Wilhelmsson, B.; Tegelberg, A. A Prospective Randomized Study Comparing Two Different Degrees of Mandibular Advancement with a Dental Appliance in Treatment of Severe Obstructive Sleep Apnea. Sleep Breath. 2003, 7, 119–130. [Google Scholar] [CrossRef]
- Narkiewicz, K.; Somers, V.K. Cardiovascular variability characteristics in obstructive sleep apnea. Auton. Neurosci. 2001, 90, 89–94. [Google Scholar] [CrossRef]
- Weinstein, A.A.; Deuster, P.A.; Kop, W.J. Heart Rate Variability as a Predictor of Negative Mood Symptoms Induced by Exercise Withdrawal. Med. Sci. Sports Exerc. 2007, 39, 735–741. [Google Scholar] [CrossRef] [PubMed]
- Guilleminault, C.; Poyares, D.; Rosa, A.; Huang, Y.-S. Heart rate variability, sympathetic and vagal balance and EEG arousals in upper airway resistance and mild obstructive sleep apnea syndromes. Sleep Med. 2005, 6, 451–457. [Google Scholar] [CrossRef]
- Bonsignore, M.R.; Romano, S.; Marrone, O.; Chiodi, M.; Bonsignore, G. Different heart rate patterns in obstructive apneas during NREM sleep. Sleep 1997, 20, 1167–1174. [Google Scholar]




| N (29) | OSA-m (39) | OSA-s (24) | |
|---|---|---|---|
| Mean ± SD | 80.86 ± 11.54 | 83.49 ± 15.12 | 84.03 ± 12.78 |
| Total number | 2345 | 3256 | 2018 |
| Indices | Correlation | N | OSA-m | OSA-s | p-Value | ||||
|---|---|---|---|---|---|---|---|---|---|
| R | P | N&OSA-m | N&OSA-s | OSA-m&OSA-s | |||||
| Time domain | Mean | −0.254 | 0.015 | 0.962 ± 0.116 | 0.951 ± 0.101 | 0.907 ± 0.087 | 0.674 | 0.058 | 0.105 |
| SDNN | 0.327 | 0.001 | 0.072 ± 0.024 | 0.076 ± 0.020 | 0.089 ± 0.026 | 0.507 | 0.008 | 0.027 | |
| RMSSD | 0.180 | 0.086 | 0.066 ± 0.022 | 0.071 ± 0.022 | 0.077 ± 0.026 | 0.351 | 0.100 | 0.381 | |
| PNN50 | 0.123 | 0.242 | 25.558 ± 15.474 | 26.572 ± 16.397 | 29.336 ± 15.624 | 0.796 | 0.392 | 0.505 | |
| CV | 0.436 | 0.000 | 0.076 ± 0.023 | 0.081 ± 0.020 | 0.099 ± 0.028 | 0.402 | <0.001 | 0.003 | |
| Frequency domain | LF | 0.268 | 0.010 | 0.002 ± 0.001 | 0.002 ± 0.001 | 0.003 ± 0.002 | 0.973 | 0.085 | 0.072 |
| HF | 0.112 | 0.288 | 0.0012 ± 0.0011 | 0.0012 ± 0.0008 | 0.0013 ± 0.0010 | 0.870 | 0.602 | 0.689 | |
| LF/HF | 0.255 | 0.014 | 2.356 ± 0.932 | 2.285 ± 0.838 | 3.052 ± 1.843 | 0.812 | 0.039 | 0.016 | |
| Nonlinear | IBS | −0.653 | 0.000 | 0.297 ± 0.016 | 0.295 ± 0.012 | 0.266 ± 0.028 | 0.634 | <0.001 | <0.001 |
| OP_IBS | −0.721 | 0.000 | 0.351 ± 0.021 | 0.348 ± 0.014 | 0.300 ± 0.040 | 0.705 | <0.001 | <0.001 | |
| Acc/% | Sen/% | Spe/% | F1 Score/% | |
|---|---|---|---|---|
| Decision tree | 85.9 | 79.2 | 88.2 | 74.5 |
| Random Forest | 83.7 | 73.0 | 88.2 | 69.7 |
| K Nearest Neighbor | 83.6 | 70.0 | 89.5 | 67.9 |
| Naive Bayes | 86.8 | 51.8 | 97.1 | 62.5 |
| Indices | p-Value | Acc/% | Sen/% | Spe/% | F1 Score/% |
|---|---|---|---|---|---|
| CV | 0.000 | 68.5 | 37.5 | 79.4 | 38.3 |
| LF/HF | 0.079 | 70.7 | 54.2 | 76.5 | 49.1 |
| IBS | 0.000 | 81.5 | 66.3 | 86.2 | 66.2 |
| OP_IBS | 0.000 | 85.9 | 79.2 | 88.2 | 74.5 |
| OP_IBS, IBS | \ | 86.8 | 72.7 | 91.0 | 74.2 |
| OP_IBS, IBS, LF/HF, CV | \ | 91.3 | 91.0 | 91.5 | 81.3 |
| Device | Signal | Subject | Feature | Classifier | Criterion | Result | ||
|---|---|---|---|---|---|---|---|---|
| Acc/% | Sen/% | Spe/% | ||||||
| Single-lead ECG patch [45] | ECG | 119 | single feature (CVHR) | ROC curve, Youden index | AHI = 15 | 64.7 * | 52.9 | 94.1 |
| Wearable ECG-Belt [46] | ECG | 241 | multiple features (11 features) | SVM | AHI = 15 | 72 | 70 | 74 |
| Wearable watch device [47] | PPG | 41 | single feature (Fcv) | ROC curve | AHI = 15 | 85 | 82 | 89 |
| Wrist-worn rPPG [48] | PPG | 188 | multiple features (212 features) | CNN | AHI = 30 | 91 * | 46 | 98 |
| Wearable bracelet [24] | PPG | 92 | multiple features (sIBS, dIBS, STD, LF.) | Random Forest | AHI = 30 | 84.7 | 76.7 | 89.6 |
| Wearable bracelet # | PPG | 92 | single feature (OP_IBS) | Decision Tree | AHI = 30 | 85.9 | 79.2 | 88.2 |
| Wearable bracelet # | multiple features (CV, LF/HF, IBS, OP_IBS) | 91.3 | 91.0 | 91.5 | ||||
| Reference | Feature | Number of Recordings | Length of RR Segment | Classification Boundary | Classification Results |
|---|---|---|---|---|---|
| Liu et al. [49] | The Hilbert–Huang transform (HHT) based cardiopulmonary coupling | 69 | 1 min | 5 | Acc = 79.1% Sen = 73.1% Spe = 71.2% |
| Li et al. [10] | Sliding trend fuzzy approximate entropy | 60 | 5 min | 5 | Acc = 85.0% Sen = 82.5% Spe = 90.0% |
| Pietrzak et al. [50] | Standard deviation of successive differences | 70 | 10,000 s | 5 | Acc = 88.5% Sen = 96.0% Spe = 70.0% |
| Our proposed method | Information-based similarity of ordinal pattern sequences | 60 | 5 min | 5 | Acc = 91.7% Sen = 95.0% Spe = 85.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Wu, S.; Chen, T.; Wang, C.; Liu, G. Information-Based Similarity of Ordinal Pattern Sequences as a Novel Descriptor in Obstructive Sleep Apnea Screening Based on Wearable Photoplethysmography Bracelets. Biosensors 2022, 12, 1089. https://doi.org/10.3390/bios12121089
Chen M, Wu S, Chen T, Wang C, Liu G. Information-Based Similarity of Ordinal Pattern Sequences as a Novel Descriptor in Obstructive Sleep Apnea Screening Based on Wearable Photoplethysmography Bracelets. Biosensors. 2022; 12(12):1089. https://doi.org/10.3390/bios12121089
Chicago/Turabian StyleChen, Mingjing, Shan Wu, Tian Chen, Changhong Wang, and Guanzheng Liu. 2022. "Information-Based Similarity of Ordinal Pattern Sequences as a Novel Descriptor in Obstructive Sleep Apnea Screening Based on Wearable Photoplethysmography Bracelets" Biosensors 12, no. 12: 1089. https://doi.org/10.3390/bios12121089
APA StyleChen, M., Wu, S., Chen, T., Wang, C., & Liu, G. (2022). Information-Based Similarity of Ordinal Pattern Sequences as a Novel Descriptor in Obstructive Sleep Apnea Screening Based on Wearable Photoplethysmography Bracelets. Biosensors, 12(12), 1089. https://doi.org/10.3390/bios12121089





