Effect of Electrolyte Concentration on Cell Sensing by Measuring Ionic Current Waveform through Micropores
Abstract
1. Introduction
2. Materials and Methods
2.1. Cell Cultures and Sample Preparation for Measuring Ionic Current
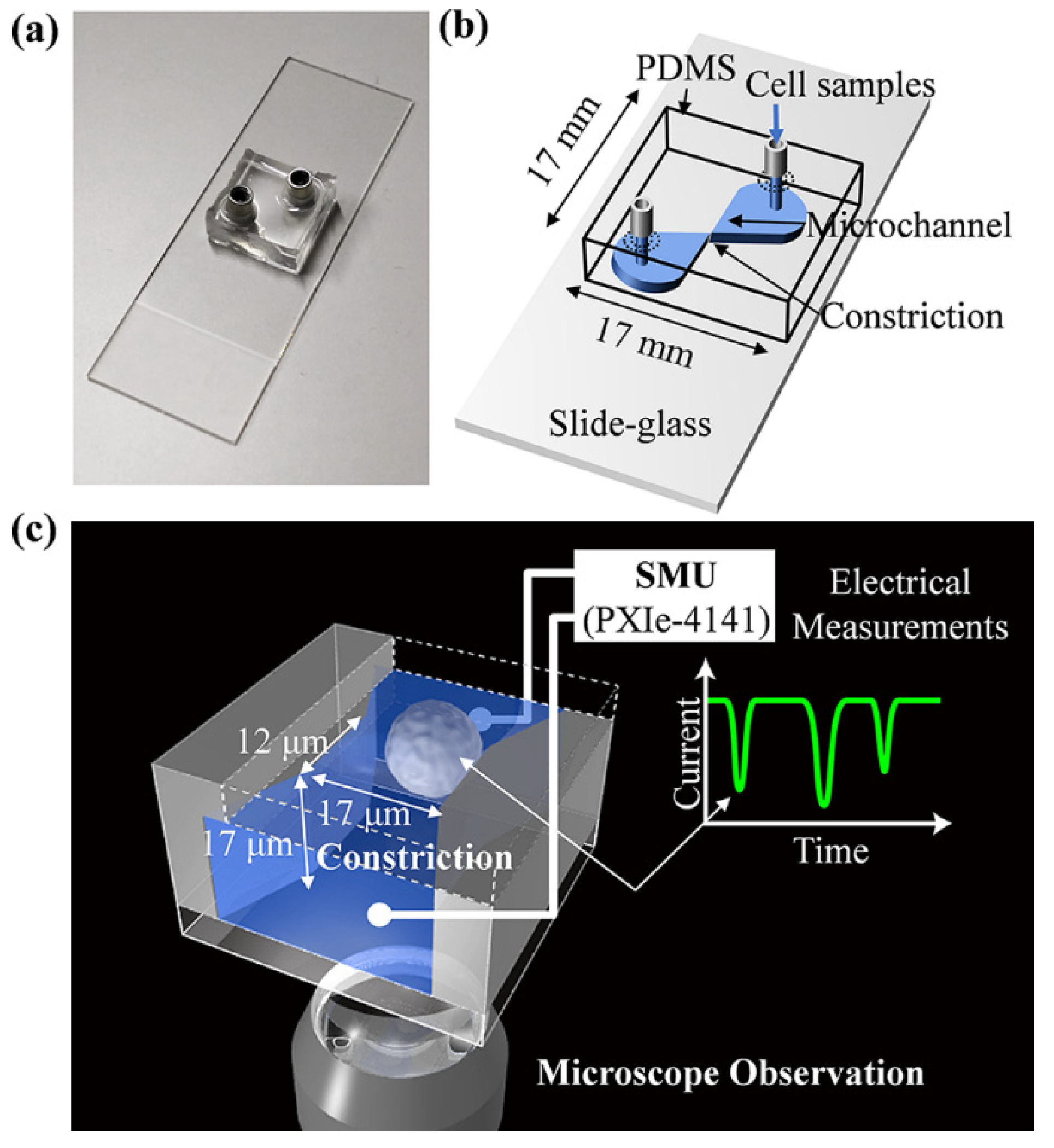
2.2. Fabrication of Microfluidic Cell Sensing Chips
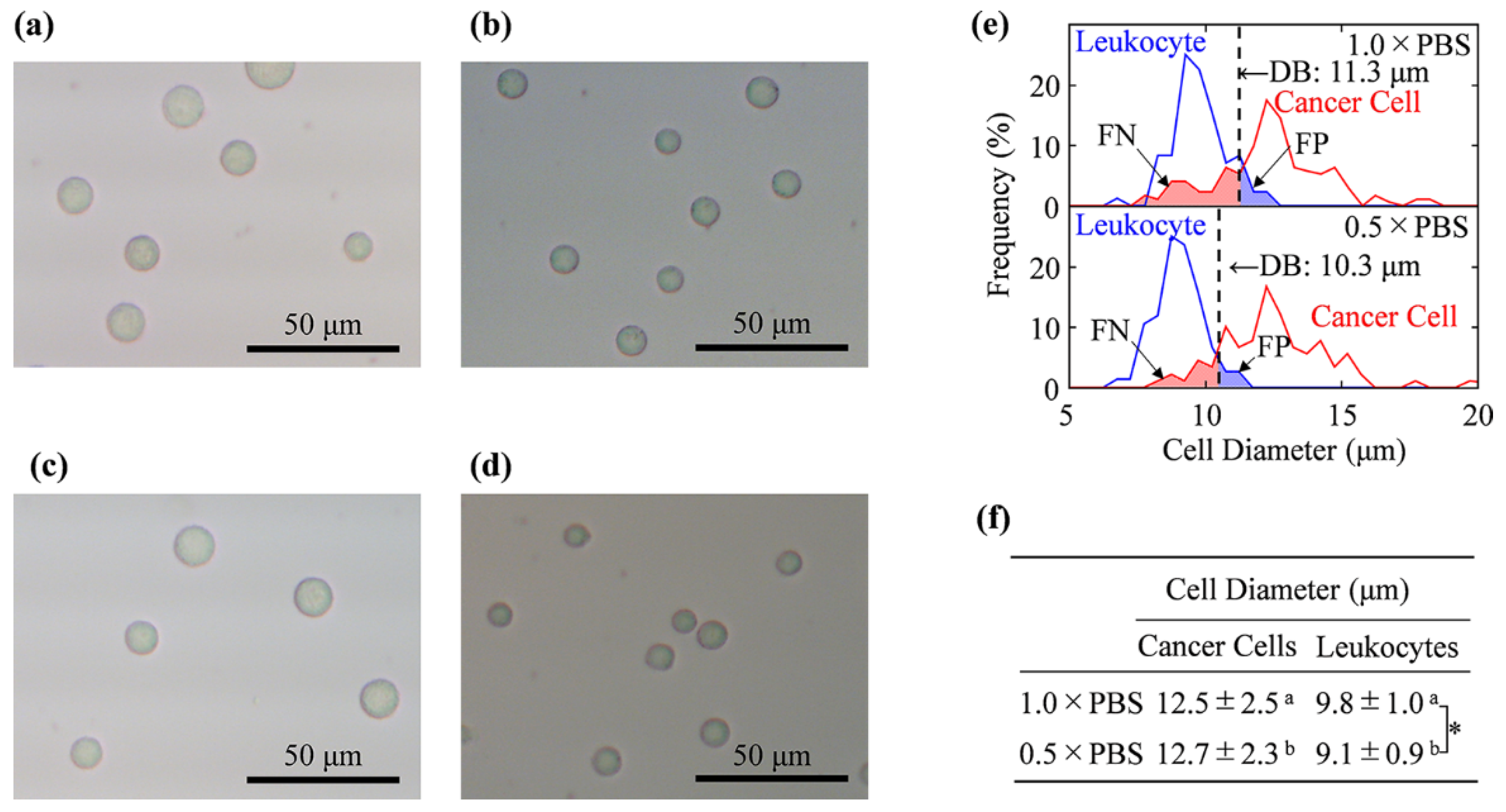
2.3. Cell Size Measurement by Using Optical Microscope
2.4. Determination of Decision Boundary and Discrimination Error
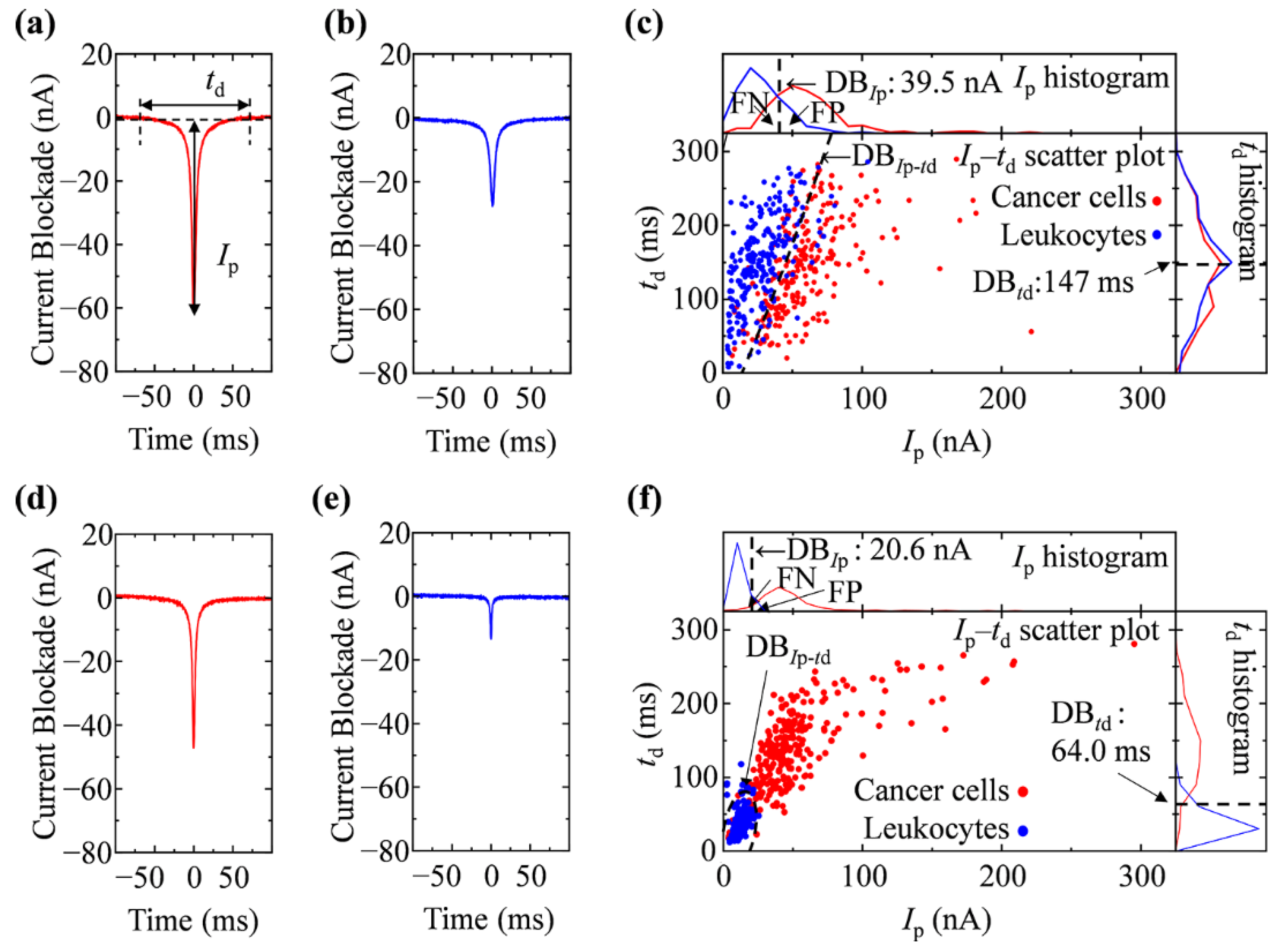
2.5. Ionic Current Measurements
2.6. Resistive Pulse Analyses and Cell Discrimination
2.7. Zeta Potential Measurements
3. Results and Discussion
3.1. Cell Size Examination by Light Microscopy
3.2. Ionic Current Measurement of Cells
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, Y.X.; Zhang, J.Y.; Li, D.Q. Microfluidic and nanofluidic resistive pulse sensing: A review. Micromachines 2017, 8, 204. [Google Scholar] [CrossRef]
- Tsutsui, M.; Yoshida, T.; Yokota, K.; Yasaki, H.; Yasui, T.; Arima, A.; Tonomura, W.; Nagashima, K.; Yanagida, T.; Kaji, N.; et al. Discriminating single-bacterial shape using low-aspect-ratio pores. Sci. Rep. 2017, 7, 17371. [Google Scholar] [CrossRef] [PubMed]
- Yusko, E.C.; Bruhn, B.R.; Eggenberger, O.M.; Houghtaling, J.; Rollings, R.C.; Walsh, N.C.; Nandivada, S.; Pindrus, M.; Hall, A.R.; Sept, D.; et al. Real-time shape approximation and fingerprinting of single proteins using a nanopore. Nat. Nanotechnol. 2017, 12, 360–367. [Google Scholar] [CrossRef] [PubMed]
- Ryuzaki, S.; Tsutsui, M.; He, Y.; Yokota, K.; Arima, A.; Morokawa, T.; Taniguchi, M.; Kawai, T. Rapid structural analysis of nanomaterials in aqueous solutions. Nanotechnology 2017, 28, 155501. [Google Scholar] [CrossRef]
- Arjmandi, N.; Van Roy, W.; Lagae, L.; Borghs, G. Measuring the electric charge and zeta potential of nanometer-sized objects using pyramidal-shaped nanopores. Anal. Chem. 2012, 84, 8490–8496. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Nguyen, J.; Wang, C.; Sun, Y. Electrical measurement of red blood cell deformability on a microfluidic device. Lab Chip 2013, 13, 3275–3283. [Google Scholar] [CrossRef] [PubMed]
- Darvish, A.; Goyal, G.; Aneja, R.; Sundaram, R.V.K.; Lee, K.; Ahn, C.W.; Kim, K.-B.; Vlahovska, P.M.; Kim, M.J. Nanoparticle mechanics: Deformation detection via nanopore resistive pulse sensing. Nanoscale 2016, 8, 14420–14431. [Google Scholar] [CrossRef]
- Luo, L.; German, S.R.; Lan, W.-J.; Holden, D.A.; Mega, T.L.; White, H.S. Resistive-pulse analysis of nanoparticles. Annu. Rev. Anal. Chem. 2014, 7, 513–535. [Google Scholar] [CrossRef] [PubMed]
- Wanunu, M. Nanopores: A journey towards DNA sequencing. Phys. Life Rev. 2012, 9, 125–158. [Google Scholar] [CrossRef]
- Howorka, S.; Siwy, Z. Nanopore analytics: Sensing of single molecules. Chem. Soc. Rev. 2009, 38, 2360–2384. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Xie, X.; Duan, Y.; Wang, L.; Cheng, Z.; Cheng, J. A review of impedance measurements of whole cells. Biosens. Bioelectron. 2016, 77, 824–836. [Google Scholar] [CrossRef]
- Fidler, I.J. Timeline—The pathogenesis of cancer metastasis: The ‘seed and soil’ hypothesis revisited. Nat. Rev. Cancer 2003, 3, 453–458. [Google Scholar] [CrossRef] [PubMed]
- Sieuwerts, A.M.; Kraan, J.; Bolt, J.; van der Spoel, P.; Elistrodt, F.; Schutte, M.; Martens, J.W.M.; Gratama, J.-W.; Sleijfer, S.; Foekens, J.A. Anti-epithelial cell adhesion molecule antibodies and the detection of circulating normal-like breast tumor cells. J. Natl. Cancer Inst. 2009, 101, 61–66. [Google Scholar] [CrossRef]
- Mostert, B.; Kraan, J.; Bolt-de Vries, J.; van der Spoel, P.; Sieuwerts, A.M.; Schutte, M.; Timmermans, A.M.; Foekens, R.; Martens, J.W.M.; Gratama, J.-W. Detection of circulating tumor cells in breast cancer may improve through enrichment with anti-CD146. Breast Cancer Res. Treat. 2011, 127, 33–41. [Google Scholar] [CrossRef] [PubMed]
- van der Toom, E.E.; Verdone, J.E.; Gorin, M.A.; Pienta, K.J. Technical challenges in the isolation and analysis of circulating tumor cells. Oncotarget 2016, 7, 62754–62766. [Google Scholar] [CrossRef] [PubMed]
- Tsutsui, M.; He, Y.; Furuhashi, M.; Rahong, S.; Taniguchi, M.; Kawai, T. Transverse electric field dragging of DNA in a nanochannel. Sci. Rep. 2012, 2, 394. [Google Scholar] [CrossRef] [PubMed]
- Sibarani, J.; Takai, M.; Ishihara, K. Surface modification on microfluidic devices with 2-methacryloyloxyethyl phosphorylcholine polymers for reducing unfavorable protein adsorption. Colloids Surf. B. Biointerfaces 2007, 54, 88–93. [Google Scholar] [CrossRef] [PubMed]
- Fukazawa, K.; Ishihara, K. Simple surface treatment using amphiphilic phospholipid polymers to obtain wetting and lubricity on polydimethylsiloxane-based substrates. Colloids Surf B Biointerfaces 2012, 97, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Pischel, D.; Buchbinder, J.H.; Sundmacher, K.; Lavrik, I.N.; Flassig, R.J. A guide to automated apoptosis detection: How to make sense of imaging flow cytometry data. PLoS ONE 2018, 13, e0197208. [Google Scholar] [CrossRef]
- Fraley, C.; Raftery, A.E. Model-based clustering, discriminant analysis, and density estimation. J. Am. Stat. Assoc. 2002, 97, 611–631. [Google Scholar] [CrossRef]
- Wernecke, K.-D. Discriminant Analysis. In Wiley Encyclopedia of Clinical Trials; D’Agostino, R.B., Sullivan, L., Massaro, J., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; pp. 1–19. [Google Scholar]
- Ballabio, D.; Todeschini, R. Multivariate Classification for Quantitative Analysis. In Infrared Spectroscopy for Food Quality Analysis and Control, 1st ed.; Sun, D.-W., Ed.; Elsevier: London, UK, 2009; pp. 83–104. [Google Scholar]
- Fagerland, M.W.; Lydersen, S.; Laake, P. Recommended tests and confidence intervals for paired binomial proportions. Stat. Med. 2014, 33, 2850–2875. [Google Scholar] [CrossRef] [PubMed]
- Smeets, R.M.; Keyser, U.F.; Dekker, N.H.; Dekker, C. Noise in solid-state nanopores. Proc. Natl. Acad. Sci. USA 2008, 105, 417–421. [Google Scholar] [CrossRef] [PubMed]
- Bondar, O.V.; Saifullina, D.V.; Shakhmaeva, I.I.; Mavlyutova, I.I.; Abdullin, T.I. Monitoring of the zeta potential of human cells upon reduction in their viability and interaction with polymers. Acta Nat. 2012, 4, 78–81. [Google Scholar] [CrossRef]
- Dobrzynska, I.; Skrzydlewska, E.; Figaszewski, Z.A. Changes in electric properties of human breast cancer cells. J. Membr. Biol. 2013, 246, 161–166. [Google Scholar] [CrossRef]
- Schoch, R.B.; Han, J.Y.; Renaud, P. Transport phenomena in nanofluidics. Rev. Mod. Phys. 2008, 80, 839–883. [Google Scholar] [CrossRef]
- de Wit, S.; van Dalum, G.; Lenferink, A.T.M.; Tibbe, A.G.J.; Hiltermann, T.J.N.; Groen, H.J.M.; van Rijn, C.J.M.; Terstappen, L. The detection of EpCAM+ and EpCAM- circulating tumor cells. Sci. Rep. 2015, 5, 12270. [Google Scholar] [CrossRef]
- Rostami, P.; Kashaninejad, N.; Moshksayan, K.; Saidi, M.S.; Firoozabadi, B.; Nguyen, N.T. Novel approaches in cancer management with circulating tumor cell clusters. J. Sci. Adv. Mater. Dev. 2019, 4, 1–18. [Google Scholar] [CrossRef]
- Gogoi, P.; Sepehri, S.; Zhou, Y.; Gorin, M.A.; Paolillo, C.; Capoluongo, E.; Gleason, K.; Payne, A.; Boniface, B.; Cristofanilli, M.; et al. Development of an Automated and Sensitive Microfluidic Device for Capturing and Characterizing Circulating Tumor Cells (CTCs) from Clinical Blood Samples. PLoS ONE 2016, 11, e0147400. [Google Scholar] [CrossRef]
- Austin, R.G.; Huang, T.J.; Wu, M.; Armstrong, A.J.; Zhang, T. Clinical utility of non-EpCAM based circulating tumor cell assays. Adv. Drug Deliv. Rev. 2018, 125, 132–142. [Google Scholar] [CrossRef] [PubMed]
| Discrimination Based on the Cell Size by a Microscopic Examination | ||||||
| Actual Classification | Predicted Classification | |||||
| 1.0 × PBS | 0.5 × PBS | |||||
| Cancer Cells | Leukocytes | ER (%) | Cancer Cells | Leukocytes | ER (%) | |
| Cancer cells | 71 (TP) | 29 (FN) | 17.5 | 90 (TP) | 10 (FN) | 8.5 |
| Leukocytes | 6 (FP) | 94 (TN) | 7 (FP) | 93 (TN) | ||
| Confidence interval of error rate (ER) | 95% CI, 12.5–23.5 | 95% CI, 5.0–13.3 | ||||
| Discrimination Based on Ip, or td Acquired by RPM | ||||||
| Actual Classification | Predicted Classification by Ip | |||||
| 1.0 × PBS | 0.5 × PBS | |||||
| Cancer Cells | Leukocytes | ER (%) | Cancer Cells | Leukocytes | ER (%) | |
| Cancer cells Leukocytes | 163 34 | 87 216 | 24.2 | 237 12 | 13 238 | 5.0 |
| Cancer cells Leukocytes | 140 23 | 110 227 | 26.6 | 230 7 | 20 243 | 5.4 |
| Cancer cells Leukocytes | 122 27 | 128 223 | 31.0 | 238 7 | 12 243 | 3.8 |
| Discrimination ER (mean ± SD %, n = 3) | 27.3 ± 3.5 | 4.7 ± 0.8 ** | ||||
| Actual Classification | Predicted Classification by td | |||||
| Cancer cells Leukocytes | 109 86 | 141 164 | 45.4 | 231 11 | 19 239 | 6.0 |
| Cancer cells Leukocytes | 96 70 | 154 180 | 44.8 | 224 9 | 26 241 | 7.0 |
| Cancer cells Leukocytes | 184 160 | 66 90 | 45.2 | 230 15 | 20 235 | 7.0 |
| Discrimination ER | 45.1 ± 0.3 | 6.7 ± 0.6 ** | ||||
| Discrimination Based on Ip–td Acquired by RPM | ||||||
| Actual Classification | Predicted Classification by Ip–td | |||||
| 1.0 × PBS | 0.5 × PBS | |||||
| Cancer Cells | Leukocytes | ER (%) | Cancer Cells | Leukocytes | ER (%) | |
| Cancer cells Leukocytes | 202 23 | 48 227 | 14.2 | 238 11 | 12 239 | 4.6 |
| Cancer cells Leukocytes | 172 23 | 78 227 | 20.2 | 234 9 | 16 241 | 5.0 |
| Cancer cells Leukocytes | 161 20 | 89 230 | 21.8 | 240 10 | 10 240 | 4.0 |
| Discrimination ER | 18.7 ± 4.0 | 4.5 ± 0.5 ** | ||||
| Ip (nA) | td (ms) | |||
|---|---|---|---|---|
| Cancer Cell | Leukocytes | Cancer Cell | Leukocytes | |
| 1.0 × PBS | 58.7 ± 1.9 | 26.3 ± 1.6** | 145.2 ± 1.9 | 150.0 ± 1.4 * |
| 0.5 × PBS | 50.8 ± 1.6 | 12.0 ± 0.2** | 136.4 ± 3.8 | 40.7 ± 1.2 ** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yokota, K.; Hashimoto, M.; Kajimoto, K.; Tanaka, M.; Murayama, S.; Tsutsui, M.; Nakajima, Y.; Taniguchi, M.; Kataoka, M. Effect of Electrolyte Concentration on Cell Sensing by Measuring Ionic Current Waveform through Micropores. Biosensors 2021, 11, 78. https://doi.org/10.3390/bios11030078
Yokota K, Hashimoto M, Kajimoto K, Tanaka M, Murayama S, Tsutsui M, Nakajima Y, Taniguchi M, Kataoka M. Effect of Electrolyte Concentration on Cell Sensing by Measuring Ionic Current Waveform through Micropores. Biosensors. 2021; 11(3):78. https://doi.org/10.3390/bios11030078
Chicago/Turabian StyleYokota, Kazumichi, Muneaki Hashimoto, Kazuaki Kajimoto, Masato Tanaka, Sanae Murayama, Makusu Tsutsui, Yoshihiro Nakajima, Masateru Taniguchi, and Masatoshi Kataoka. 2021. "Effect of Electrolyte Concentration on Cell Sensing by Measuring Ionic Current Waveform through Micropores" Biosensors 11, no. 3: 78. https://doi.org/10.3390/bios11030078
APA StyleYokota, K., Hashimoto, M., Kajimoto, K., Tanaka, M., Murayama, S., Tsutsui, M., Nakajima, Y., Taniguchi, M., & Kataoka, M. (2021). Effect of Electrolyte Concentration on Cell Sensing by Measuring Ionic Current Waveform through Micropores. Biosensors, 11(3), 78. https://doi.org/10.3390/bios11030078







