Impedance Model of Cylindrical Nanowires for Metamaterial Applications
Abstract
1. Introduction
- New cylindrical wave impedance approach (impedance defined as ) is used at optical frequency, which uses cylindrical harmonic functions to derive expression for the internal and external impedances of the metallic nanowire.
- Equivalent analytical expression for the scattering () and extinction () cross-sectional area efficiencies of the nanowire (basic unit cell in metamaterial) is derived in terms of impedances.
- Derived expressions are in terms of length, radius, and dielectric function of the nanowires, thus preserving macroscopic plasmon properties of the metal at optical frequency.
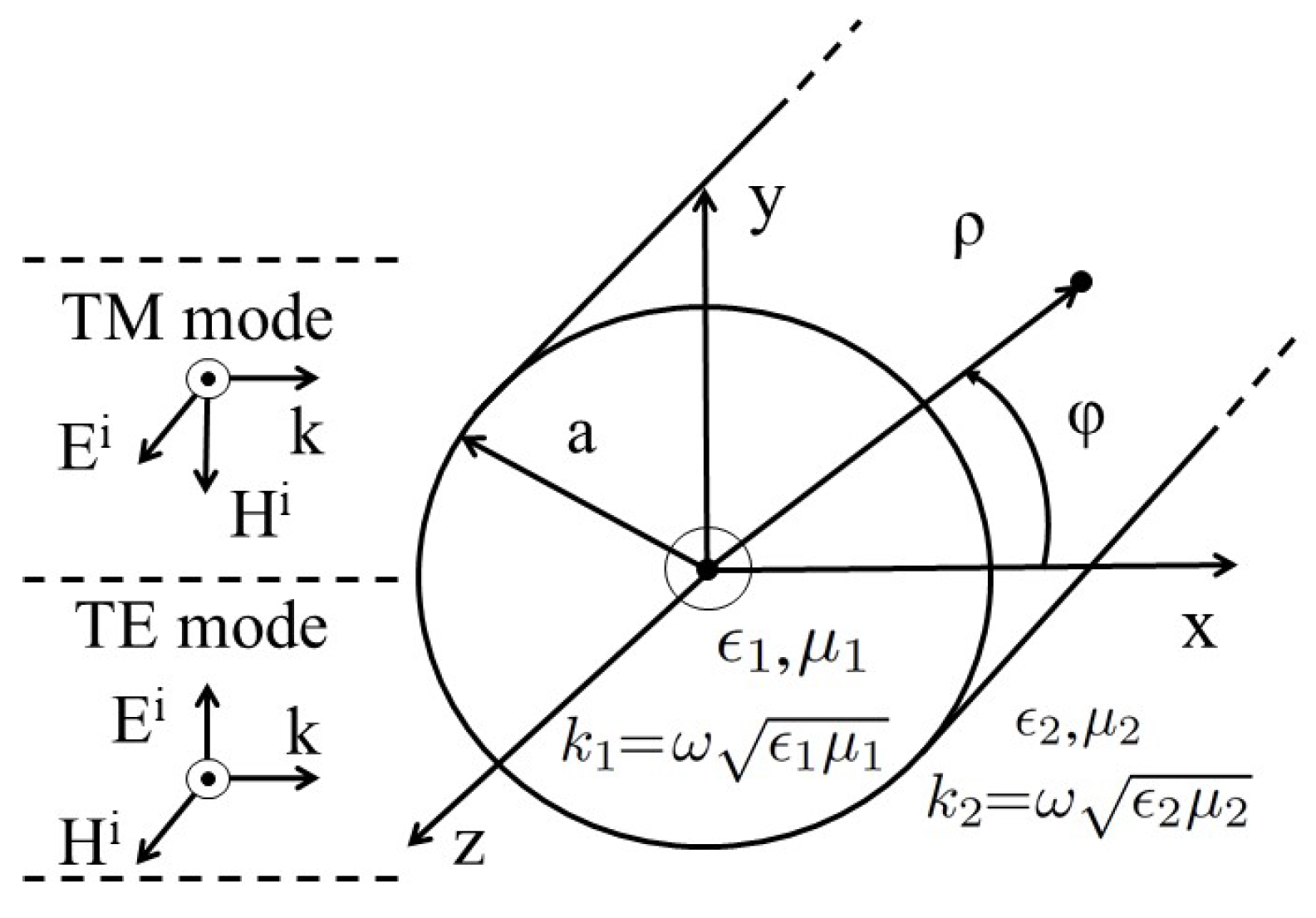
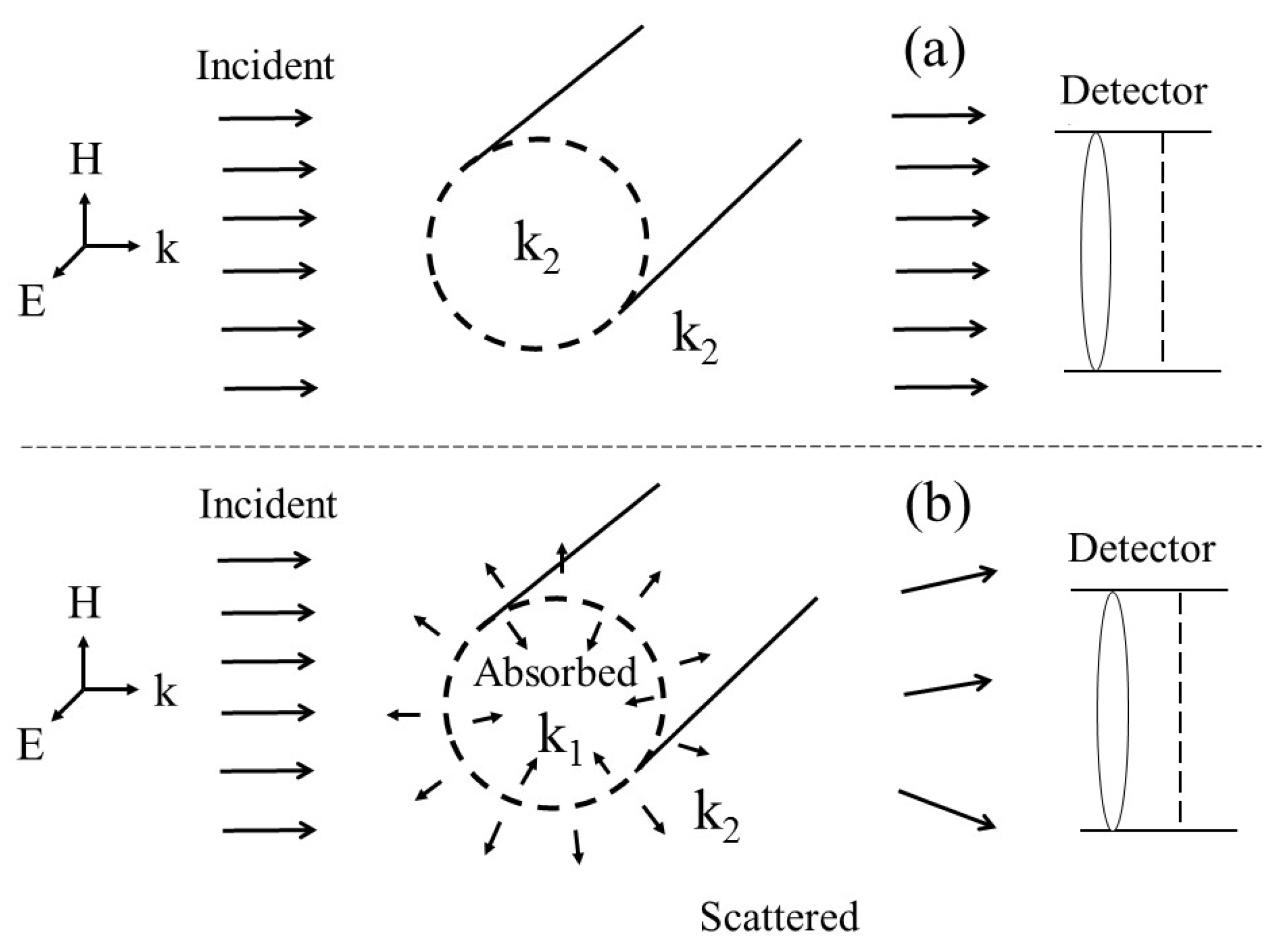
2. EM Field Solution to the Scattering, Absorption and Extinction in Circular Cylindrical Nanowire
3. Proposed Wave Impedance Model of Metallic Cylindrical Nanowires
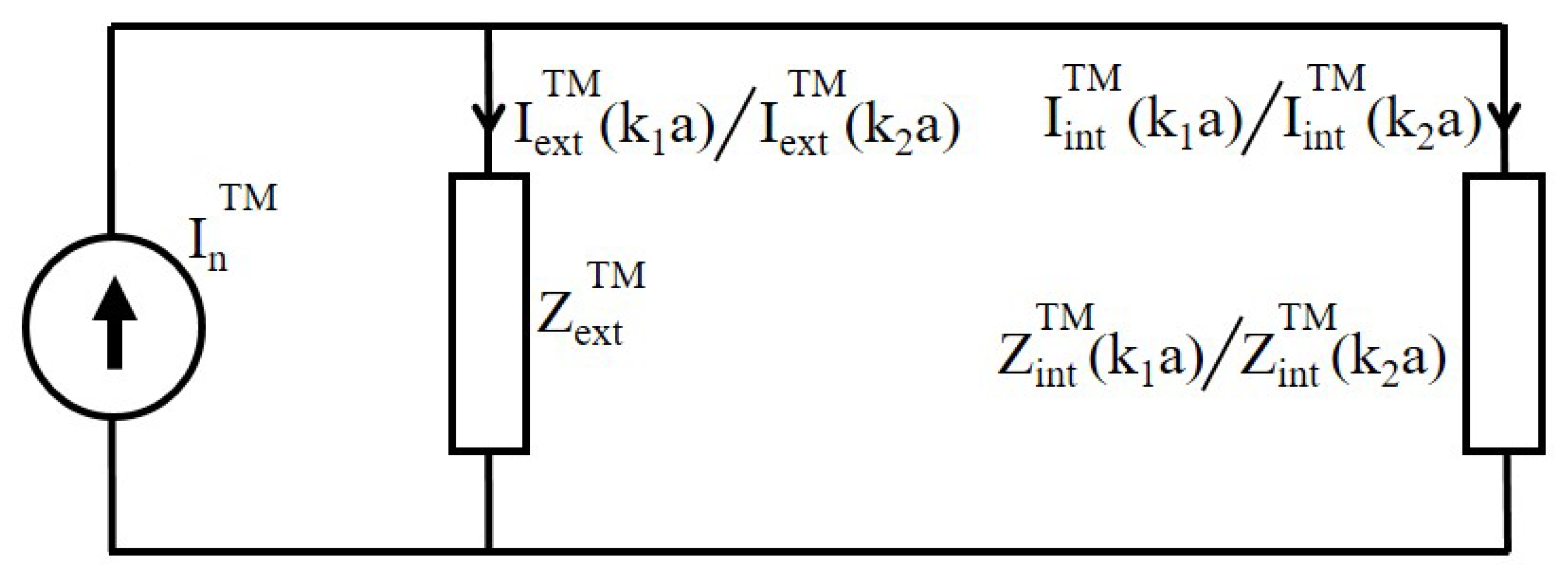
3.1. TM Mode: Wave Impedance and Cross-Sectional Areas Efficiencies (Scattering, Absorption and Extinction)
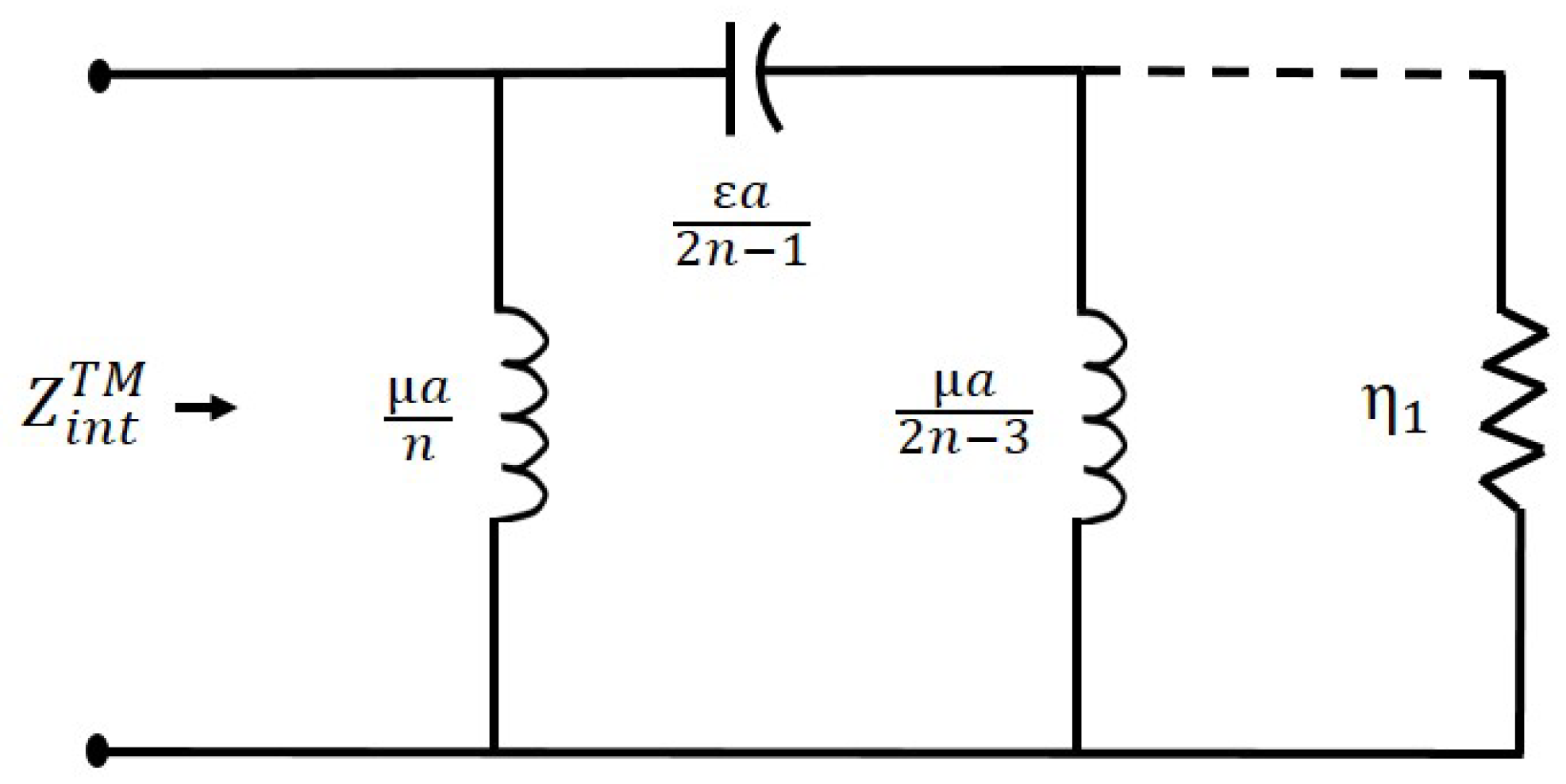
3.1.1. Internal Impedance
3.1.2. External Impedance
3.1.3. TM Mode: Cross-Sectional Areas Efficiencies Using Impedances
- -
- : Surface current due to nanowire with property , supporting scattering waves.
- -
- : Surface current due to nanowire with property , supporting scattering waves.
- -
- : Surface current due to nanowire with property , supporting waves absorption.
- -
- : Surface current due to nanowire with property , supporting waves absorption.
- -
- : The ratio between and .
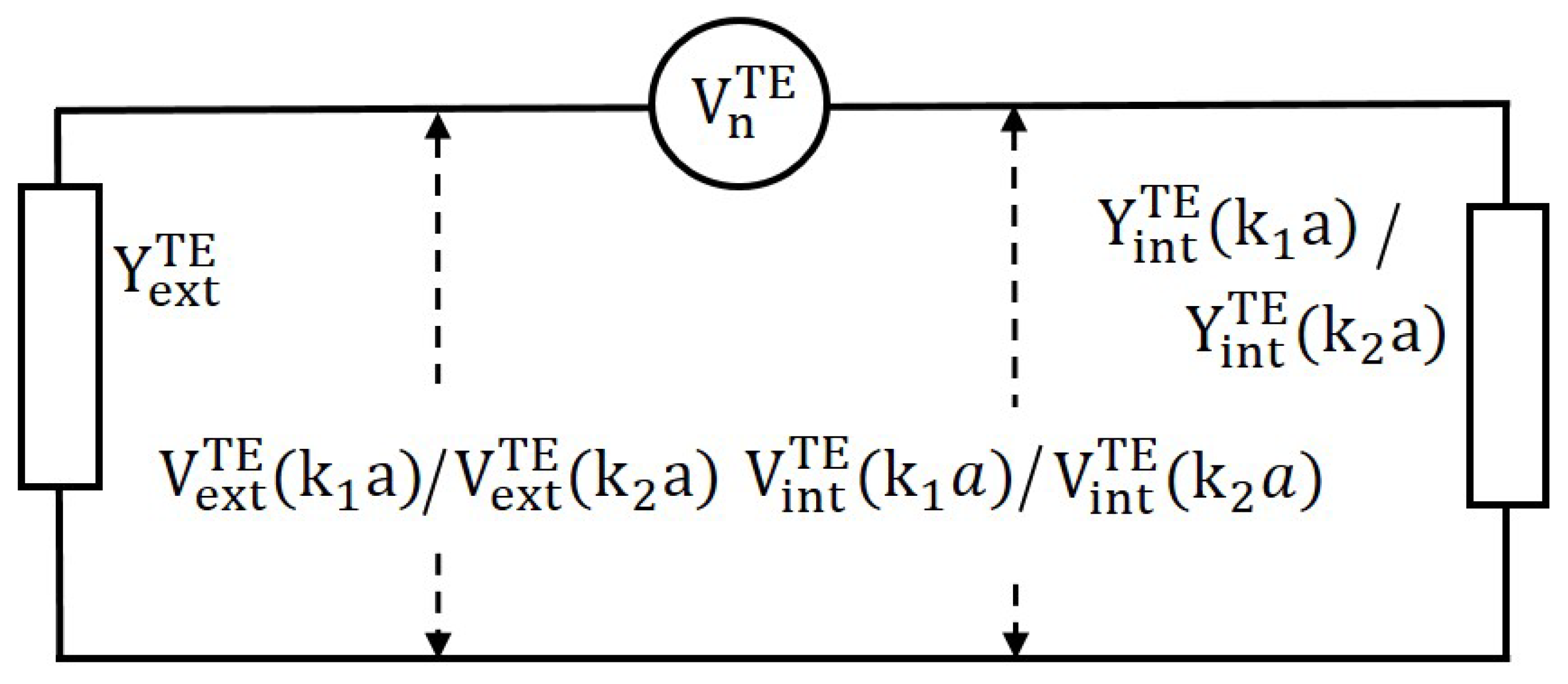
3.2. TE Mode: Wave Impedance and Cross-Sectional Area Efficiencies (Scattering, Absorption and Extinction)
3.2.1. Internal and External Admittance
3.2.2. TE Mode: Cross-Sectional Areas Efficiencies Using Admittance
- -
- : Voltage due to nanowire with property , supporting scattering waves.
- -
- : Voltage due to nanowire with property , supporting scattering waves.
- -
- : Voltage due to nanowire with property , supporting waves absorption.
- -
- : Voltage due to nanowire with property , supporting waves absorption.
- -
- : The ratio between and .
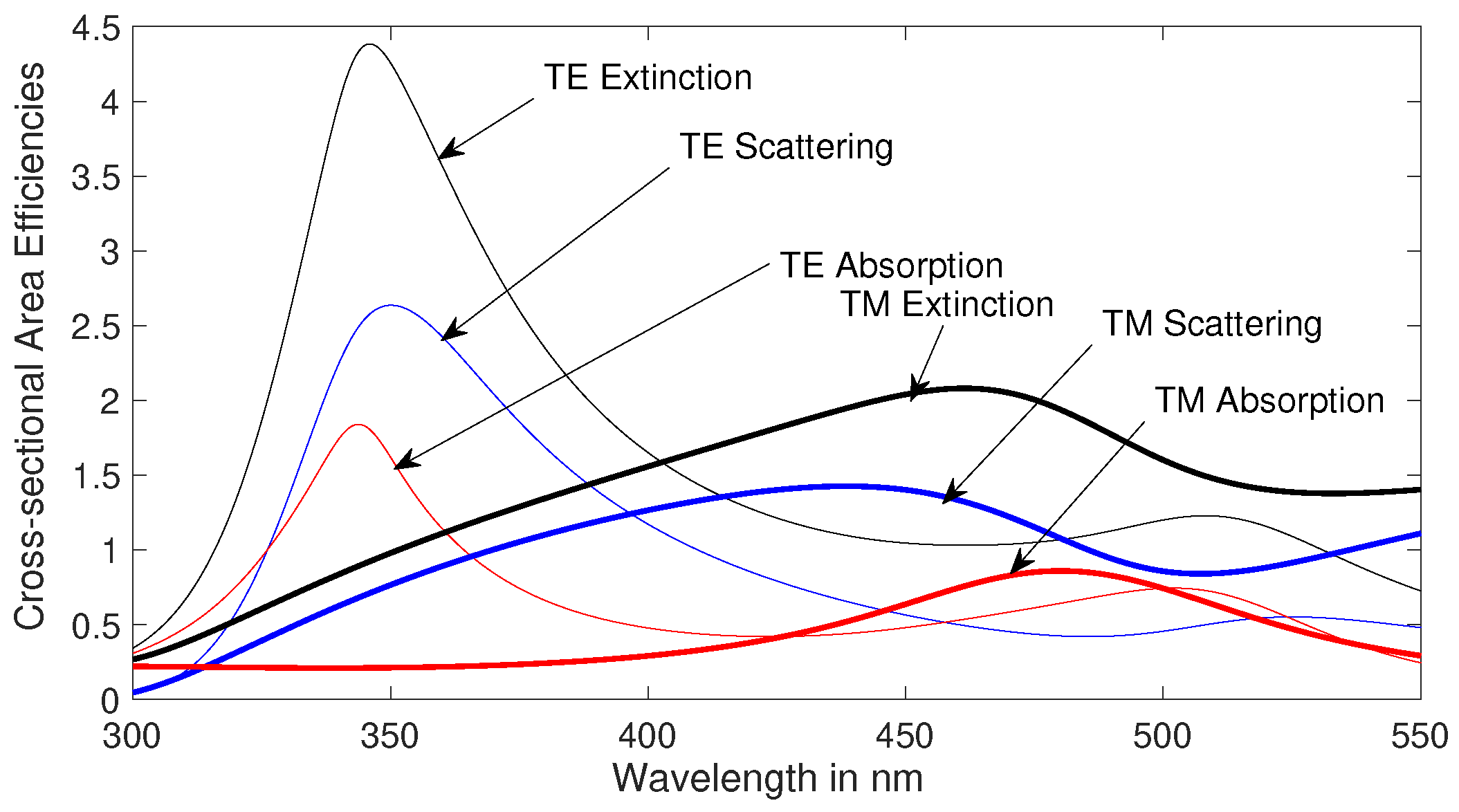
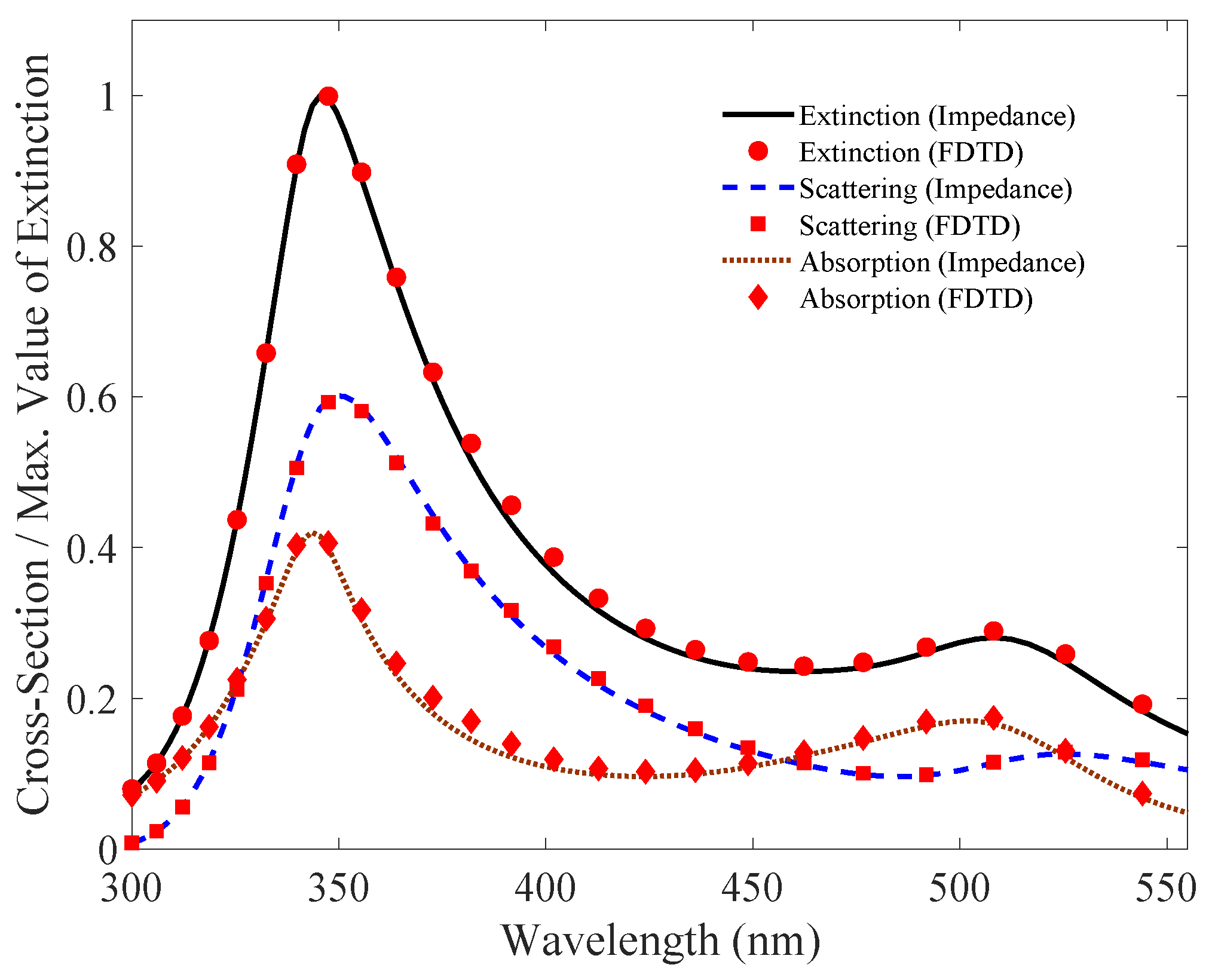
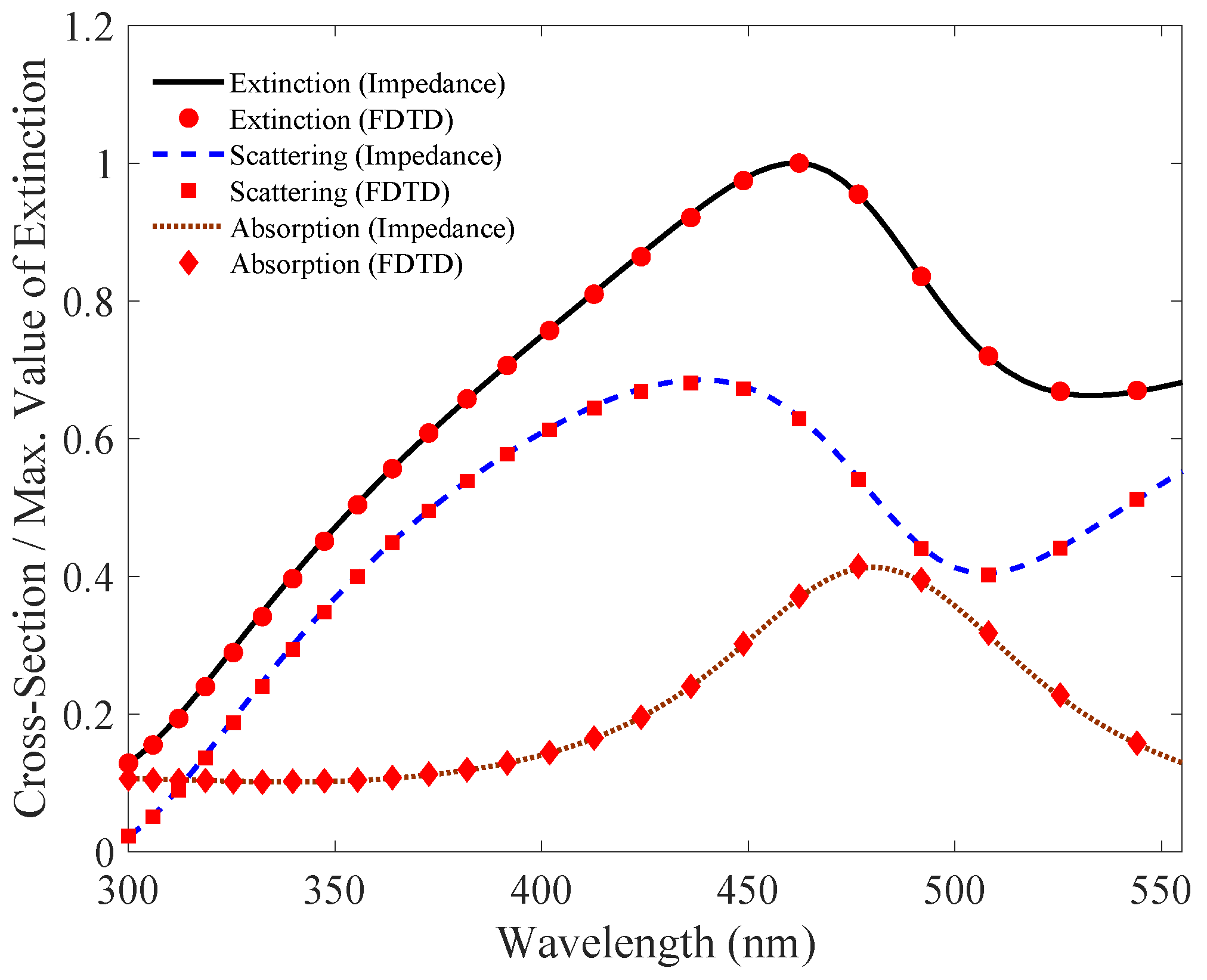
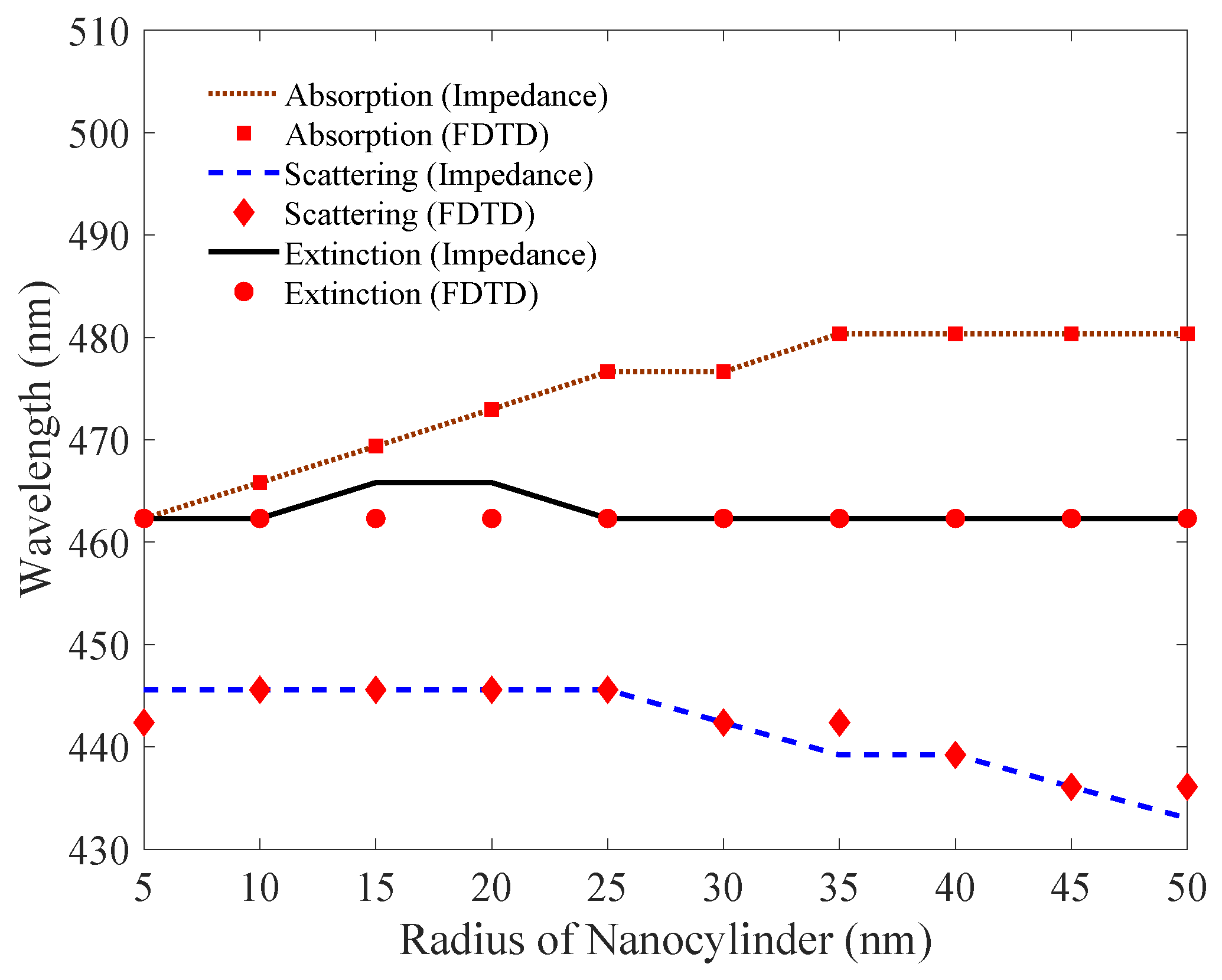
4. Simulation and Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| E | Electric |
| M | Magnetic |
| TE | Transverse Electric |
| TM | Transverse Magnetic |
| FDTD | Finite Difference Time Domain |
References
- Kadic, M.; Milton, G.W.; van Hecke, M.; Wegener, M. 3D metamaterials. Nat. Rev. Phys. 2019, 1, 198–210. [Google Scholar] [CrossRef]
- Yoo, S.; Park, Q. Metamaterials and chiral sensing: A review of fundamentals and applications. Nanophotonics 2019, 2, 249–261. [Google Scholar] [CrossRef]
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic surface lattice resonances: A review of properties and applications. Chem. Rev. 2018, 12, 5912–5951. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Kim, S.J.; Park, H.; Lee, B. Metamaterials and metasurfaces for sensor applications. Sensors 2017, 17, 1726. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, A.; Ranif, A.; Alam, M.; Massoud, Y. Effect of Dielectric Constant on the Energy Shift in Localized Surface Plasmons Resonance. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Quebec City, QC, Canada, 13–16 May 2018; pp. 1–4. [Google Scholar]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Low Frequency Plasmons in Thin Wire Structures. J. Phys. Condens. Matter 1998, 10, 4785–4809. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.J.; Stewart, W.J.; Youngs, I. Extremely Low Frequency Plasmons in Metallic Mesostructures. Phys. Rev. Lett. 1996, 76, 4773–4776. [Google Scholar] [CrossRef] [PubMed]
- Smith, K.L.; Adams, R.S. Spherical Spiral Metamaterial Unit Cell for Negative Permeability and Negative Permittivity. IEEE Trans. Antennas Propag. 2018, 66, 6425–6428. [Google Scholar] [CrossRef]
- Avitzour, Y.; Urzhumov, Y.A.; Shvets, G. Wide-angle Infrared Absorber Based on a Negative-Index Plasmonic Metamaterial. Phys. Rev. B 2009, 79, 045131. [Google Scholar] [CrossRef]
- Henzie, J.; Lee, M.H.; Odom, T.W. Multiscale Patterning of Plasmonic Metamaterials. Nat. Nanotechnol. 2007, 2, 549. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, J.; Li, L. A dual-band tunable metamaterial near-unity absorber composed of periodic cross and disk graphene arrays. IEEE Photonics J. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental Verification of a Negative Index of Refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef] [PubMed]
- Schurig, D.; Mock, J.J.; Smith, D.R. Electric-Field-Coupled Resonators for Negative Permittivity Metamaterials. Appl. Phys. Lett. 2006, 88, 041109. [Google Scholar] [CrossRef]
- Cai, W.; Chettiar, U.K.; Kildishev, A.V.; Shalaev, V.M. Optical cloaking with metamaterials. Nat. Photonics 2007, 1, 224. [Google Scholar] [CrossRef]
- Pollard, R.J.; Murphy, A.; Hendren, W.R.; Evans, P.R.; Atkinson, R.; Wurtz, G.A.; Zayats, A.V.; Podolskiy, V.A. Optical nonlocalities and additional waves in epsilon-near-zero metamaterials. Phys. Rev. Lett. 2009, 102, 127405. [Google Scholar] [CrossRef] [PubMed]
- Liberal, I.; Engheta, N. Near-zero refractive index photonics. Nat. Photonics 2017, 11, 149. [Google Scholar] [CrossRef]
- Engheta, N.; Salandrino, A.; Alù, A. Circuit elements at optical frequencies: Nanoinductors, nanocapacitors, and nanoresistors. Phys. Rev. Lett. 2005, 95, 095504. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, A.; Alam, M.; Massoud, Y. A Dynamic Approach to the Lumped Impedance Representation of a Nanoparticle. IEEE Photonics J. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Hulst, H.C.; van de Hulst, H.C. Light Scattering by Small Particles; Courier Corporation: North Chelmsford, MA, USA, 1981. [Google Scholar]
- Alam, M.; Eleftheriades, G.V. Multimode Impedance Representation of Scattering, Absorption and Extinction Cross-Sectional Areas for Plasmonic Nanoparticle. J. Lightwave Technol. 2011, 29, 2512–2526. [Google Scholar] [CrossRef]
- Alam, M.; Massoud, Y.; Eleftheriades, G.V. A Time-Varying Approach to Circuit Modeling of Plasmonic Nanospheres Using Radial Vector Wave Functions. IEEE Trans. Microw. Theory Tech. 2011, 59, 2595–2611. [Google Scholar] [CrossRef]
- Gang, Q.; Jia-Fu, W.; Ming-Bao, Y.; Wei, C.; Hong-Ya, C.; Yong-Feng, L. Lowering Plasma Frequency by Enhancing the Effective mass of Electrons: A route to deep Sub-wavelength Metamaterials. Chin. Phys. B 2013, 22, 087302. [Google Scholar]
- Alam, M.; Massoud, Y. A Closed-Form Analytical Model for Single Nanoshells. IEEE Trans. Nanotechnol. 2006, 5, 265–272. [Google Scholar] [CrossRef]
- Alam, M.; Hosseini, A.; Massoud, Y. Impedance formulation of single oscillating nanospheres at optical frequencies. In Proceedings of the IEEE 50th Midwest Symposium on Circuits and Systems, Montreal, QC, Canada, 5–8 August 2007; pp. 1249–1252. [Google Scholar]
- Alam, M.; Massoud, Y. An accurate closed-form analytical model of single nanoshells for cancer treatment. In Proceedings of the IEEE 48th Midwest Symposium on Circuits and Systems, Covington, KY, USA, 7–10 August 2005; pp. 1928–1931. [Google Scholar]
- Mie, G. Beitrage zur optik truber medien speziell kolloidaler metallosungen. Ann. Phys. 1908, 25, 377–445. [Google Scholar] [CrossRef]
- Balanis, C. Advance Engineering Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Harrington, R.F. Time-Harmonic Electromagnetic Fields; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Etchegoin, P.G.; Le Ru, E.C.; Meyer, M. An analytic model for the optical properties of gold. J. Chem. Phys. 2006, 125, 164705. [Google Scholar] [CrossRef] [PubMed]
- RoyChoudhury, S.; Rawat, V.; Jalal, A.H.; Kale, S.N.; Bhansali, S. Recent advances in metamaterial split-ring-resonator circuits as biosensors and therapeutic agents. Biosens. Bioelectron. 2016, 86, 595. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Differential sensors using microstrip lines loaded with two split-ring resonators. IEEE Sens. J. 2018, 18, 5786. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, M.; Mahmood, A.; Azam, S.; Butt, M.S.; Haq, A.U.; Massoud, Y. Impedance Model of Cylindrical Nanowires for Metamaterial Applications. Nanomaterials 2019, 9, 1104. https://doi.org/10.3390/nano9081104
Alam M, Mahmood A, Azam S, Butt MS, Haq AU, Massoud Y. Impedance Model of Cylindrical Nanowires for Metamaterial Applications. Nanomaterials. 2019; 9(8):1104. https://doi.org/10.3390/nano9081104
Chicago/Turabian StyleAlam, Mehboob, Ali Mahmood, Shahida Azam, Madiha Saher Butt, Anwar Ul Haq, and Yehia Massoud. 2019. "Impedance Model of Cylindrical Nanowires for Metamaterial Applications" Nanomaterials 9, no. 8: 1104. https://doi.org/10.3390/nano9081104
APA StyleAlam, M., Mahmood, A., Azam, S., Butt, M. S., Haq, A. U., & Massoud, Y. (2019). Impedance Model of Cylindrical Nanowires for Metamaterial Applications. Nanomaterials, 9(8), 1104. https://doi.org/10.3390/nano9081104




