A New Model to Predict Optimum Conditions for Growth of 2D Materials on a Substrate
Abstract
1. Introduction
2. Theoretical Method
3. Demonstrations of the Model
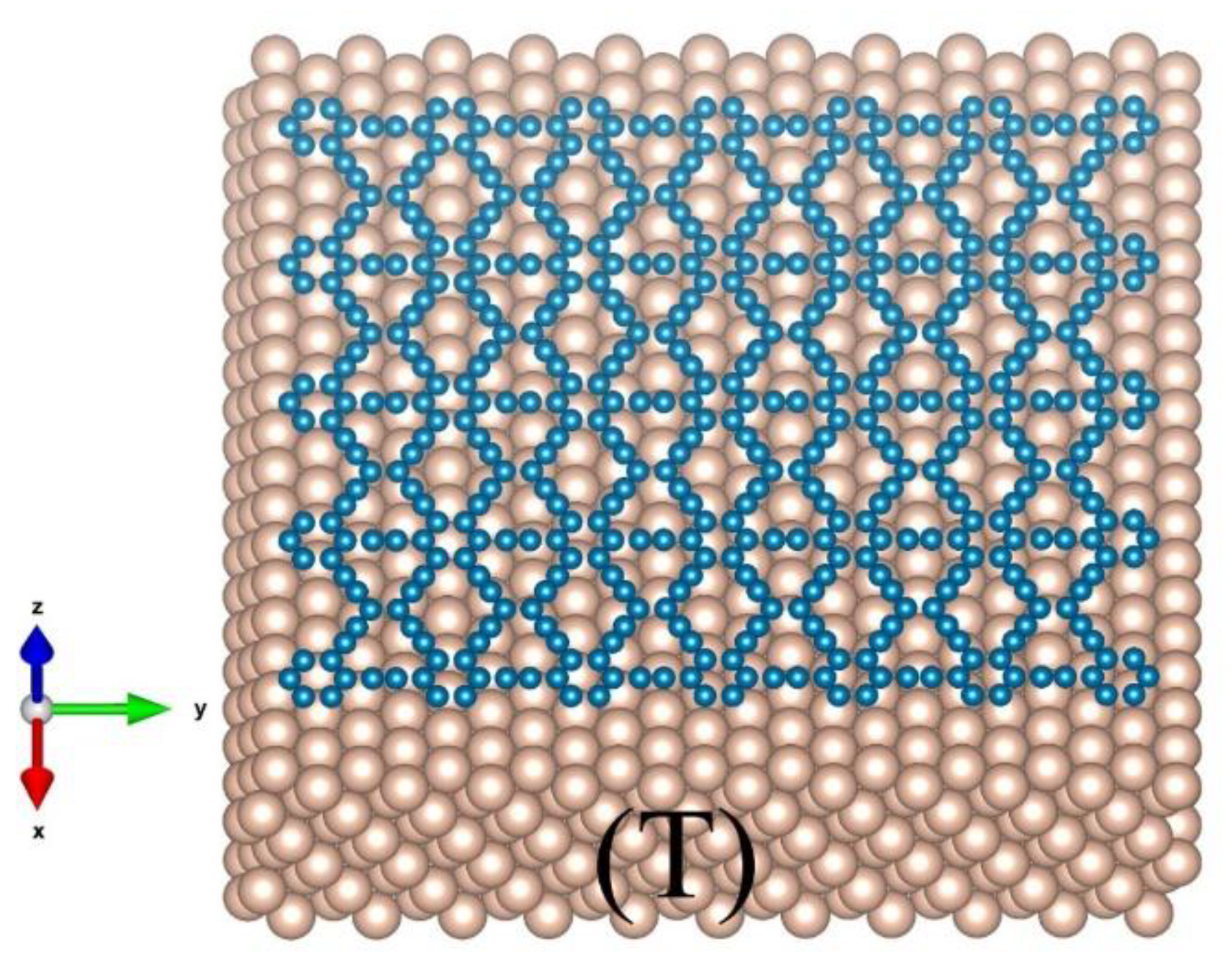
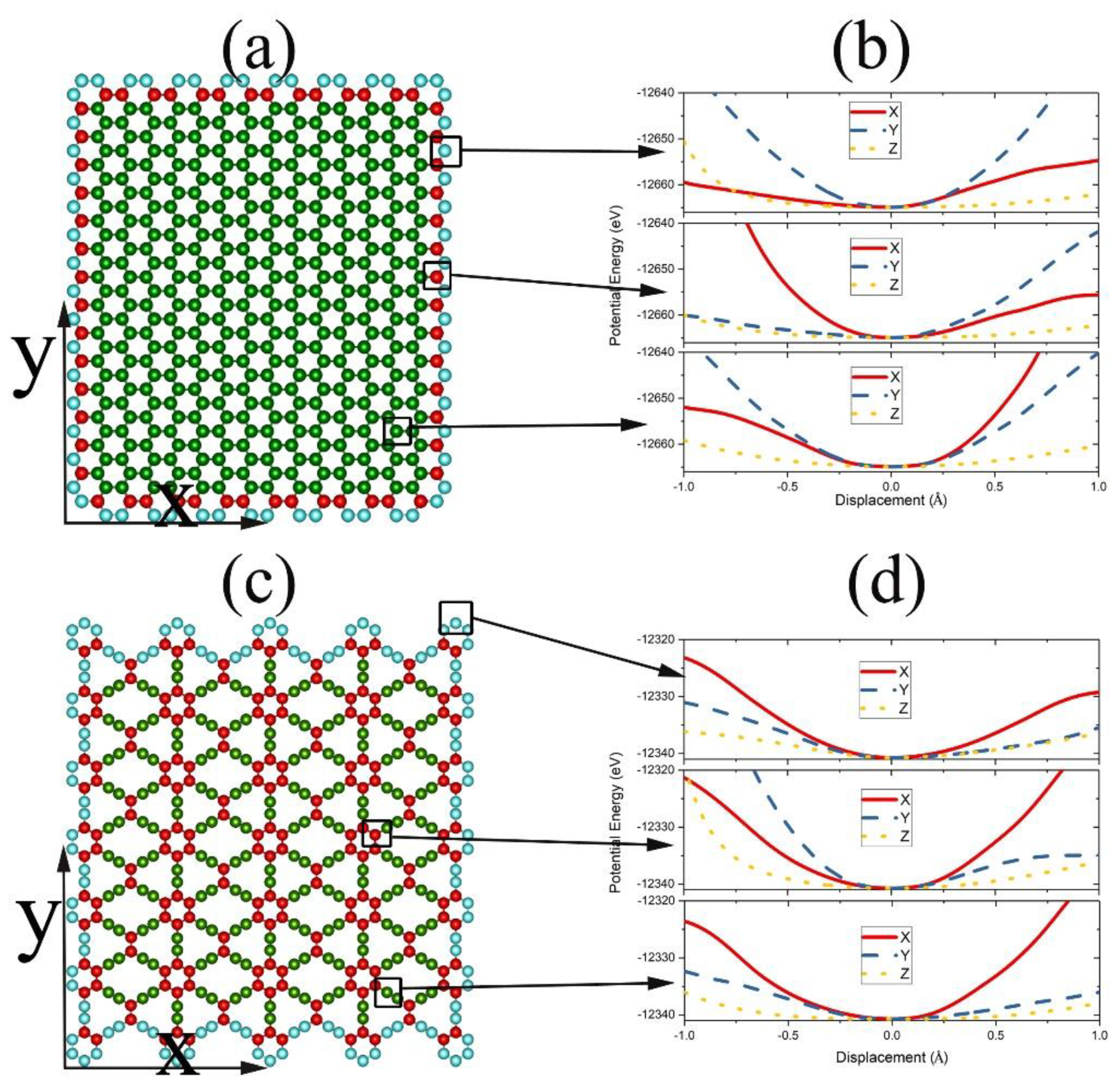
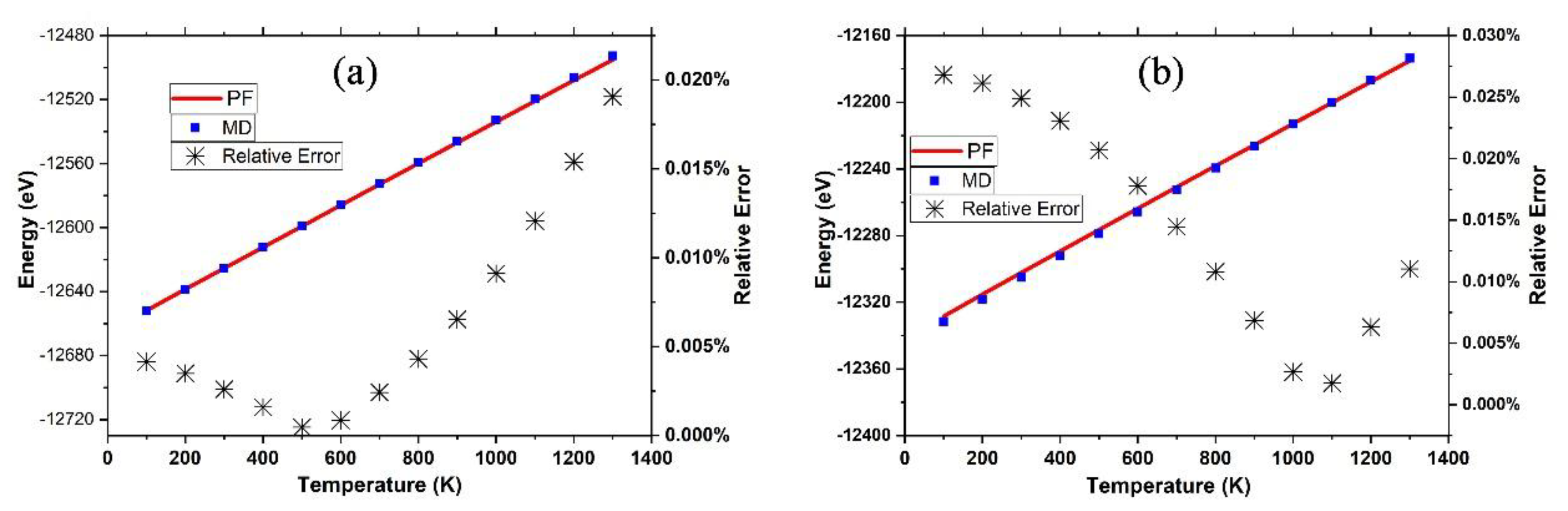
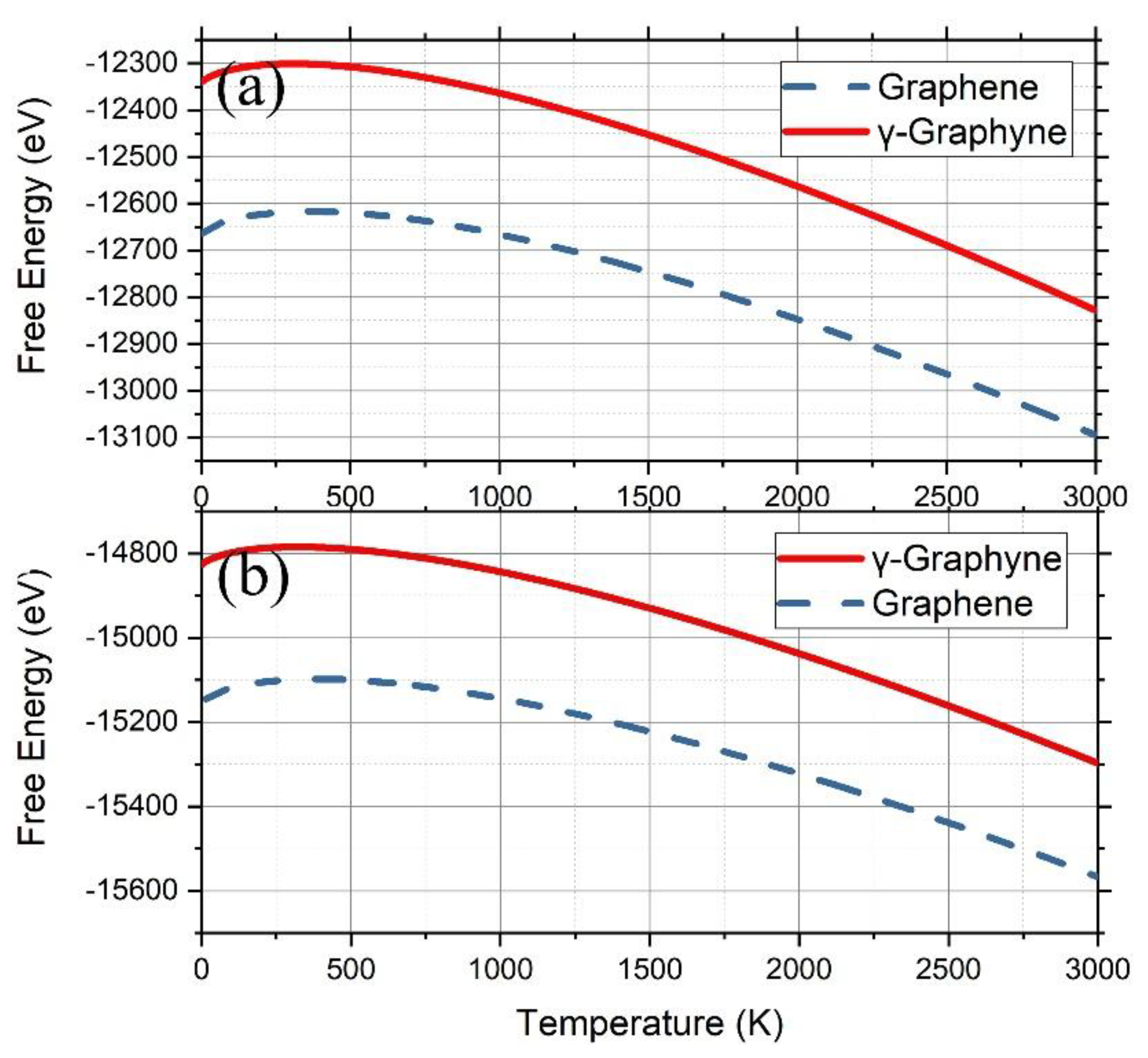
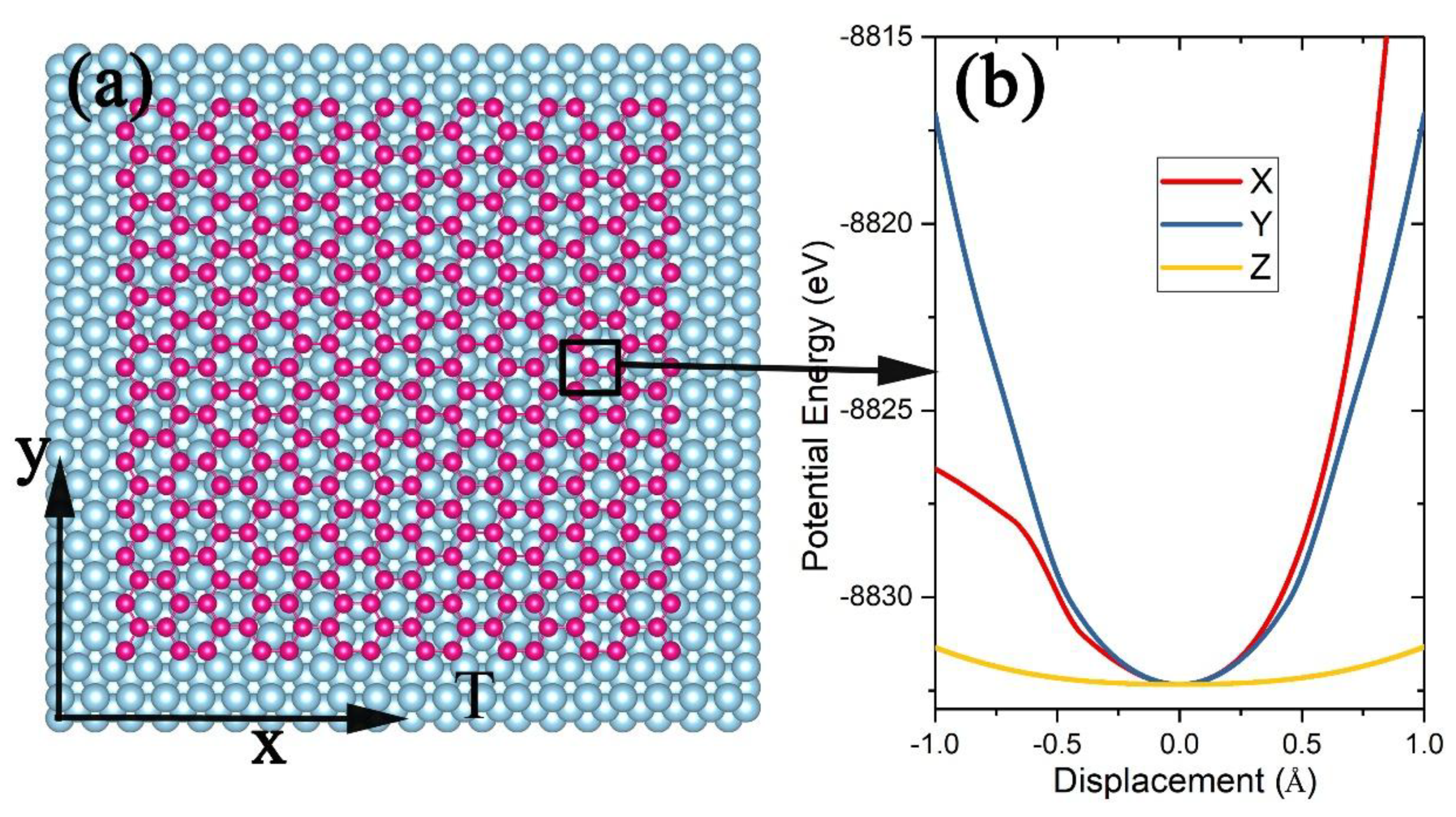
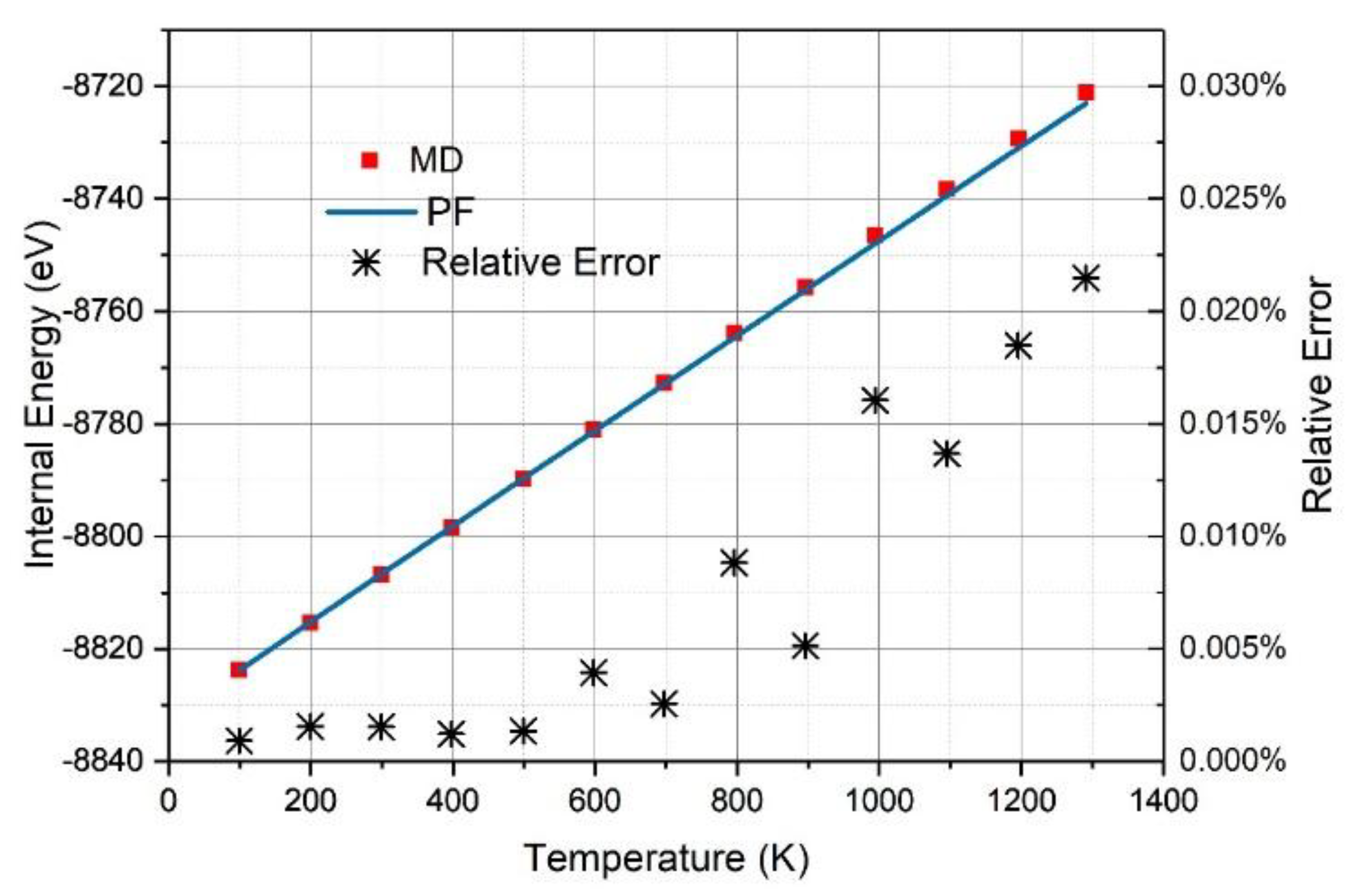
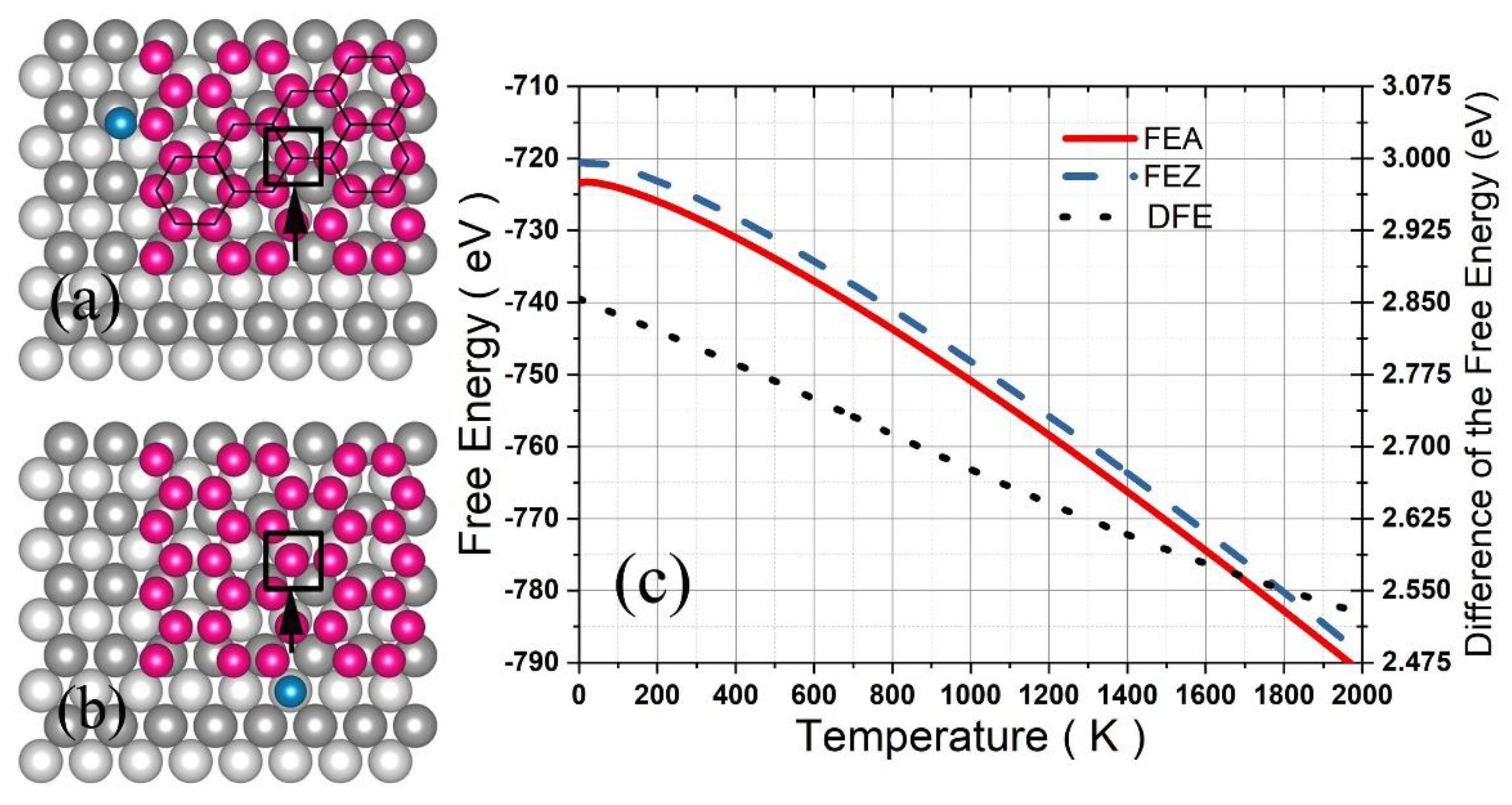
3.1. Graphene and γ-Graphyne on a Cu Substrate
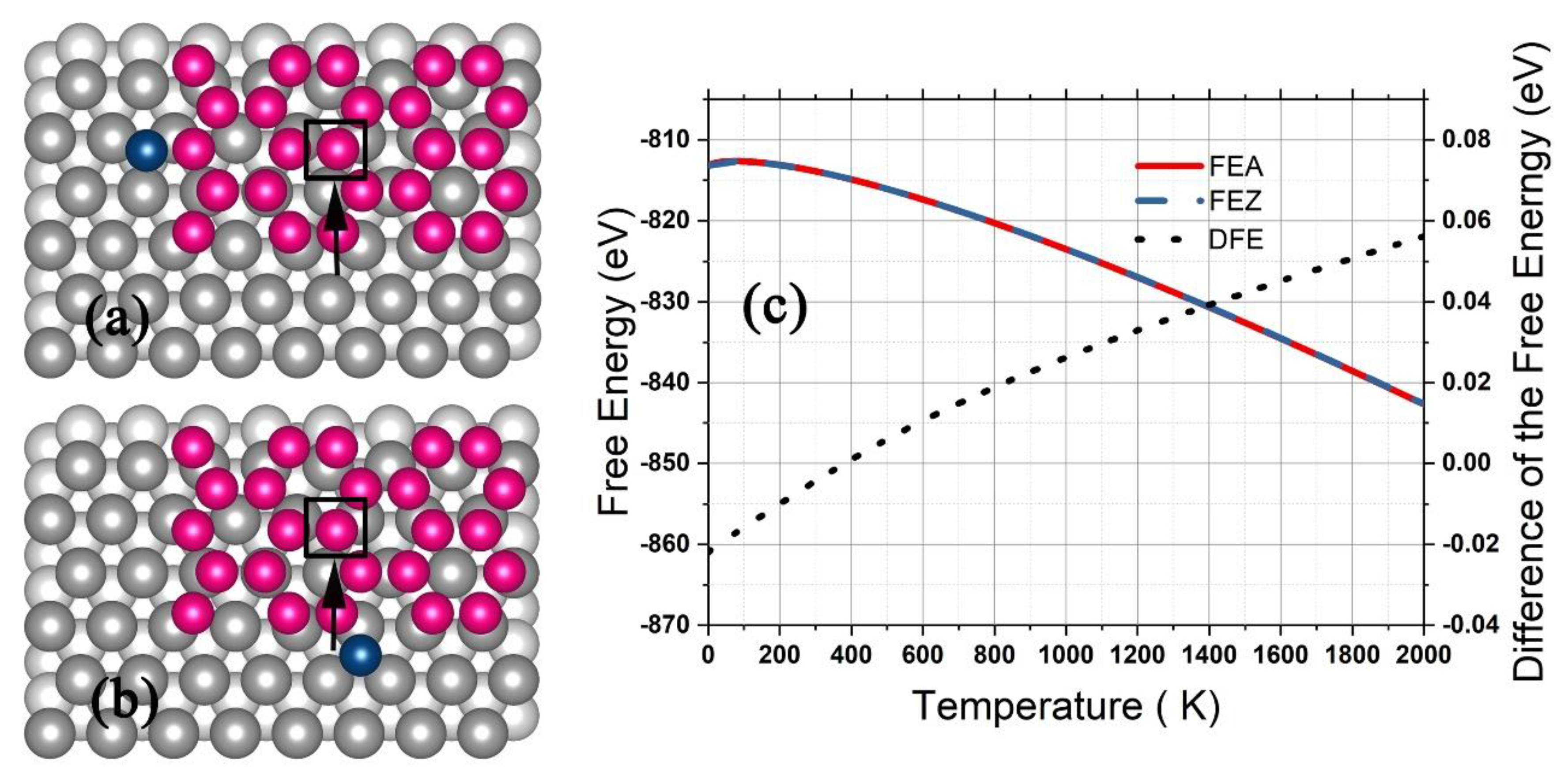
3.2. Silicene on Silver Substrate
4. Conditions for Silicene Growth on a Ag Substrate
5. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666. [Google Scholar] [CrossRef] [PubMed]
- Li, G.X.; Li, Y.L.; Liu, H.B.; Guo, Y.B.; Li, Y.J.; Zhu, D.B. Architecture of graphdiyne nanoscale films. Chem. Commun. 2010, 46, 3256. [Google Scholar] [CrossRef] [PubMed]
- Vogt, P.; De Padova, P.; Quaresima, C.; Avila, J.; Frantzeskakis, E.; Asensio, M.C.; Resta, A.; Ealet, B.; Le Lay, G. Silicene: Compelling experimental evidence for graphenelike two-dimensional silicon. Phys. Rev. Lett. 2012, 108, 155501. [Google Scholar] [CrossRef] [PubMed]
- Yuhara, J.; Shimazu, H.; Ito, K.; Ohta, A.; Araidai, M.; Kurosawa, M.; Nakatake, M.; Le Lay, G. Germanene epitaxial growth by segregation through Ag (111) thin films on Ge (111). ACS Nano 2018, 12, 11632. [Google Scholar] [CrossRef] [PubMed]
- Pakdel, A.; Zhi, C.; Bando, Y.; Golberg, D. Low-dimensional boron nitride nanomaterials. Mater. Today. 2012, 15, 256. [Google Scholar] [CrossRef]
- Kaur, H.; Yadav, S.; Srivastava, A.K.; Singh, N.; Schneider, J.J.; Sinha, O.P.; Agrawal, V.V.; Srivastava, R. Large area fabrication of semiconducting phosphorene by langmuir-blodgett assembly. Sci. Rep. 2016, 6, 34095. [Google Scholar] [CrossRef] [PubMed]
- Reis, F.; Li, G.; Dudy, L.; Bauernfeind, M.; Glass, S.; Hanke, W.; Thomale, R.; Schäfer, J.; Claessen, R. Bismuthene on a SiC substrate: A candidate for a high-temperature quantum spin Hall material. Science 2017, 357, 287. [Google Scholar] [CrossRef]
- Liu, Z.; Song, L.; Zhao, S.; Huang, J.; Ma, L.; Zhang, J.; Lou, J.; Ajayan, P.M. Direct growth of graphene/hexagonal boron nitride stacked layers. Nano Lett. 2011, 11, 2032. [Google Scholar] [CrossRef]
- Dos Santos, R.B.; de Brito Mota, F.; Rivelino, R.; Kakanakova-Georgieva, A.; Gueorguiev, G.K. Van der Waals stacks of few-layer h-AlN with graphene: An ab initio study of structural, interaction and electronic properties. Nanotechnology 2016, 27, 145601. [Google Scholar] [CrossRef]
- Freitas, R.R.; Rivelino, R.; de Brito Mota, F.; de Castilho CM, C.; Kakanakova-Georgieva, A.; Gueorguiev, G.K. Topological insulating phases in two-dimensional bismuth-containing single layers preserved by hydrogenation. J. Phys. Chem. C 2015, 119, 23599–23606. [Google Scholar] [CrossRef]
- Bosi, M. Growth and synthesis of mono and few-layers transition metal dichalcogenides by vapour techniques: A review. RSC Adv. 2015, 5, 75500. [Google Scholar] [CrossRef]
- Ghidiu, M.; Lukatskaya, M.R.; Zhao, M.-Q.; Gogotsi, Y.; Barsoum, M.W. Conductive two-dimensional titanium carbide ‘clay’ with high volumetric capacitance. Nature 2014, 516, 78. [Google Scholar] [CrossRef] [PubMed]
- Benameur, M.M.; Radisavljevic, B.; Héron, J.S.; Sahoo, S.; Berger, H.; Kis, A. Visibility of dichalcogenide nanolayers. Nanotechnology 2011, 22, 125706. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Liu, C.-C.; Feng, B.; He, X.; Cheng, P.; Ding, Z.; Meng, S.; Yao, Y.; Wu, K. Evidence for dirac fermions in a honeycomb lattice based on silicon. Phys. Rev. Lett. 2012, 109, 056804. [Google Scholar] [CrossRef] [PubMed]
- Sheng, S.; Wu, J.-B.; Cong, X.; Li, W.; Gou, J.; Zhong, Q.; Cheng, P.; Tan, P.-H.; Chen, L.; Wu, K. Vibrational properties of a monolayer silicene sheet studied by tip-enhanced raman spectroscopy. Phys. Rev. Lett. 2017, 119, 196803. [Google Scholar] [CrossRef] [PubMed]
- Fleurence, A.; Friedlein, R.; Ozaki, T.; Kawai, H.; Wang, Y.; Yamada-Takamura, Y. Experimental evidence for epitaxial silicene on diboride thin films. Phys. Rev. Lett. 2012, 108, 245501. [Google Scholar] [CrossRef]
- Ni, Z.; Liu, Q.; Tang, K.; Zheng, J.; Zhou, J.; Qin, R.; Gao, Z.; Yu, D.; Lu, J. Tunable bandgap in silicene and germanene. Nano Lett. 2012, 12, 113. [Google Scholar] [CrossRef]
- Drummond, N.D.; Zólyomi, V.; Fal’ko, V.I. Electrically tunable band gap in silicene. Phys. Rev. B 2012, 85, 075423. [Google Scholar] [CrossRef]
- Quhe, R.; Fei, R.; Liu, Q.; Zheng, J.; Li, H.; Xu, C.; Ni, Z.; Wang, Y.; Yu, D.; Gao, Z.; et al. Tunable and sizable band gap in silicene by surface adsorption. Sci. Rep. 2012, 2, 853. [Google Scholar] [CrossRef]
- Liu, C.-C.; Feng, W.; Yao, Y. Quantum spin hall effect in silicene and two-dimensional germanium. Phys. Rev. Lett. 2011, 107, 076802. [Google Scholar] [CrossRef]
- Ezawa, M. Valley-polarized metals and quantum anomalous hall effect in silicene. Phys. Rev. Lett. 2012, 109, 055502. [Google Scholar] [CrossRef] [PubMed]
- Molle, A.; Grazianetti, C.; Tao, L.; Taneja, D.; Alam, M.H.; Akinwande, D. Silicene, silicene derivatives, and their device applications. Chem. Soc. Rev. 2018, 47, 6370. [Google Scholar] [CrossRef] [PubMed]
- Bointon, T.; Barnes, M.; Russo, S.; Craciun, M. High quality monolayer graphene synthesized by resistive heating cold wall chemical vapor deposition. Adv. Mater. 2015, 27, 4200. [Google Scholar] [CrossRef] [PubMed]
- Leandri, C.; Oughaddou, H.; Aufray, B.; Gay, J.M.; Le Lay, G.; Ranguis, A.; Garreau, Y. Growth of Si nanostructures on Ag (001). Surf. Sci. 2007, 601, 262. [Google Scholar] [CrossRef]
- Leandri, C.; Lay, G.L.; Aufray, B.; Girardeaux, C.; Avila, J.; Dávila, M.E.; Asensio, M.C.; Ottaviani, C.; Cricenti, A. Self-aligned silicon quantum wires on Ag (110). Surf. Sci. 2005, 574, L9. [Google Scholar] [CrossRef]
- Aufray, B.; Kara, A.; Vizzini, S.; Oughaddou, H.; Leandri, C.; Ealet, B.; Le Lay, G. Graphene-like silicon nanoribbons on Ag (110): A possible formation of silicene. Appl. Phys. Lett. 2010, 96, 3. [Google Scholar] [CrossRef]
- Lalmi, B.; Oughaddou, H.; Enriquez, H.; Kara, A.; Vizzini, S.; Ealet, B.; Aufray, B. Epitaxial growth of a silicene sheet. Appl. Phys. Lett. 2010, 97, 2. [Google Scholar] [CrossRef]
- Swendsen, R.H.; Wang, J.-S. Replica Monte Carlo simulation of spin-glasses. Phys. Rev. Lett. 1986, 57, 2607. [Google Scholar] [CrossRef]
- Bartels, C. Analyzing biased Monte Carlo and molecular dynamics simulations. Chem. Phys. Lett. 2000, 331, 446. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping free-energy minima. PNAS 2002, 99, 12562. [Google Scholar] [CrossRef]
- Wang, F.; Landau, D.P. Efficient, multiple-range random walk algorithm to calculate the density of states. Phys. Rev. Lett. 2001, 86, 2050. [Google Scholar] [CrossRef] [PubMed]
- Pártay, L.B.; Bartók, A.P.; Csányi, G. Efficient sampling of atomic configurational spaces. J. Phys. Chem. B 2010, 114, 10502. [Google Scholar] [CrossRef] [PubMed]
- Do, H.; Wheatley, R.J. Density of states partitioning method for calculating the free energy of solids. J. Chem. Theory Comput. 2013, 9, 165. [Google Scholar] [CrossRef] [PubMed]
- Brenner, D.W. Empirical potential for hydrocarbons for use in simulating the chemical vapor-deposition of diamond films. Phys. Rev. B 1990, 42, 9458. [Google Scholar] [CrossRef] [PubMed]
- Bo-Yuan, N.; Le-Cheng, G.; Tsu-Chien, W.; Xi-Jing, N. Solution of partition function for macroscopic condensed matters-a long standing key problem in statistical physics. arXiv 2019, arXiv:1901.08233. [Google Scholar]
- Tersoff, J. modeling solid-state chemistry—Interatomic potentials for multicomponent systems. Phys. Rev. B 1989, 39, 5566. [Google Scholar] [CrossRef] [PubMed]
- Le-Cheng, G.; Bo-Yuan, N.; Tsu-Chien, W.; Xi-Jing, N. Comparison of two efficient methods for calculating partition functions. arXiv 2019, arXiv:1902.07388. [Google Scholar]
- Frenkel, D.; Smit, B. Chapter 7—Free energy calculations. In Understanding Molecular Simulation, 2nd ed.; Frenkel, D., Smit, B., Eds.; Academic Press: San Diego, CA, USA, 2002; p. 167. [Google Scholar]
- Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef] [PubMed]
- Wales, D.J.; Scheraga, H.A. Global optimization of clusters, crystals, and biomolecules. Science 1999, 285, 1368. [Google Scholar] [CrossRef] [PubMed]
- Deaven, D.M.; Ho, K.M. Molecular geometry optimization with a genetic algorithm. Phys. Rev. Lett. 1995, 75, 288. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Zhang, Q.; Buch, V. Computational study of formation dynamics and structure of amorphous ice condenstates. J. Chem. Phys. 1990, 92, 5004. [Google Scholar] [CrossRef]
- Ye, X.X.; Ming, C.; Hu, Y.C.; Ning, X.J. Evaluating the ability to form single crystal. J. Chem. Phys. 2009, 130, 6. [Google Scholar] [CrossRef] [PubMed]
- Karasiev, V.V.; Dufty, J.W.; Trickey, S.B. Nonempirical semilocal free-energy density functional for matter under extreme conditions. Phys. Rev. Lett. 2018, 120, 076401. [Google Scholar] [CrossRef] [PubMed]
- Constantin, L.A.; Fabiano, E.; Della Sala, F. Nonlocal kinetic energy functional from the jellium-with-gap model: Applications to orbital-free density functional theory. Phys. Rev. B. 2018, 97, 205137. [Google Scholar] [CrossRef]
- Do, H.; Hirst, J.D.; Wheatley, R.J. Calculation of partition functions and free energies of a binary mixture using the energy partitioning method: Application to carbon dioxide and methane. J. Phys. Chem. B 2012, 116, 4535. [Google Scholar] [CrossRef] [PubMed]
- Do, H.; Hirst, J.D.; Wheatley, R.J. Rapid calculation of partition functions and free energies of fluids. J. Chem. Phys. 2011, 135, 174105. [Google Scholar] [CrossRef]
- Shi, X.H.; Yin, Q.F.; Wei, Y.J. A theoretical analysis of the surface dependent binding, peeling and folding of graphene on single crystal copper. Carbon 2012, 50, 3055. [Google Scholar] [CrossRef]
- Yu, Q.K.; Jauregui, L.A.; Wu, W.; Colby, R.; Tian, J.F.; Su, Z.H.; Cao, H.L.; Liu, Z.H.; Pandey, D.; Wei, D.G.; et al. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nat. Mater. 2011, 10, 443. [Google Scholar] [CrossRef]
- Li, X.; Cai, W.; Colombo, L.; Ruoff, R.S. Evolution of graphene growth on Ni and Cu by carbon isotope labeling. Nano Lett. 2009, 9, 4268. [Google Scholar] [CrossRef]
- Galashev, A.Y.; Ivanichkina, K.A. Computer study of atomic mechanisms of intercalation/deintercalation of li ions in a silicene anode on an Ag (111) substrate. J. Electrochem. Soc. 2018, 165, A1788. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 1995, 117, 1. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.-P.; Ning, B.-Y.; Gong, L.-C.; Weng, T.-C.; Ning, X.-J. A New Model to Predict Optimum Conditions for Growth of 2D Materials on a Substrate. Nanomaterials 2019, 9, 978. https://doi.org/10.3390/nano9070978
Liu Y-P, Ning B-Y, Gong L-C, Weng T-C, Ning X-J. A New Model to Predict Optimum Conditions for Growth of 2D Materials on a Substrate. Nanomaterials. 2019; 9(7):978. https://doi.org/10.3390/nano9070978
Chicago/Turabian StyleLiu, Yu-Peng, Bo-Yuan Ning, Le-Cheng Gong, Tsu-Chien Weng, and Xi-Jing Ning. 2019. "A New Model to Predict Optimum Conditions for Growth of 2D Materials on a Substrate" Nanomaterials 9, no. 7: 978. https://doi.org/10.3390/nano9070978
APA StyleLiu, Y.-P., Ning, B.-Y., Gong, L.-C., Weng, T.-C., & Ning, X.-J. (2019). A New Model to Predict Optimum Conditions for Growth of 2D Materials on a Substrate. Nanomaterials, 9(7), 978. https://doi.org/10.3390/nano9070978




