Measurement of Diffusion and Segregation in Semiconductor Quantum Dots and Quantum Wells by Transmission Electron Microscopy: A Guide
Abstract
1. Introduction
2. Transmission Electron Microscopy (TEM)
- (a)
- bright-field (BF) TEM with a small objective aperture,
- (b)
- dark-field TEM with a small objective aperture,
- (c)
- high-resolution TEM (HREM) with a larger objective aperture,
- (d)
- annular dark-field scanning TEM (ADF-STEM) without any objective aperture but with a larger convergence angle of a small probe that is raster scanned over the specimen. The intensity is here registered not with a two-dimensional image detector but a ring-shaped sensitive charge integration device that produces a map of the intensity at every point. This technique necessities a scan unit but has been widely applied in the last decade because many other signals (bright-field signal, electron energy loss, characteristic X-rays produced, light emitted) can be read out simultaneously.
- (e)
- energy-dispersive X-ray spectroscopy (EDXS) and related X-ray mapping,
- (f)
- electron energy-loss spectroscopy (EELS) of ionisation core losses and their mapping in energy-filtered TEM (EFTEM),
- (g)
- plasmon spectroscopy and mapping thereof.
- Figures 2 and 9 in a JEOL Z3100 R005 cold field emission gun (cFEG)-STEM operated at 300 kV (beam convergence: 28 mrad; ADF inner collection angle: 62 mrad), equipped with a JED 2300 Si:Li X-ray detector with ultrathin polymer window (X-ray collection solid angle: 0.17srad);
- Figure 3 in a JEOL 2010F FEG-TEM operated at 197 kV and equipped with a Gatan Imaging Filter 2000 (beam convergence: 5 mrad; EFTEM collection angle: 37 mrad);
- Figure 5 in a JEOL 4000EX operated at 400 kV (beam convergence: ~1 mrad; BF collection angle: ~3 mrad);
- Figure 7 in a VG HB 501 cFEG-STEM at 100 kV (beam convergence: 7.6 mrad; high angle ADF inner collection angle: ~200 mrad).
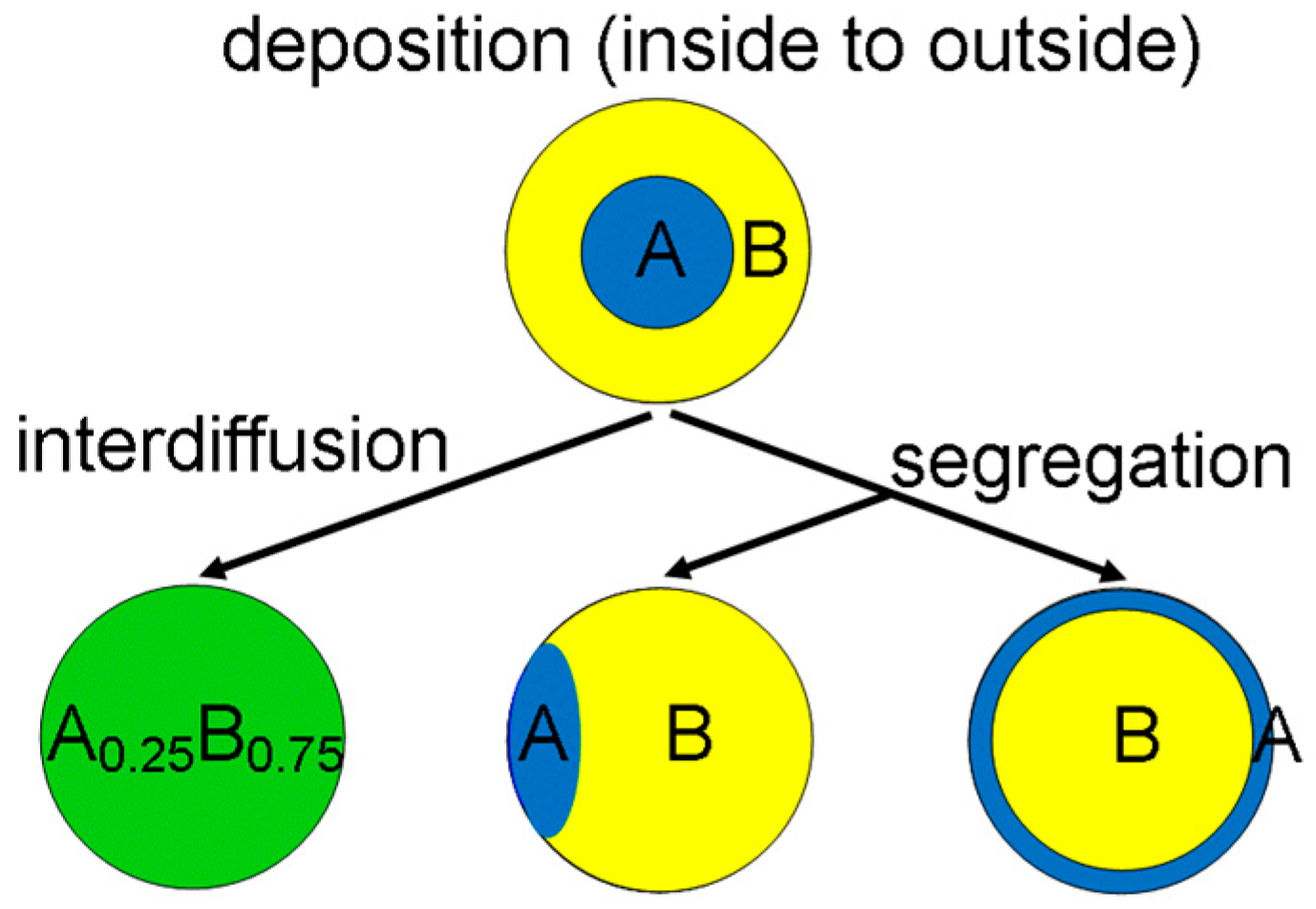
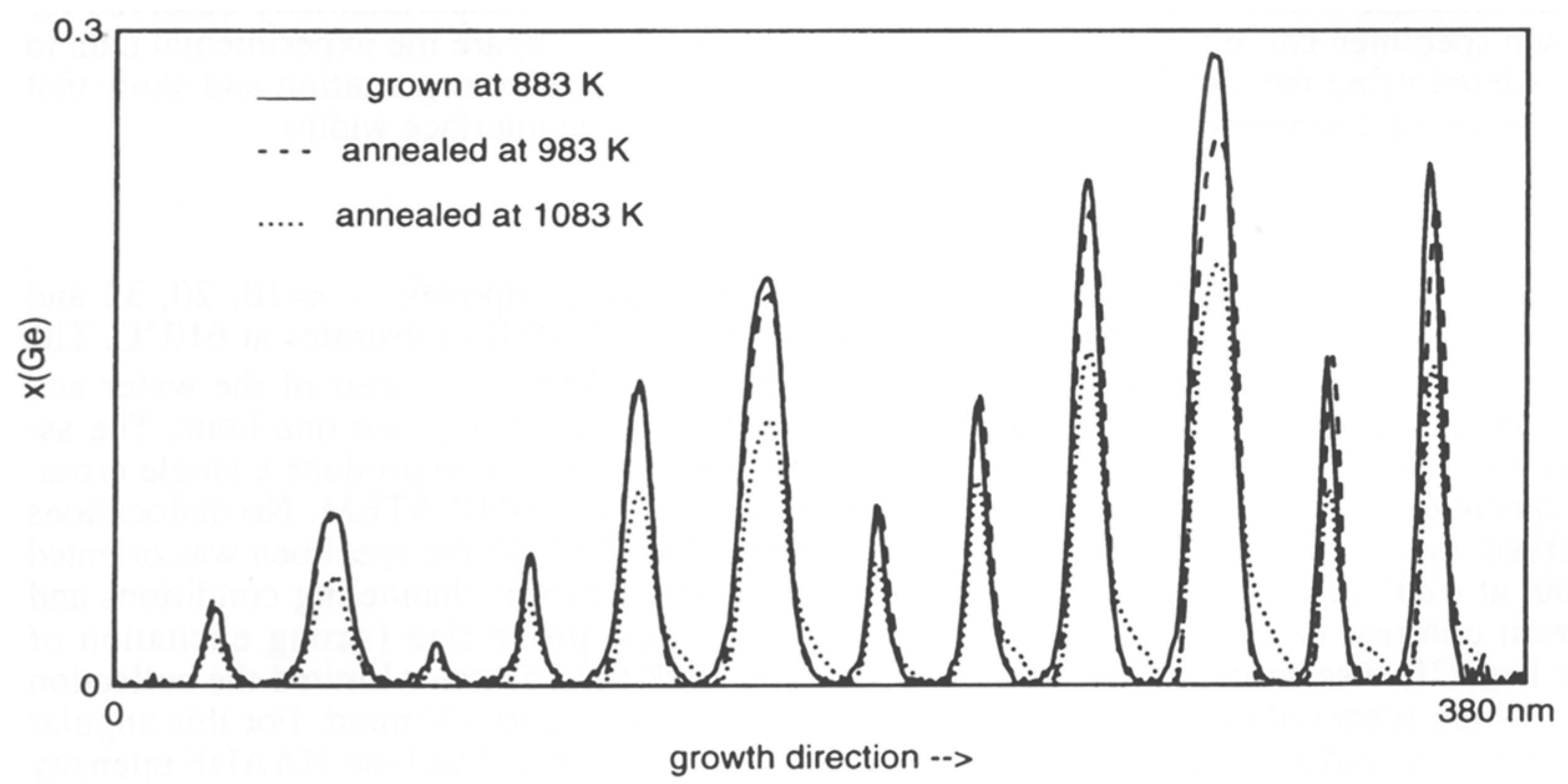
3. Quantum Dots
4. Quantum Nanowires
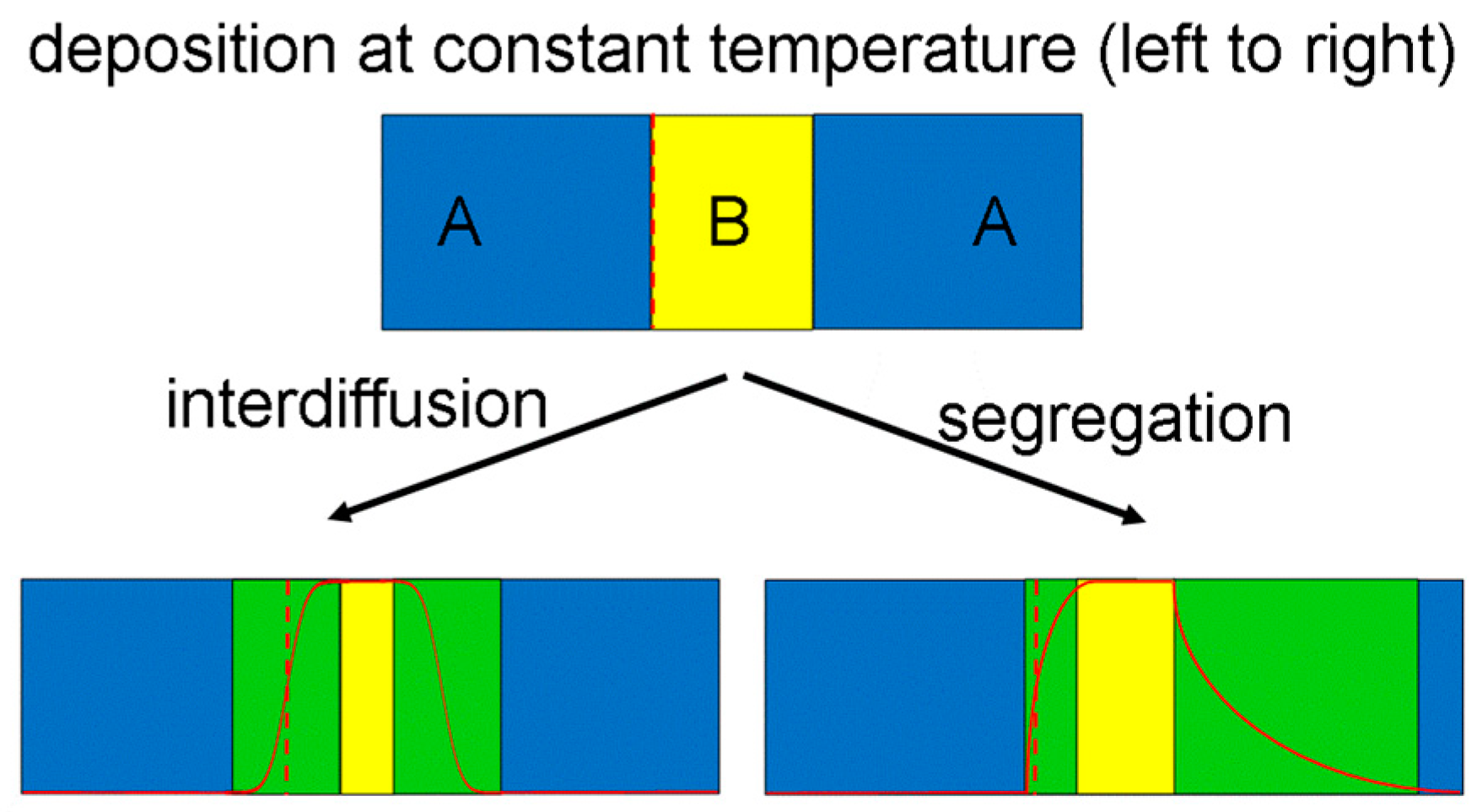
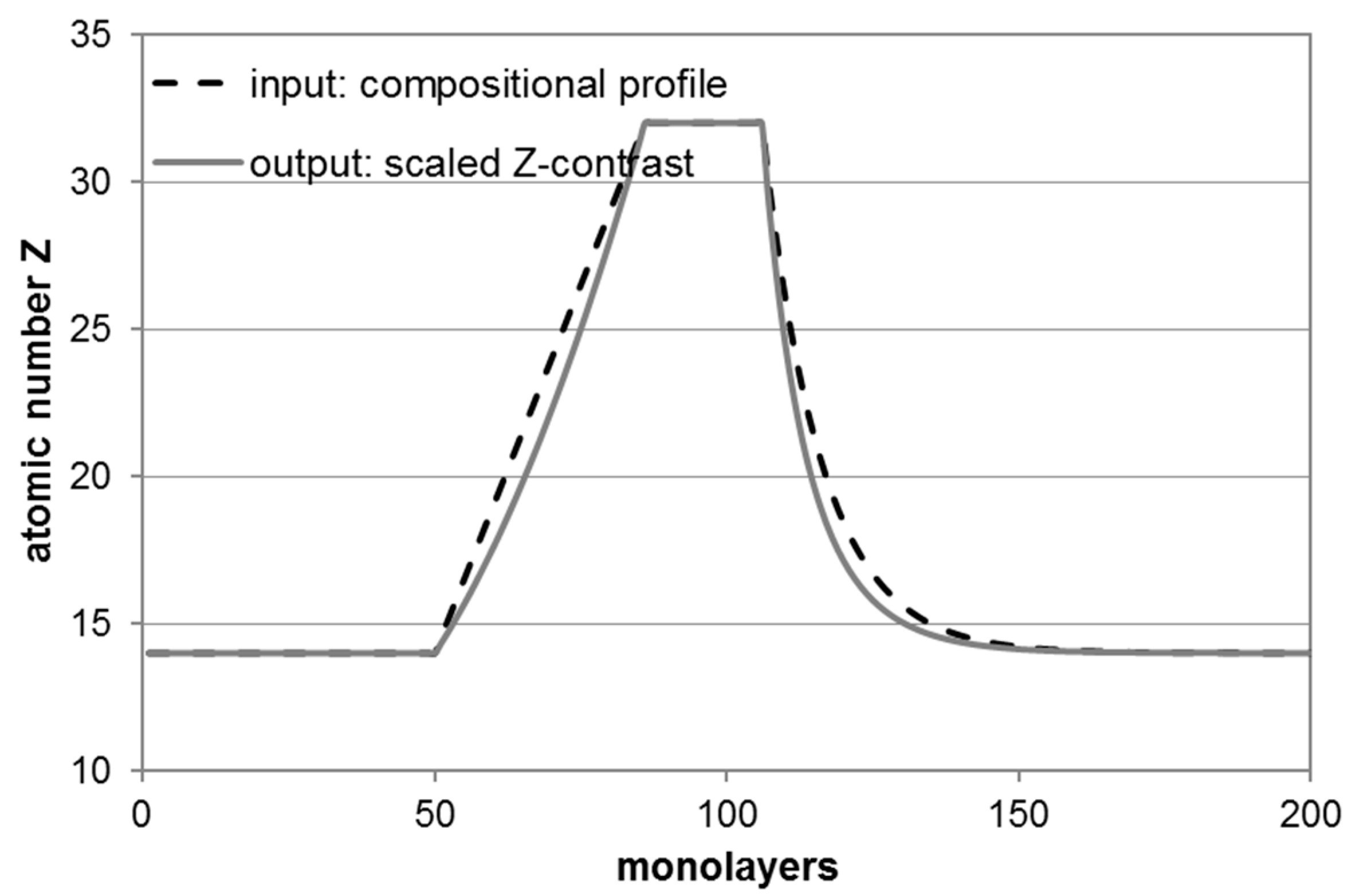
5. Quantum Wells
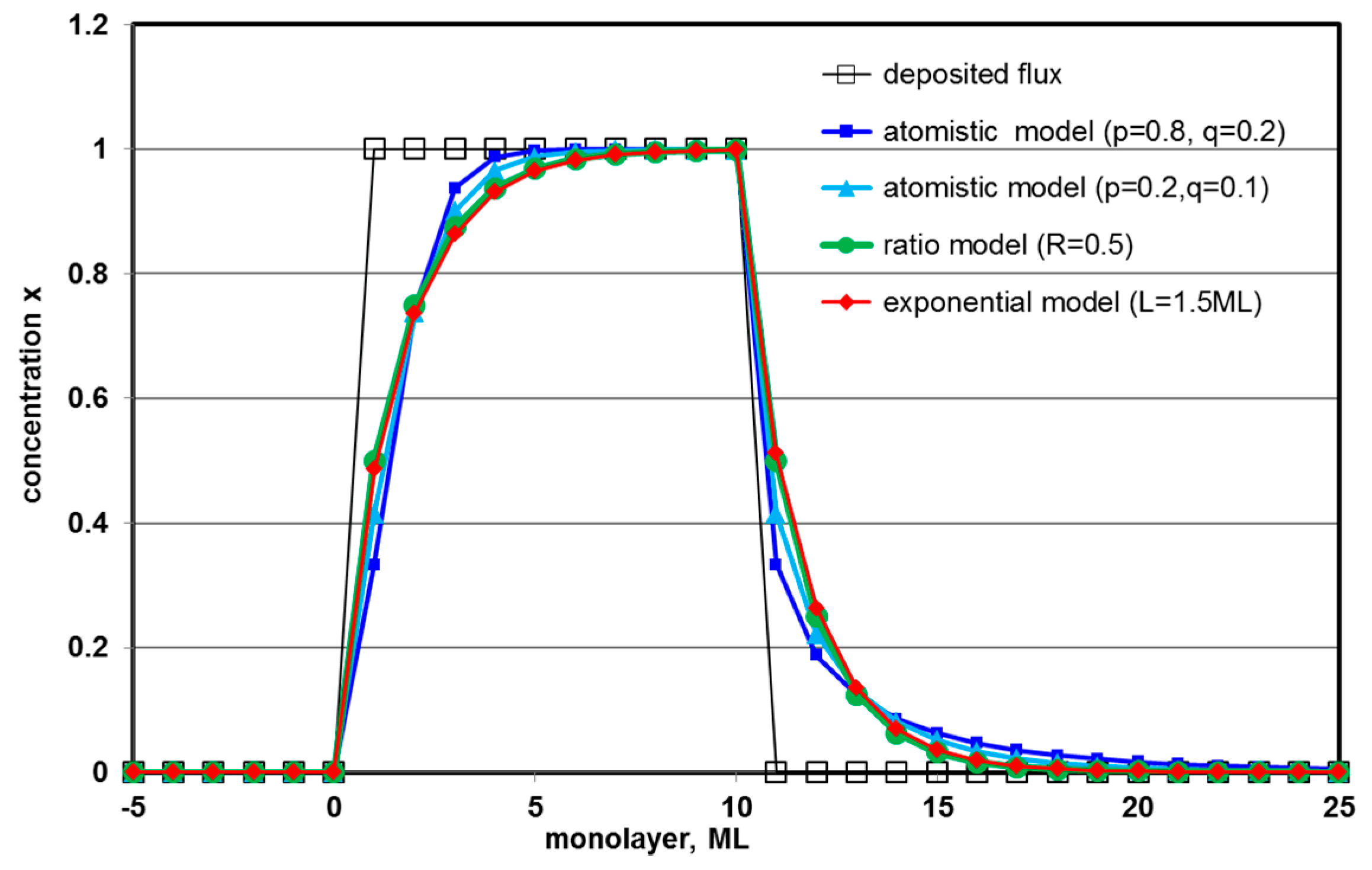
6. Segregation at Grain Boundaries, Interfaces, Defects and Surfaces
- (a)
- Grain boundary segregation can unintentionally and directly lead to the formation of extremely thin quantum wells, down to fractions of monolayers, where imaging approaches can fail even with the best electron microscopes as it is chemical sensitivity and accuracy in measuring chemical profiles that count rather than spatial resolution. Interfaces that appear atomically smooth in lattice images may in fact be chemically graded if the interference pattern is not sufficiently sensitive to those gradients, cf. the case of Ca segregation [49] vs. Ba segregation [50] at SrTiO3 on (La,Ca)MnO3 interfaces. Conversely, strained interfaces can also appear diffuse in imaging when they are actually abrupt, due to long range strain components interfering with the contrast in bright field [51,52] as well as medium-angle dark field [12].
- (b)
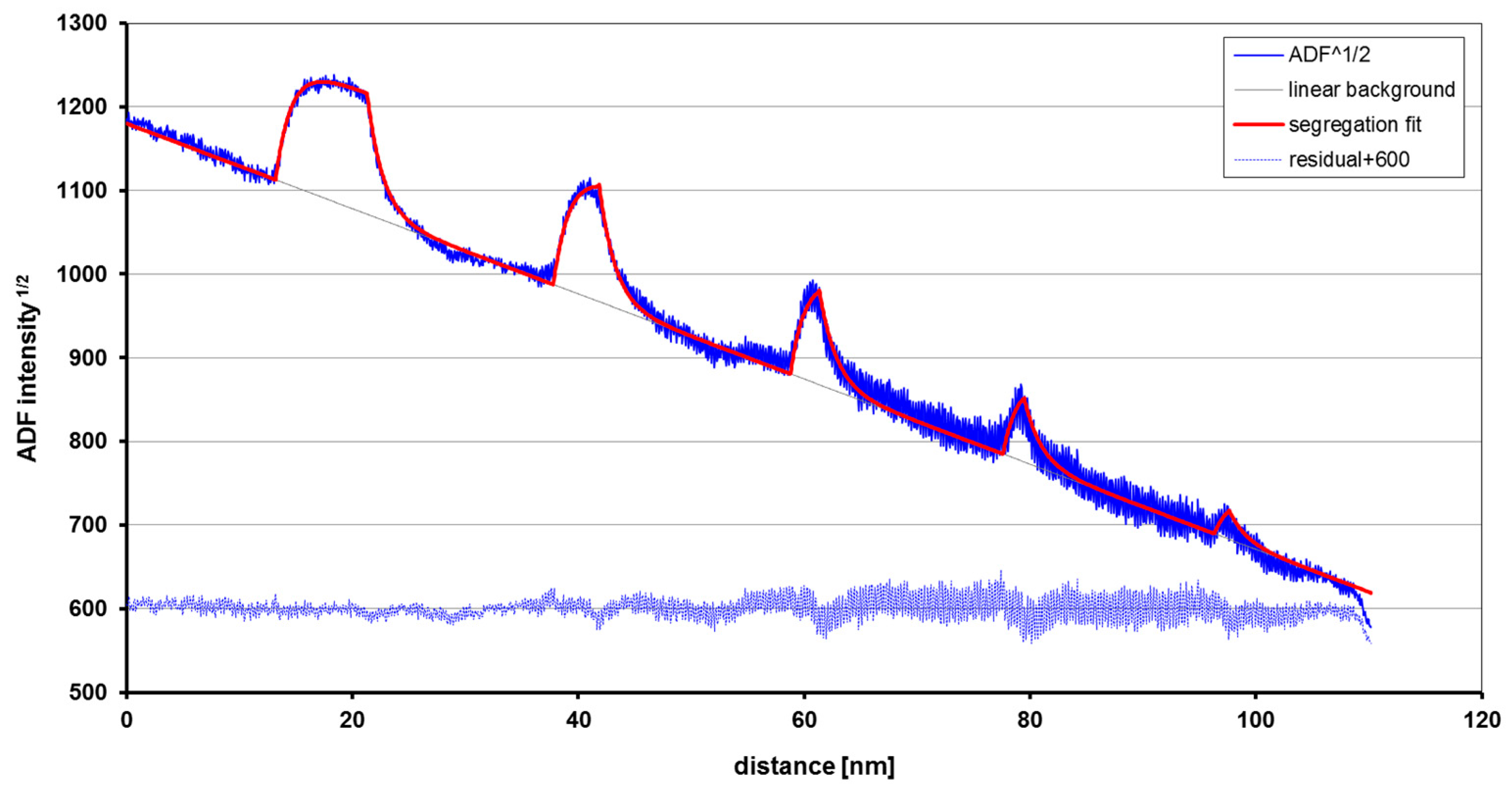
- For interfaces and grain boundaries thinner than a unit cell or a fraction of a monolayer, a method originally implemented in TEM [53] and later also STEM [54] has been successful in measuring highly accurately the effective chemical width of fractions of monolayers in many material systems, most recently for Ge/Si [28] and InAs/GaAs [55,56]. This approach uses a plot of atomic ratio measured as a function of scan window size perpendicular to the interface or defect in question. If the spatial resolution is sufficient and the sample does not damage at high electron dose, then atomic resolution images of grain boundaries, ideally correlated with simultaneously acquired EELS, can sometimes directly reveal the positions to which atoms segregate, e.g., heavy metal dopants at interfaces in polycrystalline Si3N4 [57].
- (c)
- Atomic segregation to lattice defects or surfaces can directly form quantum nanowires or quantum dots, depending on the extension of the defects structure, and both surface segregation and interdiffusion can modify the chemistry of such quantum domain structures further. While many spectroscopic methods in (S)TEM reach only nm-scale rather than lattice resolution, this is often sufficient to detect such surface layers, e.g., thin surface layers of phosphides used for passivation of the sidewalls in GaAs-based quantum nanowires (as in the supporting information to [58]). EDXS point analysis proved Al segregation to dislocation cores in AlGaN [59]. Both ADF imaging and X-ray line scans have been combined in [60] to detect indium segregation to the sidewalls of V-shaped pyramidal surface defects in (In)AlN. ADF and EELS were used to detect oxygen segregation to screw dislocations in GaN [61].
7. Conclusions
Funding
Conflicts of Interest
References
- Christen, J. Characterization of semiconductor interfaces with atomic scale resolution by luminescence. In Festkörperprobleme: Advances in Solid State Physics; Rössler, U., Ed.; Springer: Berlin/Heidelberg, Germany, 1990; Volume 30, pp. 239–265. [Google Scholar]
- Treacy, M.M.J.; Howie, A.; Wilson, C.J. Z-contrast of platinum and palladium catalysts. Philos. Mag. A 1978, 38, 569–585. [Google Scholar] [CrossRef]
- Pennycook, S.J.; Jesson, D.E. High-resolution Z-contrast imaging of crystals. Ultramicroscopy 1991, 37, 14–38. [Google Scholar] [CrossRef]
- Ashuach, Y.; Lakin, E.; Saguy, C.; Kaufmann, Y.; Zolotoyabko, E. Atomic intermixing and interface roughness in short-period InAs/GaSb superlattices for infrared photodetectors. J. Appl. Phys. 2014, 116, 124315. [Google Scholar] [CrossRef]
- Angadi, V.C.; Benz, F.; Tischer, I.; Thonke, K.; Aoki, T.; Walther, T. Evidence of terbium and oxygen co-segregation in annealed AlN:Tb. Appl. Phys. Lett. 2017, 110, 222102. [Google Scholar] [CrossRef]
- Erni, R.; Browning, N.D. Valence electron energy-loss spectroscopy in monochromated scanning transmission electron microscopy. Ultramicroscopy 2005, 104, 176–192. [Google Scholar] [CrossRef] [PubMed]
- Walther, T.; Stegmann, H. Preliminary results from the first monochromated and aberration corrected 200kV field-emission scanning transmission electron microscope. Microsc. Microanal. 2006, 12, 498–505. [Google Scholar] [CrossRef]
- Stöger-Pollach, M.; Franco, H.; Schattschneider, P.; Lazar, S.; Schaffer, B.; Grogger, W.; Zandbergen, H.W. Cerenkov losses: A limit for bandgap determination and Kramers-Kronig analysis. Micron 2006, 37, 396–402. [Google Scholar]
- Lazar, S.; Botton, G.A.; Zandbergen, H.W. Enhancement of resolution in core-loss and low-loss spectroscopy in a monochromated microscope. Ultramicroscopy 2006, 106, 1091–1103. [Google Scholar] [CrossRef]
- Walther, T. A new experimental procedure to quantify annular dark field images in scanning transmission electron microscopy. J. Microsc. 2006, 221, 137–144. [Google Scholar] [CrossRef]
- Perovic, D.D.; Rossouw, C.J.; Howie, A. Imaging elastic strains in high-angle annular dark-field scanning-transmission electron microscopy. Ultramicroscopy 2003, 52, 353–359. [Google Scholar] [CrossRef]
- Grillo, V. The effect of surface strain on HAADF imaging. Ultramicroscopy 2009, 109, 1453–1464. [Google Scholar] [CrossRef] [PubMed]
- Walther, T. Electron microscopy of quantum dots. J. Microsc. 2014, 257, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Yalcin, A.O.; Goris, B.; van Dijk-Moes, R.J.A.; Fan, Z.; Erdamar, A.K.; Tichelaar, F.D.; Vlugt, T.J.H.; van Tendeloo, G.; Bals, S.; Vanmaekelbergh, D.; et al. Heat induced transformation of CdSe-CdS-ZnS core-multishell quantum dots by Zn diffusion into inner layers. Chem. Commun. 2015, 51, 3320–3323. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Walther, T.; Cullis, A.G.; Norris, D.J.; Hopkinson, M. Nature of the Stranski-Krastanow transition during epitaxy of InGaAs on GaAs. Phys. Rev. Lett. 2001, 86, 2381–2384. [Google Scholar] [CrossRef] [PubMed]
- Walther, T. Transmission electron microscopy of nanostructures. In Microscopy Methods in Nanomaterials Characterization; Chapter 4, Elsevier Series on Micro; Thomas, S., Thomas, R., Zachariah, A.K., Mishra, R.K., Eds.; Nano Technologies: Amsterdam, The Netherlands, 2017; Volume 1, pp. 105–134. [Google Scholar]
- Rosenauer, A.; Gerthsen, D.; van Dyck, D. Quantification of segregation and mass transport in InxGa1-xAs/GaAs Stranski-Krastanow layers. Phys. Rev. B 2001, 64, 245334. [Google Scholar] [CrossRef]
- Walther, T.; Wang, X.; Angadi, V.C.; Ruterana, P.; Longo, P.; Aoki, T. Study of phase separation in an InGaN alloy by electron energy loss spectroscopy in an aberration corrected monochromated scanning transmission electron microscope. J. Mater. Res. 2017, 32, 983–995. [Google Scholar] [CrossRef][Green Version]
- Kong, X.; Albert, S.; Bengoechea-Encabo, A.; Sanchez-Garcia, M.A.; Calleja, E.; Trampert, A. Plasmon excitation in electron energy-loss spectroscopy for determination of indium concentration in (In,Ga)N/GaN nanowires. Nanotechnology 2012, 23, 485701. [Google Scholar] [CrossRef] [PubMed]
- Kauko, H.; Fimland, B.O.; Grieb, T.; Munshi, A.M.; Müller, K.; Rosenauer, A.; van Helvoort, A.T.J. Near-surface depletion of antimony during the growth of GaAsSb and GaAs/GaAsSb nanowires. J. Appl. Phys. 2014, 116, 144303. [Google Scholar] [CrossRef]
- Kehagias, T.; Kerasiotis, I.; Vajpeyi, A.P.; Häusler, I.; Neumann, W.; Georgakilas, A.; Dimitrakopulos, G.P.; Komninou, P. Electron microscopy of InGaN nanopillars spontaneously grown on Si (111) substrates. Phys Status Solidi 2010, 7, 1305–1308. [Google Scholar] [CrossRef]
- Chou, N.J.; van der Meulen, Y.J.; Hammer, R.; Cahill, J. Auger and ellipsometric study of phosphorus segregation in oxidized degenerate silicon. Appl. Phys. Lett. 1974, 24, 200–202. [Google Scholar] [CrossRef]
- Li, Y.; Hembree, G.G.; Venables, V.A. Quantitative Auger electron spectroscopic analysis of Ge surface segregation in Si/Ge/Si(100) heterostructures. Appl. Phys. Lett. 1995, 67, 276–278. [Google Scholar] [CrossRef]
- Walther, T.; Gerthsen, D. Quantitative characterization of AlAs/GaAs interfaces by high-resolution transmission electron microscopy along the <100> and <110> projection. Appl. Phys. A 1993, 57, 393–400. [Google Scholar] [CrossRef]
- Harris, J.J.; Ashenford, D.E.; Foxon, C.T.; Dobson, P.J.; Joyce, B.A. Kinetic limitations to surface segregation during MBE growth of III/V compounds: Sn in GaAs. Appl. Phys. A 1984, 33, 87–92. [Google Scholar] [CrossRef]
- Fukatsu, S.; Fujita, K.; Yaguchi, H.; Shiraki, Y.; Ito, R. Self-limitation in the surface segregation of Ge atoms during Si molecular beam epitaxial growth. Appl. Phys. Lett. 1991, 59, 2103–2105. [Google Scholar] [CrossRef]
- Godbey, D.J.; Ancona, M.G. Modeling of Ge segregation in the limits of zero and infinite surface diffusion. J. Vac. Sci Technol. A 1996, 15, 976–980. [Google Scholar] [CrossRef]
- Norris, D.J.; Qiu, Y.; Dobbie, A.; Myronov, M.; Walther, T. Similarity of Stranski-Krastanow growth of Ge/Si and SiGe/Si. J. Appl. Phys. 2014, 115, 012003. [Google Scholar] [CrossRef]
- Walther, T.; Humphreys, C.J.; Cullis, A.G.; Robbins, D.J. A correlation between compositional fluctuations and surface undulations in strained layer epitaxy. Mater. Sci. Forum 1995, 196, 505–510. [Google Scholar] [CrossRef]
- Walther, T.; Humphreys, C.J.; Cullis, A.G. Observation of vertical and lateral Ge segregation in thin undulating SiGe layers on Si by electron energy loss spectroscopy. Appl. Phys. Lett. 1997, 71, 809–811. [Google Scholar] [CrossRef]
- Muraki, K.; Fukatsu, S.; Shiraki, Y.; Ito, R. Surface segregation of in atoms during molecular-beam epitaxy and its influence on the energy levels in InGaAs/GaAs quantum-wells. Appl. Phys. Lett. 1992, 61, 557–559. [Google Scholar] [CrossRef]
- Walther, T.; Humphreys, C.J. A quantitative study of compositional profiles of chemical vapour deposited strained silicon-germanium/silicon layers by transmission electron microscopy. J. Cryst. Growth 1999, 197, 113–128. [Google Scholar] [CrossRef]
- Walther, T.; Humphreys, C.J. Quantification of the Composition of Silicon Germanium/Silicon Structures by High-Angle Annular Dark Field Imaging. In Conference Series-Institute of Physics; Rodenburg, J.M., Ed.; Proc. EMAG-97; IoP Publishing: Bristol, UK, 1997; Volume 153, pp. 303–306. [Google Scholar]
- Walther, T.; Humphreys, C.J.; Robbins, D.J. Diffusion and surface segregation in thin SiGe/Si layers studied by scanning transmission electron microscopy. Defect Diffus. Forum 1997, 143, 1135–1140. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhang, Z.Y.; Hogg, R.A.; Cullis, A.G.; Walther, T. Study of the Effect of Annealing of in(Ga)As Quantum Dots. In Journal of Physics: Conference Series; Baker, R.T., Ed.; Proc. EMAG 2009; IoP Publishing: Bristol, UK, 2010; Volume 241, p. 012054. [Google Scholar]
- Schowalter, M.; Rosenauer, A.; Gerthsen, D.; Arzberger, M.; Bichler, M.; Abstreiter, G. Investigation of in segregation in InAs/AlAs quantum-well structures. Appl. Phys. Lett. 2001, 79, 4426–4428. [Google Scholar] [CrossRef]
- Rosenauer, A.; Fischer, U.; Gerthsen, D.; Förster, A. Composition evaluation by lattice fringe analysis. Ultramicroscopy 1998, 72, 121–133. [Google Scholar] [CrossRef]
- Schowalter, M.; Rosenauer, A.; Gerthsen, D.; Grau Amann, M.-C. Quantitative measurement of the influence of growth interruptions on the Sb distribution of GaSb/GaAs quantum wells by transmission electron microscopy. Appl. Phys. Lett. 2003, 84, 3123–3125. [Google Scholar] [CrossRef]
- Volz, K.; Torunksi, T.; Rubel, O.; Stolz, W.; Kruse, P.; Gerthsen, D.; Schowalter, M.; Rosenauer, A. Annealing effects on the nanoscale indium and nitrogen distribution in Ga(NAs) and (GaIn)(NAs) quantum wells. J. Appl. Phys. 2007, 102, 083504. [Google Scholar] [CrossRef]
- Litvinov, D.; Rosenauer, A.; Gerthsen, D.; Preis, H. Transmission electron microscopy investigation of CdSe/ZnSe quantum dot structures. Phys. Status Solidi 2002, 229, 523–527. [Google Scholar] [CrossRef]
- Rosenauer, A.; Mehrtens, T.; Müller, K.; Gries, K.; Schowalter, M.; Satyam, P.V.; Bley, S.; Tessarek, C.; Hommel, D.; Sebald, K.; et al. Compositional mapping in InGaN by scanning transmission electron microscopy. Ultramicroscopy 2011, 111, 1316–1327. [Google Scholar] [CrossRef]
- Walther, T.; Amari, H.; Ross, I.M.; Wang, T.; Cullis, A.G. Lattice resolved annular dark-field scanning transmission electron microscopy of (Al,In)GaN/GaN layers for measuring segregation with sub-monolayer precision. J. Mater. Sci. 2013, 48, 2883–2892. [Google Scholar] [CrossRef]
- Piscopiello, E.; Rosenauer, A.; Passaseo, A.; Montoya Rossi, E.H.; van Tendeloo, G. Segregation in InxGa1-xAs/GaAs Stranski-Krastanow layers grown by metal-organic chemical vapour deposition. Philos. Mag. 2007, 85, 3857–3870. [Google Scholar] [CrossRef]
- Hytch, M.J.; Plamann, T. Imaging conditions for reliable measurement of displacement and strain in high-resolution electron microscopy. Ultramicroscopy 2001, 87, 199–212. [Google Scholar] [CrossRef]
- Walther, T.; Humphreys, C.J. The limitations of pattern recognition and displacement measurement techniques for evaluating HREM images of strained semiconductor interfaces. Proc. EMAG, Birmingham. Inst. Phys. Conf. Ser. 1995, 147, 103–106. [Google Scholar]
- Müller, K.; Schowalter, M.; Rubel, O.; Hu, D.Z.; Schaadt, D.M.; Hetterich, M.; Gilet, P.; Fritz, R.; Volz, K.; Rosenauer, A. TEM 3-beam study of annealing effects in InGaNAs using ab-initio structure factors for strain-relaxed supercells. Proc. 17th Microsc. Semicond. Mater. Cambridge. J. Phys. Conf. Ser. 2011, 326, 012026. [Google Scholar] [CrossRef]
- Rao, D.V.S.; Sankarasubramanian, R.; Muraleedharan, K.; Mehrtens, T.; Rosenauer, A.; Banerjee, D. Quantitative strain and compositional studies of InxGa1-xAs epilayers in a GaAs-based pHEMT device structure by TEM techniques. Microsc. Microanal. 2014, 20, 1262–1270. [Google Scholar]
- Rosenauer, A.; van Dyck, D.; Arzberger, M.; Abstreiter, G. Compositional analysis based on electron holography and a chemically sensitive reflection. Ultramicroscopy 2001, 88, 51–61. [Google Scholar] [CrossRef]
- Walther, T. Electron energy-loss spectroscopic profiling of thin film structures: 0.39nm line resolution and 0.04eV precision measurement of near-edge structure shifts at interfaces. Ultramicroscopy 2003, 96, 401–411. [Google Scholar] [CrossRef]
- Simon, J.; Walther, T.; Mader, W.; Klein, J.; Reisinger, D.; Alff, L.; Gross, R. Diffusion and segregation effects in doped manganite / titanate heterostructures. Appl. Phys. Lett. 2004, 84, 3882–3884. [Google Scholar] [CrossRef]
- Walther, T.; Ross, I.M. Aberration corrected high-resolution and scanning transmission electron microscopy of thin perovskite layers. Phys. Procedia 2013, 40, 49–55. [Google Scholar] [CrossRef]
- Walther, T.; Richards, R.D.; Bastiman, F. Scanning transmission electron microscopy measurement of bismuth segregation in thin Ga(As,Bi) layers grown by molecular beam epitaxy. Cryst. Res. Technol. 2015, 50, 38–42. [Google Scholar] [CrossRef]
- Walther, T. Development of a new analytical electron microscopy technique to quantify the chemistry of planar defects and to measure accurately solute segregation to grain boundaries. J. Microsc. 2004, 215, 191–202. [Google Scholar] [CrossRef] [PubMed]
- Walther, T. Linear least-squares fit evaluation of series of analytical spectra from planar defects: extension and possible implementations in scanning transmission electron microscopy. J. Microsc. 2006, 223, 165–170. [Google Scholar] [CrossRef] [PubMed]
- Walther, T.; Hopkinson, M. Quantitative investigation of the onset of islanding in strained layer epitaxy of InAs/GaAs by X-ray mapping in STEM. J. Phys. Conf. Ser. 2010, 209, 012035. [Google Scholar] [CrossRef]
- Walther, T. Accurate measurement of atomic segregation to grain boundaries or to planar faults by analytical transmission electron microscopy. Phys. Status. Solidi 2015, 12, 310–313. [Google Scholar] [CrossRef]
- Dwyer, C.; Ziegler, A.; Shibata, N.; Winkelmann, G.B.; Satet, R.L.; Hoffmann, M.J.; Cinibulk, M.K.; Becher, P.F.; Painter, G.S.; Browning, N.D.; et al. Interfacial structure in silicon nitride sintered with lanthanide oxide. J. Mater. Sci. 2006, 41, 4405–4412. [Google Scholar] [CrossRef]
- Makhonin, M.N.; Foster, A.P.; Krysa, A.B.; Fry, P.W.; Davies, D.G.; Grange, T.; Walther, T.; Skolnick, M.S.; Wilson, L.R. Homogeneous array of nanowire-embedded quantum light emitters. Nano Lett. 2013, 13, 861–865. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.; Lai, S.K.; Chen, F.R.; Kai, J.J. Observations of segregation of Al in AlGaN alloys. Phys. Status. Solidi 2001, 188, 811–814. [Google Scholar] [CrossRef]
- Kehagias, T.; Dimitrakopulos, G.P.; Kioseoglou, J.; Kirmse, H.; Ciesen, C.; Heuken, M.; Georgakilas, A.; Neumann, W.; Karakostas, T.; Komninou, P. Indium migration paths in V-defects of InAlN grown by metal-organic vapour phase epitaxy. Appl. Phys. Lett. 2009, 95, 071905. [Google Scholar] [CrossRef]
- Arslan, I.; Browning, N.D. Role of oxygen at screw dislocations in GaN. Phys. Rev. Lett. 2003, 91, 165501. [Google Scholar] [CrossRef] [PubMed]



© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walther, T. Measurement of Diffusion and Segregation in Semiconductor Quantum Dots and Quantum Wells by Transmission Electron Microscopy: A Guide. Nanomaterials 2019, 9, 872. https://doi.org/10.3390/nano9060872
Walther T. Measurement of Diffusion and Segregation in Semiconductor Quantum Dots and Quantum Wells by Transmission Electron Microscopy: A Guide. Nanomaterials. 2019; 9(6):872. https://doi.org/10.3390/nano9060872
Chicago/Turabian StyleWalther, Thomas. 2019. "Measurement of Diffusion and Segregation in Semiconductor Quantum Dots and Quantum Wells by Transmission Electron Microscopy: A Guide" Nanomaterials 9, no. 6: 872. https://doi.org/10.3390/nano9060872
APA StyleWalther, T. (2019). Measurement of Diffusion and Segregation in Semiconductor Quantum Dots and Quantum Wells by Transmission Electron Microscopy: A Guide. Nanomaterials, 9(6), 872. https://doi.org/10.3390/nano9060872




