Infrared Polariscopy Imaging of Linear Polymeric Patterns with a Focal Plane Array
Abstract
1. Introduction
2. Materials and Methods
3. Results
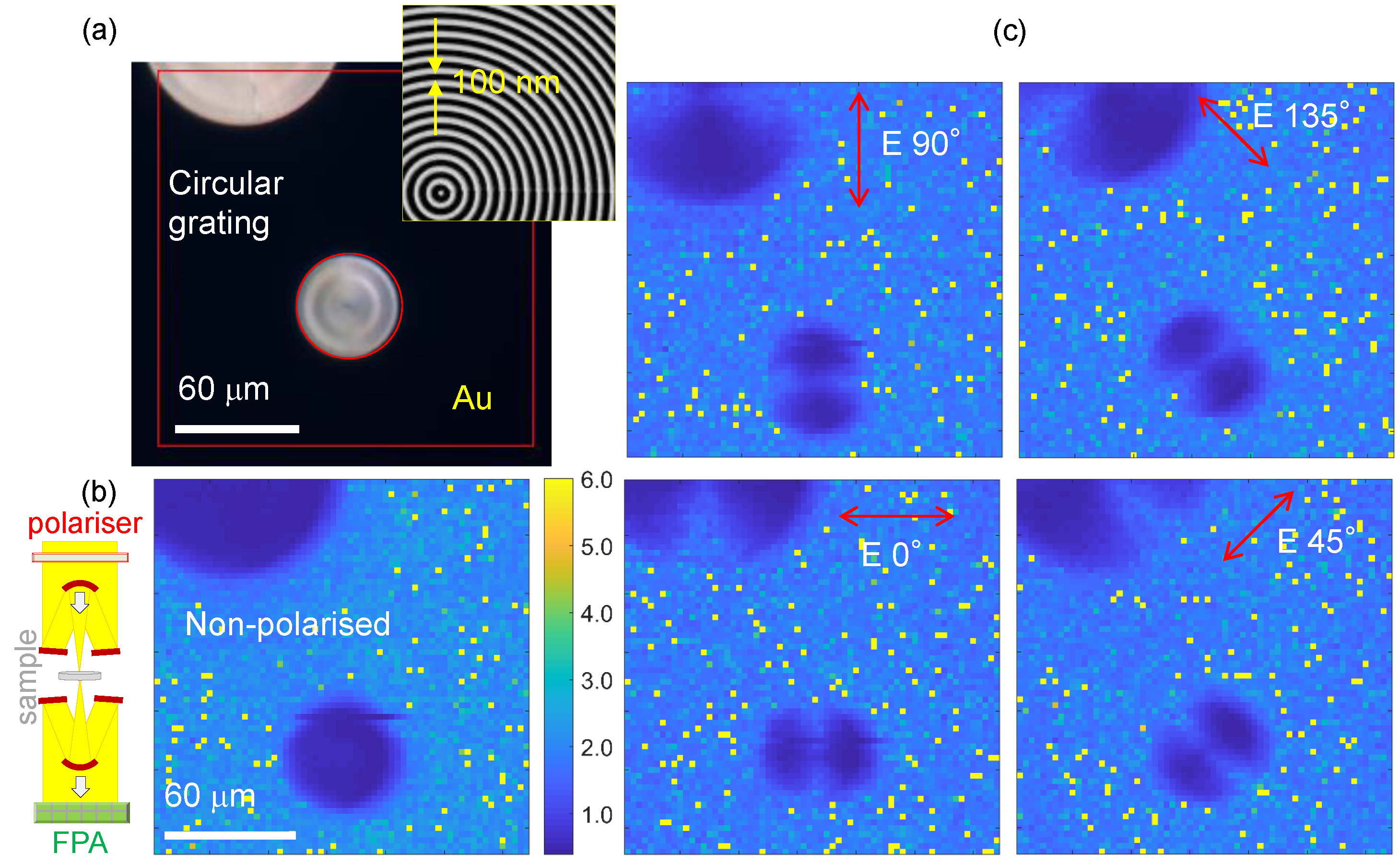
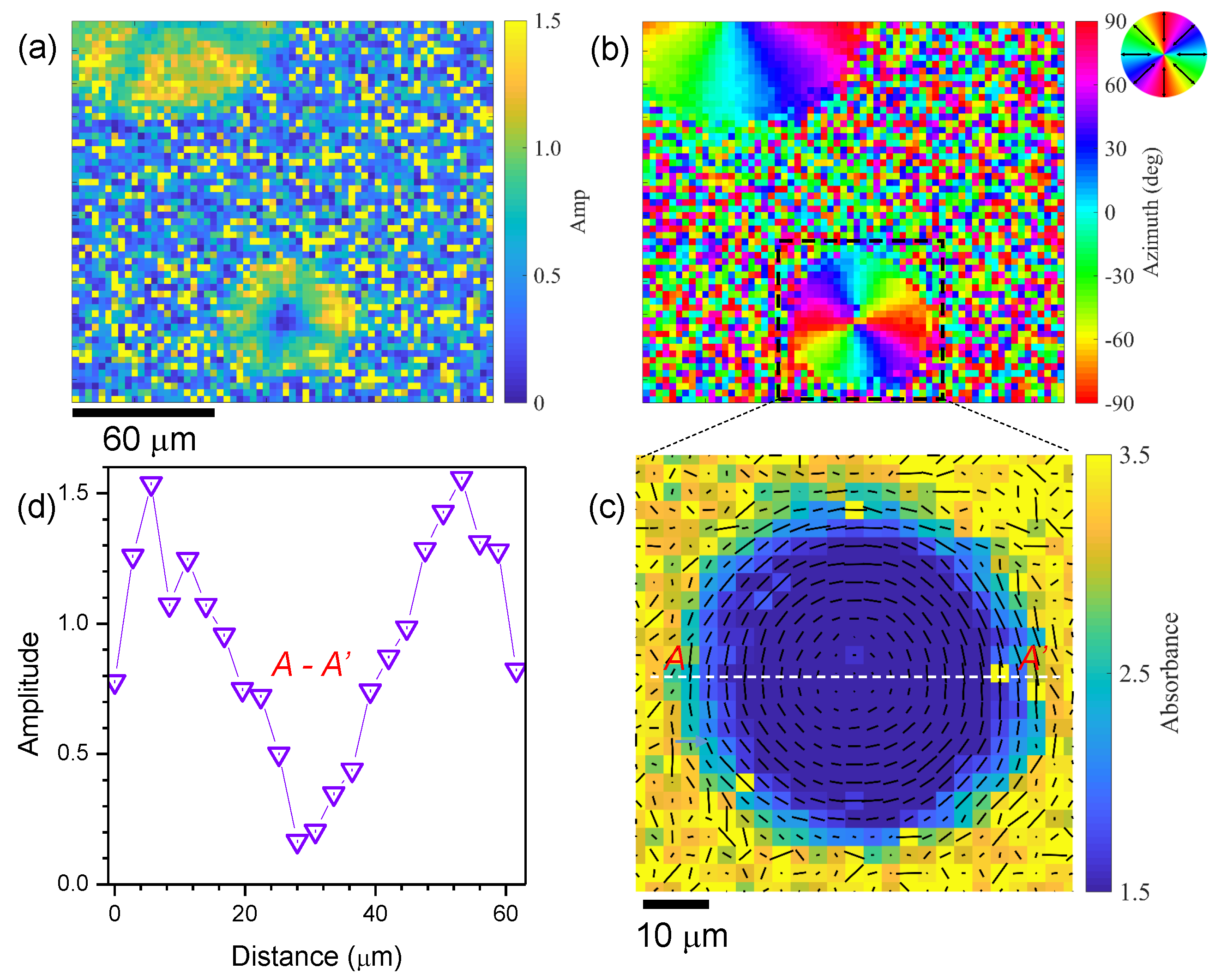
3.1. Circular Sub-Wavelength Grating
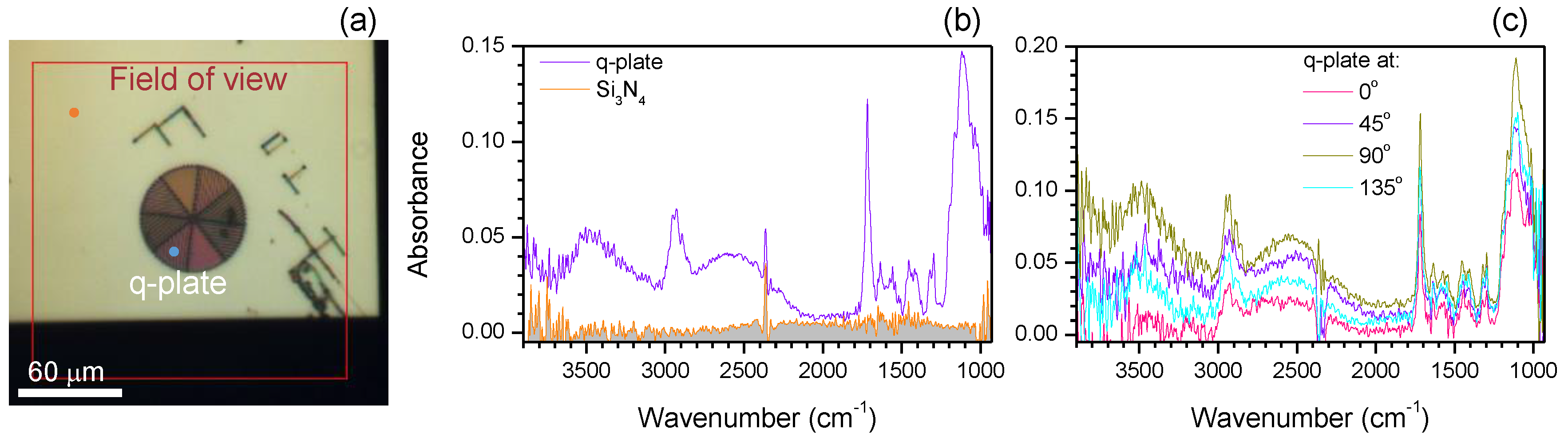
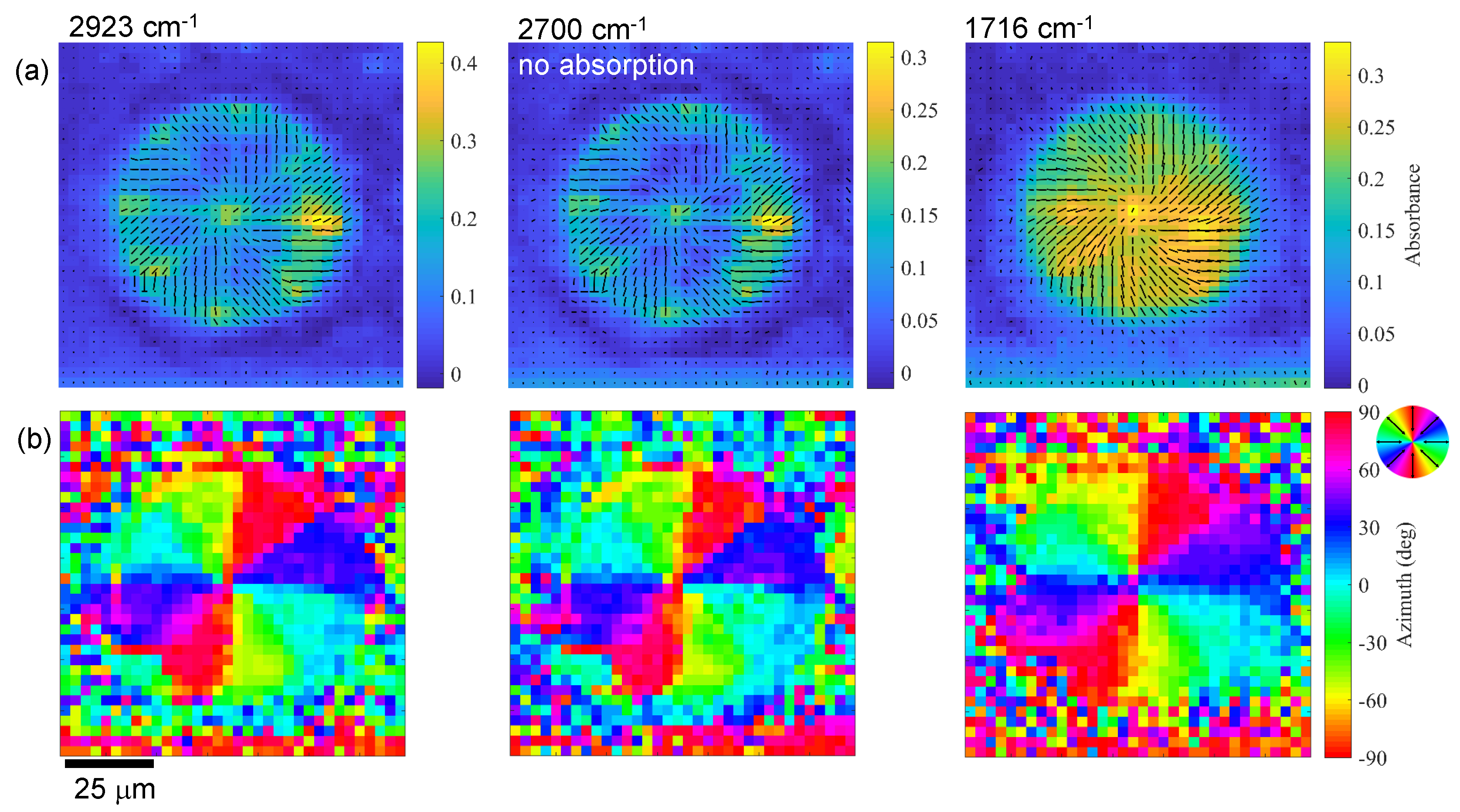
3.2. SZ2080 Polymerised Gratings
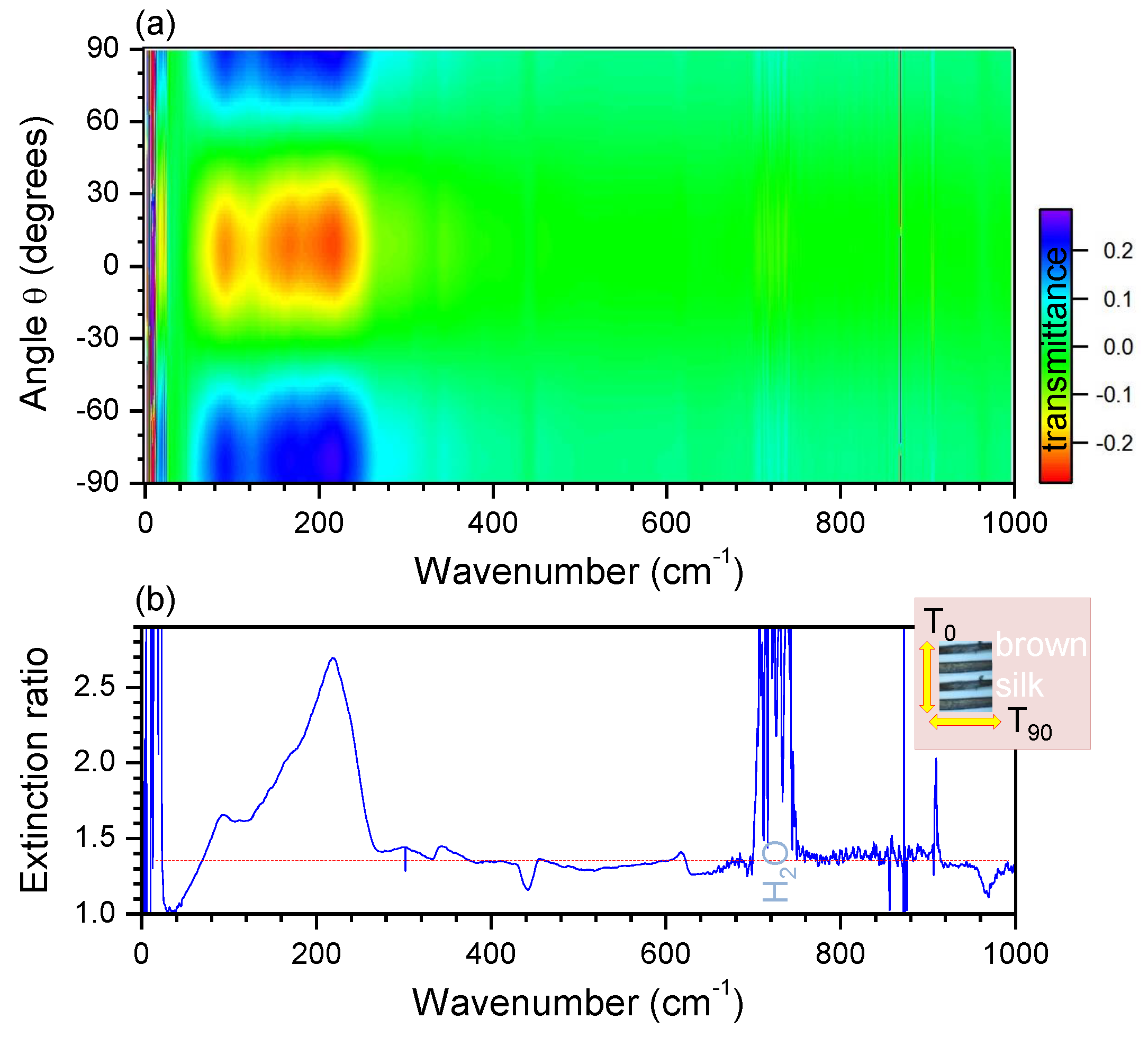
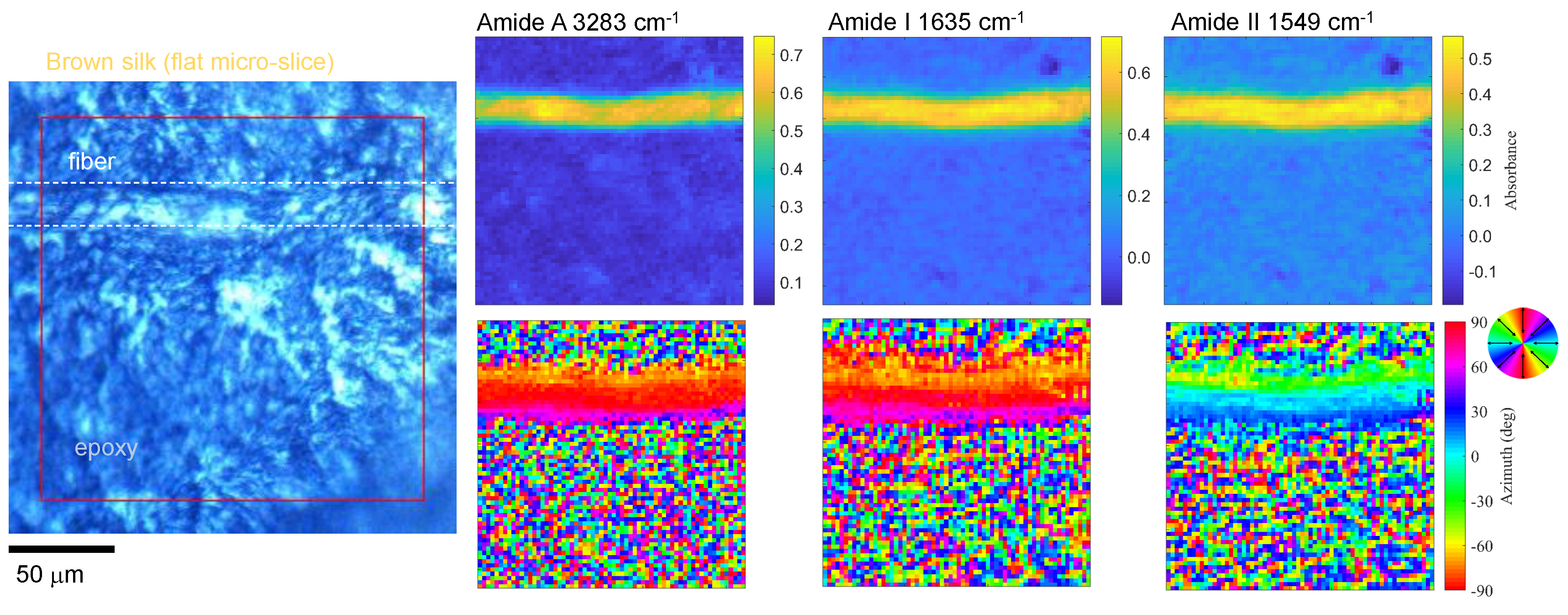
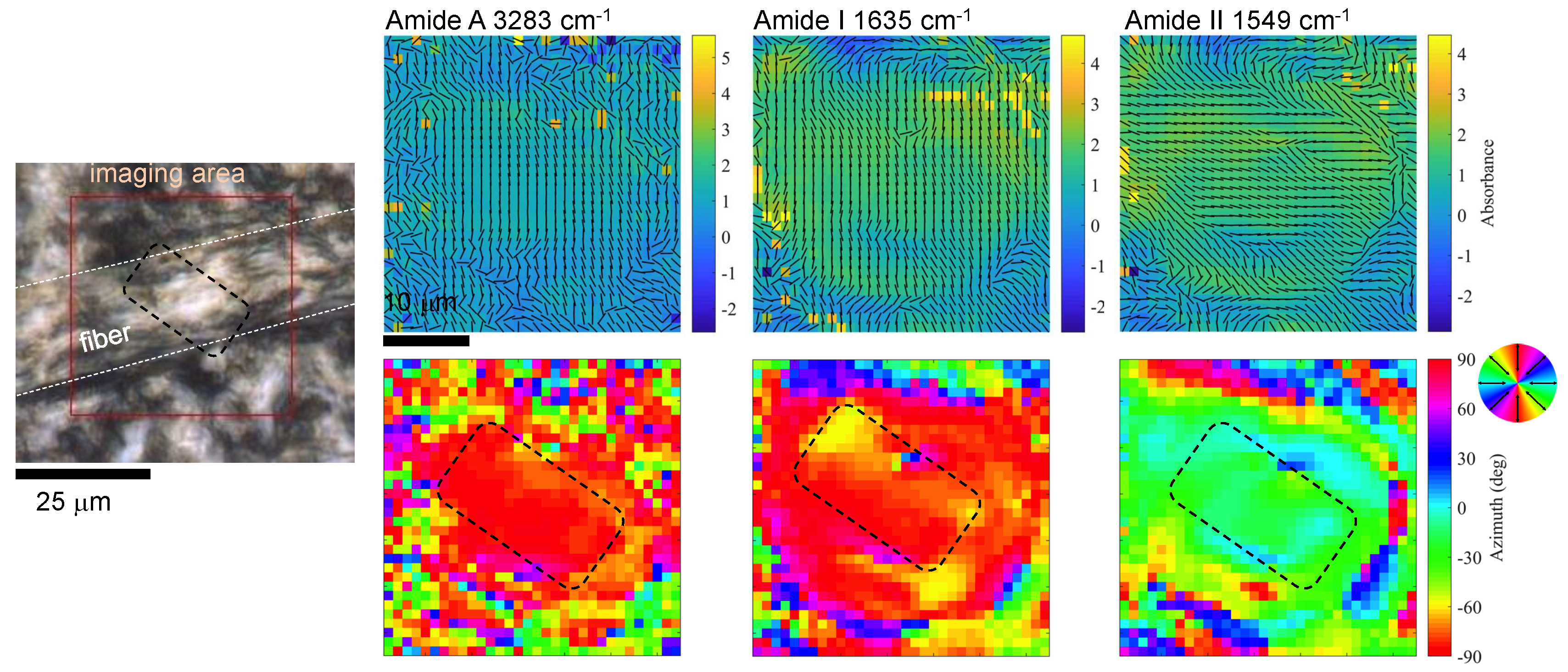
3.3. Brown Silk
4. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
Appendix A. Supplement

References
- Cheeseman, S.; Truong, V.; Vongsvivut, J.; Tobin, M.J.; Crawford, R.; Ivanova, E.P. Applications of Synchrotron-Source IR Spectroscopy for the Investigation of Insect Wings; Intechopen: Rijeka, Croatia, 2018. [Google Scholar]
- Wang, D.C.; Sun, S.; Feng, Z.; Tan, W.; Qiu, C.W. Multipolar-interference-assisted terahertz waveplates via all-dielectric metamaterials. Appl. Phys. Lett. 2018, 113, 201103. [Google Scholar] [CrossRef]
- Ryu, M.; Linklater, D.; Hart, W.; Balčytis, A.; Skliutas, E.; Malinauskas, M.; Appadoo, D.; Tan, Y.; Ivanova, E.P.; Morikawa, J.; et al. 3D Printed Polarising Grids for IR-THz Synchrotron Radiation. J. Opt. 2018, 20, 035101. [Google Scholar] [CrossRef]
- Tobin, M.; Vongsvivut, J.; Martin, D.; Sizeland, K.; Hackett, M.; Takechi, R.; Fimorgnari, N.; Lam, V.; Mamo, J.; Carter, E.; et al. Focal plane array IR imaging at the Australian Synchrotron. Infrared Phys. Technol. 2018, 94, 85–90. [Google Scholar] [CrossRef]
- Tao, H.; Kaplan, D.L.; Omenetto, F.G. Silk Materials: A Road to Sustainable High Technology. Adv. Mater. 2012, 24, 2824–2837. [Google Scholar] [CrossRef] [PubMed]
- Shao, Z.; Vollrath, F. Surprising strength of silkworm silk. Nature 2002, 418, 741. [Google Scholar] [CrossRef] [PubMed]
- Rousseau, M.E.; Lefevre, T.; Beaulieu, L.; Asakura, T.; Pezolet, M. Study of Protein Conformation and Orientation in Silkworm and Spider Silk Fibers Using Raman Microspectroscopy. Biomacromolecules 2004, 5, 2247–2257. [Google Scholar] [CrossRef] [PubMed]
- Du, N.; Liu, X.Y.; Narayanan, J.; Li, L.; Lim, M.L.M.; Li, D. Design of Superior Spider Silk: From Nanostructure to Mechanical Properties. Biophys. J. 2006, 91, 4528–4535. [Google Scholar] [CrossRef]
- Malinauskas, M.; Žukauskas, A.; Bičkauskaitė, G.; Gadonas, R.; Juodkazis, S. Mechanisms of three-dimensional structuring of photo-polymers by tightly focussed femtosecond laser pulses. Opt. Express 2010, 18, 10209–10221. [Google Scholar] [CrossRef]
- Ryu, M.; Bačytis, A.; Wang, X.; Vongsvivut, J.; Hikima, Y.; Li, J.; Tobin, M.J.; Juodkazis, S.; Morikawa, J. Orientational Mapping Augmented Sub-Wavelength Hyper-Spectral Imaging of Silk. Sci. Rep. 2017, 7, 7419. [Google Scholar] [CrossRef]
- Hikima, Y.; Morikawa, J.; Hashimoto, T. FT-IR Image Processing Algorithms for In-Plane Orientation Function and Azimuth Angle of Uniaxially Drawn Polyethylene Composite Film. Macromolecules 2011, 44, 3950–3957. [Google Scholar] [CrossRef]
- Honda, R.; Ryu, M.; Balčytis, A.; Vongsvivut, J.; Tobin, M.J.; Juodkazis, S.; Morikawa, J. Paracetamol micro-structure analysis by optical mapping. Appl. Surf. Sci. 2019, 473, 127–132. [Google Scholar] [CrossRef]
- Wang, X.; Kuchmizhak, A.A.; Brasselet, E.; Juodkazis, S. Dielectric geometric phase optical elements fabricated by femtosecond direct laser writing in photoresists. Appl. Phys. Lett. 2017, 110, 181101. [Google Scholar] [CrossRef]
- Marrucci, L.; Karimi, E.; Slussarenko, S.; Piccirillo, B.; Santamato, E.; Nagali, E.; Sciarrino, F. Spin-to-orbital conversion of the angular momentum of light and its classical and quantum applications. J. Opt. 2011, 13, 064001. [Google Scholar] [CrossRef]
- Slussarenko, S.; Murauski, A.; Du, T.; Chigrinov, V.; Marrucci, L.; Santamato, E. Tunable liquid crystal q-plates with arbitrary topological charge. Opt. Express 2011, 19, 4085–4090. [Google Scholar] [CrossRef]
- Biener, G.; Niv, A.; Kleiner, V.; Hasman, E. Formation of helical beams by use of Pancharatnam - Berry phase optical elements. Opt. Lett. 2002, 27, 1875–1877. [Google Scholar] [CrossRef]
- Hakobyan, D.; Brasselet, E. Left-handed optical radiation torque. Nat. Photonics 2014, 82, 610–614. [Google Scholar] [CrossRef]
- Rekštytė, S.; Jonavicius, T.; Gailevičius, D.; Malinauskas, M.; Mizeikis, V.; Gamaly, E.G.; Juodkazis, S. Nanoscale precision of 3D polymerisation via polarisation control. Adv. Opt. Mat. 2016, 4, 1209–1214. [Google Scholar] [CrossRef]
- Balčytis, A.; Ryu, M.; Wang, X.; Novelli, F.; Seniutinas, G.; Du, S.; Wang, X.; Li, J.; Davis, J.; Appadoo, D.; Morikawa, J.; Juodkazis, S. Silk: Optical Properties over 12.6 Octaves THz-IR-Visible-UV Range. Materials 2017, 10, 356. [Google Scholar] [CrossRef]
- Ryu, M.; Kobayashi, H.; Balčytis, A.; Wang, X.; Vongsvivut, J.; Li, J.; Urayama, N.; Mizeikis, V.; Tobin, M.; Juodkazis, S.; et al. Nanoscale chemical mapping of laser-solubilized silk. Mat. Res. Express 2017, 4, 115028. [Google Scholar] [CrossRef]
- Ryu, M.; Honda, R.; Cernescu, A.; Vailionis, A.; Balcytis, A.; Vongsvivut, J.; Li, J.L.; Linklater, D.P.; Ivanova, E.P.; Mizeikis, V.; Tobin, M.J.; Morikawa, J.; Juodkazis, S. Nanoscale optical and structural characterisation of silk. arXiv 2019, arXiv:1902.02688. [Google Scholar] [CrossRef]
- Gall, D. Electron mean free path in elemental metals. J. Appl. Phys. 2016, 110, 085101. [Google Scholar] [CrossRef]
- McMaster, W.H. Polarization and the Stokes Parameter. Am. J. Phys. 1954, 22, 351–362. [Google Scholar] [CrossRef]
- Stedmon, C.A.; Bro, R. Characterizing dissolved organic matter fluorescence with parallel factor analysis: A tutorial. Limnol. Oceanogr. Methods 2008, 6, 572–579. [Google Scholar] [CrossRef]
- Zhizhchenko, A.; Kuchmizhak, A.; Vitrik, O.; Kulchin, Y.; Juodkazis, S. On-demand concentration of an analyte on laser-printed polytetrafluoroethylene. Nanoscale 2018, 10, 21414–21424. [Google Scholar] [CrossRef]
- Xiong, X.; Jiang, S.; Hu, Y.; Peng, R.; Wang, M. Structured Metal Film as a Perfect Absorber. Adv. Mat. 2013, 25, 3994–4000. [Google Scholar] [CrossRef]
- Nishijima, Y.; Balčytis, A.; Naganuma, S.; Seniutinas, G.; Juodkazis, S. Tailoring Metal and Insulator Contributions in Plasmonic Perfect Absorber Metasurfaces. ACS Appl. Nanomater. 2018, 1, 3557–3564. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Honda, R.; Ryu, M.; Moritake, M.; Balčytis, A.; Mizeikis, V.; Vongsvivut, J.; Tobin, M.J.; Appadoo, D.; Li, J.-L.; Ng, S.H.; et al. Infrared Polariscopy Imaging of Linear Polymeric Patterns with a Focal Plane Array. Nanomaterials 2019, 9, 732. https://doi.org/10.3390/nano9050732
Honda R, Ryu M, Moritake M, Balčytis A, Mizeikis V, Vongsvivut J, Tobin MJ, Appadoo D, Li J-L, Ng SH, et al. Infrared Polariscopy Imaging of Linear Polymeric Patterns with a Focal Plane Array. Nanomaterials. 2019; 9(5):732. https://doi.org/10.3390/nano9050732
Chicago/Turabian StyleHonda, Reo, Meguya Ryu, Masayuki Moritake, Armandas Balčytis, Vygantas Mizeikis, Jitraporn Vongsvivut, Mark J. Tobin, Dominique Appadoo, Jing-Liang Li, Soon Hock Ng, and et al. 2019. "Infrared Polariscopy Imaging of Linear Polymeric Patterns with a Focal Plane Array" Nanomaterials 9, no. 5: 732. https://doi.org/10.3390/nano9050732
APA StyleHonda, R., Ryu, M., Moritake, M., Balčytis, A., Mizeikis, V., Vongsvivut, J., Tobin, M. J., Appadoo, D., Li, J.-L., Ng, S. H., Juodkazis, S., & Morikawa, J. (2019). Infrared Polariscopy Imaging of Linear Polymeric Patterns with a Focal Plane Array. Nanomaterials, 9(5), 732. https://doi.org/10.3390/nano9050732







