Multi-Scale Modeling and Simulation of Thermoplastic Automated Tape Placement: Effects of Metallic Particles Reinforcement on Part Consolidation
Abstract
1. Introduction
2. Methods
2.1. Surface Description and Its Time Evolution
2.2. Particle Orientation Model
Homogenized Thermal Conductivity
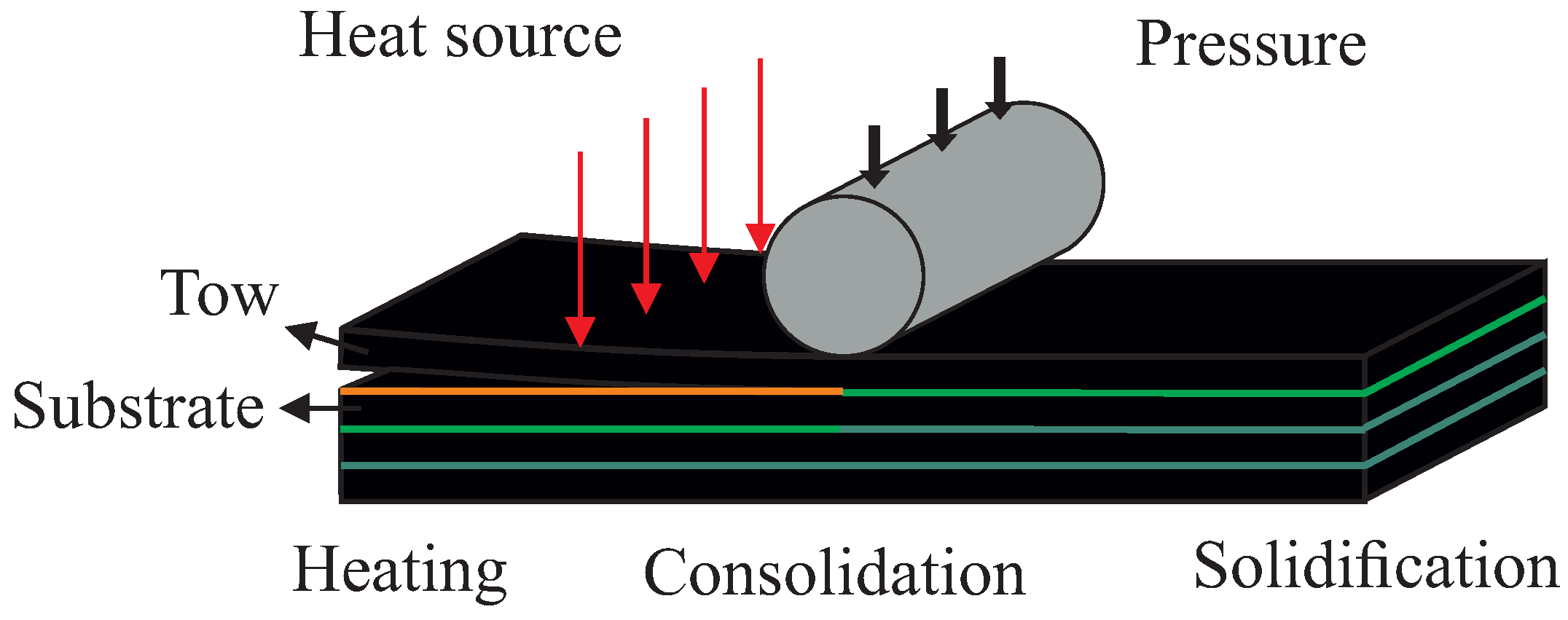
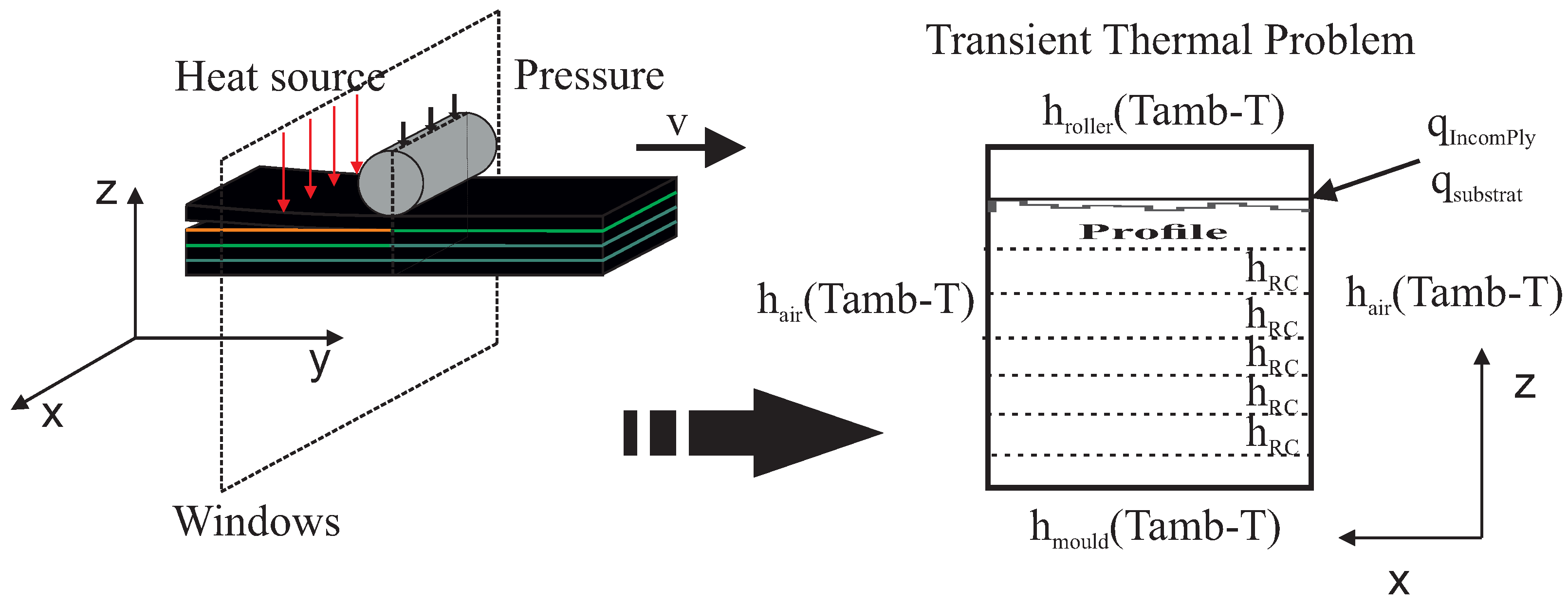
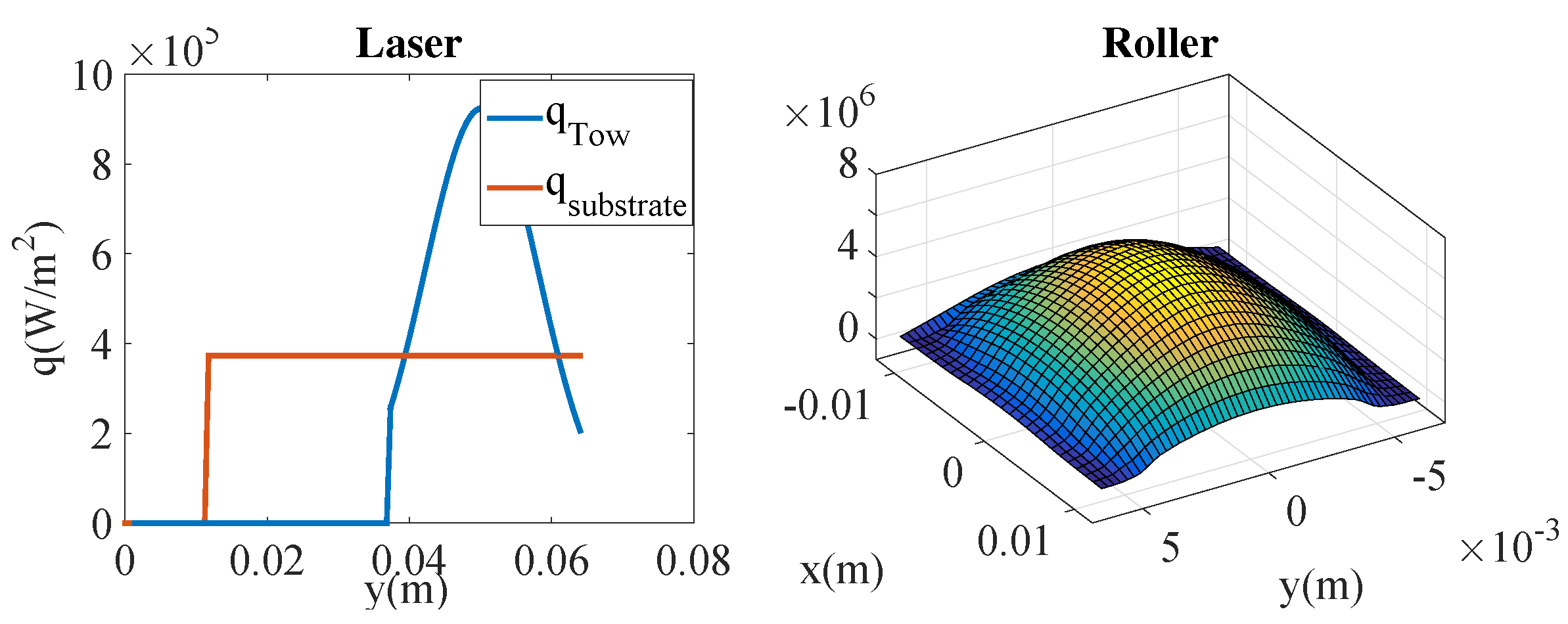
3. Process Modeling and Simulation
- An Eulerian frame, in which the tape moves while the laying head remains at rest, is considered. This frame choice allows one to reduce the thermal and squeezing flow calculation to the tape cross-section depicted in Figure 2.
- The domain of the study consists of an m-plies laminate. We consider more than 6 plies in order to limit the effect of the boundary condition between the substrate and the tool.
- The metallic particles contained in the prepreg are considered well dispersed and isotropically oriented at the beginning of the forming stage. The orientation evolution and induced properties are computed all along the consolidation process.
- Room temperature was assumed as the initial temperature of the incoming tape.
- Parameters involved in the simulation are reported in Table 2.
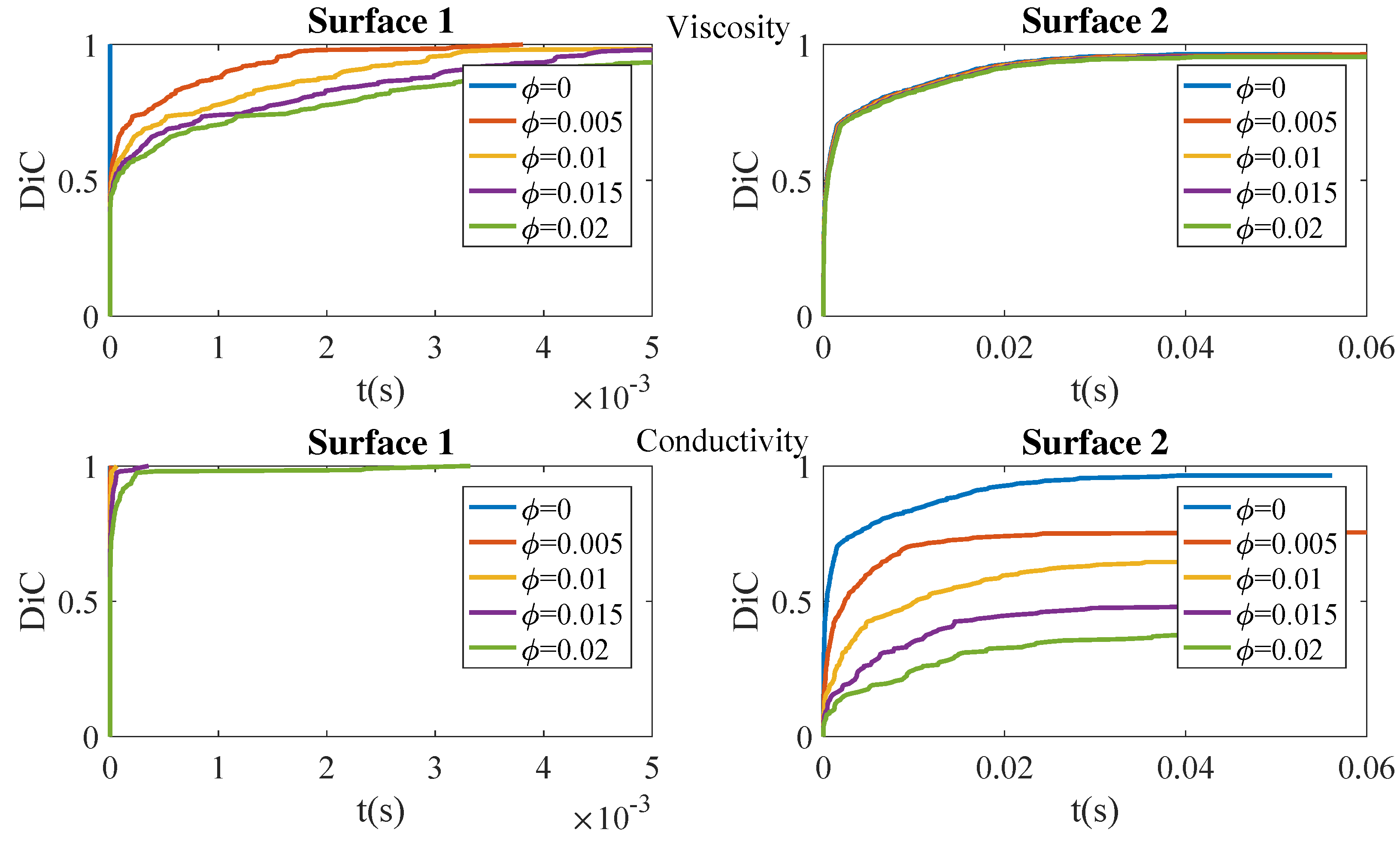
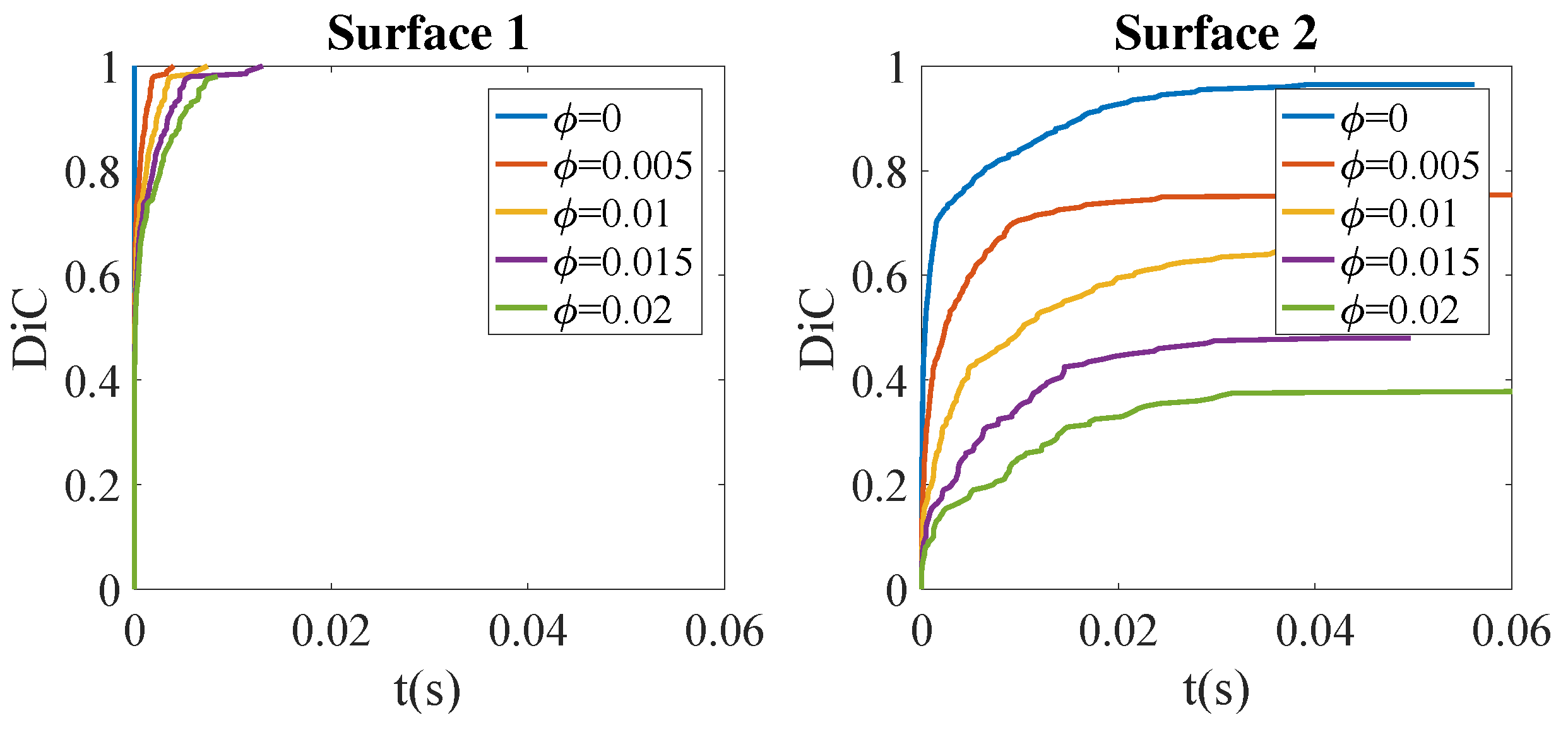
4. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goodship, V.; Middleton, B.; Cherrington, R. Design and Manufacture of Plastic Components for Multifunctionality. In Plastics Design Library; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Barasinski, A.; Leygue, A.; Soccard, E.; Poitou, A. Identification of non uniform thermal contact resistance in automated tape placement process. Int. J. Mater. Form. 2013, 7, 479–486. [Google Scholar] [CrossRef]
- Perez, M.; Barasinski, A.; Courtemanche, B.; Ghnatios, C.; Chinesta, F. Sensitivity thermal analysis in the laser-assisted tape placement process. AIMS Mater. Sci. 2018, 5, 1053–1072. [Google Scholar] [CrossRef]
- Argerich, C.; Ibanez, R.; Leon, A.; Barasinski, A.; Abisset-Chavanne, E.; Chinesta, F. Surface characterization and classification in automated tape placement processability: Modeling and numerical analysis. AIMS Mater. Sci. 2018, 5, 870–888. [Google Scholar] [CrossRef]
- Chinesta, F.; Leygue, A.; Bognet, B.; Ghnatios, C.; Poulahon, F.; Bordeu, F.; Barasinski, A.; Poitou, A.; Chatel, S.; Maison-Le-Poec, S. First steps towards an advanced simulation of composites manufacturing by automated tape placement. Int. J. Mater. Form. 2014, 7, 81–92. [Google Scholar] [CrossRef]
- Bur, N.; Joyot, P.; Ghnatios, C.; Villon, P.; Cueto, E.; Chinesta, F. On the use of model order reduction for simulating automated fibre placement processes. Adv. Model. Simul. Eng. Sci. 2016, 3, 4. [Google Scholar] [CrossRef]
- Chinesta, F.; Leygue, A.; Bordeu, F.; Aguado, J.; Cueto, E.; Gonzalez, D.; Alfaro, I.; Ammar, A.; Huerta, A. Parametric PGD based computational vademecum for efficient design, optimization and control. Arch. Comput. Methods Eng. 2013, 20, 31–59. [Google Scholar] [CrossRef]
- Bognet, B.; Leygue, A.; Chinesta, F.; Poitou, A.; Bordeu, F. Advanced simulation of models defined in plate geometries: 3D solutions with 2D computational complexity. Comput. Methods Appl. Mech. Eng. 2012, 201, 1–12. [Google Scholar] [CrossRef]
- Lee, W.; Springer, G. A model of the manufacturing process of thermoplastic matrix composites. J. Compos. Mater. 1987, 21, 1057–1082. [Google Scholar]
- Yang, F.; Pitchumani, R. A fractal Cantor set based description of interlaminar contact evolution during thermoplastic composites processing. J. Mater. Sci. 2001, 36, 4661–4671. [Google Scholar] [CrossRef]
- Leon, A.; Barasinski, A.; Nadal, E.; Chinesta, F. High-resolution thermal analysis at thermoplastic pre-impregnated acomposite interfaces. Compos. Interfaces 2015, 22, 767–777. [Google Scholar] [CrossRef]
- Leon, A.; Perez, M.; Barasinski, A.; Abisset-Chavanne, E.; Chinesta, F. On the properties evolution of engineered surfaces of thin reinforced thermoplastic tapes during consolidation. Surf. Topogr. Metrol. Prop. 2017, 5, 044003. [Google Scholar] [CrossRef]
- Leon, A.; Barasinski, A.; Chinesta, F. Microstructural analysis of pre-impreganted tapes consolidation. Int. J. Mater. Form. 2017, 10, 369–378. [Google Scholar] [CrossRef]
- Leon, A.; Argerich, C.; Barasinski, A.; Soccard, E.; Chinesta, F. Effects of material and process parameters on in-situ consolidation. Int. J. Mater. Form. 2018. [Google Scholar] [CrossRef]
- Ma, A.; Chinesta, F.; Mackley, M. The rheology and modelling of chemically treated carbon nanotube suspensions. J. Rheol. 2009, 53, 547–573. [Google Scholar] [CrossRef]
- Jeffery, G. The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. 1922, 102, 161–179. [Google Scholar] [CrossRef]
- Rivière, L.; Lonjon, A.; Dantras, E.; Lacabanne, C.; Olivier, P.; Rocher, N. Silver fillers aspect ratio influence on electrical and thermal conductivity in PEEK/Ag nanocomposites. Eur. Polym. J. 2016, 85, 15–125. [Google Scholar]
- Advani, S.; Tucker, C. Closure approximations for three dimensional structure tensors. J. Rheol. 1990, 34, 367–386. [Google Scholar] [CrossRef]
- Perez, M.; Abisset-Chavanne, E.; Barasinski, A.; Chinesta, F.; Ammar, A.; Keunings, R. On the multi-scale description of electrical conducting suspensions involving perfectly dispersed rods. Adv. Model. Simul. Eng. Sci. 2015, 1, 2–23. [Google Scholar] [CrossRef]
- Rivière, L.; Caussé, N.; Lonjon, A.; Dantras, E.; Lacabanne, C. Specific heat capacity and thermal conductivity of PEEK/Ag nanoparticles composites determined by Modulated-Temperature Differential Scanning Calorimetry. Polym. Degrad. Stab. 2016, 127, 98–104. [Google Scholar] [CrossRef]
- Dedieu, C. Mastering the Filament Winding Process with In Situ Consolidation for Launcher Application. Ph.D. Thesis, Ecole Centrale de Nantes, Nantes, France, 2017. [Google Scholar]
- Shuler, S.F.; Advani, S.G. Transverse squeeze flow of concentrated aligned fibers in viscous fluids. J. Non-Newtonian Fluid Mech. 1996, 65, 47–74. [Google Scholar] [CrossRef]
- Quiroga Cortes, L.; Lonjon, A.; Dantras, E.; Lacabanne, C. High-performance thermoplastic composites poly(ether ketone ketone)/silver nanowires: Morphological, mechanical and electrical properties. J. Non-Crystalline Solids 2014, 391, 106–111. [Google Scholar] [CrossRef]
- Quiroga Cortes, L.; Racagel, S.; Lonjon, A.; Dantras, E.; Lacabanne, C. Electrically conductive carbon fiber/PEKK/silver nanowires multifunctional composites. Compos. Sci. Technol. 2016, 137, 159–166. [Google Scholar] [CrossRef][Green Version]
- Petrie, C.J.S. The rheology of fibre suspensions. J. Non-Newtonian Fluid Mech. 1999, 87, 369–402. [Google Scholar] [CrossRef]
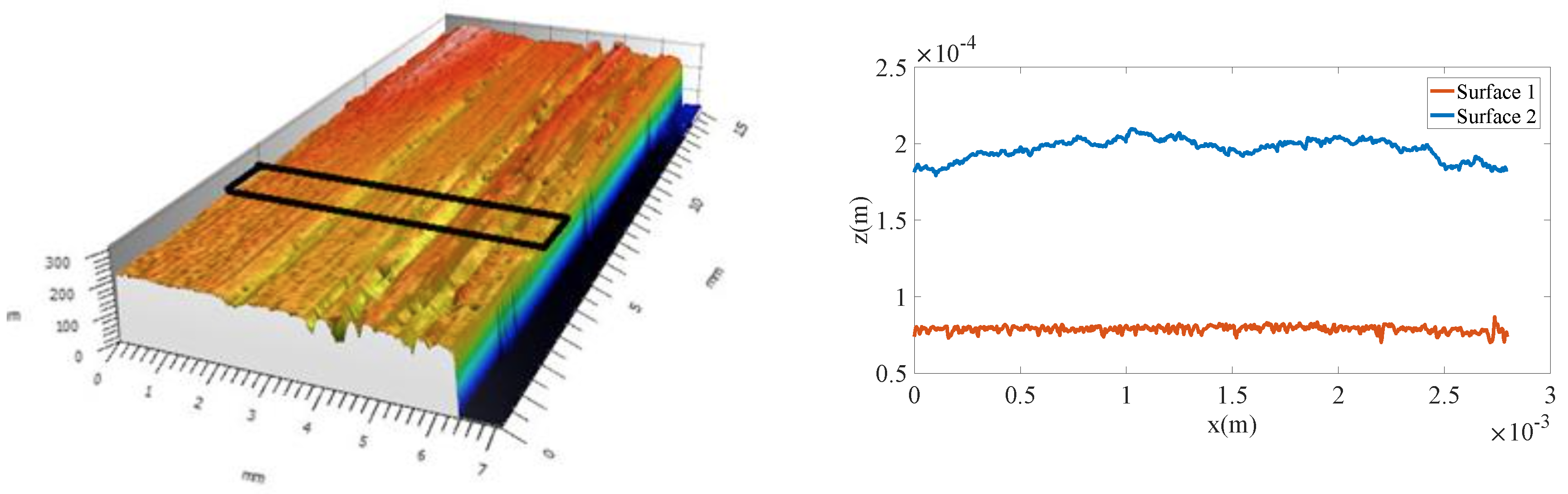
| Surface | m) | m) | m) |
|---|---|---|---|
| Surface 1 | 103 | ||
| Surface 2 | 13 |
| Parameters of Simulation | |||
|---|---|---|---|
| 2.2 × 10 | 600 N | ||
| n | 0.5 W/(m K) | ||
| 0.024 W/(mK) | 4000 K m/W | ||
| 10 K m/W | 2500 K m/W | ||
| 2000 K m/W | 0.1 m/s | ||
| m | 6 | 25 C | |
| 25 C | 720 W | ||
| 60 W/(m K) | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leon, A.; Perez, M.; Barasinski, A.; Abisset-Chavanne, E.; Defoort, B.; Chinesta, F. Multi-Scale Modeling and Simulation of Thermoplastic Automated Tape Placement: Effects of Metallic Particles Reinforcement on Part Consolidation. Nanomaterials 2019, 9, 695. https://doi.org/10.3390/nano9050695
Leon A, Perez M, Barasinski A, Abisset-Chavanne E, Defoort B, Chinesta F. Multi-Scale Modeling and Simulation of Thermoplastic Automated Tape Placement: Effects of Metallic Particles Reinforcement on Part Consolidation. Nanomaterials. 2019; 9(5):695. https://doi.org/10.3390/nano9050695
Chicago/Turabian StyleLeon, Angel, Marta Perez, Anaïs Barasinski, Emmanuelle Abisset-Chavanne, Brigitte Defoort, and Francisco Chinesta. 2019. "Multi-Scale Modeling and Simulation of Thermoplastic Automated Tape Placement: Effects of Metallic Particles Reinforcement on Part Consolidation" Nanomaterials 9, no. 5: 695. https://doi.org/10.3390/nano9050695
APA StyleLeon, A., Perez, M., Barasinski, A., Abisset-Chavanne, E., Defoort, B., & Chinesta, F. (2019). Multi-Scale Modeling and Simulation of Thermoplastic Automated Tape Placement: Effects of Metallic Particles Reinforcement on Part Consolidation. Nanomaterials, 9(5), 695. https://doi.org/10.3390/nano9050695





