Thermoelectric Properties of Hexagonal M2C3 (M = As, Sb, and Bi) Monolayers from First-Principles Calculations
Abstract
1. Introduction
2. Methods
3. Results and Analysis
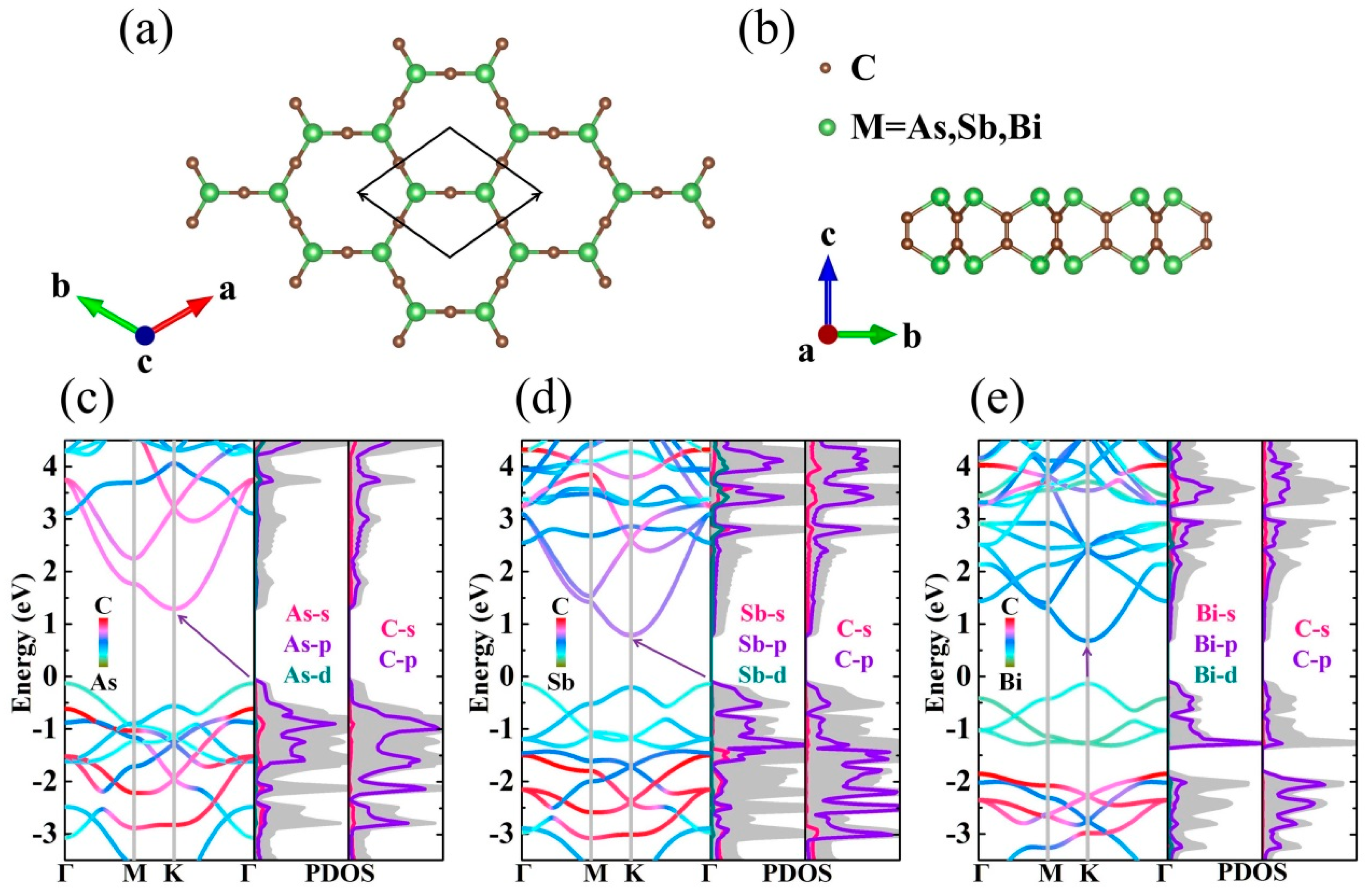
3.1. Atomic and Electronic Structures
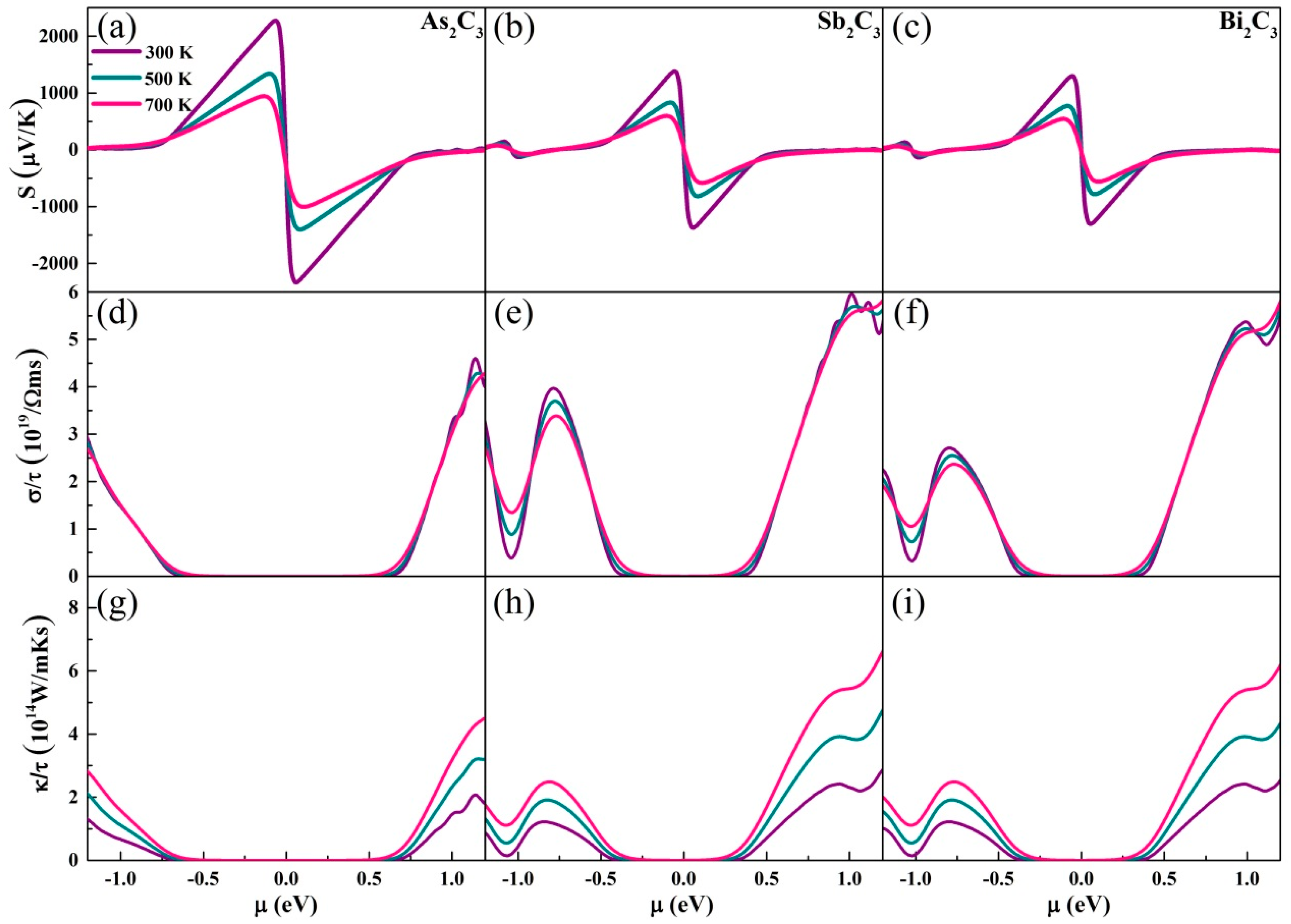
3.2. Electrical Transport Properties
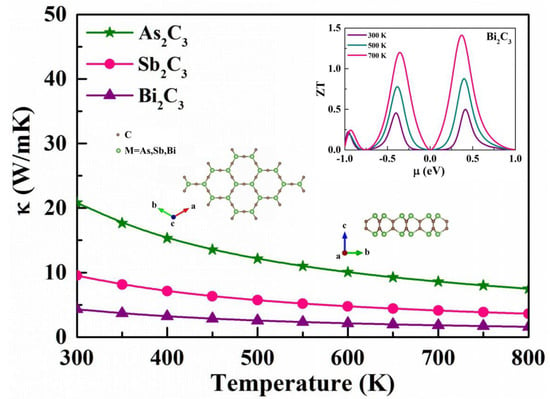
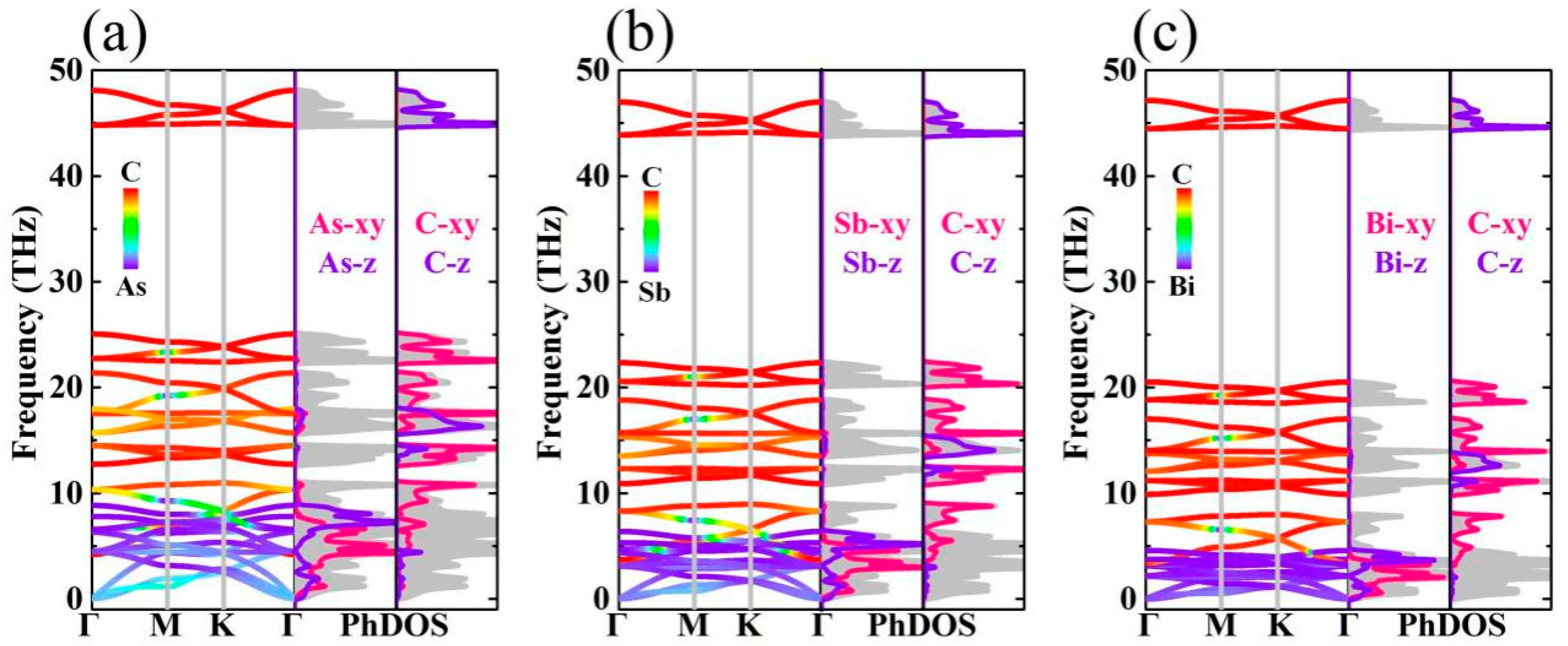
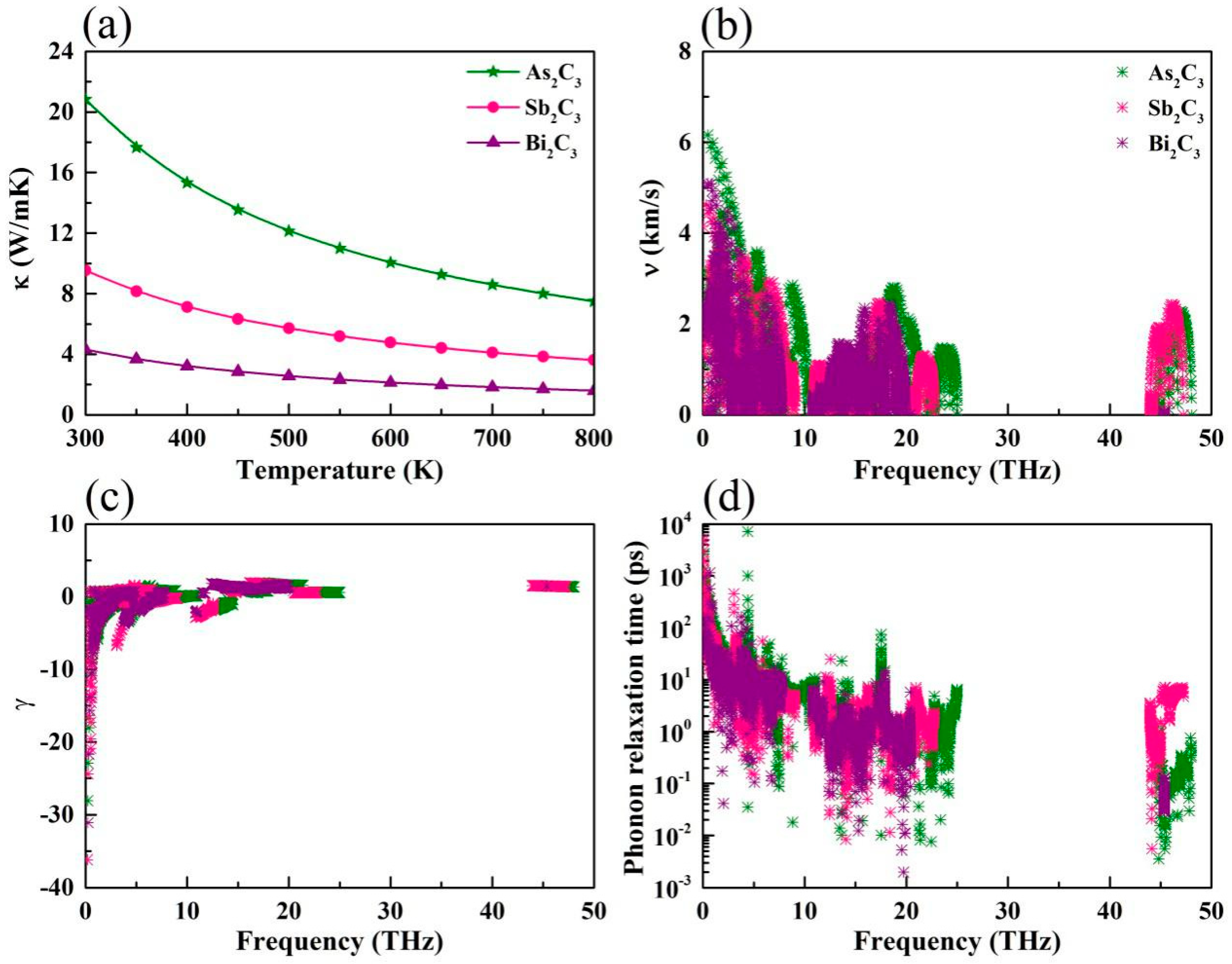
3.3. Phonon Transport Properties
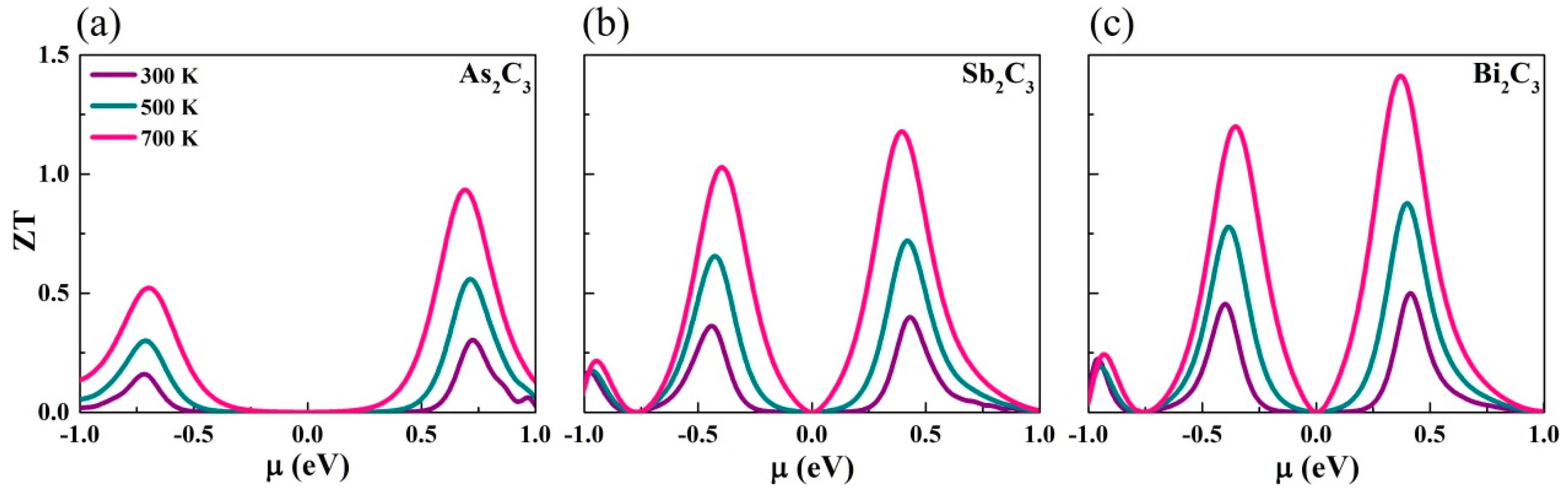
3.4. Thermoelectric Figure of Merit
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chu, S.; Cui, Y.; Liu, N. The path towards sustainable energy. Nat. Mater. 2017, 16, 16–22. [Google Scholar] [CrossRef]
- Aneke, M.; Wang, M. Energy storage technologies and real life applications—A state of the art review. Appl. Energy 2016, 179, 350–377. [Google Scholar] [CrossRef]
- Wang, J.; Xie, F.; Cao, X.H.; An, S.C.; Zhou, W.X.; Tang, L.M.; Chen, K.Q. Excellent Thermoelectric Properties in monolayer WSe2 Nanoribbons due to Ultralow Phonon Thermal Conductivity. Sci. Rep. 2017, 7, 41418. [Google Scholar] [CrossRef]
- Ouyang, Y.; Zhang, Z.; Li, D.; Chen, J.; Zhang, G. Emerging Theory, Materials, and Screening Methods: New Opportunities for Promoting Thermoelectric Performance. Ann. Phys. 2019. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, L.D. Thermoelectric materials: Energy conversion between heat and electricity. J. Materiomics 2015, 1, 92–105. [Google Scholar] [CrossRef]
- Zhao, L.D.; Dravid, V.P.; Kanatzidis, M.G. The panoscopic approach to high performance thermoelectrics. Energy Environ. Sci. 2014, 7, 251–268. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states. Science 2008, 321, 554–557. [Google Scholar] [CrossRef]
- Pei, Y.; Wang, H.; Snyder, G.J. Band engineering of thermoelectric materials. Adv. Mater. 2012, 24, 6125. [Google Scholar] [CrossRef]
- Kim, W. Strategies for engineering phonon transport in thermoelectrics. J. Mater. Chem. C 2015, 3, 10336–10348. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-like two-dimensional materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.B.; Qu, Q.; Zhu, P.; Lam, C.H. Robust intrinsic ferromagnetism and half semiconductivity in stable two-dimensional single-layer chromium trihalides. J. Mater. Chem. C 2015, 3, 12457–12468. [Google Scholar] [CrossRef]
- Xie, G.F.; Ju, Z.F.; Zhou, K.K.; Wei, X.L.; Guo, Z.X.; Cai, Y.Q.; Zhang, G. Ultra-low thermal conductivity of two-dimensional phononic crystals in the incoherent regime. npj Comput. Mater. 2018, 4, 21. [Google Scholar] [CrossRef]
- Chen, X.K.; Xie, Z.X.; Zhou, W.X.; Tang, L.M.; Chen, K.Q. Thermal rectification and negative differential thermal resistance behaviors in graphene/hexagonal boron nitride heterojunction. Carbon 2016, 100, 492–500. [Google Scholar] [CrossRef]
- Tang, L.P.; Tang, L.M.; Geng, H.; Yi, Y.P.; Wei, Z.M.; Chen, K.Q.; Deng, H.X. Tuning transport performance in two-dimensional metal-organic framework semiconductors: Role of the metal d band. Appl. Phys. Lett. 2018, 112, 012101. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Yan, Q.; Chen, H.; Zhou, W.; Hng, H.H.; Boey, F.Y.C.; Ma, J. A simple chemical approach for PbTe nanowires with enhanced thermoelectric properties. Chem. Mater. 2008, 20, 6298–6300. [Google Scholar] [CrossRef]
- Min, Y.; Roh, J.W.; Yang, H.; Park, M.; Kim, S.I.; Hwang, S.; Lee, S.M.; Lee, K.H.; Jeong, U. Surfactant-Free Scalable Synthesis of Bi2Te3 and Bi2Se3 Nanoflakes and Enhanced Thermoelectric Properties of Their Nanocomposites. Adv. Mater. 2013, 25, 1425–1429. [Google Scholar] [CrossRef]
- Androulakis, J.; Lee, Y.; Todorov, I.; Chung, D.Y.; Kanatzidis, M. High-temperature thermoelectric properties of n-type PbSe doped with Ga, In, and Pb. Phys. Rev. B 2011, 83, 195209. [Google Scholar] [CrossRef]
- Pal, K.; Anand, S.; Waghmare, U.V. Thermoelectric properties of materials with nontrivial electronic topolog. J. Mater. Chem. C 2015, 3, 12130–12139. [Google Scholar] [CrossRef]
- Zhao, L.D.; Lo, S.H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 2014, 508, 373–377. [Google Scholar] [CrossRef]
- Delaire, O.; Ma, J.; Marty, K.; May, A.F.; McGuire, M.A.; Du, M.H.; Singh, D.J.; Ehlers, G.; Lumsden, M.D.; Sales, B.C. Giant anharmonic phonon scattering in PbTe. Nat. Mater. 2011, 10, 614–619. [Google Scholar] [CrossRef]
- Liu, P.F.; Bo, T.; Liu, Z.; Eriksson, O.; Wang, F.; Zhao, J.; Wang, B.T. Hexagonal M2C3 (M= As, Sb, and Bi) monolayers: New functional materials with desirable band gaps and ultrahigh carrier mobility. J. Mater. Chem. C 2018, 6, 12689–12697. [Google Scholar] [CrossRef]
- Huang, L.F.; Gong, P.L.; Zeng, Z. Correlation between structure, phonon spectra, thermal expansion, and thermomechanics of single-layer MoS2. Phys. Rev. B 2014, 90, 045409. [Google Scholar] [CrossRef]
- Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.H.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotechnol. 2014, 9, 372–377. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef]
- Kara, A.; Enriquez, H.; Seitsonen, A.P.; Voon, L.L.Y.; Vizzini, S.; Aufray, B.; Oughaddou, H. A review on silicene—New candidate for electronics. Surf. Sci. Rep. 2012, 67, 1–18. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Madsen, G.K.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Xu, L.; Zheng, Y.; Zheng, J.C. Thermoelectric transport properties of PbTe under pressure. Phys. Rev. B 2010, 82, 195102. [Google Scholar] [CrossRef]
- Zhu, X.L.; Liu, P.F.; Gao, H.; Xie, G.F.; Wang, B.T. Thermoelectric properties of hexagonal WN6 from first-principles calculation. ES Energy Environ. 2018, 3, 80–87. [Google Scholar] [CrossRef][Green Version]
- Li, W.; Carrete, J.; Katcho, N.A.; Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Li, W.; Lindsay, L.; Broido, D.A.; Stewart, D.A.; Mingo, N. Thermal conductivity of bulk and nanowire Mg2SixSn1−x alloys from first principles. Phys. Rev. B 2012, 86, 174307. [Google Scholar] [CrossRef]
- Pumera, M.; Sofer, Z. 2D monoelemental arsenene, antimonene, and bismuthene: Beyond black phosphorus. Adv. Mater. 2017, 29, 1605299. [Google Scholar] [CrossRef]
- Peng, H.; Kioussis, N.; Snyder, G.J. Elemental tellurium as a chiral p-type thermoelectric material. Phys. Rev. B 2014, 89, 195206. [Google Scholar] [CrossRef]
- Ding, G.; Wang, C.; Gao, G.; Yao, K.; Dun, C.; Feng, C.; Li, D.; Zhang, G. Engineering of charge carriers via a two-dimensional heterostructure to enhance the thermoelectric figure of merit. Nanoscale 2018, 10, 7077–7084. [Google Scholar] [CrossRef]
- May, A.F.; Toberer, E.S.; Saramat, A.; Snyder, G.J. Characterization and Analysis of Thermoelectric Transport in n-type Ba8Ga16−xGe30+x. Phys. Rev. B 2009, 80, 125205. [Google Scholar] [CrossRef]
- Singh, D.J. Electronic and thermoelectric properties of CuCoO2: Density functional calculations. Phys. Rev. B 2007, 76, 085110. [Google Scholar] [CrossRef]
- Parker, D.; Singh, D.J. Potential thermoelectric performance from optimization of hole-doped Bi2Se3. Phys. Rev. X 2011, 1, 021005. [Google Scholar]
- Yu, J.; Sun, Q. Bi2O2Se nanosheet: An excellent high-temperature n-type thermoelectric material. Appl. Phys. Lett. 2018, 112, 053901. [Google Scholar] [CrossRef]
- Heremans, J.P.; Dresselhaus, M.S. 27 Low-Dimensional Thermoelectricity. Acta Phys. Pol. A 2005, 108, 609–634. [Google Scholar] [CrossRef]
- Jonson, M.; Mahan, G.D. Mott’s formula for the thermopower and the Wiedemann-Franz law. Phys. Rev. B 1980, 21, 4223. [Google Scholar] [CrossRef]
- Nika, D.L.; Pokatilov, E.P.; Askerov, A.S.; Balandin, A.A. Phonon thermal conduction in graphene: Role of Umklapp and edge roughness scattering. Phys. Rev. B 2009, 79, 155413. [Google Scholar] [CrossRef]
- Liu, P.F.; Bo, T.; Xu, J.; Yin, W.; Zhang, J.; Wang, F.; Erillsson, O.; Wang, B.T. First-principles calculations of the ultralow thermal conductivity in two-dimensional group-IV selenides. Phys. Rev. B 2018, 98, 235426. [Google Scholar] [CrossRef]
- Xie, G.F.; Ding, D.; Zhang, G. Phonon coherence and its effect on thermal conductivity of nanostructures. Adv. Phys. X. 2018, 3, 1480417. [Google Scholar] [CrossRef]
- Qin, G.; Qin, Z.; Fang, W.Z.; Zhang, L.C.; Yue, S.Y.; Yan, Q.B.; Hu, M.; Su, G. Diverse anisotropy of phonon transport in two-dimensional group IV–VI compounds: A comparative study. Nanoscale 2016, 8, 11306–11319. [Google Scholar] [CrossRef]
- Bardeen, J.; Shockley, W. Deformation potentials and mobilities in non-polar crystals. Phys. Rev. 1950, 80, 72–80. [Google Scholar] [CrossRef]
- Harman, T.C.; Taylor, P.J.; Walsh, M.P.; LaForge, B.E. Quantum dot superlattice thermoelectric materials and devices. Science 2002, 297, 2229–2232. [Google Scholar] [CrossRef]
| Type | la (Å) | lC-C (Å) | lM-C (Å) | PBE (eV) | HES06 (eV) |
|---|---|---|---|---|---|
| As2C3 | 5.86 | 1.33 | 2.00 | 1.42 | 2.27 |
| Sb2C3 | 6.39 | 1.33 | 2.20 | 0.92 | 1.53 |
| Bi2C3 | 6.70 | 1.33 | 2.31 | 0.81 | 1.28 |
| Type | ||||
|---|---|---|---|---|
| As2C3 | 20.82 | 2.59 | 2.61 | 4.18 |
| Sb2C3 | 9.53 | 2.15 | 4.25 | 3.08 |
| Bi2C3 | 4.31 | 2.07 | 4.46 | 2.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.-L.; Liu, P.-F.; Xie, G.; Zhou, W.-X.; Wang, B.-T.; Zhang, G. Thermoelectric Properties of Hexagonal M2C3 (M = As, Sb, and Bi) Monolayers from First-Principles Calculations. Nanomaterials 2019, 9, 597. https://doi.org/10.3390/nano9040597
Zhu X-L, Liu P-F, Xie G, Zhou W-X, Wang B-T, Zhang G. Thermoelectric Properties of Hexagonal M2C3 (M = As, Sb, and Bi) Monolayers from First-Principles Calculations. Nanomaterials. 2019; 9(4):597. https://doi.org/10.3390/nano9040597
Chicago/Turabian StyleZhu, Xue-Liang, Peng-Fei Liu, Guofeng Xie, Wu-Xing Zhou, Bao-Tian Wang, and Gang Zhang. 2019. "Thermoelectric Properties of Hexagonal M2C3 (M = As, Sb, and Bi) Monolayers from First-Principles Calculations" Nanomaterials 9, no. 4: 597. https://doi.org/10.3390/nano9040597
APA StyleZhu, X.-L., Liu, P.-F., Xie, G., Zhou, W.-X., Wang, B.-T., & Zhang, G. (2019). Thermoelectric Properties of Hexagonal M2C3 (M = As, Sb, and Bi) Monolayers from First-Principles Calculations. Nanomaterials, 9(4), 597. https://doi.org/10.3390/nano9040597