Measuring Device and Material ZT in a Thin-Film Si-Based Thermoelectric Microgenerator
Abstract
1. Introduction
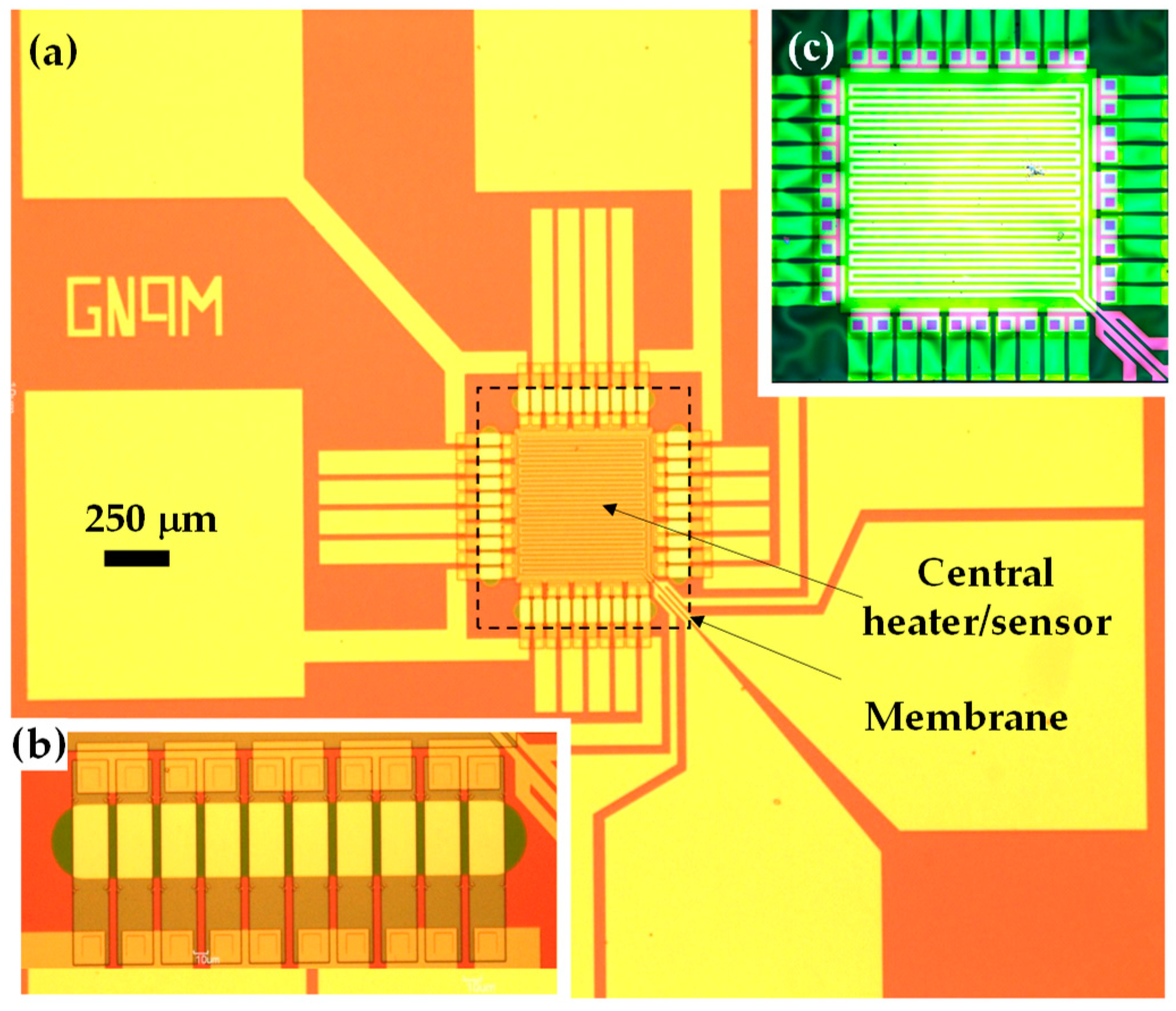
2. Experimental Methods
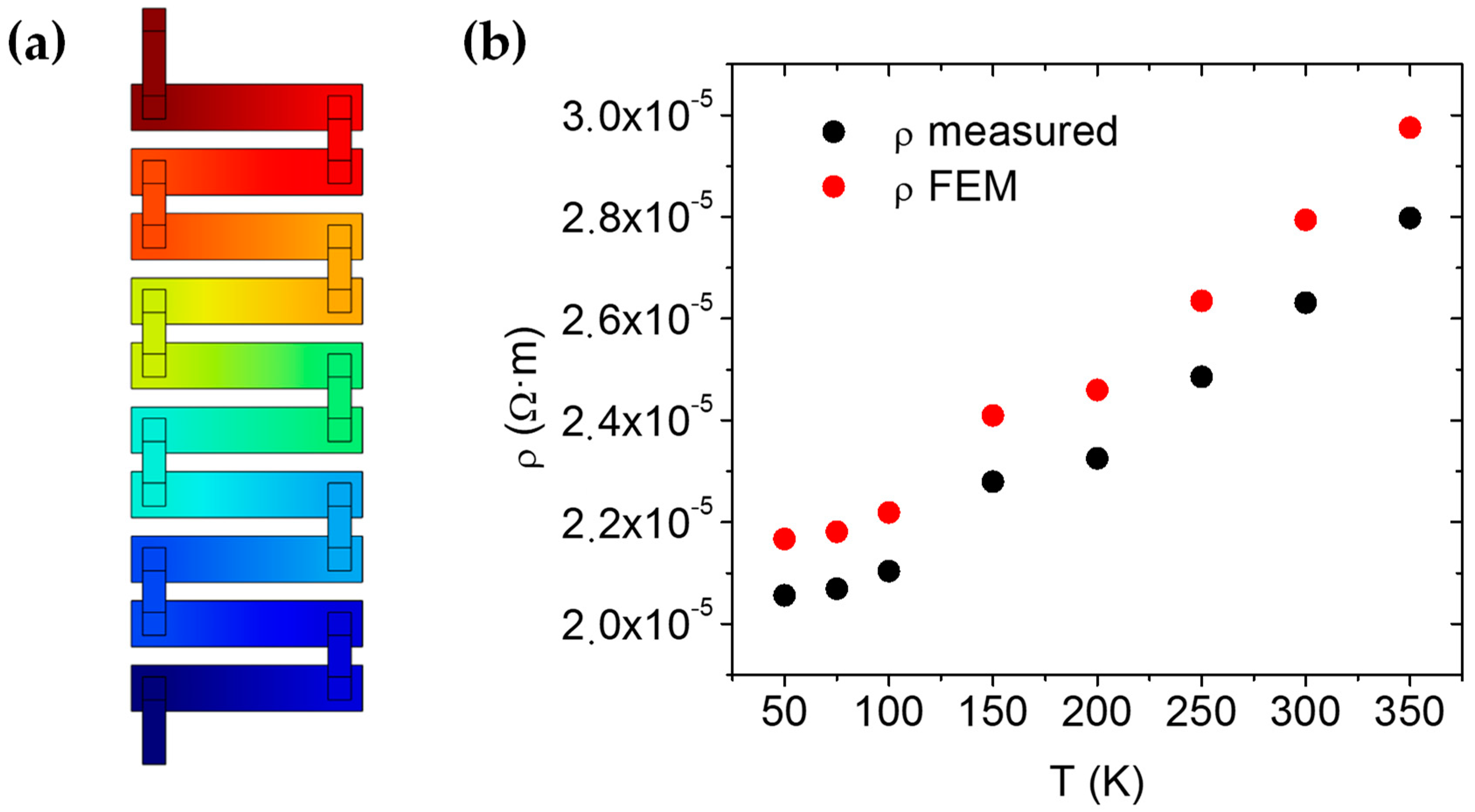
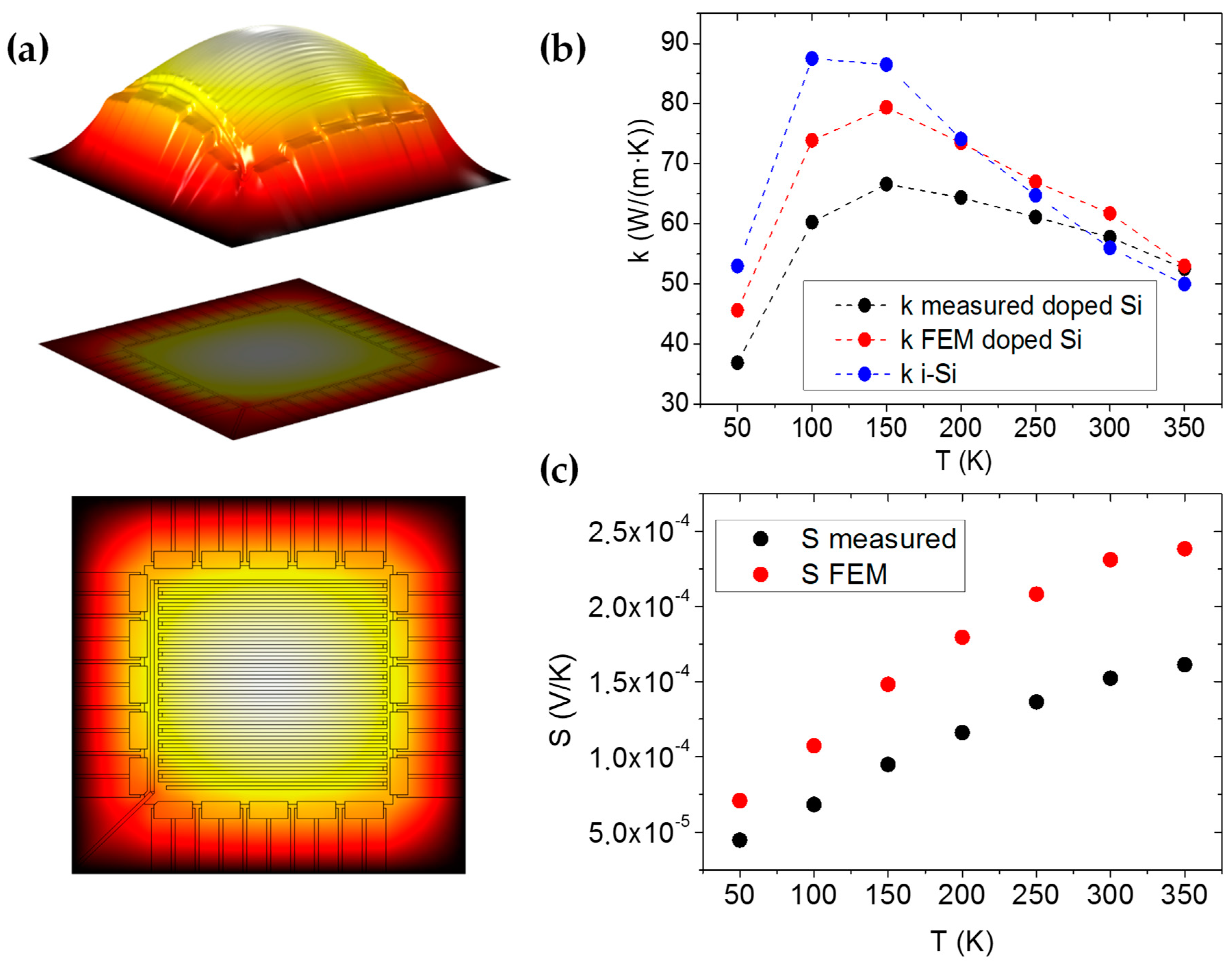
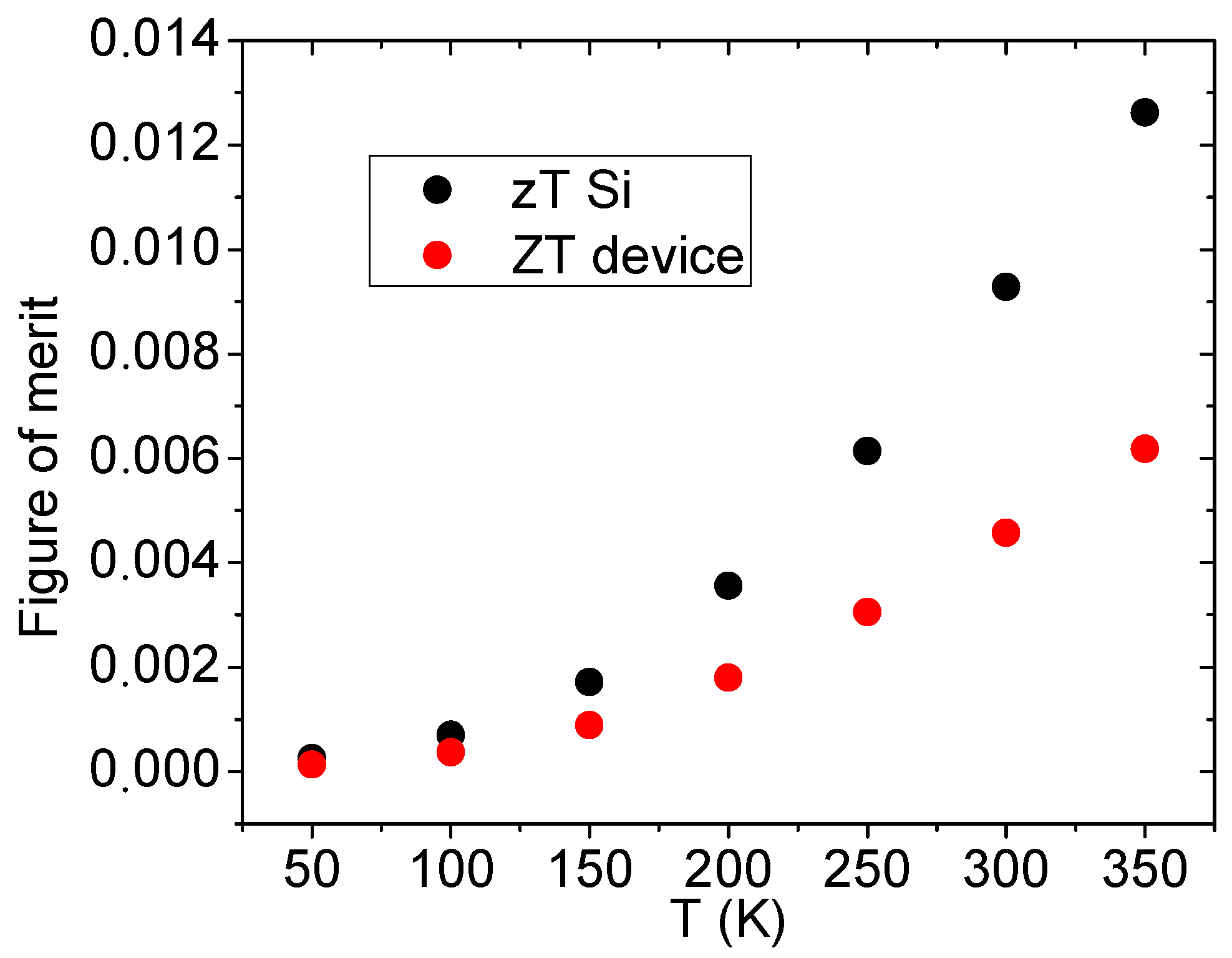
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
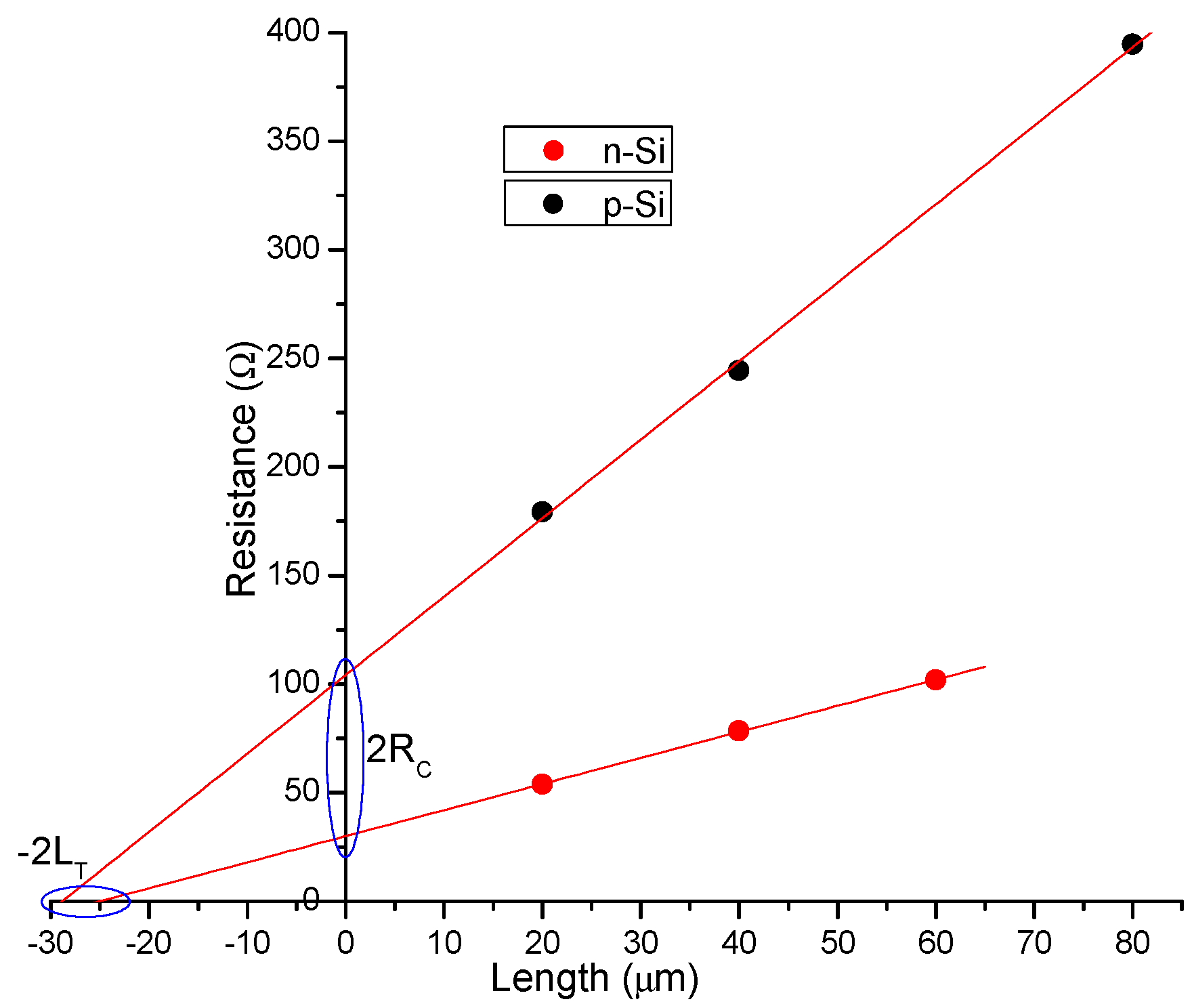
Appendix A. Measurement of the Contact Resistivity
Appendix B. COMSOL Model
References
- Dresselhaus, M.S.; Chen, G.; Tang, M.Y.; Yang, R.G.; Lee, H.; Wang, D.Z.; Ren, Z.F.; Fleurial, J.-P.; Gogna, P. New Directions for Low-Dimensional Thermoelectric Materials. Adv. Mater. 2007, 19, 1043–1053. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Kim, P.; Shi, L.; Yang, P.; Majumdar, A. Thermal conductivity of individual silicon nanowires. Appl. Phys. Lett. 2003, 83, 2934–2936. [Google Scholar] [CrossRef]
- Hicks, L.D.; Dresselhaus, M.S. Thermoelectric figure of merit of a one-dimensional conductor. Phys. Rev. B 1993, 47, 16631–16634. [Google Scholar] [CrossRef]
- Pei, Y.; Wang, H.; Snyder, G.J. Band engineering of thermoelectric materials. Adv. Mater. 2012, 24, 6125–6135. [Google Scholar] [CrossRef] [PubMed]
- Bennett, N.S.; Byrne, D.; Cowley, A. Enhanced Seebeck coefficient in silicon nanowires containing dislocations. Appl. Phys. Lett. 2015, 107, 013903. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Brovman, Y.M.; Kim, P.; Lee, W. Diameter-dependent thermoelectric figure of merit in single-crystalline Bi nanowires. Nanoscale 2015, 7, 5053–5059. [Google Scholar] [CrossRef] [PubMed]
- Markussen, T.; Jauho, A.-P.; Brandbyge, M. Surface-decorated silicon nanowires: a route to high-ZT thermoelectrics. Phys. Rev. Lett. 2009, 103, 55502. [Google Scholar] [CrossRef] [PubMed]
- Snyder, G.J.; Lim, J.R.; Huang, C.-K.; Fleurial, J.-P. Thermoelectric microdevice fabricated by a MEMS-like electrochemical process. Nat. Mater. 2003, 2, 528–531. [Google Scholar] [CrossRef] [PubMed]
- Vizel, R.; Bargig, T.; Beeri, O.; Gelbstein, Y. Bonding of Bi2Te3-Based Thermoelectric Legs to Metallic Contacts Using Bi0.82Sb0.18 Alloy. J. Electron. Mater. 2016, 45, 1296–1300. [Google Scholar] [CrossRef]
- Kim, I.-H. (Bi,Sb)2(Te,Se)3-based thin film thermoelectric generators. Mater. Lett. 2000, 43, 221–224. [Google Scholar] [CrossRef]
- Beeri, O.; Rotem, O.; Hazan, E.; Katz, E.A.; Braun, A.; Gelbstein, Y. Hybrid photovoltaic-thermoelectric system for concentrated solar energy conversion: Experimental realization and modeling. J. Appl. Phys. 2015, 118, 115104. [Google Scholar] [CrossRef]
- Venkatasubramanian, R.; Siivola, E.; Colpitts, T.; O’Quinn, B. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature 2001, 413, 597–602. [Google Scholar] [CrossRef]
- Dávila, D.; Tarancón, A.; Calaza, C.; Salleras, M.; Fernández-Regúlez, M.; San Paulo, A.; Fonseca, L. Monolithically integrated thermoelectric energy harvester based on silicon nanowire arrays for powering micro/nanodevices. Nano Energy 2012, 1, 812–819. [Google Scholar] [CrossRef]
- Strasser, M.; Aigner, R.; Lauterbach, C.; Sturm, T.F.; Franosch, M.; Wachutka, G. Micromachined CMOS thermoelectric generators as on-chip power supply. Sensors Actuators A Phys. 2004, 114, 362–370. [Google Scholar] [CrossRef]
- Wang, Z.; Leonov, V.; Fiorini, P.; Van Hoof, C. Micromachined Polycrystalline Sige-Based Thermopiles for Micropower Generation on Human Body. CMP-TIMA 2007, 284–289. [Google Scholar]
- Curtin, B.M.; Fang, E.W.; Bowers, J.E. Highly Ordered Vertical Silicon Nanowire Array Composite Thin Films for Thermoelectric Devices. J. Electron. Mater. 2012, 41, 887–894. [Google Scholar] [CrossRef]
- Fan, P.; Zheng, Z.; Cai, Z.; Chen, T.; Liu, P.; Cai, X.; Zhang, D.; Liang, G.; Luo, J. The high performance of a thin film thermoelectric generator with heat flow running parallel to film surface. Appl. Phys. Lett. 2013, 102, 033904. [Google Scholar] [CrossRef]
- Perez-Marín, A.P.; Lopeandía, A.F.; Abad, L.; Ferrando-Villaba, P.; Garcia, G.; Lopez, A.M.; Muñoz-Pascual, F.X.; Rodríguez-Viejo, J. Micropower thermoelectric generator from thin Si membranes. Nano Energy 2014, 4, 73–80. [Google Scholar] [CrossRef]
- Rowe, D.M.; Volklein, F. Integrated thin film thermoelectric cooler. Electron. Lett. 1998, 34, 222. [Google Scholar]
- Min, G.; Rowe, D.M.; Kontostavlakis, K. Thermoelectric figure-of-merit under large temperature differences. J. Phys. D. Appl. Phys. 2004, 37, 1301–1304. [Google Scholar] [CrossRef]
- Min, G.; Singh, T.; Garcia-Canadas, J.; Ellor, R. Evaluation of Thermoelectric Generators by I–V Curves. J. Electron. Mater. 2015, 45, 1700–1704. [Google Scholar] [CrossRef]
- Chantrenne, P.; Barrat, J.L.; Blase, X.; Gale, J.D. An analytical model for the thermal conductivity of silicon nanostructures. J. Appl. Phys. 2005, 97, 104318. [Google Scholar] [CrossRef]
- Asheghi, M.; Touzelbaev, M.N.; Goodson, K.E.; Leung, Y.K.; Wong, S.S. Temperature-Dependent Thermal Conductivity of Single-Crystal Silicon Layers in SOI Substrates. J. Heat Transfer 1998, 120, 30–36. [Google Scholar] [CrossRef]
- Ju, Y.S. Phonon heat transport in silicon nanostructures. Appl. Phys. Lett. 2005, 87, 1–3. [Google Scholar] [CrossRef]
- Ju, Y.S.; Goodson, K.E. Phonon scattering in silicon films with thickness of order 100 nm. Appl. Phys. Lett. 1999, 74, 3005. [Google Scholar] [CrossRef]
- Asheghi, M.; Leung, Y.K.; Wong, S.S.; Goodson, K.E. Phonon-boundary scattering in thin silicon layers. Appl. Phys. Lett. 1997, 71, 1798. [Google Scholar] [CrossRef]
- Asheghi, M.; Kurabayashi, K.; Kasnavi, R.; Goodson, K.E. Thermal conduction in doped single-crystal silicon films. J. Appl. Phys. 2002, 91, 5079. [Google Scholar] [CrossRef]
- Liu, W.; Asheghi, M. Thermal conductivity measurements of ultra-thin single crystal silicon layers. J. Heat Transfer 2006, 128, 75–83. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, Z.; Tian, L.; Tan, Z.; Liu, L.; Li, Z. Measurement of thermal conductivity of ultra-thin single crystal silicon film using symmetric structure. Bandaoti Xuebao(Chinese J. Semicond. 2006, 27, 1961–1965. [Google Scholar]
- Bux, S.K.; Blair, R.G.; Gogna, P.K.; Lee, H.; Chen, G.; Dresselhaus, M.S.; Kaner, R.B.; Fleurial, J.-P. Nanostructured Bulk Silicon as an Effective Thermoelectric Material. Adv. Funct. Mater. 2009, 19, 2445–2452. [Google Scholar] [CrossRef]
- Stavitski, N.; van Dal, M.J.H.; Lauwers, A.; Vrancken, C.; Kovalgin, A.Y.; Wolters, R.A.M. Systematic TLM measurements of NiSi and PtSi specific contact resistance to n- and p-type Si in a broad doping range. IEEE Electron Device Lett. 2008, 29, 378–381. [Google Scholar] [CrossRef]
| [22] | [23] | |||
|---|---|---|---|---|
| K | Ω·m | W/(m·K) | W/(m·K) | W/(m·K) |
| 50 | 2.821 × 10−8 | 53 | 31.51 | 0.317 |
| 100 | 3.258 × 10−8 | 87.5 | 54.57 | 0.628 |
| 150 | 3.680 × 10−8 | 86.5 | 72.47 | 0.910 |
| 200 | 4.067 × 10−8 | 74.1 | 87.44 | 1.180 |
| 250 | 4.497 × 10−8 | 64.75 | 98.85 | 1.335 |
| 300 | 4.890 × 10−8 | 56 | 109.08 | 1.410 |
| 350 | 5.282 × 10−8 | 50 | 116.2 | 1.45 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrando-Villalba, P.; Pérez-Marín, A.P.; Abad, L.; Dalkiranis, G.G.; Lopeandia, A.F.; Garcia, G.; Rodriguez-Viejo, J. Measuring Device and Material ZT in a Thin-Film Si-Based Thermoelectric Microgenerator. Nanomaterials 2019, 9, 653. https://doi.org/10.3390/nano9040653
Ferrando-Villalba P, Pérez-Marín AP, Abad L, Dalkiranis GG, Lopeandia AF, Garcia G, Rodriguez-Viejo J. Measuring Device and Material ZT in a Thin-Film Si-Based Thermoelectric Microgenerator. Nanomaterials. 2019; 9(4):653. https://doi.org/10.3390/nano9040653
Chicago/Turabian StyleFerrando-Villalba, Pablo, Antonio Pablo Pérez-Marín, Llibertat Abad, Gustavo Gonçalves Dalkiranis, Aitor F. Lopeandia, Gemma Garcia, and Javier Rodriguez-Viejo. 2019. "Measuring Device and Material ZT in a Thin-Film Si-Based Thermoelectric Microgenerator" Nanomaterials 9, no. 4: 653. https://doi.org/10.3390/nano9040653
APA StyleFerrando-Villalba, P., Pérez-Marín, A. P., Abad, L., Dalkiranis, G. G., Lopeandia, A. F., Garcia, G., & Rodriguez-Viejo, J. (2019). Measuring Device and Material ZT in a Thin-Film Si-Based Thermoelectric Microgenerator. Nanomaterials, 9(4), 653. https://doi.org/10.3390/nano9040653





