On the Formation of Nanocrystalline Grains in Metallic Glasses by Means of In-Situ Nuclear Forward Scattering of Synchrotron Radiation
Abstract
1. Introduction
2. Experimental Details
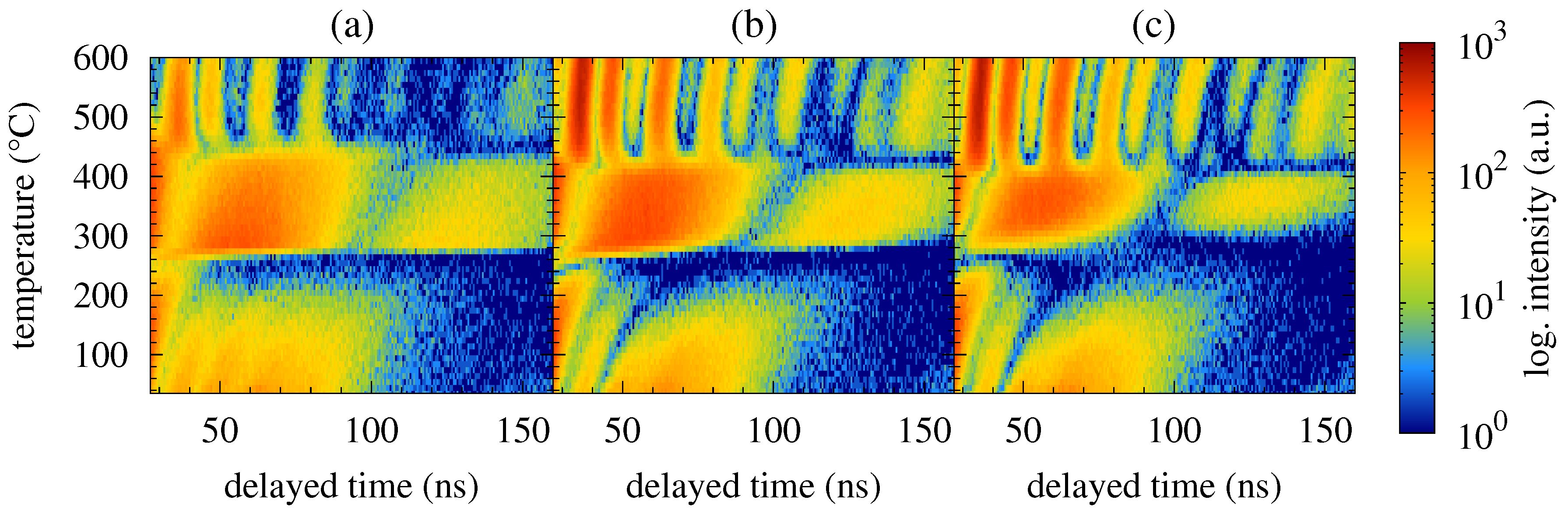
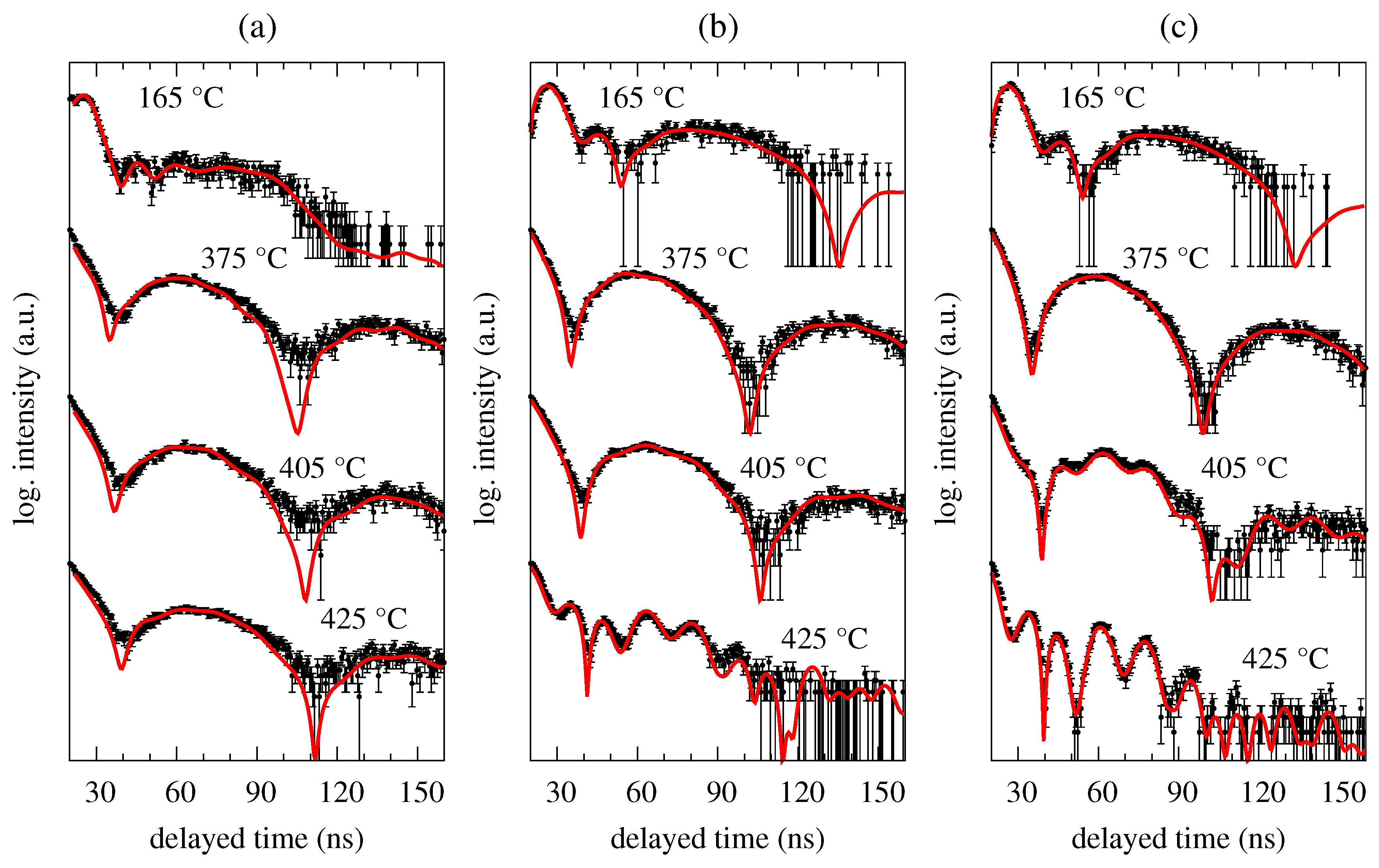
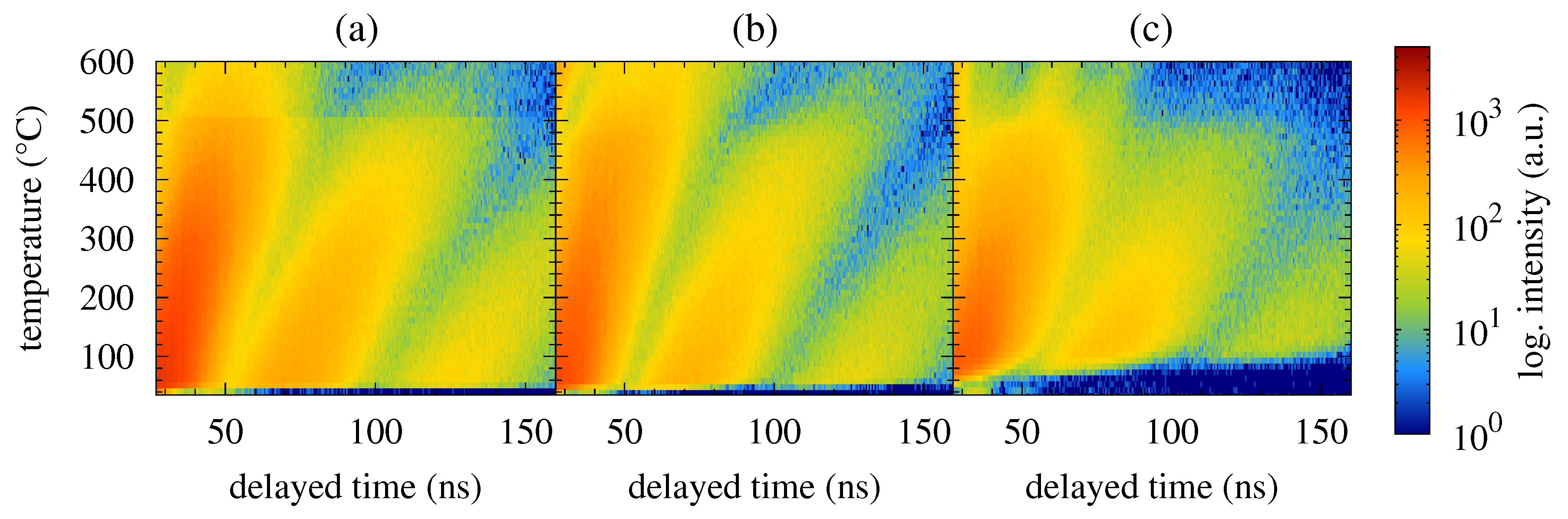
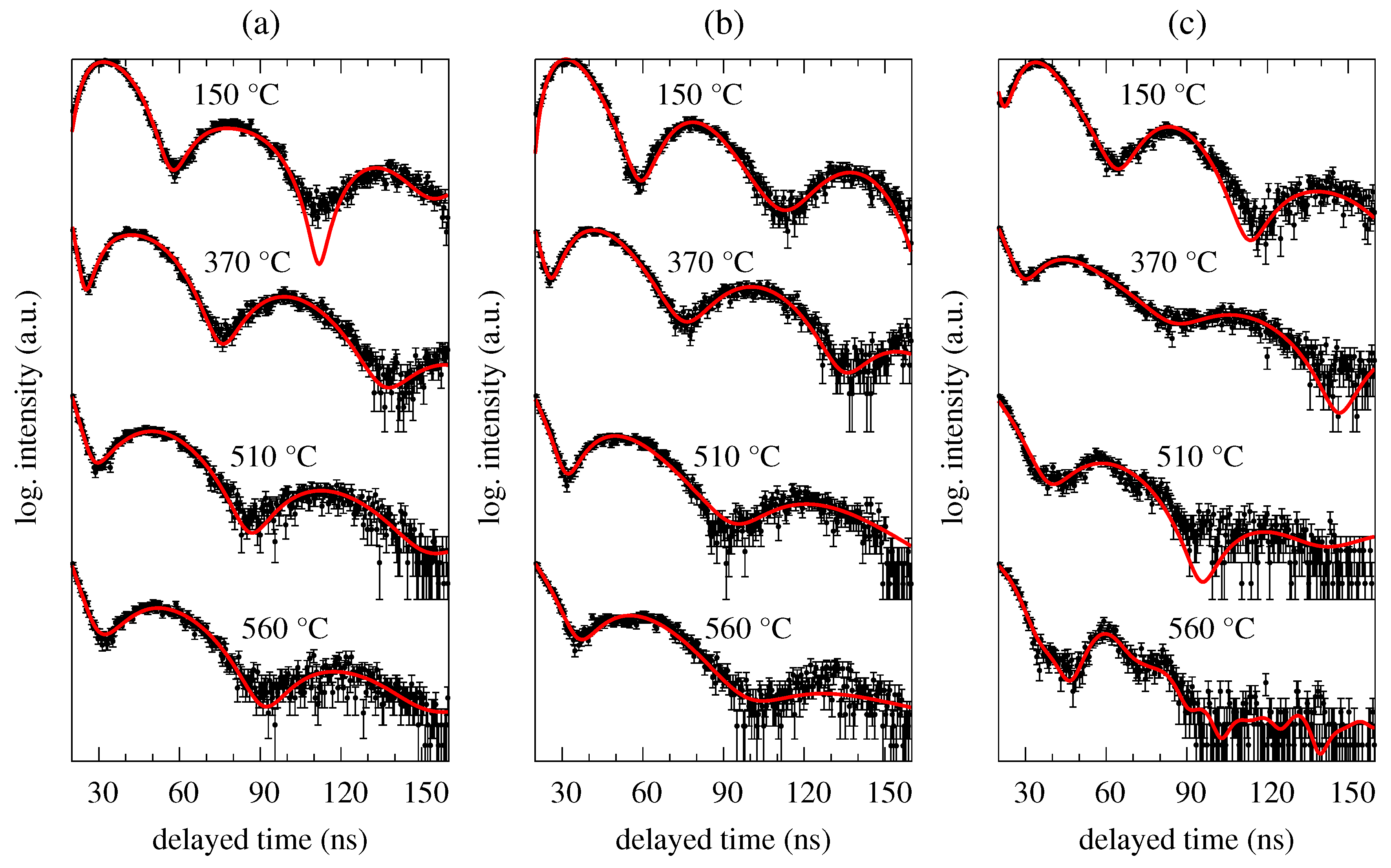
3. Results and Discussion
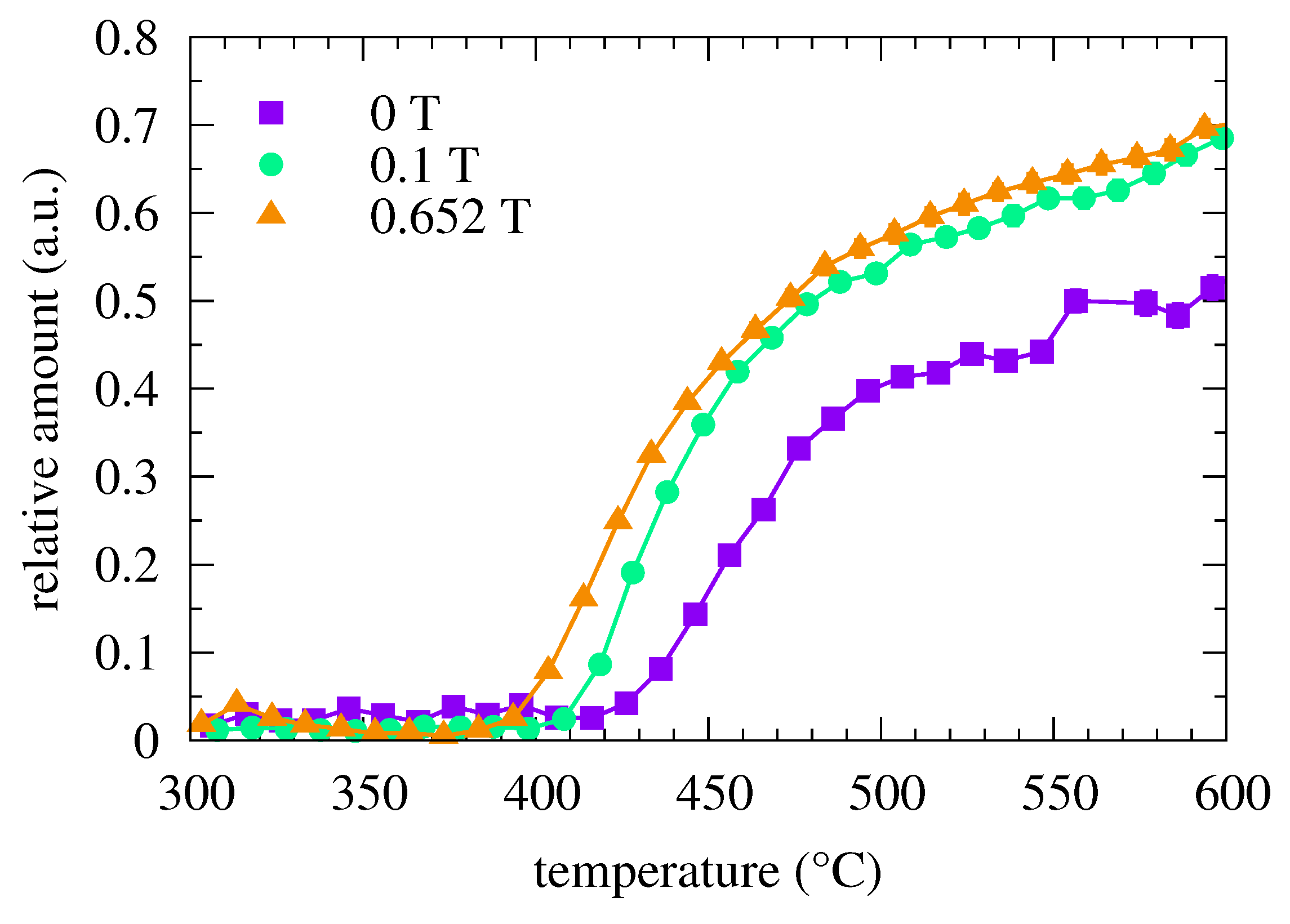
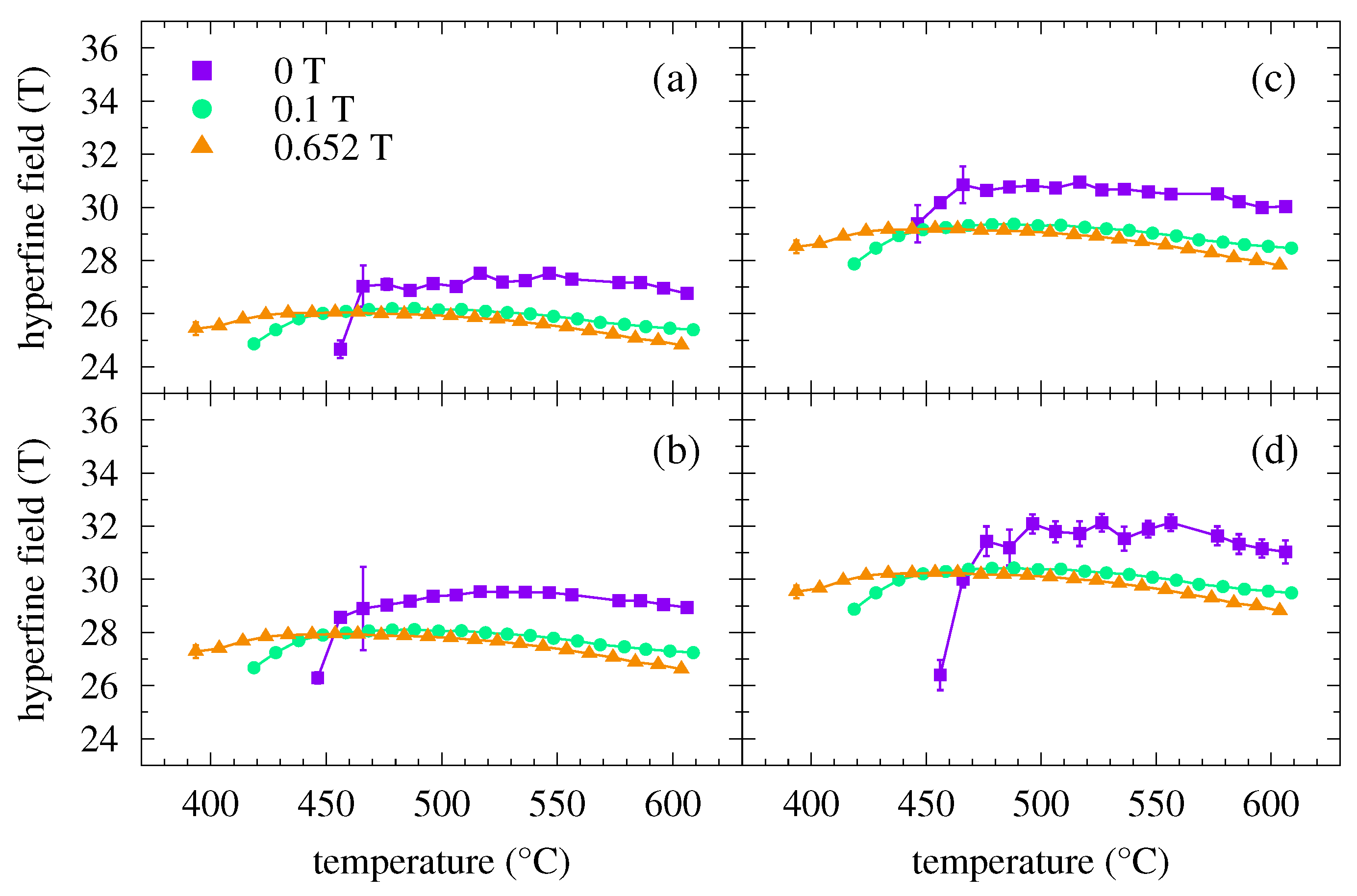
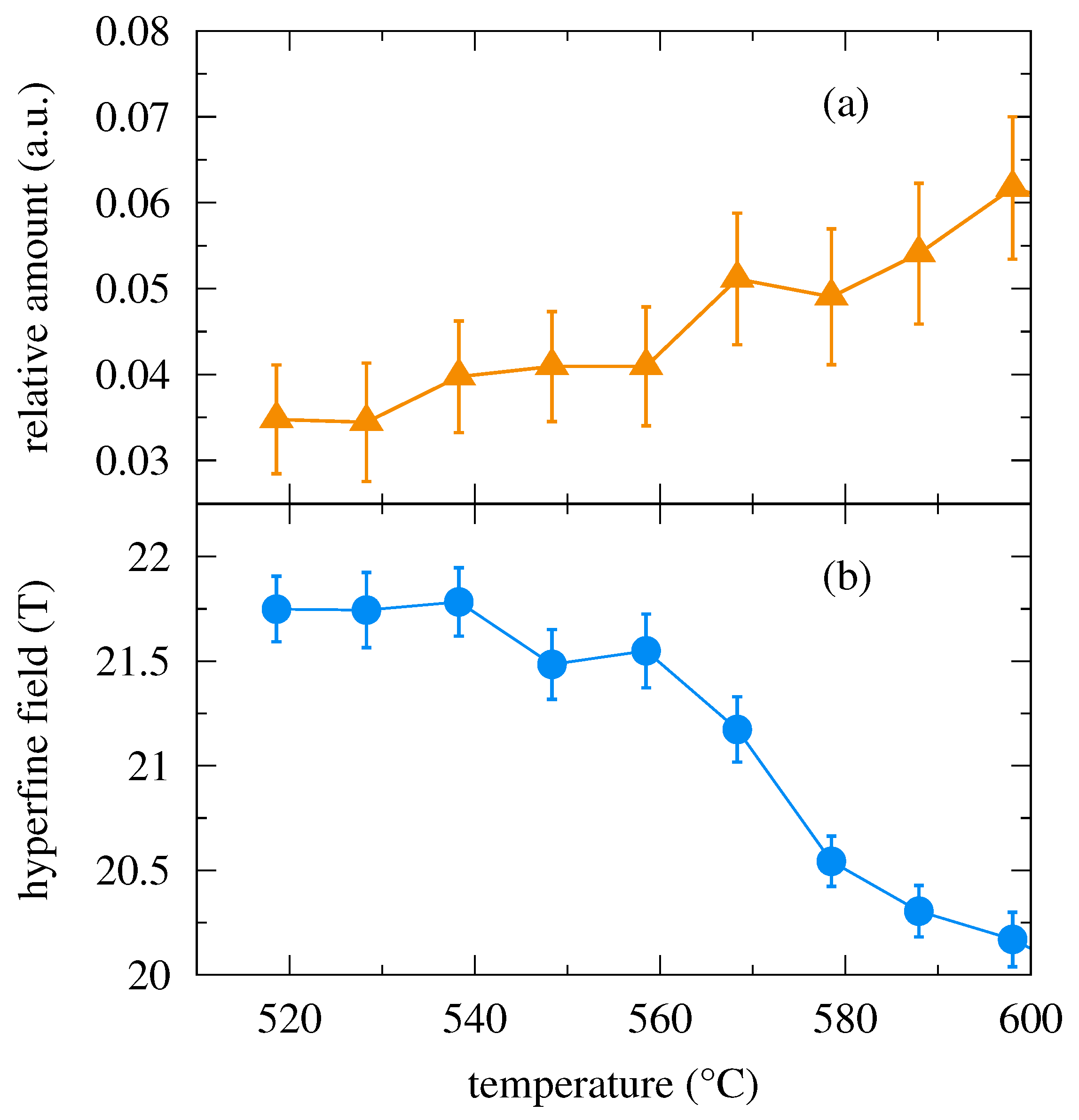
3.1. Ferromagnetic Fe57Co20Mo8Cu1B14 Metallic Glass
3.2. Weak Magnetic Fe75Mo8Cu1B16 Metallic Glass
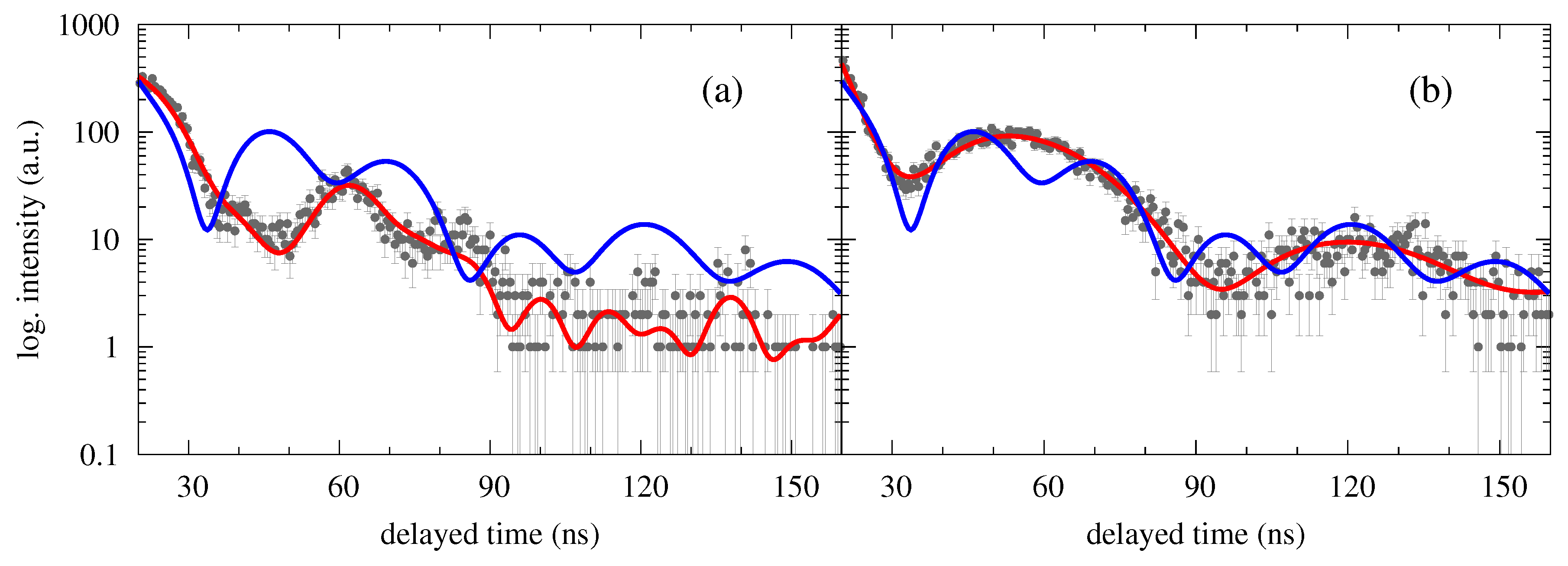
3.3. Simulations of the Impact of Magnetic Field on NFS Time Spectra
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MG | Metallic glass |
| NFS | Nuclear Forward Scattering |
| ESRF | European Synchrotron Radiation Facility |
References
- Chang, Y.H.; Hsu, C.H.; Chu, H.L.; Chang, C.W.; Chan, W.S.; Lee, C.Y.; Yao, C.S.; He, Y.L. Effect of uneven surface on magnetic properties of Fe-based amorphous transformer. World Acad. Sci. Eng. Technol. 2011, 56, 1435–1439. [Google Scholar]
- Herzer, G.; Hilzinger, H. Surface crystallization and magnetic properties in amorphous iron rich alloys. J. Magn. Magn. Mater. 1986, 62, 143–151. [Google Scholar] [CrossRef]
- Wu, C. Development of amorphous ribbon manufacturing technology. China Steel Tech. Rep. 2014, 27, 28–42. [Google Scholar]
- Hasegawa, R. Present status of amorphous soft magnetic alloys. J. Magn. Magn. Mater. 2000, 215, 240–245. [Google Scholar] [CrossRef]
- Zhao, L.Z.; Yu, H.Y.; Li, W.; Liao, X.F.; Zhang, J.S.; Zhong, X.C.; Liu, Z.W.; Su, K.P.; Greneche, J.M. Magnetic characteristics of the ferromagnetic Fe-rich clusters in bulk amorphous Nd60Fe30Al10 alloy. J. Magn. Magn. Mater. 2019, 469, 151–154. [Google Scholar] [CrossRef]
- Parsons, R.; Zang, B.; Onodera, K.; Kishimoto, H.; Kato, A.; Suzuki, K. Soft magnetic properties of rapidly-annealed nanocrystalline Fe-Nb-B-(Cu) alloys. J. Alloy. Compd. 2017, 723, 408–417. [Google Scholar] [CrossRef]
- Salazar, D.; Martín-Cid, A.; Madugundo, R.; Garitaonandia, J.S.; Barandiaran, J.M.; Hadjipanayis, G.C. Effect of Nb and Cu on the crystallization behavior of under-stoichiometric Nd–Fe–B alloys. J. Phys. D Appl. Phys. 2016, 50, 015305. [Google Scholar] [CrossRef]
- Barandiarán, J.M.; Gutiérrez, J.; García-Arribas, A. Magneto-elasticity in amorphous ferromagnets: Basic principles and applications. Phys. Status Solidi (A) 2011, 208, 2258–2264. [Google Scholar] [CrossRef]
- Gutiérrez, J.; Lasheras, A.; Martins, P.; Pereira, N.; Barandiarán, J.M.; Lanceros-Mendez, S. Metallic Glass/PVDF Magnetoelectric Laminates for Resonant Sensors and Actuators: A Review. Sensors 2017, 17, 1251. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ramanujan, R. A study of the crystallization behavior of an amorphous Fe77.5Si13.5B9 alloy. Mater. Sci. Eng. A 2006, 416, 161–168. [Google Scholar] [CrossRef]
- Li, Z.; Dong, Y.; Li, F.; Chang, C.; Wang, X.M.; Li, R.W. Fe78Si9B13 amorphous powder core with improved magnetic properties. J. Mater. Sci.-Mater. Electron. 2017, 28, 1180–1185. [Google Scholar] [CrossRef]
- Li, Z.; Dong, Y.; Pauly, S.; Chang, C.; Wei, R.; Li, F.; Wang, X.M. Enhanced soft magnetic properties of Fe-based amorphous powder cores by longitude magnetic field annealing. J. Alloy. Compd. 2017, 706, 1–6. [Google Scholar] [CrossRef]
- Yardley, V.A.; Tsurekawa, S.; Fujii, H.; Matsuzaki, T. Thermodynamic Study of Magnetic Field-Enhanced Nanocrystallisation in Amorphous Fe-Si-B(-Nb-Cu). Mater. Trans. 2007, 48, 2826–2832. [Google Scholar] [CrossRef]
- Miglierini, M.; Pavlovič, M.; Procházka, V.; Hatala, T.; Schumacher, G.; Rüffer, R. Evolution of structure and local magnetic fields during crystallization of HITPERM glassy alloys studied by in situ diffraction and nuclear forward scattering of synchrotron radiation. Phys. Chem. Chem. Phys. 2015, 17, 28239–28249. [Google Scholar] [CrossRef]
- Miglierini, M.; Procházka, V.; Rüffer, R.; Zbořil, R. In situ crystallization of metallic glasses during magnetic field annealing. Acta Mater. 2015, 91, 50–56. [Google Scholar] [CrossRef]
- Procházka, V.; Vrba, V.; Smrčka, D.; Rüffer, R.; Matúš, P.; Mašláň, M.; Miglierini, M.B. Structural transformation of NANOPERM-type metallic glasses followed in situ by synchrotron radiation during thermal annealing in an external magnetic field. J. Alloys Compd. 2015, 638, 398–404. [Google Scholar] [CrossRef]
- Preston, R.; Heberle, J.; Hanna, S. Mössbauer Effect in Metallic Iron. Phys. Rev. 1962, 128, 2207–2218. [Google Scholar] [CrossRef]
- Miglierini, M.B.; Procházka, V. Nanocrystallization of Metallic Glasses Followed by in situ Nuclear Forward Scattering of Synchrotron Radiation. In X-ray Characterization of Nanomaterials by Synchrotron Radiation; InTech: London, UK, 2017; pp. 7–29. [Google Scholar]
- Röhlsberger, R. Nuclear Condensed Matter Physics with Synchrotron Radiation; Springer: Berlin/Heidelberg, Germany, 2005; Volume 208, p. 318. [Google Scholar]
- Rüffer, R. Nuclear resonance scattering. Comptes Rendus Phys. 2008, 9, 595–607. [Google Scholar] [CrossRef]
- Sturhahn, W.; Gerdau, E. Evaluation of time-differential measurements of nuclear-resonance scattering of x rays. Phys. Rev. B 1994, 49, 9285–9294. [Google Scholar] [CrossRef]
- Sturhahn, W. CONUSS and PHOENIX: Evaluation of nuclear resonant scattering data. Hyperfine Interact. 2000, 125, 149–172. [Google Scholar] [CrossRef]
- Vrba, V.; Procházka, V.; Smrčka, D.; Miglierini, M. Advanced approach to the analysis of a series of in-situ nuclear forward scattering experiments. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2017, 847, 111–116. [Google Scholar] [CrossRef]
- Baron, A.Q.R.; Chumakov, A.I.; Grünsteudel, H.F.; Grünsteudel, H.; Niesen, L.; Rüffer, R. Transverse X-Ray Coherence in Nuclear Scattering of Synchrotron Radiation. Phys. Rev. Lett. 1996, 77, 4808–4811. [Google Scholar] [CrossRef] [PubMed]
- Baron, A.Q.R. Transverse coherence in nuclear resonant scattering of synchrotron radiation. Hyperfine Interact. 1999, 123, 667–680. [Google Scholar] [CrossRef]
- Paluga, M.; Švec, P.; Janičkovič, D.; Muller, D.; Mrafko, P.; Miglierini, M. Nanocrystallization in rapidly quenched Fe-Mo-Cu-B: Surface and volume effects. Rev. Adv. Mater. Sci. 2008, 18, 481–493. [Google Scholar]
- Smrčka, D.; Procházka, V.; Vrba, V.; Miglierini, M. Nuclear forward scattering analysis of crystallization processes in weakly magnetic metallic glasses. J. Alloys Compd. under review.
- Craig, P.; Perisho, R.; Segnan, R.; Steyert, W. Temperature and field dependence of hyperfine fields and magnetization in a dilute random substitutional ferromagnetic alloy: Fe2.65Pd97.35. Phys. Rev. 1965, 138, 1460–1471. [Google Scholar] [CrossRef]
- Delavari, H.; Madaah Hosseini, H.; Simchi, A. A simple model for the size and shape dependent Curie temperature of freestanding Ni and Fe nanoparticles based on the average coordination number and atomic cohesive energy. Chem. Phys. 2011, 383, 1–5. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smrčka, D.; Procházka, V.; Vrba, V.; Miglierini, M.B. On the Formation of Nanocrystalline Grains in Metallic Glasses by Means of In-Situ Nuclear Forward Scattering of Synchrotron Radiation. Nanomaterials 2019, 9, 544. https://doi.org/10.3390/nano9040544
Smrčka D, Procházka V, Vrba V, Miglierini MB. On the Formation of Nanocrystalline Grains in Metallic Glasses by Means of In-Situ Nuclear Forward Scattering of Synchrotron Radiation. Nanomaterials. 2019; 9(4):544. https://doi.org/10.3390/nano9040544
Chicago/Turabian StyleSmrčka, David, Vít Procházka, Vlastimil Vrba, and Marcel B. Miglierini. 2019. "On the Formation of Nanocrystalline Grains in Metallic Glasses by Means of In-Situ Nuclear Forward Scattering of Synchrotron Radiation" Nanomaterials 9, no. 4: 544. https://doi.org/10.3390/nano9040544
APA StyleSmrčka, D., Procházka, V., Vrba, V., & Miglierini, M. B. (2019). On the Formation of Nanocrystalline Grains in Metallic Glasses by Means of In-Situ Nuclear Forward Scattering of Synchrotron Radiation. Nanomaterials, 9(4), 544. https://doi.org/10.3390/nano9040544




