Anomalous Elastic Properties of Attraction-Dominated DNA Self-Assembled 2D Films and the Resultant Dynamic Biodetection Signals of Microbeam Sensors
Abstract
1. Introduction
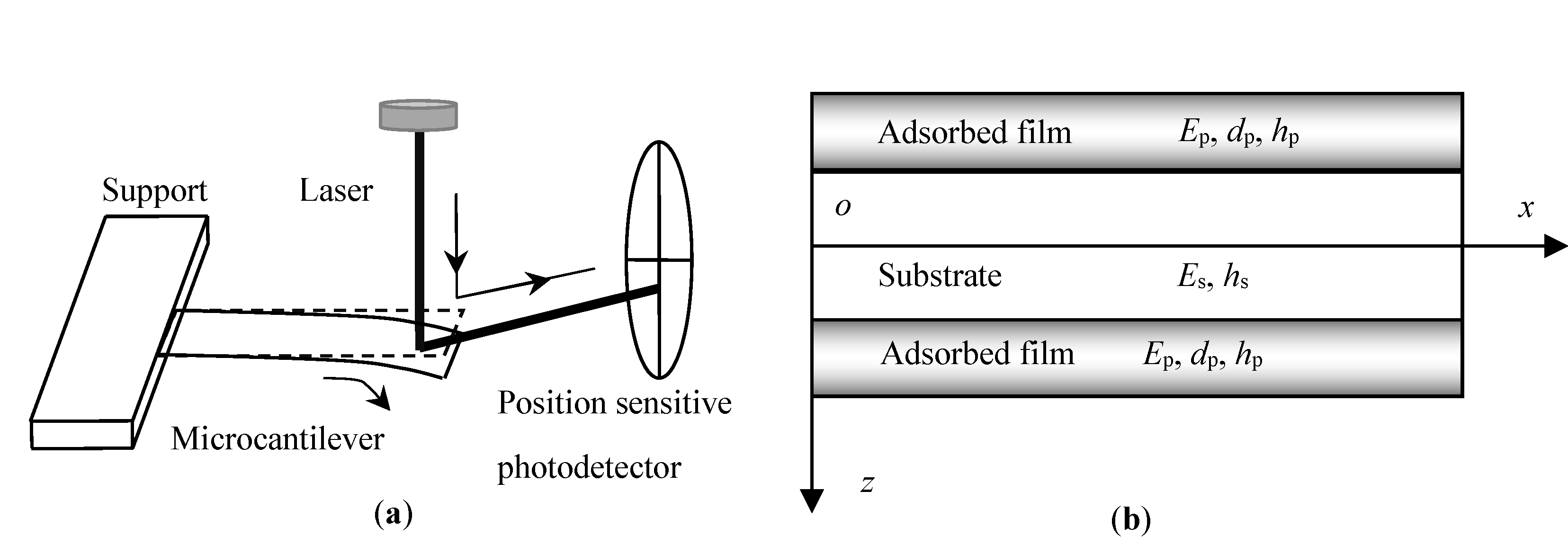
2. Multiscale Analytical Model
2.1. Elastic Properties of Adsorbed DNA Films
2.2. Natural Frequency of DNA-Microbeam System
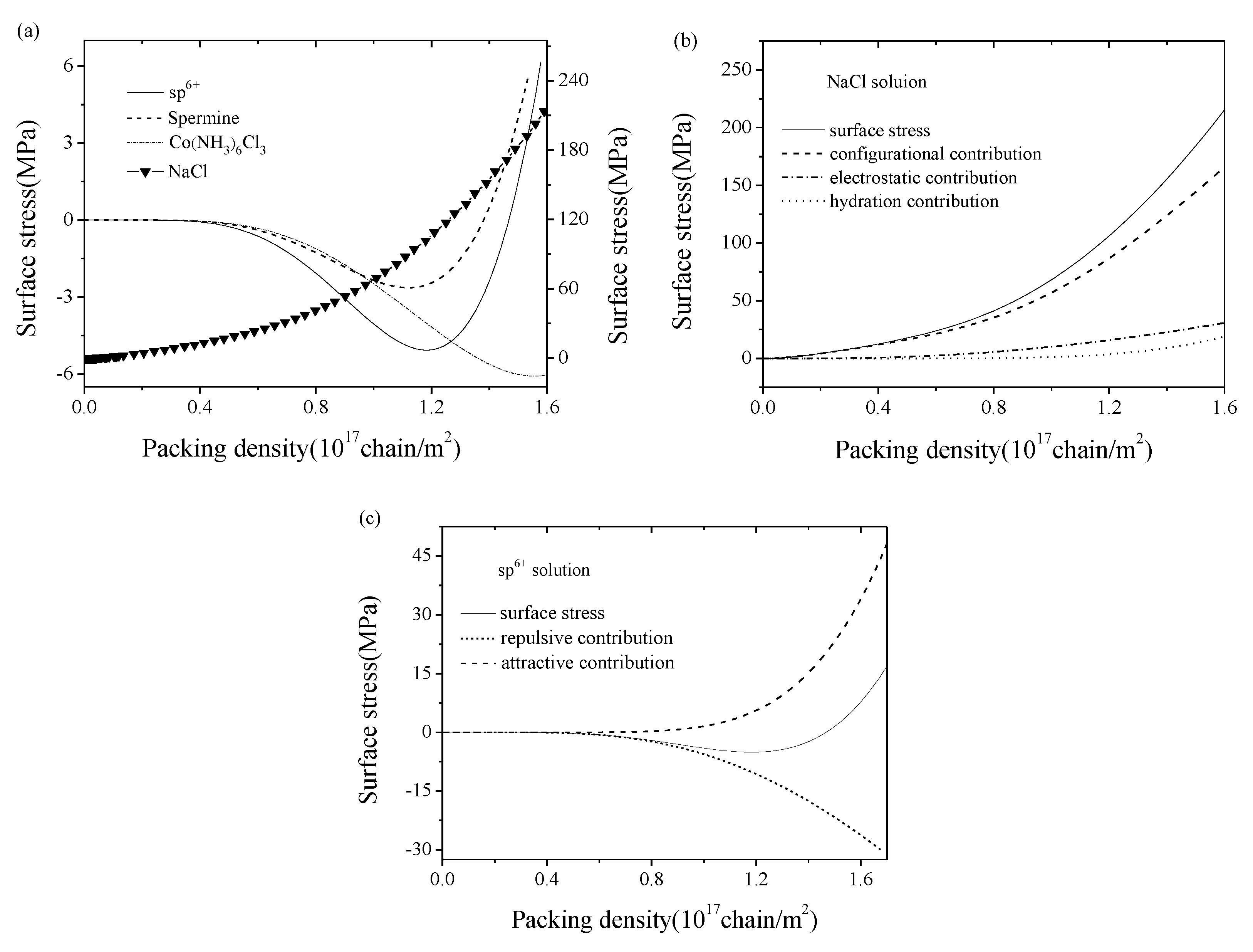
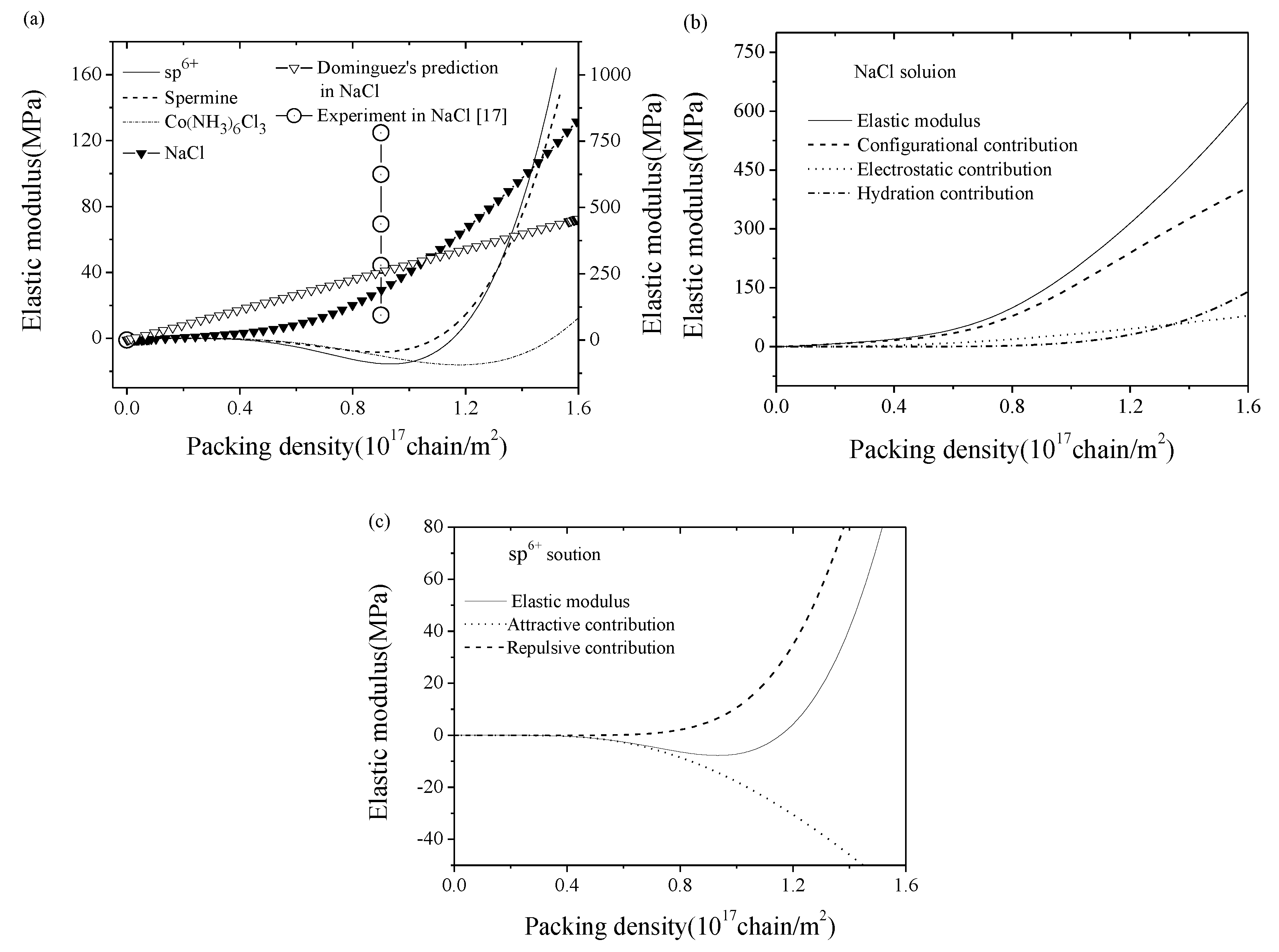
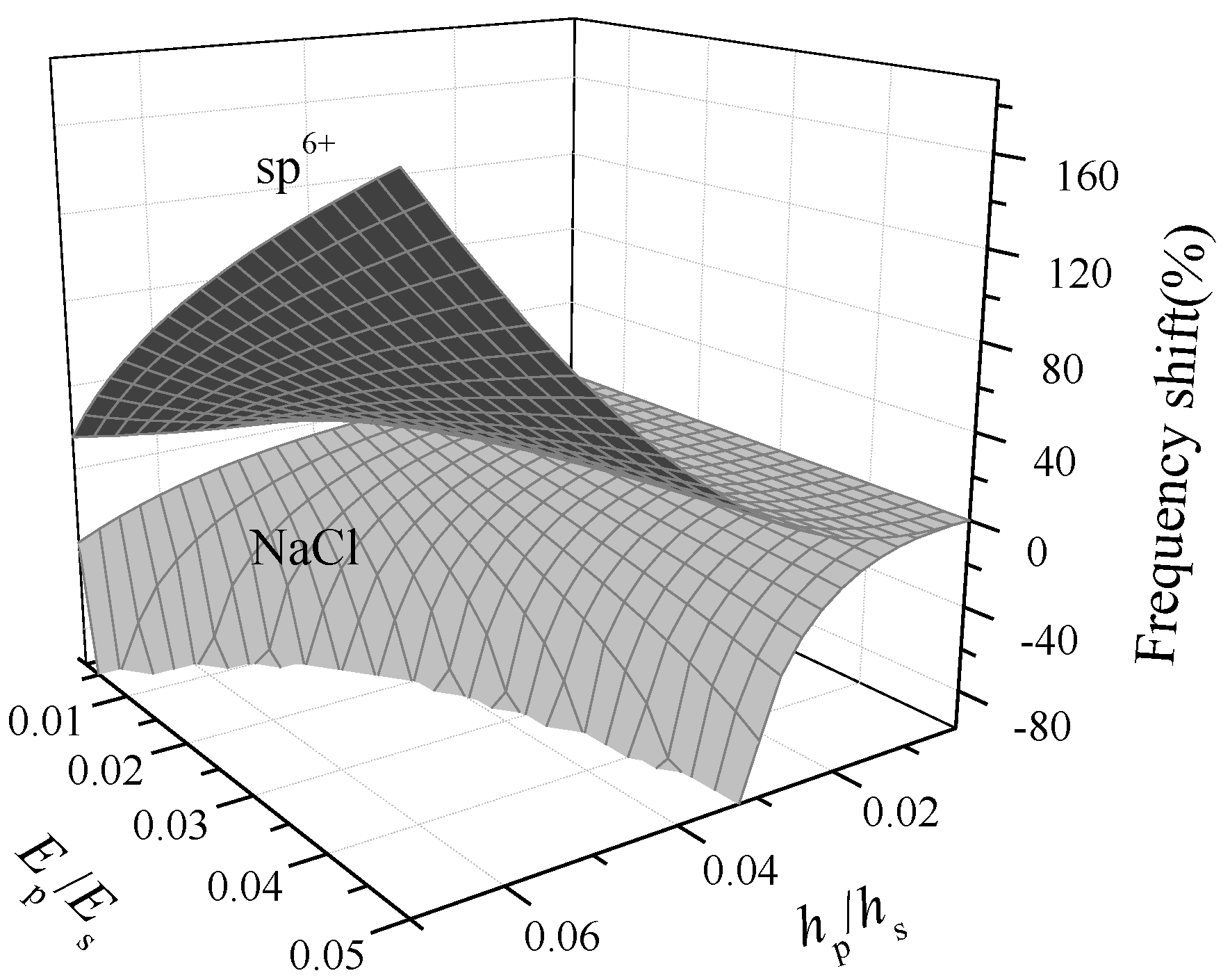
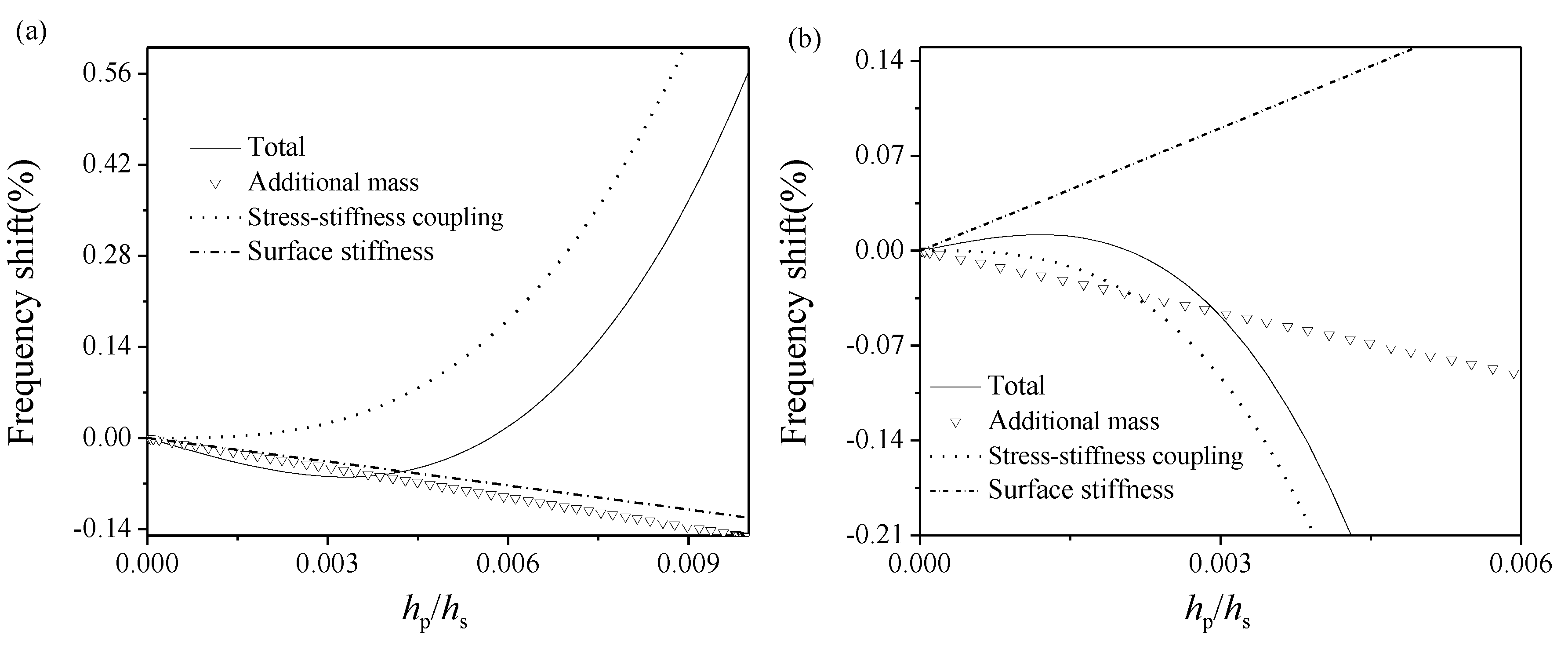
3. Results and Discussion
- (i)
- When the relation between the modulus ratio and the thickness ratio satisfies the following relation, , the microbeam vibrates in a linear phase, in which the frequency shift of a periodic vibration could be taken as an indication of DNA adsorptions;
- (ii)
- When their relation satisfies the following relation, , the microbeam vibrates in a non-periodic way, which means a dynamic instability region (i.e., the anomalous blank area in Figure 4 appears.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bloomfield, V.A. DNA condensation by multivalent cations. Biopolymers 1997, 44, 269–282. [Google Scholar] [CrossRef]
- Cortini, R.; Caré, B.R.; Victor, J.; Barbi, M. Theory and simulations of toroidal and rod-like structures in single-molecule DNA condensation. J. Chem. Phys. 2015, 142, 105102. [Google Scholar] [CrossRef]
- Li, G.Y.; Guan, R.L.; Ji, L.N.; Chao, H. DNA condensation induced by metal complexes. Coord. Chem. Rev. 2014, 281, 100–113. [Google Scholar] [CrossRef]
- Todd, B.A.; Parsegian, V.A.; Shirahata, A.; Thomas, T.J.; Rau, D.C. Attractive forces between cation condensed DNA double helices. Biophys. J. 2008, 94, 4775–4782. [Google Scholar] [CrossRef] [PubMed]
- Mertens, J.; Tamayo, J.; Kosaka, P.; Calleja, M. Observation of spermidine-induced attractive forces in self-assembled monolayers of single stranded DNA using a microcantilever sensor. Appl. Phys. Lett. 2011, 98, 153704. [Google Scholar] [CrossRef]
- Montasser, I.; Coleman, A.W.; Tauran, Y.; Perret, G.; Jalabert, L.; Collard, D.; Kim, B.J.; Tarhan, M.C. Direct measurement of the mechanism by which magnesium specifically modifies the mechanical properties of DNA. Biomicrofluidics 2017, 11, 051102. [Google Scholar] [CrossRef]
- Jeltsch, A.; Maschke, H.; Selent, U.; Wenz, C.; Köhler, E.; Connolly, B.A.; Thorogood, H.; Pingoud, A. DNA binding specificity of the EcoRV restriction endonuclease ss increased by Mg2+ binding to a metal ion binding site distinct from the catalytic center of the Enzyme. Biochemistry 1995, 34, 6239–6246. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.S.; Chou, C.C.; Chang, S.W. Multiscale analysis of adsorption-induced surface stress of alkanethiol on microcantilever. J. Phys. D Appl. Phys. 2013, 46, 035301. [Google Scholar] [CrossRef]
- Mathew, R.; Sankar, A.R. Design of a triangular platform piezoresistive affinity microcantilever sensor for biochemical sensing applications. J. Phys. D Appl. Phys. 2015, 48, 205402. [Google Scholar] [CrossRef]
- Zhang, G.M.; Zhao, L.B.; Jiang, Z.D.; Yang, S.M.; Zhao, Y.L.; Huang, E.; Hebibul, R.; Wang, X.P.; Liu, Z.G. Surface stress-induced deflection of a microcantilever with various widths and overall microcantilever sensitivity enhancement via geometry modification. J. Phys. D Appl. Phys. 2011, 44, 425402. [Google Scholar] [CrossRef]
- Stachowiak, J.C.; Yue, M.; Castelino, K.; Chakraborty, A.; Majumdar, A. Chemomechanics of surface stresses induced by DNA hybridization. Langmuir 2006, 22, 263–268. [Google Scholar] [CrossRef]
- Biswal, S.L.; Raorane, D.; Chaiken, A.; Majumdar, H.B.A. Nanomechanical Detection of DNA Melting on Microcantilever Surfaces. Anal. Chem. 2006, 78, 7104–7109. [Google Scholar] [CrossRef]
- Eom, K.; Kwon, T.Y.; Yoon, D.S.; Lee, H.L.; Kim, T.S. Dynamical response of nanomechanical resonators to biomolecular interactions. Phys. Rev. B 2007, 76, 113408. [Google Scholar] [CrossRef]
- Lee, J.H.; Hwang, K.S.; Yoon, D.S.; Kim, H.; Song, S.H.; Kang, J.Y.; Kim, T.S. Anomalous resonant frequency changes in piezoelectric microcantilevers by monolayer formation of Au films. Appl. Phys. Lett. 2011, 99, 143701. [Google Scholar] [CrossRef]
- Tamayo, J.; Ramos, D.; Mertens, J.; Calleja, M. Effect of the adsorbate stiffness on the resonance response of microcantilever sensors. Appl. Phys. Lett. 2006, 89, 224104. [Google Scholar] [CrossRef]
- Wu, J.Z.; Zhou, M.H.; Zhang, N.H. The effect of microscopic attractive interactions on piezoelectric coefficients of nanoscale DNA films and its resultant mirocantilever-based biosensor signals. J. Phys. D Appl. Phys. 2017, 50, 415403. [Google Scholar] [CrossRef]
- Domínguez, C.M.; Ramos, D.; Mendieta-Moreno, J.I.; Fierro, J.L.G.; Mendieta, J.; Tamayo, J.; Calleja, M. Effect of water-DNA interactions on elastic properties of DNA self-assembled monolayers. Sci. Rep. 2017, 7, 536. [Google Scholar] [CrossRef] [PubMed]
- Shu, W.M.; Laue, E.D.; Seshia, A.A. Investigation of biotin–streptavidin binding interactions using microcantilever sensors. Biosens. Bioelectron. 2007, 22, 2003–2009. [Google Scholar] [CrossRef]
- Shu, W.M.; Laurenson, S.; Knowles, T.P.J.; Ferrigno, P.K.; Seshia, A.A. Highly specific label-free protein detection from lysed cells using internally referenced microcantilever sensors. Biosens. Bioelectron. 2008, 24, 233–237. [Google Scholar] [CrossRef]
- Zhou, M.H.; Meng, M.L.; Zhang, C.Y.; Li, X.B.; Wu, J.Z.; Zhang, N.H. The pH-dependent elastic properties of nanoscale DNA films and the resultant bending signals for microcantilever biosensors. Soft Matter 2018, 14, 3028–3039. [Google Scholar] [CrossRef] [PubMed]
- Zhang, N.H.; Shan, J.Y. An energy model for nanomechanical deflection of cantilever-DNA chip. J. Mech. Phys. Solids 2008, 56, 2328–2337. [Google Scholar] [CrossRef]
- Zhang, N.H.; Meng, W.L.; Tan, Z.Q. A multi-scale model for the analysis of the inhomogeneity of elastic properties of DNA biofilm on microcantilevers. Biomaterials 2013, 34, 1833–1842. [Google Scholar] [CrossRef]
- Hagan, M.F.; Majumdar, A.; Chakraborty, A.K. Nanomechanical Forces Generated by Surface Grafted DNA. J. Phys. Chem. B 2002, 106, 10163–10173. [Google Scholar] [CrossRef]
- Rekesh, D.; Lyubchenko, Y.; Shlyakhtenko, L.S.; Lindsay, S.M. Scanning tunneling microscopy of mercapto-hexyl-oligonucleotides attached to gold. Biophys. J. 1996, 71, 1079–1086. [Google Scholar] [CrossRef]
- Strey, H.H.; Parsegian, V.A.; Podgornik, R. Equation of State for DNA Liquid Crystals: Fluctuation Enhanced Electrostatic Double Layer Repulsion. Phys. Rev. Lett. 1997, 78, 895–898. [Google Scholar] [CrossRef]
- Ambia-Garrido, J.; Vainrub, A.; Pettitt, B.M. A model for structure and thermodynamics of ssDNA and dsDNA near a surface: A coarse grained approach. Comput. Phys. Commun. 2010, 181, 2001–2007. [Google Scholar] [CrossRef]
- Zhang, N.H.; Xing, J.J. An alternative model for elastic bending deformation of multilayered beams. J. Appl. Phys. 2006, 100, 103519. [Google Scholar] [CrossRef]
- Ilic, B.; Yang, Y.; Aubin, K.L.; Reichenbach, R.; Krylov, S.; Craiqhead, H.G. Enumeration of DNA molecules bound to a nanomechanical oscillator. Nano Lett. 2005, 5, 925–929. [Google Scholar] [CrossRef]
- Wang, G.F.; Feng, X.Q. Effects of surface elasticity and residual surface tension on the natural frequency of microbeams. Appl. Phys. Lett. 2007, 90, 231904. [Google Scholar] [CrossRef]
- Lu, P.; Lee, H.P.; Lu, C.; O’Shea, S.J.O. Surface stress effects on the resonance properties of cantilever sensors. Phys. Rev. B 2005, 72, 085405. [Google Scholar] [CrossRef]
- Yasar, S.; Podgornik, R.; Valle-Orero, J.; Johnson, M.R.; Parsegian, V.A. Continuity of states between the cholesteric → line hexatic transition and the condensation transition in DNA solutions. Sci. Rep. 2014, 4, 6877. [Google Scholar] [CrossRef]
- Legay, G.; Finot, E.; Meunier-Prest, R.; Cherkaoui-Malki, M.; Latruffe, N.; Dereux, A. DNA nanofilm thickness measurement on microarray in air and in liquid using an atomic force microscope. Biosens. Bioelectron. 2005, 21, 627–636. [Google Scholar] [CrossRef] [PubMed]
- Lakes, R.S.; Rosakis, P.; Ruina, A. Microbuckling instability in elastomeric cellular solids. J. Mater. Sci. 1993, 28, 4667–4672. [Google Scholar] [CrossRef]
- Lakes, R.S. Extreme damping in composite materials with a negative stiffness phase. Phys. Rev. Lett. 2001, 86, 2897–2900. [Google Scholar] [CrossRef] [PubMed]
- Karabalin, R.B.; Villanueva, L.G.; Matheny, M.H.; Sader, J.E.; Roukes, M.L. Stress-induced variations in the stiffness of micro- and nanocantilever beams. Phys. Rev. Lett. 2012, 108, 236101. [Google Scholar] [CrossRef]
- Lachut, M.J.; Sader, J.E. Effect of surface stress on the stiffness of thin elastic plates and beams. Phys. Rev. B 2012, 85, 085440. [Google Scholar] [CrossRef]
- Kozinsky, I.; Postma, H.W.C.; Kogan, O.; Husain, A.; Roukes, M.L. Basins of attraction of a nonlinear nanomechanical resonator. Phys. Rev. Lett. 2007, 99, 207201. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Choi, J.H.; Lee, S.M.; Hwang, K.S.; Kim, S.K.; Kim, T.S. Analysis of DNA hybridization regarding the conformation of molecular layer with piezoelectric microcantilevers. Lab Chip 2011, 11, 63–69. [Google Scholar] [CrossRef]
| d, Å | aWb2, kBT/a | aΔGrep, kBT/a | CA, MPa | CR, MPa | |
|---|---|---|---|---|---|
| Co(NH3)6Cl3 | 27.75 | −0.21 | 0.17 | 755.83 | 303, 444 |
| Spermine | 28.15 | −0.33 | 0.29 | 945.89 | 508, 714 |
| sp6+ | 27.65 | −0.38 | 0.39 | 1503.26 | 668, 743 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Zhang, Y.; Zhang, N. Anomalous Elastic Properties of Attraction-Dominated DNA Self-Assembled 2D Films and the Resultant Dynamic Biodetection Signals of Microbeam Sensors. Nanomaterials 2019, 9, 543. https://doi.org/10.3390/nano9040543
Wu J, Zhang Y, Zhang N. Anomalous Elastic Properties of Attraction-Dominated DNA Self-Assembled 2D Films and the Resultant Dynamic Biodetection Signals of Microbeam Sensors. Nanomaterials. 2019; 9(4):543. https://doi.org/10.3390/nano9040543
Chicago/Turabian StyleWu, Junzheng, Ying Zhang, and Nenghui Zhang. 2019. "Anomalous Elastic Properties of Attraction-Dominated DNA Self-Assembled 2D Films and the Resultant Dynamic Biodetection Signals of Microbeam Sensors" Nanomaterials 9, no. 4: 543. https://doi.org/10.3390/nano9040543
APA StyleWu, J., Zhang, Y., & Zhang, N. (2019). Anomalous Elastic Properties of Attraction-Dominated DNA Self-Assembled 2D Films and the Resultant Dynamic Biodetection Signals of Microbeam Sensors. Nanomaterials, 9(4), 543. https://doi.org/10.3390/nano9040543






