Moment Dynamics of Zirconia Particle Formation for Optimizing Particle Size Distribution
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Dynamic Light Scattering
2.2.2. Optical Emission Spectrometry with Inductively Coupled Plasma
2.2.3. Liquid Pycnometry
2.2.4. Zeta Potential Measurements
3. Results
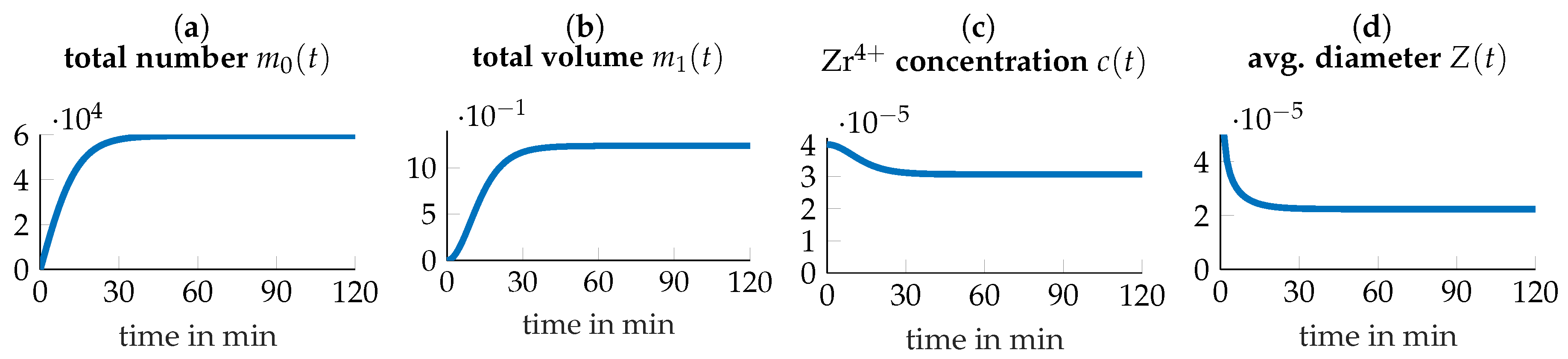
3.1. Mineralization of ZrbM
3.2. Model
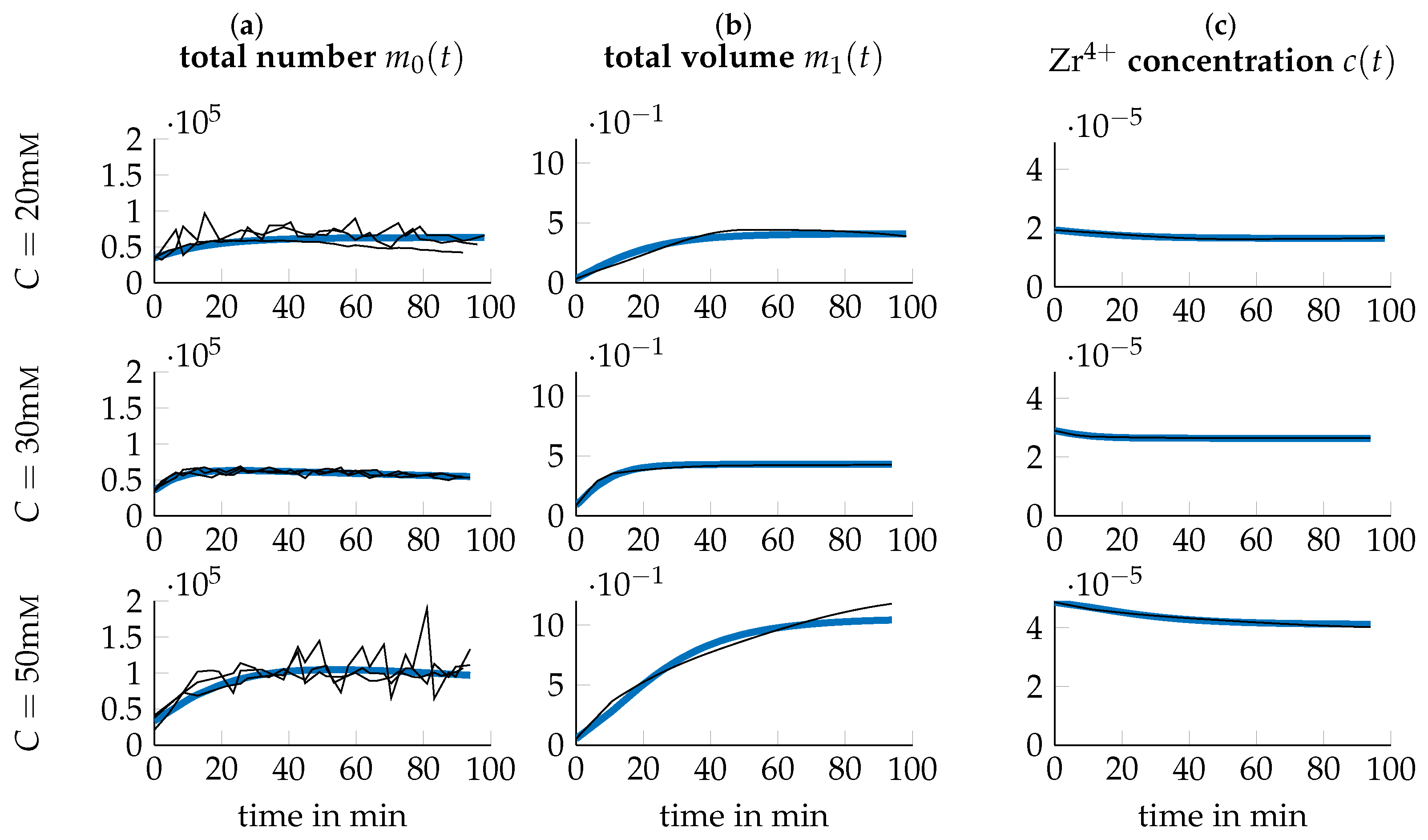
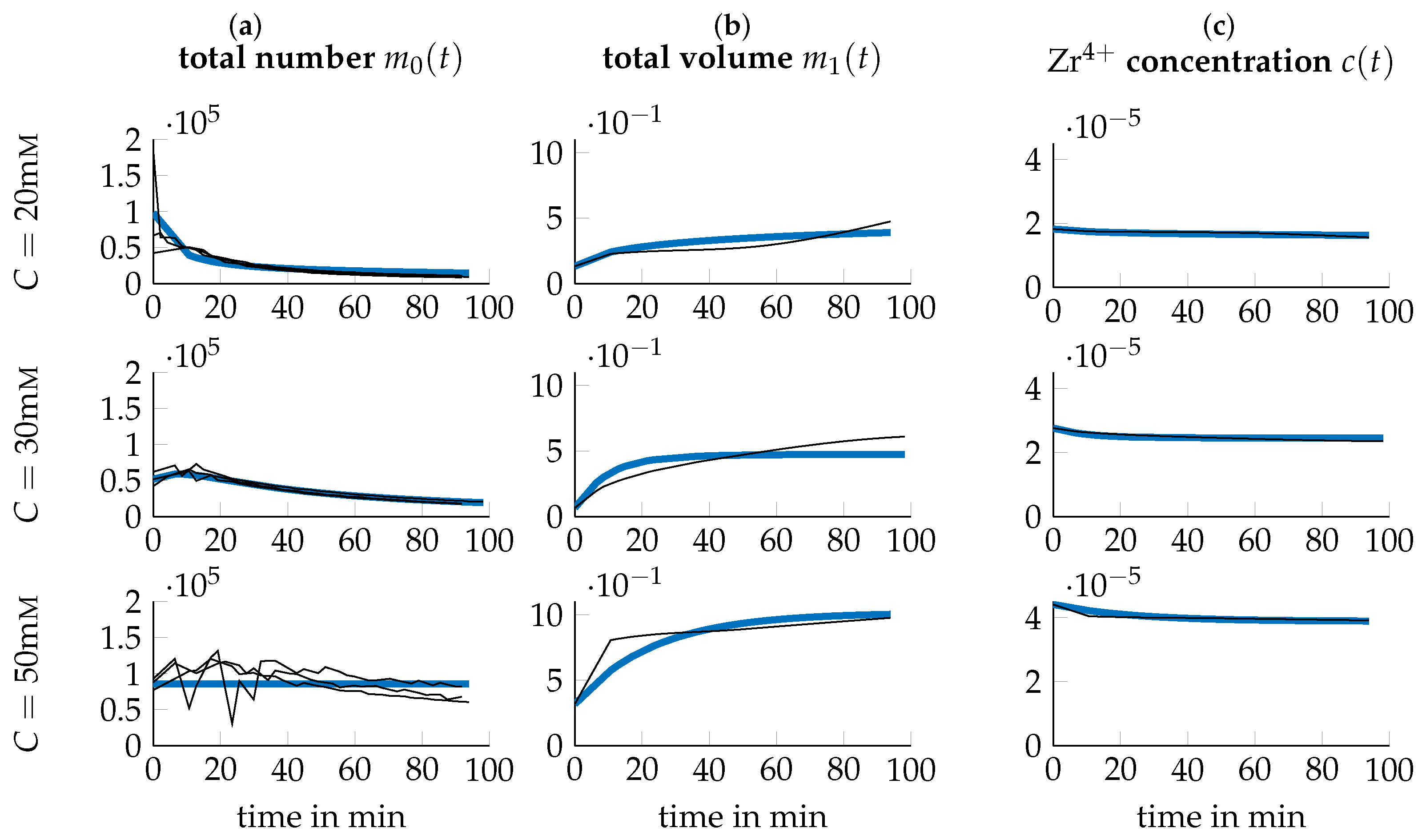
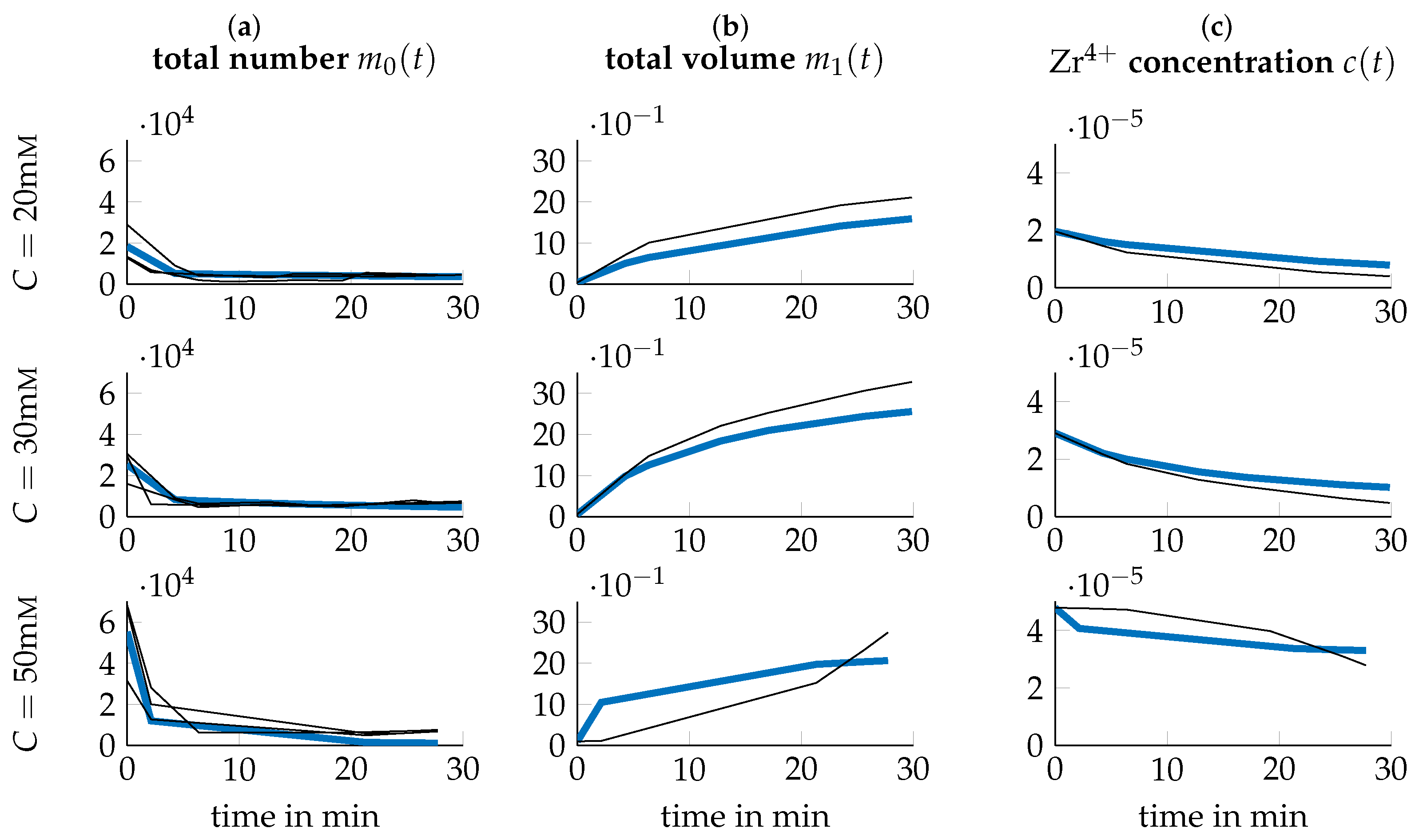
3.3. Data Transformation
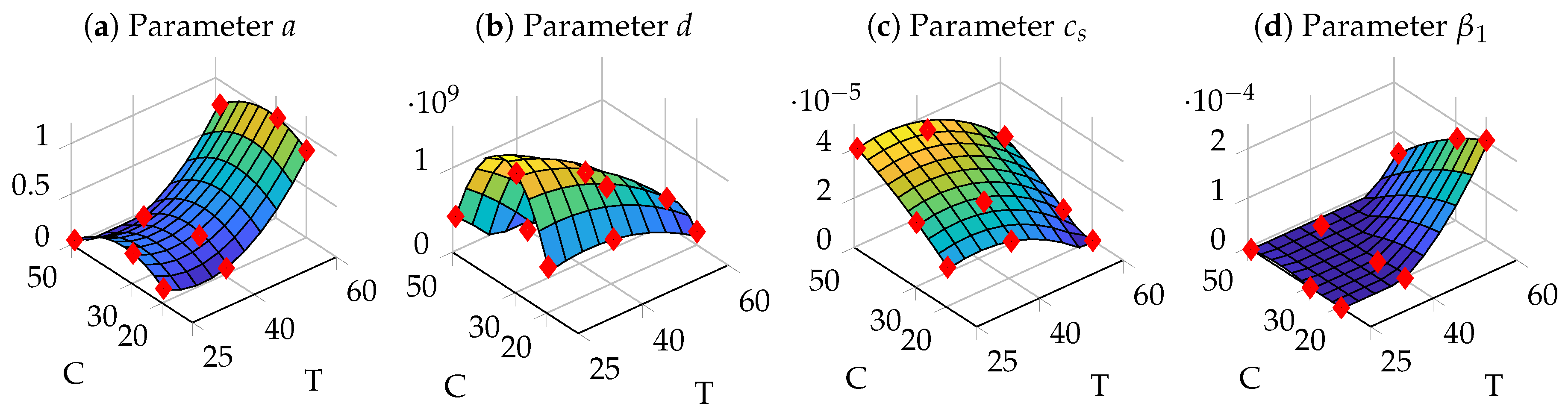
3.4. Parameter Identification
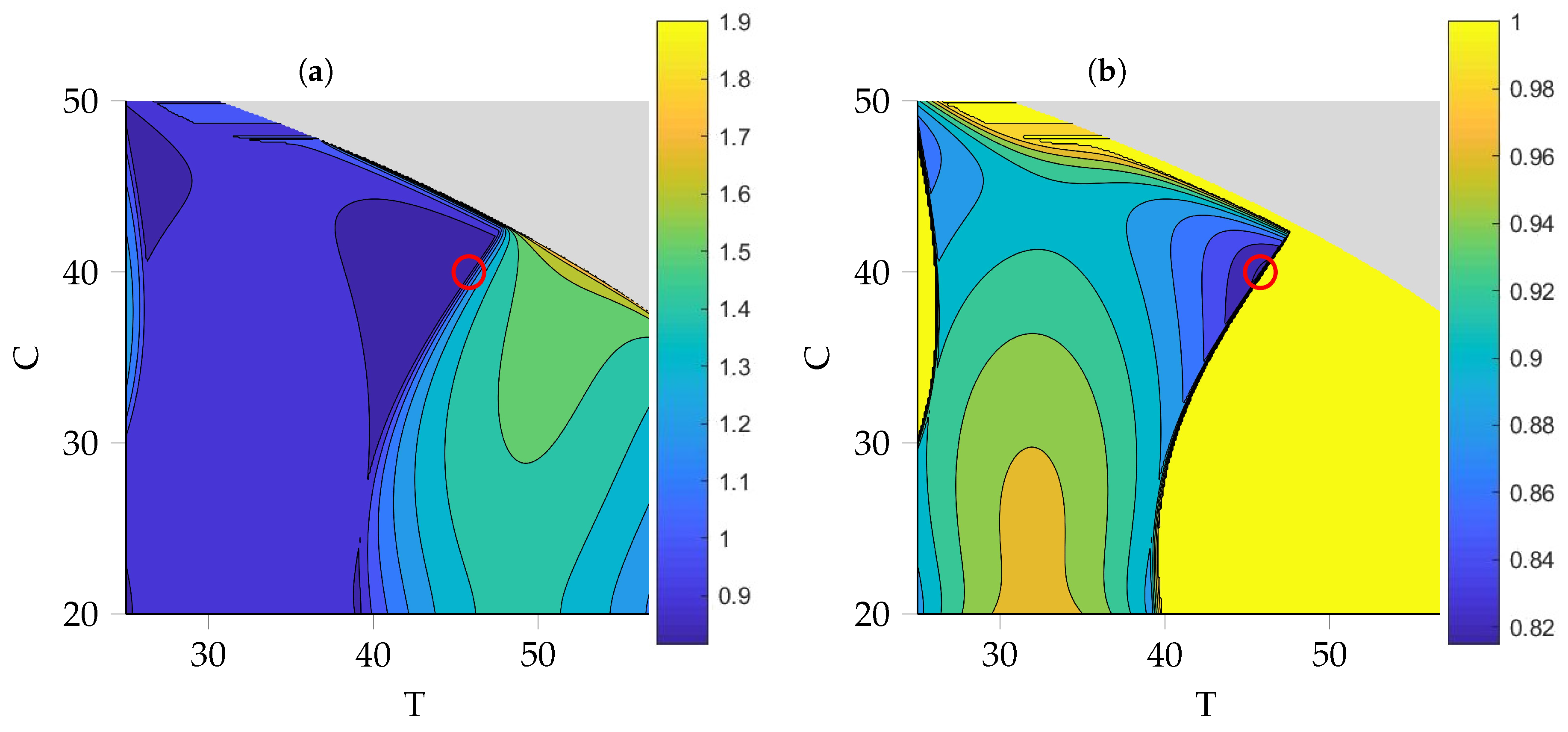
3.5. Optimization of Process Parameters
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thomas, I.M. Preparation of dielectric highly reflective (HR) mirrors from colloidal oxide suspensions containing organic polymer binders. Proc. SPIE 2288 1994, 50. [Google Scholar] [CrossRef]
- Perkins, C.M.; Triplett, B.B.; McIntyre, P.C.; Saraswat, K.C.; Haukka, S.; Tuominen, M. Electrical and materials properties of ZrO2 gate dielectrics grown by atomic layer chemical vapor deposition. Appl. Phys. Lett. 2001, 78, 2357–2359. [Google Scholar] [CrossRef]
- Wu, C.C.; Wei, C.K.; Ho, C.C.; Ding, S.J. Enhanced Hydrophilicity and Biocompatibility of Dental Zirconia Ceramics by Oxygen Plasma Treatment. Materials 2015, 8, 684–699. [Google Scholar] [CrossRef] [PubMed]
- Scarano, A.; Piattelli, M.; Caputi, S.; Favero, G.A.; Piattelli, A. Bacterial Adhesion on Commercially Pure Titanium and Zirconium Oxide Disks: An In Vivo Human Study. J. Periodontol. 2004, 75, 292–296. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Vassen, R.; Stoever, D. Ceramic materials for thermal barrier coatings. J. Eur. Ceram. Soc. 2004, 24, 1–10. [Google Scholar] [CrossRef]
- Li, H.; Liang, K.; Mei, L.; Gu, S.; Wang, S. Oxidation protection of mild steel by zirconia sol–gel coatings. Mater. Lett. 2001, 51, 320–324. [Google Scholar] [CrossRef]
- Uribe López, M.C.; Alvarez Lemus, M.A.; Hidalgo, M.C.; López González, R.; Quintana Owen, P.; Oros-Ruiz, S.; Uribe López, S.A.; Acosta, J. Synthesis and Characterization of ZnO-ZrO2 Nanocomposites for Photocatalytic Degradation and Mineralization of Phenol. J. Nanomater. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Alzari, V.; Sanna, V.; Biccai, S.; Caruso, T.; Politano, A.; Scaramuzza, N.; Sechi, M.; Nuvoli, D.; Sanna, R.; Mariani, A. Tailoring the physical properties of nanocomposite films by the insertion of graphene and other nanoparticles. Compos. Part B Eng. 2014, 60, 29–35. [Google Scholar] [CrossRef]
- Gionco, C.; Hernández, S.; Castellino, M.; Gadhi, T.A.; Muñoz-Tabares, J.A.; Cerrato, E.; Tagliaferro, A.; Russo, N.; Paganini, M.C. Synthesis and characterization of Ce and Er doped ZrO22 nanoparticles as solar light driven photocatalysts. J. Alloy. Compd. 2019, 775, 896–904. [Google Scholar] [CrossRef]
- Li, W.; Nie, X.; Jiang, X.; Zhang, A.; Ding, F.; Liu, M.; Liu, Z.; Guo, X.; Song, C. ZrO2 support imparts superior activity and stability of Co catalysts for CO2 methanation. Appl. Catal. B Environ. 2018, 220, 397–408. [Google Scholar] [CrossRef]
- Schipper, F.; Bouzaglo, H.; Dixit, M.; Erickson, E.M.; Weigel, T.; Talianker, M.; Grinblat, J.; Burstein, L.; Schmidt, M.; Lampert, J.; et al. From Surface ZrO2 Coating to Bulk Zr Doping by High Temperature Annealing of Nickel-Rich Lithiated Oxides and Their Enhanced Electrochemical Performance in Lithium Ion Batteries. Adv. Energy Mater. 2018, 8, 1701682. [Google Scholar] [CrossRef]
- Brodbeck, U. The ZiReal Post: A new ceramic implant abutment. J. Esthet. Restor. Dent. Off. Publ. Am. Acad. Esthet. Dent. 2003, 15, 10–23; discussion 24. [Google Scholar] [CrossRef]
- Tinschert, J.; Natt, G.; Mautsch, W.; Spekermann, H.; Anusavice, K. Marginal fit of alumina and zirconia-based fixed partial dentures produced by a CAD/CAM system. Oper. Dent. 2001, 26, 396–400. [Google Scholar]
- Meyenberg, K.H.; Lüthy, H.; Schärer, P. Zirconia posts: A new all-ceramic concept for nonvital abutment teeth. J. Esthet. Dent. 1995, 7, 73–80. [Google Scholar] [CrossRef] [PubMed]
- Christel, P.; Meunier, A.; Dorlot, J.M.; Crolet, J.M.; Witvoet, J.; Sedel, L.; Boutin, P. Biomechanical compatibility and design of ceramic implants for orthopedic surgery. Ann. N. Y. Acad. Sci. 1988, 523, 234–256. [Google Scholar] [CrossRef] [PubMed]
- Chevalier, J. What future for zirconia as a biomaterial? Biomaterials 2006, 27, 535–543. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.Z.; Harris, M.T.; Byers, C.H. Nucleation and Growth for Synthesis of Nanometric Zirconia Particles by Forced Hydrolysis. J. Colloid Interface Sci. 1998, 198, 87–99. [Google Scholar] [CrossRef]
- Moon, Y.T.; Park, H.K.; Kim, D.K.; Kim, C.H.; Seog, I.S. Preparation of Monodisperse and Spherical Zirconia Powders by Heating of Alcohol-Aqueous Salt Solutions. J. Am. Ceram. Soc. 1995, 78, 2690–2694. [Google Scholar] [CrossRef]
- Hu, M.Z.C.; Hunt, R.D.; Payzant, E.A.; Hubbard, C.R. Nanocrystallization and Phase Transformation in Monodispersed Ultrafine Zirconia Particles from Various Homogeneous Precipitation Methods. J. Am. Ceram. Soc. 1999, 82, 2313–2320. [Google Scholar] [CrossRef]
- Hu, M.Z.; Payzant, E.; Byers, C.H. Sol–Gel and Ultrafine Particle Formation via Dielectric Tuning of Inorganic Salt–Alcohol–Water Solutions. J. Colloid Interface Sci. 2000, 222, 20–36. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Gao, L.; Guo, J.K. Synthesis of yttria-stabilized zirconia nanoiparticles by heating of alcohol-aqueous salt solutions. Nanostruct. Mater. 1998, 10, 1043–1049. [Google Scholar] [CrossRef]
- Gao, Y.; Masuda, Y.; Yonezawa, T.; Koumoto, K. Site-Selective Deposition and Micropatterning of Zirconia Thin films on Templates of Self-Assembled Monolayers. J. Ceram. Soc. Japan 2002, 110, 379–385. [Google Scholar] [CrossRef]
- Nudelman, F.; Sommerdijk, N.A.J.M. Biomineralisation als Inspirationsquelle für die Materialchemie. Angew. Chem. 2012, 124, 6686–6700. [Google Scholar] [CrossRef]
- Gao, Y.; Koumoto, K. Bioinspired Ceramic Thin Film Processing: Present Status and Future Perspectives. Growth (Lakeland) 2005, 5, 1983–2017. [Google Scholar] [CrossRef]
- Heinemann, F.; Launspach, M.; Gries, K.; Fritz, M. Gastropod nacre: Structure, properties and growth—Biological, chemical and physical basics. Biophys. Chem. 2011, 153, 126–153. [Google Scholar] [CrossRef] [PubMed]
- Jochum, K.P.; Wang, X.; Vennemann, T.W.; Sinha, B.; Müller, W.E. Siliceous deep-sea sponge Monorhaphis chuni: A potential paleoclimate archive in ancient animals. Chem. Geol. 2012, 300–301, 143–151. [Google Scholar] [CrossRef]
- Wang, X.; Gan, L.; Jochum, K.P.; Schröder, H.C.; Müller, W.E.G. The Largest Bio-Silica Structure on Earth: The Giant Basal Spicule from the Deep-Sea Glass Sponge Monorhaphis chuni. Evid. Based Complement. Altern. Med. 2011, 2011, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Mann, S. Molecular recognition in biomineralization. Nature 1988, 332, 119–124. [Google Scholar] [CrossRef]
- Nudelman, F. Nacre biomineralisation: A review on the mechanisms of crystal nucleation. Semin. Cell Dev. Biol. 2015, 46, 2–10. [Google Scholar] [CrossRef] [PubMed]
- Merk, V.; Chanana, M.; Keplinger, T.; Gaan, S.; Burgert, I. Hybrid wood materials with improved fire retardance by bio-inspired mineralisation on the nano- and submicron level. Green Chem. 2015, 17, 1423–1428. [Google Scholar] [CrossRef]
- Patrício, T.M.F.; Panseri, S.; Sandri, M.; Tampieri, A.; Sprio, S. New bioactive bone-like microspheres with intrinsic magnetic properties obtained by bio-inspired mineralisation process. Mater. Sci. Eng. C 2017, 77, 613–623. [Google Scholar] [CrossRef] [PubMed]
- Kilper, S.; Facey, S.J.; Burghard, Z.; Hauer, B.; Rothenstein, D.; Bill, J. Macroscopic Properties of Biomimetic Ceramics Are Governed by the Molecular Recognition at the Bioorganic–Inorganic Interface. Adv. Funct. Mater. 2018, 28, 1–8. [Google Scholar] [CrossRef]
- Bunker, B.C.; Rieke, P.C.; Tarasevich, B.J.; Campbell, A.A.; Fryxell, G.E.; Graff, G.L.; Song, L.; Liu, J.; Virden, J.W.; Mcvay, G.L. Ceramic Thin-Film Formation on Functionalized Interfaces Through Biomimetic Processing. Science 1994, 264, 48–55. [Google Scholar] [CrossRef] [PubMed]
- Smoluchowski, M. Contribution to the theory of electro-osmosis and related phenomena. Bull. Int. Acad. Sci. Cracovie 1903, 3, 184–199. [Google Scholar]
- Clearfield, A.; Vaughan, P.A. The crystal structure of zirconyl chloride octahydrate and zirconyl bromide octahydrate. Acta Crystallogr. 1956, 9, 555–558. [Google Scholar] [CrossRef]
- Jolivet, J.P.; Henry, M.; Livage, J.; Bescher, E. Metal Oxide Chemistry and Synthesis: From Solution to Solid State; John Wiley & Sons: Chichester, UK, 2000. [Google Scholar]
- Singhal, A.; Toth, L.M.; Lin, J.S.; Affholter, K. Zirconium(IV) Tetramer/Octamer Hydrolysis Equilibrium in Aqueous Hydrochloric Acid Solution. J. Am. Chem. Soc. 1996, 118, 11529–11534. [Google Scholar] [CrossRef]
- Cölfen, H.; Schnablegger, H.; Fischer, A.; Jentoft, F.C.; Weinberg, G.; Schlögl, R. Particle Growth Kinetics in Zirconium Sulfate Aqueous Solutions Followed by Dynamic Light Scattering and Analytical Ultracentrifugation: Implications for Thin Film Deposition. Langmuir 2002, 18, 3500–3509. [Google Scholar] [CrossRef]
- Randolph, A.D.; Larson, M.A. Theory of Particulate Processes: Analysis and Techniques of Continuous Crystallization; Academic Press: San Diego, CA, USA, 1988. [Google Scholar] [CrossRef]
- Worlitschek, J.; Mazzotti, M. Model-Based Optimization of Particle Size Distribution in Batch-Cooling Crystallization of Paracetamol. Cryst. Growth Des. 2004, 4, 891–903. [Google Scholar] [CrossRef]
- Hounslow, M.J.; Ryall, R.L.; Marshall, V.R. A discretized population balance for nucleation, growth, and aggregation. AIChE J. 1988, 34, 1821–1832. [Google Scholar] [CrossRef]
- Marchisio, D.L.; Vigil, R.; Fox, R.O. Quadrature method of moments for aggregation–breakage processes. J. Colloid Interface Sci. 2003, 258, 322–334. [Google Scholar] [CrossRef]
- Roy, P.; Vashishtha, M.; Khanna, R.; Subbarao, D. Size-dependent coalescence kernel in fertilizer granulation—A comparative study. Particuology 2009, 7, 445–450. [Google Scholar] [CrossRef]
- Aamir, E.; Nagy, Z.K.; Rielly, C.D.; Kleinert, T.; Judat, B. Combined Quadrature Method of Moments and Method of Characteristics Approach for Efficient Solution of Population Balance Models for Dynamic Modeling and Crystal Size Distribution Control of Crystallization Processes. Ind. Eng. Chem. Res. 2009, 48, 8575–8584. [Google Scholar] [CrossRef]
- Gerstlauer, A.; Mitrović, A.; Motz, S.; Gilles, E.D. A population model for crystallization processes using two independent particle properties. Chem. Eng. Sci. 2001, 56, 2553–2565. [Google Scholar] [CrossRef]
- Hu, M.Z.C.; Zielke, J.T.; Lin, J.S.; Byers, C.H. Small-angle x-ray scattering studies of early-stage colloid formation by thermohydrolytic polymerization of aqueous zirconyl salt solutions. J. Mater. Res. 1999, 14, 103–113. [Google Scholar] [CrossRef]
- Livage, J. Sol-gel synthesis of heterogeneous catalysts from aqueous solutions. Catal. Today 1998, 41, 3–19. [Google Scholar] [CrossRef]
- Chen, H.I.; Chang, H.Y. Homogeneous precipitation of cerium dioxide nanoparticles in alcohol/water mixed solvents. Colloids Surf. A Physicochem. Eng. Asp. 2004, 242, 61–69. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 2nd ed.; Academic Press Limited: London, UK, 1992. [Google Scholar]
- Hunter, R.J. Foundations of Colloid Science, 2nd ed.; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Feke, D.L.; Prabhu, N.D.; Mann, J.A.J.; Mann, J.A. A Formulation of the Short-Range Repulsion between Spherical Colloidal Particles. J. Phys. Chem. 1984, 88, 5735–5739. [Google Scholar] [CrossRef]
- Kallay, N.; Barouch, E.; Matijevlc, E. Diffusional Detachment of Colloidal Particles from Solid/Solution Interfaces. Adv. Colloid Interface 1987, 27, 1–42. [Google Scholar] [CrossRef]
- Shin, H.; Agarwal, M.; De Guire, M.R.; Heuer, A.H. Deposition mechanism of oxide thin films on self-assembled organic monolayers. Acta Mater. 1998, 46, 801. [Google Scholar] [CrossRef]
- Raveendran, P.; Amirtharajah, A. Role of short-range forces in particle detachment during filter backwashing. J. Environ. Eng. 1995, 121, 860–868. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halter, W.; Eisele, R.; Rothenstein, D.; Bill, J.; Allgöwer, F. Moment Dynamics of Zirconia Particle Formation for Optimizing Particle Size Distribution. Nanomaterials 2019, 9, 333. https://doi.org/10.3390/nano9030333
Halter W, Eisele R, Rothenstein D, Bill J, Allgöwer F. Moment Dynamics of Zirconia Particle Formation for Optimizing Particle Size Distribution. Nanomaterials. 2019; 9(3):333. https://doi.org/10.3390/nano9030333
Chicago/Turabian StyleHalter, Wolfgang, Rahel Eisele, Dirk Rothenstein, Joachim Bill, and Frank Allgöwer. 2019. "Moment Dynamics of Zirconia Particle Formation for Optimizing Particle Size Distribution" Nanomaterials 9, no. 3: 333. https://doi.org/10.3390/nano9030333
APA StyleHalter, W., Eisele, R., Rothenstein, D., Bill, J., & Allgöwer, F. (2019). Moment Dynamics of Zirconia Particle Formation for Optimizing Particle Size Distribution. Nanomaterials, 9(3), 333. https://doi.org/10.3390/nano9030333





