Thermo-Electro-Mechanical Vibrations of Porous Functionally Graded Piezoelectric Nanoshells
Abstract
:1. Introduction
2. Preliminaries
2.1. Nonlocal Elasticity Theory for FGPMs
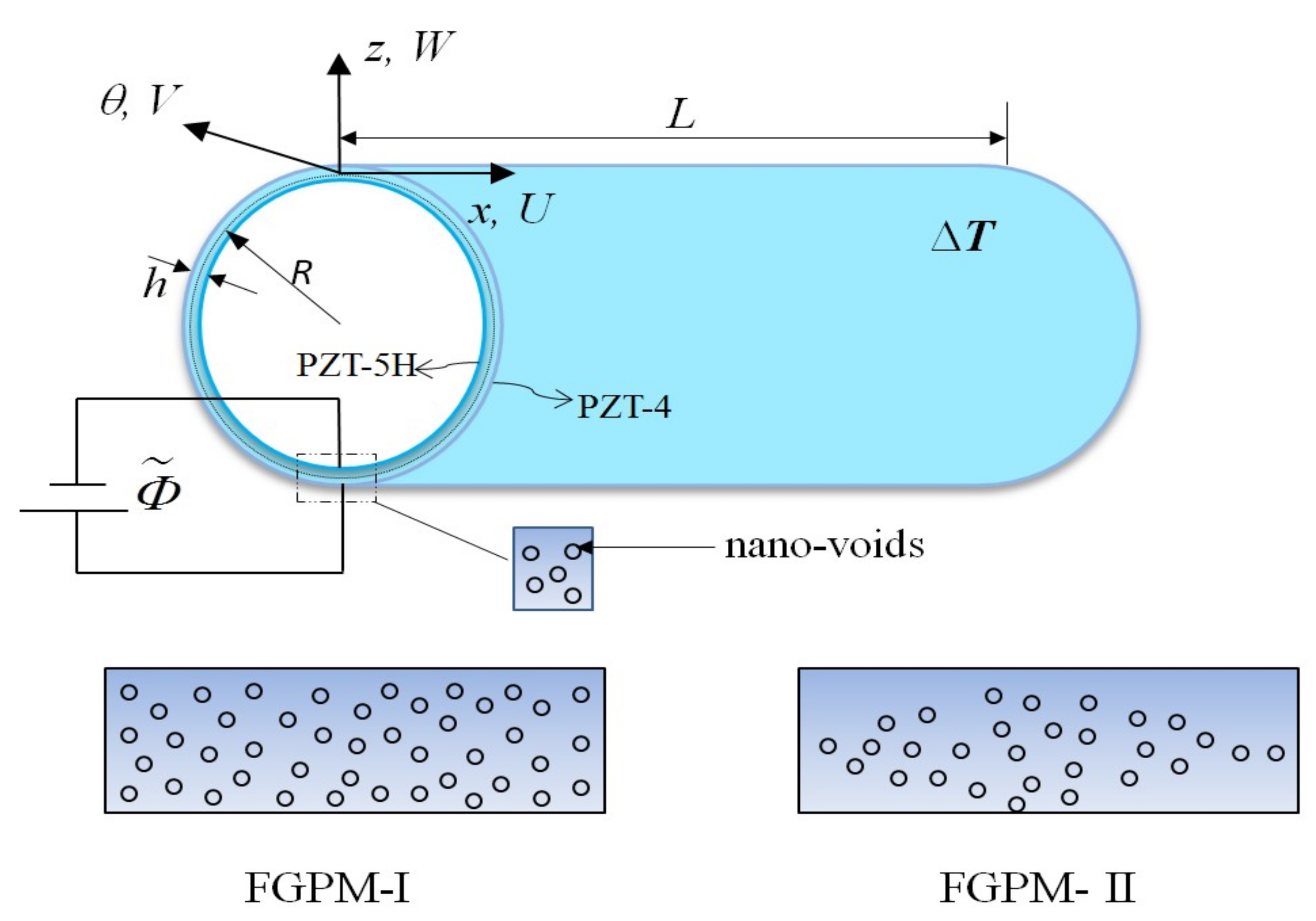
2.2. Nonlocal Porous FGPM Cylindrical Nanoshell Model
3. Solution Procedure
3.1. Navier Procedure
3.2. Galerkin Solution
4. Results and Discussion
m = 1, N = 1, α = 0.1, V0 = 0, ΔT = 0, e0a = 2 nm
5. Conclusions
- (1)
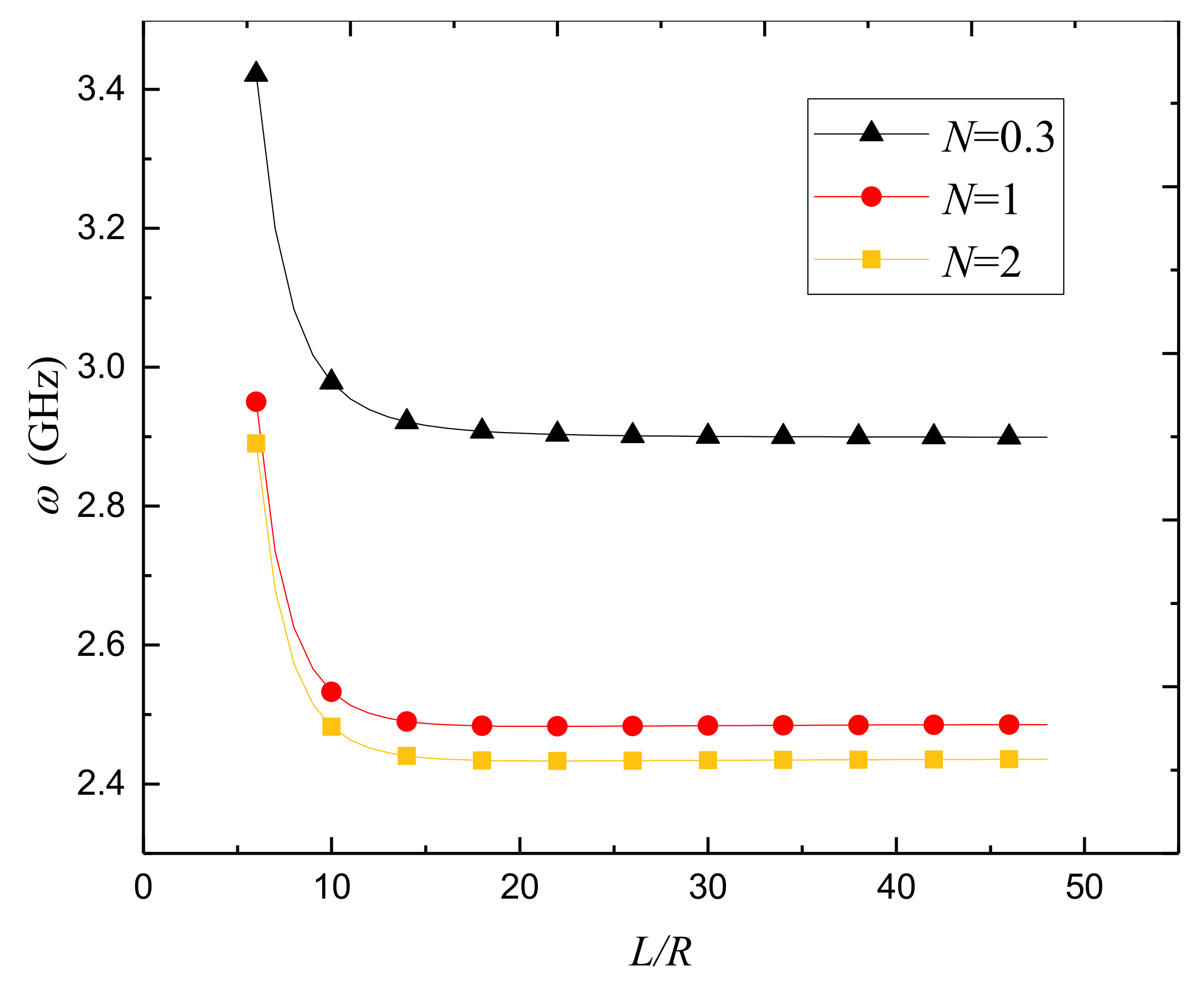
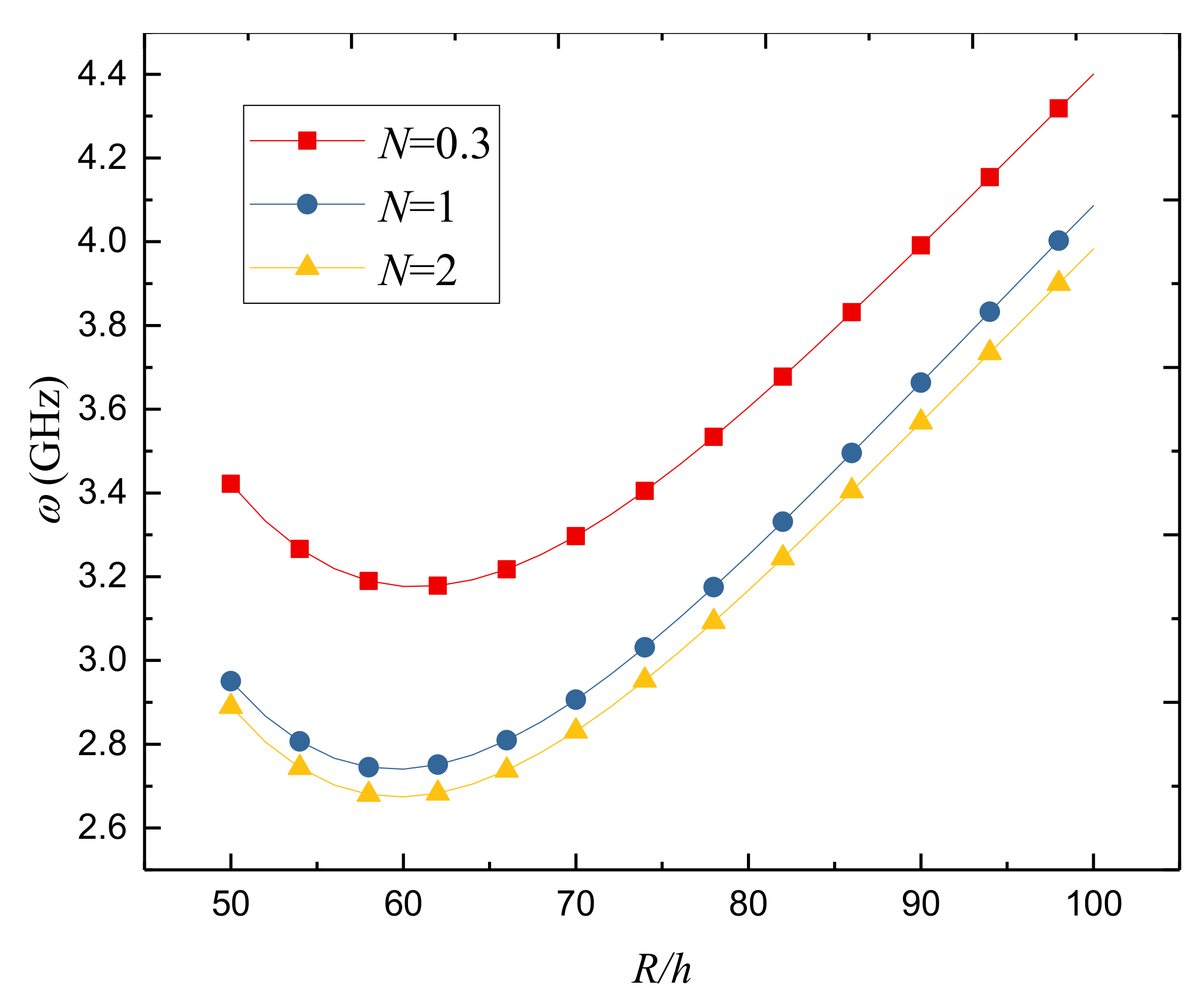
- The fundamental natural frequency of the porous FGPM nanoshell decreases initially and then increases as the radius-to-thickness ratio increases. Furthermore, the fundamental frequency decreases with the rise of the length-to-radius ratio; especially, the frequency changes notably when the length-to-radius ratio is small;
- (2)
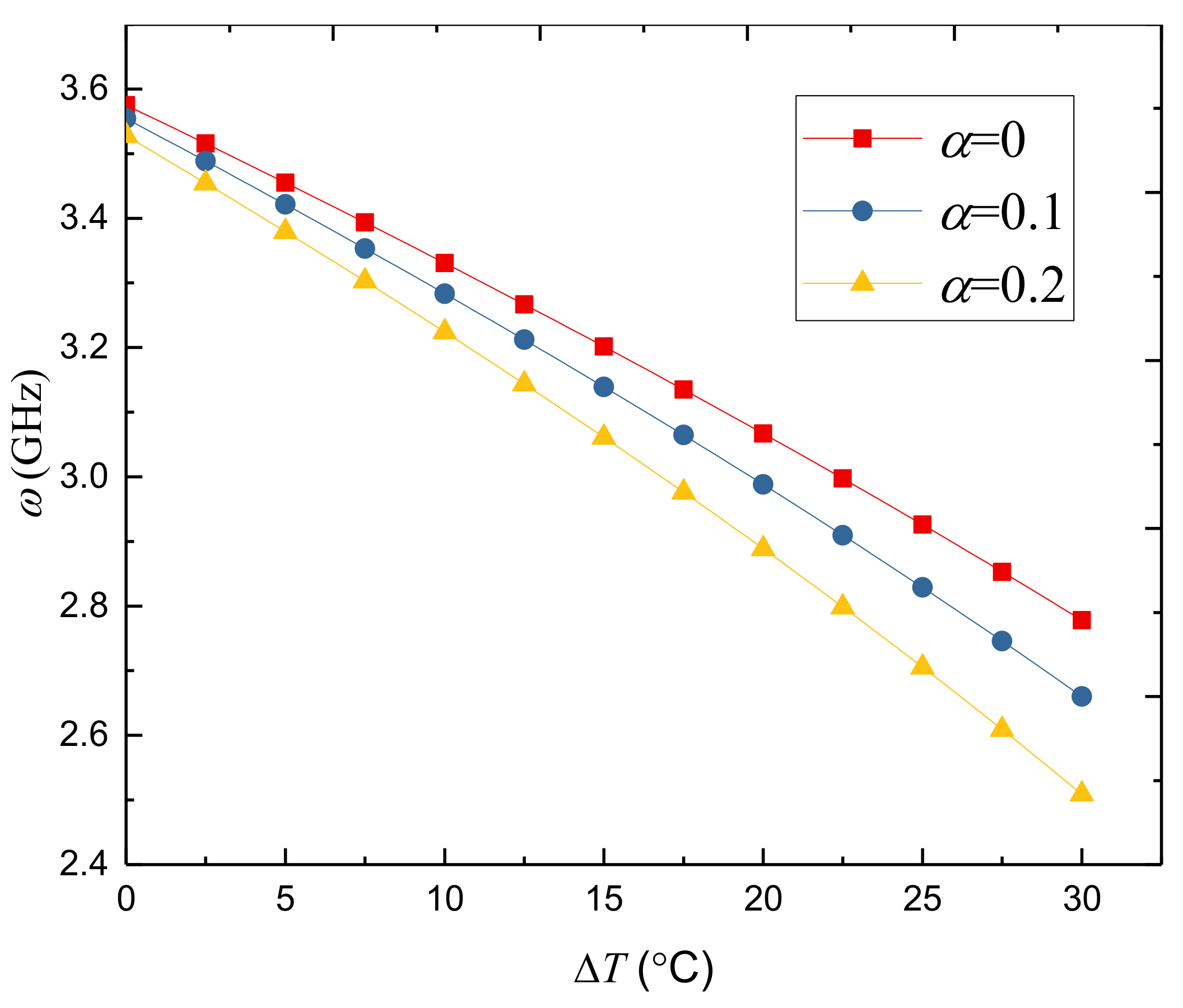
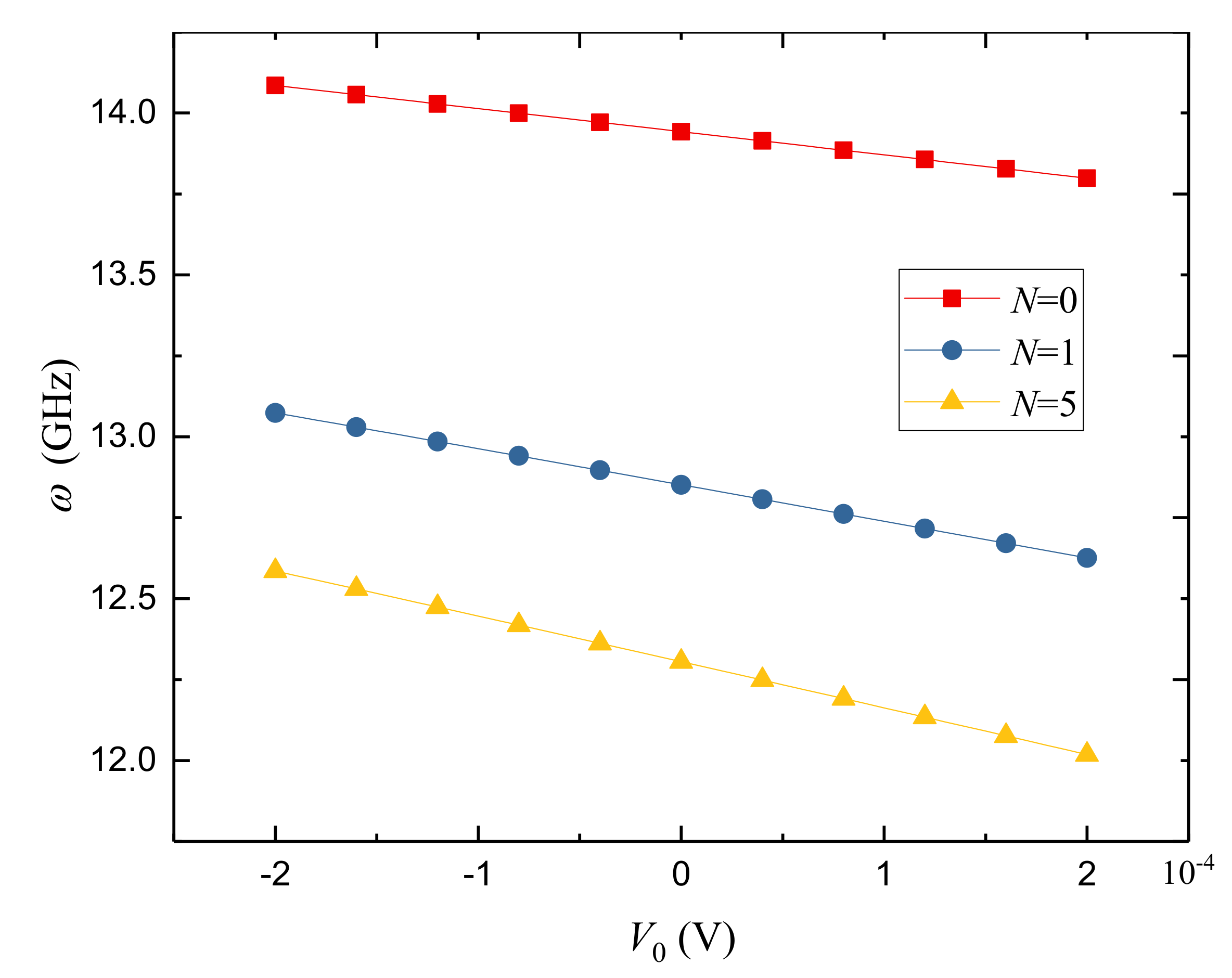
- Applying positive voltage decreases the stiffness while applying negative voltage increases the stiffness of the porous FGPM cylindrical nanoshell. Furthermore, the temperature rise results in a reduction in the stiffness. In addition, the larger power-law index leads to the lower natural frequencies of the porous FGPM cylindrical nanoshell;
- (3)
- The nonlocal parameter has a softening effect on the free vibrations of the porous FGPM nanoscale shells;
- (4)
- The Galerkin solution procedure is an alternative method, which can give numerical results with satisfactory accuracy;
- (5)
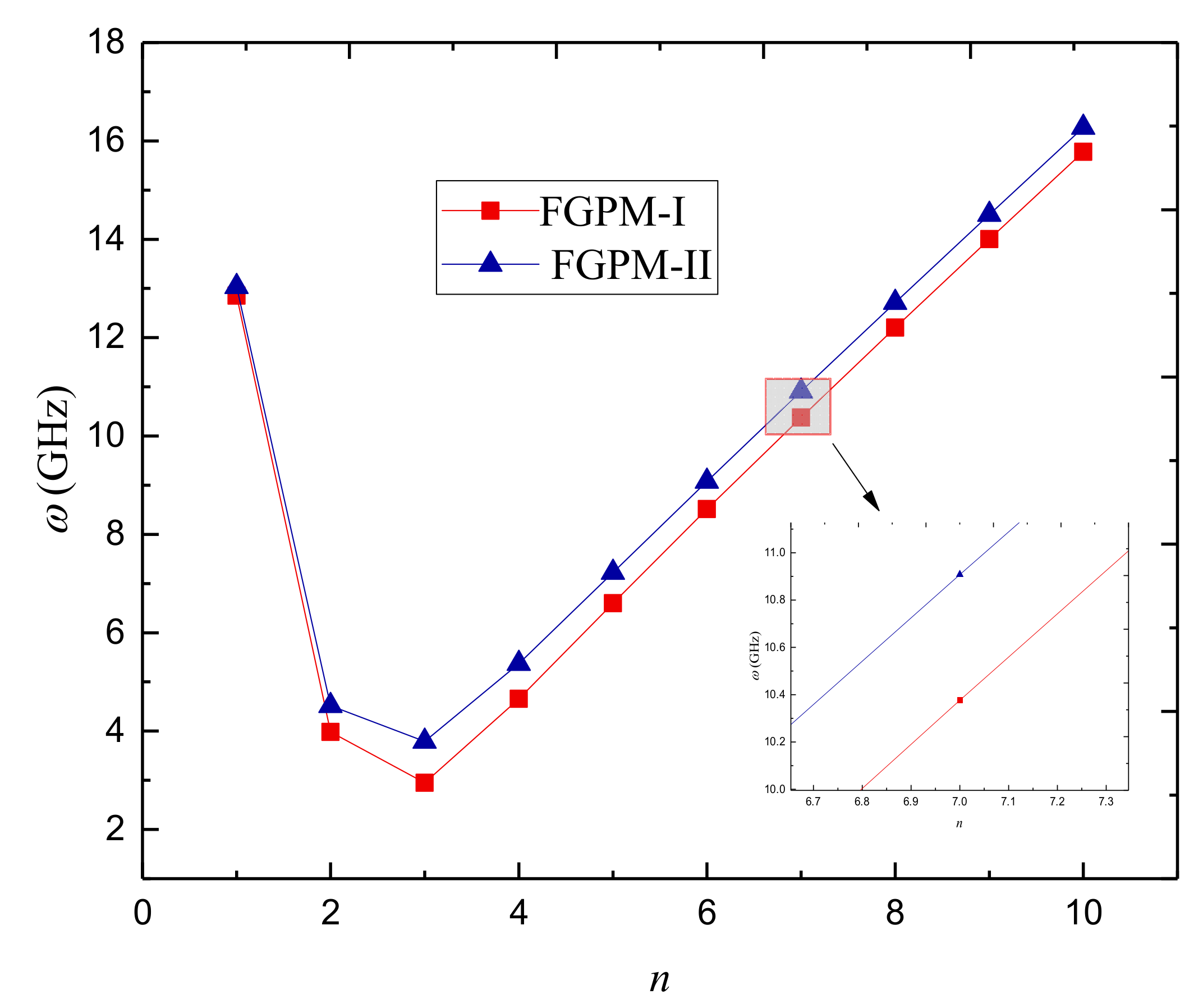
- Increasing the porosity volume fraction has a different effect on the natural frequencies of the FGPM-I and FGPM-II nanoshells, which shows that the porosity distribution type plays a notable role on vibration characteristics of the FGPM nanoscale shells.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Gupta, V.; Sharma, M.; Thakur, N. Optimization criteria for optimal placement of piezoelectric sensors and actuators on a smart structure: A technical review. J. Intell. Mater. Syst. Struct. 2010, 21, 1227–1243. [Google Scholar] [CrossRef]
- Yang, M.; Qiao, P. Modeling and experimental detection of damage in various materials using the pulse-echo method and piezoelectric sensors/actuators. Smart Mater. Struct. 2005, 14, 1083–1100. [Google Scholar] [CrossRef]
- Aksel, E.; Jones, J.L. Advances in lead-free piezoelectric materials for sensors and actuators. Sensors 2010, 10, 1935–1954. [Google Scholar] [CrossRef] [PubMed]
- Rama, G. A 3-node piezoelectric shell element for linear and geometrically nonlinear dynamic analysis of smart structures. Facta Univ. Ser. Mech. Eng. 2017, 15, 31–44. [Google Scholar] [CrossRef]
- Schindel, D.W.; Hutchins, D.A.; Grandia, W.A. Capacitive and piezoelectric air-coupled transducers for resonant ultrasonic inspection. Ultrasonics 1996, 34, 621–627. [Google Scholar] [CrossRef]
- Lu, F.; Lee, H.P.; Lim, S.P. Modeling and analysis of micro piezoelectric power generators for micro-electromechanical-systems applications. Smart Mater. Struct. 2003, 13, 57–63. [Google Scholar] [CrossRef]
- Araneo, R.; Rinaldi, A.; Notargiacomo, A.; Bini, F.; Pea, M.; Celozzi, S.; Marinozzi, F.; Lovat, G. Design concepts, fabrication and advanced characterization methods of innovative piezoelectric sensors based on ZnO nanowires. Sensors 2014, 14, 23539–23562. [Google Scholar] [CrossRef]
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, Q.; Meng, Z. A functionally gradient piezoelectric actuator prepared by powder metallurgical process in PNN-PZ-PT system. J. Mater. Sci. Lett. 1995, 14, 516–518. [Google Scholar] [CrossRef]
- Wu, C.; Kahn, M.; Moy, W. Piezoelectric ceramics with functional gradients: A new application in material design. J. Am. Ceram. Soc. 1996, 79, 809–812. [Google Scholar] [CrossRef]
- Sakamura, J.; Yamada, K.; Nakamura, K. Equivalent network analysis of functionally graded piezoelectric transducers. Jpn. J. Appl. Phys. 2000, 39, 3150. [Google Scholar]
- Ballato, J.; Schwartz, R.; Ballato, A. Network formalism for modeling functionally gradient piezoelectric plates and stacks and simulations of RAINBOW ceramic actuators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 462–476. [Google Scholar] [CrossRef]
- Takahashi, S.; Miyamoto, N.; Ichinose, N. Functionally gradient piezoelectric ceramics for ultrasonic transducers. Jpn. J. Appl. Phys. 2002, 41, 7103. [Google Scholar] [CrossRef]
- Zhu, J.; Lai, Z.; Yin, Z.; Jeon, J.; Lee, S. Fabrication of ZrO2–NiCr functionally graded material by powder metallurgy. Mater. Chem. Phys. 2001, 68, 130–135. [Google Scholar] [CrossRef]
- Chen, C.Q.; Shi, Y.; Zhang, Y.S.; Zhu, J.; Yan, Y.J. Size dependence of Young’s modulus in ZnO nanowires. Phys. Rev. Lett. 2006, 96, 75505. [Google Scholar] [CrossRef]
- Park, T.-J.; Papaefthymiou, G.C.; Viescas, A.J.; Moodenbaugh, A.R.; Wong, S.S. Size-dependent magnetic properties of single-crystalline multiferroic BiFeO3 nanoparticles. Nano Lett. 2007, 7, 766–772. [Google Scholar] [CrossRef]
- Araneo, R.; Rinaldi, A.; Notargiacomo, A.; Bini, F.; Marinozzi, F.; Pea, M.; Lovat, G.; Celozzi, S. Effect of the scaling of the mechanical properties on the performances of ZnO piezo-semiconductive nanowires. AIP Conf. Proc. 2014, 1603, 14–22. [Google Scholar]
- Araneo, R.; Bini, F.; Rinaldi, A.; Notargiacomo, A.; Pea, M.; Celozzi, S. Thermal-electric model for piezoelectric ZnO nanowires. Nanotechnology 2015, 26, 265402. [Google Scholar] [CrossRef] [PubMed]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2002; ISBN 0387952756. [Google Scholar]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S. Thermoelectric-mechanical vibration of piezoelectric nanobeams based on the nonlocal theory. Smart Mater. Struct. 2012, 21, 025018. [Google Scholar] [CrossRef]
- Jandaghian, A.A.; Rahmani, O. Vibration analysis of functionally graded piezoelectric nanoscale plates by nonlocal elasticity theory: An analytical solution. Superlattices Microstruct. 2016, 100, 57–75. [Google Scholar] [CrossRef]
- Jandaghian, A.A.; Rahmani, O. Size-dependent free vibration analysis of functionally graded piezoelectric plate subjected to thermo-electro-mechanical loading. J. Intell. Mater. Syst. Struct. 2017, 28, 3039–3053. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.; Shen, S. Size-dependent buckling and vibration behaviors of piezoelectric nanostructures due to flexoelectricity. Smart Mater. Struct. 2015, 24, 105012. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Vibration and buckling analysis of a piezoelectric nanoplate considering surface effects and in-plane constraints. Proc. R. Soc. A 2012, 468, 3458–3475. [Google Scholar] [CrossRef]
- Ghadiri, M.; Safarpour, H. Free vibration analysis of embedded magneto-electro-thermo-elastic cylindrical nanoshell based on the modified couple stress theory. Appl. Phys. A 2016, 122, 833. [Google Scholar] [CrossRef]
- Fang, X.-Q.; Zhu, C.-S.; Liu, J.-X.; Liu, X.-L. Surface energy effect on free vibration of nano-sized piezoelectric double-shell structures. Phys. B Condens. Matter 2018, 529, 41–56. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R.; Norouzzadeh, A. Size-dependent thermo-mechanical vibration and instability of conveying fluid functionally graded nanoshells based on Mindlin’s strain gradient theory. Thin-Walled Struct. 2016, 105, 172–184. [Google Scholar] [CrossRef]
- Sun, J.; Lim, C.W.; Zhou, Z.; Xu, X.; Sun, W. Rigorous buckling analysis of size-dependent functionally graded cylindrical nanoshells. J. Appl. Phys. 2016, 119, 214303. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S.; Reddy, J.N. Thermo-electro-mechanical vibration of size-dependent piezoelectric cylindrical nanoshells under various boundary conditions. Compos. Struct. 2014, 116, 626–636. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S.; Yang, J.; Kitipornchai, S. The size-dependent vibration of embedded magneto-electro-elastic cylindrical nanoshells. Smart Mater. Struct. 2014, 23, 125036. [Google Scholar] [CrossRef]
- Komijani, M.; Reddy, J.N.; Eslami, M.R. Nonlinear analysis of microstructure-dependent functionally graded piezoelectric material actuators. J. Mech. Phys. Solids 2014, 63, 214–227. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Vibration behaviors of functionally graded rectangular plates with porosities and moving in thermal environment. Aerosp. Sci. Technol. 2017, 69, 550–562. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Nonlinear steady-state responses of longitudinally traveling functionally graded material plates in contact with liquid. Compos. Struct. 2017, 164, 130–144. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Nonlinear dynamics of a translational FGM plate with strong mode interaction. Int. J. Struct. Stab. Dyn. 2018, 18, 1850031. [Google Scholar] [CrossRef]
- Wang, Y.Q. Electro-mechanical vibration analysis of functionally graded piezoelectric porous plates in the translation state. Acta Astronaut. 2018, 143, 263–271. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Chaikittiratana, A. Flexural vibration of imperfect functionally graded beams based on Timoshenko beam theory: Chebyshev collocation method. Meccanica 2015, 50, 1331–1342. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press: Cambridge, UK, 2008; ISBN 1139469029. [Google Scholar]
- Soedel, W. Vibrations of Shells and Plates; CRC Press: Boca Raton, FL, USA, 2004; ISBN 0203026306. [Google Scholar]
- Wang, Q. On buckling of column structures with a pair of piezoelectric layers. Eng. Struct. 2002, 24, 199–205. [Google Scholar] [CrossRef]
- Zhang, D.P.; Lei, Y.J.; Shen, Z.B. Thermo-electro-mechanical vibration analysis of piezoelectric nanoplates resting on viscoelastic foundation with various boundary conditions. Int. J. Mech. Sci. 2017, 131–132, 1001–1015. [Google Scholar] [CrossRef]
- Zhao, M.; Qian, C.; Lee, S.W.R.; Tong, P.; Suemasu, H.; Zhang, T.Y. Electro-elastic analysis of piezoelectric laminated plates. Adv. Compos. Mater. 2007, 16, 63–81. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Wan, Y.H.; Zu, J.W. Nonlinear dynamic characteristics of functionally graded sandwich thin nanoshells conveying fluid incorporating surface stress influence. Thin-Walled Struct. 2019, 135, 537–547. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Ye, C.; Zu, J.W. Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aerosp. Sci. Technol. 2019, 85, 359–370. [Google Scholar] [CrossRef]
- Loy, C.T.; Lam, K.Y. Vibration of cylindrical shells with ring support. Int. J. Mech. Sci. 1997, 39, 455–471. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos. Part B Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Kamarian, S.; Salim, M.; Dimitri, R.; Tornabene, F. Free vibration analysis of conical shells reinforced with agglomerated Carbon Nanotubes. Int. J. Mech. Sci. 2016, 108, 157–165. [Google Scholar] [CrossRef]
- Nejati, M.; Dimitri, R.; Tornabene, F.; Hossein Yas, M. Thermal buckling of nanocomposite stiffened cylindrical shells reinforced by functionally graded wavy carbon nanotubes with temperature-dependent properties. Appl. Sci. 2017, 7, 1223. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Bacciocchi, M.; Dimitri, R. Free vibration analysis of arbitrarily shaped Functionally Graded Carbon Nanotube-reinforced plates. Compos. Part B Eng. 2017, 115, 384–408. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M.; Fantuzzi, N.; Reddy, J.N. Multiscale approach for three-phase CNT/polymer/fiber laminated nanocomposite structures. Polym. Compos. 2017. [Google Scholar] [CrossRef]
- Nejati, M.; Asanjarani, A.; Dimitri, R.; Tornabene, F. Static and free vibration analysis of functionally graded conical shells reinforced by carbon nanotubes. Int. J. Mech. Sci. 2017, 130, 383–398. [Google Scholar]
- Kiani, Y.; Dimitri, R.; Tornabene, F. Free vibration study of composite conical panels reinforced with FG-CNTs. Eng. Struct. 2018, 172, 472–482. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Huang, X.B.; Li, J. Hydroelastic dynamic analysis of axially moving plates in continuous hot-dip galvanizing process. Int. J. Mech. Sci. 2016, 110, 201–216. [Google Scholar] [CrossRef]
- Yang, J. Special Topics in the Theory of Piezoelectricity; Springer Science & Business Media: Berlin, Germany, 2010; ISBN 0387894985. [Google Scholar]
- Eltaher, M.A.; Hamed, M.A.; Sadoun, A.M.; Mansour, A. Mechanical analysis of higher order gradient nanobeams. Appl. Math. Comput. 2014, 229, 260–272. [Google Scholar] [CrossRef]
- Lim, C.W. Is a nanorod (or nanotube) with a lower Young’s modulus stiffer? Is not Young’s modulus a stiffness indicator? Sci. China Phys. Mech. Astron. 2010, 53, 712–724. [Google Scholar] [CrossRef]
- Ke, L.-L.; Liu, C.; Wang, Y.-S. Free vibration of nonlocal piezoelectric nanoplates under various boundary conditions. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 66, 93–106. [Google Scholar] [CrossRef]
| Boundary Condition | c1 | c2 | c3 | c4 | ζi | λi | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| C-SS | 1 | −1 | 1 | −1 | 3.9266 | 7.0686 | 10.2102 | 13.3518 | … | |
| C-C | 1 | −1 | 1 | −1 | 4.7300 | 7.8532 | 10.9956 | 14.1372 | … | |
| n | μ = 0.02 | μ = 0.04 | ||
|---|---|---|---|---|
| Ke et al. [31] | Present | Ke et al. [31] | Present | |
| 1 | 0.4448 | 0.4448 | 0.4105 | 0.4105 |
| 2 | 0.2190 | 0.2190 | 0.1748 | 0.1748 |
| 3 | 0.4296 | 0.4296 | 0.3016 | 0.3016 |
| 4 | 0.7235 | 0.7235 | 0.4630 | 0.4630 |
| 5 | 1.0361 | 1.0361 | 0.6223 | 0.6223 |
| 6 | 1.3532 | 1.3532 | 0.7780 | 0.7780 |
| 7 | 1.6694 | 1.6694 | 0.9309 | 0.9309 |
| 8 | 1.9829 | 1.9829 | 1.0827 | 1.0827 |
| 9 | 2.2933 | 2.2933 | 1.2310 | 1.2310 |
| 10 | 2.6008 | 2.6008 | 1.3791 | 1.3791 |
| n | μ = 0.02 | μ = 0.04 | ||
|---|---|---|---|---|
| Ke et al. [31] | Present | Ke et al. [31] | Present | |
| 1 | 0.6189 | 0.6539 | 0.5710 | 0.6031 |
| 2 | 0.2701 | 0.2751 | 0.2155 | 0.2195 |
| 3 | 0.4357 | 0.4362 | 0.3058 | 0.3061 |
| 4 | 0.7247 | 0.7248 | 0.4637 | 0.4638 |
| 5 | 1.0365 | 1.0367 | 0.6225 | 0.6226 |
| 6 | 1.3534 | 1.3535 | 0.7781 | 0.7782 |
| 7 | 1.6695 | 1.6696 | 0.9309 | 0.9310 |
| 8 | 1.9830 | 1.9831 | 1.0817 | 1.0818 |
| 9 | 2.2934 | 2.2935 | 1.2310 | 1.2311 |
| 10 | 2.6008 | 2.6009 | 1.3791 | 1.3792 |
| n | μ = 0.02 | μ = 0.04 | ||
|---|---|---|---|---|
| Ke et al. [31] | Present | Ke et al. [31] | Present | |
| 1 | 0.7987 | 0.8487 | 0.7368 | 0.7823 |
| 2 | 0.3386 | 0.3488 | 0.2702 | 0.2782 |
| 3 | 0.4458 | 0.4472 | 0.3129 | 0.3138 |
| 4 | 0.7266 | 0.7268 | 0.4649 | 0.4651 |
| 5 | 1.0371 | 1.0373 | 0.6228 | 0.6229 |
| 6 | 1.3536 | 1.3538 | 0.7782 | 0.7783 |
| 7 | 1.6696 | 1.6698 | 0.9310 | 0.9311 |
| 8 | 1.9830 | 1.9832 | 1.0818 | 1.0819 |
| 9 | 2.2934 | 2.2936 | 1.2310 | 1.2311 |
| 10 | 2.6008 | 2.6010 | 1.3791 | 1.3792 |
| Material | PZT-4 | PZT-5H |
|---|---|---|
| Elastic constants (GPa) | c11 = 132, c12 = 71, c13 = 73, c22 = 132, c23 = 73, c33 = 115, c66 = 30.5 | c11 = 126, c12 = 79.1, c13 = 83.9, c22 = 139, c23 = 83.9, c33 = 117, c66 = 23.5 |
| Piezoelectric constants (C/m2) | e31 = −4.1, e32 = −4.1, e33 = 14.1 | e31 = −6.5, e32 = −6.5, e33 = 23.3 |
| Dielectric constants (10−9 C/Vm) | s11 = 5.841, s33 = 7.124 | s11 = 15.05, s33 = 13.02 |
| Thermal moduli (105 N/km2) | β11 = 4.738, β22 = 4.738, β33 = 4.529 | β11 = 4.738, β22 = 4.738, β33 = 4.529 |
| Pyroelectric constant (10−6 C/N) | p3 = 25 | p3 = 25 |
| Mass density (kg/m3) | ρ = 7500 | ρ = 7500 |
| n | α = 0 | α = 0.1 | α = 0.2 |
|---|---|---|---|
| 1 | 12.216 | 12.120 | 11.998 |
| 2 | 4.212 | 4.176 | 4.131 |
| 3 | 3.575 | 3.554 | 3.528 |
| 4 | 5.129 | 5.109 | 5.084 |
| 5 | 6.934 | 6.912 | 6.884 |
| 6 | 8.737 | 8.712 | 8.680 |
| 7 | 10.514 | 10.486 | 10.450 |
| 8 | 12.267 | 12.235 | 12.195 |
| 9 | 14.000 | 13.965 | 13.920 |
| 10 | 15.718 | 15.679 | 15.630 |
| n | α = 0 | α = 0.1 | α = 0.2 |
|---|---|---|---|
| 1 | 15.958 | 15.833 | 15.675 |
| 2 | 6.000 | 5.951 | 5.889 |
| 3 | 4.042 | 4.017 | 3.985 |
| 4 | 5.223 | 5.202 | 5.176 |
| 5 | 6.961 | 6.939 | 6.911 |
| 6 | 8.750 | 8.724 | 8.692 |
| 7 | 10.522 | 10.493 | 10.458 |
| 8 | 12.273 | 12.241 | 12.201 |
| 9 | 14.005 | 13.969 | 13.925 |
| 10 | 15.722 | 15.683 | 15.634 |
| n | α = 0 | α = 0.1 | α = 0.2 |
|---|---|---|---|
| 1 | 18.371 | 18.228 | 18.048 |
| 2 | 7.670 | 7.609 | 7.531 |
| 3 | 4.657 | 4.626 | 4.587 |
| 4 | 5.365 | 5.343 | 5.314 |
| 5 | 7.000 | 6.977 | 6.948 |
| 6 | 8.763 | 8.738 | 8.706 |
| 7 | 10.529 | 10.500 | 10.464 |
| 8 | 12.277 | 12.245 | 12.205 |
| 9 | 14.008 | 13.972 | 13.928 |
| 10 | 15.724 | 15.685 | 15.636 |
| R/h | α = 0 | α = 0.1 | α = 0.2 |
|---|---|---|---|
| 50 | 3.575 | 3.554 | 3.528 |
| 55 | 3.353 | 3.332 | 3.304 |
| 60 | 3.239 | 3.217 | 3.189 |
| 65 | 3.211 | 3.187 | 3.158 |
| 70 | 3.248 | 3.223 | 3.192 |
| 75 | 3.333 | 3.307 | 3.274 |
| 80 | 3.452 | 3.425 | 3.390 |
| 85 | 3.594 | 3.565 | 3.529 |
| 90 | 3.751 | 3.721 | 3.683 |
| 95 | 3.917 | 3.885 | 3.845 |
| 100 | 3.575 | 3.554 | 3.528 |
| n | N = 0.3 | N = 1 | N = 5 |
|---|---|---|---|
| 1 | 13.474 | 12.852 | 12.305 |
| 2 | 4.437 | 3.982 | 3.967 |
| 3 | 3.422 | 2.950 | 3.088 |
| 4 | 5.027 | 4.656 | 4.735 |
| 5 | 6.929 | 6.602 | 6.630 |
| 6 | 8.822 | 8.512 | 8.503 |
| 7 | 10.680 | 10.376 | 10.336 |
| 8 | 12.508 | 12.203 | 12.135 |
| 9 | 14.312 | 14.002 | 13.908 |
| 10 | 16.097 | 15.779 | 15.661 |
| n | e0a = 0 | e0a = 1 nm | e0a = 1.5 nm | e0a = 2 nm |
|---|---|---|---|---|
| 1 | 14.101 | 13.755 | 13.356 | 14.101 |
| 2 | 5.168 | 4.775 | 4.392 | 5.168 |
| 3 | 4.650 | 3.971 | 3.433 | 4.650 |
| 4 | 8.839 | 6.879 | 5.630 | 8.839 |
| 5 | 14.826 | 10.455 | 8.193 | 14.826 |
| 6 | 22.203 | 14.182 | 10.752 | 22.203 |
| 7 | 30.928 | 17.943 | 13.267 | 30.928 |
| 8 | 40.993 | 21.693 | 15.738 | 40.993 |
| 9 | 52.398 | 25.414 | 18.172 | 52.398 |
| 10 | 65.143 | 29.101 | 20.575 | 65.143 |
| L/R | α = 0 | α = 0.1 | α = 0.2 | ||
|---|---|---|---|---|---|
| Prefect | FGPM-I | FGPM-II | FGPM-I | FGPM-II | |
| 6 | 3.575 | 3.554 | 3.609 | 3.528 | 3.643 |
| 12 | 3.168 | 3.151 | 3.208 | 3.130 | 3.249 |
| 18 | 3.137 | 3.121 | 3.177 | 3.100 | 3.218 |
| 24 | 3.130 | 3.114 | 3.170 | 3.093 | 3.211 |
| 30 | 3.127 | 3.111 | 3.168 | 3.091 | 3.209 |
| 36 | 3.126 | 3.110 | 3.166 | 3.090 | 3.208 |
| 42 | 3.126 | 3.109 | 3.166 | 3.089 | 3.207 |
| 48 | 3.125 | 3.109 | 3.165 | 3.089 | 3.207 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.F.; Wang, Y.Q. Thermo-Electro-Mechanical Vibrations of Porous Functionally Graded Piezoelectric Nanoshells. Nanomaterials 2019, 9, 301. https://doi.org/10.3390/nano9020301
Liu YF, Wang YQ. Thermo-Electro-Mechanical Vibrations of Porous Functionally Graded Piezoelectric Nanoshells. Nanomaterials. 2019; 9(2):301. https://doi.org/10.3390/nano9020301
Chicago/Turabian StyleLiu, Yun Fei, and Yan Qing Wang. 2019. "Thermo-Electro-Mechanical Vibrations of Porous Functionally Graded Piezoelectric Nanoshells" Nanomaterials 9, no. 2: 301. https://doi.org/10.3390/nano9020301
APA StyleLiu, Y. F., & Wang, Y. Q. (2019). Thermo-Electro-Mechanical Vibrations of Porous Functionally Graded Piezoelectric Nanoshells. Nanomaterials, 9(2), 301. https://doi.org/10.3390/nano9020301





