Second Harmonic Generation for Moisture Monitoring in Dimethoxyethane at a Gold-Solvent Interface Using Plasmonic Structures
Abstract
1. Introduction
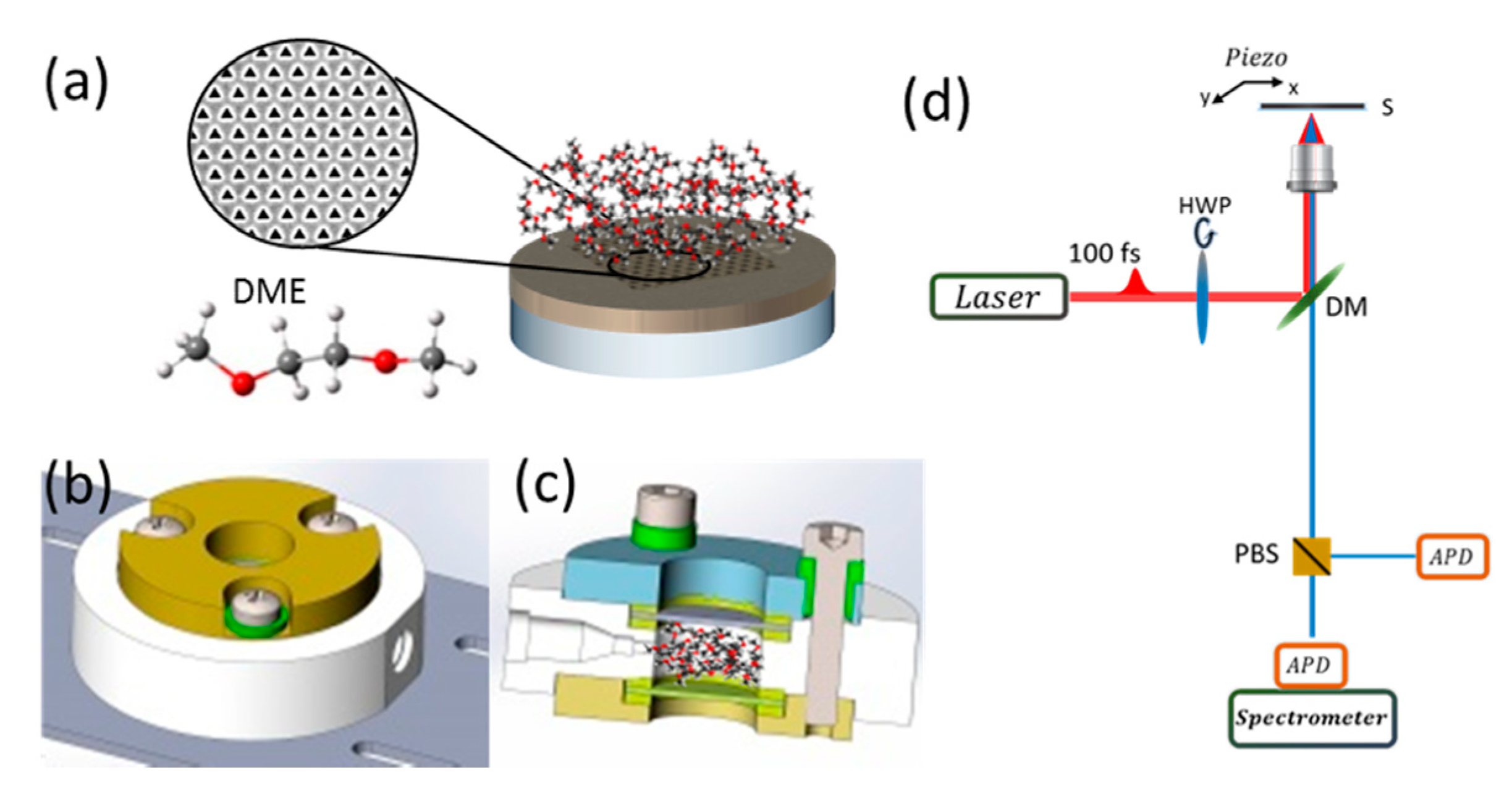
2. Materials and Methods
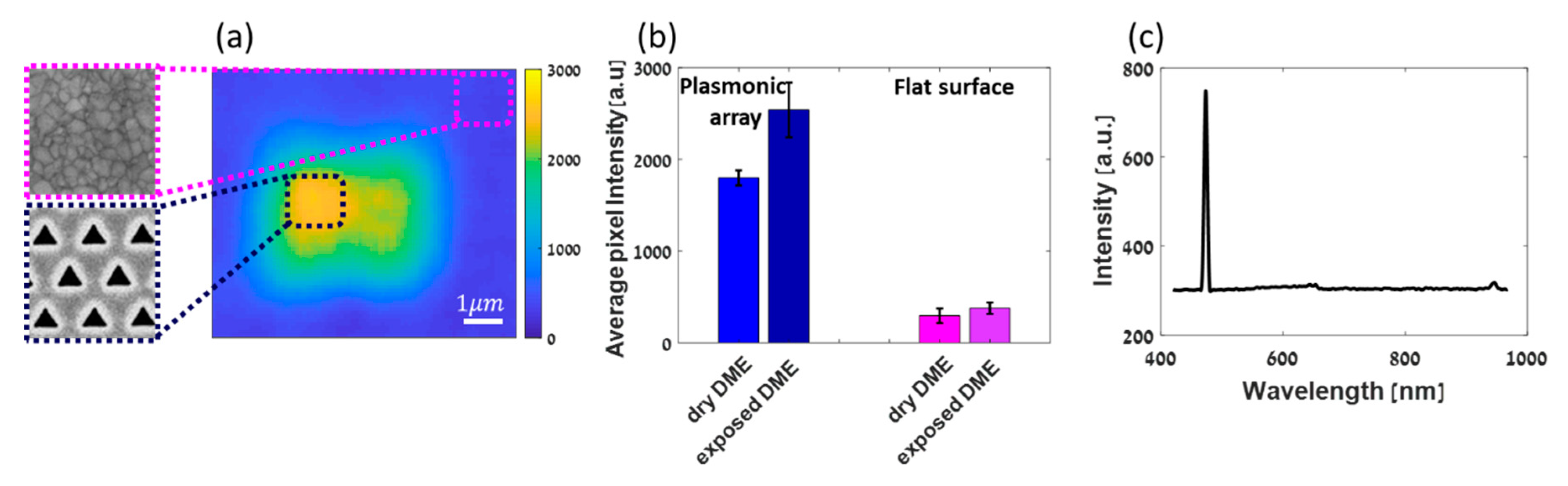
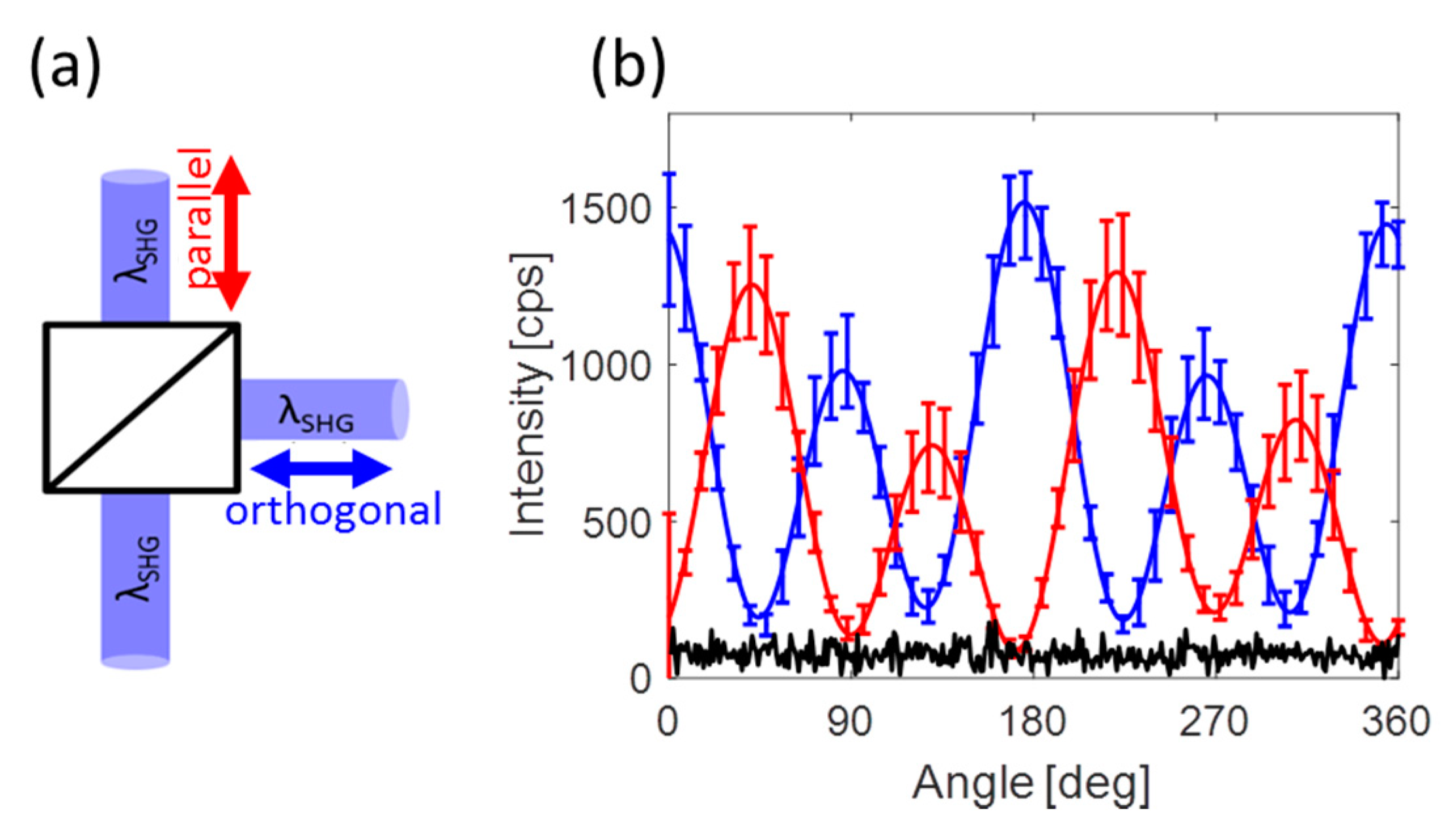
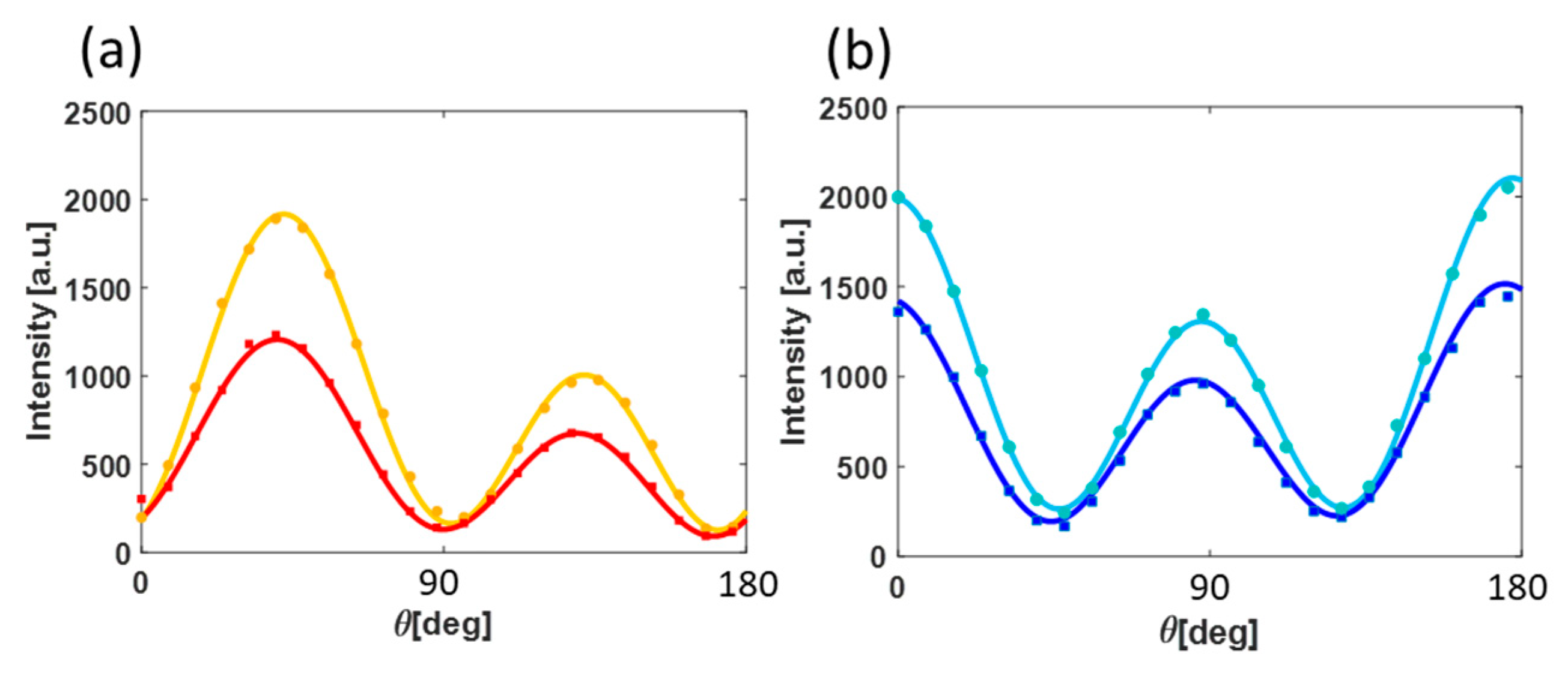
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McDowell, M.T.; Lee, S.W.; Harris, J.T.; Korgel, B.A.; Wang, C.; Nix, W.D.; Cui, Y. In situ TEM of two-phase lithiation of amorphous silicon nanospheres. Nano Lett. 2013, 13, 758–764. [Google Scholar] [CrossRef] [PubMed]
- Jensen, E.; Købler, C.; Jensen, P.S.; Mølhave, K. In-situ SEM microchip setup for electrochemical experiments with water based solutions. Ultramicroscopy 2013, 129, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Strelcov, E.; Cothren, J.; Leonard, D.; Borisevich, A.Y.; Kolmakov, A. In situ SEM study of lithium intercalation in individual V 2 O 5 nanowires. Nanoscale 2015, 7, 3022–3027. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.M.; Li, X.; Wang, Z.; Xu, W.; Liu, J.; Gao, F.; Kovarik, L.; Zhang, J.G.; Howe, J.; Burton, D.J.; et al. In situ TEM investigation of congruent phase transition and structural evolution of nanostructured silicon/carbon anode for lithium ion batteries. Nano Lett. 2012, 12, 1624–1632. [Google Scholar] [CrossRef]
- Yang, J.; Kraytsberg, A.; Ein-Eli, Y. In-situ Raman spectroscopy mapping of Si based anode material lithiation. J. Power Sources 2015, 282, 294–298. [Google Scholar] [CrossRef]
- Luo, Y.; Cai, W.-B.; Xing, X.; Scherson, D.A. In Situ, Time-Resolved Raman Spectromicrotopography of an Operating Lithium-Ion Battery. Electrochem. Solid-State Lett. 2004, 7, 5. [Google Scholar] [CrossRef][Green Version]
- Amalraj, S.F.; Aurbach, D. The use of in situ techniques in R D of Li and Mg rechargeable batteries. J Solid State Electrochem 2011, 15, 877–890. [Google Scholar]
- Moskovits, M. Surface-enhanced spectroscopy. Rev. Mod. Phys. 1985, 57, 783–826. [Google Scholar] [CrossRef]
- Corn, R.M.; Higgins, D.A. Optical second harmonic generation as a probe of surface chemistry. Chem. Rev. 1994, 94, 107–125. [Google Scholar] [CrossRef]
- Shen, Y.R. Optical Second Harmonic Generation at Interfaces. Annu. Rev. Phys. Chem. 1989, 40, 327–350. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Elsevier Inc.: London, UK, 2008; ISBN 0080485960. [Google Scholar]
- Giuliano Nicolau, B.; Garcia-Rey, N.; Dryzhakov, B.; Dlott, D.D. Interfacial Processes of a Model Lithium Ion Battery Anode Observed, in situ, with Vibrational Sum-Frequency Generation Spectroscopy. J. Phys. Chem. C 2015, 119, 10227–10233. [Google Scholar] [CrossRef]
- Johansson, P.K.; Schmüser, L.; Castner, D.G. Nonlinear Optical Methods for Characterization of Molecular Structure and Surface Chemistry. Top. Catal. 2018, 61, 1101–1124. [Google Scholar] [CrossRef] [PubMed]
- Peng, Q.; Chen, J.; Ji, H.; Morita, A.; Ye, S. Origin of the Overpotential for the Oxygen Evolution Reaction on a Well-Defined Graphene Electrode Probed by in Situ Sum Frequency Generation Vibrational Spectroscopy. J. Am. Chem. Soc. 2018. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.-T.; Shen, Y.R. In situ sum-frequency vibrational spectroscopy of electrochemical interfaces with surface plasmon resonance. PNAS 2014, 111, 1293–1297. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Li, Y.; Liu, X.; Cao, Y.; Gao, Y.; Shen, Y.R.; Liu, W.-T. Facet-specific interaction between methanol and TiO2 probed by sum-frequency vibrational spectroscopy. Proc. Natl. Acad. Sci. USA 2018, 115, E3888–E3894. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.K.; de Castro, A.R.B.; Shen, Y.R. Surface-Enhanced Second-Harmonic Generation. Phys. Rev. Lett. 1981, 46, 145–148. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, Z.; Zhu, H.; Jin, L.; Chiu, M.-H.; Li, L.-J.; Xu, Q.-H.; Eda, G.; Maier, S.A.; Wee, A.T.S.; et al. Selectively Plasmon-Enhanced Second-Harmonic Generation from Monolayer Tungsten Diselenide on Flexible Substrates. ACS Nano 2018, 12, 1859–1867. [Google Scholar] [CrossRef]
- De Hoogh, A.; Opheij, A.; Wulf, M.; Rotenberg, N.; Kuipers, L. Harmonics Generation by Surface Plasmon Polaritons on Single Nanowires. ACS Photonics 2016, 3, 1446–1452. [Google Scholar] [CrossRef]
- Naraoka, R.; Okawa, H.; Hashimoto, K.; Kajikawa, K. Surface plasmon resonance enhanced second-harmonic generation in Kretschmann configuration. Opt. Commun. 2005, 248, 249–256. [Google Scholar] [CrossRef]
- Shen, Y. Surfaces probed by nonlinear optics. Surf. Sci. 1994, 299–300, 551–562. [Google Scholar] [CrossRef]
- Zhuang, X.; Miranda, P.B.; Kim, D.; Shen, Y.R. Mapping molecular orientation and conformation at interfaces by surface nonlinear optics. Phys. Rev. B 1999, 59, 632–640. [Google Scholar] [CrossRef]
- Valev, V.K.; De Clercq, B.; Biris, C.G.; Zheng, X.; Vandendriessche, S.; Hojeij, M.; Denkova, D.; Jeyaram, Y.; Panoiu, N.C.; Ekinci, Y.; et al. Distributing the Optical Near-Field for Efficient Field-Enhancements in Nanostructures. Adv. Mater. 2012, 24, OP208–OP215. [Google Scholar] [CrossRef] [PubMed]
- Zielinski, M.; Oron, D.; Chauvat, D.; Zyss, J. Second-Harmonic Generation from a Single Core/Shell Quantum Dot. Small 2009, 5, 2835–2840. [Google Scholar] [CrossRef] [PubMed]
- Guyot-Sionnest, P.; Chen, W.; Shen, Y.R. General considerations on optical second-harmonic generation from surfaces and interfaces. Phys. Rev. B 1986, 33, 8254. [Google Scholar] [CrossRef]
- Salomon, A.; Zielinski, M.; Kolkowski, R.; Zyss, J.; Prior, Y. Size and Shape Resonances in Second Harmonic Generation from Silver Nanocavities. J. Phys. Chem. C 2013, 117, 22377–22382. [Google Scholar] [CrossRef]
- Galanty, M.; Shavit, O.; Weissman, A.; Aharon, H.; Gachet, D.; Segal, E.; Salomon, A. Second harmonic generation hotspot on a centrosymmetric smooth silver surface. Light Sci. Appl. 2018, 7, 49. [Google Scholar] [CrossRef] [PubMed]
- Salomon, A.; Prior, Y.; Fedoruk, M.; Feldmann, J.; Kolkowski, R.; Zyss, J. Plasmonic coupling between metallic nanocavities. J. Opt. 2014, 16. [Google Scholar] [CrossRef]
- Segal, E.; Haleva, E.; Salomon, A. Ultrasensitive Plasmonic Sensor for Detecting Sub-PPB Levels of Alachlor. ACS Appl. Nano Mater. 2019, 2, 1285–1293. [Google Scholar] [CrossRef]
- Segal, E.; Weissman, A.; Gachet, D.; Salomon, A. Hybridization between nanocavities for a polarimetric color sorter at the sub-micron scale. Nanoscale 2016. [Google Scholar] [CrossRef]
- Weissman, A.; Galanty, M.; Gachet, D.; Segal, E.; Shavit, O.; Salomon, A. Spatial Confinement of Light onto a Flat Metallic Surface Using Hybridization between Two Cavities. Adv. Opt. Mater. 2017. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007; ISBN 0387331506. [Google Scholar]
- Kauranen, M.; Zayats, A.V. Nonlinear plasmonics. Nat. Photonics 2012, 6, 737–748. [Google Scholar] [CrossRef]
- Almeida, E.; Bitton, O.; Prior, Y. Nonlinear metamaterials for holography. Nat. Commun. 2016, 7, 12533. [Google Scholar] [CrossRef]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2006; ISBN 9780511813535. [Google Scholar]
- Lerman, G.M.; Yanai, A.; Levy, U. Demonstration of Nanofocusing by the use of Plasmonic Lens Illuminated with Radially Polarized Light. Nano Lett. 2009, 9, 2139–2143. [Google Scholar] [CrossRef] [PubMed]
- García de Abajo, F.J. Colloquium: Light scattering by particle and hole arrays. Rev. Mod. Phys. 2007, 79, 1267–1290. [Google Scholar] [CrossRef]
- Genet, C.; Ebbesen, T.W. Light in tiny holes. Nature 2007, 445, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Wokaun, A.; Bergman, J.G.; Heritage, J.P.; Glass, A.M.; Liao, P.F.; Olson, D.H. Surface second-harmonic generation from metal island films and microlithographic structures. Phys. Rev. B 1981, 24, 849–856. [Google Scholar] [CrossRef]
- O’Brien, K.; Suchowski, H.; Rho, J.; Salandrino, A.; Kante, B.; Yin, X.; Zhang, X. Predicting nonlinear properties of metamaterials from the linear response. Nat. Mater. 2015, 14, 379–383. [Google Scholar] [CrossRef]
- Wurtz, G.A.; Pollard, R.; Hendren, W.; Wiederrecht, G.P.; Gosztola, D.J.; Podolskiy, V.A.; Zayats, A.V. Designed ultrafast optical nonlinearity in a plasmonic nanorod metamaterial enhanced by nonlocality. Nat. Nanotechnol. 2011, 6, 107–111. [Google Scholar] [CrossRef]
- Ngo, H.M.; Luong, T.T.; Ledoux-Rak, I. Surface area-dependent second harmonic generation from silver nanorods. Phys. Chem. Chem. Phys. 2016, 18, 23215–23219. [Google Scholar] [CrossRef]
- Butet, J.; Brevet, P.-F.; Martin, O.J.F. Optical Second Harmonic Generation in Plasmonic Nanostructures: From Fundamental Principles to Advanced Applications. ACS Nano 2015, 9, 10545–10562. [Google Scholar] [CrossRef]
- Butet, J.; Yang, K.-Y.; Dutta-Gupta, S.; Martin, O.J.F. Maximizing Nonlinear Optical Conversion in Plasmonic Nanoparticles through Ideal Absorption of Light. ACS Photonics 2016, 3, 1453–1460. [Google Scholar] [CrossRef]
- Anceau, C.; Brasselet, S.; Zyss, J.; Gadenne, P. Local second-harmonic generation enhancement on gold nanostructures probed by two-photon microscopy. Opt. Lett. 2003, 28, 713. [Google Scholar] [CrossRef]
- Breit, M.; von Plessen, G.; Feldmann, J.; Gresillon, S.; Rivoal, J.C.; Gadenne, P.; Podolskiy, V.A.; Sarychev, A.K.; Shalaev, V.M. Experimental observation of percolation-enhanced nonlinear light scattering from semicontinuous metal films. Phys. Rev. B 2001, 64, 125106. [Google Scholar] [CrossRef]
- Celebrano, M.; Wu, X.; Baselli, M.; Großmann, S.; Biagioni, P.; Locatelli, A.; De Angelis, C.; Cerullo, G.; Osellame, R.; Hecht, B.; et al. Mode matching in multiresonant plasmonic nanoantennas for enhanced second harmonic generation. Nat. Nanotechnol. 2015, 10, 412–417. [Google Scholar] [CrossRef] [PubMed]
- Valev, V.K. Characterization of Nanostructured Plasmonic Surfaces with Second Harmonic Generation. Langmuir 2012, 28, 15454–15471. [Google Scholar] [CrossRef] [PubMed]
- Viter, R.; Balevicius, Z.; Abou Chaaya, A.; Baleviciute, I.; Tumenas, S.; Mikoliunaite, L.; Ramanavicius, A.; Gertnere, Z.; Zalesska, A.; Vataman, V.; et al. The influence of localized plasmons on the optical properties of Au/ZnO nanostructures. J. Mater. Chem. C 2015, 3, 6815–6821. [Google Scholar] [CrossRef]
- Salama, M.; Shterenberg, I.; Gizbar, H.; Eliaz, N.N.; Kosa, M.; Keinan-Adamsky, K.; Afri, M.; Shimon, L.J.W.; Gottlieb, H.E.; Major, D.T.; et al. Unique Behavior of Dimethoxyethane (DME)/Mg(N(SO2CF3)2)2Solutions. J. Phys. Chem. C 2016, 120, 19586–19594. [Google Scholar] [CrossRef]
- Cheng, Y.; Stolley, R.M.; Han, K.S.; Shao, Y.; Arey, B.W.; Washton, N.M.; Mueller, K.T.; Helm, M.L.; Sprenkle, V.L.; Liu, J.; et al. Highly active electrolytes for rechargeable Mg batteries based on a [Mg 2 (μ-Cl) 2 ] 2+ cation complex in dimethoxyethane. Phys. Chem. Chem. Phys. 2015, 17, 13307–13314. [Google Scholar] [CrossRef] [PubMed]
- Nickolov, Z.S.; Goutev, N.; Matsuura, H. Hydrogen bonding in concentrated aqueous solutions of 1,2-dimethoxyethane: Formation of water clusters. J. Phys. Chem. A 2001, 105, 10884–10889. [Google Scholar] [CrossRef]
- Hou, R.; Shynkar, V.; Lafargue, C.; Kolkowski, R.; Zyss, J.; Lagugné-Labarthet, F. Second harmonic generation from gold meta-molecules with three-fold symmetry. Phys. Chem. Chem. Phys. 2016, 18, 7956–7965. [Google Scholar] [CrossRef]
- Grande, M.D.C.; Alvarez Juliá, J.; Barrero, C.R.; Marschoff, C.M. Density, sound velocity and refractive index in the water + 1,2-dimethoxyethane system. Phys. Chem. Liq. 2015, 53, 403–417. [Google Scholar] [CrossRef]
- Duboisset, J.; Brevet, P.F. Salt-induced Long-to-Short Range Orientational Transition in Water. Phys. Rev. Lett. 2018, 120, 263001. [Google Scholar] [CrossRef]
- Macias-romero, C.; Nahalka, I.; Okur, H.I.; Roke, S. Optical imaging of surface chemistry and dynamics in confinement. Science. 2017, 357, 784–788. [Google Scholar] [CrossRef]
- Flauraud, V.; Regmi, R.; Winkler, P.M.; Alexander, D.T.L.; Rigneault, H.; Van Hulst, N.F.; García-Parajo, M.F.; Wenger, J.; Brugger, J. In-Plane Plasmonic Antenna Arrays with Surface Nanogaps for Giant Fluorescence Enhancement. Nano Lett. 2017, 17, 1703–1710. [Google Scholar] [CrossRef] [PubMed]
- Esteban, R.; Borisov, A.G.; Nordlander, P.; Aizpurua, J. Bridging quantum and classical plasmonics with a quantum-corrected model. Nat. Commun. 2012, 3, 825. [Google Scholar] [CrossRef] [PubMed]
- Kausaite-Minkstimiene, A.; Ramanaviciene, A.; Ramanavicius, A. Surface plasmon resonance biosensor for direct detection of antibodies against human growth hormone. Analyst 2009, 134, 2051–2057. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aharon, H.; Shavit, O.; Galanty, M.; Salomon, A. Second Harmonic Generation for Moisture Monitoring in Dimethoxyethane at a Gold-Solvent Interface Using Plasmonic Structures. Nanomaterials 2019, 9, 1788. https://doi.org/10.3390/nano9121788
Aharon H, Shavit O, Galanty M, Salomon A. Second Harmonic Generation for Moisture Monitoring in Dimethoxyethane at a Gold-Solvent Interface Using Plasmonic Structures. Nanomaterials. 2019; 9(12):1788. https://doi.org/10.3390/nano9121788
Chicago/Turabian StyleAharon, Hannah, Omer Shavit, Matan Galanty, and Adi Salomon. 2019. "Second Harmonic Generation for Moisture Monitoring in Dimethoxyethane at a Gold-Solvent Interface Using Plasmonic Structures" Nanomaterials 9, no. 12: 1788. https://doi.org/10.3390/nano9121788
APA StyleAharon, H., Shavit, O., Galanty, M., & Salomon, A. (2019). Second Harmonic Generation for Moisture Monitoring in Dimethoxyethane at a Gold-Solvent Interface Using Plasmonic Structures. Nanomaterials, 9(12), 1788. https://doi.org/10.3390/nano9121788




