Influence of Nanoscale Textured Surfaces and Subsurface Defects on Friction Behaviors by Molecular Dynamics Simulation
Abstract
1. Introduction
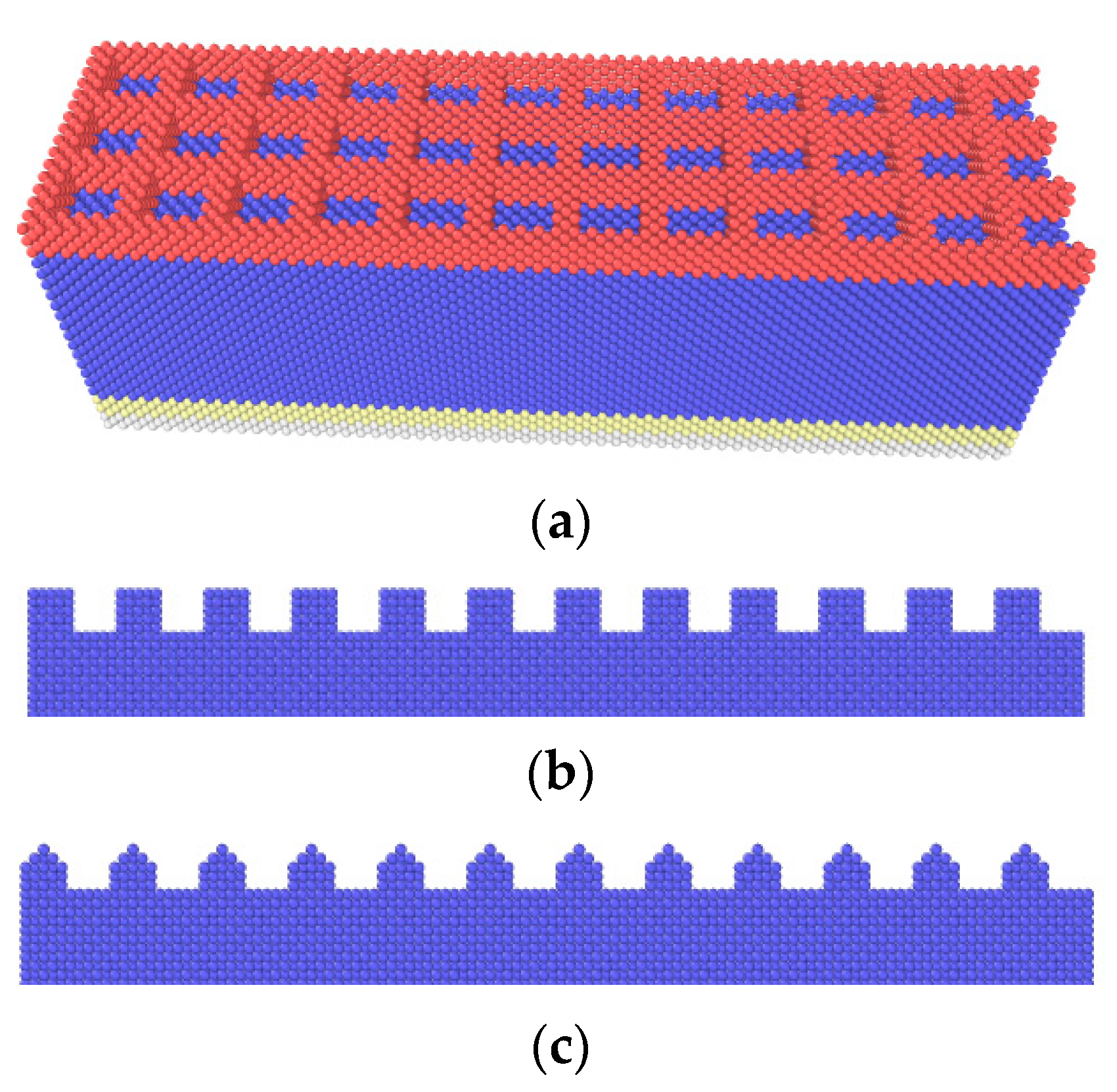
2. Model Description
3. Results and Discussion
3.1. The Influence of Textured Surface on Sliding Contacts
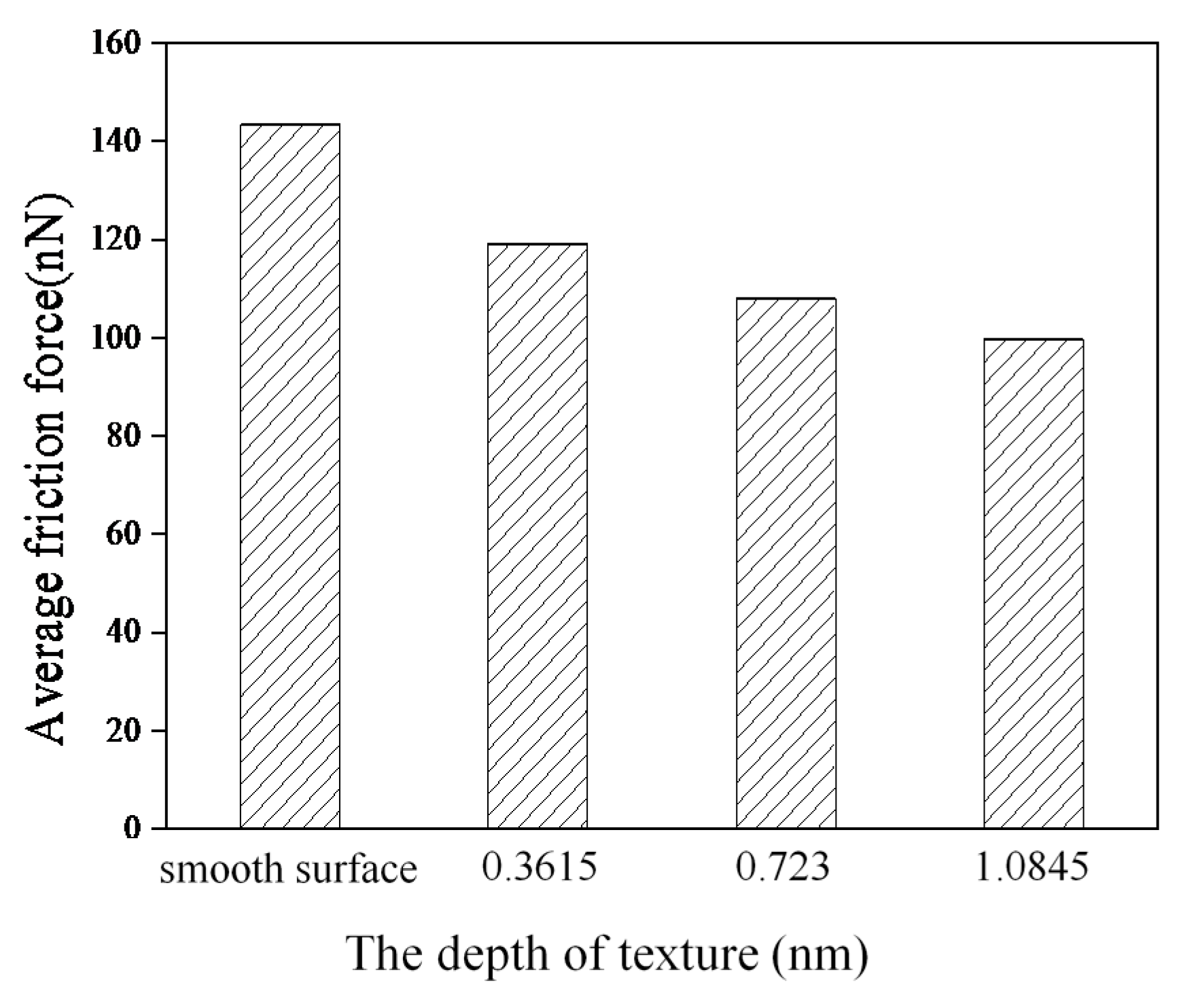
3.1.1. Effects of Texture Depth
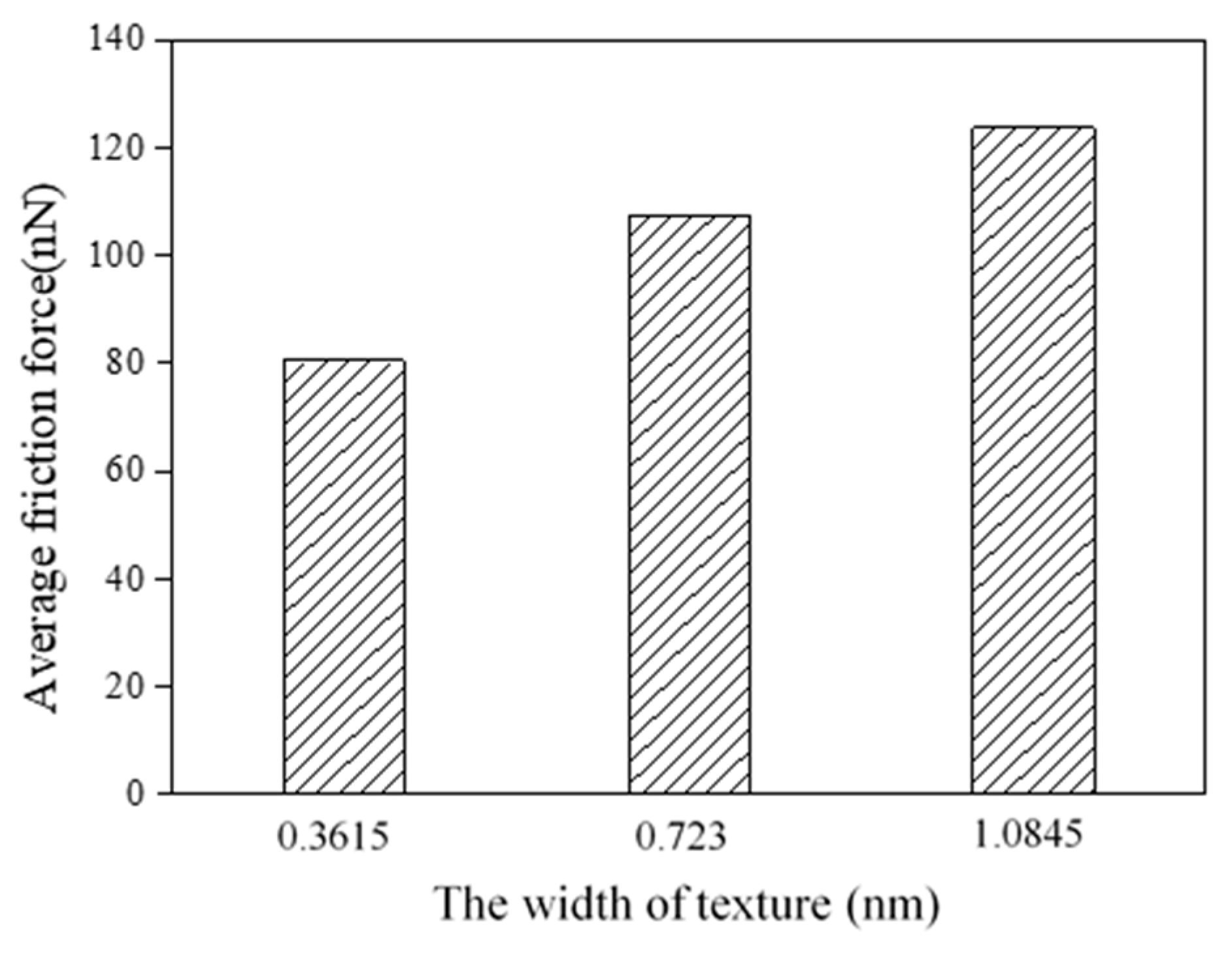
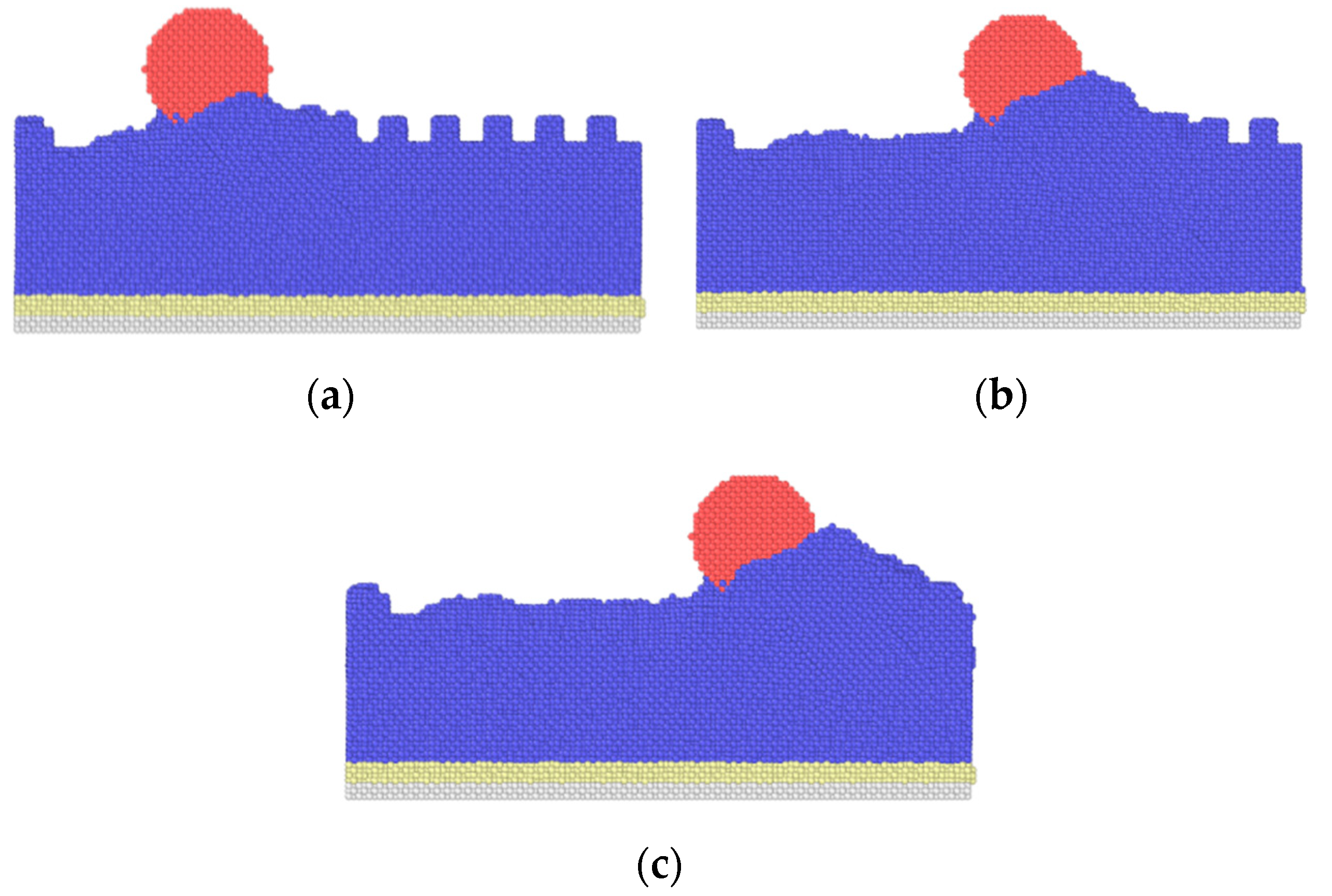
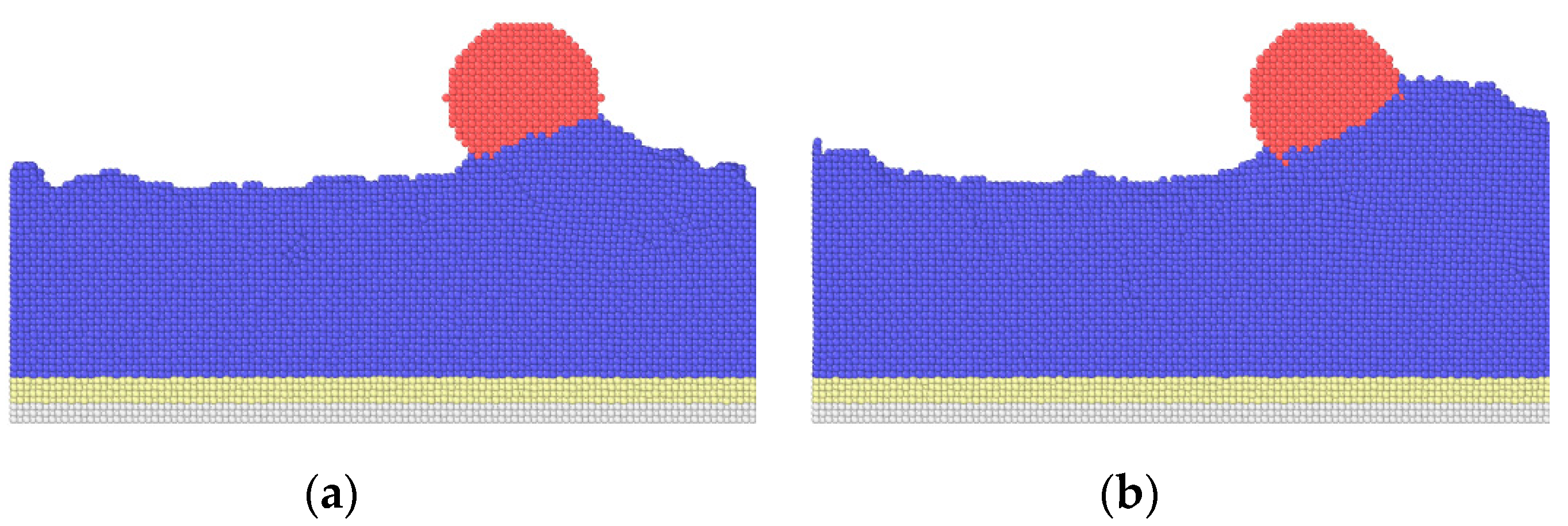
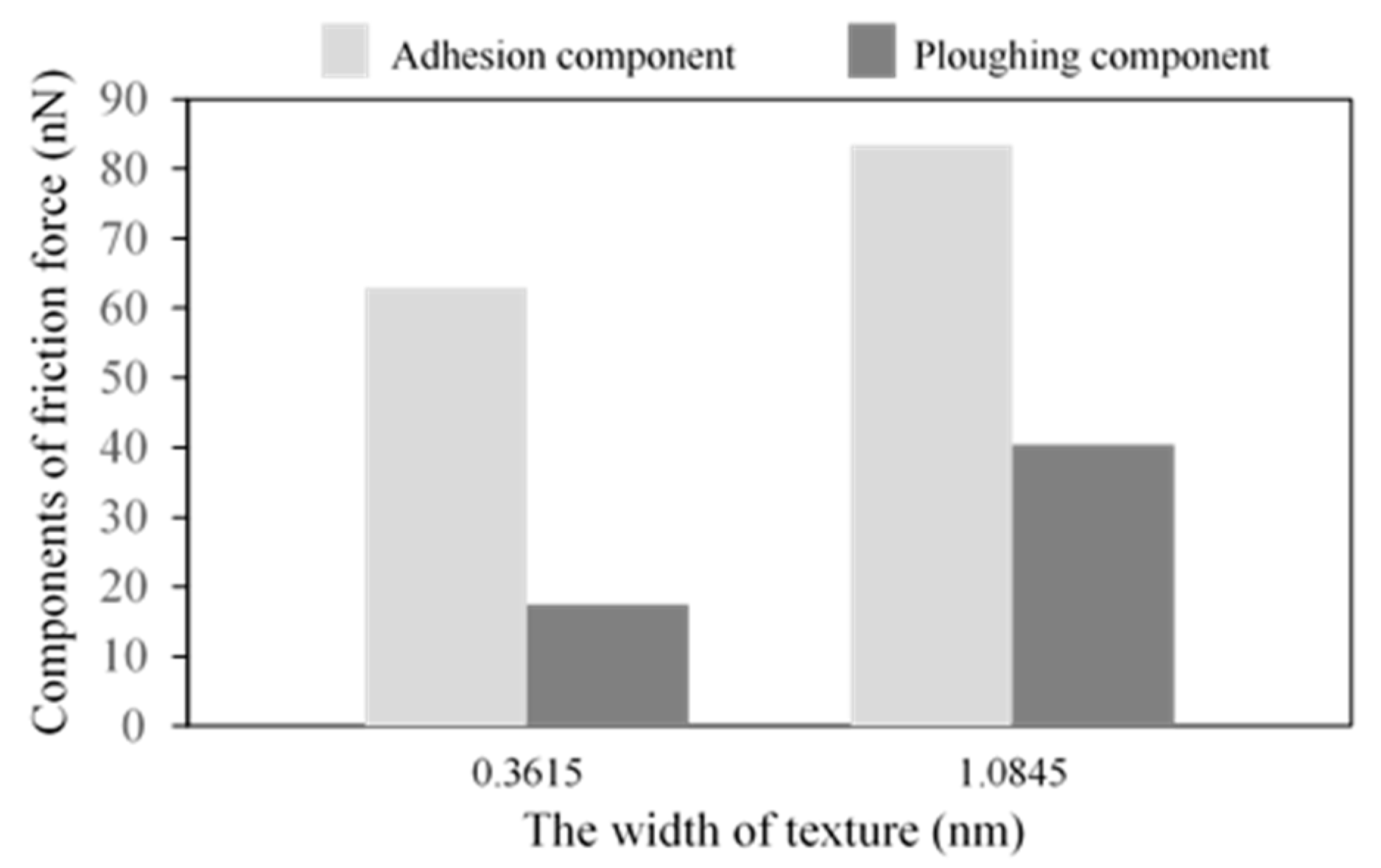
3.1.2. Effects of Texture Width
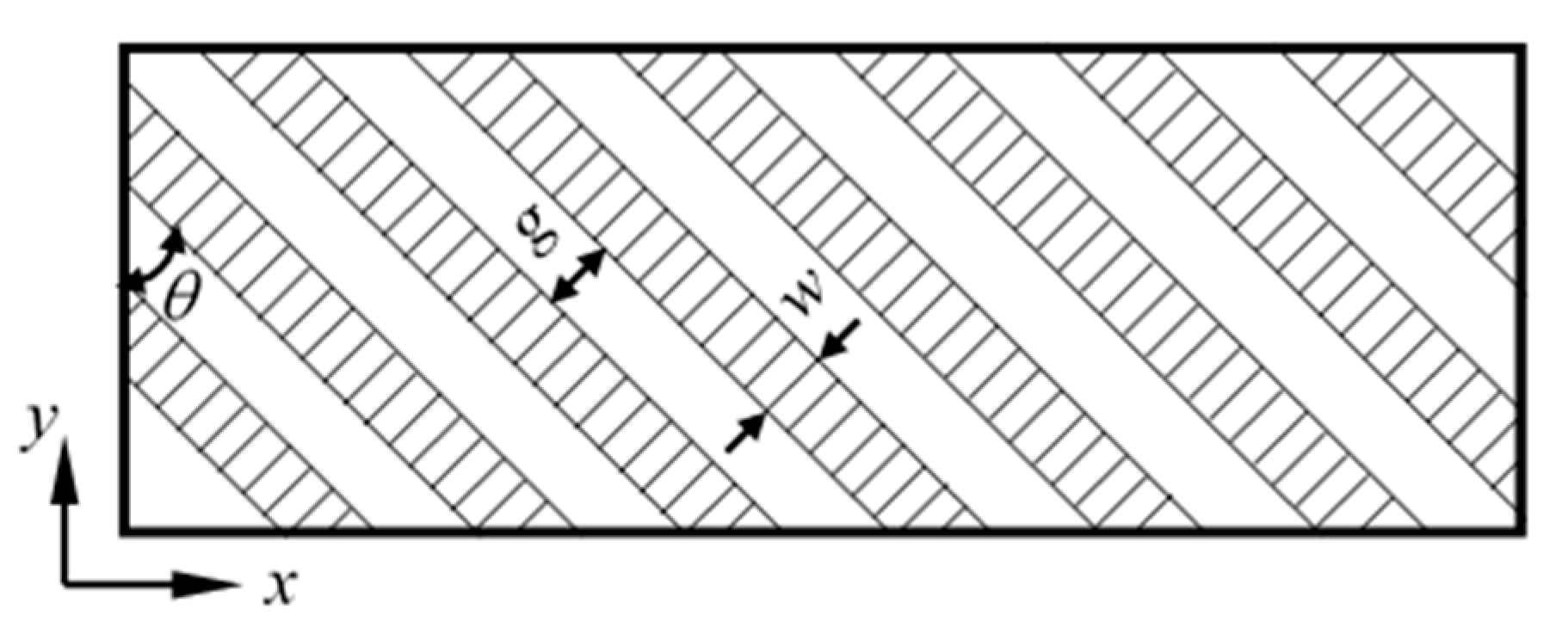
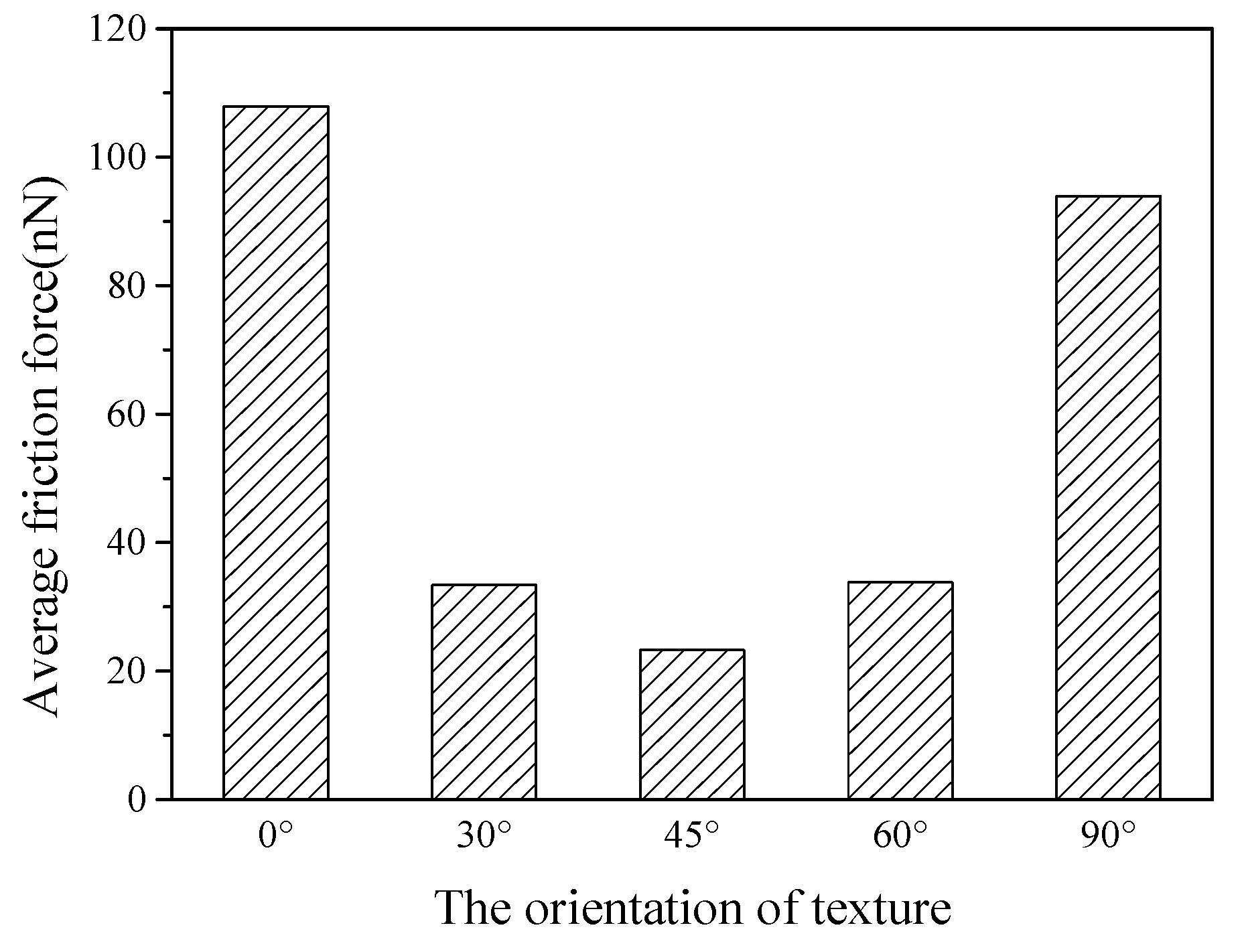
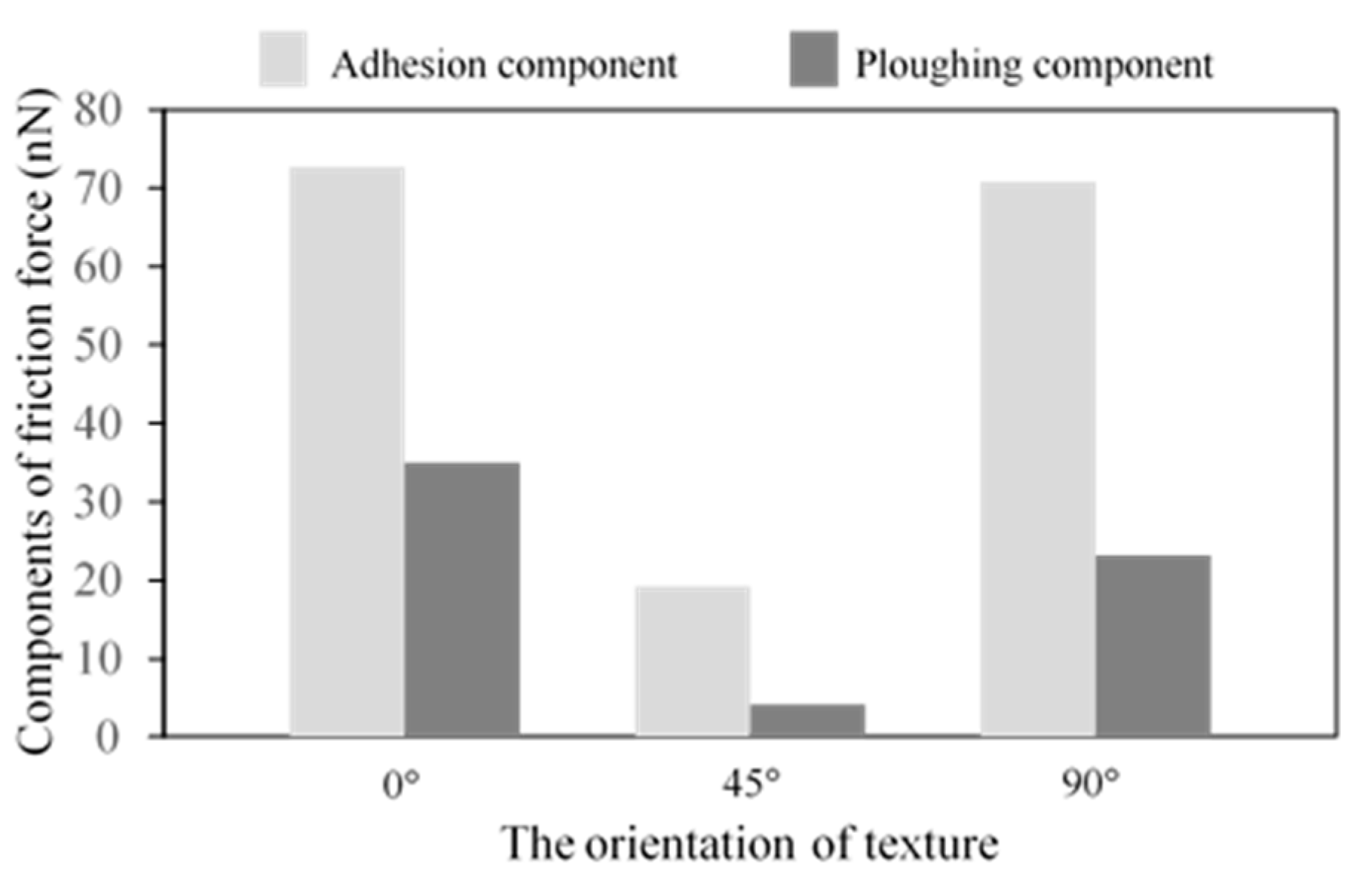
3.1.3. Effects of Texture Orientation
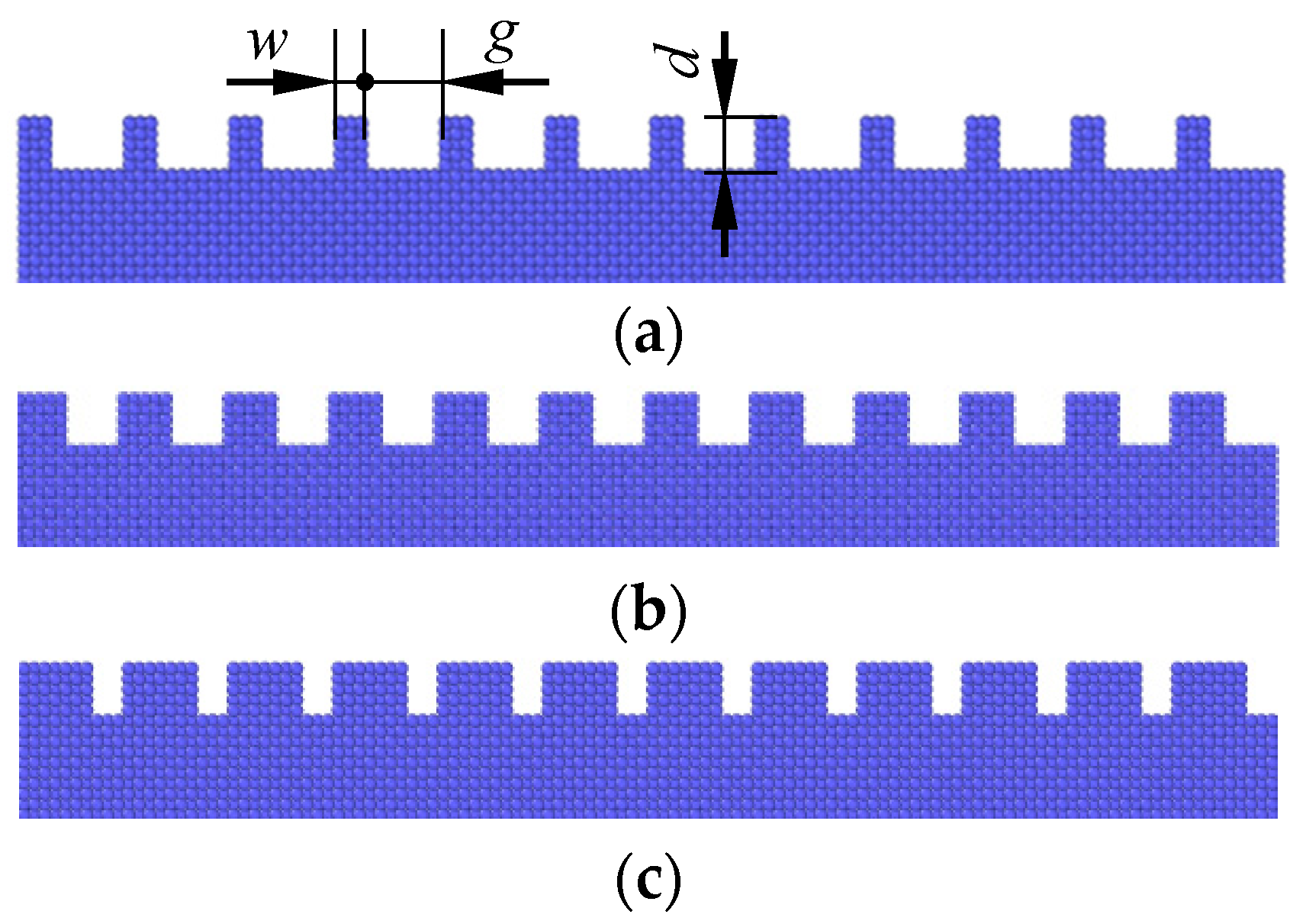
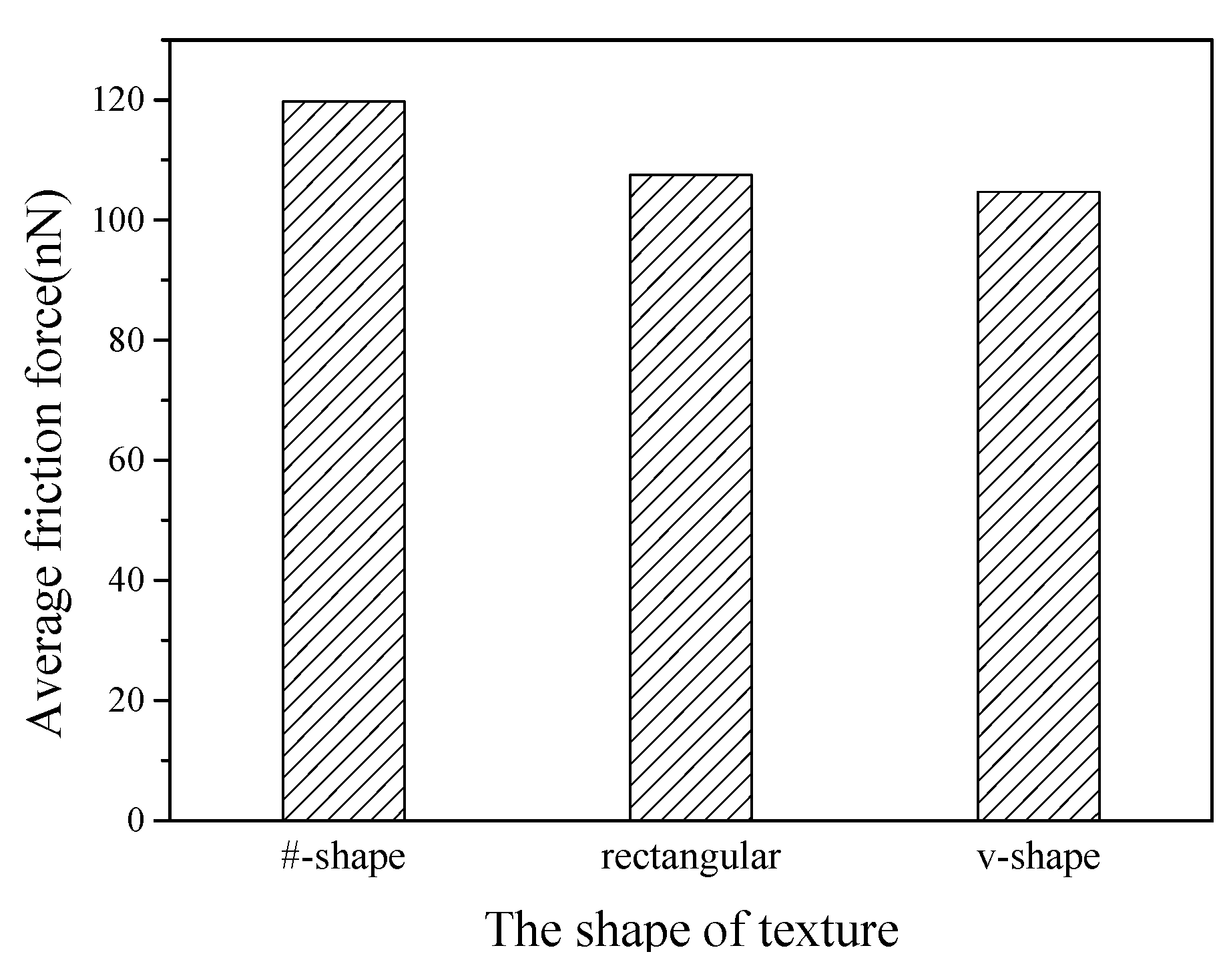
3.1.4. Effects of Texture Shape
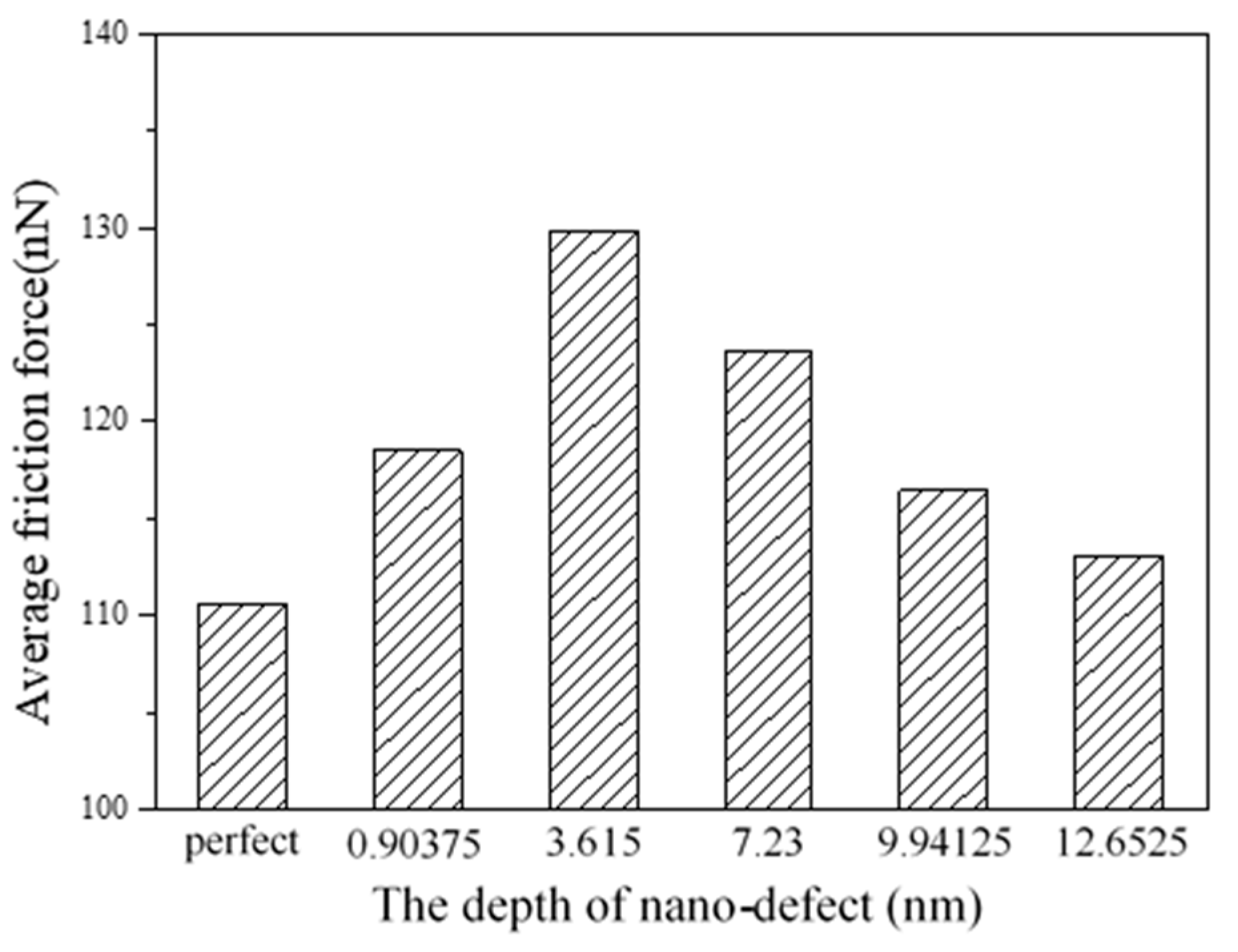
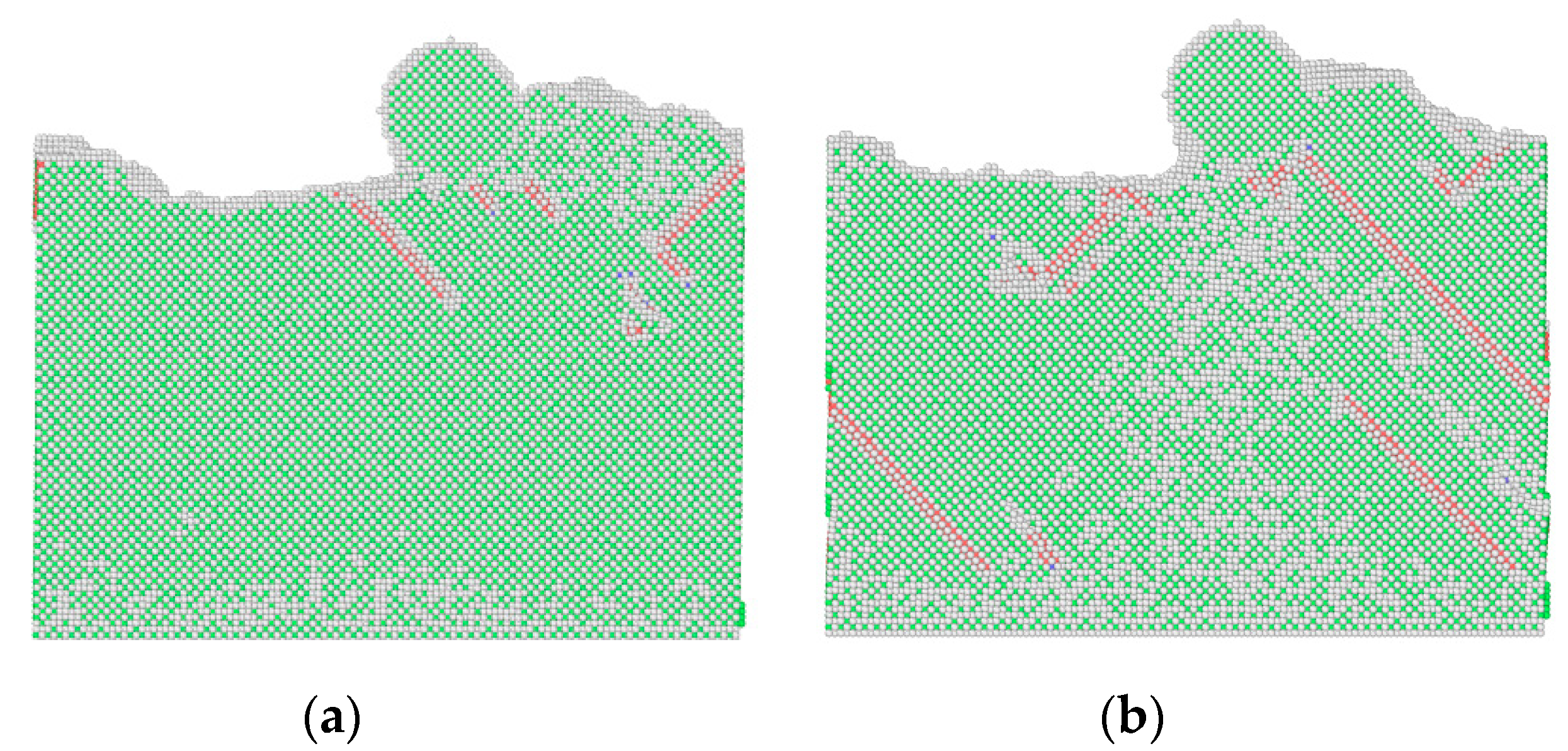
3.2. The Influence of Subsurface Defect on Sliding Contact
4. Conclusions
- (1)
- Compared with a smooth surface, textured surfaces can reduce friction forces effectively. In addition, the textured surfaces with a higher depth and smaller width lead to lower average friction forces.
- (2)
- For the texture surfaces with the orientations of 0° and 90°, the average friction forces are higher than those with orientations of 30°, 45° and 60°, and the textured surface with 45° orientation produces the lowest average friction force.
- (3)
- The effects of texture shape on friction behaviors are slight compared with the effects of depth, width and orientation, and the v-shape shows a lower average friction force.
- (4)
- The nanoscale ball defects in the substrate make the sliding process unstable. In this paper, when the depth of the ball defects is h = 3.615 nm, the influence of defects on the average friction force is the greatest. When the depth is greater than 3.615 nm, the average friction forces decrease with the increase in depth, and they tend to be close to that of a perfect substrate.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bhushan, B. Nanotribology and Nanomechanics of MEMS/NEMS and BioMEMS/BioNEMS Materials and Devices. Microelectron. Eng. 2007, 84, 387–412. [Google Scholar] [CrossRef]
- Qi, Y.; Cheng, Y.T.; Çağin, T.; Goddard, W.A., III. Friction Anisotropy at Ni(100)/(100) Interfaces: Molecular Dynamics Studies. Phys. Rev. B 2002, 66, 085420. [Google Scholar] [CrossRef]
- Jung, Y.C.; Bhushan, B. Contact Angle, Adhesion and Friction Properties of Micro-and Nanopatterned Polymers for Superhydrophobicity. Nanotechnology 2006, 17, 4970–4980. [Google Scholar] [CrossRef]
- Wang, H.; Nair, R.; Zou, M.; Larson, P.R.; Pollack, A.L.; Hobbs, K.; Johnson, M.B.; Awitor, O. Friction Study of a Ni Nanodot-Patterned Surface. Tribol. Lett. 2007, 28, 183–189. [Google Scholar] [CrossRef]
- Song, Y.; Nair, R.; Zou, M.; Wang, Y.A. Adhesion and Friction Properties of Micro/Nanoengineered Superhydrophobic/Hydrophobic Surfaces. Thin Solid Films 2010, 518, 3801–3807. [Google Scholar] [CrossRef]
- Fleming, R.A.; Zou, M. Nanostructure-Textured Surfaces with Low Friction and High Deformation Resistance. Tribol. Trans. 2018, 61, 80–87. [Google Scholar] [CrossRef]
- Yee, Y.; Chun, K.; Lee, J.D.; Kim, C.-J. Polysilicon Surface-Modification Technique to Reduce Sticking of Microstructures. Sens. Actuators A 1996, 52, 145–150. [Google Scholar] [CrossRef]
- Zou, M.; Cai, L.; Wang, H. Adhesion and Friction Studies of a Nano-Textured Surface Produced by Spin Coating of Colloidal Silica Nanoparticle Solution. Tribol. Lett. 2006, 21, 25–30. [Google Scholar] [CrossRef]
- Nair, R.P.; Zou, M. Surface-Nano-Texturing by Aluminum-Induced Crystallization of Amorphous Silicon. Surf. Coat. Technol. 2008, 203, 675–679. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Xue, Q. Design and Fabrication of Nanopillar Patterned Au Textures for Improving Nanotribological Performance. ACS Appl. Mater. Interfaces 2010, 2, 788–794. [Google Scholar] [CrossRef]
- Zhang, X.L.; Lu, Y.J.; Zhong, X.H.; Yi, G.W.; Jia, J.H. Adhesion and Friction Studies of Au Nanoparticle-Textured Surfaces with Colloidal Tips. Surf. Interface Anal. 2012, 44, 126–132. [Google Scholar] [CrossRef]
- Yu, C.J.; Yu, H.L.; Liu, G.; Chen, W.; He, B.; Wang, Q.J. Understanding Topographic Dependence of Friction with Micro- and Nano-Grooved Surfaces. Tribol. Lett. 2014, 53, 145–156. [Google Scholar] [CrossRef]
- Wu, C.X.; Jia, J.H.; Che, H.W.; Mu, J.B.; Zhao, S.F.; Zhang, X.L. Frictional Behaviors of Three Kinds of Nanotextured Surfaces. Surf. Interface Anal. 2016, 48, 1056–1061. [Google Scholar] [CrossRef]
- Steck, J.G.; Afshar-Mohajer, M.; Sun, Q.; Meng, X.B.; Zou, M. Fabrication and Tribological Characterization of Deformation-Resistant Nanotextured Surfaces Produced by Two-Photon Lithography and Atomic Layer Deposition. Tribol. Int. 2019, 132, 75–84. [Google Scholar] [CrossRef]
- Zhang, Q.; Qi, Y.; Hector, L.G., Jr.; Çağın, T.; Goddard, W.A., III. Atomic Simulations of Kinetic Friction and Its Velocity Dependence at Al/Al and α-Al2O3/α-Al2O3 Interfaces. Phys. Rev. B 2005, 72, 045406. [Google Scholar] [CrossRef]
- Chen, M.Y.; Hong, Z.H.; Fang, T.H.; Kang, S.H.; Kuo, L.M. Atomistic Scale Simulation of Textured Surfaces on Dry Sliding Friction. Trans. Can. Soc. Mech. Eng. 2013, 27, 927–936. [Google Scholar] [CrossRef]
- Li, J.; Fang, Q.H.; Zhang, L.C.; Li, Y.W. The Effect of Rough Surface on Nanoscale High Speed Grinding by a Molecular Dynamics Simulation. Comput. Mater. Sci. 2015, 98, 252–262. [Google Scholar] [CrossRef]
- Santhapuram, R.R.; Nair, A.K. Frictional Properties of Multi-Asperity Surfaces at the Nanoscale. Comput. Mater. Sci. 2017, 136, 253–263. [Google Scholar] [CrossRef]
- Tong, R.T.; Liu, G.; Liu, T.X. Multiscale Analysis on Two Dimensional Nanoscale Sliding Contacts of Textured Surfaces. ASME J. Tribol. 2011, 133, 041401. [Google Scholar] [CrossRef]
- Tong, R.T.; Liu, G. Nanoscale Reciprocating Sliding Contacts of Textured Surfaces: Influence of Structure Parameters and Indentation Depth. Chin. J. Mech. Eng. 2018, 31, 62. [Google Scholar] [CrossRef]
- Tong, R.T.; Quan, Z.F.; Han, B.; Liu, G. Coarse-Grained Molecular Dynamics Simulation on Friction Behaviors of Textured Ag-Coating under Vacuum and Microgravity Environments. Surf. Coat. Technol. 2019, 359, 265–271. [Google Scholar] [CrossRef]
- Tong, R.T.; Han, B.; Quan, Z.F.; Liu, G. Molecular Dynamics Simulation of Friction and Heat Properties of Nano-texture Gold Film in Space Environment. Surf. Coat. Technol. 2019, 358, 775–784. [Google Scholar] [CrossRef]
- Hone, J.; Whitney, M.; Piskoti, C.; Zettl, A. Thermal Conductivity of Single-Walled Carbon Nanotubes. Phys. Rev. B 1999, 59, 2514–2516. [Google Scholar] [CrossRef]
- Che, J.; Cagin, T.; Goddard, W.A., III. Thermal Conductivity of Carbon Nanotubes. Nanotechnology 2000, 11, 65–69. [Google Scholar] [CrossRef]
- Li, M.Y.; Deng, T.Z.X.; Zheng, B.; Zhang, Y.; Liao, Y.G.; Zhou, H.M. Effect of Defects on the Mechanical and Thermal Properties of Graphene. Nanomaterials 2019, 9, 347. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.; An, H.J.; He, C.W.; Qin, Q.; Peng, Q. Mechanical Properties of Vacancy Tuned Carbon Honeycomb. Nanomaterials 2019, 9, 156. [Google Scholar] [CrossRef] [PubMed]
- Kopta, S.; Salmeron, M. The Atomic Scale Origin of Wear on Mica and Its Contribution to Friction. J. Chem. Phys. 2000, 113, 8249–8252. [Google Scholar] [CrossRef]
- Gajurel, P.; Kim, M.; Wang, Q.; Dai, W.T.; Liu, H.T.; Cen, C. Vacancy-Controlled Contact Friction in Graphene. Adv. Funct. Mater. 2017, 27, 1702832. [Google Scholar] [CrossRef]
- Guo, Y.F.; Guo, W.L.; Chen, C.F. Modifying Atomic-Scale Friction between Two Graphene Sheets: A Molecular-Force-Field Study. Phys. Rev. B 2007, 76, 155429. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, Y.W. A Theoretical Analysis of Frictional and Defect Characteristics of Graphene Probed by a Capped Single-Walled Carbon Nanotube. Carbon 2011, 49, 3687–3697. [Google Scholar] [CrossRef]
- Sun, X.Y.; Wu, R.N.; Xia, R.; Chu, X.H.; Xu, Y.J. Effects of Stone-Wales and Vacancy Defects in Atomic-Scale Friction on Defective Graphite. Appl. Phys. Lett. 2014, 104, 183109. [Google Scholar] [CrossRef]
- Chen, Z.T.; Xiong, W.; Xu, G.; Li, Y.M.; Mei, H.P.; Ding, T.; Xiao, S.F. Study on Molecular Dynamics of the Effect of Defects on the Friction Properties of Single Crystal Metals. Ferroelectrics 2019, 546, 98–108. [Google Scholar]
- LAMMPS Molecular Dynamics Simulator. Available online: http://lammps.sandia.gov (accessed on 13 November 2019).
- OVITO Open Visualization Tool. Available online: http://www.ovito.org (accessed on 13 November 2019).
- Dai, H.F.; Chen, G.Y.; Li, S.B.; Fang, Q.H.; Hu, B. Influence of Laser Nanostructured Diamond Tools on the Cutting Behavior of Silicon by Molecular Dynamics Simulation. R. Soc. Chem. 2017, 7, 15596–15612. [Google Scholar] [CrossRef]
- Swope, W.C.; Andersen, H.C.; Berens, P.H. A Computer Simulation Method for the Calculation of Equilibrium Constants for the Formation of Physical Clusters of Molecules: Application to Small Water Cluster. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Moore, D.F. Principles and Applications of Tribology, 1st ed.; Pergamon Press: Oxford, UK, 1975; pp. 44–46. [Google Scholar]
- Stephen, H.; Charles, Y.; Fei, Z. The Nature of Friction: A Critical Assessment. Friction 2014, 2, 1–26. [Google Scholar]
- Kim, H.J.; Kim, D.E. Nano-Scale Friction: A Review. Int. J. Precis. Eng. Manuf. 2009, 10, 141–151. [Google Scholar] [CrossRef]
- Müser, M.H. Structural Lubricity: Role of Dimension and Symmetry. Europhys. Lett. 2003, 66, 97–103. [Google Scholar] [CrossRef]
- Dienwiebel, M.; Verhoeven, G.S.; Pradeep, N.; Frenken, J.W.M.; Heimberg, J.A.; Zandbergen, H.W. Superlubricity of Graphite. Phys. Rev. Lett. 2004, 92, 126101. [Google Scholar] [CrossRef]
- Hu, Y.Z.; Zhang, T.; Ma, T.B.; Wang, H. Molecular Dynamics Simulations on Atomic Friction between Self-Assembled Monolayers: Commensurate and in Commensurate Sliding. Comput. Mater. Sci. 2007, 38, 98–104. [Google Scholar] [CrossRef]
- Ruan, J.A.; Bhushan, B. Friction Behavior of Highly Oriented Pyrolytic Graphite. J. Appl. Phys. 1994, 76, 8117–8120. [Google Scholar] [CrossRef]
- Makkonen, L. A Thermodynamic Model of Sliding Friction. AIP Adv. 2012, 2, 012179. [Google Scholar] [CrossRef]
- Tong, R.T.; Liu, G.; Liu, L. Multiscale Analysis on Two-dimensional Nanoscale Adhesive Contacts. Chin. J. Mech. Eng. 2012, 25, 446–455. [Google Scholar] [CrossRef]
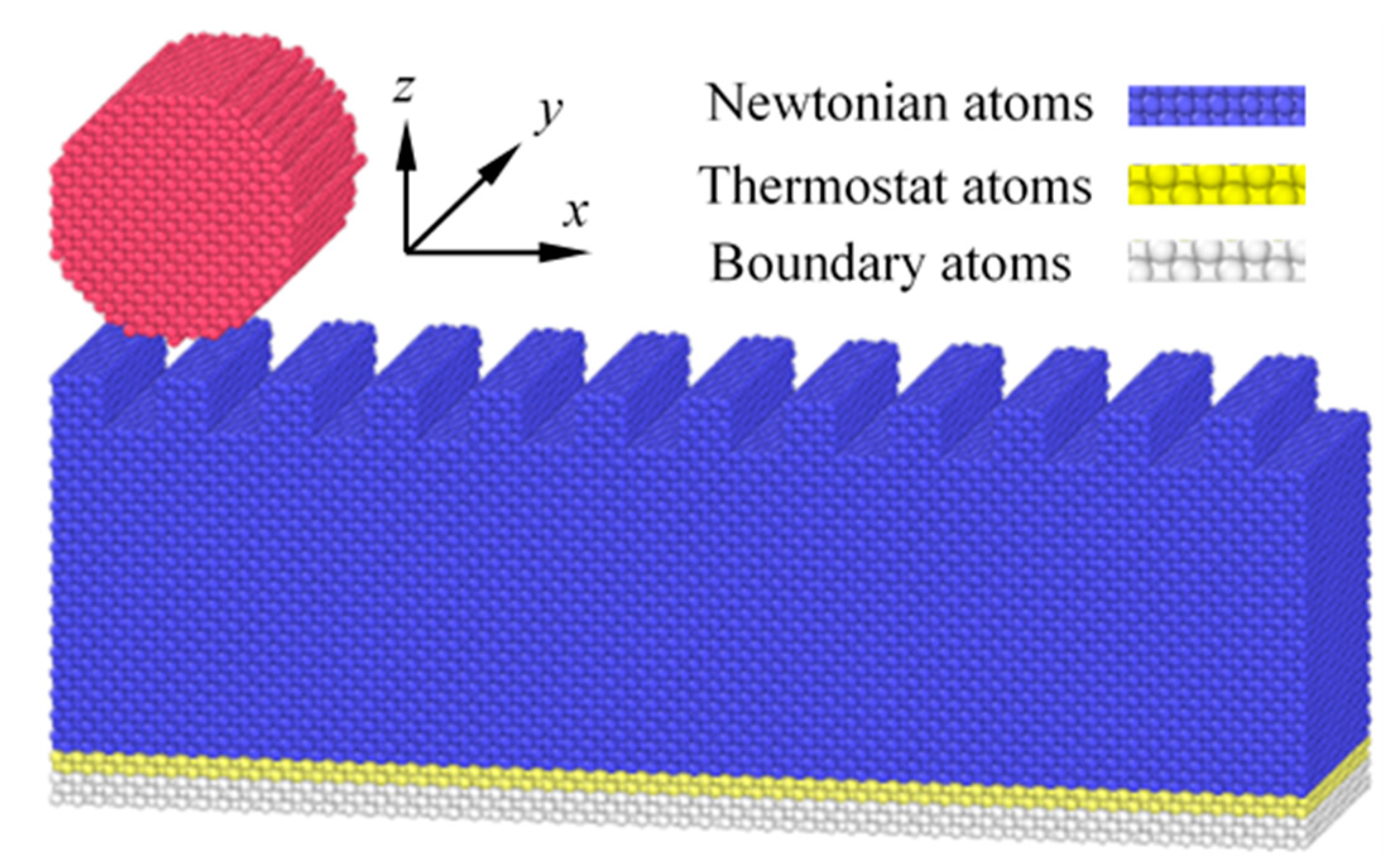
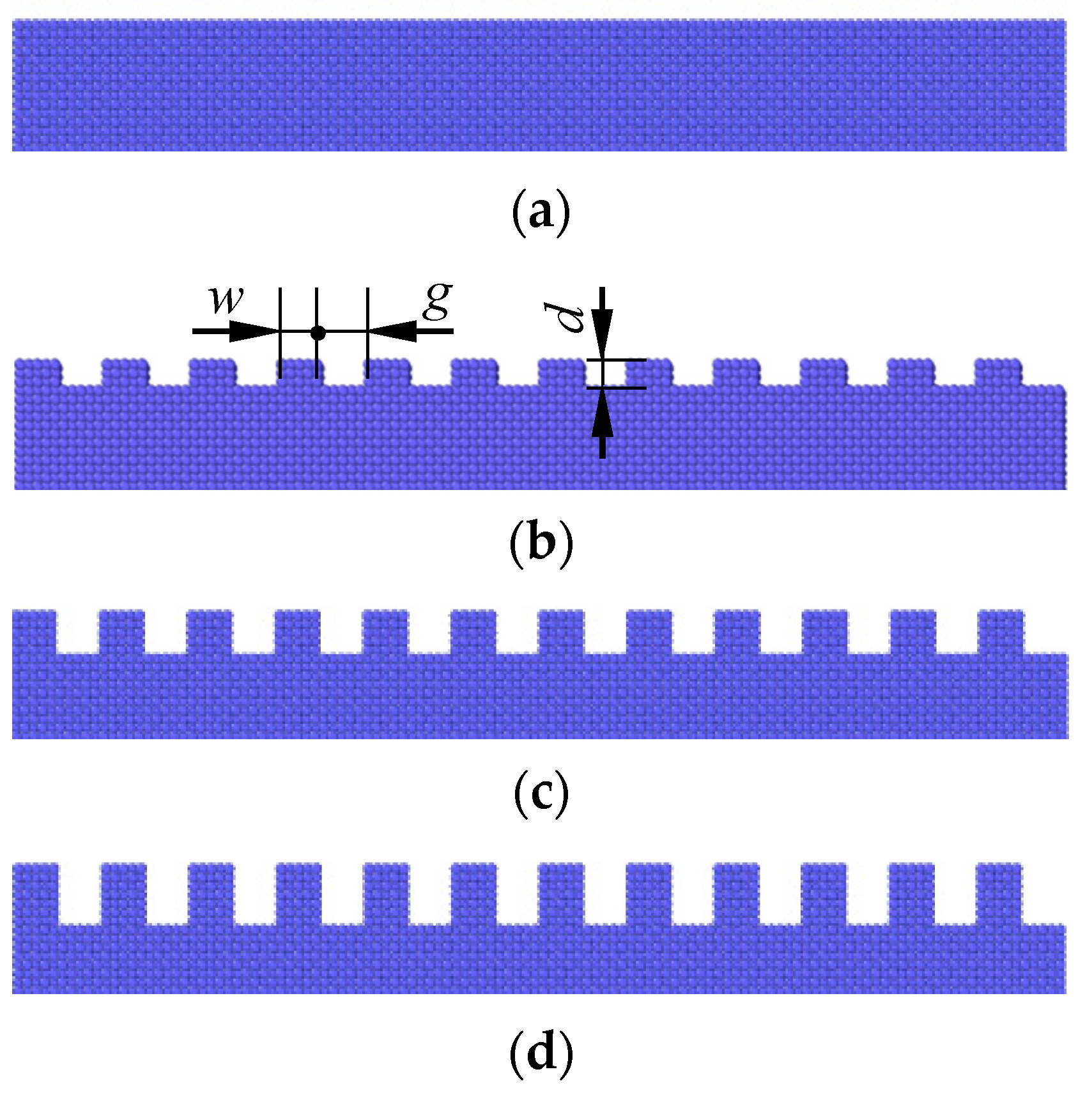


| Parameter | Value |
|---|---|
| material | single crystal copper |
| dimension of substrate | 21.69 nm × 5.784 nm × 7.23 nm |
| radius of tip | 2.169 nm |
| potential | EAM |
| time step | 0.01 ps |
| sliding velocity | 5 m/s |
| sliding distance | 15 nm |
| texture depth | 0.3615 nm, 0.723 nm, 1.0845 nm |
| texture width | 0.3615 nm, 0.723 nm, 1.0845 nm |
| texture orientation | 0°, 30°, 45°, 60°, 90° |
| texture shape | #-shape, rectangular, v-shape |
| depth of subsurface defects | 0.90375 nm, 3.615 nm, 7.23 nm, 9.94125 nm, 12.6525 nm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, R.; Quan, Z.; Zhao, Y.; Han, B.; Liu, G. Influence of Nanoscale Textured Surfaces and Subsurface Defects on Friction Behaviors by Molecular Dynamics Simulation. Nanomaterials 2019, 9, 1617. https://doi.org/10.3390/nano9111617
Tong R, Quan Z, Zhao Y, Han B, Liu G. Influence of Nanoscale Textured Surfaces and Subsurface Defects on Friction Behaviors by Molecular Dynamics Simulation. Nanomaterials. 2019; 9(11):1617. https://doi.org/10.3390/nano9111617
Chicago/Turabian StyleTong, Ruiting, Zefen Quan, Yangdong Zhao, Bin Han, and Geng Liu. 2019. "Influence of Nanoscale Textured Surfaces and Subsurface Defects on Friction Behaviors by Molecular Dynamics Simulation" Nanomaterials 9, no. 11: 1617. https://doi.org/10.3390/nano9111617
APA StyleTong, R., Quan, Z., Zhao, Y., Han, B., & Liu, G. (2019). Influence of Nanoscale Textured Surfaces and Subsurface Defects on Friction Behaviors by Molecular Dynamics Simulation. Nanomaterials, 9(11), 1617. https://doi.org/10.3390/nano9111617






