Highly Sensitive Plasmonic Sensor Based on a Dual-Side Polished Photonic Crystal Fiber for Component Content Sensing Applications
Abstract
1. Introduction
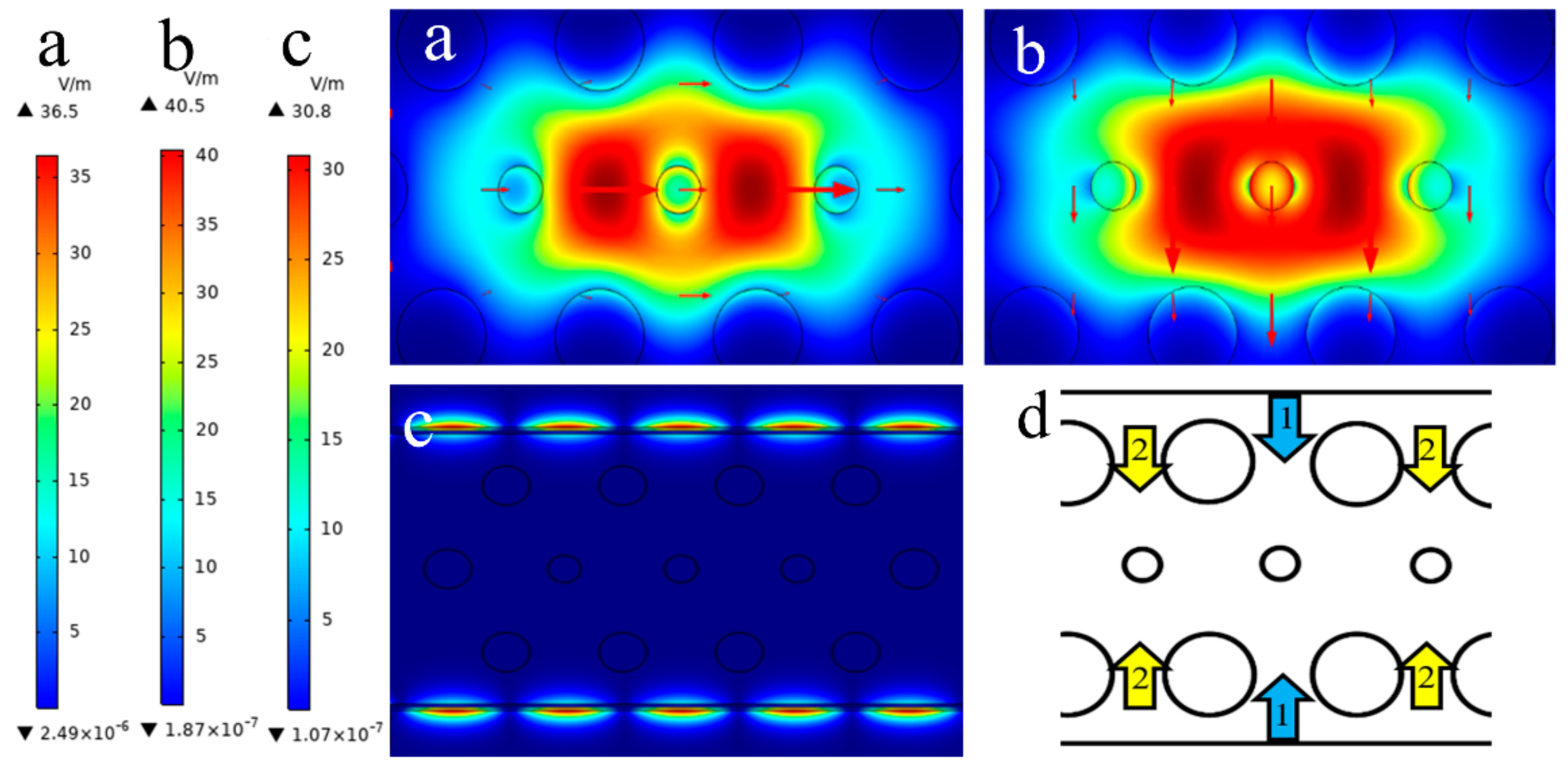
2. Geometry Design and Theoretical Modeling
3. Simulation Results and Discussions
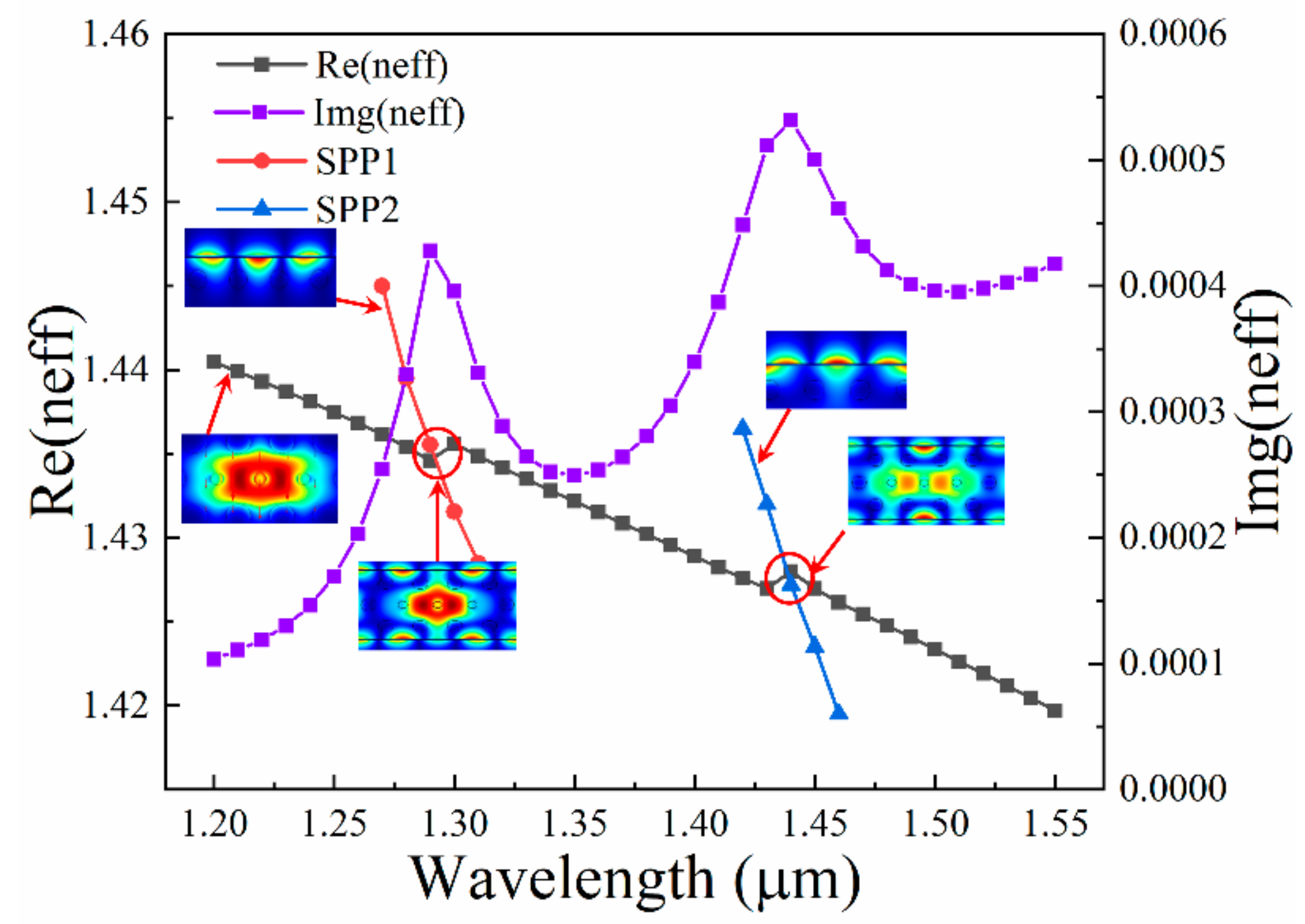
3.1. Dispersion Relationship
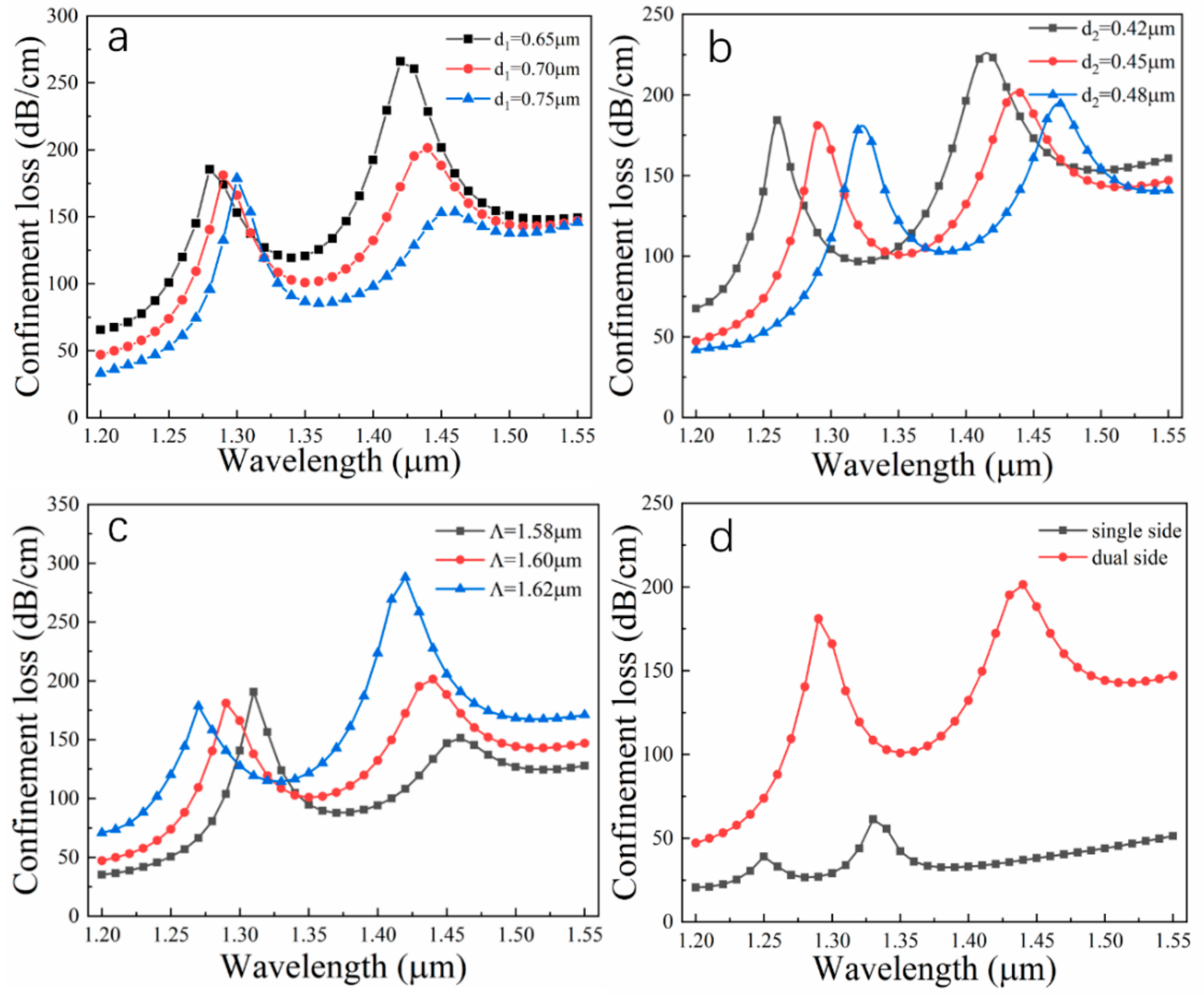
3.2. Structural Parameter Effects
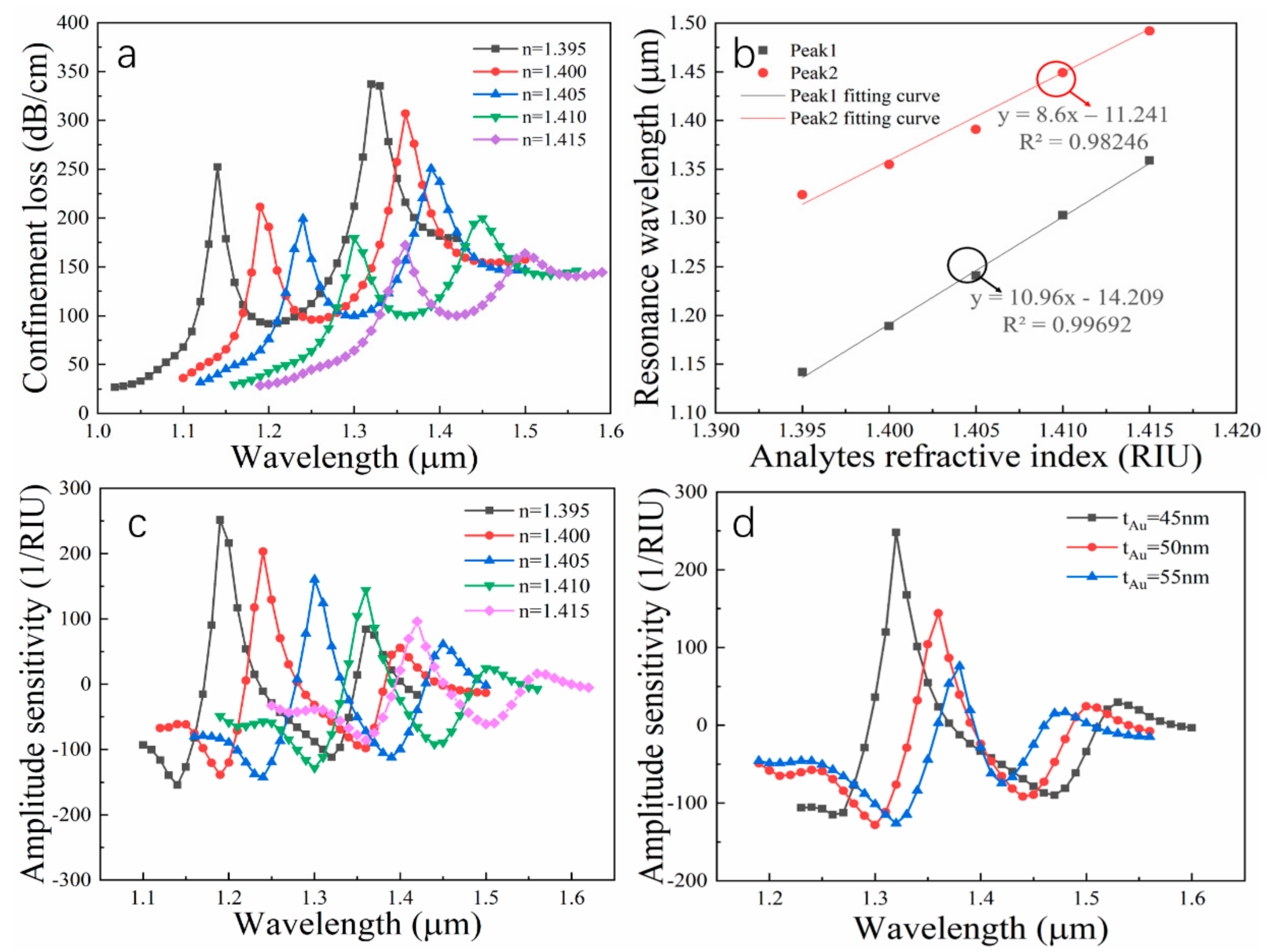
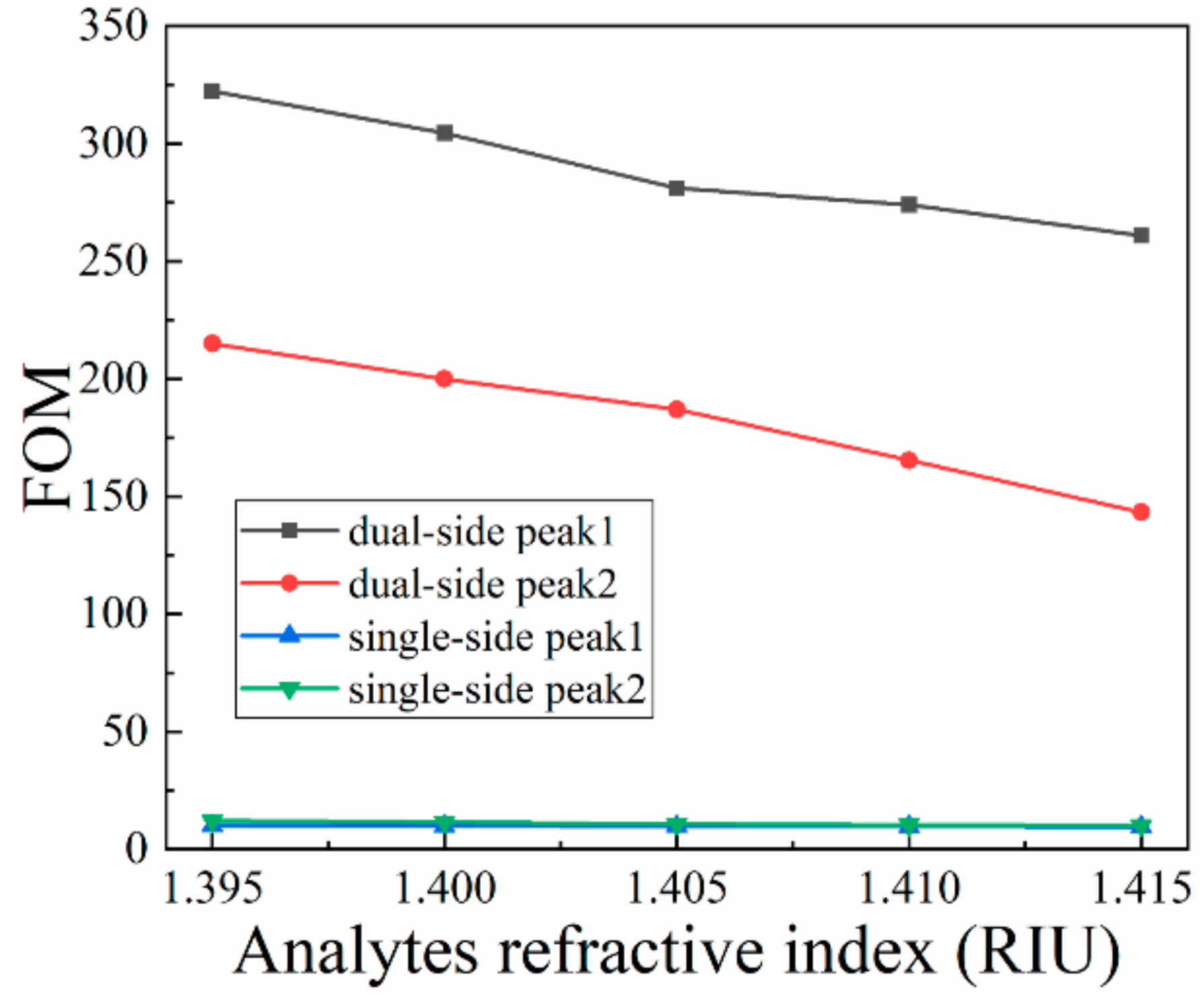
3.3. Sensor Performance
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef]
- Ozbay, E. Plasmonics: Merging Photonics and Electronics at Nanoscale Dimensions. Science 2006, 311, 189–193. [Google Scholar] [CrossRef]
- Hu, D.J.J.; Ho, H.P. Recent advances in plasmonic photonic crystal fibers: Design, fabrication and applications. Adv. Opt. Photonics 2017, 9, 257–314. [Google Scholar] [CrossRef]
- Russell, P.W. Photonic crystal fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef] [PubMed]
- Russell, P.S.J. Photonic-Crystal Fibers. J. Lightwave Technol. 2007, 24, 4729–4749. [Google Scholar] [CrossRef]
- John, S. Photonics: Light control at will. Nature 2009, 460, 337. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Schmidt, M.A.; Tyagi, H.K.; Sempere, L.P.; Russell, P.S.J. Polarization-Dependent coupling to plasmon modes on submicron gold wire in photonic crystal fiber. Appl. Phys. Lett. 2008, 93, 111102. [Google Scholar] [CrossRef]
- Shuai, B.; Xia, L.; Zhang, Y.; Liu, D. A multi-core holey fiber based plasmonic sensor with large detection range and high linearity. Opt. Express 2012, 20, 5974–5986. [Google Scholar] [CrossRef]
- Rifat, A.A.; Haider, F.; Ahmed, R.; Mahdiraji, G.A.; Adikan, F.R.; Miroshnichenko, A.E. Highly sensitive selectively coated photonic crystal fiber-based plasmonic sensor. Opt. Lett. 2018, 43, 891–894. [Google Scholar] [CrossRef]
- Rifat, A.A.; Mahdiraji, G.A.; Sua, Y.M.; Shee, Y.G.; Ahmed, R.; Chow, D.M.; Adikan, F.R. Surface Plasmon Resonance Photonic Crystal Fiber Biosensor: A Practical Sensing Approach. IEEE Photonic Technol. Lett. 2015, 27, 1628–1631. [Google Scholar] [CrossRef]
- Lu, Y.; Hao, C.; Wu, B.; Musideke, M.; Duan, L.; Wen, W.; Yao, J. Surface Plasmon Resonance Sensor Based on Polymer Photonic Crystal Fibers with Metal Nanolayers. Sensors 2013, 13, 956–965. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.S.; Sultana, J.; Rifat, A.A.; Ahmed, R.; Dinovitser, A.; Ng, B.W.; Ebendorffheidepriem, H.; Abbott, D. Dual-polarized highly sensitive plasmonic sensor in the visible to near-IR spectrum. Opt. Express 2018, 26, 30347–30361. [Google Scholar] [CrossRef] [PubMed]
- Santos, D.F.; Guerreiro, A.; Baptista, J.M. SPR Microstructured D-Type Optical Fiber Sensor Configuration for Refractive Index Measurement. IEEE Sens. J. 2015, 15, 5472–5477. [Google Scholar] [CrossRef]
- Luan, N.; Wang, R.; Lv, W.; Yao, J. Surface plasmon resonance sensor based on D-shaped microstructured optical fiber with hollow core. Opt. Express 2015, 23, 8576–8582. [Google Scholar] [CrossRef]
- Luan, N.; Han, H.; Zhao, L.; Liu, J.; Yao, J. Opening up dual-core microstructured optical fiber-based plasmonic sensor with large detection range and linear sensitivity. Opt. Mater. Express 2019, 9, 819–825. [Google Scholar] [CrossRef]
- Liu, C.; Yang, L.; Lu, X.; Liu, Q.; Wang, F.; Lv, J.; Sun, T.; Mu, H.; Chu, P.K. Mid-infrared surface plasmon resonance sensor based on photonic crystal fibers. Opt. Express 2017, 25, 14227–14237. [Google Scholar] [CrossRef]
- Hassani, A.; Skorobogatiy, M. Photonic crystal fiber-based plasmonic sensors for the detection of biolayer thickness. J. Opt. Soc. Am. B 2009, 26, 1550–1557. [Google Scholar] [CrossRef]
- Saitoh, K.; Koshiba, M. Numerical modeling of photonic crystal fibers. J. Lightwave Technol. 2005, 23, 3580–3590. [Google Scholar] [CrossRef]
- Kalnins, C.A.; Spooner, N.A.; Monro, T.M.; Ebendorffheidepriem, H. Surface Analysis and Treatment of Extruded Fluoride Phosphate Glass Preforms for Optical Fiber Fabrication. J. Am. Ceram. Soc. 2016, 99, 1874–1877. [Google Scholar] [CrossRef][Green Version]
- Hameed, M.F.; Heikal, A.M.; Younis, B.M.; Abdelrazzak, M.M.; Obayya, S.S. Ultra-high tunable liquid crystal-plasmonic photonic crystal fiber polarization filter. Opt. Express 2015, 23, 7007–7020. [Google Scholar] [CrossRef]
- Nagasaki, A.; Saitoh, K.; Koshiba, M. Polarization characteristics of photonic crystal fibers selectively filled with metal wires into cladding air holes. Opt. Express 2011, 19, 3799–3808. [Google Scholar] [CrossRef] [PubMed]
- Cao, S.; Shao, Y.; Wang, Y.; Wu, T.; Zhang, L.; Huang, Y.; Zhang, F.; Liao, C.; He, J.; Wang, Y. Highly sensitive surface plasmon resonance biosensor based on a low-index polymer optical fiber. Opt. Express 2018, 26, 3988–3994. [Google Scholar] [CrossRef] [PubMed]
- Luke, K.; Okawachi, Y.; Lamont, M.R.; Gaeta, A.L.; Lipson, M. Broadband mid-infrared frequency comb generation in a Si3N4 microresonator. Opt. Lett. 2015, 40, 4823–4826. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Li, S.; Li, J.; Dou, C.; Wang, X.; Wang, G.; Shi, M. Tunable Fiber Polarization Filter by Filling Different Index Liquids and Gold Wire Into Photonic Crystal Fiber. J. Lightwavve. Technol. 2016, 34, 2484–2490. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, L.; Liu, Z.; Zhang, Y.; Zhang, Y. Surface-plasmon-resonance-based optical-fiber temperature sensor with high sensitivity and high figure of merit. Opt. Lett. 2017, 42, 2948–2951. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Su, W.; Liu, Q.; Lu, X.; Wang, F.; Sun, T.; Chu, P.K. Symmetrical dual D-shape photonic crystal fibers for surface plasmon resonance sensing. Opt. Express 2018, 26, 9039–9049. [Google Scholar] [CrossRef] [PubMed]
- Rifat, A.A.; Mahdiraji, G.A.; Sua, Y.M.; Ahmed, R.; Shee, Y.G.; Adikan, F.R. Highly sensitive multi-core flat fiber surface plasmon resonance refractive index sensor. Opt. Express 2016, 24, 2485–2495. [Google Scholar] [CrossRef]
- Hasan, M.R.; Akter, S.; Rifat, A.A.; Rana, S.; Ahmed, K.; Ahmed, R.; Subbaraman, H.; Abbott, D. Spiral Photonic Crystal Fiber Based Dual-Polarized Surface Plasmon Resonance Biosensor. IEEE Sens. J. 2018, 18, 133–140. [Google Scholar] [CrossRef]
- Otupiri, R.; Akowuah, E.K.; Haxha, S. Multi-channel SPR biosensor based on PCF for multi-analyte sensing applications. Opt. Express 2015, 23, 15716–15727. [Google Scholar] [CrossRef]
- Dash, J.N.; Jha, R. Highly sensitive D shaped PCF sensor based on SPR for near IR. Opt. Quantum Electron. 2016, 48, 137. [Google Scholar] [CrossRef]


| Ref | Structure Type | Max. Wav. Sens. (nm/RIU) | Max. Amp. Sens. (RIU−1) | Resolution (RIU) | Linearity |
|---|---|---|---|---|---|
| [10] | Outer coating | 4000 | 320 | 3.125 × 10−5 | N/A |
| [12] | Dual-polarized | 62,000 | 1415 | 1.6 × 10−6 | N/A |
| [13] | Side polished | 10,000 | N/A | 9.8 × 10−6 | N/A |
| [16] | Open-ring channels | 5500 | 333.8 | 7.69 × 10−6 | N/A |
| [26] | Dual D-shape | 43,200 | 1222 | 6.82 × 10−6 | N/A |
| [27] | Side polished | 23,000 | 820 | 1.22 × 10−5 | 0.9432 |
| [28] | Dual-polarized | 4600 | 420.4 | N/A | 0.9720 |
| [29] | Multi-channel | 4600 | N/A | 2 × 10−5 | N/A |
| [30] | Side polished | 5200 | N/A | 1.92 × 10−5 | N/A |
| The present paper | Dual-side polished | 12,400 | 252 | 9.39 × 10−6 | 0.99692 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, N.; Chang, M.; Zhang, X.; Zhou, J.; Lu, X.; Zhuang, S. Highly Sensitive Plasmonic Sensor Based on a Dual-Side Polished Photonic Crystal Fiber for Component Content Sensing Applications. Nanomaterials 2019, 9, 1587. https://doi.org/10.3390/nano9111587
Chen N, Chang M, Zhang X, Zhou J, Lu X, Zhuang S. Highly Sensitive Plasmonic Sensor Based on a Dual-Side Polished Photonic Crystal Fiber for Component Content Sensing Applications. Nanomaterials. 2019; 9(11):1587. https://doi.org/10.3390/nano9111587
Chicago/Turabian StyleChen, Nan, Min Chang, Xuedian Zhang, Jun Zhou, Xinglian Lu, and Songlin Zhuang. 2019. "Highly Sensitive Plasmonic Sensor Based on a Dual-Side Polished Photonic Crystal Fiber for Component Content Sensing Applications" Nanomaterials 9, no. 11: 1587. https://doi.org/10.3390/nano9111587
APA StyleChen, N., Chang, M., Zhang, X., Zhou, J., Lu, X., & Zhuang, S. (2019). Highly Sensitive Plasmonic Sensor Based on a Dual-Side Polished Photonic Crystal Fiber for Component Content Sensing Applications. Nanomaterials, 9(11), 1587. https://doi.org/10.3390/nano9111587





