A Mechanics Based Surface Image Interpretation Method for Multifunctional Nanocomposites
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Manufacturing
2.3. Tensile Tests
2.4. Scanning Electron Microscopy
2.5. Thermal Conductivity Tests
3. Theory
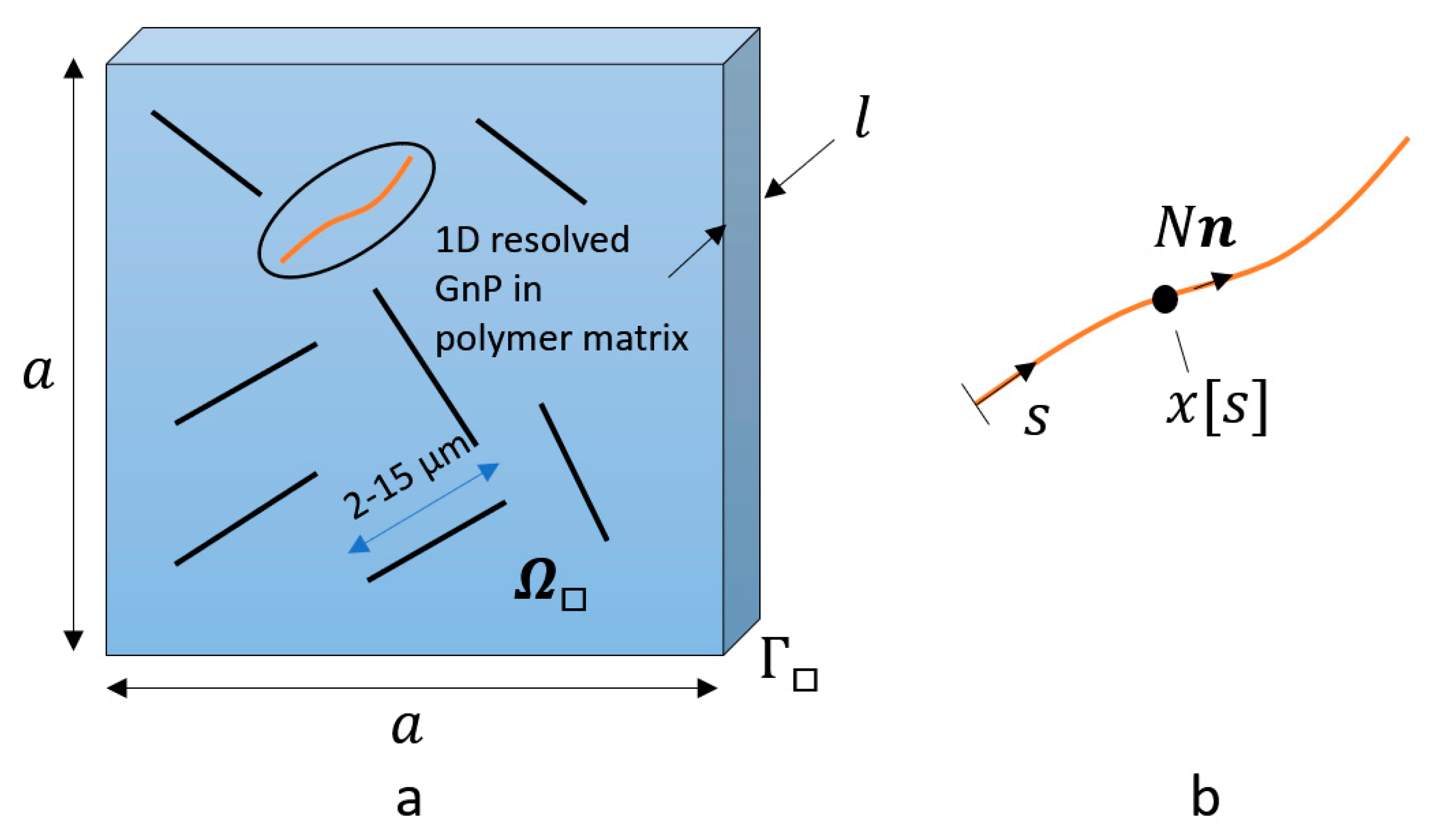
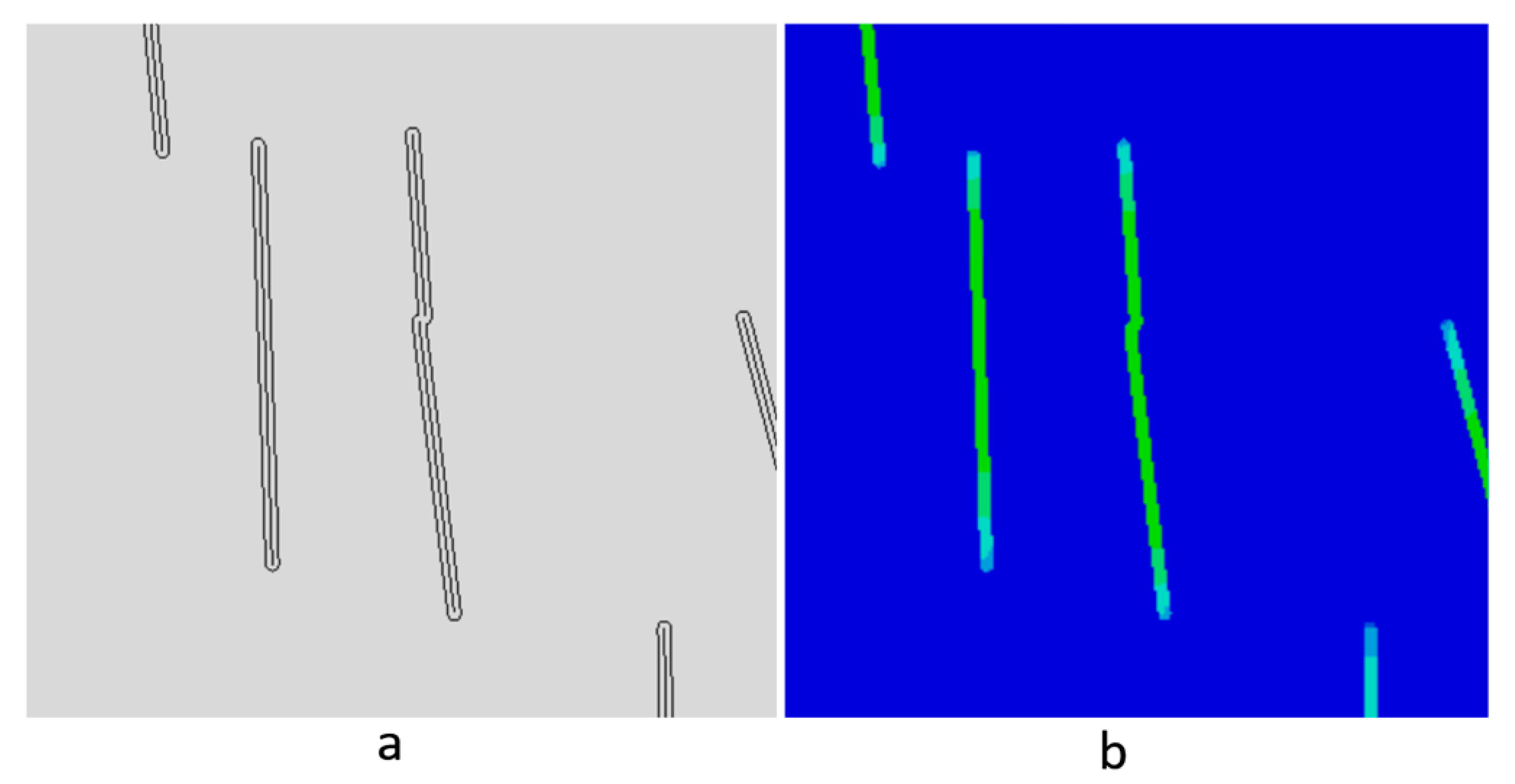
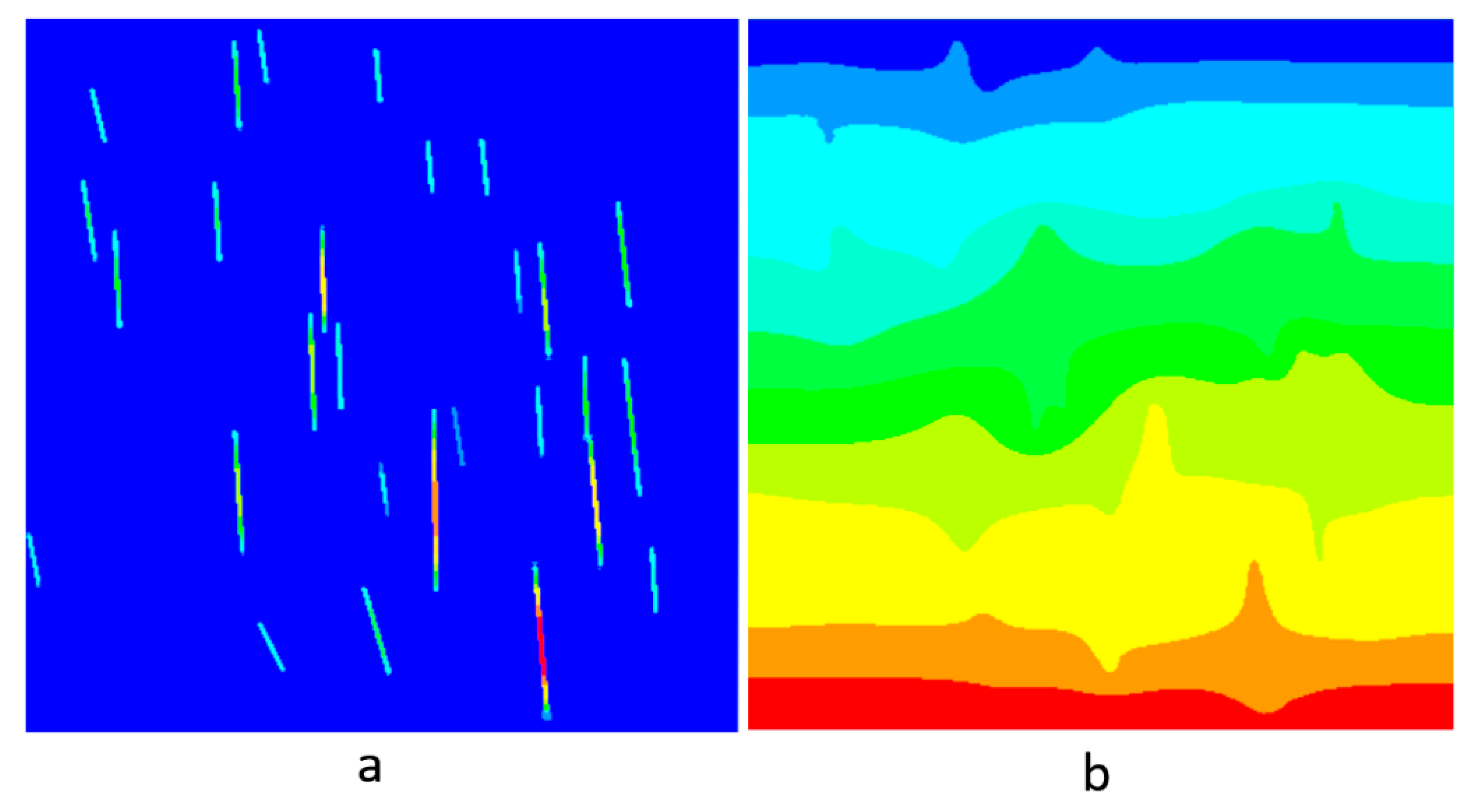
3.1. Image Interpretation
3.2. Mechanical Property Calculations
3.2.1. Effective In-Plane Stiffness of Graphene
3.2.2. Computational Homogenization of Mechanical Properties
3.3. Computational Homogenization of Thermal Properties
3.3.1. Thermal Conductivity of Constituents
3.3.2. Approximation of the Kapitza Effect
3.3.3. Computational Homogenization of Thermal Properties
4. Results
4.1. Computational Results
4.1.1. Mechanical Property Results
Effective In-Plane Stiffness of Graphene
Computational Homogenization of Mechanical Properties
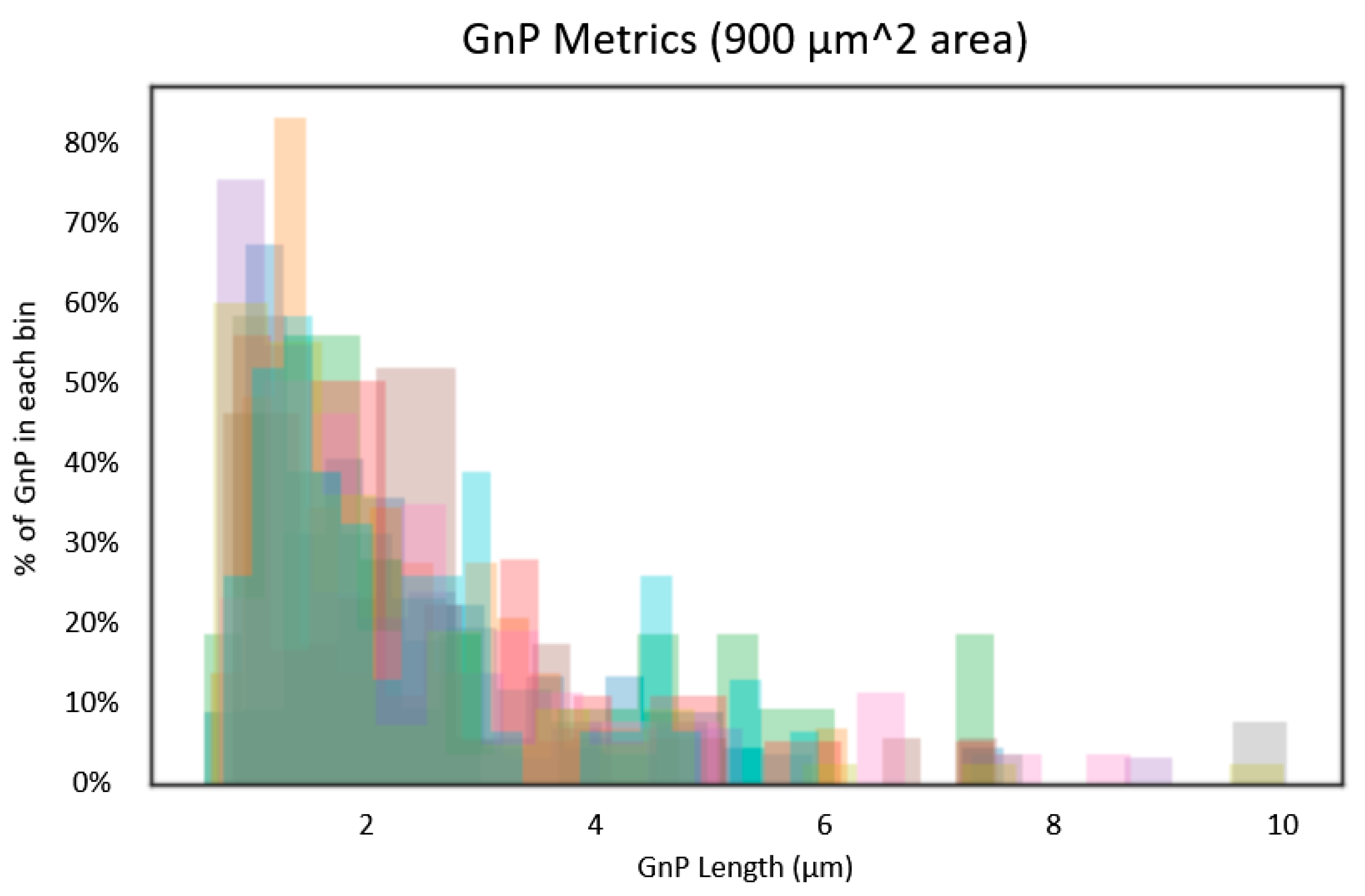
Calculation of Volume Fraction of Graphene from Surface Images
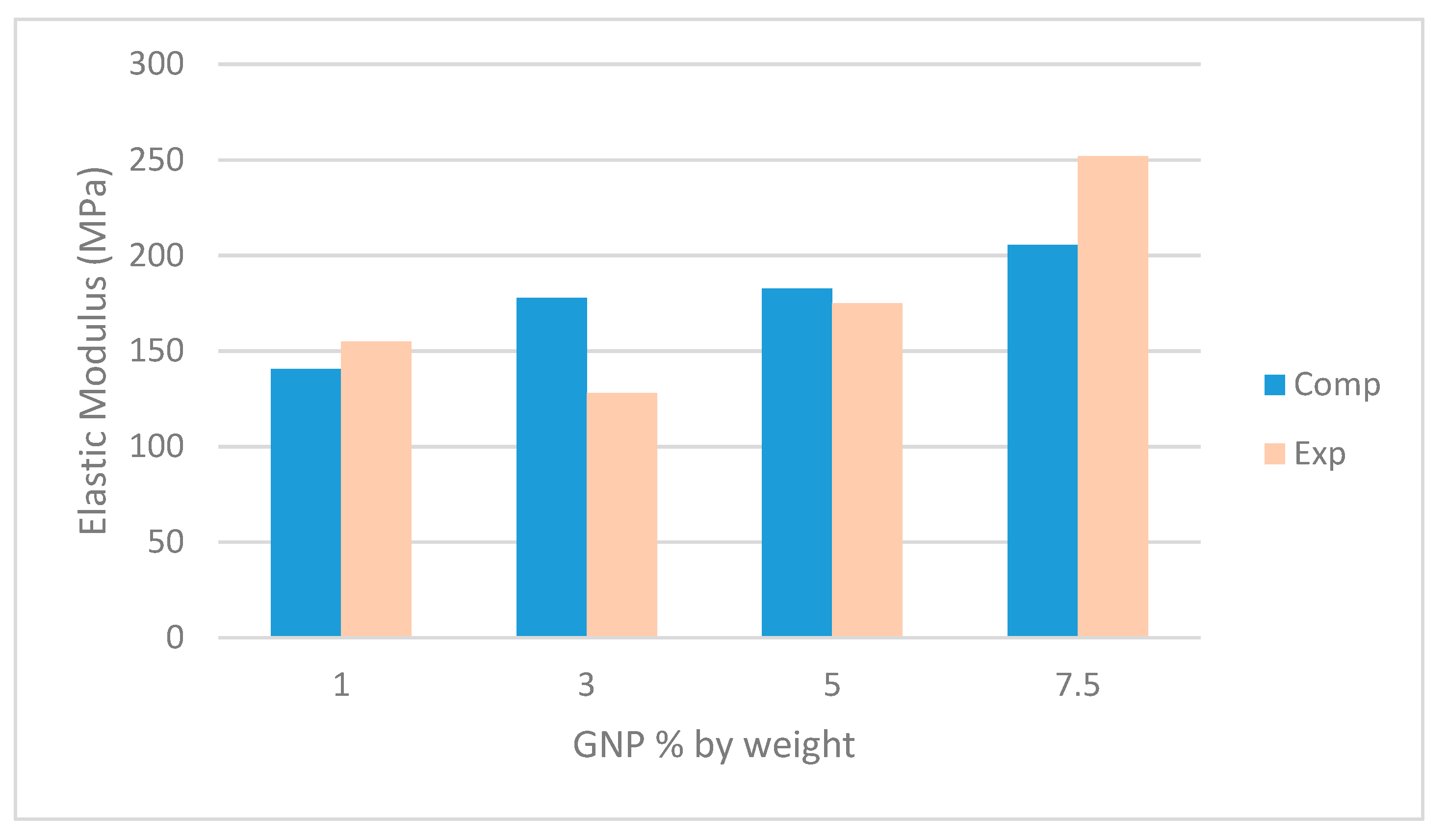
Comparison with Analytical Approaches
4.1.2. Thermal Property Results
Thermal Conductivity of Constituents
Computational Homogenization of Thermal Properties
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gaska, K.; Kádar, R.; Rybak, A.; Siwek, A.; Gubanski, S. Gas Barrier, Thermal, Mechanical and Rheological Properties of Highly Aligned Graphene-LDPE Nanocomposites. Polymers 2017, 9, 294. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, A.; Bonaccorso, F.; Fal’ko, V.; Novoselov, K.; Roche, S.; Bøggild, P.; Borini, S.; Koppens, F.H.; Palermo, V.; Pugno, N.; et al. Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems. Nanoscale 2015, 7, 4598–4810. [Google Scholar] [PubMed]
- Kim, H.; Abdala, A.; Macosko, C. Graphene/polymer nanocomposites. Macromolecules 2010, 43, 6515–6530. [Google Scholar] [CrossRef]
- Papageorgiou, D.; Kinloch, I.; Young, R. Mechanical properties of graphene and graphene-based nanocomposites. Prog. Mater. Sci. 2017, 90, 75–127. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Young, R.; Liu, M.; Kinloch, I.A.; Li, S.; Zhao, X.; Vallés, C.; Papageorgiou, D.G. The mechanics of reinforcement of polymers by graphene nanoplatelets. Compos. Sci. Technol. 2018, 154, 110–116. [Google Scholar] [CrossRef]
- Liu, M.; Papageorgiou, D.; Li, S.; Lin, K.; Kinloch, I.; Young, R. Micromechanics of reinforcement of a graphene-based thermoplastic elastomer nanocomposite. Compos. Part A Appl. Sci. Manuf. 2018, 110, 84–92. [Google Scholar] [CrossRef]
- Feng, C.; Wang, Y.; Yang, J. Effects of Reorientation of Graphene Platelets (GPLs) on Young’s Modulus of Polymer Composites under Bi-Axial Stretching. Nanomaterials 2018, 8, 27. [Google Scholar] [CrossRef]
- Caro, C.; Quaresma, P.; Pereira, E.; Franco, J.; Leal, M.P.; Garcia-Martin, M.L.; Royo, J.L.; Oliva-Montero, J.M.; Merkling, P.J.; Zaderenka, A.P.; et al. Synthesis and Characterization of Elongated-Shaped Silver Nanoparticles as a Biocompatible Anisotropic SERS Probe for Intracellular Imaging: Theoretical Modeling and Experimental Verification. Nanomaterials 2019, 9, 256. [Google Scholar] [CrossRef]
- Chu, L.; Shi, J.; Souza de Cursi, E. Vibration Analysis of Vacancy Defected Graphene Sheets by Monte Carlo Based Finite Element Method. Nanomaterials 2018, 8, 489. [Google Scholar] [CrossRef]
- Fang, H.; Bai, S.; Wong, C. Microstructure engineering of graphene towards highly thermal conductive composites. Compos. Part A Appl. Sci. Manuf. 2018, 112, 216–238. [Google Scholar] [CrossRef]
- Nan, C.; Birringer, R.; Clarke, D.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1998, 81, 6692. [Google Scholar] [CrossRef]
- Dunn, M.; Taya, M. The effective thermal conductivity of composites with coated reinforcement and the application to imperfect interfaces. J. Appl. Phys. 1993, 73, 1711–1722. [Google Scholar] [CrossRef]
- Gresil, M.; Wang, Z.; Poutrel, Q.; Soutis, C. Thermal Diffusivity Mapping of Graphene Based Polymer Nanocomposites. Sci. Rep. 2017, 7, 5536. [Google Scholar] [CrossRef] [PubMed]
- Manta, A.; Gresil, M.; Soutis, C. Predictive Model of Graphene Based Polymer Nanocomposites: Electrical Performance. Appl. Compos. Mater. 2017, 24, 281–300. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Sezgin, M.; Sankur, B. Survey over Image Thresholding Techniques and Quantitative Performance Evaluation. Electron. Imaging 2004, 13, 146–165. [Google Scholar]
- Gaska, K.; Xu, X.; Gubanski, S.; Kadar, R. Electrical, Mechanical, and Thermal Properties of LDPE Graphene Nanoplatelets Composites Produced by Means of Melt Extrusion Process. Polymers 2017, 9, 11. [Google Scholar] [CrossRef]
- Gaska, K.; Kadar, R.; Xu, X.; Gubanski, S.; Muller, C.; Pandit, S.; Mokkapati, V.R.S.S.; Mijakovic, I.; Rybak, A.; Siwek, A.; et al. Highly structured graphene polyethylene nanocomposites. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2019; Volume 2065. [Google Scholar]
- Pandit, S.; Gaska, K.; Mokkapati, V.R.S.S.; Forsberg, S.; Svensson, M.; Kádár, R.; Mijakovic, I. Antibacterial effect of boron nitride flakes with controlled orientation in polymer composites. RSC Advances 2019, 9, 33454–33459. [Google Scholar] [CrossRef]
- Kadar, R.; Abbasi, M.; Figuli, R.; Rigdahl, M. Linear and Nonlinear Rheology Combined with Dielectric Spectroscopy of Hybrid Polymer Nanocomposites for Semiconductive Applications. Nanomaterials 2017, 7, 2. [Google Scholar] [CrossRef]
- Li, C.; Tam, P. An Iterative Algorithm for Minimum Cross Entropy Thresholding. Pattern Recognit. Lett. 1998, 18, 771–776. [Google Scholar] [CrossRef]
- Benveniste, Y. A new approach to the application of mori-tanaka’s theory in composite materials. Mech. Mater. 1987, 6, 147–157. [Google Scholar] [CrossRef]
- Suquet, P. Local and Global Aspects in the Mathematical Theory of Plasticity. Plasticity Today: Modelling, Methods and Applications; Elsevier: London, UK, 1985. [Google Scholar]
- Dassault Systems Simulia Corporation. SIMULIA User Guide. Dassault Systems; Dassault Systems Simulia Corporation: Providence, RI, USA, 2016. [Google Scholar]
- Iijima, K. Carbon Nanotubes and Graphene; Elsevier: Oxford, UK, 2014. [Google Scholar]
- Potts, J.; Dreyer, D.; Bielawski, C.; Ruoff, R. Graphene-based polymer nanocomposites. Polymer 2011, 52, 5–25. [Google Scholar] [CrossRef]
- Vallés, C.; Beckert, F.; Burk, L.; Mülhaupt, R.; Young, R.; Kinloch, I. Effect of the C/O ratio in graphene oxide materials on the reinforcement of epoxy-based nanocomposites. J. Polymer Sci. Part B Polymer Phys. 2016, 54, 281–291. [Google Scholar] [CrossRef]
- Geers, M.; Kouznetsova, V.; Brekelmans, W. Multi-scale computational homogenization: Trends and challenges. J. Comput. Appl. Math. 2010, 234, 2175–2182. [Google Scholar] [CrossRef]
- Zhai, S.; Zhang, P.; Xian, Y.; Zeng, J.; Shi, B. Effective thermal conductivity of polymer composites: Theoretical models and simulation models. Int. J. Heat Mass Transf. 2018, 117, 358–374. [Google Scholar] [CrossRef]
- Mortazavi, B.; Benzerara, O.; Meyer, H.; Bardon, J.; Ahzi, S. Combined molecular dynamics-finite element multiscale modeling of thermal conduction in graphene epoxy nanocomposites. Carbon 2013, 60, 356–365. [Google Scholar] [CrossRef]
- Shin, H.; Yang, S.; Chang, S.; Yu, S.; Cho, M. Multiscale homogenization modeling for thermal transport properties of polymer nanocomposites with Kapitza thermal resistance. Polymer 2013, 54, 1543–1554. [Google Scholar] [CrossRef]
- He, B.; Mortazavi, B.; Zhuang, X.; Rabczuk, T. Modeling Kapitza resistance of two-phase composite material. Compos. Struct. 2016, 152, 939–946. [Google Scholar] [CrossRef]
- Özdemir, I.; Brekelmans, W.; Geers, M. Computational homogenization for heat conduction. Int. J. Numer. Meth. Eng. 2008, 73, 185–204. [Google Scholar] [CrossRef]
- Clegg, D.W.; Collyer, A.A. Mechanical Properties of Reinforced Thermoplastics; Elsevier Applied Science Publishers: London, UK, 1986; Chapter 2. [Google Scholar]
- Nielsen, L.E.; Landel, R.F. Mechanical Properties of Polymers and Composites, 2nd ed.; Marcel Dekker Inc.: New York, NY, USA, 1994; Chapters 7 and 8. [Google Scholar]
- Mascia, L. Thermoplastics: Materials Engineering; Applied Science Publishers Ltd.: Barking, UK, 1982; Chapter 4. [Google Scholar]
- Balandin, A. Thermal Properties of Graphene, Carbon Nanotubes and Nanostructured Carbon Materials; University of California: Riverside, CA, USA, 2011. [Google Scholar]
- Sun, S.; Samani, M.; Fu, Y.; Xu, T.; Ye, L.; Satwara, M.; Jeppson, K.; Nilsson, T.; Sun, L.; Liu, J. Improving Thermal Transport at Carbon Hybrid Interfaces by Covalent Bonds. Adv. Mater. Interfaces 2018, 5, 15. [Google Scholar] [CrossRef]
- Shahil, K.; Balandin, A. Thermal properties of graphene and multilayer graphene: Applications in thermal interface matrials. Solid State Commun. 2012, 152, 1331–1340. [Google Scholar] [CrossRef]


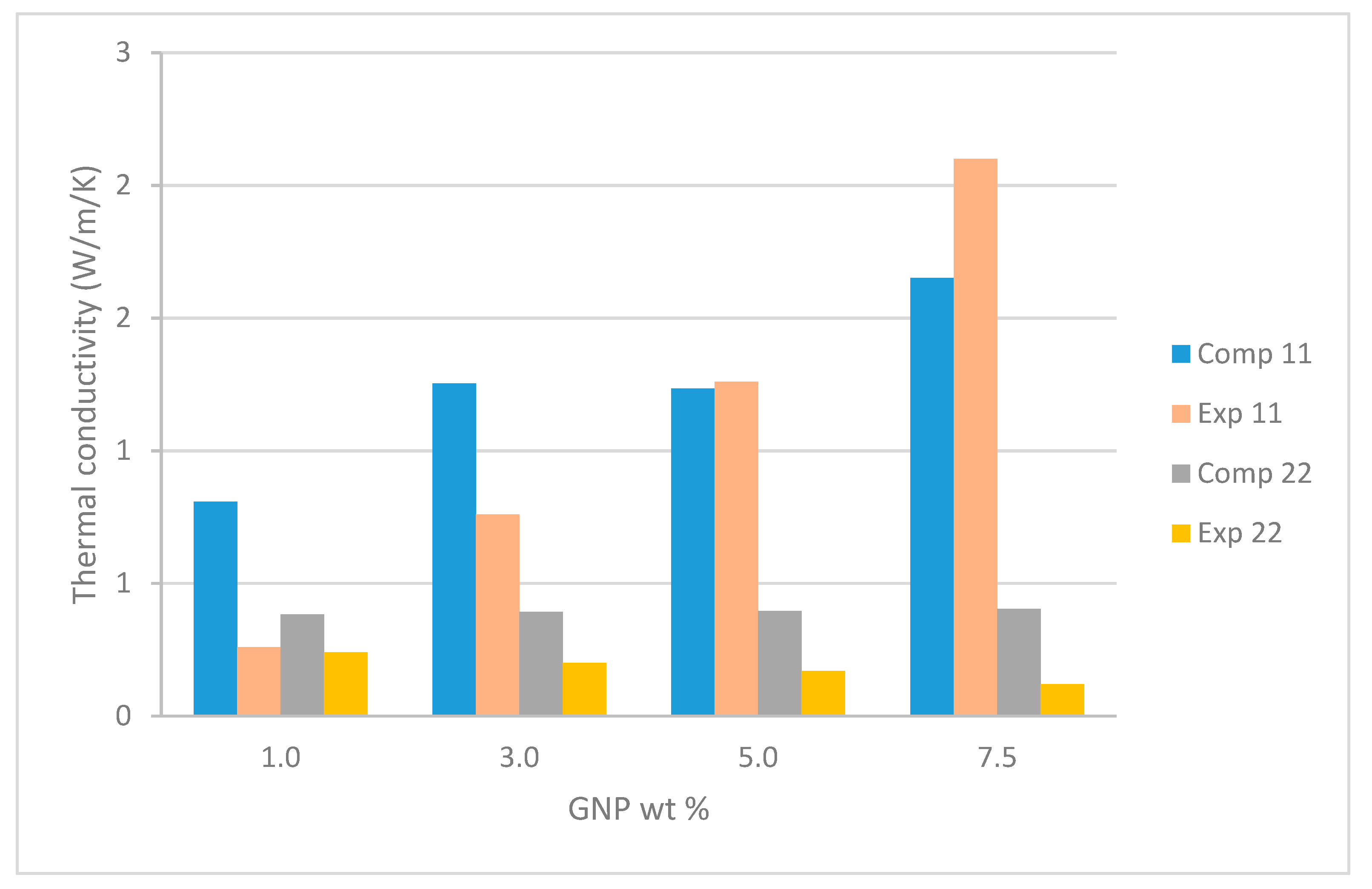
| E11 | 125 | MPa |
| E22 | 120 | MPa |
| 12 | 0.38 |
| Multiplier | 10 | 50 | 100 | 500 | 1000 |
|---|---|---|---|---|---|
| 1 wt. % E11(MPa) | 137.49 | 139.87 | 140.21 | 140.50 | 140.54 |
| 3 wt. % E11(MPa) | 166.37 | 175.12 | 176.47 | 177.60 | 177.75 |
| 5 wt. % E11(MPa) | 171.17 | 180.09 | 181.45 | 182.58 | 182.72 |
| 7.5 wt. % E11(MPa) | 186.15 | 200.72 | 203.10 | 205.13 | 205.39 |
| 1 wt. % | E11(MPa) | E22(MPa) | G12(MPa) |
|---|---|---|---|
| 136.84 | 126.35 | 47.68 | |
| 127.97 | 123.19 | 45.50 | |
| 125.36 | 122.08 | 44.83 | |
| 134.40 | 125.34 | 47.05 | |
| 129.60 | 123.96 | 45.93 | |
| 135.62 | 124.93 | 47.20 | |
| 133.82 | 123.70 | 46.65 | |
| 134.31 | 125.40 | 47.05 | |
| Average | 132.24 | 124.37 | 46.49 |
| 3 wt. % | E11(MPa) | E22(MPa) | G12(MPa) |
|---|---|---|---|
| 139.95 | 126.35 | 48.24 | |
| 151.26 | 127.54 | 50.51 | |
| 148.68 | 125.67 | 49.70 | |
| 140.60 | 123.94 | 47.92 | |
| 156.29 | 128.53 | 51.60 | |
| 142.65 | 126.61 | 48.78 | |
| 156.87 | 125.22 | 51.10 | |
| 150.40 | 124.83 | 49.86 | |
| 155.50 | 132.62 | 52.20 | |
| Average | 149.13 | 126.81 | 49.99 |
| 5 wt. % | E11(MPa) | E22(MPa) | G12(MPa) |
|---|---|---|---|
| 157.07 | 130.69 | 52.13 | |
| 144.97 | 127.02 | 49.27 | |
| 154.19 | 128.17 | 51.15 | |
| 151.81 | 130.58 | 51.16 | |
| 148.38 | 125.52 | 49.62 | |
| 157.54 | 125.24 | 51.23 | |
| 155.72 | 127.05 | 51.23 | |
| Average | 152.81 | 127.75 | 50.83 |
| 7.5 wt. % | E11(MPa) | E22(MPa) | G12(MPa) |
|---|---|---|---|
| 153.83 | 125.86 | 50.67 | |
| 151.83 | 123.15 | 49.82 | |
| 157.08 | 130.70 | 52.13 | |
| 177.74 | 129.69 | 55.69 | |
| 163.55 | 129.61 | 53.11 | |
| 149.84 | 126.04 | 49.98 | |
| 164.39 | 131.12 | 53.54 | |
| Average | 159.75 | 128.02 | 52.13 |
| E11 | E22 | |
|---|---|---|
| Experimental Result | 175 | -- |
| Computational Homogenization | 183 | 123 |
| Analytical Method | 131 | 127 |
| (k)LDPE | 0.37 | W m−1 K−1 |
| (k)GnP | 1000 | W m−1 K−1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blinzler, B.J.; Larsson, R.; Gaska, K.; Kádár, R. A Mechanics Based Surface Image Interpretation Method for Multifunctional Nanocomposites. Nanomaterials 2019, 9, 1578. https://doi.org/10.3390/nano9111578
Blinzler BJ, Larsson R, Gaska K, Kádár R. A Mechanics Based Surface Image Interpretation Method for Multifunctional Nanocomposites. Nanomaterials. 2019; 9(11):1578. https://doi.org/10.3390/nano9111578
Chicago/Turabian StyleBlinzler, Brina J., Ragnar Larsson, Karolina Gaska, and Roland Kádár. 2019. "A Mechanics Based Surface Image Interpretation Method for Multifunctional Nanocomposites" Nanomaterials 9, no. 11: 1578. https://doi.org/10.3390/nano9111578
APA StyleBlinzler, B. J., Larsson, R., Gaska, K., & Kádár, R. (2019). A Mechanics Based Surface Image Interpretation Method for Multifunctional Nanocomposites. Nanomaterials, 9(11), 1578. https://doi.org/10.3390/nano9111578






