Dewetting Metal Nanofilms—Effect of Substrate on Refractive Index Sensitivity of Nanoplasmonic Gold
Abstract
1. Introduction
2. Materials and Methods
2.1. Reagents
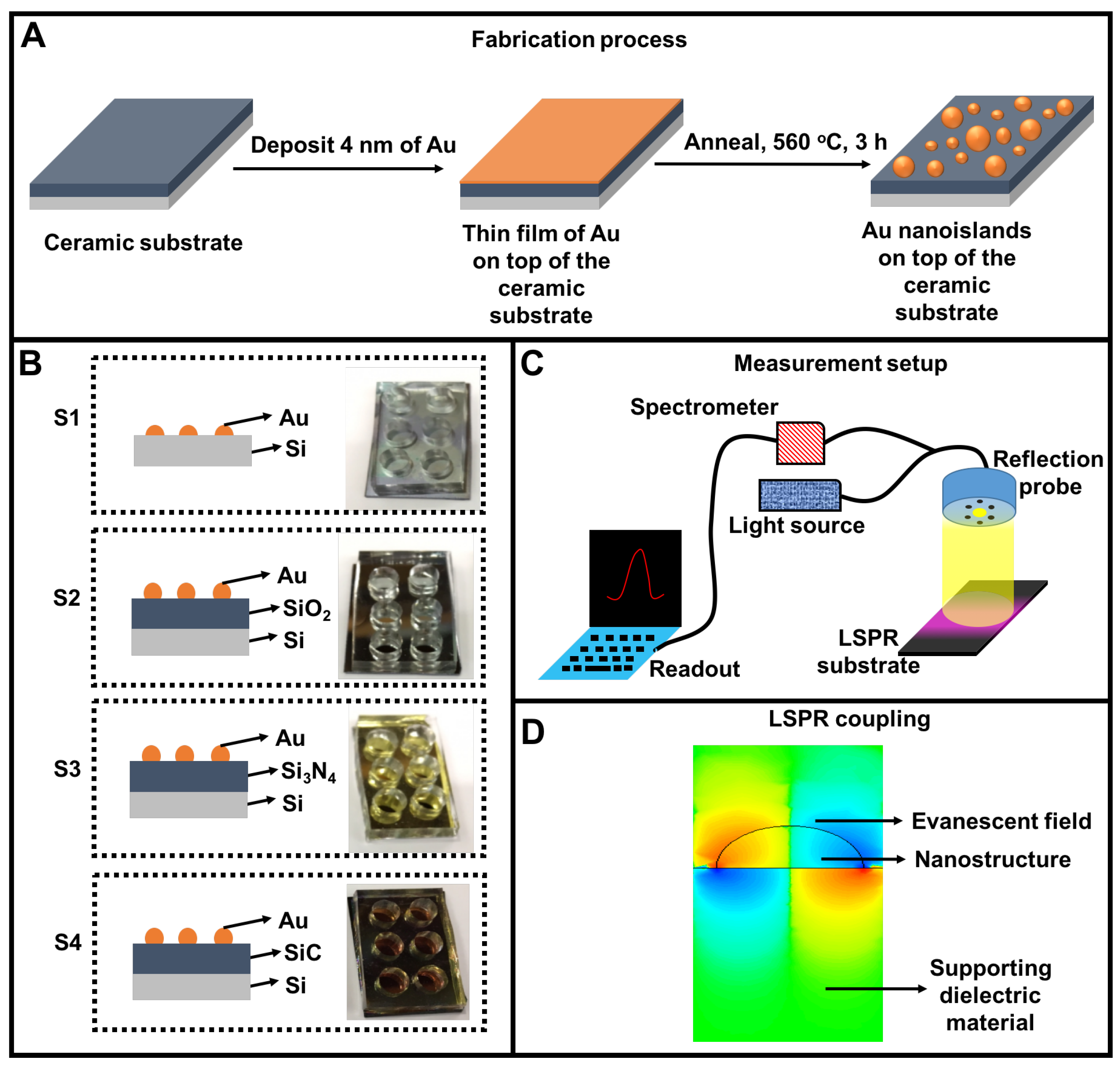
2.2. Nanoplasmonic Substrate Preparation
2.3. Modeling
2.4. Refractive Index Sensing
2.5. Electron Microscopy
2.6. Data Analysis
3. Results and Discussion
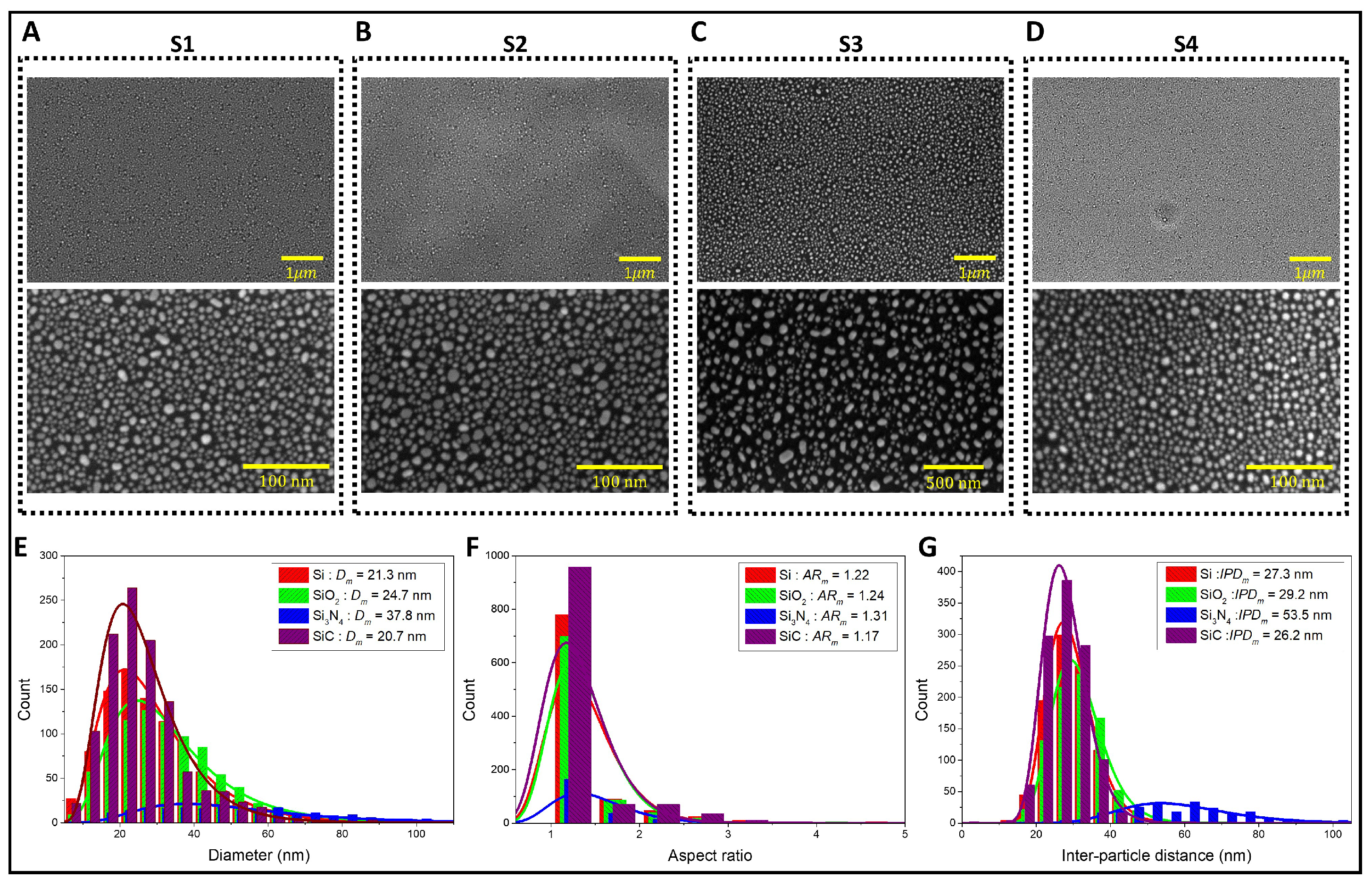
3.1. Morphological Characterizations
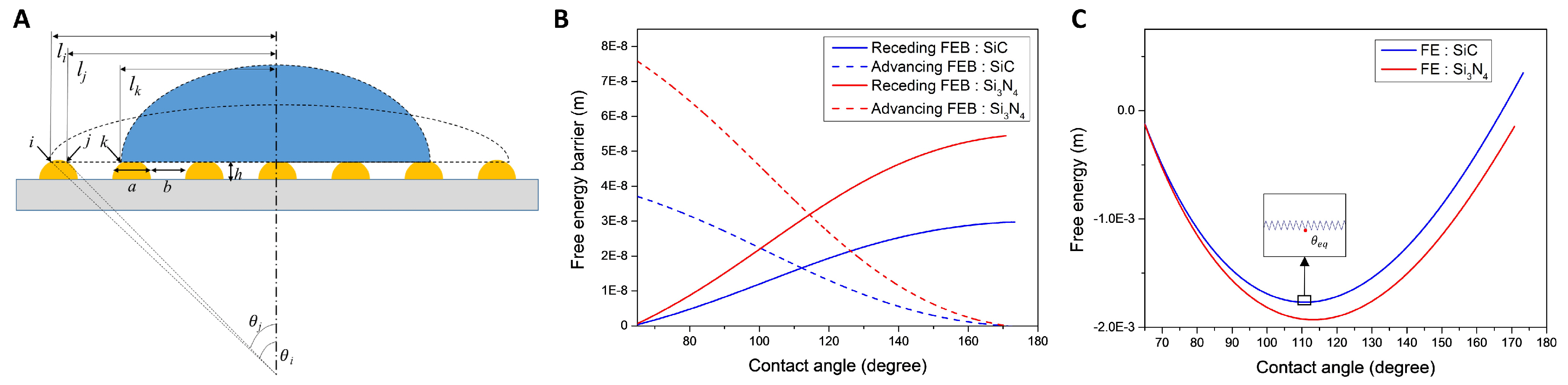
3.2. Surface Energy and Dewetting
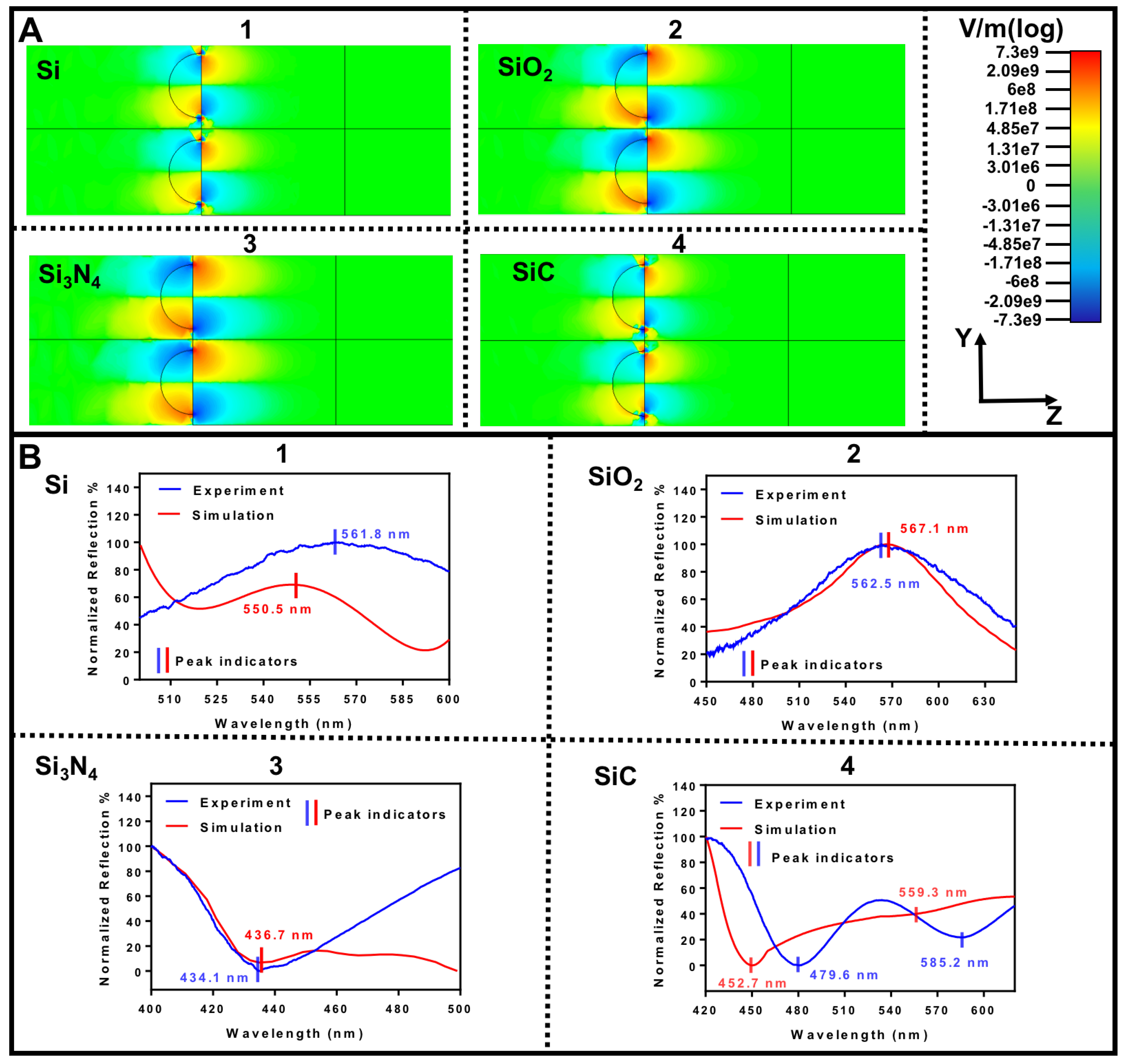
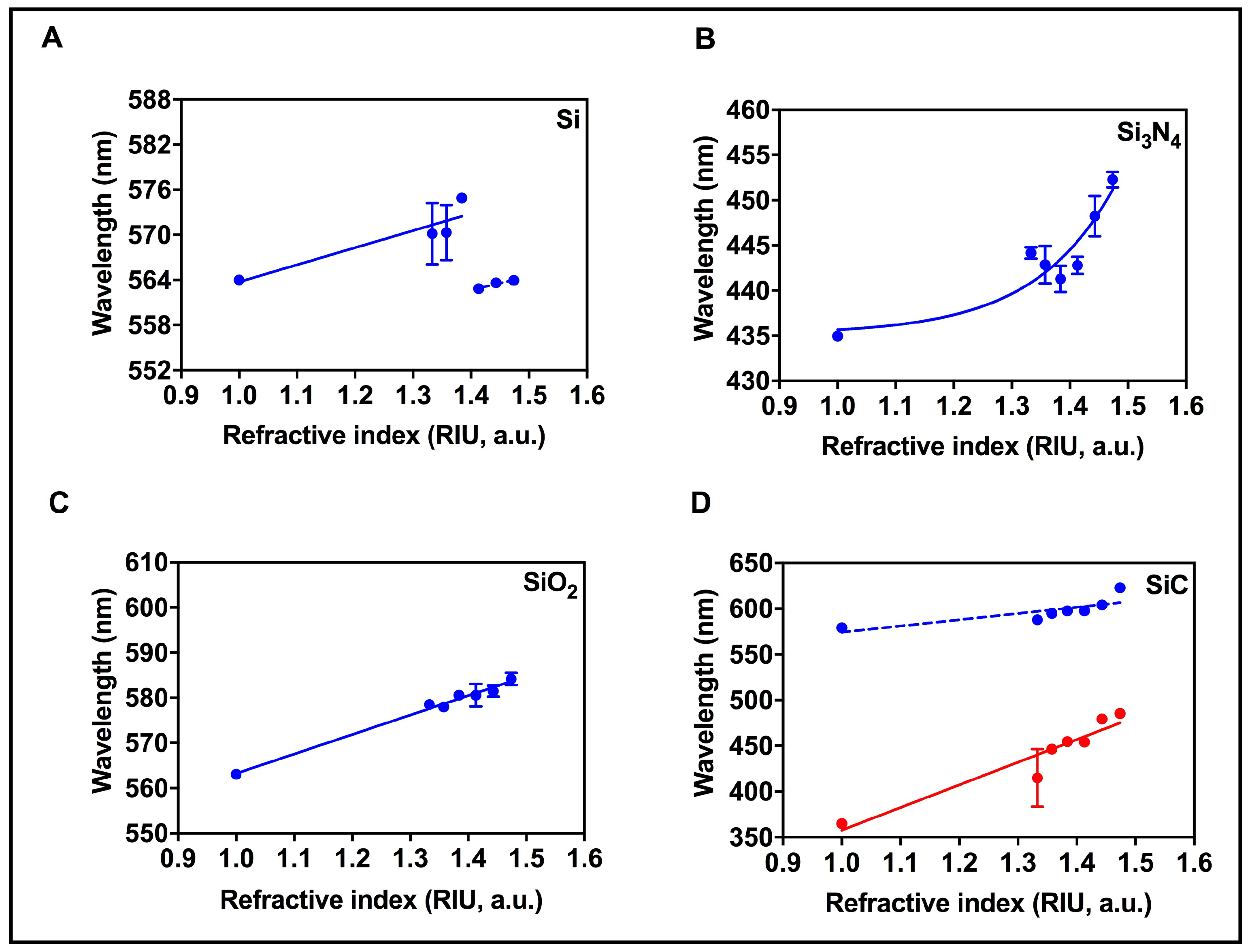
3.3. LSPR Characterization
3.4. RI Sensitivity
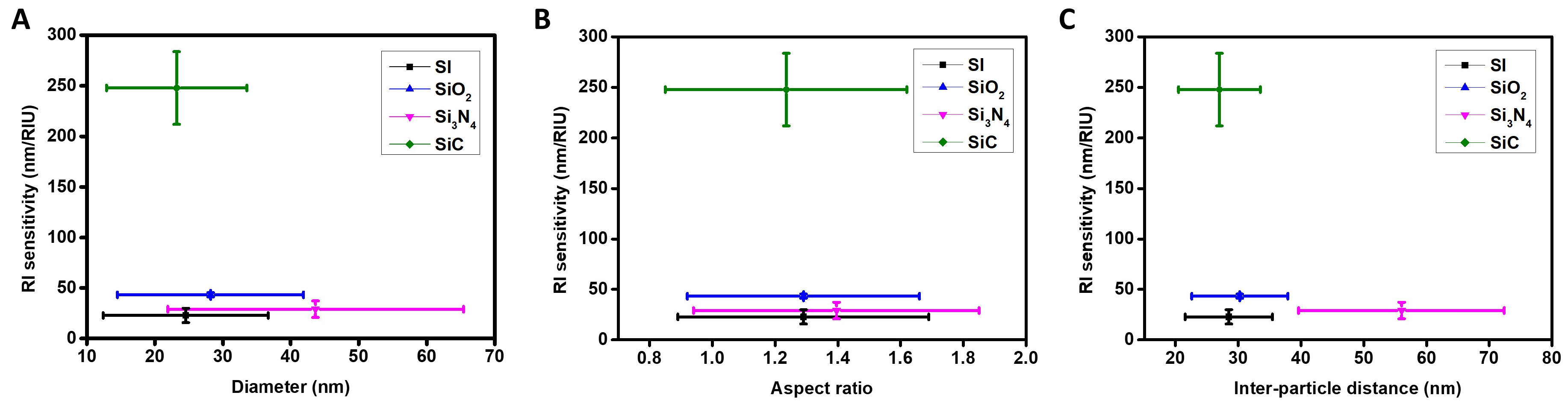
3.5. RI Sensitivity and Morphology
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Mukherjee, S.; Sobhani, H.; Lassiter, J.B.; Bardhan, R.; Nordlander, P.; Halas, N.J. Fanoshells: Nanoparticles with built-in Fano resonances. Nano Lett. 2010, 10, 2694–2701. [Google Scholar] [CrossRef] [PubMed]
- Hooshmand, N.; Panikkanvalappil, S.R.; El-Sayed, M.A. Effects of the Substrate Refractive Index, the Exciting Light Propagation Direction, and the Relative Cube Orientation on the Plasmonic Coupling Behavior of Two Silver Nanocubes at Different Separations. J. Phys. Chem. C 2016, 120, 20896–20904. [Google Scholar] [CrossRef]
- Willets, K.A.; Van Duyne, R.P. Localized surface plasmon resonance spectroscopy and sensing. Annu. Rev. Phys. Chem. 2007, 58, 267–297. [Google Scholar] [CrossRef] [PubMed]
- Bhalla, N.; Sathish, S.; Galvin, C.J.; Campbell, R.A.; Sinha, A.; Shen, A.Q. Plasma assisted large-scale nanoassembly of metal-insulator bioplasmonic mushrooms. ACS Appl. Mater. Interfaces 2017, 10, 219–226. [Google Scholar] [CrossRef]
- Saha, K.; Agasti, S.S.; Kim, C.; Li, X.; Rotello, V.M. Gold nanoparticles in chemical and biological sensing. Chem. Rev. 2012, 112, 2739–2779. [Google Scholar] [CrossRef]
- Mayer, K.M.; Hafner, J.H. Localized surface plasmon resonance sensors. Chem. Rev. 2011, 111, 3828–3857. [Google Scholar] [CrossRef]
- Jiang, R.; Li, B.; Fang, C.; Wang, J. Metal/Semiconductor Hybrid Nanostructures for Plasmon-Enhanced Applications. Adv. Mater. 2014, 26, 5274–5309. [Google Scholar] [CrossRef]
- Xiao, M.; Jiang, R.; Wang, F.; Fang, C.; Wang, J.; Jimmy, C.Y. Plasmon-enhanced chemical reactions. J. Mater. Chem. A 2013, 1, 5790–5805. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, R.; You, P.; Zhu, X.; Wang, J.; Yan, F. Au/Ag core–shell nanocuboids for high-efficiency organic solar cells with broadband plasmonic enhancement. Energy Environ. Sci. 2016, 9, 898–905. [Google Scholar] [CrossRef]
- Neumann, O.; Urban, A.S.; Day, J.; Lal, S.; Nordlander, P.; Halas, N.J. Solar vapor generation enabled by nanoparticles. ACS Nano 2012, 7, 42–49. [Google Scholar] [CrossRef]
- Kosako, T.; Kadoya, Y.; Hofmann, H.F. Directional control of light by a nano-optical Yagi–Uda antenna. Nat. Photonics 2010, 4, 312. [Google Scholar] [CrossRef]
- Curto, A.G.; Volpe, G.; Taminiau, T.H.; Kreuzer, M.P.; Quidant, R.; van Hulst, N.F. Unidirectional emission of a quantum dot coupled to a nanoantenna. Science 2010, 329, 930–933. [Google Scholar] [CrossRef] [PubMed]
- Sreekanth, K.V.; Alapan, Y.; ElKabbash, M.; Ilker, E.; Hinczewski, M.; Gurkan, U.A.; De Luca, A.; Strangi, G. Extreme sensitivity biosensing platform based on hyperbolic metamaterials. Nat. Mater. 2016, 15, 621. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Guo, H.; Fu, L.; Kaiser, S.; Schweizer, H.; Giessen, H. Three-dimensional photonic metamaterials at optical frequencies. Nat. Mater. 2008, 7, 31. [Google Scholar] [CrossRef]
- Limaj, O.; Etezadi, D.; Wittenberg, N.J.; Rodrigo, D.; Yoo, D.; Oh, S.H.; Altug, H. Infrared plasmonic biosensor for real-time and label-free monitoring of lipid membranes. Nano Lett. 2016, 16, 1502–1508. [Google Scholar] [CrossRef]
- Qin, F.; Cui, X.; Ruan, Q.; Lai, Y.; Wang, J.; Ma, H.; Lin, H.Q. Role of shape in substrate-induced plasmonic shift and mode uncovering on gold nanocrystals. Nanoscale 2016, 8, 17645–17657. [Google Scholar] [CrossRef]
- Dokhlikova, N.; Kolchenko, N.; Grishin, M.; Gatin, A.; Shub, B. Substrate effect on hydrogen adsorption on gold cluster. Nanotechnol. Russ. 2016, 11, 735–742. [Google Scholar] [CrossRef]
- Duval Malinsky, M.; Kelly, K.L.; Schatz, G.C.; Van Duyne, R.P. Nanosphere lithography: Effect of substrate on the localized surface plasmon resonance spectrum of silver nanoparticles. J. Phys. Chem. B 2001, 105, 2343–2350. [Google Scholar] [CrossRef]
- Bhalla, N.; Estrela, P. Exploiting the signatures of nanoplasmon–exciton coupling on proton sensitive insulator–semiconductor devices for drug discovery applications. Nanoscale 2018, 10, 13320–13328. [Google Scholar] [CrossRef]
- Knight, M.W.; Wu, Y.; Lassiter, J.B.; Nordlander, P.; Halas, N.J. Substrates matter: Influence of an adjacent dielectric on an individual plasmonic nanoparticle. Nano Lett. 2009, 9, 2188–2192. [Google Scholar] [CrossRef]
- Chen, H.; Shao, L.; Ming, T.; Woo, K.C.; Man, Y.C.; Wang, J.; Lin, H.Q. Observation of the Fano resonance in gold nanorods supported on high-dielectric-constant substrates. ACS Nano 2011, 5, 6754–6763. [Google Scholar] [CrossRef] [PubMed]
- Dement, D.B.; Quan, M.K.; Ferry, V.E. Nanoscale Patterning of Colloidal Nanocrystal Films for Nanophotonic Applications Using Direct Write Electron Beam Lithography. ACS Appl. Mater. Interfaces 2019, 11, 14970–14979. [Google Scholar] [CrossRef] [PubMed]
- Barreca, D.; Gri, F.; Gasparotto, A.; Carraro, G.; Bigiani, L.; Altantzis, T.; Žener, B.; Štangar, U.L.; Alessi, B.; Padmanaban, D.B.; et al. Multi-functional MnO2 nanomaterials for photo-activated applications by a plasma-assisted fabrication route. Nanoscale 2019, 11, 98–108. [Google Scholar] [CrossRef] [PubMed]
- Garg, V.; Mote, R.G.; Fu, J. Focused Ion Beam Direct Fabrication of Subwavelength Nanostructures on Silicon for Multicolor Generation. Adv. Mater. Technol. 2018, 3, 1800100. [Google Scholar] [CrossRef]
- Smith, J.D.; Bunch, C.M.; Li, Y.; Koczkur, K.M.; Skrabalak, S.E. Surface versus solution chemistry: manipulating nanoparticle shape and composition through metal–thiolate interactions. Nanoscale 2019, 11, 512–519. [Google Scholar] [CrossRef]
- Thompson, C.V. Solid-state dewetting of thin films. Annu. Rev. Mater. Res. 2012, 42, 399–434. [Google Scholar] [CrossRef]
- Siegel, J.; Kvitek, O.; Lyutakov, O.; Řezníčková, A.; Švorčík, V. Low pressure annealing of gold nanostructures. Vacuum 2013, 98, 100–105. [Google Scholar] [CrossRef]
- Siegel, J.; Lyutakov, O.; Rybka, V.; Kolská, Z.; Švorčík, V. Properties of gold nanostructures sputtered on glass. Nanoscale Res. Lett. 2011, 6, 96. [Google Scholar] [CrossRef]
- Sachan, P.; Kulkarni, M.; Sharma, A. Hierarchical micro/nano structures by combined self-organized dewetting and photopatterning of photoresist thin films. Langmuir 2015, 31, 12505–12511. [Google Scholar] [CrossRef]
- Palik, E. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1985; Volume 19852. [Google Scholar]
- Available online: https://refractiveindex.info/?shelf=main&book=SiO2&page=Malitson (accessed on 1 June 2019).
- Lifshitz, I.M.; Slyozov, V.V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
- Söderlund, J.; Kiss, L.; Niklasson, G.; Granqvist, C. Lognormal size distributions in particle growth processes without coagulation. Phys. Rev. Lett. 1998, 80, 2386. [Google Scholar] [CrossRef]
- Heintzenberg, J. Properties of the log-normal particle size distribution. Aerosol Sci. Technol. 1994, 21, 46–48. [Google Scholar] [CrossRef]
- Smith, J.E.; Jordan, M.L. Mathematical and graphical interpretation of the log-normal law for particle size distribution analysis. J. Colloid Sci. 1964, 19, 549–559. [Google Scholar] [CrossRef]
- Gleiter, H. Materials with ultrafine microstructures: Retrospectives and perspectives. Nanostruct. Mater. 1992, 1, 1–19. [Google Scholar] [CrossRef]
- Srolovitz, D.J.; Goldiner, M.G. The thermodynamics and kinetics of film agglomeration. J. Miner. Met. Mater. Soc. 1995, 47, 31–36. [Google Scholar] [CrossRef]
- Li, W.; Amirfazli, A. A thermodynamic approach for determining the contact angle hysteresis for superhydrophobic surfaces. J. Colloid Interface Sci. 2005, 292, 195–201. [Google Scholar] [CrossRef]
- Li, W.; Amirfazli, A. Microtextured superhydrophobic surfaces: A thermodynamic analysis. Adv. Colloid Interface Sci. 2007, 132, 51–68. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, H.; Li, W. Thermodynamic analysis on wetting behavior of hierarchical structured superhydrophobic surfaces. Langmuir 2011, 27, 6260–6267. [Google Scholar] [CrossRef]
- Lee, D.J.; Kim, H.M.; Song, Y.S.; Youn, J.R. Water droplet bouncing and superhydrophobicity induced by multiscale hierarchical nanostructures. ACS Nano 2012, 6, 7656–7664. [Google Scholar] [CrossRef]
- Lee, D.J.; Song, Y.S. Anomalous water drop bouncing on a nanotextured surface by the Leidenfrost levitation. Appl. Phys. Lett. 2016, 108, 201604. [Google Scholar] [CrossRef]
- Erb, R.A. Wettability of gold. J. Phys. Chem. 1968, 72, 2412–2417. [Google Scholar] [CrossRef]
- Krajcar, R.; Siegel, J.; Slepička, P.; Fitl, P.; Švorčík, V. Silver nanowires prepared on PET structured by laser irradiation. Mater. Lett. 2014, 117, 184–187. [Google Scholar] [CrossRef]
- Krajcar, R.; Siegel, J.; Lyutakov, O.; Slepička, P.; Švorčík, V. Optical response of anisotropic silver nanostructures on polarized light. Mater. Lett. 2014, 137, 72–74. [Google Scholar] [CrossRef]
- Lohrmann, A.; Iwamoto, N.; Bodrog, Z.; Castelletto, S.; Ohshima, T.; Karle, T.; Gali, A.; Prawer, S.; McCallum, J.; Johnson, B. Single-photon emitting diode in silicon carbide. Nat. Commun. 2015, 6, 7783. [Google Scholar] [CrossRef]
- Zheng, Y.; Pu, M.; Yi, A.; Chang, B.; You, T.; Huang, K.; Kamel, A.N.; Henriksen, M.R.; Jørgensen, A.A.; Ou, X.; et al. High-quality factor, high-confinement microring resonators in 4H-silicon carbide-on-insulator. Opt. Express 2019, 27, 13053–13060. [Google Scholar] [CrossRef]
| Si | SiO2 | Si3N4 | SiC | ||
|---|---|---|---|---|---|
| D | 3.27 | 3.41 | 3.85 | 3.20 | |
| 0.28 | 0.28 | 0.36 | 0.24 | ||
| 3.35 | 3.42 | 4.05 | 3.31 | ||
| D | 0.46 | 0.45 | 0.46 | 0.41 | |
| 0.27 | 0.25 | 0.29 | 0.28 | ||
| 0.22 | 0.22 | 0.26 | 0.21 |
| Substrate | Without AuNI () | With AuNI () |
|---|---|---|
| SiC | 98.93–100.61 | 110.58–113 |
| Si3N4 | 45.27–48.81 | 102.00–103.08 |
| Si | 73.89–74.37 | 110.95–109.38 |
| SiO2 | 73.49–74.10 | 95.93–99.55 |
| RI Range | Type | Equation | Slope | |
|---|---|---|---|---|
| Si | 1–1.4 | Linear, R sq. = 0.84 | = 22.74RI + 541 | 22.74 ± 7.05 nm/RIU |
| 1.4–1.473 | Linear, R sq. = 0.94 | = 18.09RI + 537.04 | 18.98 ± 4.55 nm/RIU | |
| Si3N4 | 1–1.473 | Exponential | - | - |
| SiO2 | 1–1.473 | Linear, R sq. = 0.99 | = 43.71RI + 520.1 | 43.17 ± 2.07 nm/RIU |
| SiC | 1–1.473 | Linear, R sq. = 0.91 | = 247.80RI + 109.9 | 247.80 ± 35.83 nm/RIU |
| 1–1.473 | Linear, R sq. = 0.63 | = 68.47RI + 35.83 | 68.47 ± 23.36 nm/RIU |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhalla, N.; Jain, A.; Lee, Y.; Shen, A.Q.; Lee, D. Dewetting Metal Nanofilms—Effect of Substrate on Refractive Index Sensitivity of Nanoplasmonic Gold. Nanomaterials 2019, 9, 1530. https://doi.org/10.3390/nano9111530
Bhalla N, Jain A, Lee Y, Shen AQ, Lee D. Dewetting Metal Nanofilms—Effect of Substrate on Refractive Index Sensitivity of Nanoplasmonic Gold. Nanomaterials. 2019; 9(11):1530. https://doi.org/10.3390/nano9111530
Chicago/Turabian StyleBhalla, Nikhil, Aditya Jain, Yoonjoo Lee, Amy Q. Shen, and Doojin Lee. 2019. "Dewetting Metal Nanofilms—Effect of Substrate on Refractive Index Sensitivity of Nanoplasmonic Gold" Nanomaterials 9, no. 11: 1530. https://doi.org/10.3390/nano9111530
APA StyleBhalla, N., Jain, A., Lee, Y., Shen, A. Q., & Lee, D. (2019). Dewetting Metal Nanofilms—Effect of Substrate on Refractive Index Sensitivity of Nanoplasmonic Gold. Nanomaterials, 9(11), 1530. https://doi.org/10.3390/nano9111530








