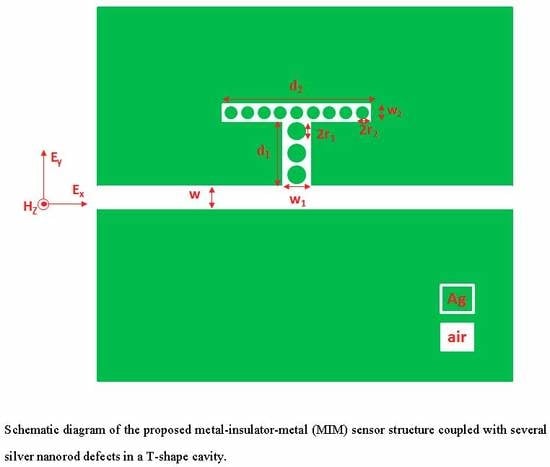
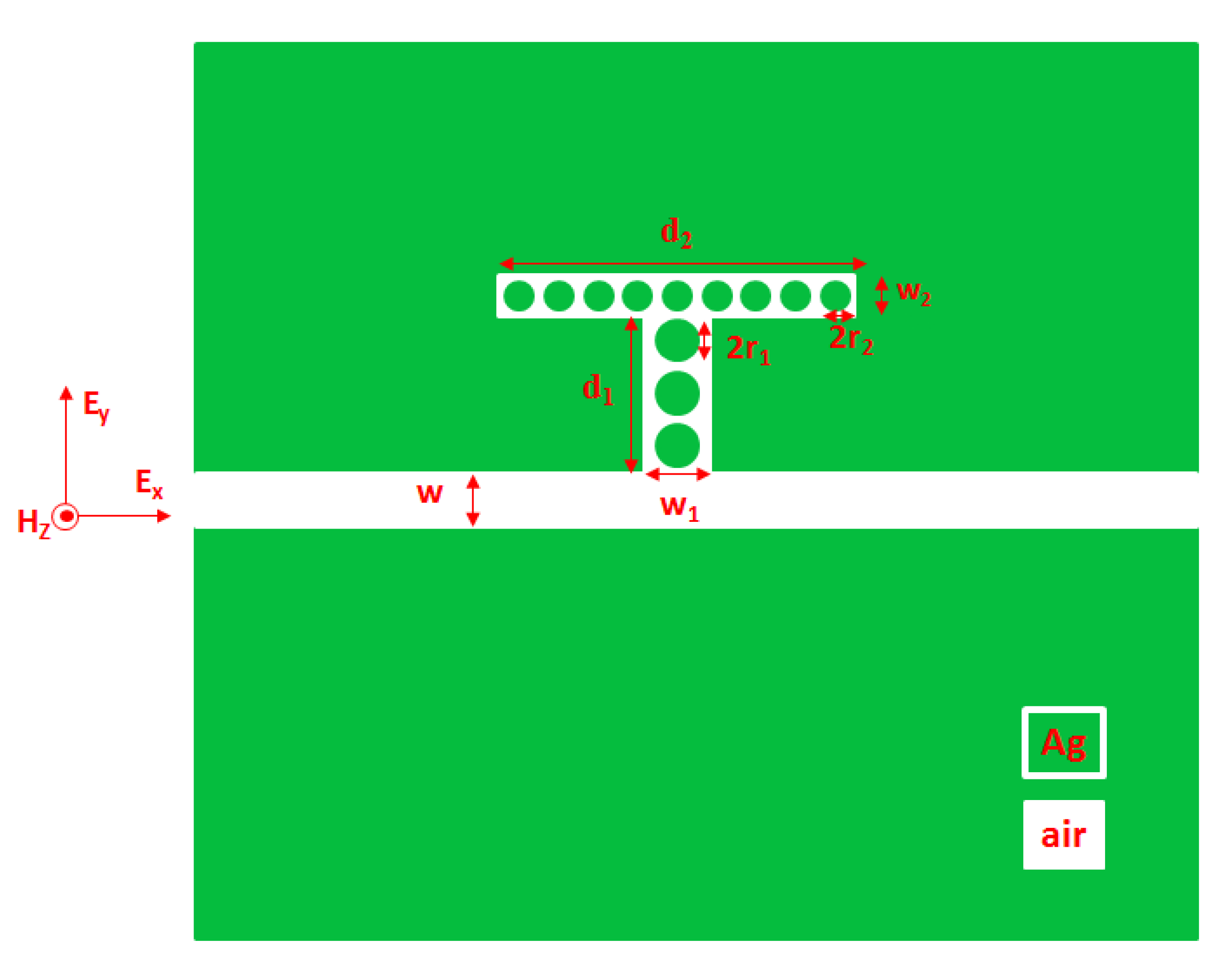
Ultra-High Refractive Index Sensing Structure Based on a Metal-Insulator-Metal Waveguide-Coupled T-Shape Cavity with Metal Nanorod Defects
Abstract
1. Introduction
2. Simulation Method and Models
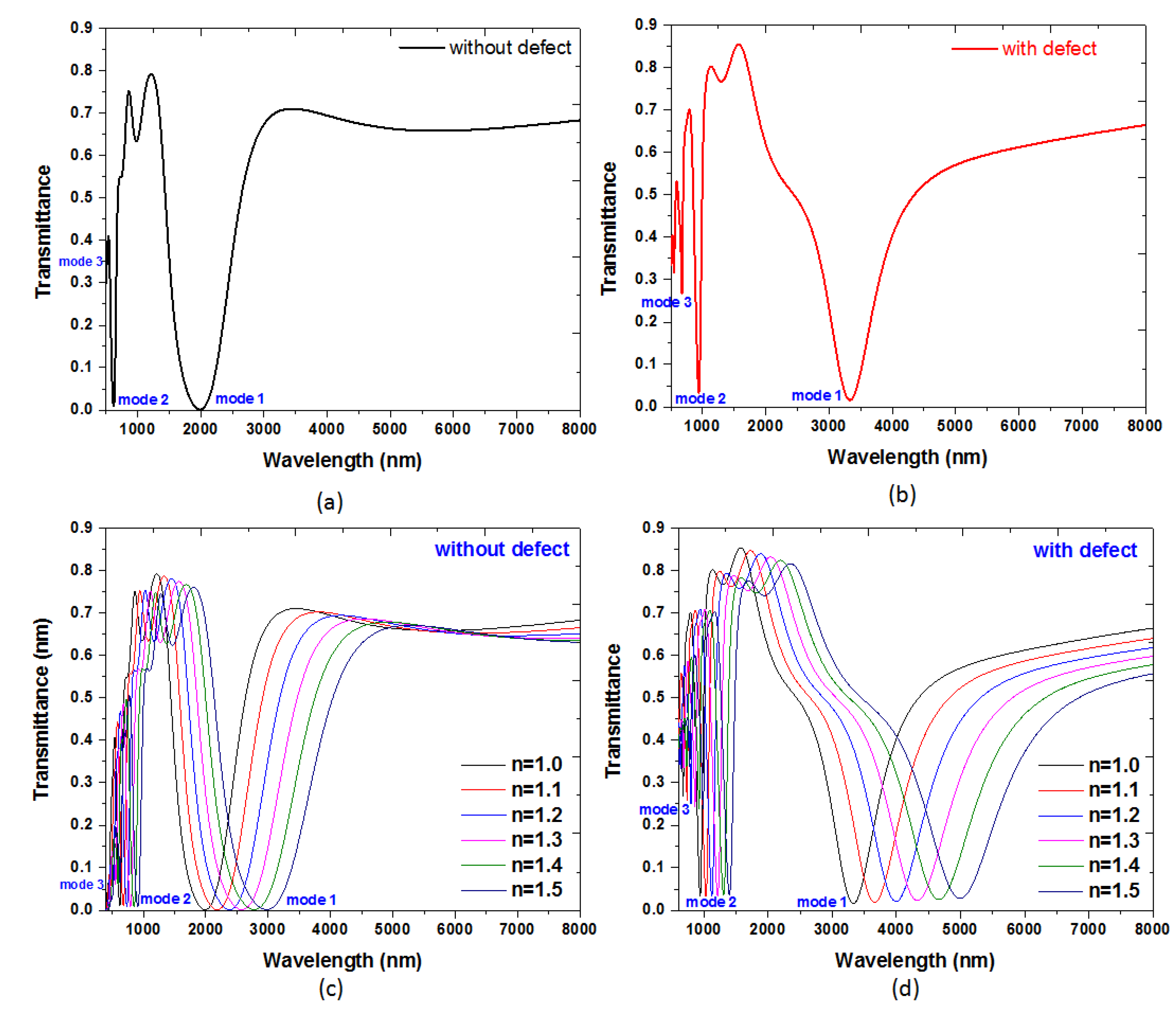
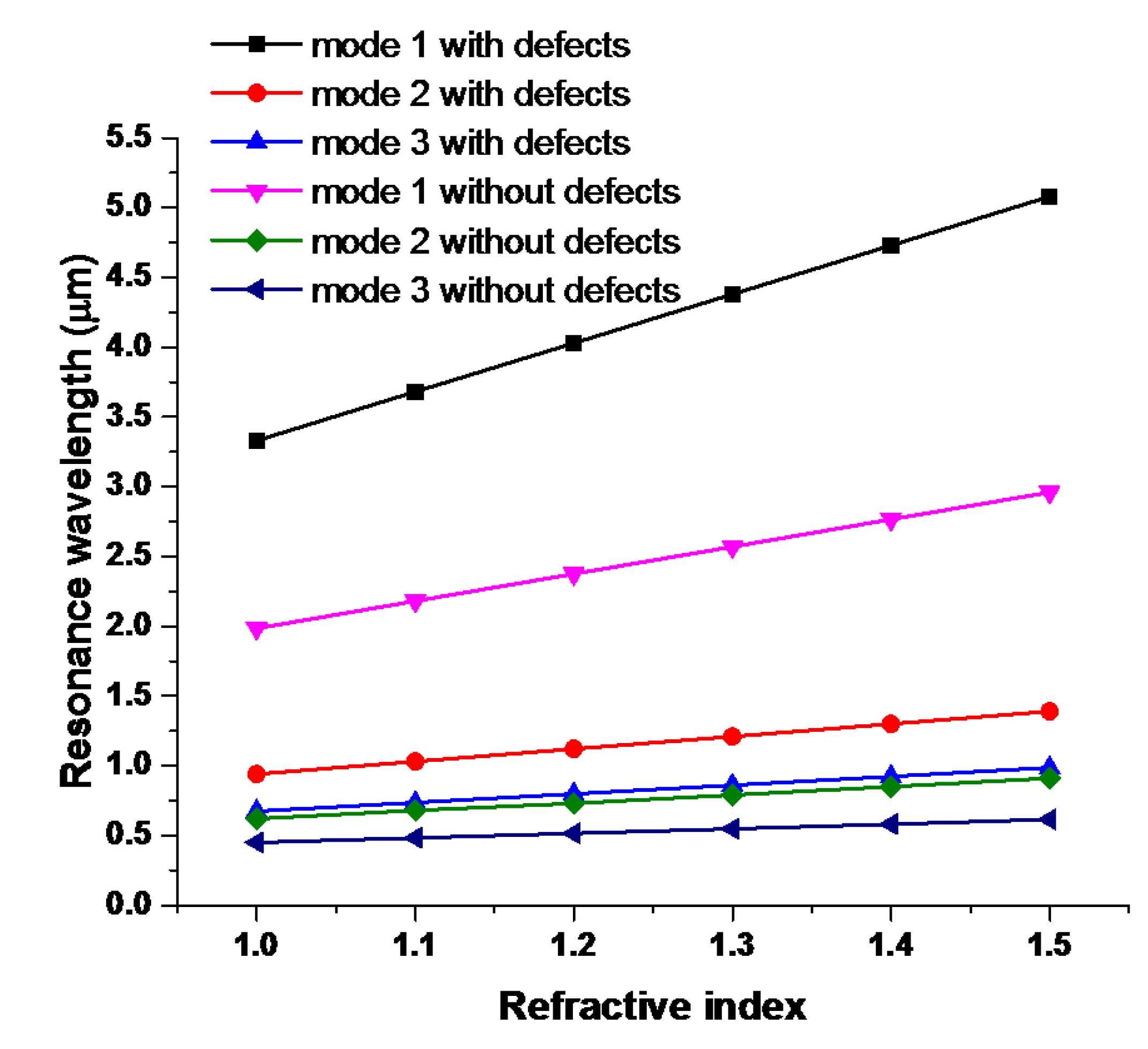
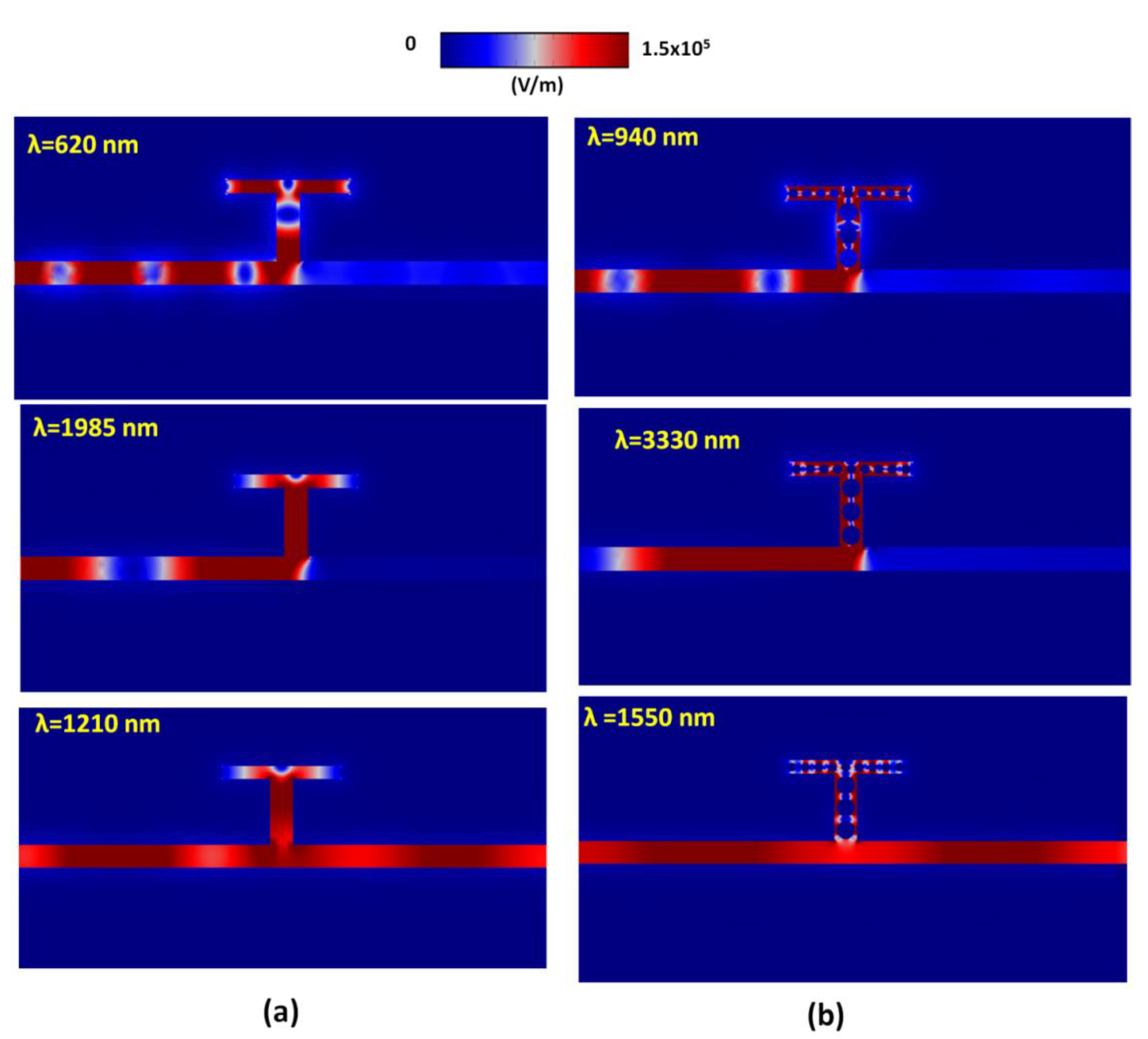
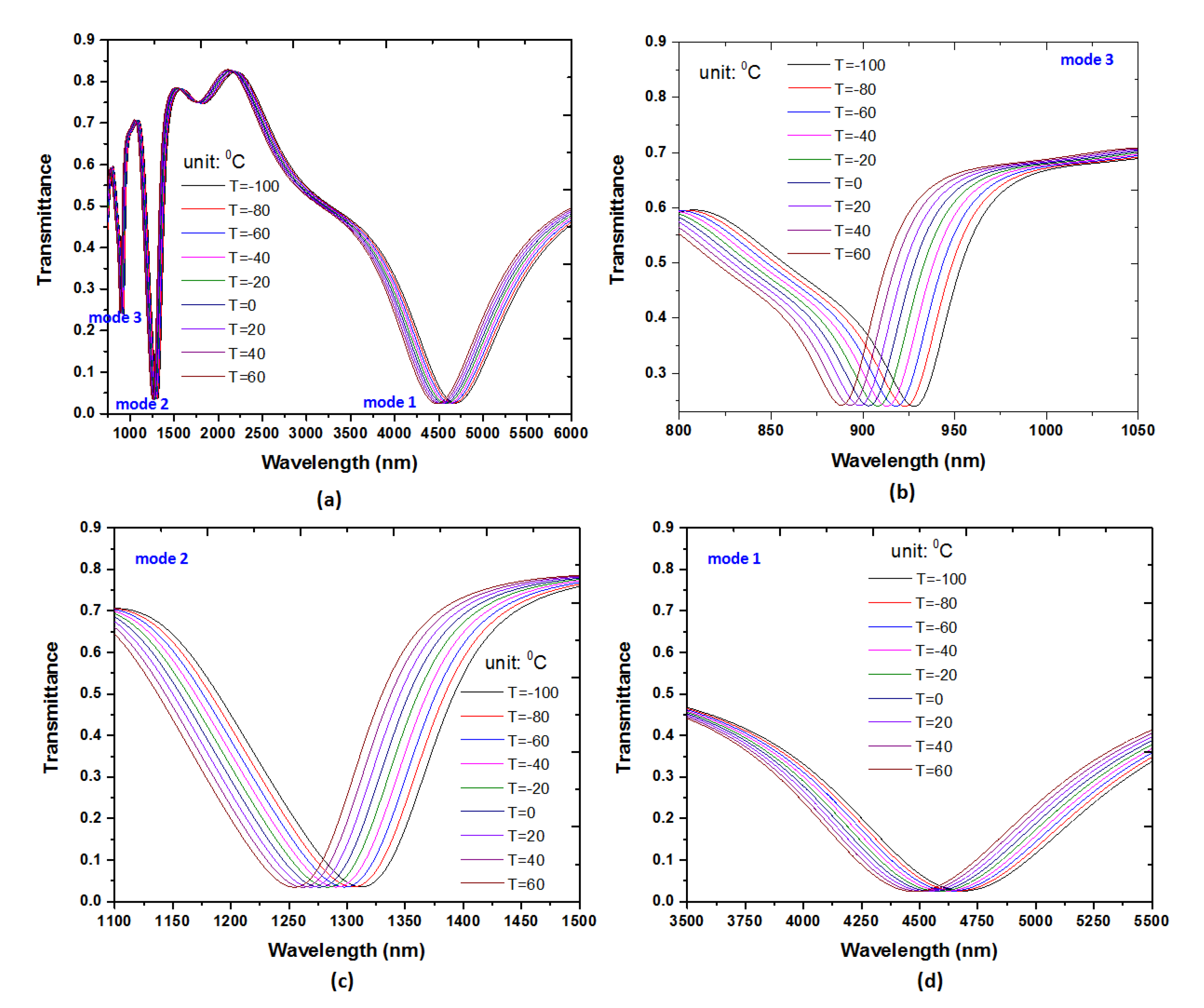
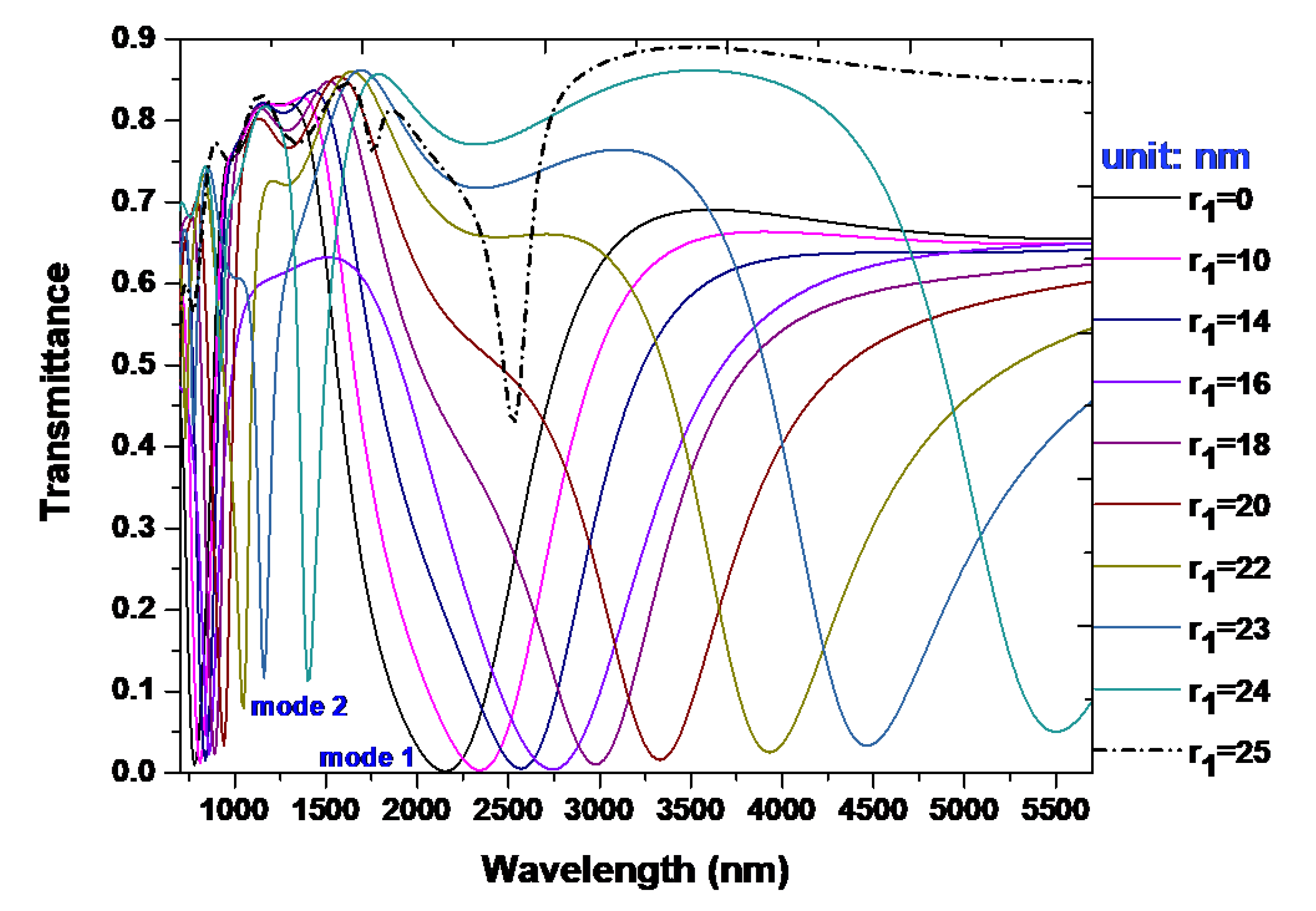
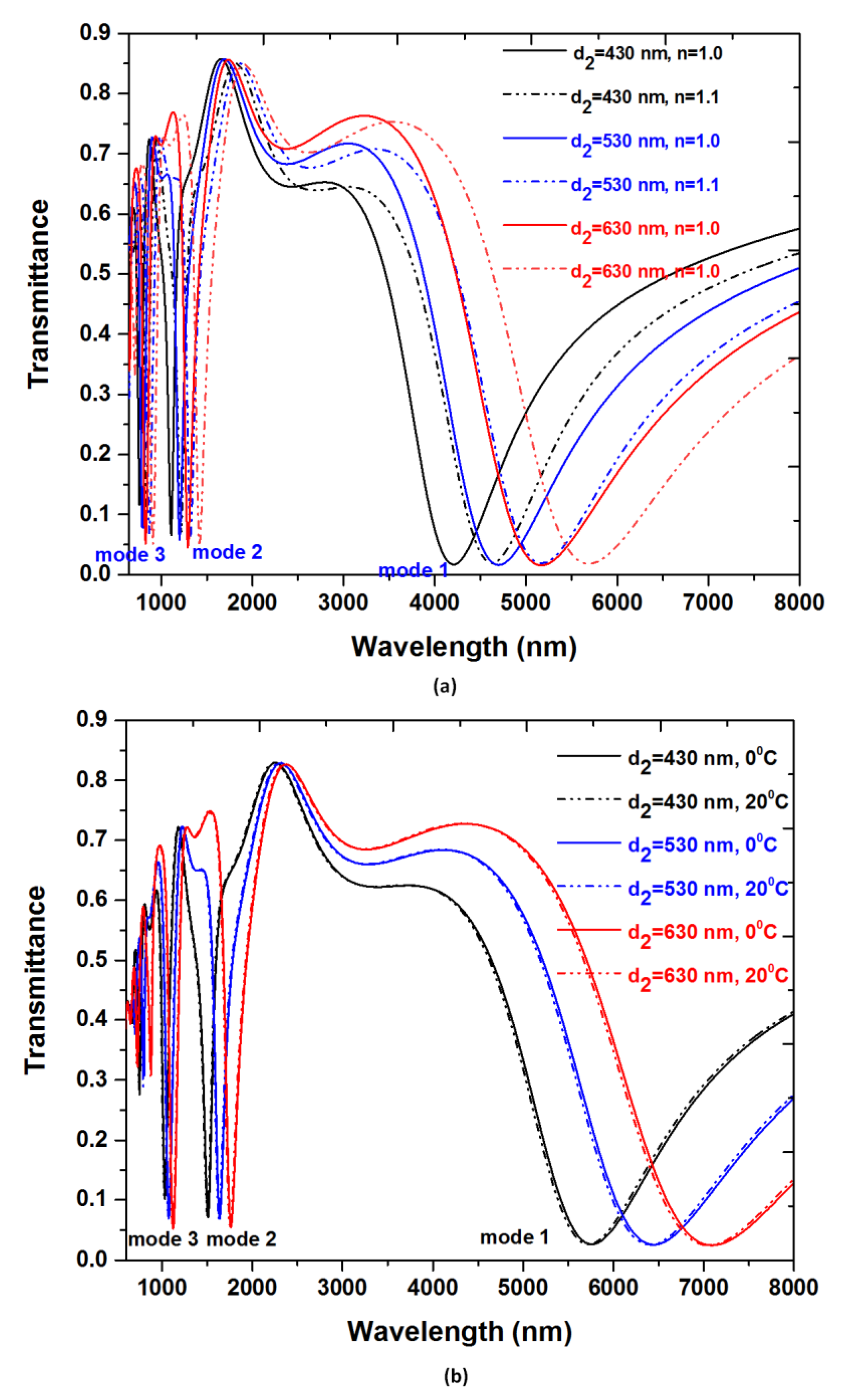
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, W.; Chau, Y.F.C.; Jheng, S.C. Analysis of transmittance properties of surface plasmon modes on periodic solid/outline bowtie nanoantenna arrays. Phys. Plasmas 2013, 20, 064503. [Google Scholar] [CrossRef]
- Chen, W.T.; Wu, P.C.; Chen, C.J.; Chung, H.Y.; Chau, Y.F.; Kuan, C.H.; Tsai, D.P. Electromagnetic energy vortex associated with sub-wavelength plasmonic Taiji marks. Opt. Express 2010, 18, 19665–19671. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.C.; Jen, H.C.; Chen, C.L.; Hwang, D.F.; Chang, R.; Hwang, J.S.; Chiang, H.P. SERS Study of Tetrodotoxin (TTX) by Using Silver Nanoparticle Arrays. Plasmonics 2009, 4, 187–192. [Google Scholar] [CrossRef]
- Yan, S.B.; Luo, L.; Xue, C.Y.; Zhang, Z.D. A Refractive Index Sensor Based on a Metal-Insulator-Metal Waveguide-Coupled Ring Resonator. Sensors 2015, 15, 29183–29191. [Google Scholar] [CrossRef] [PubMed]
- Fitrakis, E.P.; Kamalakis, T.; Sphicopoulos, T. Slow light in insulator–metal–insulator plasmonic waveguides. J. Opt. Soc. Am. B 2011, 28, 2159–2164. [Google Scholar] [CrossRef]
- Tong, L.M.; Wei, H.; Zhang, S.P.; Xu, H.X. Recent Advances in Plasmonic Sensors. Sensors 2014, 14, 7959–7973. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Tian, X.R.; Pan, D.; Chen, L.; Jia, Z.L.; Xu, H.G. Directionally-Controlled Periodic Collimated Beams of Surface Plasmon Polaritons on Metal Film in Ag Nanowire/Al2O3/Ag Film Composite Structure. Nano Lett. 2015, 15, 560–564. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, P.; Liu, X.; Di, Y.; Han, S.; Cui, X.; He, L. Sensing performance analysis on Fano resonance of metallic double-baffle contained MDM waveguide coupled ring resonator. Opt. Laser Technol. 2018, 101, 273–278. [Google Scholar] [CrossRef]
- Zhou, W.; Li, K.; Song, C.; Hao, P.; Chi, M.; Yu, M.; Wu, Y. Polarization-independent and omnidirectional nearly perfect absorber with ultra-thin 2D subwavelength metal grating in the visible region. Opt. Express 2015, 23, A413–A418. [Google Scholar] [CrossRef]
- Chen, M.W.; Chau, Y.F.; Tsai, D.P. Three-dimensional analysis of scattering field interactions and surface plasmon resonance in coupled silver nanospheres. Plasmonics 2008, 3, 157–164. [Google Scholar] [CrossRef]
- He, Z.; Li, H.; Zhan, S.; Li, B. Oscillator Model Analysis for Slow Light in Bright-Dark-Dark Waveguide Systems. IEEE Photonic. Technol. Lett. 2015, 27, 2371–2374. [Google Scholar] [CrossRef]
- Wu, T.; Liu, Y.; Yu, Z.; Peng, Y.W.; Shu, C.G.; He, H.F. The sensing characteristics of plasmonic waveguide with a single defect. Opt. Commun. 2014, 323, 44–48. [Google Scholar] [CrossRef]
- Chen, C.H.; Liao, K.S. 1xN plasmonic power splitters based on metal-insulator-metal waveguides. Opt. Express 2013, 21, 4036–4043. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Hu, R.; Cui, L.N.; Yu, L.; Wang, L.L.; Xiao, J.H. Plasmonic wavelength demultiplexers based on tunable Fano resonance in coupled-resonator systems. Opt. Commun. 2014, 320, 6–11. [Google Scholar] [CrossRef]
- Neutens, P.; Lagae, L.; Borghs, G.; Dorpe, P.V. Plasmon filters and resonators in metal-insulator-metal waveguides. Opt. Express 2012, 20, 3408–3423. [Google Scholar] [CrossRef]
- Lin, J.M.; Chau, Y.F. Radome slope compensation using multiple-model kalman filters. J. Guidance Control Dynam. 1995, 18, 637–640. [Google Scholar] [CrossRef]
- Wang, H.; Yang, J.; Zhang, J.; Huang, J.; Wu, W.; Chen, D.; Xiao, G. Tunable band-stop plasmonic waveguide filter with symmetrical multiple-teeth-shaped structure. Opt. Lett. 2016, 41, 1233–1236. [Google Scholar] [CrossRef]
- Tao, J.; Huang, X.G.; Lin, X.; Zhang, Q.; Jin, X. A narrow-band subwavelength plasmonic waveguide filter with asymmetrical multiple-teeth-shaped structure. Opt. Express 2009, 17, 13989–13994. [Google Scholar] [CrossRef]
- Lin, X.; Huang, X. Numerical modeling of a teeth-shaped nanoplasmonic waveguide filter. J. Opt. Soc. Am. B 2009, 26, 1263–1268. [Google Scholar] [CrossRef]
- Tao, J.; Huang, X.G.; Lin, X.; Chen, J.; Zhang, Q.; Jin, X. Systematical research on characteristics of double-sided teeth-shaped nanoplasmonic waveguide filters. J. Opt. Soc. Am. B 2010, 27, 323–327. [Google Scholar] [CrossRef]
- Yan, X.; Lin, B.; Cheng, T.; Li, S. Analysis of High Sensitivity Photonic Crystal Fiber Sensor Based on Surface Plasmon Resonance of Refractive Indexes of Liquids. Sensors 2018, 18, 2922. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Lou, J. Ultrasensitive and Multifunction Plasmonic Temperature Sensor with Ethanol-Sealed Asymmetric Ellipse Resonators. Molecules 2018, 23, 2700. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Luo, P.; Zhao, Z.Y.; He, L.; Cui, X.N. Study on Fano resonance regulating mechanism of Si contained metal–dielectric–metal waveguide coupled rectangular cavity. Phys. Lett. A 2017, 381, 3472–3476. [Google Scholar] [CrossRef]
- Xie, Y.; Huang, Y.; Xu, W.; Zhao, W.; He, C. A Plasmonic Temperature-Sensing Structure Based on Dual Laterally Side-Coupled Hexagonal Cavities. Sensors 2016, 16, 706. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ng, G.I.; Hu, T.; Qiu, H.; Guo, X.; Wang, W.; Rouifed, M.S.; Liu, C.; Sia, J.; Zhou, J.; et al. Mid-Infrared Sensor Based on a Suspended Micro racetrack Resonator with Lateral Subwavelength-Grating Metamaterial Cladding. IEEE Photonics J. 2018, 10, 6801608. [Google Scholar]
- Ogawa, S.; Kimata, M. Wavelength- or Polarization-Selective Thermal Infrared Detectors for Multi-Color or Polarimetric Imaging Using Plasmonics and Metamaterials. Materials 2017, 10, 493. [Google Scholar] [CrossRef]
- Hasan, D.; Lee, C. Hybrid Metamaterial Absorber Platform for Sensing of CO2 Gas at Mid-IR. Adv. Sci. 2018, 5. [Google Scholar] [CrossRef]
- Luo, J.; Lin, Y.S. High-efficiency of infrared absorption by using composited metamaterial nanotubes. Appl. Phys. Lett. 2019, 114, 051601. [Google Scholar] [CrossRef]
- Xu, R.; Lin, Y.S. Characterizations of reconfigurable infrared metamaterial absorbers. Opt. Lett. 2018, 43, 4783–4786. [Google Scholar] [CrossRef]
- Zhao, Z.M.; Wu, B.; Wang, X.S.; Pan, Z.H.; Liu, Z.J.; Zhang, P.Q.; Shen, X.; Nie, Q.H.; Dai, S.X.; Wang, R.P. Mid-infrared supercontinuum covering 2.0–16 μm in a low-loss telluride single-mode fiber. Laser Photonics Rev. 2017, 11, 5. [Google Scholar] [CrossRef]
- Xiao, T.H.; Zhao, Z.; Zhou, W.; Takenaka, M.; Tsang, H.K.; Cheng, Z.; Goda, K. High-Q germanium optical nanocavity. Photonics Res. 2018, 6, 925. [Google Scholar] [CrossRef]
- Ustun, K.; Turhan-Sayan, G. Wideband long wave infrared metamaterial absorbers based on silicon nitride. J. Appl. Phys. 2016, 120, 203101. [Google Scholar] [CrossRef]
- Lu, J.; Li, Y.; Han, Y.; Liu, Y.; Gao, J. D-shaped photonic crystal fiber plasmonic refractive index sensor based on gold grating. Appl. Opt. 2018, 57, 5268–5272. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Li, S.; Gao, X. Highly sensitive plasmonics temperature sensor based on photonic crystal fiber with a liquid core. Opt. Commun. 2018, 427, 622–627. [Google Scholar] [CrossRef]
- Sun, Y.S.; Chau, Y.F.; Yeh, H.H.; Tsai, D.P. Highly birefringent index-guiding photonic crystal fiber with squeezed differently sized air-holes in cladding. Jpn. J. Appl. Phys. 2008, 47, 3755–3759. [Google Scholar] [CrossRef]
- Chau, Y.F.; Yeh, H.H.; Tsai, D.P. Significantly enhanced birefringence of photonic crystal fiber using rotational binary unit cell in fiber cladding. Jpn. J. Appl. Phys. 2007, 46, L1048–L1051. [Google Scholar] [CrossRef]
- Wu, T.; Liu, Y.; Yu, Z.; Peng, Y.; Shu, C.; Ye, H. The sensing characteristics of plasmonic waveguide with a ring resonator. Opt. Express 2014, 22, 7669–7677. [Google Scholar] [CrossRef]
- COMSOL Multiphysics Reference Manual. Available online: http://www.comsol.com/ (accessed on 3 October 2018).
- Shen, L.; Yang, T.J.; Chau, Y.F. Effect of internal period on the optical dispersion of indefinite-medium materials. Phys. Rev. B 2008, 77, 205124. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Y.; Yu, Z.; Wu, D.; Ma, R.; Zhang, Y.; Ye, H. Numerical analysis of a near infrared plasmonic refractive index sensor with high figure of merit based on a fillet cavity. Opt. Express 2016, 24, 9975–9983. [Google Scholar] [CrossRef]
- Chau, Y.F.C.; Chao, C.T.C.; Chiang, H.P.; Lim, C.M.; Voo, N.Y.; Mahadi, A.H. Plasmonic effects in composite metal nanostructures for sensing applications. J. Nanopart. Res. 2018, 20, 190. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Gai, H.F.; Wang, J.; Tian, Q. Modified Debye model parameters of metals applicable for broadband calculations. Appl. Opt. 2007, 46, 2229–2233. [Google Scholar] [CrossRef] [PubMed]
- Chau, Y.F.; Yang, T.J.; Lee, W.D. Coupling technique for efficient interfacing between silica waveguides and planar photonic crystal circuits. Appl. Opt. 2004, 43, 6656–6663. [Google Scholar] [CrossRef] [PubMed]
- Dionne, J.; Sweatlock, L.; Atwater, H.; Polman, A. Plasmon slot waveguides: Towards chip-scale propagation with subwavelength-scale localization. Phys. Rev. B 2006, 73, 035407. [Google Scholar] [CrossRef]
- Boltasseva, A.; Bozhevolnyi, S.I.; Nikolajsen, T.; Leosson, K. Compact Bragg gratings for long-range surface Plasmon palaritons. J. Lighwave Technol. 2006, 24, 912–918. [Google Scholar] [CrossRef]
- Chau, Y.F.; Jheng, C.Y.; Joe, S.F.; Wang, S.F.; Yang, W.; Jheng, S.C.; Sun, Y.S.; Wei, J.H. Structurally and materially sensitive hybrid surface plasmon modes in periodic silver-shell nanopearl and its dimer arrays. J. Nanopart. Res. 2013, 15, 1424. [Google Scholar] [CrossRef]
- Xie, Y.; Huang, Y.; Zhao, W.; Xu, W.; He, C. A Novel Plasmonic Sensor Based on Metal–Insulator-Metal Waveguide with Side-Coupled Hexagonal Cavity. IEEE Photonics J. 2015, 7. [Google Scholar] [CrossRef]
- Wang, T.; Wen, X.; Yin, C.; Wang, H. The transmission characteristics of surface plasmon polaritons in ring resonator. Opt. Express 2009, 17, 24096–24101. [Google Scholar] [CrossRef]
- Al-Mahmod, M.J.; Hyder, R.; Islam, M.Z. Numerical Studies on a Plasmonic Temperature Nanosensor Based on a Metal-Insulator-Metal Ring Resonator Structure for Optical Integrated Circuit Applications. Photonics Nanostruct. Fundam. Appl. 2017, 25, 52–57. [Google Scholar] [CrossRef]
- Kong, Y.; Qiu, P.; Wei, Q.; Quan, W.; Wang, S.Y.; Qian, W.Y. Refractive index and temperature nanosensor with plasmonic waveguide system. Opt. Commun. 2016, 371, 132–137. [Google Scholar] [CrossRef]
- Shevchenko, Y.Y.; Albert, J. Plasmon resonances in gold-coated tilted fiber Bragg gratings. Opt. Lett. 2007, 32, 211–213. [Google Scholar] [CrossRef] [PubMed]
- Homes, C.; Daly, K.R.; Sparrow, I.J.G.; Gates, J.C.; D’Alessandro, G.; Smith, P.G.R. Excitation of Surface Plasmons Using Tilted Planar-Waveguide Bragg Gratings. IEEE Photonics 2011, 3, 777–788. [Google Scholar] [CrossRef]
- Chou Chau, Y.F.; Chou Chao, C.T.; Huang, H.J.; Anward, U.; Lim, C.M.; Voo, N.Y.; Mahadi, A.H.; Kumara, N.T.R.N.; Chiang, H.P. Plasmonic perfect absorber based on metal nanorod arrays connected with veins. Results Phys. 2019, 15, 102567. [Google Scholar] [CrossRef]
- Chou Chau, Y.F.; Chou Chao, C.T.; Huang, H.J.; Irdis, M.N.S.M.; Wang, Y.C.; Masri, Z.; Chiang, H.P.; Lim, C.M. Strong and tunable plasmonic field coupling and enhancement generating from the protruded metal nanorods and dielectric cores. Results Phys. 2019, 13, 102290. [Google Scholar] [CrossRef]
- Afridi, A.; Kocabaş, Ş.E. Beam steering and impedance matching of plasmonic horn nanoantennas. Opt. Express 2016, 24, 25647–25652. [Google Scholar] [CrossRef] [PubMed]
- Hung, Y.T.; Huang, C.B.; Huang, J.S. Plasmonic mode converter for controlling optical impedance and nanoscale light-matter interaction. Opt. Express 2012, 20, 20342–20355. [Google Scholar] [CrossRef] [PubMed]
- Chau, Y.F.; Yeh, H.H.; Tsai, D.P. Surface plasmon resonances effects on different patterns of solid-silver and silver-shell nanocylindrical pairs. J. Electromagn. Waves 2010, 24, 1005–1014. [Google Scholar] [CrossRef]
- Luo, S.; Zhao, J.; Zuo, D.L.; Wang, X.B. Perfect narrow band absorber for sensing applications. Opt. Express 2016, 24, 9288–9294. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, Z.; Yu, H.; Yang, L.; Gou, P.G.; Cao, J.; Zou, Y.; Qian, J.; Shi, T.; Ren, Q.; et al. Design of triple-band metamaterial absorbers with refractive index sensitivity at infrared frequencies. Opt. Express 2016, 24, 25742–25751. [Google Scholar] [CrossRef]
- Kumara, N.; Chau, Y.F.C.; Huang, J.W.; Huang, H.J.; Lin, C.T.; Chiang, H.P. Plasmonic spectrum on 1D and 2D periodic arrays of rod-shape metal nanoparticle pairs with different core patterns for biosensor and solar cell applications. J. Opt. 2016, 18, 115003. [Google Scholar] [CrossRef]
- Chau, Y.F.C.; Chou Chao, C.T.; Lim, C.M.; Huang, H.J.; Chiang, H.P. Depolying tunable metal-shell/dielectric core nanorod arrays as the virtually perfect absorber in the near-infrared regime. ACS Omega 2018, 3, 7508–7516. [Google Scholar] [CrossRef] [PubMed]
- Chou Chau, Y.F.; Wang, C.K.; Shen, L.; Lim, C.M.; Chiang, H.P.; Chou Chao, C.T.; Huang, H.J.; Lin, C.T.; Kumara, N.T.R.N.; Voo, N.Y. Simultaneous realization of high sensing sensitivity and tunability in plasmonic nanostructures arrays. Sci. Rep. 2017, 7, 16817. [Google Scholar] [CrossRef] [PubMed]
- Ben Salah, H.; Hocini, A.; Temmar, M.N.; Khedrouche, D. Design of mid infrared high sensitive metal-insulator-metal plasmonic sensor. Chin. J. Phys. 2019, 61, 86–97. [Google Scholar] [CrossRef]
| r1 (nm) | Mode 1 | Mode 2 | Mode 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| λres (nm) | S (nm/RIU) | λres (nm) | S (nm/RIU) | λres (nm) | S (nm/RIU) | ||||
| n = 1.0 | n = 1.1 | n = 1.0 | n = 1.1 | n = 1.0 | n = 1.1 | ||||
| 0 | 2153 | 2367 | 2140.0 | 780 | 854 | 740.0 | 548 | 593 | 450 |
| 5.0 | 2197 | 2416 | 2190.0 | 787 | 862 | 750.0 | 551 | 597 | 460 |
| 8.0 | 2270 | 2496 | 2260.0 | 798 | 874 | 760.0 | 557 | 604 | 470 |
| 10.0 | 2343 | 2576 | 2330.0 | 810 | 887 | 770.0 | 563 | 611 | 480 |
| 12.0 | 2440 | 2683 | 2430.0 | 822 | 900 | 780.0 | 573 | 622 | 490 |
| 14.0 | 2569 | 2825 | 2560.0 | 838 | 919 | 810.0 | 586 | 637 | 510 |
| 16.0 | 2741 | 3015 | 2740.0 | 860 | 942 | 820.0 | 606 | 660 | 540 |
| 18.0 | 2978 | 3275 | 2970.0 | 890 | 976 | 860.0 | 634 | 691 | 570 |
| 20.0 | 3330 | 3663 | 3330.0 | 940 | 1031 | 910.0 | 674 | 736 | 620 |
| 22.0 | 3931 | 4325 | 3940.0 | 1046 | 1148 | 1020.0 | 730 | 798 | 680 |
| 23.0 | 4465 | 4914 | 4490.0 | 1160 | 1273 | 1130.0 | 775 | 847 | 720 |
| 24.0 | 5502 | 6056 | 5540.0 | 1404 | 1542 | 1380.0 | 923 | 1010 | 870 |
| 25.0 | 2528 | 2778 | 2500.0 | 1760 | 1933 | 1730.0 | |||
| d2 (nm) | Mode 1 | Mode 2 | Mode 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| λres (nm) | S (nm/RIU) | λres (nm) | S (nm/RIU) | λres (nm) | S (nm/RIU) | ||||
| n = 1.0 | n = 1.1 | n = 1.0 | n = 1.1 | n = 1.0 | n = 1.1 | ||||
| 430 | 6778 | 7463 | 6850 | 1470 | 1616 | 1460 | 998 | 1095 | 970 |
| 530 | 7484 | 8246 | 7620 | 1513 | 1663 | 1500 | 1079 | 1184 | 1050 |
| 630 | 8146 | 8974 | 8280 | 1563 | 1717 | 1540 | 1154 | 1267 | 1130 |
| d2 (nm) | Mode 1 | Mode 2 | Mode 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| λres (nm) | S (nm/°C) | λres (nm) | S (nm/°C) | λres (nm) | S (nm/°C) | ||||
| T = 0 °C | T = 20 °C | T = 0 °C | T = 20 °C | T = 0 °C | T = 20 °C | ||||
| 430 | 9262 | 9317 | 2.75 | 2006 | 1995 | 0.55 | 1354 | 1347 | 0.35 |
| 530 | 10,300 | 10,239 | 3.05 | 2066 | 2050 | 0.80 | 1467 | 1459 | 0.40 |
| 630 | 11,214 | 11,148 | 3.30 | 2133 | 2121 | 0.60 | 1570 | 1562 | 0.40 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chou Chau, Y.-F.; Chou Chao, C.-T.; Huang, H.J.; Kumara, N.T.R.N.; Lim, C.M.; Chiang, H.-P. Ultra-High Refractive Index Sensing Structure Based on a Metal-Insulator-Metal Waveguide-Coupled T-Shape Cavity with Metal Nanorod Defects. Nanomaterials 2019, 9, 1433. https://doi.org/10.3390/nano9101433
Chou Chau Y-F, Chou Chao C-T, Huang HJ, Kumara NTRN, Lim CM, Chiang H-P. Ultra-High Refractive Index Sensing Structure Based on a Metal-Insulator-Metal Waveguide-Coupled T-Shape Cavity with Metal Nanorod Defects. Nanomaterials. 2019; 9(10):1433. https://doi.org/10.3390/nano9101433
Chicago/Turabian StyleChou Chau, Yuan-Fong, Chung-Ting Chou Chao, Hung Ji Huang, N. T. R. N. Kumara, Chee Ming Lim, and Hai-Pang Chiang. 2019. "Ultra-High Refractive Index Sensing Structure Based on a Metal-Insulator-Metal Waveguide-Coupled T-Shape Cavity with Metal Nanorod Defects" Nanomaterials 9, no. 10: 1433. https://doi.org/10.3390/nano9101433
APA StyleChou Chau, Y.-F., Chou Chao, C.-T., Huang, H. J., Kumara, N. T. R. N., Lim, C. M., & Chiang, H.-P. (2019). Ultra-High Refractive Index Sensing Structure Based on a Metal-Insulator-Metal Waveguide-Coupled T-Shape Cavity with Metal Nanorod Defects. Nanomaterials, 9(10), 1433. https://doi.org/10.3390/nano9101433