Linear and Nonlinear Intersubband Optical Properties of Direct Band Gap GeSn Quantum Dots
Abstract
1. Introduction
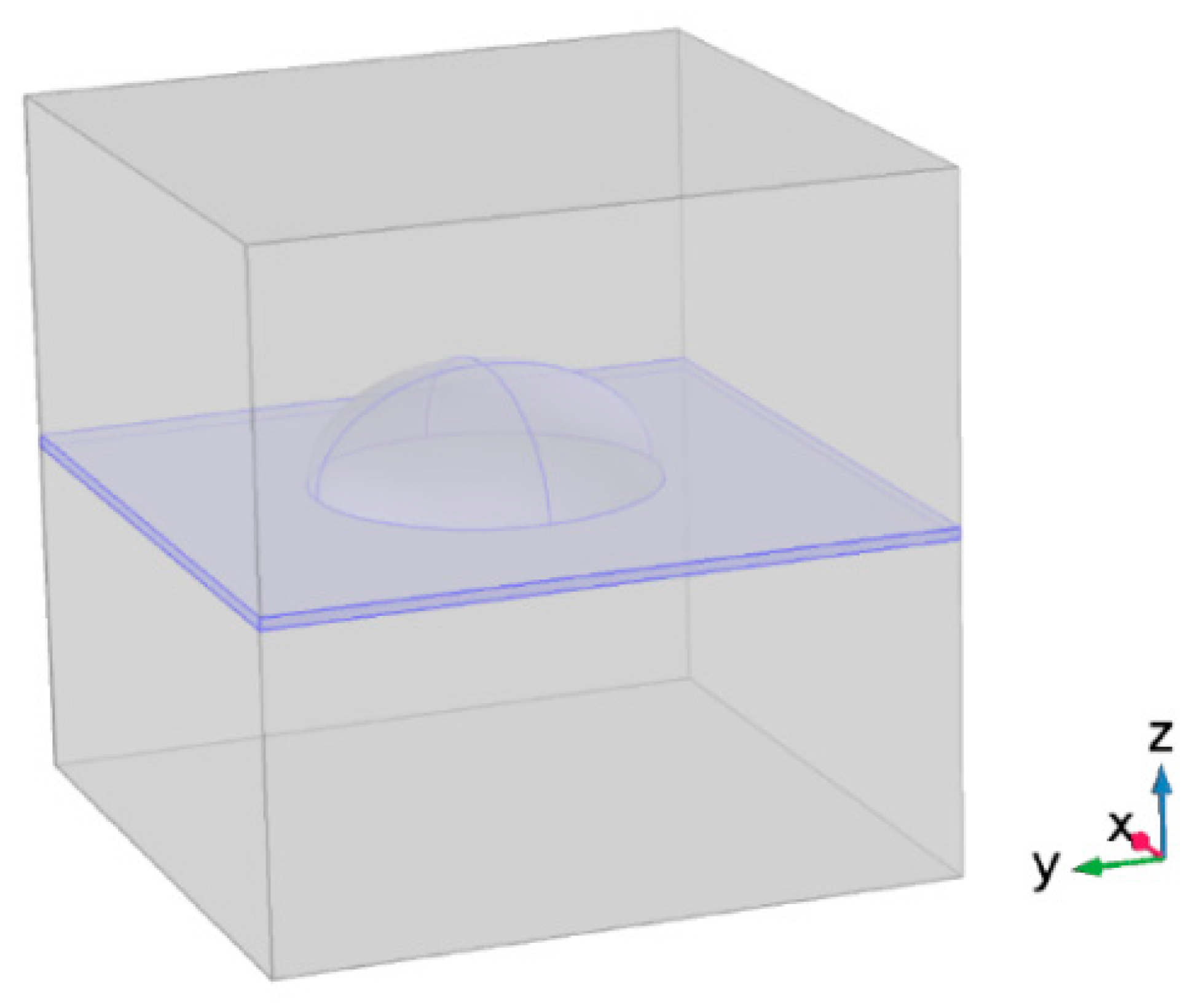
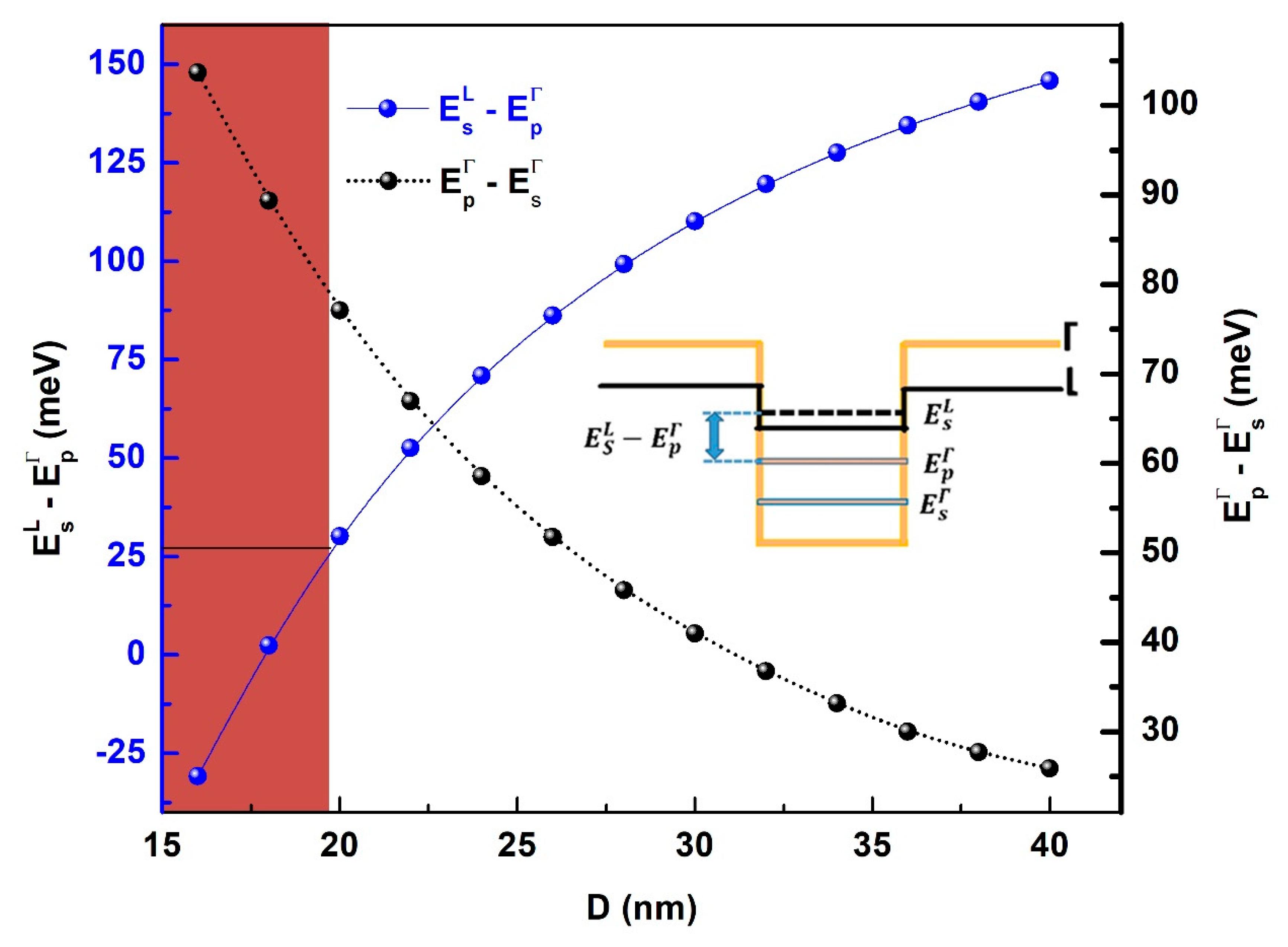
2. Intersubband Transition Energies
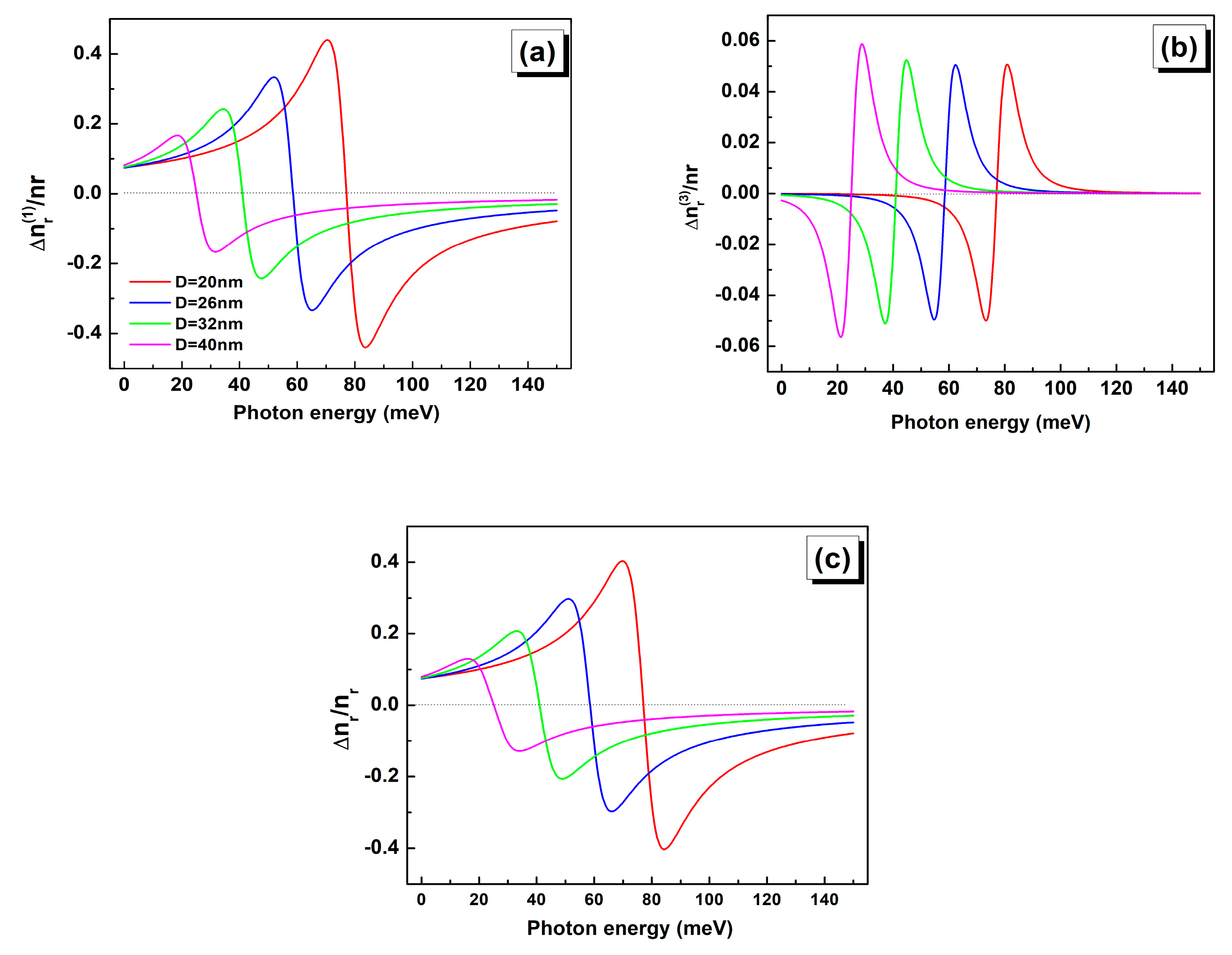
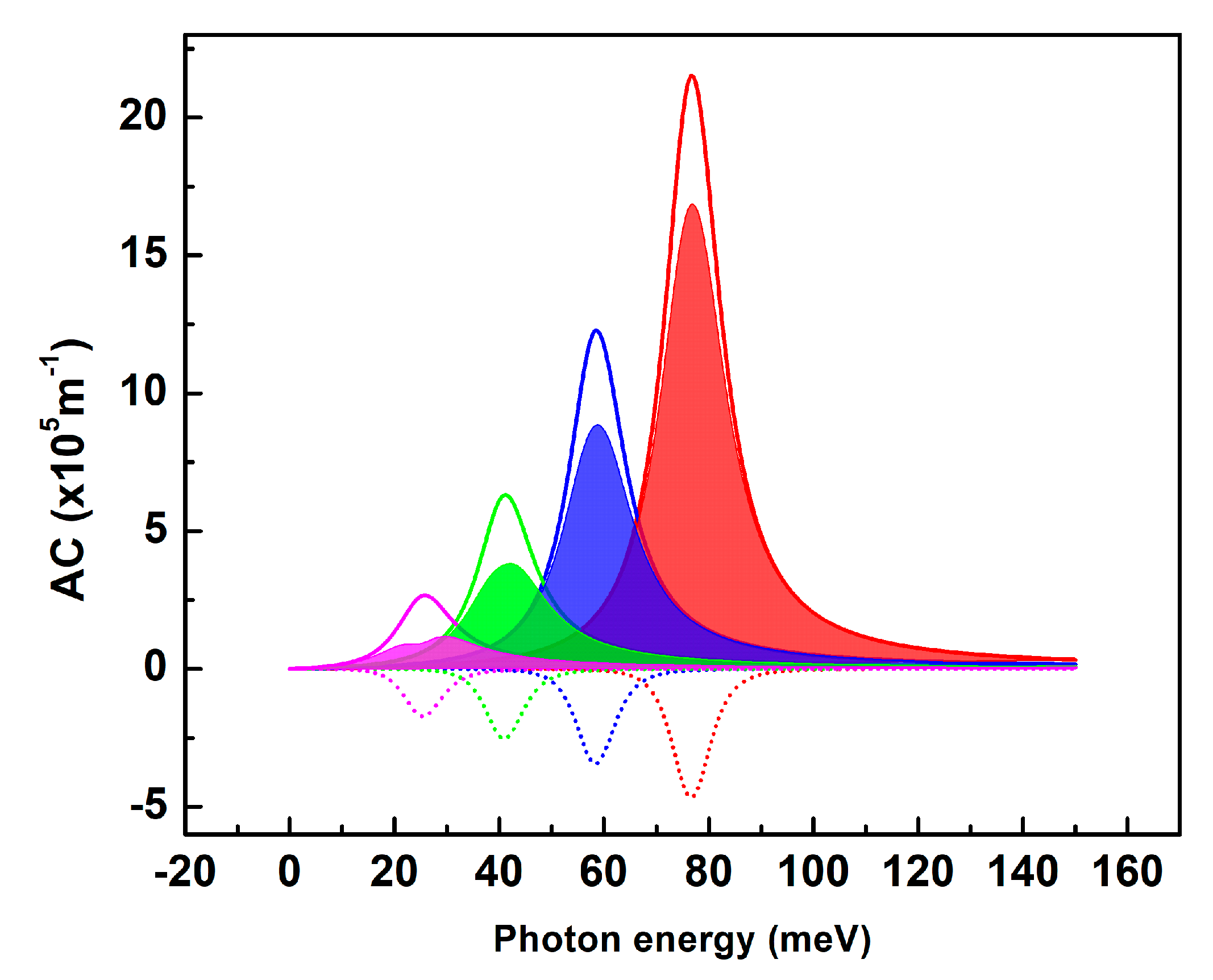
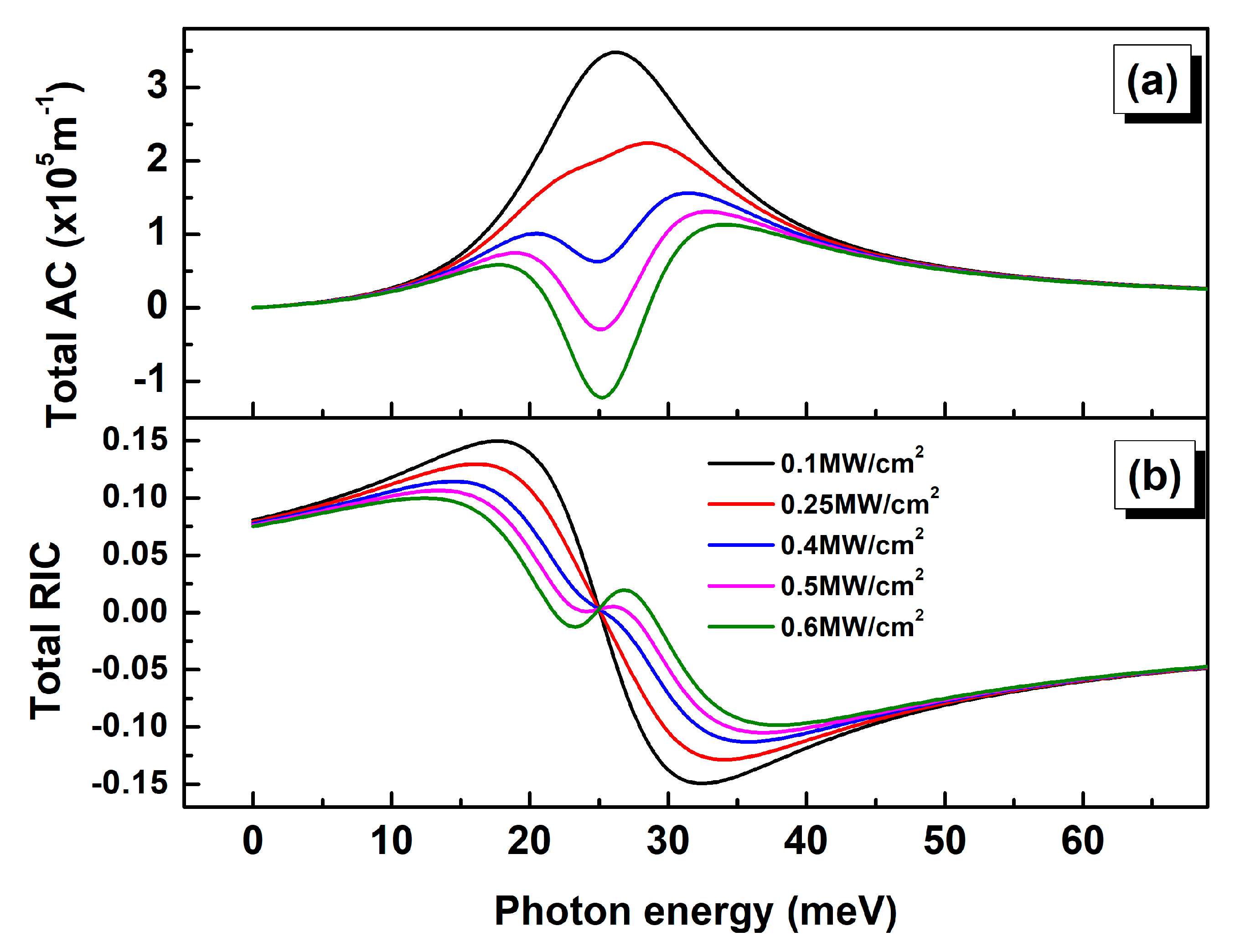
3. Linear and Nonlinear Optical Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| QD | Quantum Dots |
| AC | absorption coefficient |
| RIC | refractive index change |
| CMO | Complementary Metal Oxide Semiconductor |
References
- He, G.; Atwater, H. Interband transitions in SnxGe1−x alloys. Phys. Rev. Lett. 1997, 79, 1937–1940. [Google Scholar] [CrossRef]
- Chen, R.; Lin, H.; Huo, Y.; Hitzman, C.; Kamins, T.I.; Harris, J.S. Increased photoluminescence of strain-reduced, high-Sn composition Ge1−xSnx alloys grown by molecular beam epitaxy. Appl. Phys. Lett. 2011, 99, 181125. [Google Scholar] [CrossRef]
- Jiang, L.; Gallagher, J.D.; Senaratne, C.L.; Aoki, T.; Mathews, J.; Kouvetakis, J.; Menéndez, J. Compositional dependence of the direct and indirect band gaps in Ge1−ySny alloys from room temperature photoluminescence: Implications for the indirect to direct gap crossover in intrinsic and n-type materials. Semicond. Sci. Technol. 2014, 29, 115028. [Google Scholar] [CrossRef]
- Toko, K.; Oya, N.; Saitoh, N.; Yoshizawa, N.; Suemasu, T. 70 °C synthesis of high-Sn content (25%) GeSn on insulator by Sn-induced crystallization of amorphous Ge. Appl. Phys. Lett. 2015, 106, 082109. [Google Scholar] [CrossRef]
- Taoka, N.; Capellini, G.; Schlykow, V.; Montanari, M.; Zaumseil, P.; Nakatsuk, O.; Zaima, S.; Schroeder, T. Electrical and optical properties improvement of GeSn layers formed at high temperature under well-controlled Sn migration. Mater. Sci. Semicond. Process. 2017, 57, 48–53. [Google Scholar] [CrossRef]
- Chang, C.; Chang, T.-W.; Li, H.; Cheng, H.H.; Soref, R.; Sun, G.; Hendrickson, J.R. Room-temperature 2-μm GeSn P-I-N homojunction light-emitting diode for inplane coupling to group-IV waveguides. Appl. Phys. Lett. 2017, 111, 141105. [Google Scholar] [CrossRef]
- Wirths, S.; Geiger, R.; von den Driesch, N.; Mussler, G.; Stoica, T.; Mantl, S.; Ikonic, Z.; Luysberg, M.; Chiussi, S.; Hartmann, J.M.; et al. Lasing in direct-bandgap GeSn alloy grown on Si. Nat. Photonics 2015, 9, 88–92. [Google Scholar] [CrossRef]
- Dou, W.; Zhou, Y.; Margetis, J.; Ghetmiri, S.A.; Al-Kabi, S.; Du, W.; Liu, J.; Sun, G.; Soref, R.A.; Tolle, J.; et al. Optically pumped lasing at 3 μm from compositionally graded GeSn with tin up to 22.3%. Opt. Lett. 2018, 43, 4558–4561. [Google Scholar] [CrossRef] [PubMed]
- Stange, D.; Wirths, S.; Geiger, R.; Schulte-Braucks, C.; Marzban, B.; von den Driesch, N.; Mussler, G.; Zabel, T.; Stoica, T.; Hartmann, J.-M.; et al. Optically Pumped GeSn Microdisk Lasers on Si. ACS Photonics 2016, 3, 1279–1285. [Google Scholar] [CrossRef]
- Ibrahim, T.A.; Cao, W.; Kim, Y.; Li, J.; Goldhar, J.; Ho, P.-T.; Lee, C.H. All-optical switching in a laterally coupled microring resonator by carrier injection. IEEE Photonics Technol. Lett. 2003, 15, 36–38. [Google Scholar] [CrossRef]
- Van, V.; Ibrahim, T.A.; Ritter, K.; Absil, P.P.; Johnson, F.G.; Grover, R.; Goldhar, J.; Ho, P.-T. All-optical nonlinear switching in GaAs–AlGaAs microring resonators. IEEE Photonics Technol. Lett. 2002, 14, 74–76. [Google Scholar] [CrossRef]
- Almeida, V.R.; Barrios, C.A.; Panepucci, R.; Lipson, M. All-optical control of light on a silicon chip. Nature 2004, 431, 1081–1084. [Google Scholar] [CrossRef] [PubMed]
- Eiichi, H. Very large optical nonlinearity of semiconductor microcrystallites. Phys. Rev. B 1988, 37, 1273D. [Google Scholar] [CrossRef]
- Stange, D.; von den Driesch, N.; Zabel, T.; Armand-Pilon, F.; Rainko, D.; Marzban, B.; Zaumseil, P.; Hartmann, J.-M.; Ikonic, Z.; Capellini, G.; et al. GeSn/SiGeSn Heterostructure and Multi Quantum Well Lasers. ACS Photonics 2018, 5, 4628–4636. [Google Scholar] [CrossRef]
- Albani, M.; Assali, S.; Verheijen, M.A.; Koelling, S.; Bergamaschini, R.; Pezzoli, F.; Bakkers, E.P.A.M.; Miglio, L. Critical strain for Sn incorporation into spontaneously graded Ge/GeSn core/shell nanowires Critical strain for Sn incorporation into spontaneously graded Ge/GeSn core/shell nanowires. Nanoscale 2018, 10, 7250–7256. [Google Scholar] [CrossRef] [PubMed]
- Haffner, T.; Zeghouane, M.; Bassani, F.; Gentile, P.; Gassenq, A.; Chouchane, F.; Pauc, N.; Martinez, E.; Robin, E.; David, S.; et al. Growth of Ge1− xSn x Nanowires by chemical vapor deposition via vapor–liquid–solid mechanism using GeH4 and SnCl4. Phys. Status Solidi A 2018, 215, 1700743. [Google Scholar] [CrossRef]
- Seifner, M.S.; Hernandez, S.; Bernardi, J.; Romano-Rodriguez, A.; Barth, S. Pushing the composition limit of anisotropic Ge1−xSnx nanostructures and determination of their thermal stability. Chem. Mater. 2017, 29, 9802–9813. [Google Scholar] [CrossRef]
- Esteves, R.J.A.; Ho, M.Q.; Arachchige, I.U. Nanocrystalline Group IV Alloy Semiconductors: Synthesis and Characterization of Ge1–xSnx Quantum Dots for Tunable Bandgaps. Chem. Mater. 2015, 27, 1559–1568. [Google Scholar] [CrossRef]
- Nakamura, Y. Quantum-confinement effect in individual Ge1−xSnx quantum dots on Si(111) substrates covered with ultrathin SiO2 films using scanning tunneling spectroscopy. Appl. Phys. Lett. 2007, 91, 013109. [Google Scholar] [CrossRef]
- Moontragoon, P.; Vukmirović, N.; Ikonić, Z.; Harrison, P. Electronic structure and optical properties of Sn and SnGe quantum dots. J. Appl. Phys. 2008, 103, 103712. [Google Scholar] [CrossRef]
- Ilahi, B. Design of direct band gap type I GeSn/Ge quantum dots for mid-IR light emitters on Si substrate. Phys. Status Solidi RRL 2017, 11, 1700047. [Google Scholar] [CrossRef]
- Baira, M.; Salem, B.; Madhar, N.A.; Ilahi, B. Tuning direct bandgap GeSn/Ge quantum dots’ interband and intraband useful emission wavelength: Towards CMOS compatible infrared optical devices. Superlattice Microst. 2018, 117, 31–35. [Google Scholar] [CrossRef]
- Ilahi, B.; Al-Saigh, R.; Salem, B. Impact of the wetting layer thickness on the emission wavelength of direct band gap GeSn/Ge quantum dots. Mater. Res. Express 2017, 4, 075026. [Google Scholar] [CrossRef]
- Souaf, M.; Baira, M.; Nasr, O.; Alouane, M.H.H.; Maaref, H.; Sfaxi, L.; Ilahi, B. Investigation of the InAs/GaAs quantum dots’ size: Dependence on the strain reducing layer’s position. Materials 2015, 8, 4699–4709. [Google Scholar] [CrossRef] [PubMed]
- Berbezier, I.; Ronda, A.; Portavoce, A. SiGe nanostructures: New insights into growth processes. J. Phys. Condens. Matter 2002, 14, 8283. [Google Scholar] [CrossRef]
- Zheng, U.; Liu, Z.; Zhang, Y.; Zuo, Y.; Li, C.; Xue, C.; Cheng, B.; Wang, Q. Growth of high-Sn content (28%) GeSn alloy films by sputtering epitaxy. J. Cryst. Growth 2018, 492, 29–34. [Google Scholar] [CrossRef]
- Melnik, R.V.N.; Willatzen, M. Bandstructures of conical quantum dots with wetting layers. Nanotechnology 2004, 15. [Google Scholar] [CrossRef]
- Al-Saigh, R.; Baira, M.; Salem, B.; Ilahi, B. Design of Strain-Engineered GeSn/GeSiSn Quantum Dots for Mid-IR Direct Bandgap Emission on Si Substrate. Nanoscale Res. Lett. 2018, 13, 172. [Google Scholar] [CrossRef]
- Williamson, A.J.; Wang, L.W.; Zunger, A. Theoretical interpretation of the experimental electronic structure of lens-shaped self-assembled InAs/GaAs quantum dots. Phys. Rev. B 2000, 62, 12963. [Google Scholar] [CrossRef]
- Narvaez, G.A.; Zunger, A. Calculation of conduction-to-conduction and valence-to-valence transitions between bound states in InGaAs/GaAs quantum dots. Phys. Rev. B 2007, 75, 085306. [Google Scholar] [CrossRef]
- Sabaeian, M.; Riyahi, M. Truncated pyramidal-shaped InAs/GaAs quantum dots in the presence of a vertical magnetic field: An investigation of THz wave emission and absorption. Physica E 2017, 89, 105. [Google Scholar] [CrossRef]
- Fock, V. Bemerkung zur Quantelung des harmonischen Oszillators im Magnetfeld. Zeitschrift für Physik 1928, 47, 446. [Google Scholar] [CrossRef]
- Darwin, C. The Diamagnetism of the Free Electron. Math. Proc. Camb. Philos. Soc. 1931, 27, 86. [Google Scholar] [CrossRef]
- Ünlü, S.; Karabulut, İ.; Şafak, H. Linear and nonlinear intersubband optical absorption coefficients and refractive index changes in a quantum box with finite confining potential. Physica E 2006, 33, 319–324. [Google Scholar] [CrossRef]
- Vahdani, M.R.K.; Rezaei, G. Linear and nonlinear optical properties of a hydrogenic donor in lens-shaped quantum dots. Phys. Lett. A 2009, 373, 3079–3084. [Google Scholar] [CrossRef]
- Şahin, M. Third-order nonlinear optical properties of a one- and two-electron spherical quantum dot with and without a hydrogenic impurity. J. App. Phys. 2009, 106, 063710. [Google Scholar] [CrossRef]
- Ranjan, R.; Das, M.K. Theoretical estimation of optical gain in Tinincorporated group IV alloy based transistor laser. Opt. Quant. Electron. 2016, 48, 201. [Google Scholar] [CrossRef]
- Mączko, H.S.; Kudrawiec, R.; Gladysiewicz, M. Material gain engineering in GeSn/Ge quantum wells integrated with an Si platform. Sci. Rep. 2016, 6, 34082. [Google Scholar] [CrossRef]
- Karabulut, I.; Baskoutas, S. Linear and nonlinear optical absorption coefficients and refractive index changes in spherical quantum dots: Effects of impurities, electric field, size, and optical intensity. J. Appl. Phys. 2008, 103, 073512. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baira, M.; Salem, B.; Madhar, N.A.; Ilahi, B. Linear and Nonlinear Intersubband Optical Properties of Direct Band Gap GeSn Quantum Dots. Nanomaterials 2019, 9, 124. https://doi.org/10.3390/nano9010124
Baira M, Salem B, Madhar NA, Ilahi B. Linear and Nonlinear Intersubband Optical Properties of Direct Band Gap GeSn Quantum Dots. Nanomaterials. 2019; 9(1):124. https://doi.org/10.3390/nano9010124
Chicago/Turabian StyleBaira, Mourad, Bassem Salem, Niyaz Ahmad Madhar, and Bouraoui Ilahi. 2019. "Linear and Nonlinear Intersubband Optical Properties of Direct Band Gap GeSn Quantum Dots" Nanomaterials 9, no. 1: 124. https://doi.org/10.3390/nano9010124
APA StyleBaira, M., Salem, B., Madhar, N. A., & Ilahi, B. (2019). Linear and Nonlinear Intersubband Optical Properties of Direct Band Gap GeSn Quantum Dots. Nanomaterials, 9(1), 124. https://doi.org/10.3390/nano9010124






