Optical Study and Experimental Realization of Nanostructured Back Reflectors with Reduced Parasitic Losses for Silicon Thin Film Solar Cells
Abstract
:1. Introduction
2. Experimental Details
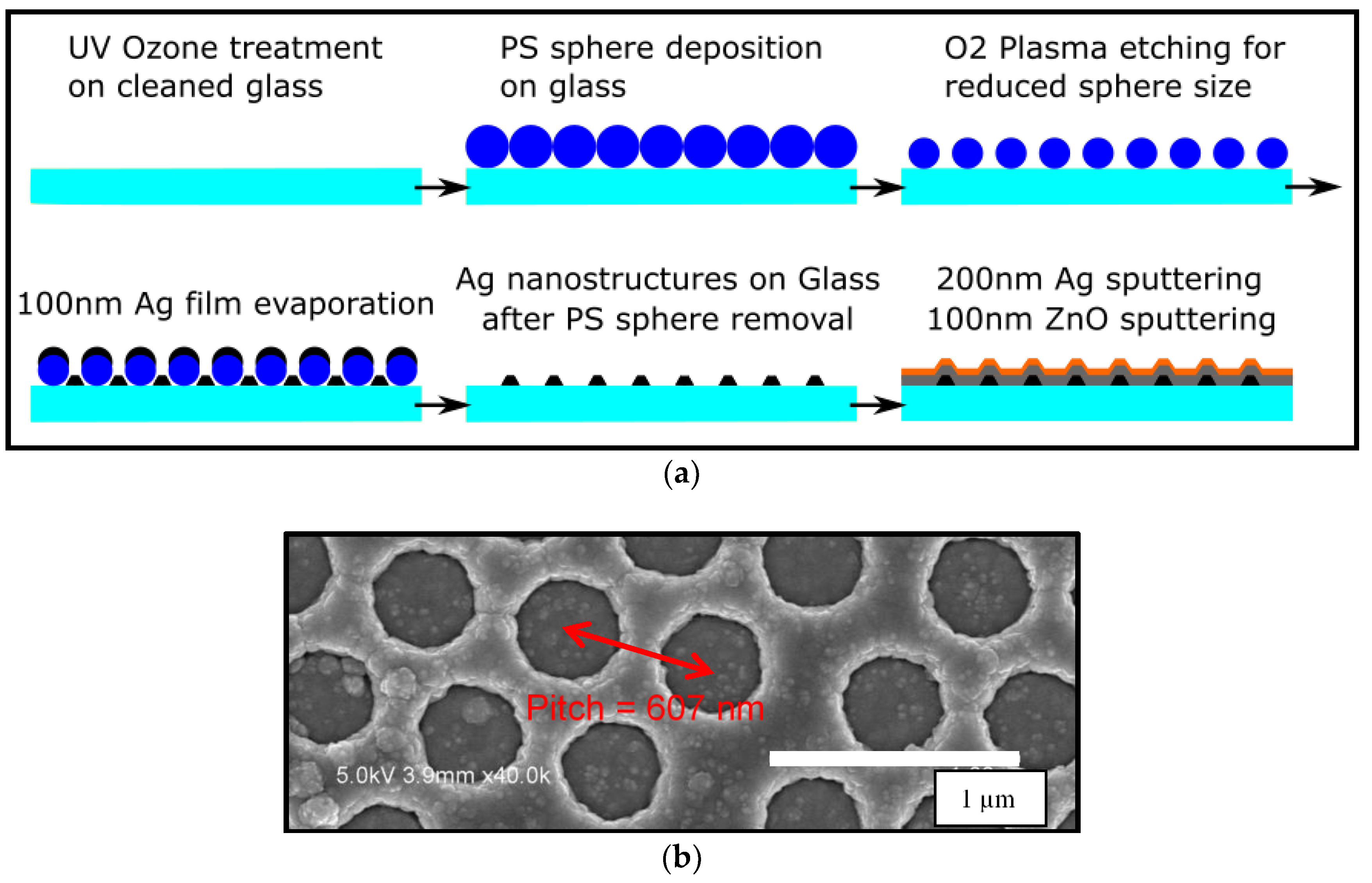
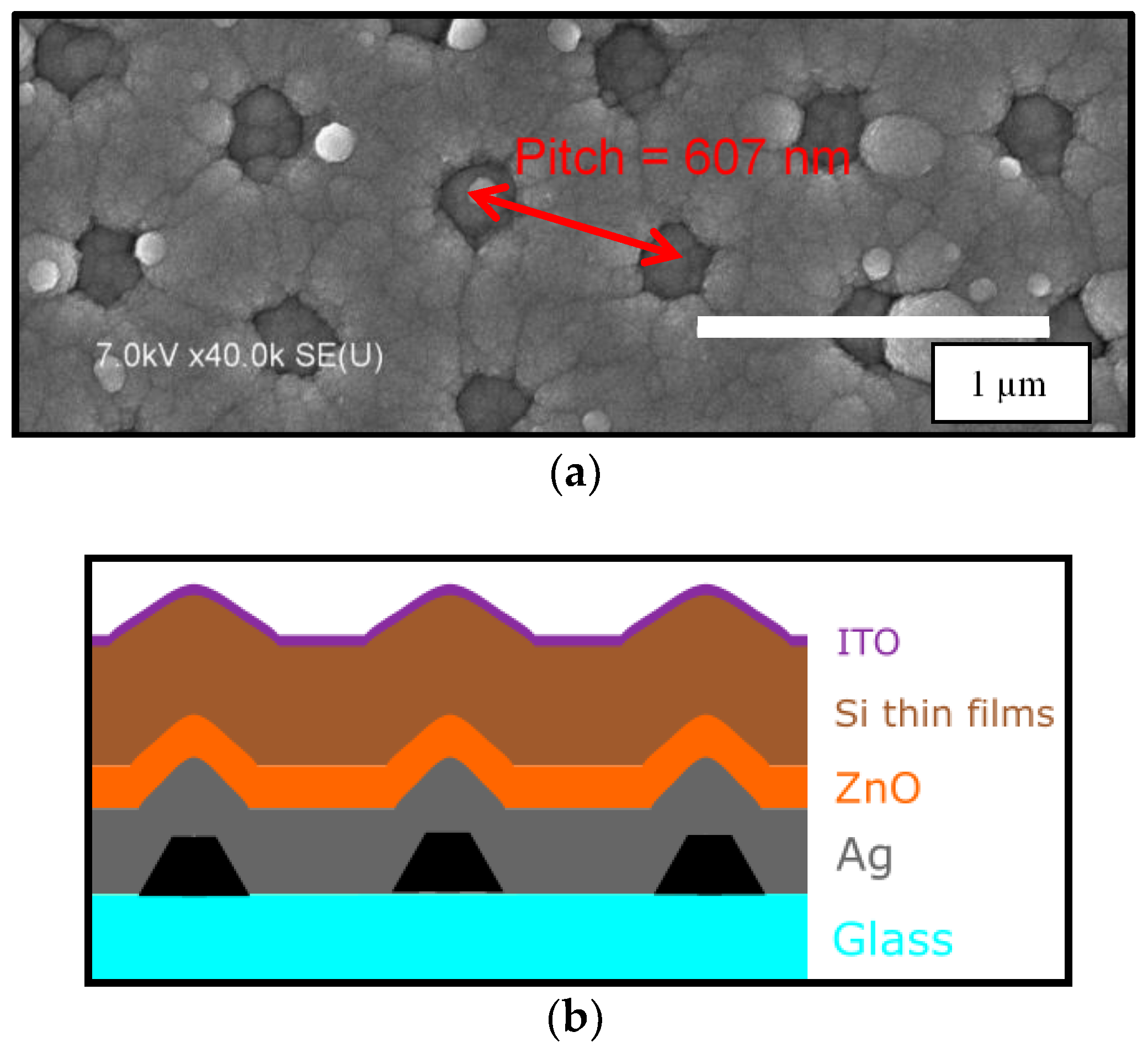
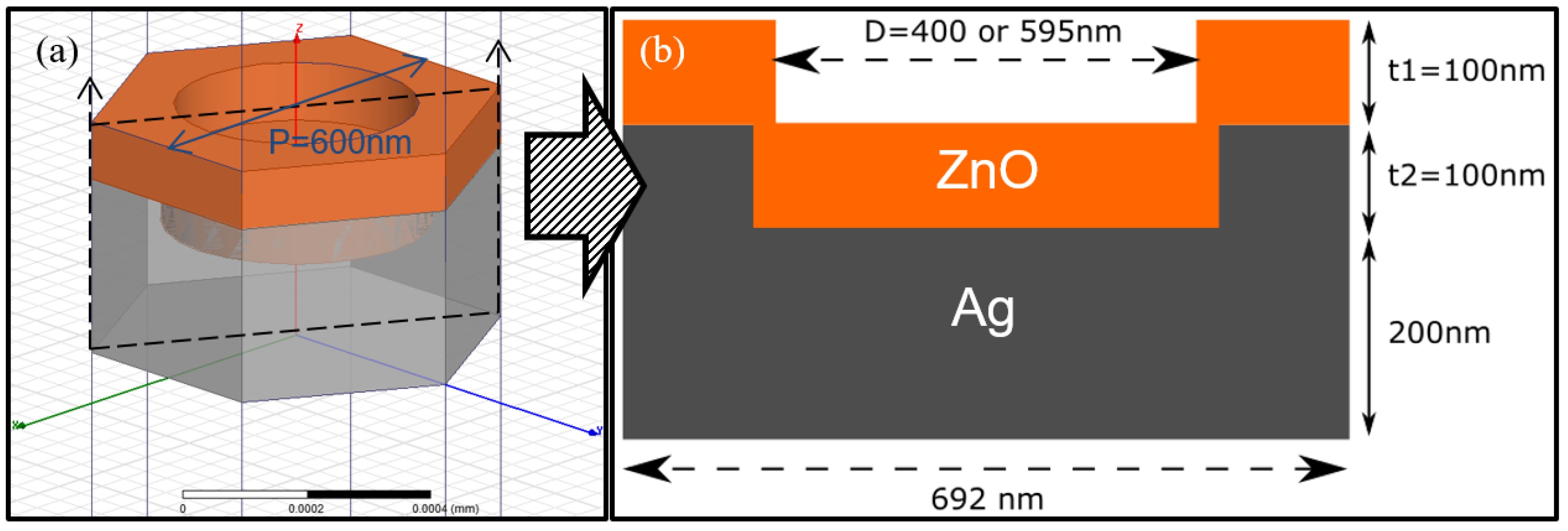
2.1. PS Assisted Lithography for Ag Nanostructures on Glass and Hexagonal Back Reflectors
2.2. Solar Cell Fabrication and Characterization
3. Results and Discussion
3.1. Optical Characterization of Flat and ASAHI Back Reflectors
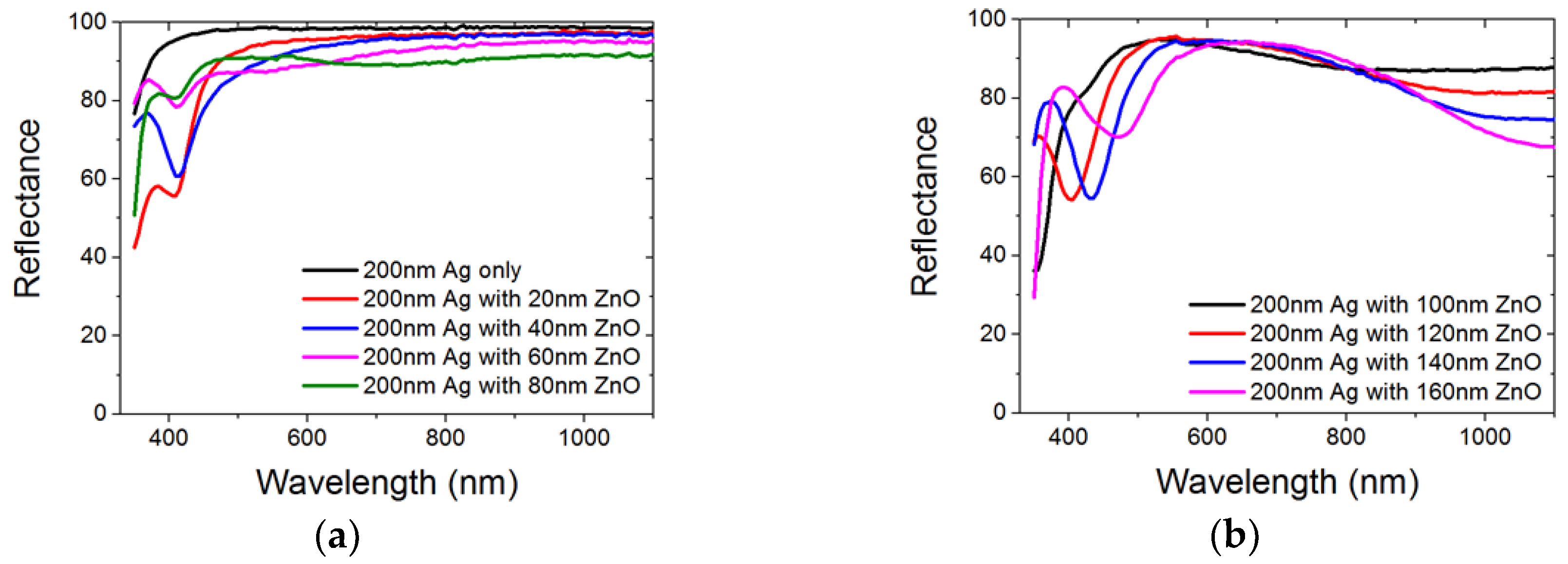
3.1.1. Total Reflectance from Flat and ASAHI Back Reflectors
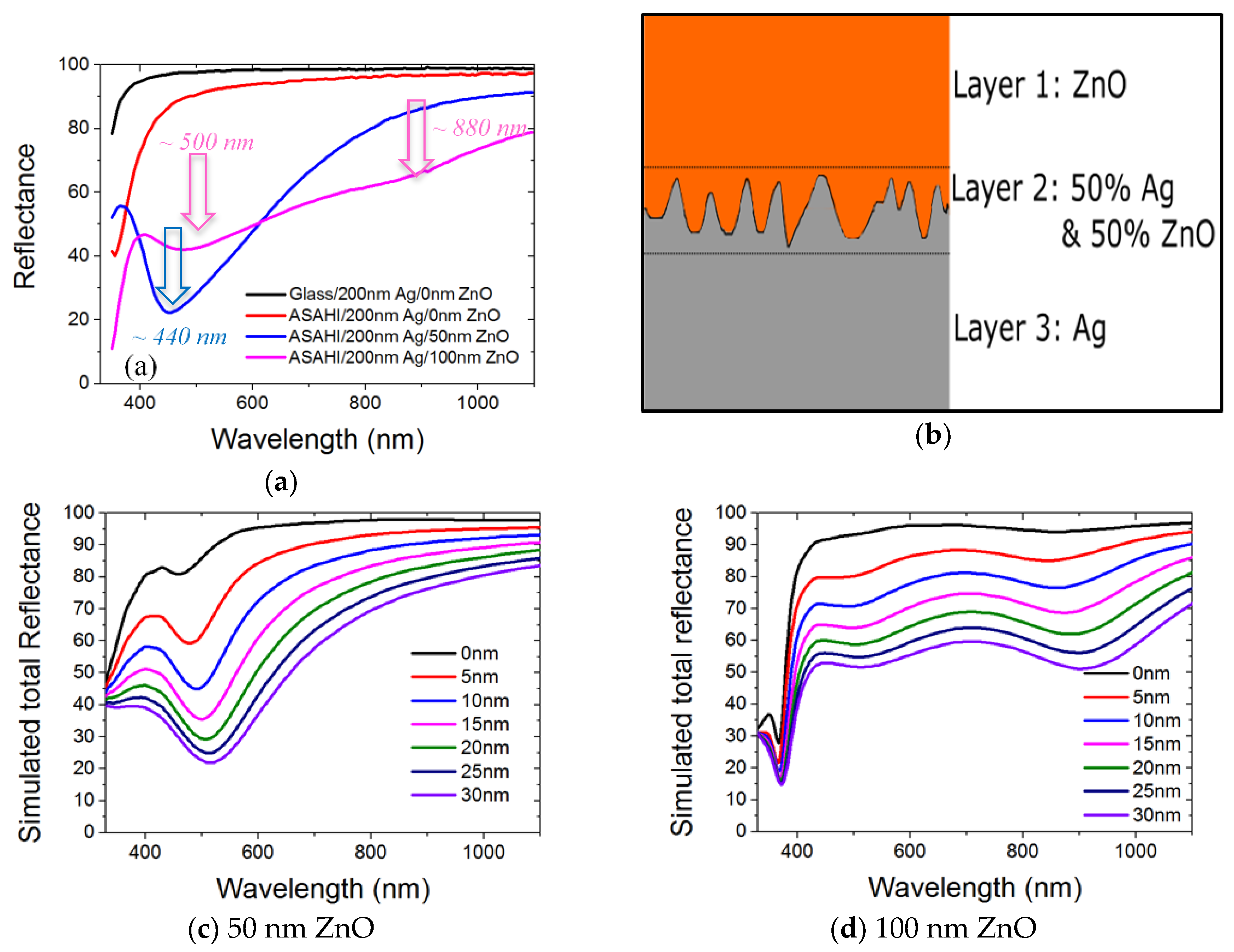
3.1.2. Bruggeman Effective Medium Approximation Simulation
3.2. Experiment and Simulation Results on Hexagonal Ag/ZnO Nanostructured Back Reflectors
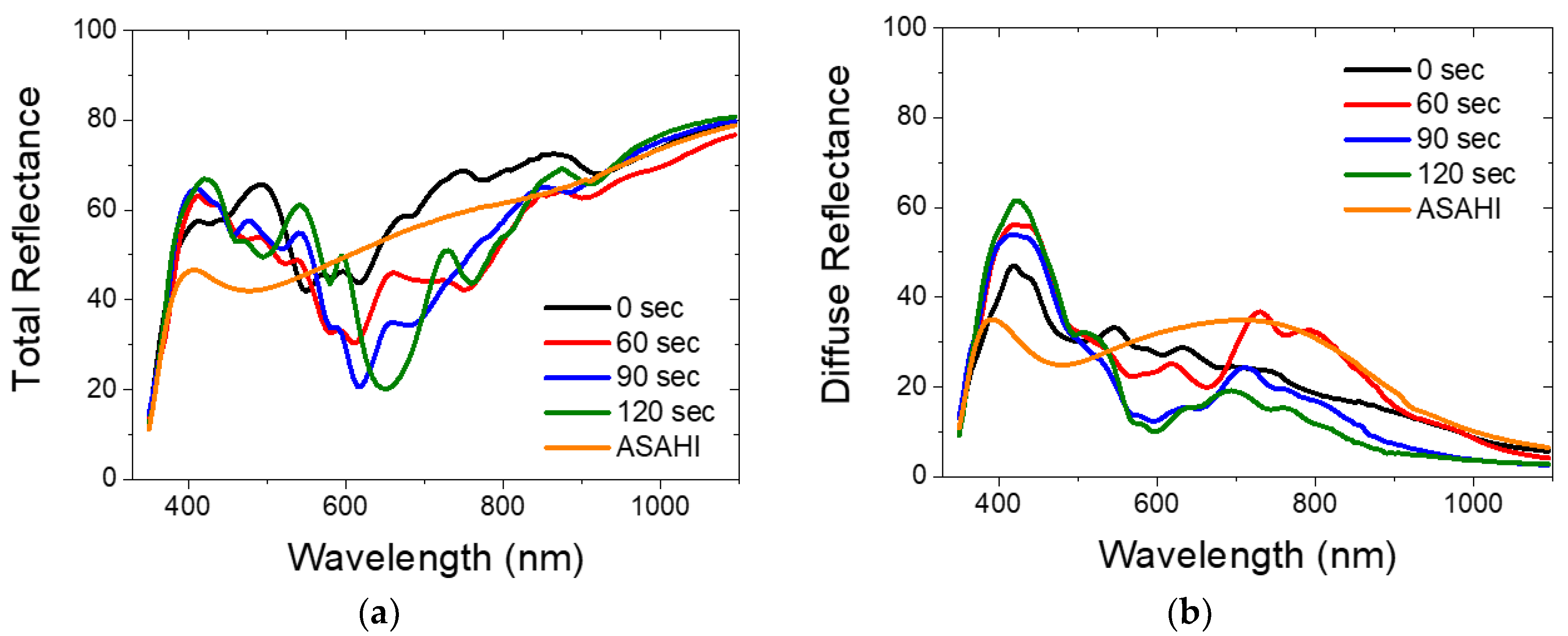
3.2.1. Total and Diffused Reflectance of Hexagonal Ag/ZnO Nanostructured Back Reflectors
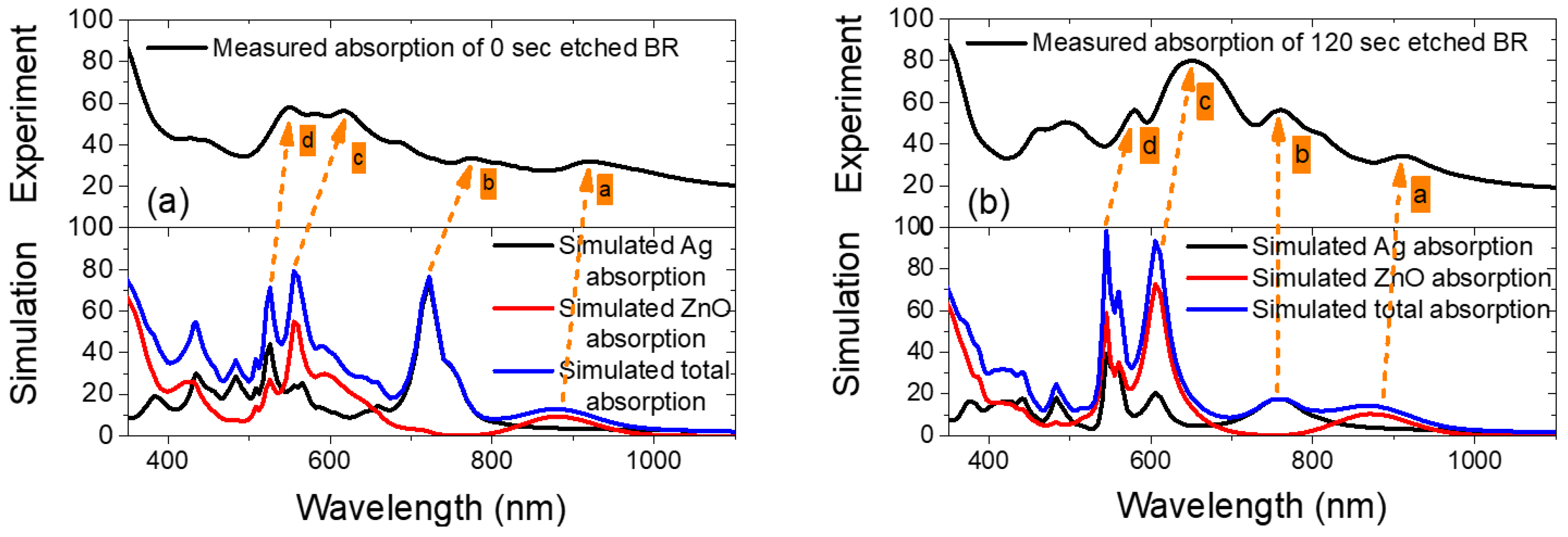
3.2.2. Simulated Absorption of Hexagonal Ag/ZnO Nanostructured Back Reflectors
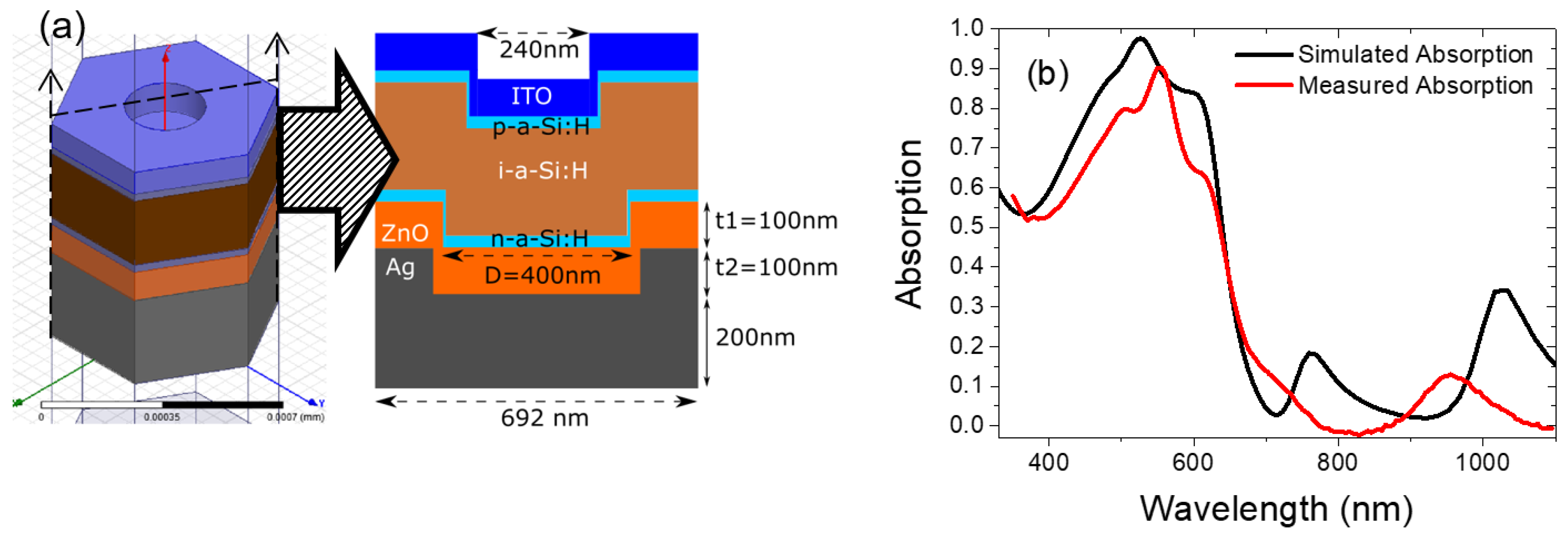
3.3. Experiment and Simulation Results on Hexagonal Ag/ZnO Back Reflector Solar Cells
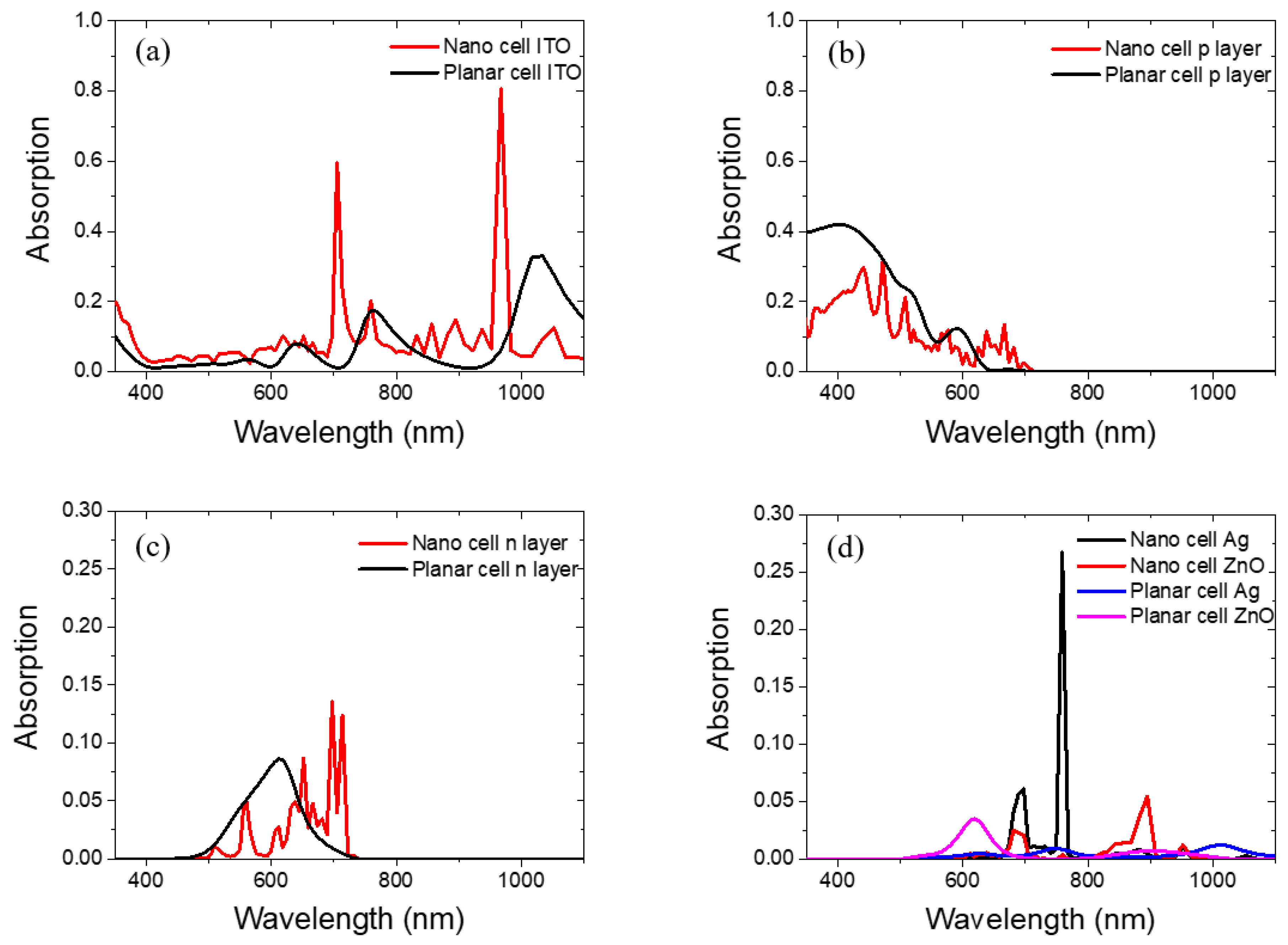
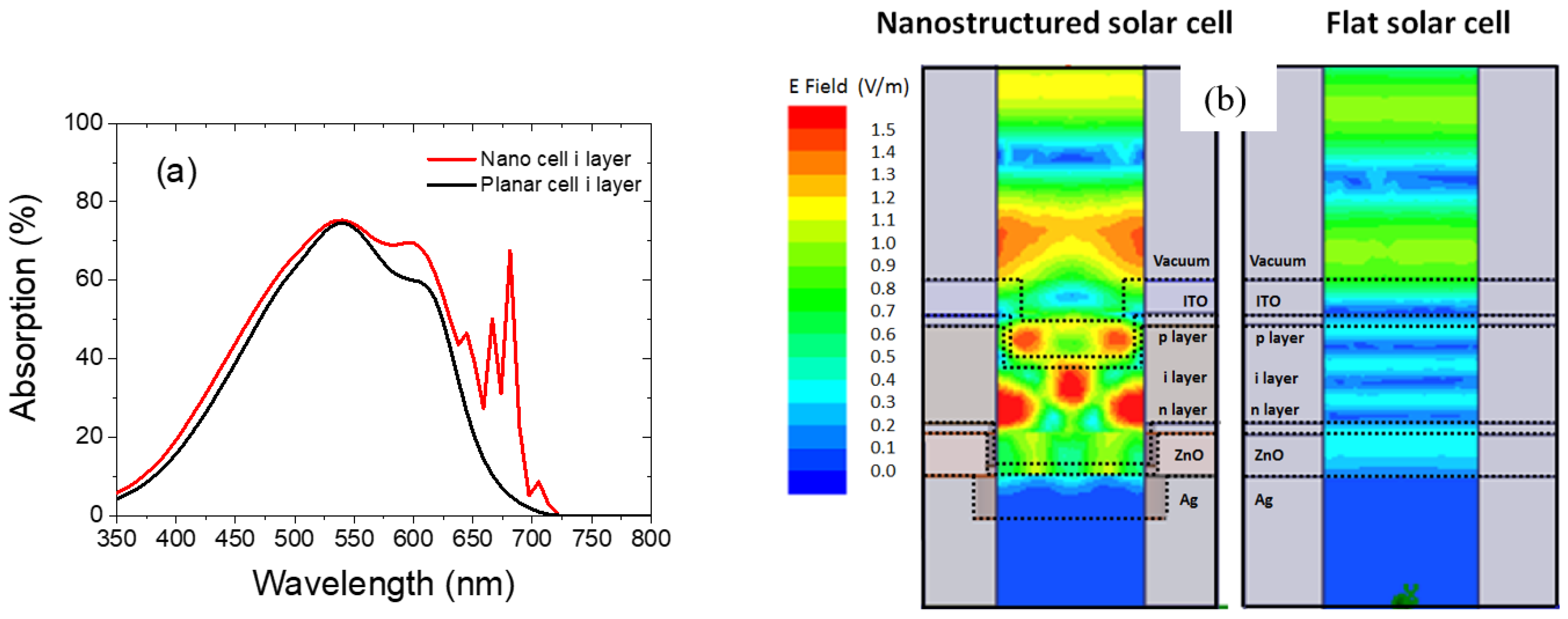
3.3.1. Parasitic Losses and Absorption Enhancement Analysis
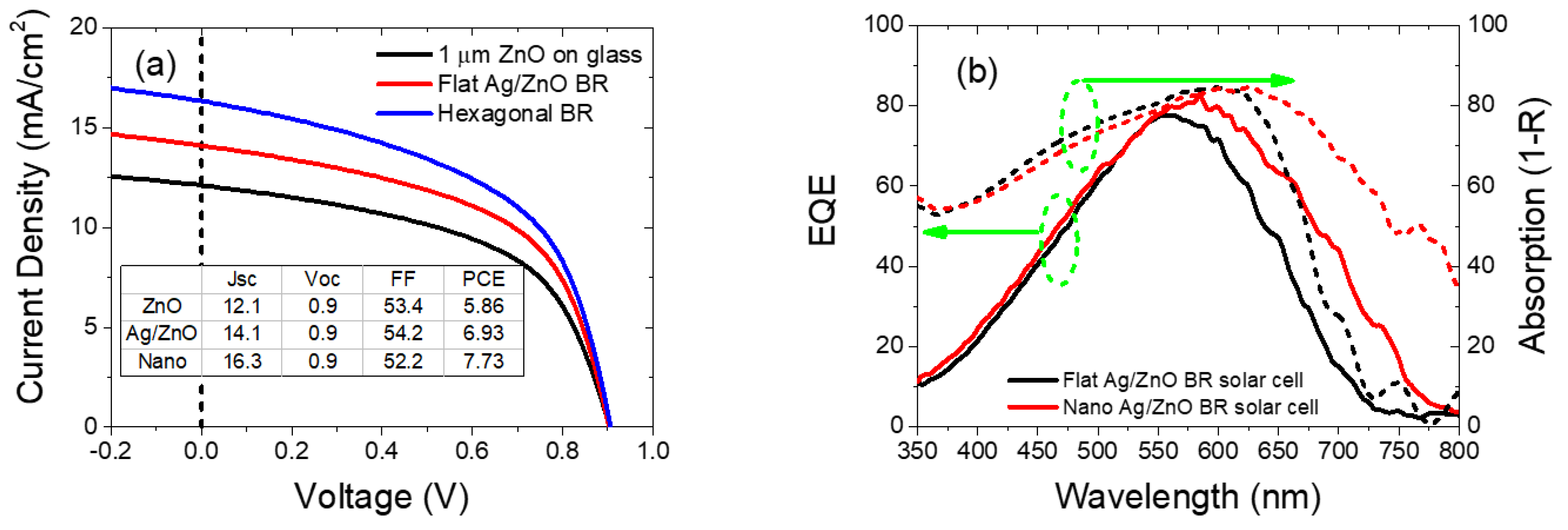
3.3.2. Experimental Results
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Sai, H.; Matsui, T.; Matsubara, K. Stabilized 14.0%-efficient triple-junction thin-film silicon solar cell. Appl. Phys. Lett. 2016, 109, 183506. [Google Scholar]
- Chen, X.; Jia, B.; Saha, J.K.; Cai, B.; Stokes, N.; Qiao, Q.; Wang, Y.; Shi, Z.; Gu, M. Broadband enhancement in thin-film amorphous silicon solar cells enabled by nucleated silver nanoparticles. Nano Lett. 2012, 12, 2187–2192. [Google Scholar] [CrossRef] [PubMed]
- Khazaka, R.; Moulin, E.; Boccard, M.; Garcia, L.; Hänni, S.; Haug, F.J.; Meillaud, F.; Ballif, C. Silver versus white sheet as a back reflector for microcrystalline silicon solar cells deposited on LPCVD-ZnO electrodes of various textures. Prog. Photovolt. Res. Appl. 2015, 23, 1182–1189. [Google Scholar] [CrossRef]
- Bhattacharya, J.; Chakravarty, N.; Pattnaik, S.; Slafer, W.D.; Biswas, R.; Dalal, V.L. A photonic-plasmonic structure for enhancing light absorption in thin film solar cells. Appl. Phys. Lett. 2011, 99, 131114. [Google Scholar] [CrossRef]
- Smeets, M.; Smirnov, V.; Meier, M.; Bittkau, K.; Carius, R.; Rau, U.; Paetzold, U.W. On the geometry of plasmonic reflection grating back contacts for light trapping in prototype amorphous silicon thin-film solar cells. J. Photonics Energy 2014, 5, 057004. [Google Scholar] [CrossRef]
- Li, Z.; Rusli, E.; Foldyna, M.; Wang, J.; Chen, W.; Prakoso, A.B.; Lu, C.; Cabarrocas, P.R. Nanostructured back reflectors produced using polystyrene assisted lithography for enhanced light trapping in silicon thin film solar cells. Sol. Energy 2018, 167, 108–115. [Google Scholar] [CrossRef]
- Jang, Y.H.; Jang, Y.J.; Kim, S.; Quan, L.N.; Chung, K.; Kim, D.H. Plasmonic Solar Cells: From Rational Design to Mechanism Overview. Chem. Rev. 2016, 116, 14982–15034. [Google Scholar] [CrossRef] [PubMed]
- Dahal, L.R.; Sainju, D.; Podraza, N.J.; Marsillac, S.; Collins, R.W. Real time spectroscopic ellipsometry of Ag/ZnO and Al/ZnO interfaces for back-reflectors in thin film Si:H photovoltaics. Thin Solid Films 2011, 519, 2682–2687. [Google Scholar] [CrossRef]
- Wienke, J.; van der Zanden, B.; Tijssen, M.; Zeman, M. “Performance of spray-deposited ZnO:In layers as front electrodes in thin-film silicon solar cells. Sol. Energy Mater. Sol. Cells 2008, 92, 884–890. [Google Scholar] [CrossRef]
- Paetzold, U.W.; Moulin, E.; Pieters, B.E.; Carius, R.; Rau, U. Design of nanostructured plasmonic back contacts for thin-film silicon solar cells. Opt. Express 2011, 19, A1219–A1230. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Guney, D.O.; Pearce, J.M. Plasmonic enhancement of amorphous silicon solar photovoltaic cells with hexagonal silver arrays made with nanosphere lithography. Mater. Res. Express 2016, 3, 10. [Google Scholar] [CrossRef]
- Isabella, O.; Solntsev, S.; Caratelli, D.; Zeman, M. 3-D optical modeling of thin-film silicon solar cells on diffraction gratings. Prog. Photovolt. Res. Appl. 2013, 21, 94–108. [Google Scholar] [CrossRef]
- Khoury, R.; Li, Z.; Bulkin, P.; Roca i Cabarrocas, P.; Johnson, E.V. Detailed study of Electron Cyclotron Resonance Oxygen Plasma Etching of Polystyrene Nanosphere Arrays. Unpublished work.
- Roca i Cabarrocas, P.; Chevrier, B.J.; Huc, J.; Lloret, A.; Parey, Y.J.; Schmitt, M.J.P. A Fully Automated Hot-wall Multiplasma monochamber Reactor for Thin Film Deposition. J. Vac. Sci. Technol. A 1991, 9, 2331–2341. [Google Scholar] [CrossRef]
- Abolmasov, S.N.; Woo, H.; Planques, R.; Holovský, J.; Johnson, E.V.; Purkrt, A.; Roca i Cabarrocas, P. Substrate and p-layer effects on polymorphous silicon solar cells. Eur. Phys. J. Photovolt. 2014, 5, 55206. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.H.; Kasouit, S.; Johnson, E.V.; Cabarrocas, P.R.I. Substrate versus superstrate configuration for stable thin film silicon solar cells. Sol. Energy Mater. Sol. Cells 2013, 119, 124–128. [Google Scholar] [CrossRef]
- Sainju, D. Spectroscopic Ellipsometry Studies of Ag and ZnO Thin Films and Their Interfaces for Thin Film Photovoltaics. Ph.D. Thesis, University of Toledo, Toledo, USA, 2015. [Google Scholar]
- Dejneka, A.; Aulika, I.; Makarova, M.V.; Hubicka, Z.; Churpita, A.; Chvostova, D.; Jastrabik, L.; Trepakov, V.A. Optical Spectra and Direct Optical Transitions in Amorphous and Crystalline ZnO Thin Films and Powders. J. Electrochem. Soc. 2010, 157, G67–G70. [Google Scholar] [CrossRef]
- Moulin, E.; Paetzold, U.W.; Kirchhoff, J.; Bauer, A.; Carius, R. Study of detached back reflector designs for thin-film silicon solar cells. Phys. Status Solidi Rapid Res. Lett. 2012, 6, 65–67. [Google Scholar] [CrossRef]
- Sainju, D.; Van Den Oever, P.J.; Podraza, N.J.; Syed, M.; Stoke, J.A.; Chen, J.; Yang, X.; Deng, X.; Collins, R.W. Origin of optical losses in Ag/ZnO back-reflectors for thin film Si photovoltaics. In Proceedings of the Conference Record of the 2006 IEEE 4th World Conference on Photovoltaic Energy Conversion, Waikoloa, HI, USA, 7–12 May 2006; pp. 1732–1735. [Google Scholar]
- Owen, J.I. Growth, Etching, and Stability of Sputtered ZnO:AI for Thin-Film Silicon Solar Cells; Forschungszentrum Jülich: Jülich, Germany, 2011. [Google Scholar]
- McPeak, K.M.; Jayanti, S.V.; Kress, S.J.P.; Meyer, S.; Iotti, S.; Rossinelli, A.; Norris, D.J. Plasmonic films can easily be better: Rules and recipes. Am. Chem. Soc. Photonics 2015, 2, 326–333. [Google Scholar] [CrossRef] [PubMed]
- Jovanov, V.; Xu, X.; Shrestha, S.; Schulte, M.; Hüpkes, J.; Zeman, M.; Knipp, D. Influence of interface morphologies on amorphous silicon thin film solar cells prepared on randomly textured substrates. Sol. Energy Mater. Sol. Cells 2013, 112, 182–189. [Google Scholar] [CrossRef]
- Springer, J.; Poruba, A.; Müllerova, L.; Vanecek, M.; Kluth, O.; Rech, B. Absorption loss at nanorough silver back reflector of thin-film silicon solar cells. J. Appl. Phys. 2004, 95, 1427–1429. [Google Scholar] [CrossRef] [Green Version]
- Mendes, M.J.; Morawiec, S.; Simone, F.; Priolo, F.; Crupi, I. Colloidal plasmonic back reflectors for light trapping in solar cells. Nanoscale 2014, 6, 4796–4805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ko, Y.H.; Yu, J.S. Optical absorption enhancement of embedded Ag nanoparticles with ZnO nanorod arrays. Phys. Status Solidi 2011, 208, 2778–2782. [Google Scholar] [CrossRef]
- Tiedje, T.; Yablonovitch, E.; Cody, G.D.; Brooks, B.G. Limiting Efficiency of Silicon Solar Cells. IEEE Trans. Electron Devices 1984, 31, 711–716. [Google Scholar] [CrossRef]
- Paetzold, U.W.; Smeets, M.; Meier, M.; Bittkau, K.; Merdzhanova, T.; Smirnov, V.; Michaelis, D.; Waechter, C.; Carius, R.; Rau, U. Disorder improves nanophotonic light trapping in thin-film solar cells. Appl. Phys. Lett. 2014, 104, 131102. [Google Scholar] [CrossRef] [Green Version]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; E, R.; Lu, C.; Prakoso, A.B.; Foldyna, M.; Khoury, R.; Bulkin, P.; Wang, J.; Chen, W.; Johnson, E.; et al. Optical Study and Experimental Realization of Nanostructured Back Reflectors with Reduced Parasitic Losses for Silicon Thin Film Solar Cells. Nanomaterials 2018, 8, 626. https://doi.org/10.3390/nano8080626
Li Z, E R, Lu C, Prakoso AB, Foldyna M, Khoury R, Bulkin P, Wang J, Chen W, Johnson E, et al. Optical Study and Experimental Realization of Nanostructured Back Reflectors with Reduced Parasitic Losses for Silicon Thin Film Solar Cells. Nanomaterials. 2018; 8(8):626. https://doi.org/10.3390/nano8080626
Chicago/Turabian StyleLi, Zeyu, Rusli E, Chenjin Lu, Ari Bimo Prakoso, Martin Foldyna, Rasha Khoury, Pavel Bulkin, Junkang Wang, Wanghua Chen, Erik Johnson, and et al. 2018. "Optical Study and Experimental Realization of Nanostructured Back Reflectors with Reduced Parasitic Losses for Silicon Thin Film Solar Cells" Nanomaterials 8, no. 8: 626. https://doi.org/10.3390/nano8080626





