High Temperature Flow Behavior of Ultra-Strong Nanoporous Au assessed by Spherical Nanoindentation
Abstract
1. Introduction
2. Materials and Methods.
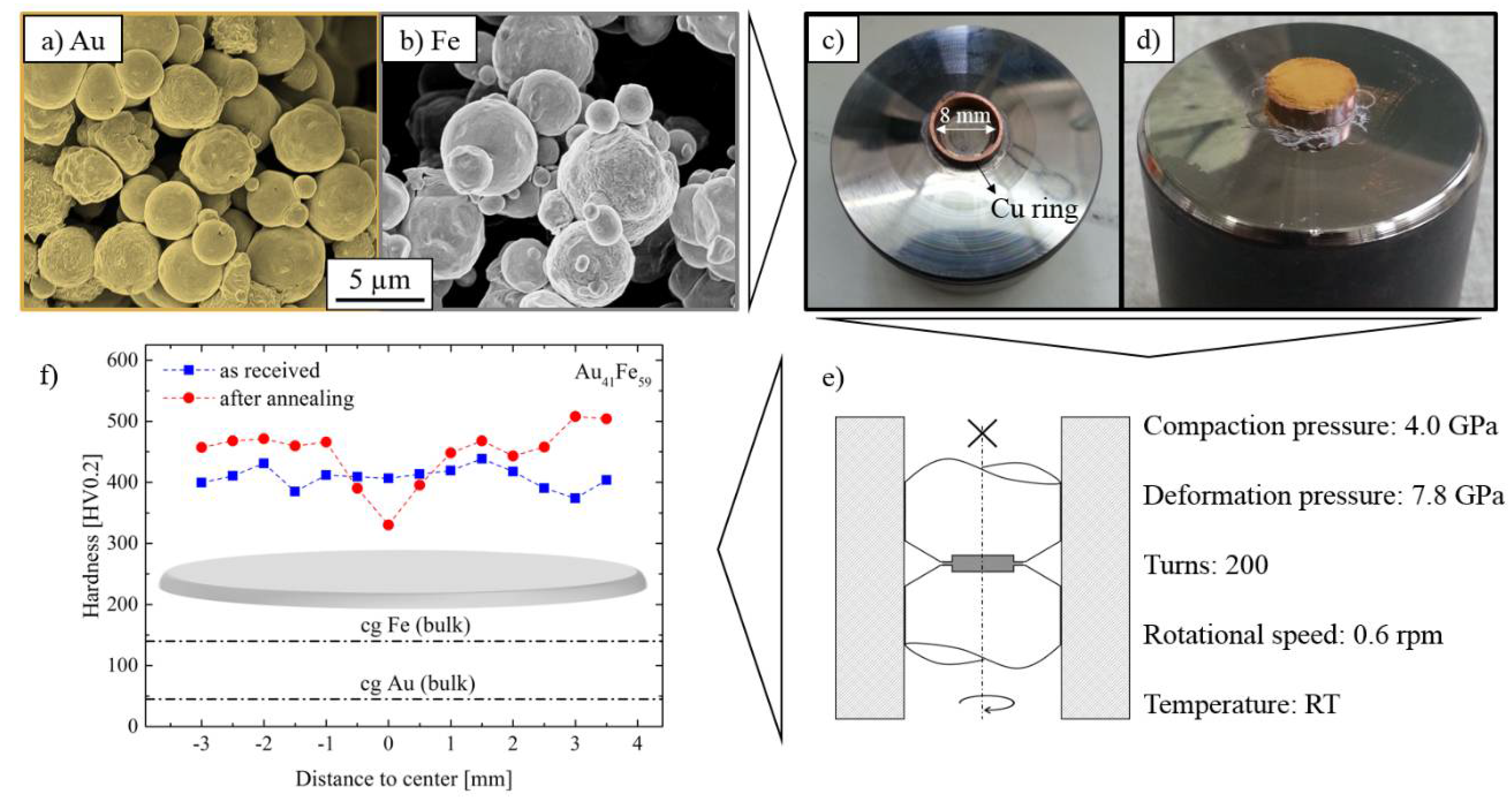
2.1. Precursor Synthesis
2.2. Selective Etching Process
2.3. Mechanical Characterization by Spherical Nanoindentation
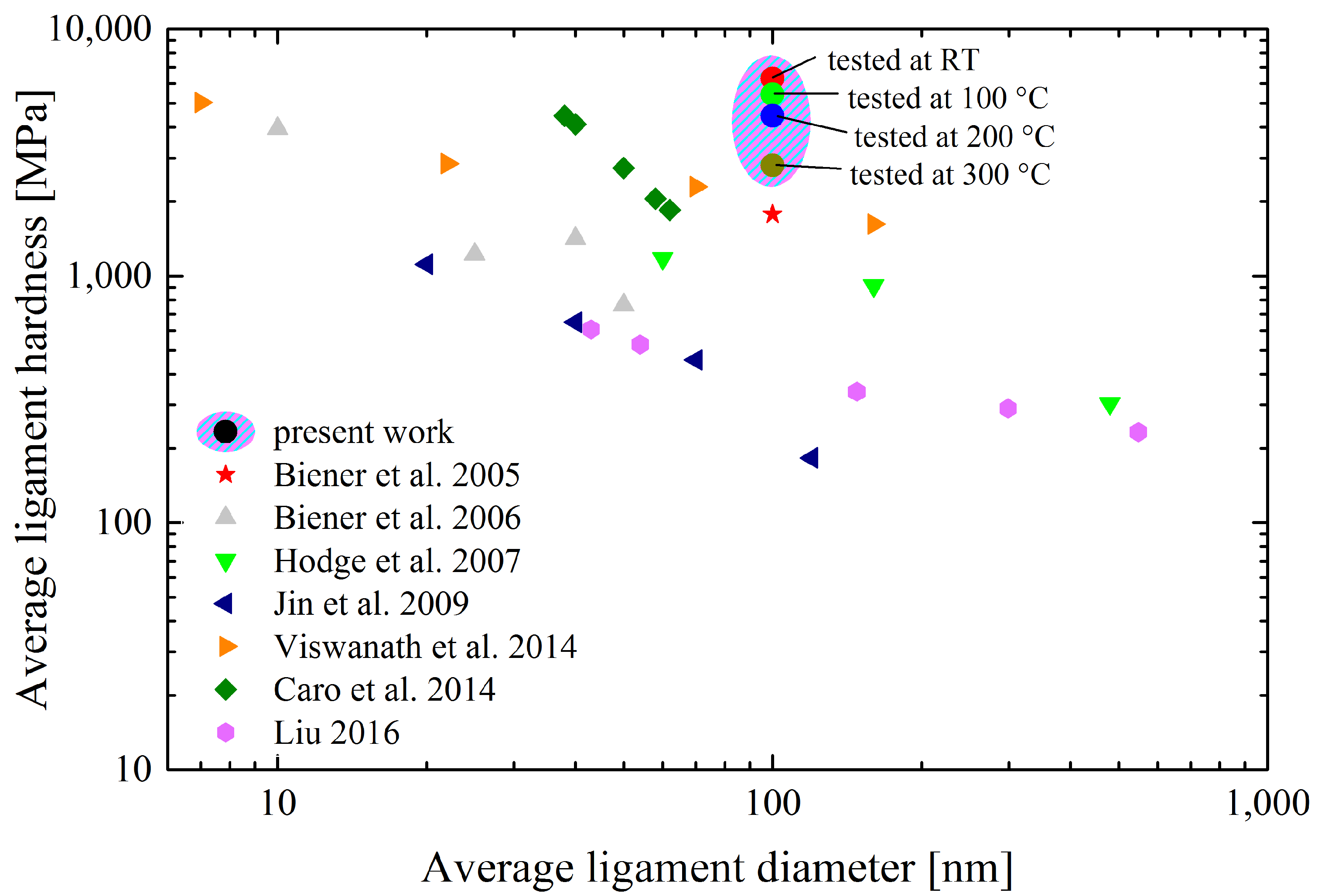
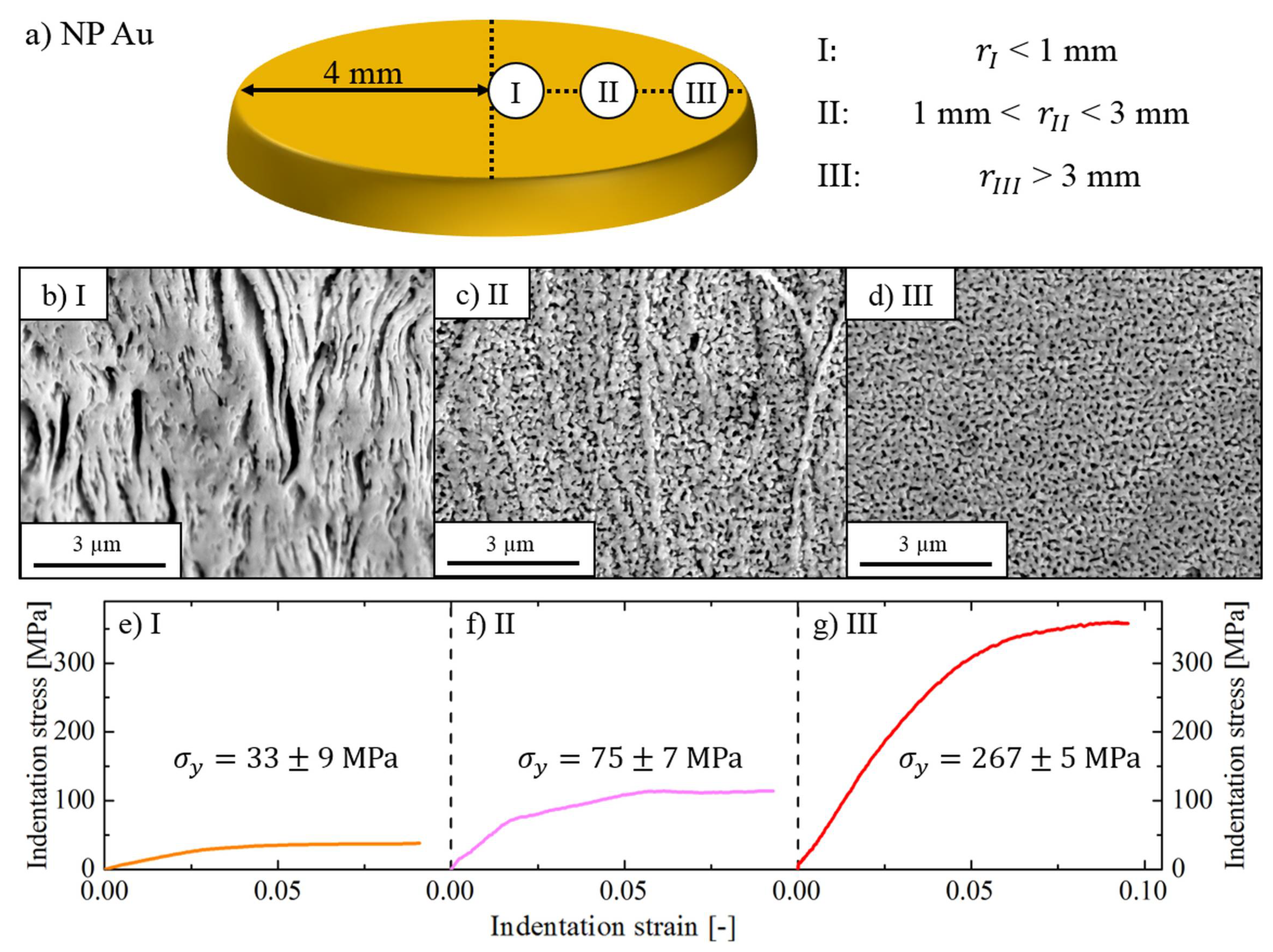
3. Results and Discussion
3.1. Characterization of Nanoporous Au
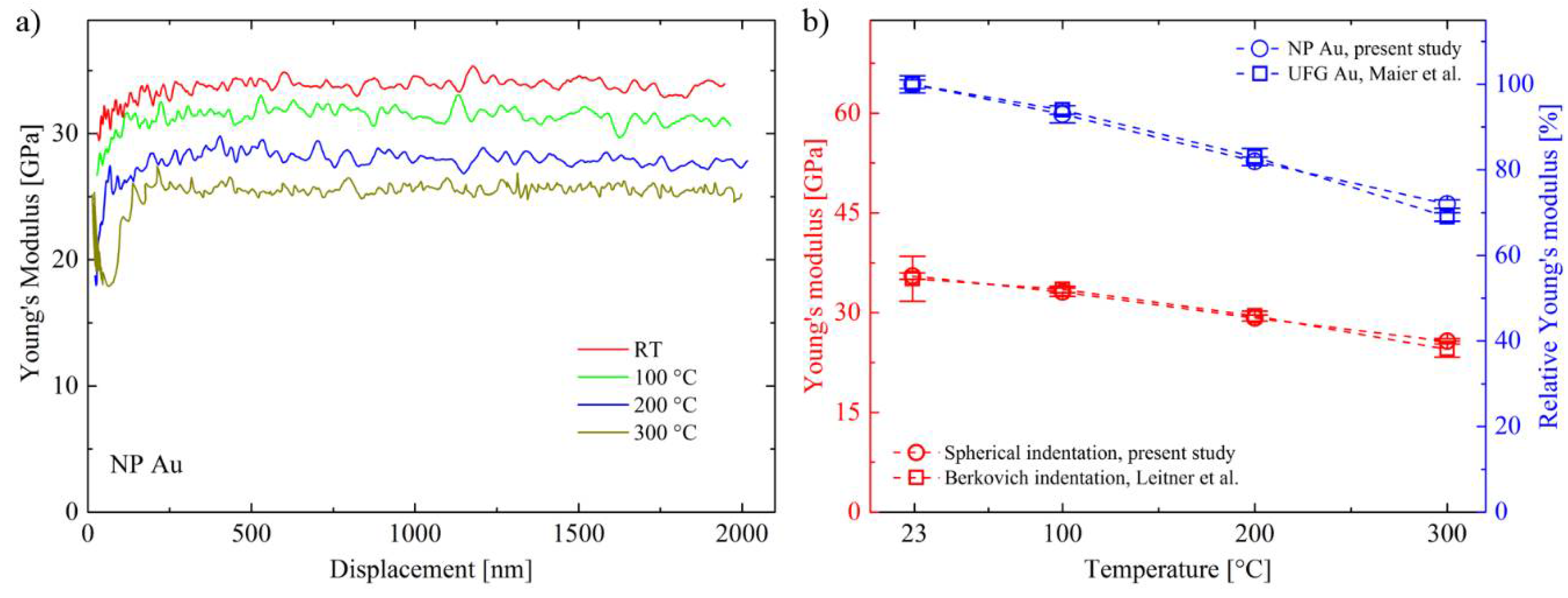
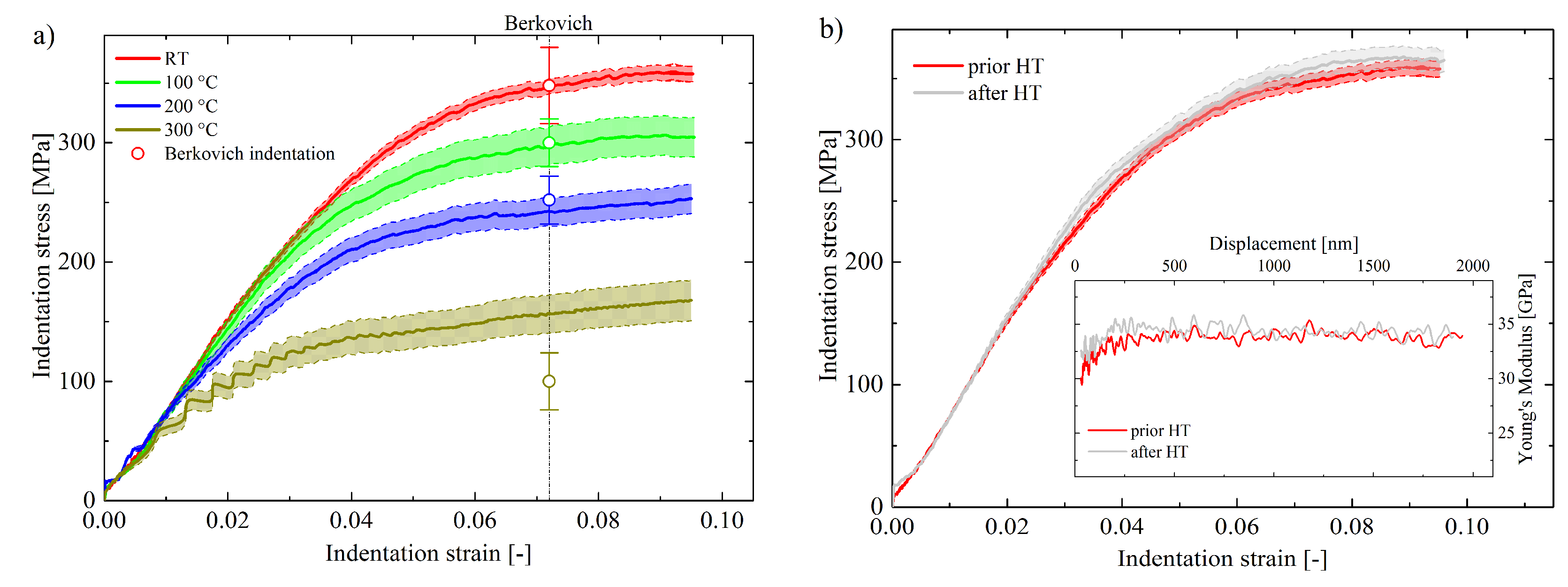
3.2. High Temperature Nanoindentation
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Biener, J.; Hodge, A.M.; Hamza, A.V. Microscopic failure behavior of nanoporous gold. Appl. Phys. Lett. 2005, 87. [Google Scholar] [CrossRef]
- Biener, J.; Hodge, A.M.; Hamza, A.V.; Hsiun, L.M.; Satcher, J.H. Nanoporous Au: A high yield strength material. J. Appl. Phys. 2005, 97. [Google Scholar] [CrossRef]
- Volkert, C.A.; Lilleodden, E.T.; Kramer, D.; Weissmüller, J. Approaching the theoretical strength in nanoporous Au. Appl. Phys. Lett. 2006, 89. [Google Scholar] [CrossRef]
- Hodge, A.M.; Biener, J.; Hayes, J.R.; Bythrow, P.M.; Volkert, C.A.; Hamza, A.V. Scaling equation for yield strength of nanoporous open-cell foams. Acta Mater. 2007, 55, 1343–1349. [Google Scholar] [CrossRef]
- Balk, T.J.; Eberl, C.; Sun, Y.; Hemker, K.J.; Gianola, D.S. Tensile and compressive microspecimen testing of bulk nanoporous gold. JOM 2009, 61, 26–31. [Google Scholar] [CrossRef]
- Briot, N.J.; Kennerknecht, T.; Eberl, C.; Balk, T.J. Mechanical properties of bulk single crystalline nanoporous gold investigated by millimetre-scale tension and compression testing. Philos. Mag. 2014, 94, 847–866. [Google Scholar] [CrossRef]
- Mameka, N.; Wang, K.; Markmann, J.; Lilleodden, E.T.; Weissmüller, J. Nanoporous Gold—Testing Macro-scale Samples to Probe Small-scale Mechanical Behavior. Mater. Res. Lett. 2016, 4, 27–36. [Google Scholar] [CrossRef]
- Jin, H.J.; Weissmüller, J. A material with electrically tunable strength and flow stress. Science 2011, 332, 1179–1182. [Google Scholar] [CrossRef] [PubMed]
- Pickering, H.W. Characteristic features of alloy polarization curves. Corros. Sci. 1983, 23. [Google Scholar] [CrossRef]
- Erlebacher, J.; Aziz, M.J.; Karma, A.; Dimitrov, N.; Sieradzki, K. Evolution of nanoporosity in dealloying. Nature 2001, 410, 450–453. [Google Scholar] [CrossRef] [PubMed]
- Seker, E.; Reed, M.L.; Begley, M.R. Nanoporous gold: Fabrication, characterization, and applications. Materials (Basel) 2009, 2, 2188–2215. [Google Scholar] [CrossRef]
- Seker, E.; Gaskins, J.T.; Bart-Smith, H.; Zhu, J.; Reed, M.L.; Zangari, G.; Kelly, R.; Begley, M.R. The effects of post-fabrication annealing on the mechanical properties of freestanding nanoporous gold structures. Acta Mater. 2007, 55, 4593–4602. [Google Scholar] [CrossRef]
- Hakamada, M.; Mabuchi, M. Mechanical strength of nanoporous gold fabricated by dealloying. Scr. Mater. 2007, 56, 1003–1006. [Google Scholar] [CrossRef]
- Viswanath, R.N.; Polaki, S.R.; Rajaraman, R.; Abhaya, S.; Chirayath, V.A.; Amarendra, G.; Sundar, C.S. On the scaling behavior of hardness with ligament diameter of nanoporous-Au: Constrained motion of dislocations along the ligaments. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Leitner, A.; Maier-Kiener, V.; Jeong, J.; Abad, M.D.; Hosemann, P.; Oh, S.H.; Kiener, D. Interface dominated mechanical properties of ultra-fine grained and nanoporous Au at elevated temperatures. Acta Mater. 2016, 121, 104–116. [Google Scholar] [CrossRef]
- Bachmaier, A.; Kerber, M.; Setman, D.; Pippan, R. The formation of supersaturated solid solutions in Fe-Cu alloys deformed by high-pressure torsion. Acta Mater. 2012, 60, 860–871. [Google Scholar] [CrossRef] [PubMed]
- Kormout, K.S.; Pippan, R.; Bachmaier, A. Deformation-induced supersaturation in immiscible material systems during High-Pressure Torsion. Adv. Eng. Mater. 2017, 19, 1–19. [Google Scholar] [CrossRef]
- Tabor, D. The Hardness of Metals; Monographs on the Physics and Chemistry of Materials; OUP Oxford: Oxford, UK, 1951; ISBN 9780198507765. [Google Scholar]
- Kalidindi, S.R.; Pathak, S. Determination of the effective zero-point and the extraction of spherical nanoindentation stress—Strain curves. Acta Mater. 2008, 56, 3523–3532. [Google Scholar] [CrossRef]
- Pathak, S.; Kalidindi, S.R. Spherical nanoindentation stress-strain curves. Mater. Sci. Eng. R Rep. 2015, 91, 1–36. [Google Scholar] [CrossRef]
- Leitner, A.; Maier-Kiener, V.; Kiener, D. Essential refinements of spherical nanoindentation protocols for the reliable determination of mechanical flow curves. Mater. Des. 2018, 146, 69–80. [Google Scholar] [CrossRef]
- Pippan, R.; Scheriau, S.; Hohenwarter, A.; Hafok, M. Advantages and Limitations of HPT: A Review. Mater. Sci. Forum 2008, 584–586, 16–21. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Islamgaliev, R.K.; Alexandrov, I.V. Bulk nanostructured materials from severe plastic deformation. Prog. Mater. Sci. 2000, 45, 103–189. [Google Scholar] [CrossRef]
- Huang, X.; Hansen, N.; Tsuji, N. Hardening by Annealing and Softening by Deformation in Nanostructured Metals. Science 2006, 312, 249–251. [Google Scholar] [CrossRef] [PubMed]
- Renk, O.; Hohenwarter, A.; Eder, K.; Kormout, K.S.; Cairney, J.M.; Pippan, R. Increasing the strength of nanocrystalline steels by annealing: Is segregation necessary? Scr. Mater. 2015, 95, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Taylor, G.I. The Mechanism of Plastic Deformation of Crystals. Part II. Comparison with Observations. Proc. R. Soc. A Math. Phys. Eng. Sci. 1934, 145, 388–404. [Google Scholar] [CrossRef]
- Vorhauer, A.; Pippan, R. On the homogeneity of deformation by high pressure torsion. Scr. Mater. 2004, 51, 921–925. [Google Scholar] [CrossRef]
- Pourbaix, M. Atlas of Electrochemical Equilibria in Aqueous Solutions; Pergamon Press: New York, NY, USA, 1966; Volume 1. [Google Scholar]
- Kreuzeder, M.; Abad, M.-D.; Primorac, M.-M.; Hosemann, P.; Maier, V.; Kiener, D. Fabrication and thermo-mechanical behavior of ultra-fine porous copper. J. Mater. Sci. 2015, 50, 634–643. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Uchic, M.D.; Dimiduk, D.M. A methodology to investigate size scale effects in crystalline plasticity using uniaxial compression testing. Mater. Sci. Eng. A 2005, 400–401, 268–278. [Google Scholar] [CrossRef]
- Sabirov, I.; Estrin, Y.; Barnett, M.R.; Timokhina, I.; Hodgson, P.D. Tensile deformation of an ultrafine-grained aluminium alloy: Micro shear banding and grain boundary sliding. Acta Mater. 2008, 56, 2223–2230. [Google Scholar] [CrossRef]
- Patel, D.K.; Kalidindi, S.R. Correlation of spherical nanoindentation stress-strain curves to simple compression stress-strain curves for elastic-plastic isotropic materials using finite element models. Acta Mater. 2016, 112, 295–302. [Google Scholar] [CrossRef]
- Prandtl, L. Über die Härte plastischer Körper. In Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen; Vandenhoeck & Ruprecht: Göttingen, Germany, 1920; pp. 74–85. [Google Scholar]
- Atkins, A.G.; Tabor, D. Plastic indentation in metals with cones. J. Mech. Phys. Solids 1965, 13, 149–164. [Google Scholar] [CrossRef]
- Mesarovic, S.-D.; Fleck, N.A. Spherical indentation of elastic-plastic solids. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1999, 455, 2707–2728. [Google Scholar] [CrossRef]
- Luehrs, L.; Soyarslan, C.; Markmann, J.; Bargmann, S.; Weissmüller, J. Elastic and plastic Poisson’s ratios of nanoporous gold. Scr. Mater. 2016, 110, 65–69. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular solids: Structure and properties. Chap 1997, 11, 429–452. [Google Scholar]
- Ruestes, C.J.; Schwen, D.; Millán, E.N.; Aparicio, E.; Bringa, E.M. Mechanical properties of Au foams under nanoindentation. Comput. Mater. Sci. 2018, 147, 154–167. [Google Scholar] [CrossRef]
- Briot, N.J.; Balk, T.J. Focused ion beam characterization of deformation resulting from nanoindentation of nanoporous gold. MRS Commun. 2018, 1–5. [Google Scholar] [CrossRef]
- Jin, H.-J.; Kurmanaeva, L.; Schmauch, J.; Rösner, H.; Ivanisenko, Y.; Weissmüller, J. Deforming nanoporous metal: Role of lattice coherency. Acta Mater. 2009, 57, 2665–2672. [Google Scholar] [CrossRef]
- Mangipudi, K.R.; Epler, E.; Volkert, C.A. On the multiaxial yielding and hardness to yield stress relation of nanoporous gold. Scr. Mater. 2018, 146, 150–153. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Sneddon, I. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Kim, Y.C.; Gwak, E.J.; Ahn, S.M.; Jang, J.I.; Han, H.N.; Kim, J.Y. Indentation size effect in nanoporous gold. Acta Mater. 2017, 138, 52–60. [Google Scholar] [CrossRef]
- Kim, Y.C.; Gwak, E.J.; Ahn, S.M.; Kang, N.R.; Han, H.N.; Jang, J.I.; Kim, J.Y. Indentation size effect for spherical nanoindentation on nanoporous gold. Scr. Mater. 2018, 143, 10–14. [Google Scholar] [CrossRef]
- Bigl, S.; Schöberl, T.; Wurster, S.; Cordill, M.J.; Kiener, D. Correlative microstructure and topography informed nanoindentation of copper films. Surf. Coat. Technol. 2016, 308, 404–413. [Google Scholar] [CrossRef]
- Hall, E.O. The Deformation and Ageing of Mild Steel: Discussion of Results. Proc. Phys. Soc. Sect. B 1951, 64, 747. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Lee, D.; Wei, X.; Chen, X.; Zhao, M.; Jun, S.C.; Hone, J.; Herbert, E.G.; Oliver, W.C.; Kysar, J.W. Microfabrication and mechanical properties of nanoporous gold at the nanoscale. Scr. Mater. 2007, 56, 437–440. [Google Scholar] [CrossRef]
- Wheeler, J.M.; Michler, J. Invited Article: Indenter materials for high temperature nanoindentation. Rev. Sci. Instrum. 2013, 84. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, J.M.; Armstrong, D.E.J.; Heinz, W.; Schwaiger, R. High temperature nanoindentation: The state of the art and future challenges. Curr. Opin. Solid State Mater. Sci. 2015. [Google Scholar] [CrossRef]
- Durst, K.; Maier, V. Dynamic nanoindentation testing for studying thermally activated processes from single to nanocrystalline metals. Curr. Opin. Solid State Mater. Sci. 2015, 19, 340–353. [Google Scholar] [CrossRef]
- Maier, V.; Merle, B.; Göken, M.; Durst, K. An improved long-term nanoindentation creep testing approach for studying the local deformation processes in nanocrystalline metals at room and elevated temperatures. J. Mater. Res. 2013, 28, 1177–1188. [Google Scholar] [CrossRef]
- Hay, J.L.; Oliver, W.C.; Bolshakov, A.; Pharr, G.M. Using the ratio of loading slope and elastic stiffness to predict pile-up and constraint factor during indentation. MRS Proc. 1998, 522, 101–106. [Google Scholar] [CrossRef]
- Bolshakov, A.; Pharr, G.M. Influences of pileup on the measurement of mechanical properties by load and depth sensing indentation techniques. J. Mater. Res. 1998, 13, 1049–1058. [Google Scholar] [CrossRef]
- Randall, N.X.; Julia-Schmutz, C. Evalution of contact area and pile-up during the nanoindentation of soft coatings on hard substrates. Mat. Res. Soc. Symp. Proc. 1998, 522, 21–26. [Google Scholar] [CrossRef]
- Maier, V.; Leitner, A.; Pippan, R.; Kiener, D. Thermally Activated Deformation Behavior of ufg-Au: Environmental Issues during Long-Term and High-Temperature Nanoindentation Testing. JOM 2015, 67, 2934–2944. [Google Scholar] [CrossRef] [PubMed]
- Hodge, A.M.; Doucette, R.T.; Biener, M.M.; Biener, J.; Cervantes, O.; Hamza, A.V. Ag effects on the elastic modulus values of nanoporous Au foams. J. Mater. Res. 2009, 24, 1600–1606. [Google Scholar] [CrossRef]
- Soyarslan, C.; Bargmann, S.; Pradas, M.; Weissmüller, J. 3D stochastic bicontinuous microstructures: Generation, topology and elasticity. Acta Mater. 2018, 149, 326–340. [Google Scholar] [CrossRef]
- Hu, K.; Ziehmer, M.; Wang, K.; Lilleodden, E.T. Nanoporous gold: 3D structural analyses of representative volumes and their implications on scaling relations of mechanical behaviour. Philos. Mag. 2016, 96, 3322–3335. [Google Scholar] [CrossRef]
- Huber, N.; Viswanath, R.N.; Mameka, N.; Markmann, J.; Weißmüller, J. Scaling laws of nanoporous metals under uniaxial compression. Acta Mater. 2014, 67, 252–265. [Google Scholar] [CrossRef]
- Gangulee, A. Stress-enhanced diffusion in thin films. Philos. Mag. 1970, 22, 865–870. [Google Scholar] [CrossRef]
- Koifman Khristosov, M.; Dishon, S.; Noi, I.; Katsman, A.; Pokroy, B. Pore and Ligament Size Control, Thermal Stability and Mechanical Properties of Nanoporous Single Crystals of Gold. Nanoscale 2017, 9, 14458–14466. [Google Scholar] [CrossRef] [PubMed]
- Leitner, A.; Maier-Kiener, V.; Kiener, D. Extraction of Flow Behavior and Hall–Petch Parameters Using a Nanoindentation Multiple Sharp Tip Approach. Adv. Eng. Mater. 2017, 19, 1–9. [Google Scholar] [CrossRef]
- Biener, J.; Hodge, A.M.A.; Hayes, J.R.J.; Volkert, C.A.; Zepeda-Ruiz, L.A.; Hamza, A.V.; Abraham, F.F. Size effects on the mechanical behavior of nanoporous Au. Nano Lett. 2006, 6, 2379–2382. [Google Scholar] [CrossRef] [PubMed]
- Caro, M.; Mook, W.M.; Fu, E.G.; Wang, Y.Q.; Sheehan, C.; Martinez, E.; Baldwin, J.K.; Caro, A. Radiation induced effects on mechanical properties of nanoporous gold foams. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Liu, L.Z.; Ye, X.L.; Jin, H.J. Interpreting anomalous low-strength and low-stiffness of nanoporous gold: Quantification of network connectivity. Acta Mater. 2016, 118, 77–87. [Google Scholar] [CrossRef]
- Kiely, J.D.; Houston, J.E. Nanomechanical properties of Au (111), (001), and (110) surfaces. Phys. Rev. B 1998, 57, 12588–12594. [Google Scholar] [CrossRef]
- Stalder, A.; Dürig, U. Study of yielding mechanics in nanometer-sized Au contacts. Appl. Phys. Lett. 1996, 68, 637–639. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leitner, A.; Maier-Kiener, V.; Kiener, D. High Temperature Flow Behavior of Ultra-Strong Nanoporous Au assessed by Spherical Nanoindentation. Nanomaterials 2018, 8, 366. https://doi.org/10.3390/nano8060366
Leitner A, Maier-Kiener V, Kiener D. High Temperature Flow Behavior of Ultra-Strong Nanoporous Au assessed by Spherical Nanoindentation. Nanomaterials. 2018; 8(6):366. https://doi.org/10.3390/nano8060366
Chicago/Turabian StyleLeitner, Alexander, Verena Maier-Kiener, and Daniel Kiener. 2018. "High Temperature Flow Behavior of Ultra-Strong Nanoporous Au assessed by Spherical Nanoindentation" Nanomaterials 8, no. 6: 366. https://doi.org/10.3390/nano8060366
APA StyleLeitner, A., Maier-Kiener, V., & Kiener, D. (2018). High Temperature Flow Behavior of Ultra-Strong Nanoporous Au assessed by Spherical Nanoindentation. Nanomaterials, 8(6), 366. https://doi.org/10.3390/nano8060366