1. Introduction
Topological defects in nematic liquid crystals (LCs) are known to drive the self-assembly of included colloidal particles through elastic interactions with the medium [
1,
2,
3]. Colloidal particles can be located and arranged in two- and three-dimensional packings by the action of defect lines [
1] to produce custom lattice-like structures. In general, several types of self-assembled structures have been constructed in different media such as linear chains [
4], clusters [
5], and structured arrays [
6,
7]. These self-assembled structures can be driven by a variety of forces, such as kinetics of the particles themselves [
8]. Two-dimensional (2D) structures composed of colloidal particles have also been formed on the surface of liquid crystal droplets suspended in water and localized at topological defects on LC droplet surfaces [
9,
10,
11]. This has been successfully achieved using both nano- and micro-particles [
12,
13] as well as biological molecules [
14], to achieve unique structures.
The assembly of very small particles (~10 nm in diameter or less) presents more of a challenge as the particles become subject to strong Brownian fluctuations where the size of the particles approaches that of the solvent molecules. If the energy scale of these thermal fluctuations (~kT) also becomes comparable to the free energy cost of inserting a particle into the anisotropic liquid crystal medium, spontaneous assembly mediated by the Frank elastic constants [
3] can occur. Dispersed particles in the liquid crystal are able to explore the anisotropic fluid thermally and assemble at free energy minima by clustering together and/or locating in topological defect cores.
There have been several recent attempts to use liquid crystal defects to assemble and cluster nanoparticles of several types, including semiconducting (e.g., quantum dots), metallic (e.g., gold, silver), and magnetic particles [
15]. Such assemblies may exhibit collective electronic, photonic, or magnetic properties not seen in isolated nanoparticles [
16,
17]. Typically, particle clustering experiments result in the formation of isolated aggregates with no internal ordering or position control, although the deliberate seeding of defect points [
18] or lines [
19] can provide an organizing mechanism. An alternative approach to forming nanoparticle assemblies uses monodisperse particles and carefully designed ligands [
20]. This work has resulted in fascinating 2D arrangements of particles; however, the technique has not been expanded into large-scale structures in the third dimension.
In this work we were interested in finding a way to reliably direct the spatial organization of nanoparticle clusters and other assemblies. For example, can we make a regular array of small nanoparticle clusters, each of a well-defined size? Our approach is to use liquid crystal droplets in the nematic phase to control the positioning and size of these clusters. Micron-scale droplets containing clusters should be easy to manipulate by external methods (including, optical trapping and surface patterning).
The nematic liquid crystal phase is an anisotropic fluid characterized by orientational order defined locally by the director [
21]. Stable topological defects in liquid crystals occur where there is orientational frustration, for example, in bulk, at the center of a spherical nematic droplet or at the poles of a sphere coated with a thin film of smectic liquid crystal [
22]. When considering a thin film of nematic liquid crystal, four +1/2 defects occur at locations that form a tetrahedron through a sphere [
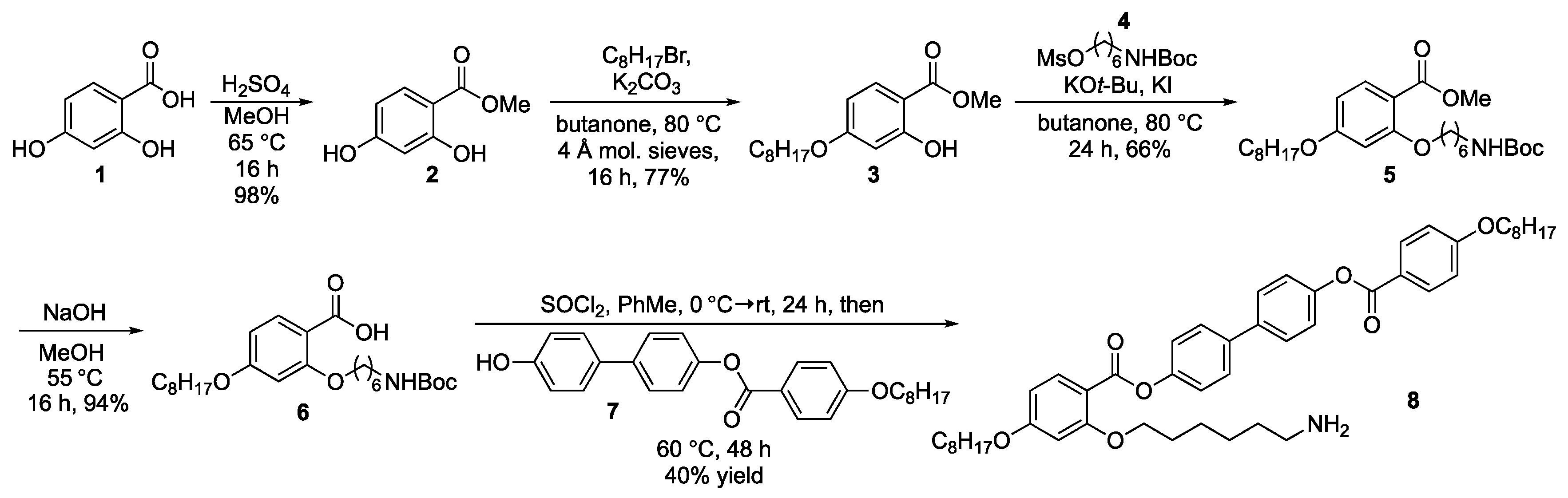
23]. One way to reliably control the location of these topological defects in liquid crystals is to control the geometry of the material and anchoring conditions at its interfaces. Take for example, a spherical liquid crystal droplet. Homeotropic anchoring conditions (whereby molecules are oriented perpendicular to the interface) will lead to a radial droplet structure, with a hedgehog defect located at the center (
Figure 1a,b). In contrast, planar anchoring conditions (whereby molecules lie parallel to the LC/solution interface) will tend to lead to a bipolar structure with two defects located at opposite poles of the droplet (
Figure 1c,d).
In previous work, large particles ranging from hundreds of nanometers to several microns in diameter were shown to pin to surface defects in liquid crystal droplets [
9]. In these experiments the particle is placed near the defect and subsequently moves to the defect core. We take a different approach, by dispersing nanoparticles into droplets in the isotropic phase, and then subsequently cooling the droplets to the nematic phase. This approach is partially motivated by the inherent difficulties in manipulating individual nanoparticles. It also allows us to begin with a uniform particle distribution and observe cluster formation free from outside manipulation.
To allow spontaneous self-assembly at a defect without the influence of any external force, the particles must be very small and therefore mobile in the liquid crystal phase, taking advantage of Brownian fluctuations to locate at defect points. For this reason, we chose to work with 6-nm quantum dots (QDs) for their bright emission properties, although similar experiments using any nanoparticle type (gold, metal oxide, etc.) would be equivalent.
While self-assembly via topological defect locations is an effective strategy to pursue, recently another mechanism for spatial nanoparticle sorting in liquid crystals was developed [
18,
20]. Results demonstrated that the moving isotropic to nematic phase front can act as an elastic sorting mechanism for the tiny nanoparticles. Of particular interest is the formation of stable microcapsules or “shells”. These structures were formed using quantum dots with mesogenic ligands [
24] providing an added degree of control in particle dispersion and cluster stabilization. When closely packed, the mesogenic ligands provide a short-range attractive interaction between nanoparticles.
In this paper we explore these two assembly mechanisms in liquid crystal droplets with different surface anchoring conditions (planar and homeotropic). These two mechanisms we title “equilibrium defect sorting” and “phase transition sorting”. By varying the droplet cooling rate through the isotropic to nematic phase transition, we observed different particle distributions in the liquid crystal droplets induced by defect locations and particle assembly at energetically unfavorable locations. In addition, we found that it was also possible to form single nanoparticle microcapsules [
24] at the center of liquid crystal droplets.
Understanding the competition between the defect-based assembly and phase-transition-induced assembly is important for controlling the position of nanoparticle clusters over large length-scales without the need for chemical alignment layers or expensive lithography techniques. By investigating assembly with a controlled spherical droplet geometry, we can compare assembly mechanisms more directly, probing the effects of droplet geometry and size, as well as cooling rate, on cluster formation. In addition, we propose that clusters isolated in individual droplets can be close-packed to produce macroscopic assemblies of nanoparticle clusters in two and three dimensions.
2. Materials and Methods
In this work we used quantum dots functionalized with a mesogenic ligand (
8,
Scheme 1). This ligand is an amine-terminated variant of the calamitic side-on attaching liquid crystals investigated by the groups of Dunmur [
25] and Vashchenko [
26]. It was prepared following the sequence of reactions reported by Quint and coworkers [
27], and then exchanged with octadecylamine surface ligands on commercial CdSe core/ZnO shell quantum dots (NN Lab Inc., Fayetteville, AR, USA) following our reported procedure [
28]. It was targeted for its ability to stabilize particle clusters via short range non-covalent interactions [
19], which would facilitate particle dispersion in the host liquid crystal matrix (4-cyano-4′-pentylbiphenyl, “5CB”) and produce a uniform dispersion of modified QDs in the isotropic phase [
20]. In addition, above a threshold concentration, the ligand allows the formation of micron-scale capsules [
24,
27] by a unique phase separation process. Herein, we aimed to form these structures in the more controlled liquid crystal droplet geometry.
The degree of ligand exchange under different conditions was quantified using
1H NMR spectroscopy as previously reported [
28], revealing a 9:1 surface ratio of
8 to octadecylamine.
The modified particles are uniformly dispersed in 5CB via heat bath sonication at 50 °C for 2 h, verified by fluorescence microscopy. Particle concentrations used in these experiments varied between 0.05 and 0.2 wt %.
Once a uniform particle dispersion in 5CB is achieved, the droplets can be formed. We pipette 3 μL of the QD-5CB composite into 300 μL of either Millipure water or 1.0 wt % polyvinyl alcohol (PVA)/water solution at a temperature of 55 °C. 5CB droplets in water typically exhibit homeotropic boundary conditions resulting in a radial configuration which was verified by cross-polarized microscopy, whereas droplets in PVA/water solution exhibit planar boundary conditions resulting in a bipolar configuration [
29], as illustrated in
Figure 1c. To follow standard practice for creating nematic droplets, we also dispersed the droplets in a solution of 1 wt % sodium dodecyl sulfate (SDS) to achieve homeotropic boundary conditions, and pure glycerol to produce planar boundary conditions. After adding the QD-5CB composite to the aqueous solution, the system was then tip sonicated using a cell disrupter for approximately one second, until the resulting emulsion appeared cloudy, keeping the system above the nematic–isotropic transition temperature. The rapid motion of the tip sonicator forms droplets of varying sizes in a very small amount of time. Isotropic droplets were then cooled into the nematic phase at two different cooling rates, 1 °C/min and ~200 °C/min, and QD cluster formation and location were observed using a fluorescence microscope.
Fluorescence microscopy was used to image the spatial distribution of QDs in the liquid crystal droplets. In the experiments presented here we used CdSe/ZnS core shell QDs (NN-labs) with an emission wavelength centered at 620 nm. Fluorescence imaging was carried out on an upright Leica DM2500P microscope in reflection mode using a 20× objective. A white-light mercury lamp illumination source with a 515–560 nm band-pass filter was used for QD excitation. Emission was detected using a 580 nm dichroic mirror and a 590 nm long pass filter. The microscope can also be used in transmission mode with a white light source and crossed polarizers to image birefringence. The droplet suspensions were mounted on standard glass slides under a cover slip for observations.
4. Discussion
Our initial hypothesis was that QD cluster patterning would be achieved through equilibrium defect formation in a liquid crystal droplet in a similar mechanism to that recently reported for micron-scale particles [
10,
11,
12]. However, we also proposed that rapid cooling might lead to the formation and stabilization of out-of-equilibrium structures such as the recently reported QD spherical shells reported at high cooling rates in a similar system [
24]. To investigate these mechanisms, we carried out two sets of experiments, focused on slow cooling and rapid cooling through the isotropic to nematic transition. The droplet geometry was particularly useful in these experiments because the ground-state topological defect configurations are well defined. In addition, the particle concentration within the droplet is easily controlled.
Two Different Mechanisms for Assembly
In this paper we considered two separate mechanisms responsible for the spatial organization of particles in liquid crystal droplets. Overall, the collection of quantum dots occurred at the defect location (i.e., center) of the droplet by a simple free energy argument. There are three major contributions to the free energy for quantum dots inside a liquid crystal droplet: elastic forces, phase transition dynamics (Landau theory (order parameter)), and the actual insertion of quantum dots. This can be expressed as . The elastic free energy is the classic Frank Free energy which consists of splay, twist, and bend energies; these are the common deformations of a liquid crystal. The Landau de Gennes (LdG) free energy governs the phase transition, and the quantum dot free energy can be considered to represent the particle fraction inside the liquid crystal medium. The particles are swept up due to the changes governed by FLdG, and the location is then governed by the elastic forces that could possibly move the formed cluster to defect locations.
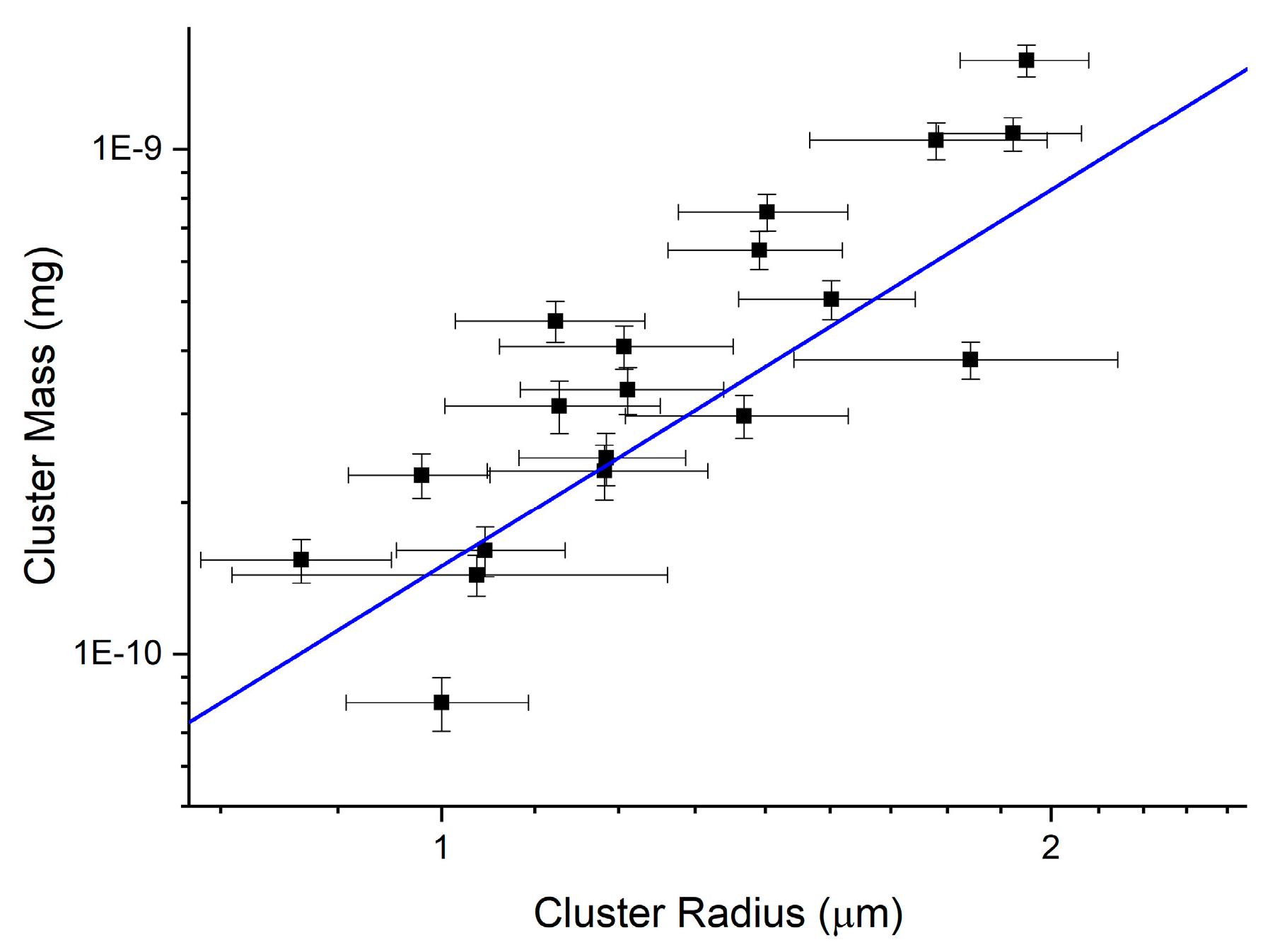
In the first mechanism, “equilibrium defect assembly”, the transition particles assemble in the topological defects, producing an 3D aggregate with a fractal-like mass scaling. This is consistent with our previous observations in bulk liquid crystal [
20]. Given sufficient time, particles initially not located at defects will eventually migrate there by thermal motion and “fall in” to the aggregate. This process is most likely to occur at very low particle concentrations.
The second mechanism is through “phase transition assembly”. In this mechanism, recently reported by our group [
20,
24], particles preferentially locate in a shrinking isotropic domain within the droplet as it cools through the isotropic to nematic phase transition. The particles are pushed close together as the isotropic phase shrinks to form a cluster.
The first mechanism for nanoparticle sorting in the droplets concerns their tendency to cluster and localize at topological defects in the liquid crystal. Spherical particles of all sizes have been shown to accumulate at defect points in liquid crystals [
3]. This is a relatively slow size-dependent process, whereby particles in the nematic phase tend to locate at points of low order to minimize the elastic deformation of the liquid crystal by radially symmetric particles.
The second mechanism is related to the propagation of the isotropic to nematic phase front. In this case, particles preferentially locate in shrinking isotropic domains at the phase transition and are effectively pushed together by the nucleating, growing nematic domains [
20,
24], entropically repelled by the ordered environment of the nematic phase. This sorting process can occur rapidly and, if the particles are small enough, provides an excellent mechanism to assemble nanoparticle-based structures.
In all of our droplets, we started with a uniform particle distribution in the isotropic liquid crystal phase. Then, following a cooling step, the liquid crystal transitioned into the nematic phase. Our results highlight several possibilities for controlling particle organization.
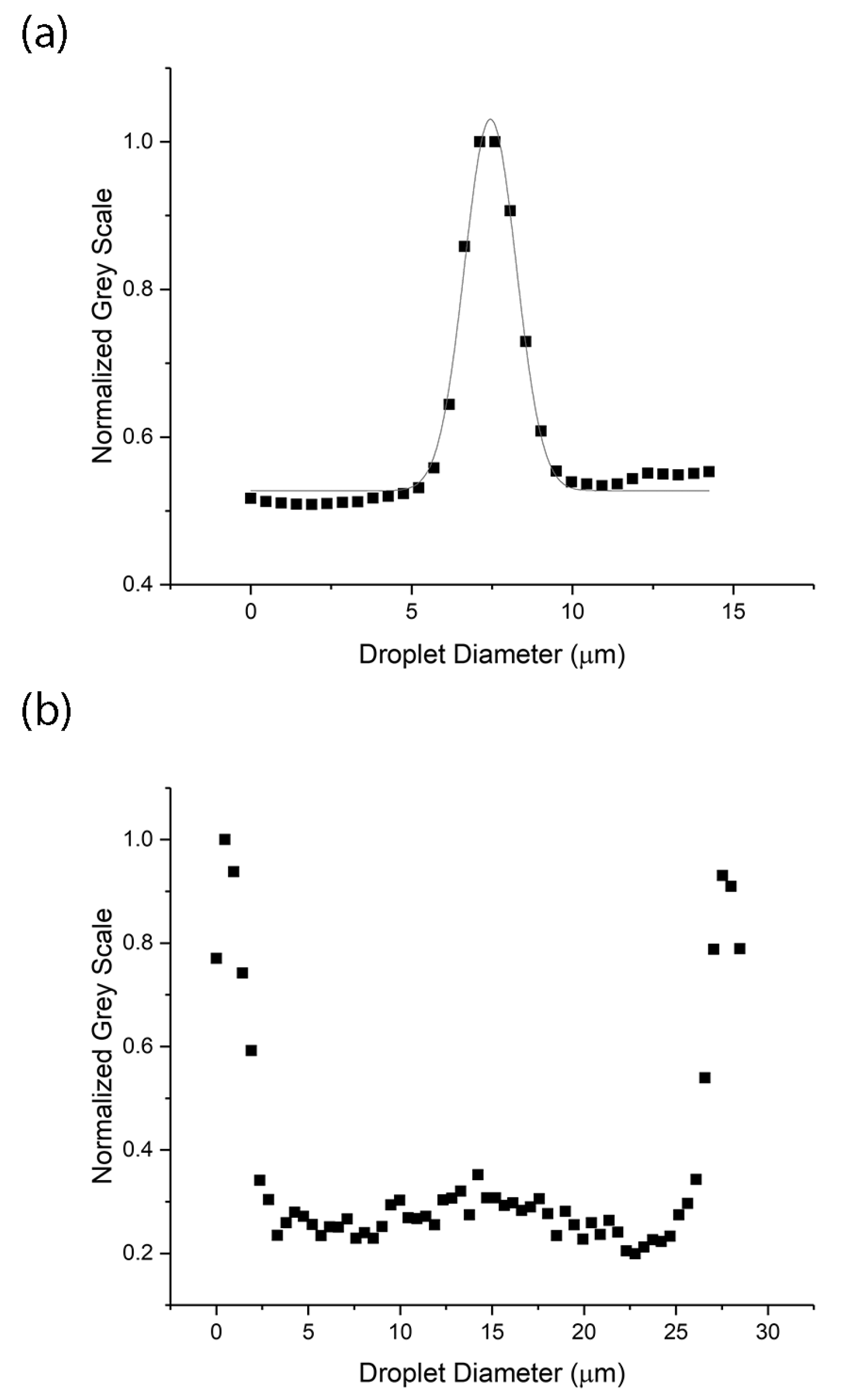
Using different cooling rates, we observed evidence of competition between the two different assembly mechanisms. Six-nanometer nanoparticle diffusion in the nematic phase can be generally considered as an Brownian random walk, modified by local director orientation. Particles and small clusters will explore the droplet until they locate in a topological defect. We can characterize this motion by timescale, τQD, the time for a particle to travel a mean squared displacement (MSD) equal to the radius of the droplet.
As nanoparticles and small clusters of particles move randomly, they may encounter other particles or clusters, increasing their size. This will further slow their diffusion rate, increasing τ
QD, and thus can be described as cluster-cluster aggregation in an anisotropic environment. Slow cooling the droplet through the phase transition tends to produce many small nematic domains which nucleate and grow. At slow cooling rates this process does not appear to impact the migration of the nanoparticles to topological defects, either at the center of a radial droplet, or on the surface of a bipolar droplet (
Figure 1a,c).
Rapid cooling through the phase transition allows the second assembly mechanism to dominate. In this case we typically observe a single-phase front rapidly moving across the droplet. If the phase front transition timescale, τ
PF (the time for the phase front to travel the radius of the droplet) is short compared to the QD clustering timescale (τ
PF < τ
QD), we expect the phase front particle sorting to dominate over Brownian motion. A simple analysis supports our assumptions. The diffusion constant of a quantum dot in isotropic 5CB was estimated to be 4 μm
2/s. This was obtained from viscosity measurements from Reference [
32] and from using the Einstein–Stokes relation for diffusion, with T above the isotropic–nematic phase transition point. These values yield a linear diffusion length for the QDs of ~5 μm/s in a 3D droplet. To quantify the phase front timescale (τ
PF), we analyzed a 60-μm diameter droplet and measured the phase front velocity to be 27 μm/s. These numbers illustrate that we can expect the phase front to move approximately five times faster than the linear diffusion of an average QD in the nematic phase.
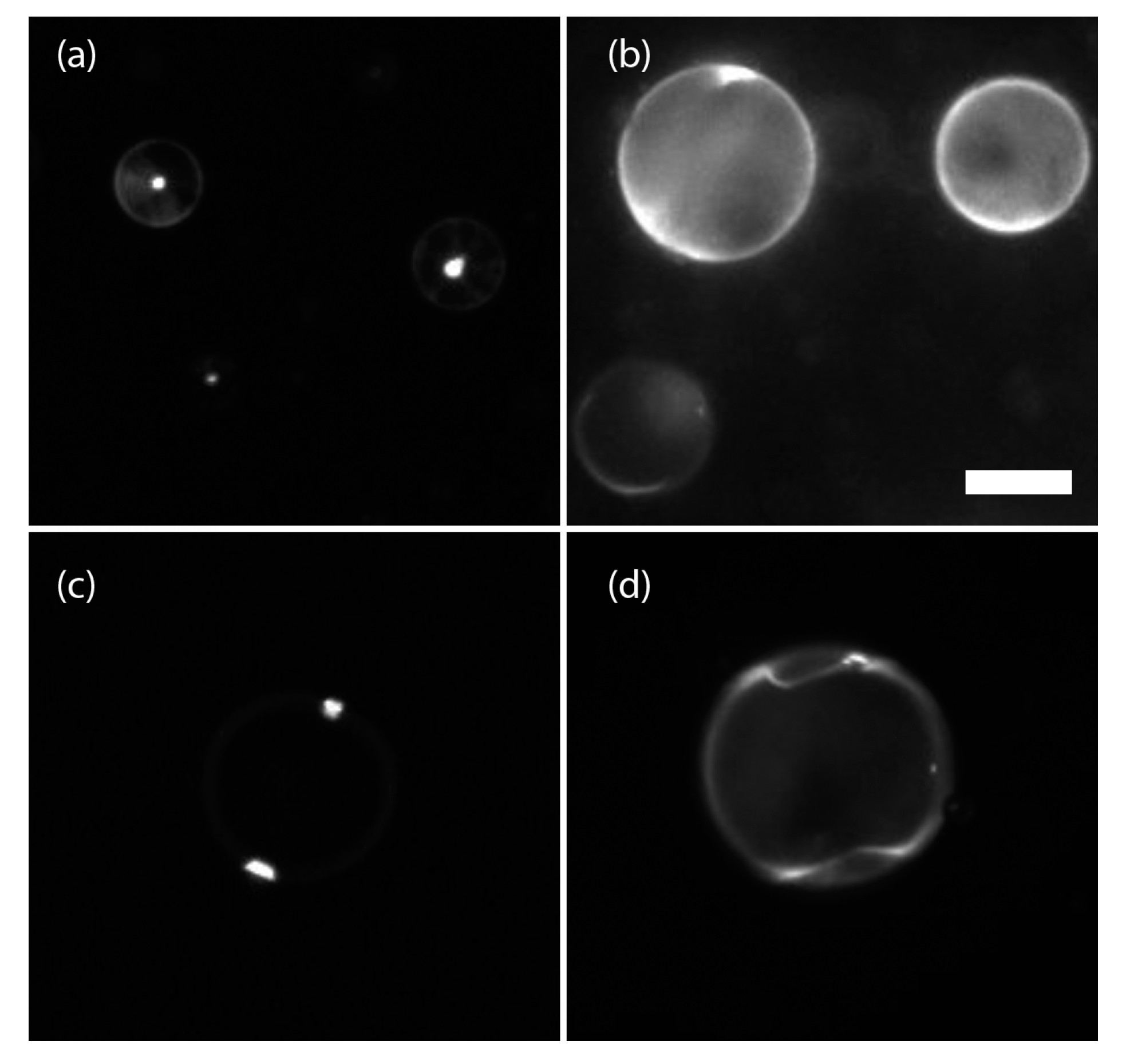
We can relate the phase transition assembly process to a non-quasistatic compression. In the case that phase transition assembly dominates, the particles are not able to diffuse away before being swept up by the phase boundary. The particles then follow the direction of the phase front, which depends on the temperature gradient direction in the liquid crystal droplet. If all of the particles are swept up, and the cluster is of sufficient size compared to the size of the droplet, Frank elastic effects are insufficient to move the large cluster, and so the liquid crystal will reorient itself around the cluster to minimize the free energy of the system. This reorientation may not always be the lowest energy state possible, as seen with the surprising example of a cluster stabilized at the center of a bipolar droplet (
Figure 3). This phase front aggregation process could be described as a ballistic diffusion-limited aggregation process as particles are pushed together in the shrinking isotropic domain.