Effect of Dimensions and Agglomerations of Carbon Nanotubes on Synchronous Enhancement of Mechanical and Damping Properties of Epoxy Nanocomposites
Abstract
1. Introduction
2. Methods and Materials
2.1. Materials
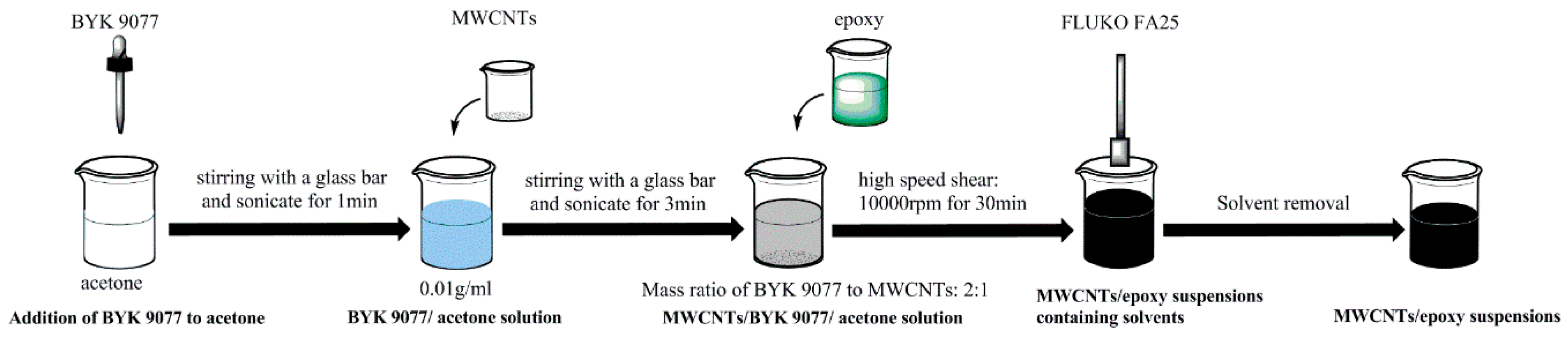
2.2. Preparation of Composites
2.3. Testing and Characterization
3. Results and Discussion
3.1. Morphologies of MWCNT Agglomerates
3.2. Dispersion of MWCNTs
3.3. Tensile Properties
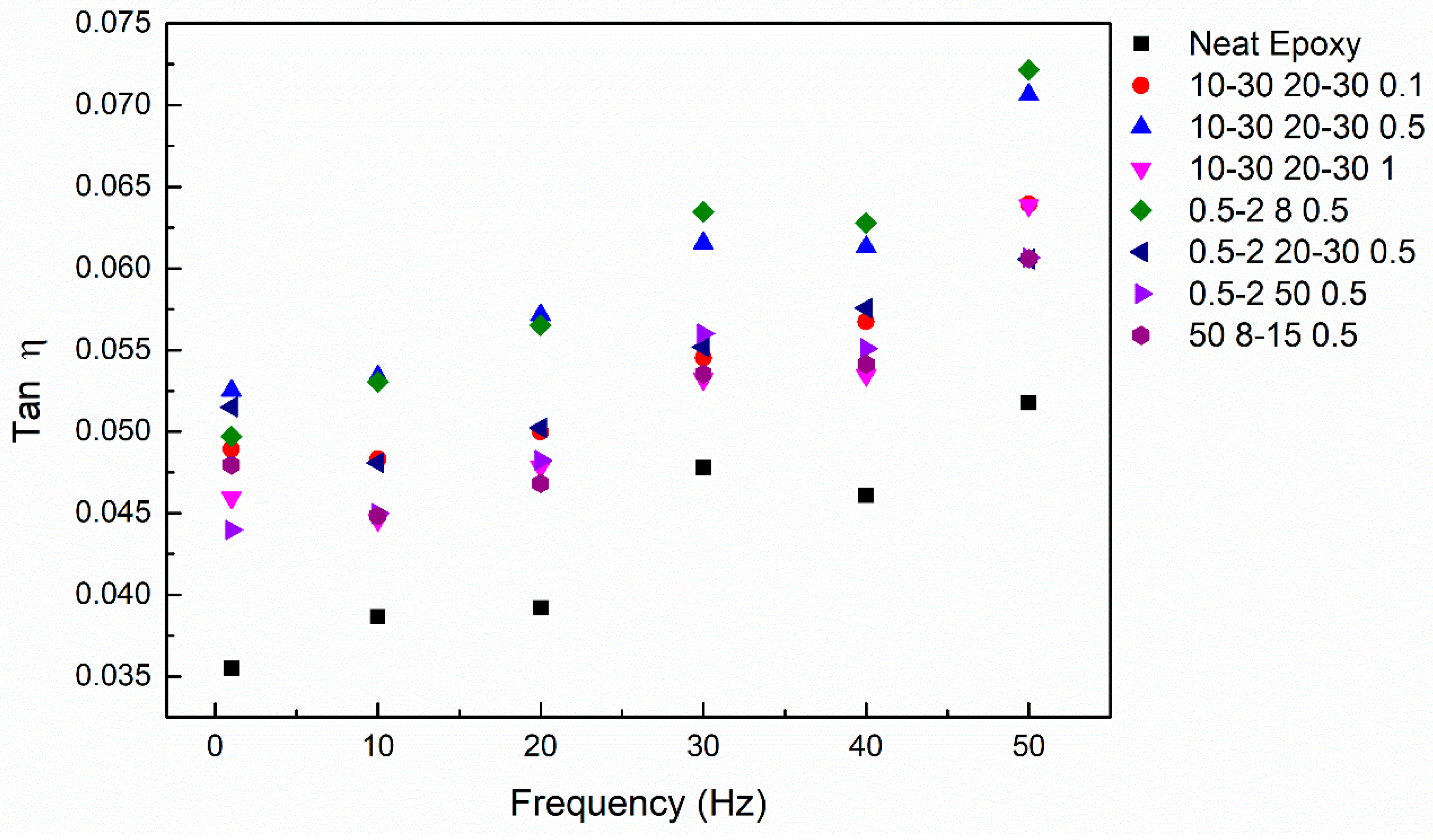
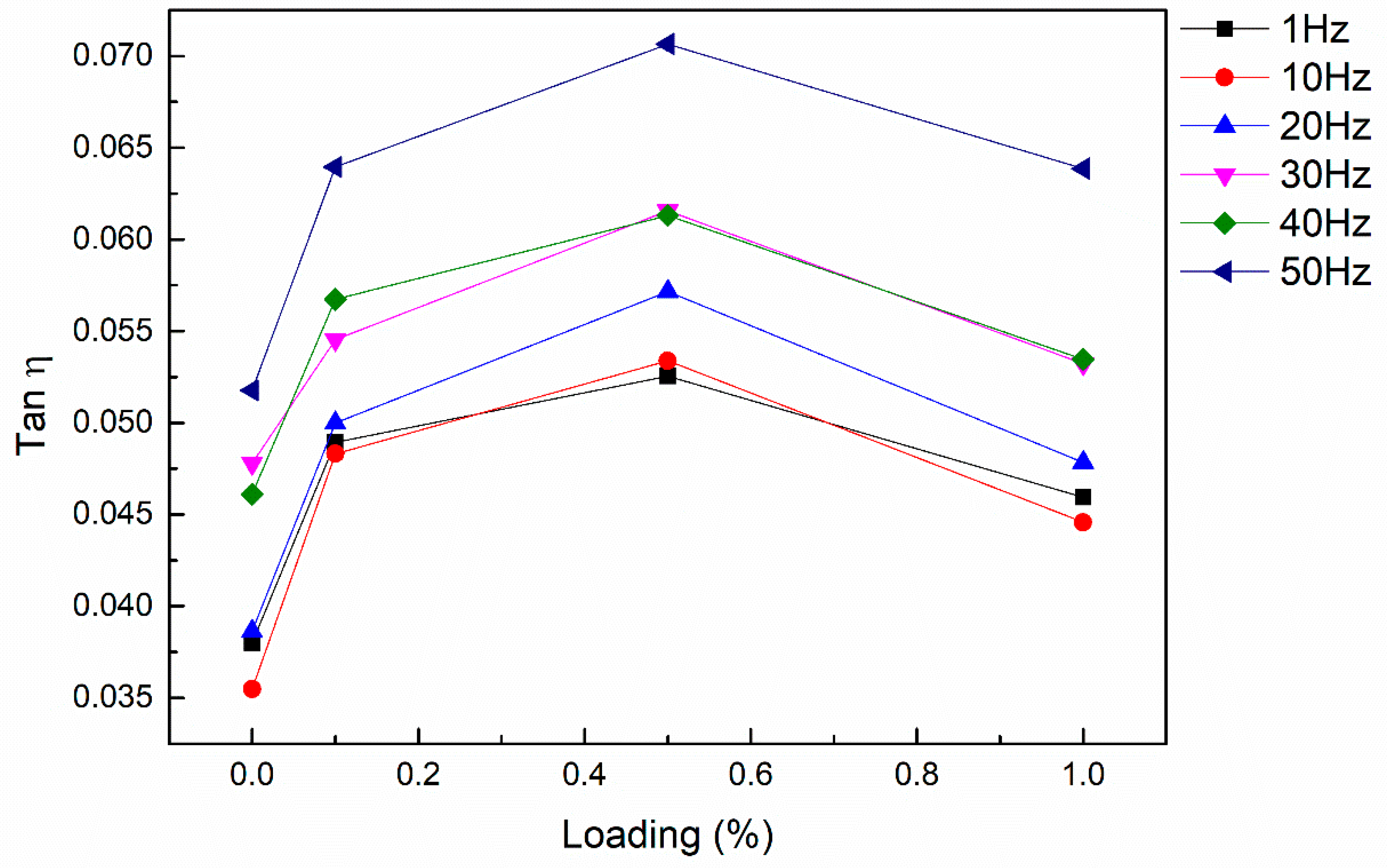
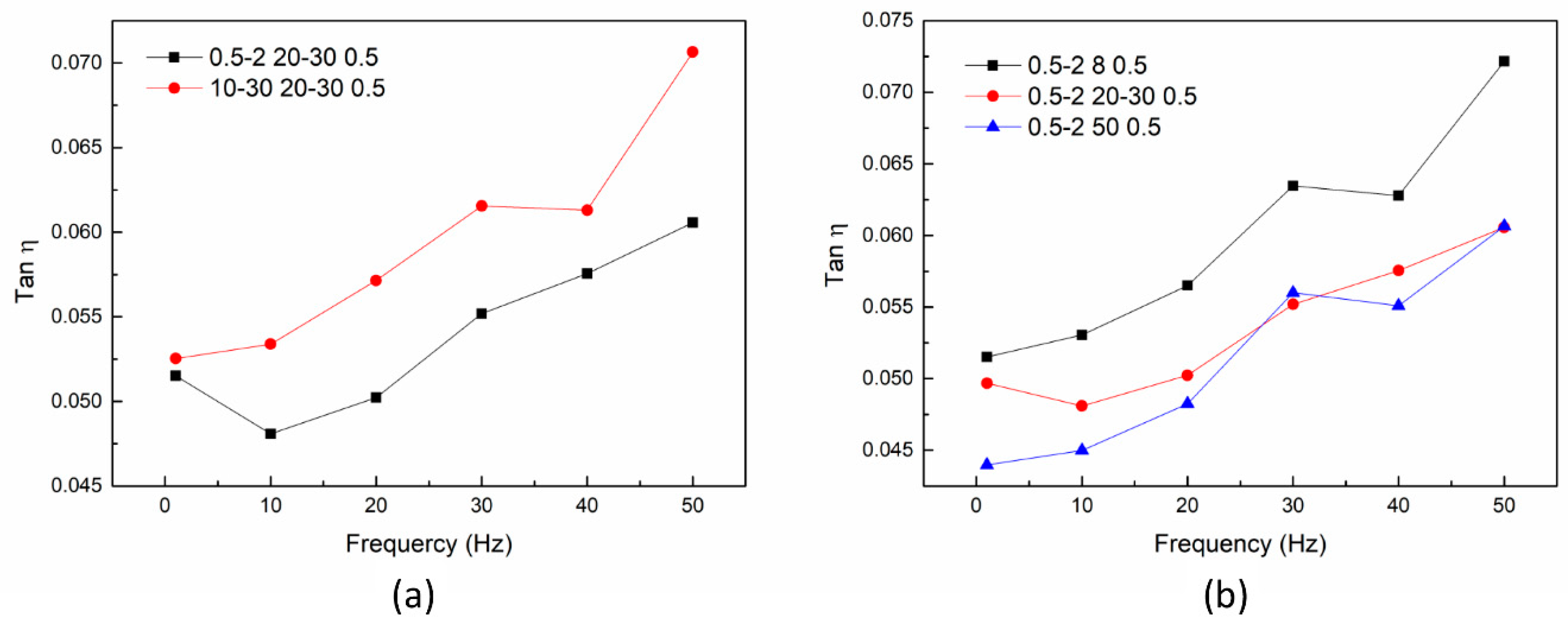
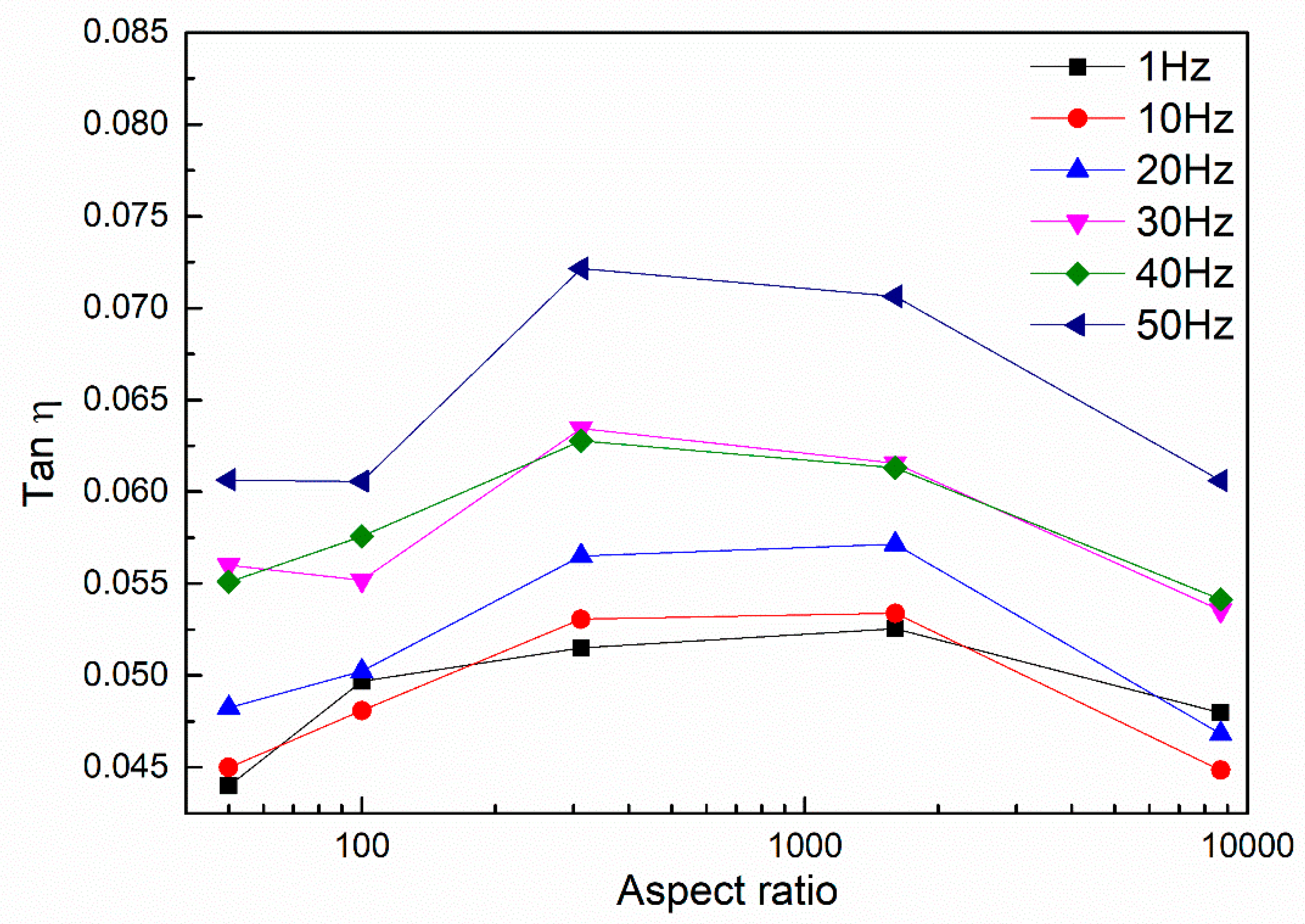
3.4. Damping Properties
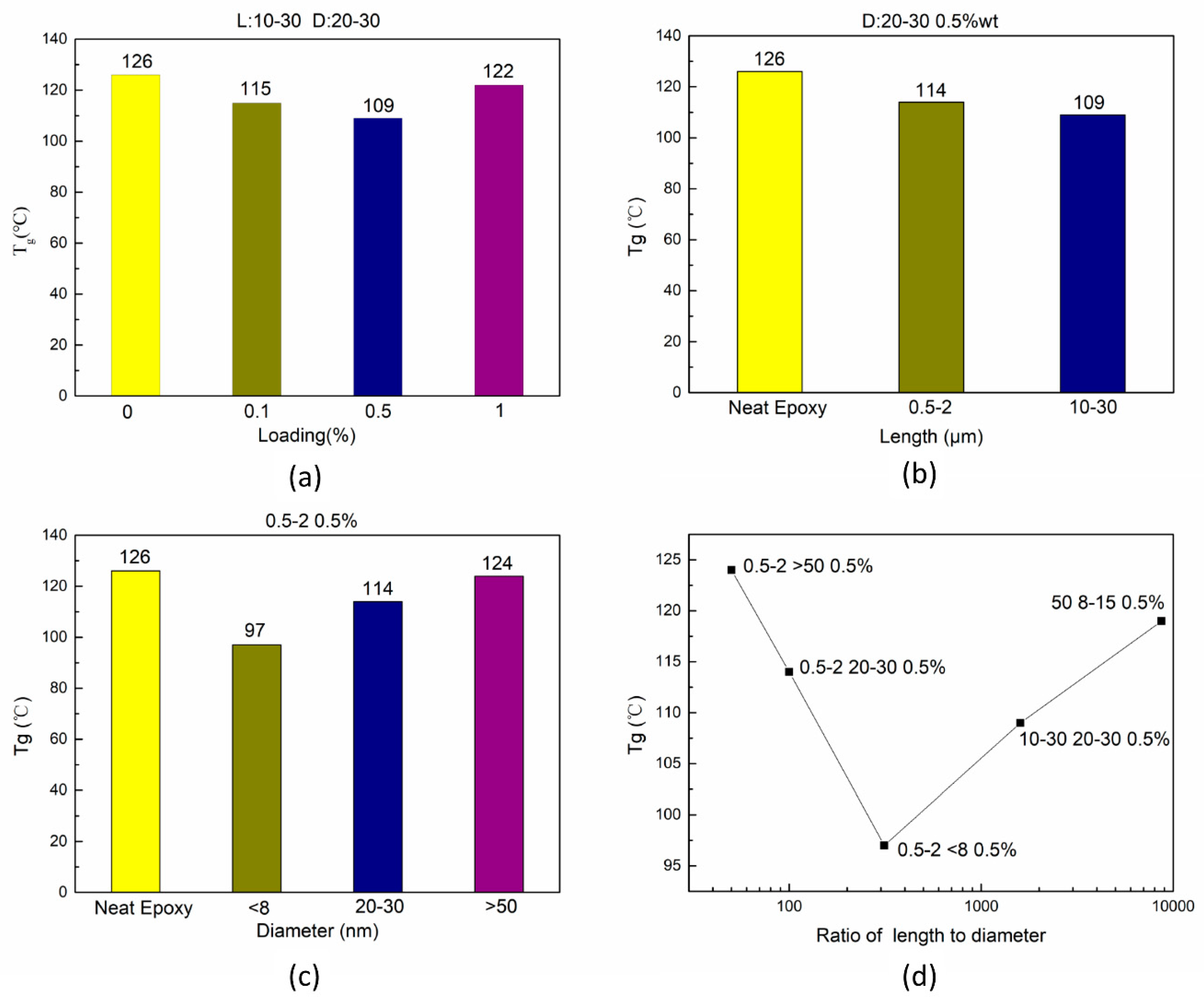
3.5. Tg of Nanocomposites
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, S.H.; Chen, H.L. A study on the damping characteristics of laminated composites with integral viscoelastic layers. Compos. Struct. 2006, 74, 63–69. [Google Scholar] [CrossRef]
- Chandra, R.; Singh, S.P.; Gupta, K. Damping studies in fiber-reinforced composites—A review. Compos. Struct. 1999, 46, 41–51. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Overney, G.; Zhong, W.; Tománek, D. Structural rigidity and low frequency vibrational modes of long carbon tubules. Z. Phys. D At. Mol. Clust. 1993, 27, 93–96. [Google Scholar] [CrossRef]
- Lu, J.P. Elastic properties of single and multilayered nanotubes. J. Phys. Chem. Solids 1997, 58, 1649–1652. [Google Scholar] [CrossRef]
- Treacy, M.M.J.; Ebbesen, T.W.; Gibson, J.M. Exceptionally high young’s modulus observed for individual carbon nanotubes. Nature 1996, 381, 678–680. [Google Scholar] [CrossRef]
- Wong, E.W.; Sheehan, P.E.; Lieber, C.M. Nanobeam mechanics: elasticity, strength, and toughness of nanorods and nanotubes. Science 1997, 277, 1971–1975. [Google Scholar] [CrossRef]
- Chang, T.E.; Jensen, L.R.; Kisliuk, A.; Pipes, R.B.; Pyrz, R.; Sokolov, A.P. Microscopic mechanism of reinforcement in single-wall carbon nanotube/polypropylene nanocomposite. Polymer 2005, 46, 439–444. [Google Scholar] [CrossRef]
- Xu, X.; Thwe, M.M.; Shearwood, C.; Liao, K. Mechanical properties and interfacial characteristics of carbon-nanotube-reinforced epoxy thin films. Appl. Phys. Lett. 2002, 81, 2833–2835. [Google Scholar] [CrossRef]
- Xu, M.; Futaba, D.N.; Yamada, T.; Yumura, M.; Hata, K. Carbon nanotubes with temperature-invariant viscoelasticity from −196 to 1000 °C. Science 2010, 330, 1364–1368. [Google Scholar] [CrossRef]
- Zhou, X.; Shin, E.; Wang, K.W.; Bakis, C.E. Interfacial damping characteristics of carbon nanotube-based composites. Compos. Sci. Technol. 2004, 64, 2425–2437. [Google Scholar] [CrossRef]
- Buldum, A.; Jian, P.L. Atomic scale sliding and rolling of carbon nanotubes. Phys. Rev. Lett. 1999, 83, 5050–5053. [Google Scholar] [CrossRef]
- Coleman, J.N.; Khan, U.; Blau, W.J.; Gun’ko, Y.K. Small but strong: A review of the mechanical properties of carbon nanotube–polymer composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
- Dubnikova, I.; Kuvardina, E.; Krasheninnikov, V.; Lomakin, S.; Tchmutin, I.; Kuznetsov, S. The effect of multiwalled carbon nanotube dimensions on the morphology, mechanical, and electrical properties of melt mixed polypropylene-based composites. J. Appl. Polym. Sci. 2010, 117, 259–272. [Google Scholar] [CrossRef]
- Su, F.; Miao, M. Effect of mwcnt dimension on the electrical percolation and mechanical properties of poly (vinylidenefluoride-hexafluoropropylene) based nanocomposites. Synth. Met. 2014, 191, 99–103. [Google Scholar] [CrossRef]
- Singh, B.P.; Saini, K.; Choudhary, V.; Teotia, S.; Pande, S.; Saini, P.; Mathur, R.B. Effect of length of carbon nanotubes on electromagnetic interference shielding and mechanical properties of their reinforced epoxy composites. J. Nanopart. Res. 2014, 16, 2161. [Google Scholar] [CrossRef]
- Song, Y.S.; Youn, J.R. Influence of dispersion states of carbon nanotubes on physical properties of epoxy nanocomposites. Carbon 2005, 43, 1378–1385. [Google Scholar] [CrossRef]
- Liu, C.; Choi, J. Improved dispersion of carbon nanotubes in polymers at high concentrations. Nanomaterials 2012, 2, 329–347. [Google Scholar] [CrossRef]
- Chen, B.; Li, S.; Imai, H.; Jia, L.; Umeda, J.; Takahashi, M.; Kondoh, K. An approach for homogeneous carbon nanotube dispersion in al matrix composites. Mater. Des. 2015, 72, 1–8. [Google Scholar] [CrossRef]
- Kumar, A.; Ghosh, P.K.; Yadav, K.L.; Kumar, K. Thermo-mechanical and anti-corrosive properties of mwcnt/epoxy nanocomposite fabricated by innovative dispersion technique. Compos. Part B Eng. 2017, 113, 291–299. [Google Scholar] [CrossRef]
- Hsiao, A.; Tsai, S.; Hsu, M.; Chang, S. Decoration of multi-walled carbon nanotubes by polymer wrapping and its application in mwcnt/polyethylene composites. Nanoscale Res. Lett. 2012, 7, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Ghozatloo, A.; Rashidi, A.M.; Shariaty-Niasar, M. Effects of surface modification on the dispersion and thermal conductivity of cnt/water nanofluids. Int. J. Heat Mass. Trans. 2014, 54, 1–7. [Google Scholar] [CrossRef]
- Gröschel, A.H.; Löbling, T.I.; Petrov, P.D.; Müllner, M.; Kuttner, C.; Wieberger, F.; Müller, A.H.E. Janus micelles as effective supracolloidal dispersants for carbon nanotubes. Angew. Chem. Int. Ed. 2013, 52, 3602–3606. [Google Scholar] [CrossRef] [PubMed]
- Parveen, S.; Rana, S.; Fangueiro, R.; Paiva, M.C. Microstructure and mechanical properties of carbon nanotube reinforced cementitious composites developed using a novel dispersion technique. Cement. Concr. Res. 2015, 73, 215–227. [Google Scholar] [CrossRef]
- Rahman, M.M.; Zainuddin, S.; Hosur, M.V.; Malone, J.E.; Salam, M.B.A.; Kumar, A.; Jeelani, S. Improvements in mechanical and thermo-mechanical properties of e-glass/epoxy composites using amino functionalized mwcnts. Compos. Struct. 2012, 94, 2397–2406. [Google Scholar] [CrossRef]
- Zeiler, R.; Khalid, U.; Kuttner, C.; Kothmann, M.; Dijkstra, D.J.; Fery, A.; Altstädt, V. Liquid composite molding-processing and characterization of fiber-reinforced composites modified with carbon nanotubes. Aip. Conf. Proc. 2014, 1593, 503–507. [Google Scholar]
- Yang, S.; Lin, W.; Huang, Y.; Tien, H.; Wang, J.; Ma, C.M.; Li, S.; Wang, Y. Synergetic effects of graphene platelets and carbon nanotubes on the mechanical and thermal properties of epoxy composites. Carbon 2011, 49, 793–803. [Google Scholar] [CrossRef]
- Zhou, Y.; Pervin, F.; Lewis, L.; Jeelani, S. Fabrication and characterization of carbon/epoxy composites mixed with multi-walled carbon nanotubes. Mater. Sci. Eng. R 2008, 475, 157–165. [Google Scholar] [CrossRef]
- Graf, A.; Zakharko, Y.; Schießl, S.P.; Backes, C.; Pfohl, M.; Flavel, B.S.; Zaumseil, J. Large scale, selective dispersion of long single-walled carbon nanotubes with high photoluminescence quantum yield by shear force mixing. Carbon 2016, 105, 593–599. [Google Scholar] [CrossRef]
- Kasaliwal, G.R.; Pegel, S.; Göldel, A.; Pötschke, P.; Heinrich, G. Analysis of agglomerate dispersion mechanisms of multiwalled carbon nanotubes during melt mixing in polycarbonate. Polymer 2010, 51, 2708–2720. [Google Scholar] [CrossRef]
- Hansen, S.; Khakhar, D.V.; Ottino, J.M. Dispersion of solids in nonhomogeneous viscous flows. Chem. Eng. Sci. 1998, 53, 1803–1817. [Google Scholar] [CrossRef]
- Ottino, J.M.; DeRoussel, P.; Hansen, S.; Khakhar, D.V. Mixing and dispersion of viscous liquids and powerdered solids. In Advances in Chemical Engineering; Academic Press: Cambridge, MA, USA, 1999; pp. 105–204. [Google Scholar]
- Rumpf, H.C.H. Zur theorie der zugfestigkeit von agglomeraten bei kraftübertragung an kontaktpunkten. Chem. Ing. Tech. 1970, 42, 538–540. [Google Scholar] [CrossRef]
- Williams, S.R.; Philipse, A.P. Random packings of spheres and spherocylinders simulated by mechanical contraction. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2003, 67, 051301. [Google Scholar] [CrossRef] [PubMed]
- Akita, S.; Nishijima, H.; Nakayama, Y. Influence of stiffness of carbon-nanotube probes in atomic force microscopy. J. Appl. Phys. 2000, 33, 2673. [Google Scholar] [CrossRef]
- Bücking, W.; Nann, T. Electrophoretic analysis of gold nanoparticles: size-dependent electrophoretic mobility of nanoparticles. IEEE Proc. Nanobiotechnol. 2006, 153, 47. [Google Scholar]
- Rance, G.A.; Marsh, D.H.; Bourne, S.J.; Reade, T.J.; Khlobystov, A.N. Van Der Waals interactions between nanotubes and nanoparticles for controlled assembly of composite nanostructures. ACS Nano 2010, 4, 4920–4928. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884. [Google Scholar] [CrossRef]
- Mallick, P.K. Fiber-Reinforced Composites: Materials, Manufacturing, And Design; CRC Press: Boca Raton, FL, USA, 2007; p. 587. [Google Scholar]
- Xie, S.; Li, W.; Pan, Z.; Chang, B.; Sun, L. Mechanical and physical properties on carbon nanotube. J. Phys. Chem. Solids 2000, 61, 1153–1158. [Google Scholar] [CrossRef]
- Schießl, S.P.; Fröhlich, N.; Held, M.; Gannott, F.; Schweiger, M.; Forster, M.; Scherf, U.; Zaumseil, J. Polymer-sorted semiconducting carbon nanotube networks for high-performance ambipolar field-effect transistors. ACS Appl. Mater. Interface 2015, 7, 682–689. [Google Scholar] [CrossRef]
- Jangam, S.; Raja, S.; Gowd, B.U.M. Influence of multiwall carbon nanotube alignment on vibration damping of nanocomposites. J. Reinf. Plast. Comp. 2016, 35, 1–11. [Google Scholar] [CrossRef]
- Abhinav, A.; Raja, S. Damping characteristics of epoxy-reinforced composite with multiwall carbon nanotubes. Mech. Compos. Mater. 2014, 21, 197–206. [Google Scholar]
- Putz, K.W.; Palmeri, M.J.; Cohn, R.B.; Andrews, R.; Brinson, L.C. Effect of cross-link density on interphase creation in polymer nanocomposites. Macromolecules 2008, 41, 6752–6756. [Google Scholar] [CrossRef]
- Babal, A.S.; Gupta, R.; Singh, B.P.; Dhakate, S.R. Depression in glass transition temperature of multiwalled carbon nanotubes reinforced polycarbonate composites: effect of functionalization. RSC Adv. 2015, 5, 43462–43472. [Google Scholar] [CrossRef]



| Length (μm) | OD 1 (nm) | ID 2 (nm) | SSA 3 (m2/g) | Purity (%) | Functional Group | Group Content (wt. %) | |
|---|---|---|---|---|---|---|---|
| 1 | 10–30 | 20–30 | 5–10 | >110 | >95 | –COOH | 1.23 |
| 2 | 0.5–2 | <8 | 2–5 | >500 | 3.86 | ||
| 3 | 0.5–2 | 20–30 | 5–10 | >110 | 1.23 | ||
| 4 | 0.5–2 | >50 | 5–15 | >40 | 0.49 | ||
| 5 | 50 | 8–15 | 3–5 | >233 | 2.56 |
| Property | Value |
|---|---|
| Viscosity at 25 °C (mPa·s) | 1100 ± 200 |
| Curing agent | Amines |
| Viscosity of mixed at 25 °C (mPa·s) | 250 ± 50 |
| Operable time (min) | 80 |
| Tg (°C) | 115–125 |
| Tensile strength (MPa) | 74.5 |
| Tensile modulus (GPa) | 2.65 |
| Flexural strength (MPa) | 117.67 |
| Flexural modulus (GPa) | 3.2 |
| Compressive strength (MPa) | 105 |
| Code | Length (μm) | OD (nm) | CNT Loading (wt. %) | |
|---|---|---|---|---|
| 1 | Neat Epoxy | - | - | - |
| 2 | 10–30, 20–30, 0.1 | 10–30 | 20–30 | 0.1 |
| 3 | 10–30, 20–30, 0.5 | 10–30 | 20–30 | 0.5 |
| 4 | 10–30, 20–30, 1 | 10–30 | 20–30 | 1 |
| 5 | 0.5–2, 8, 0.5 | 0.5–2 | <8 | 0.5 |
| 6 | 0.5–2, 20–30, 0.5 | 0.5–2 | 20–30 | 0.5 |
| 7 | 0.5–2, 50, 0.5 | 0.5–2 | >50 | 0.5 |
| 8 | 50, 8–15, 0.5 | 50 | 8–15 | 0.5 |
| CNT Type | 10–30, 20–30 | 0.5–2, 8 | 0.5–2, 20–30 | 0.5–2, 50 | 50, 8–15 |
|---|---|---|---|---|---|
| Aspect ratio | 1600 | 312 | 100 | 50 | 8695 |
| F (N) | −2.6204 × 10−5 | −9.2645 × 10−7 | −1.6378 × 10−6 | −2.3161 × 10−6 | −4.4431 × 10−5 |
| σ (MPa) | −25.0229 | −44.2347 | −25.0229 | −17.6939 | −36.8943 |
| Materials | Tensile Modulus/MPa | Tensile Strength (MPa) | Lc (μm) | |||
|---|---|---|---|---|---|---|
| Experiment | Calculation | Deviation (%) | ||||
| 1 | Neat epoxy | 2666.28 | 74.36 | |||
| 2 | 10–30, 20–30, 0.1 | 2753.72 | 2833.56 | 2.90. | 75.46 | 1500–2916.67 |
| 3 | 10–30, 20–30, 0.5 | 3177.84 | 3378.17 | 6.30 | 78.46 | 1500–2916.67 |
| 4 | 10–30, 20–30, 1 | 2890.66 | 4157.26 | 39.59 | 72.13 | 1500–2916.67 |
| 5 | 0.5–2, <8, 0.5 | 3030.09 | 3162.90 | 4.38 | 72.30 | 487.5–750 |
| 6 | 0.5–2, 20–30, 0.5 | 2931.09 | 2964.60 | 1.15 | 72.07 | 1500–2916.67 |
| 7 | 0.5–2, >50, 0.5 | 2753.90 | 2812.87 | 2.14 | 75.25 | 4550–4950 |
| 8 | 50, 8–15, 0.5 | 2959.17 | 3443.02 | 18.35 | 72.66 | 487.5–1440 |
| Code | Tg (°C) | |
|---|---|---|
| 1 | Neat Epoxy | 126 |
| 2 | 10–30, 20–30, 0.1 | 115 |
| 3 | 10–30, 20–30, 0.5 | 109 |
| 4 | 10–30 20–30, 1 | 122 |
| 5 | 0.5–2, 8, 0.5 | 97 |
| 6 | 0.5–2, 20–30, 0.5 | 114 |
| 7 | 0.5–2, 50, 0.5 | 124 |
| 8 | 50, 8–15, 0.5 | 120 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Song, B.; Qiao, K.; Huang, Y.; Wang, L. Effect of Dimensions and Agglomerations of Carbon Nanotubes on Synchronous Enhancement of Mechanical and Damping Properties of Epoxy Nanocomposites. Nanomaterials 2018, 8, 996. https://doi.org/10.3390/nano8120996
Wang T, Song B, Qiao K, Huang Y, Wang L. Effect of Dimensions and Agglomerations of Carbon Nanotubes on Synchronous Enhancement of Mechanical and Damping Properties of Epoxy Nanocomposites. Nanomaterials. 2018; 8(12):996. https://doi.org/10.3390/nano8120996
Chicago/Turabian StyleWang, Tingting, Bo Song, Kun Qiao, Yudong Huang, and Li Wang. 2018. "Effect of Dimensions and Agglomerations of Carbon Nanotubes on Synchronous Enhancement of Mechanical and Damping Properties of Epoxy Nanocomposites" Nanomaterials 8, no. 12: 996. https://doi.org/10.3390/nano8120996
APA StyleWang, T., Song, B., Qiao, K., Huang, Y., & Wang, L. (2018). Effect of Dimensions and Agglomerations of Carbon Nanotubes on Synchronous Enhancement of Mechanical and Damping Properties of Epoxy Nanocomposites. Nanomaterials, 8(12), 996. https://doi.org/10.3390/nano8120996






