1. Introduction
All polycrystalline materials, including block and powder materials, exhibit preferred orientation of crystallites, to some degree, i.e., texture, due to the mechanical deformation and microstructure evolution during material processing [
1,
2,
3]. It is of great importance to analyze and determine the preferred orientation when the material properties are orientation-dependent. Electrical, magnetic and mechanical properties of crystals with cubic symmetry are independent on the orientation [
4,
5,
6].
There are several techniques available to determine the degree of the preferred orientation of powder materials, including optical microscopy (OM), scanning electron microscopy (SEM) and transmission electron microscopy (TEM). The principle in TEM using to determine the preferred growth degree of powder materials is based on the analysis of TEM images and the corresponding diffraction pattern or phase-contrast images along appropriate crystal axis [
7]. However, both SEM and TEM can only reveal limited portion of the preferred growth of powder materials, and OM can only be used to analyze the structures with characteristic dimensions more than 200 nm. Also, it is easy to introduce artifacts in replicating real 3-D morphology from projected 2-D images from optical/electronic images, especially TEM images. It is very difficult to use the imaging-related techniques to determine the degree of the preferred growth of nanostructures.
X-ray diffraction (XRD) is another effective way to determine the preferred orientation degree in polycrystalline materials. With a tilting holder in the X-ray diffractometer, pole figure/inverse pole figure or the orientation distribution function can be used to characterize the blocking materials, such as metals. Yet, there are limited reports on the XRD use in the analysis of the preferred growth degree of powder materials, such as nanostructured Ni(OH)
2 and Cd(OH)
2 with hexagonal or trigonal symmetry, which have specific preferred growth of [001] [
8,
9]. In this study, we synthesize Ni(OH)
2 nanoplates without the use of any complex anion, and calculate the March parameter (r
n) of the preferred growth with fitting the XRD spectra of the Ni(OH)
2 nanoplates by the whole powder pattern fitting method (WPPF) in the framework of the March-Dollase function [
10,
11]. Afterwards, the degree of the preferred growth degree (η) of the Ni(OH)
2 nanoplates is determined with using Zolotoyabko’s normalized equation (η
X) [
1], the ellipsoidal model (η
E) and direct measurement (η
M) in SEM and TEM images. The preferred growth degree within the ellipsoidal model and direct measurement in SEM and TEM is defined by the ratio of the short axis and long axis in average (η = D
00l/D
hk0). The overall aim in this study is to offer a simpler way to determine the degree in the preferred powder materials.
3. Results and Discussion
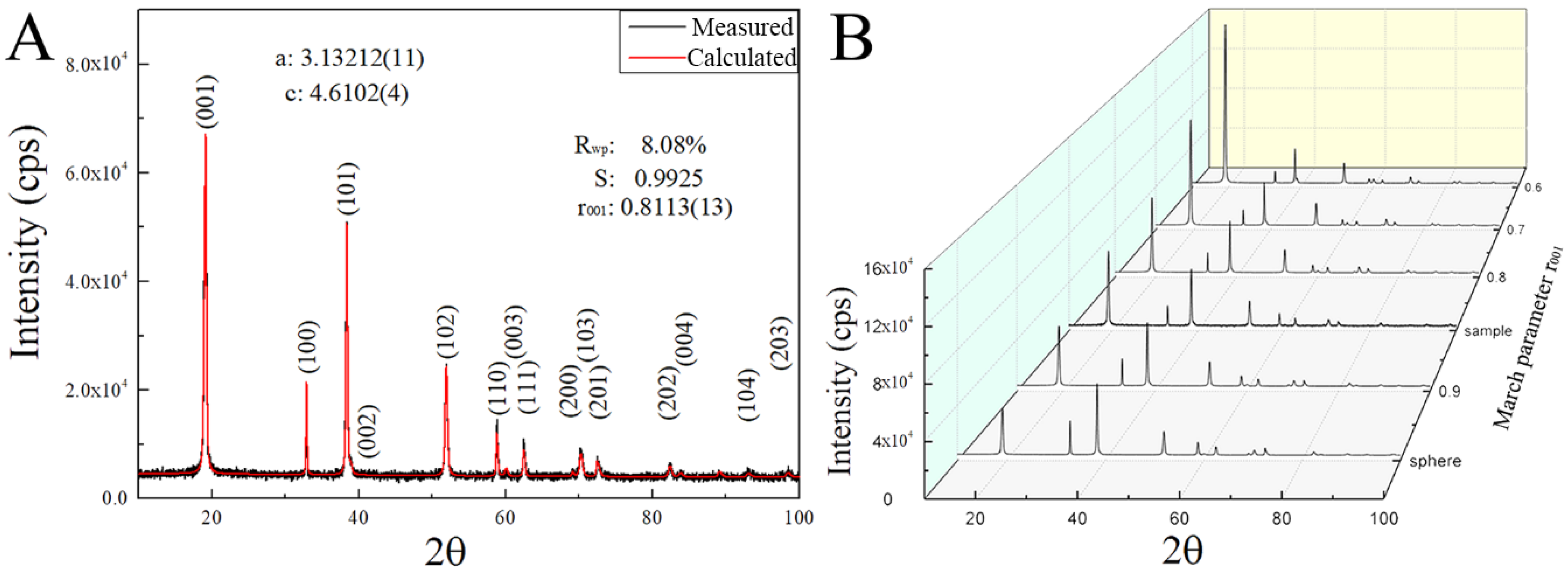
In
Figure 1A, the XRD pattern of the synthesized product is shown, in which all the diffraction peaks can be indexed by the trigonal structure of theophrastite (Ni(OH)
2 mineral) with the space group P-3m1 [
13]. However, comparing with the peaks calculated from the crystallographic information file (ICSD 24015), as shown by the calculated XRD pattern, a slight offset is observed in the diffraction angles (2θ) between measured data and calculated results, which likely is due to the difference in the lattice constants. After performing the refinement calculation of the lattice constants (a, b and c) and the profile function parameters, we obtain lattice constants of the synthesized Ni(OH)
2: a = 3.13212(11) and c = 4.6102(4) Å.
Figure 1A also depicts the calculated XRD pattern of the synthesized Ni(OH)
2 with indexed planes. The modified crystallographic file was used in the further profile and texture refinement to determine the preferred direction degree.
It is known that diffraction peak experiences an angle broadening in crystalline materials with grain size less than 100 nm or under lattice strain [
14]. The diffraction peak broadening for the synthesized Ni(OH)
2 is likely due to the submicron crystallite sizes. From
Figure 1A, we note that the FWHM (full width at half maximum) of the (001) diffraction peak of Ni(OH)
2 is much wider than those of (100) and (110), suggesting that the crystallite size along the [001] direction is much smaller than those along the [100] and [110] directions and the crystallites of Ni(OH)
2 are ellipsoidal instead of spherical shape.
To separate the instrumental broadening from the peak broadening of Ni(OH)
2, we used a silicon standard specimen for the instrumental broadening estimation during the comprehensive analysis of the synthesized Ni(OH)
2 by SmartLab Studio II.
Table 1 lists the corrected FWHM values of the synthesized Ni(OH)
2. The FWHM of the peaks (001), (002), (003) and (004) are 0.395, 0.54, 0.43 and 0.33°, respectively, which are much larger than those of the other peaks; the FWHM of the peaks (100), (110) and (200) are 0.083, 0.143 and 0.09°, respectively. The analysis of the widest peak (00l) and the narrowest peak (hk0) parameters suggests that the synthesized Ni(OH)
2 crystallites are two-dimensional in shape, and the diameter of synthesized Ni(OH)
2 crystallites along [hk0], D
hk0, is much larger than that along the [00l] direction, D
00l. Thus, the synthesized Ni(OH)
2 is present in the two-dimension nanoplate shapes.
In the standard diffraction spectra calculated with spherical crystallites, the integrated intensity of (101) should be larger than that of (001), as shown in
Figure 1B (sphere). According to the measured diffraction data, there exists the preferred growth of Ni(OH)
2 crystallites responsible for the abnormal integrated intensity ratio between (001) and (101). Using the March-Dollase function in the smartLab Studio II, we performed the profile and texture refinement to determine the degree of the preferred direction [001], i.e., the smallest dimension of the two-dimensional Ni(OH)
2 crystallites. The calculation gives the March parameter of r
001 = 0.8113, as shown in the calculated XRD spectrum of
Figure 1A with R
wp = 8.08% and S = 0.9925.
Figure 1B depicts the variation of the simulated diffraction spectra with the March parameter r
00l. Increasing the March parameter r
00l leads to the increase of the intensity ratio between (001) and (101). This ratio likely represents the preferred growth degree of the synthesized Ni(OH)
2. The standard theophrastite (JCPDS. No.14-0117) given by ICDD also shows preferred growth because the ratio of the diffraction intensity of (001) and (101) is 1. Yet, the March parameter r
00l cannot effectively represent the preferred growth degree of the 2-D Ni(OH)
2 crystallites.
Zolotoyabko established a relationship between the degree of preferred growth and the March parameter r
n extracted from diffraction measurements using the nominalized March-Dollase function W(α). He proposed that the degree of preferred growth can be expressed by η as
for r
001 = 0.8113, we obtain the degree of the [001] preferred growth deduced in X-ray diffraction, η
X, as 12.00%.
Žunić and Dohrup demonstrated that an ellipsoid in reference to crystallographic axes (triclinic case) can be expressed as [
15]
where b
ij (i, j = 1, 2, 3) are the coefficients related to reciprocal axes. The symbols x
c, y
c and z
c stand for the parameters in describing the surface function. Thus, the simulated ellipsoid can be expressed as
here, D
hkl is the surface average diameter of the ellipsoidal crystallites (D
00l and D
hk0) obtained from the normalized expressions of anisotropic line broadening, and d
hkl is the interplanar spacing. The meanings of the letters: h, k and l are consistent with the subscript in D
hkl and d
hkl.
Table 2 lists the coefficients of the refined ellipsoidal crystallites of the synthesized Ni(OH)
2. Using the fitting coefficients for the synthesized Ni(OH)
2, we obtain the main diameters of D
00l and D
hk0 as 31.40 and 185.95 nm, respectively. The synthesized Ni(OH)
2 indeed is present in the shape of nanoplates with the [001] preferred growth and the degree (η
E) of the [001] preferred growth is 16.89%.
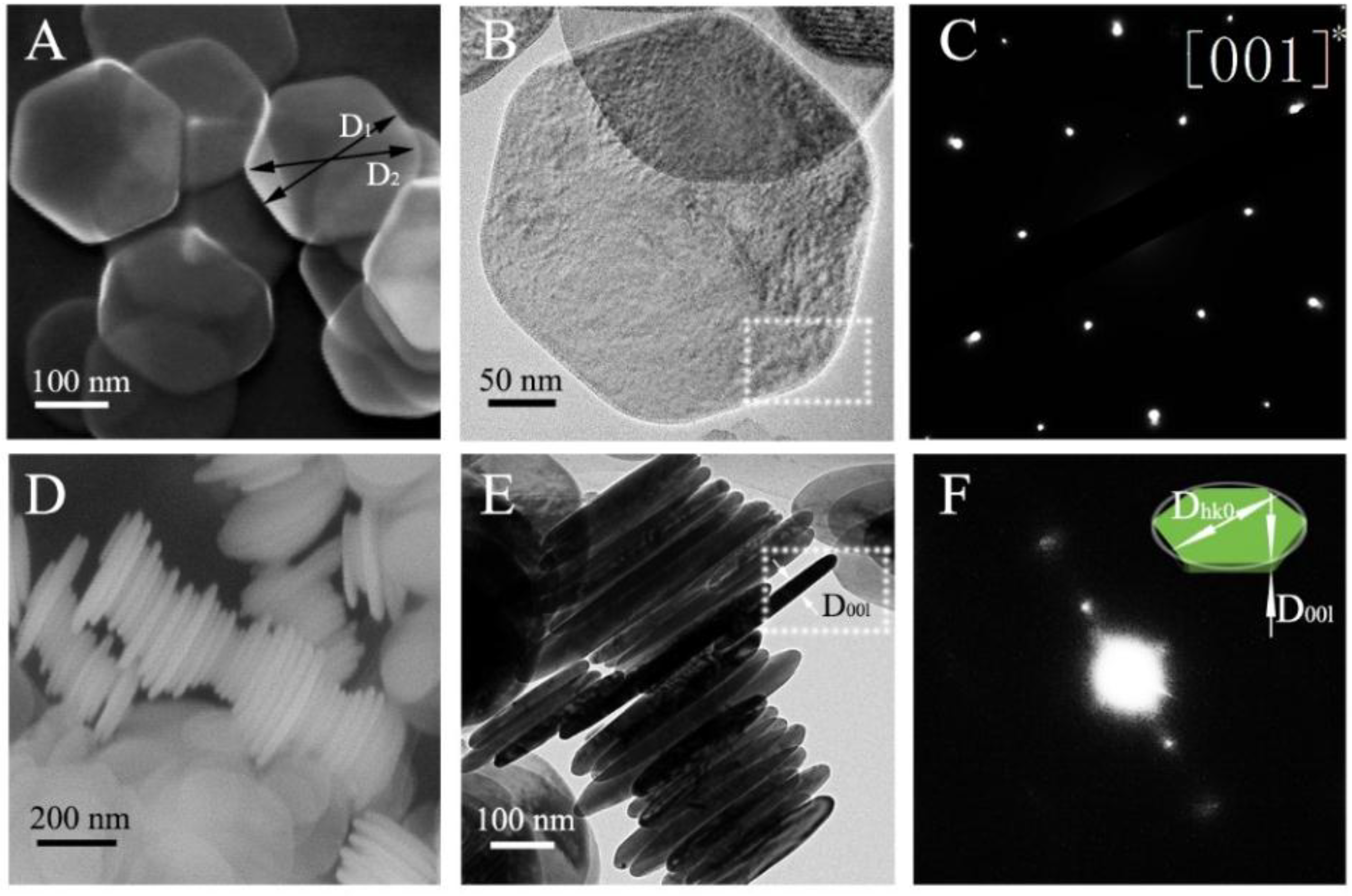
Figure 2A,B,D,E shows the SEM and TEM images of the synthesized Ni(OH)
2, confirming the shape of nanoplates determined by the analysis of the XRD pattern via the whole powder pattern.
Figure 2C depicts the selected area electron diffraction (SAED) pattern of the Ni(OH)
2 nanoplates. If the diameter of a grain in the preferred direction is much longer or shorter than that of its normal directions, it can be rendered as the preferred growth. Thus, the Ni(OH)
2 nanoplates exhibit six-fold symmetry about the [001] direction in accordance with the preferred growth obtained by X-ray diffraction. The synthesized Ni(OH)
2 powder contains two-dimension nanoplates with the normal of the surface of the nanoplates being (001) and D
001 being much smaller than D
hk0. To confirm the trigonal symmetry, in
Figure 2C, the SAED pattern is shown for a single crystal Ni(OH)
2 nanoplate. Thus, the degree of the preferred growth of Ni(OH)
2 grains characterized by the X-ray diffraction could be revealed by the Ni(OH)
2 nanoplates observation by SEM and TEM. It needs to point out that the phase-contrast images may not reveal the structure of the Ni(OH)
2 nanoplates due to possible damage induced by electron beam with an energy of 200 KeV.
Figure 2D,E shows the SEM and TEM images of the side surfaces of the synthesized Ni(OH)
2 nanoplates. The SAED pattern of the square area in
Figure 2E is shown in
Figure 2F. The one-way diffraction spots revel the spacing of [001] for the Ni(OH)
2 nanoplates in consistence with the plane (001) normal of the surface of the nanoplates. Note that the crystal orientation cannot be indexed by the one-way diffraction pattern.
With using an ellipsoid model, Žunić and Dohrup proved that the average ellipsoid size follows an equivalent ellipsoidal function in X-ray diffraction [
15]. As follows from Equation 1, the orientation distribution depends only on March parameter (r) and angle (θ), with no crystallite size being involved. However, the degree of the preferred Ni(OH)
2 nanoplates could be determined from measuring the edge length of the preferred growth and its normal diameter. Thus, the preferred direction and normal direction diameters are measured to confirm the results in X-ray diffraction. In this paper, the degree of averaged crystallite shape in [001] preferred Ni(OH)
2 is simply defined as the ratio of D
00l and D
hk0 labelled in
Figure 2F. From
Figure 2D,E, we note that there are some Ni(OH)
2 nanoplates tilted or truncated, and expect to obtain a distribution of the diameters of D
hk0 and D
00l. Statistical analysis of the SEM and TEM images of the side surfaces of 288 Ni(OH)
2 nanoplates was performed in Image J to calculate the diameters of D
hk0 and D
00l. We obtain D
00l of 24.34 ± 3.54 nm.
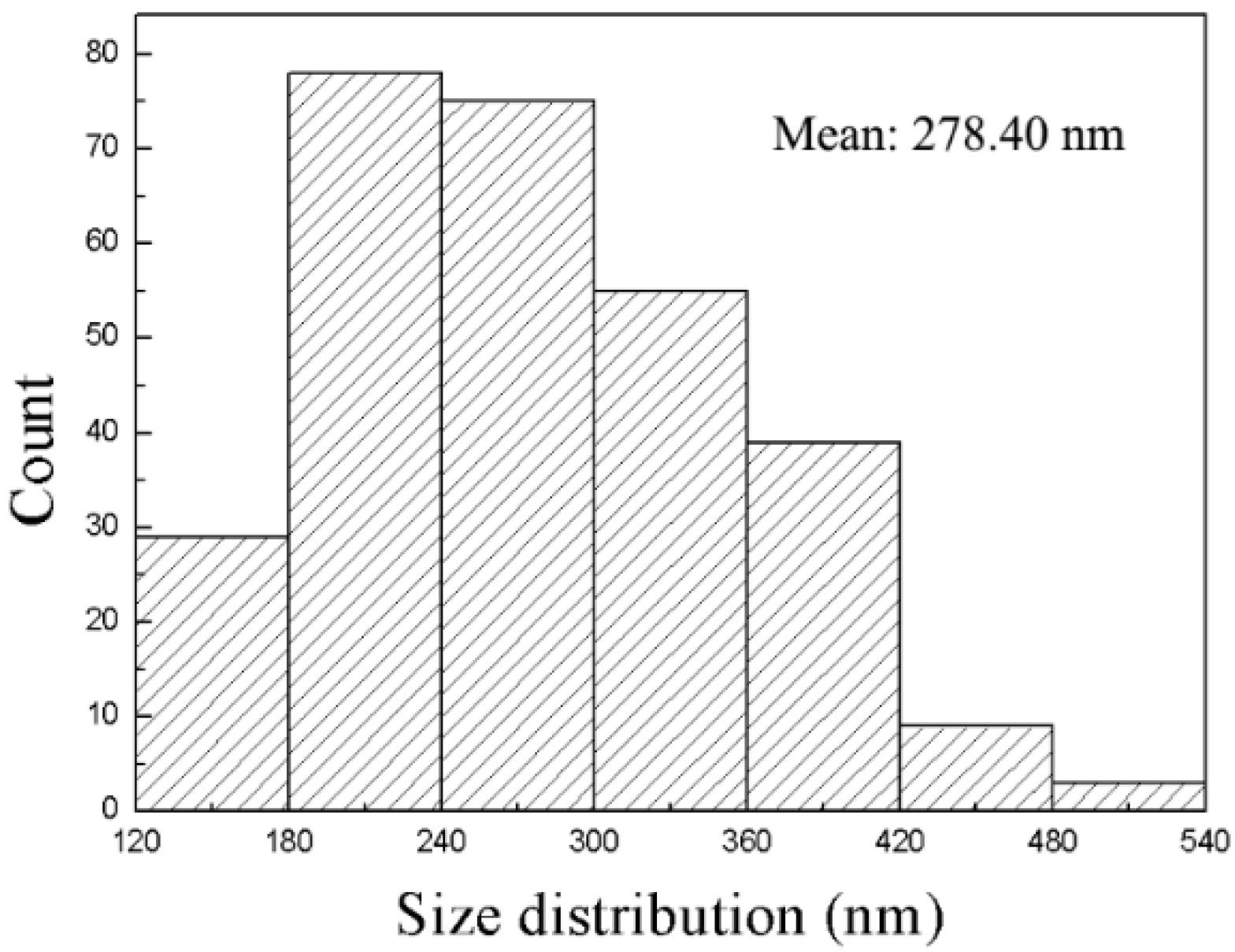
Figure 3 shows the distribution of D
hk0 of the Ni(OH)
2 nanoplates over 288 nanoplates. The D
hk0 is in the range of 129.31–539.68 nm, and the averaged D
hk0 is 278.4 nm. Using the D
hk0 and D
00l, we obtain the degree of [001] preferred growth as 8.74%. The λ-like distribution of the D
hk0 of the Ni(OH)
2 nanoplates, as shown in
Figure 3, reveals the difficulty in the counting of Ni(OH)
2 nanoplates of small diameters, resulting in smaller η
M than η
X. We conclude that the degree of the [001] preferred growth of the Ni(OH)
2 nanoplates, η
X, calculated by the WPPF reflects the degree of the [001] preferred growth of the Ni(OH)
2 nanoplates, η
M.
Compared the values of 278.40 and 24.34 nm of Dhk0 and D00l measured by SEM and TEM with those of 185.95 and 31.40 nm calculated from the ellipsoidal model, we note that there are significant differences between the corresponding values. The shape function of crystallites is not suitable for the description of the shape of nanoplates, and the calculated values cannot be used to represent diameters of Dhk0 and D00l of the Ni(OH)2 nanoplates.
For the situation when the shape parameters of crystallites cannot be accounted for the actual sizes, an average spherical shape can be assumed. Using the Halder-Wagner’s method, we can calculate D
hk0 from the slope of the line plotting of
vs.
for the FWHM of (100), (110)and (200) and D
00l from the FWHM of (001), (002), (003) and (004) [
16]. As shown in
Figure S1 the calculated diameters of D
00l and D
hk0 are 22.2 ± 1.3 and 93.7 ± 14.1 nm, respectively. The edge length in [001] of the Ni(OH)
2 is in good relation to the results 24.34 nm determined by SEM and TEM images. The diameter of the crystallites below 100 nm will result the widening in the diffraction peaks, which may be accounted for the inappropriate edge length in [hk0] [
14].