Impact of Nano-Scale Distribution of Atoms on Electronic and Magnetic Properties of Phases in Fe-Al Nanocomposites: An Ab Initio Study
Abstract
1. Introduction
2. Methods
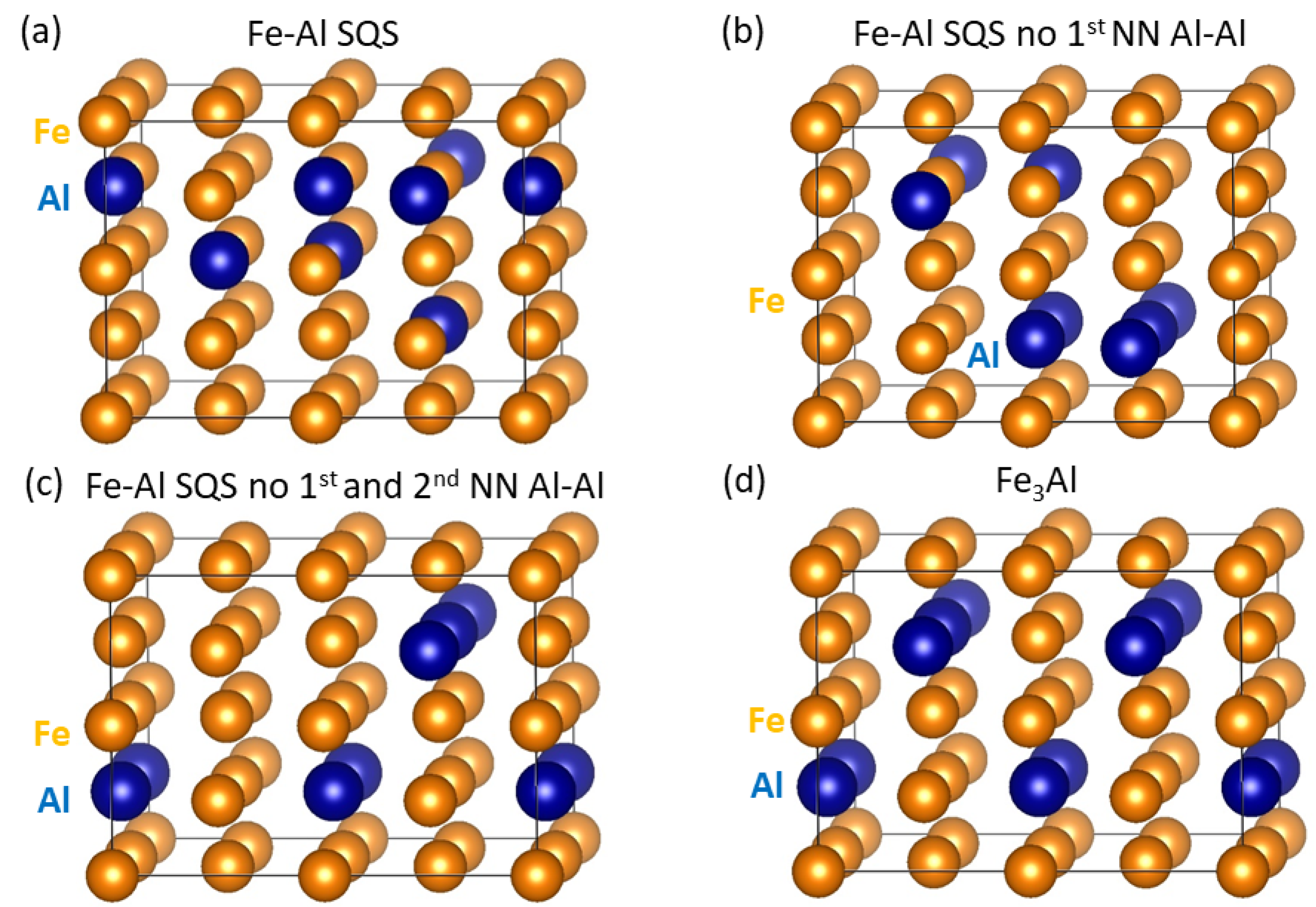
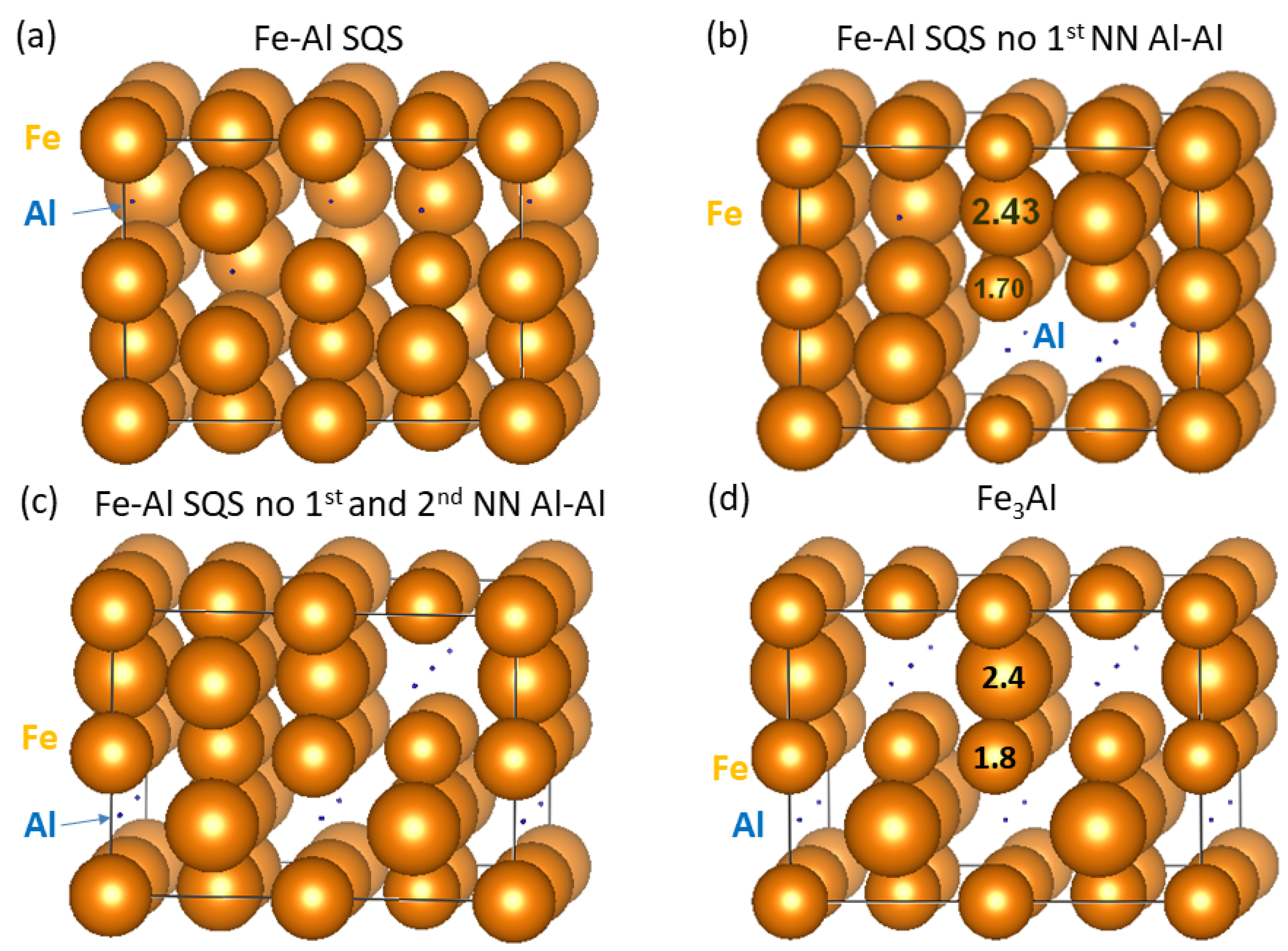
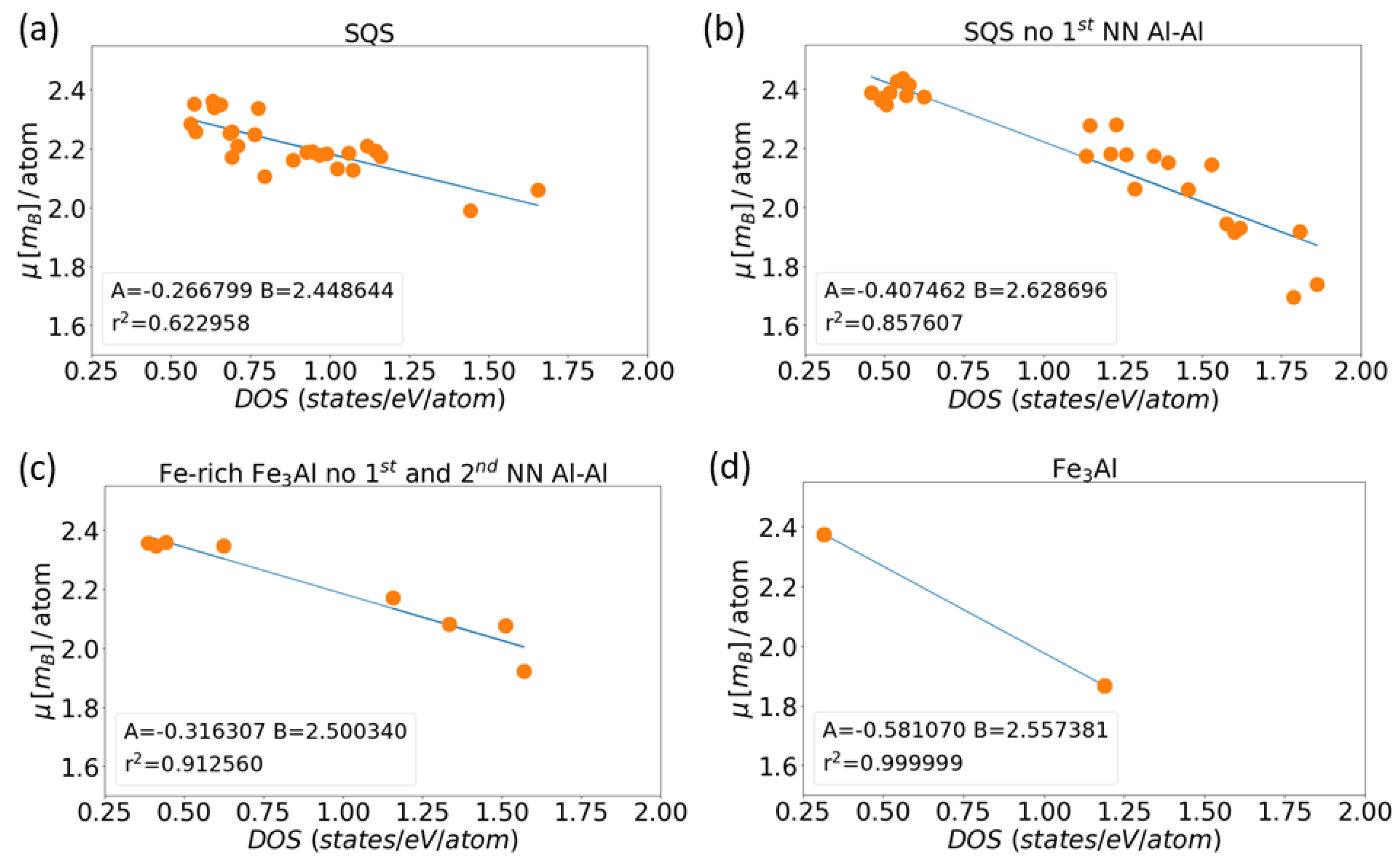
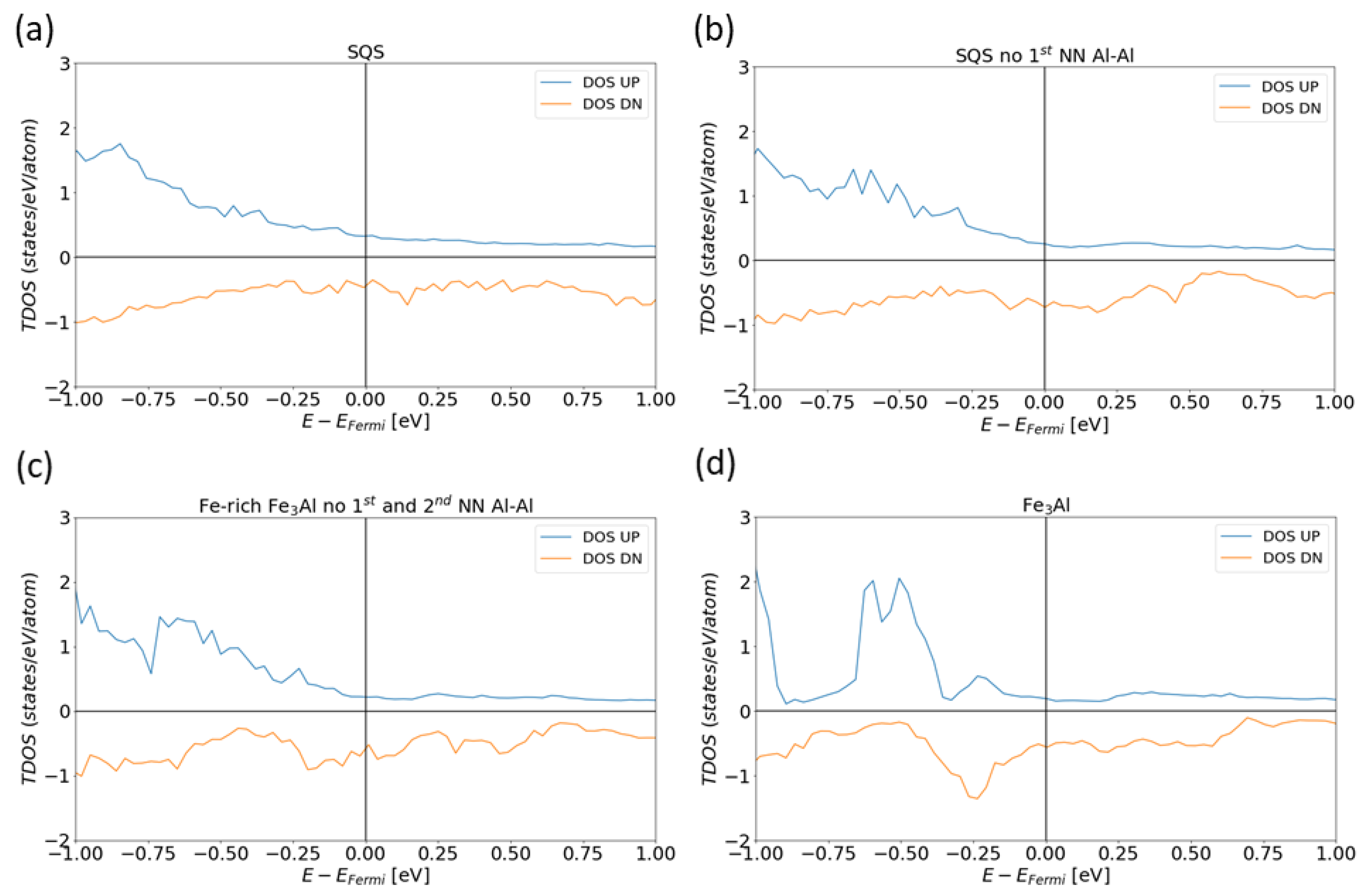
3. Results for Individual Phases
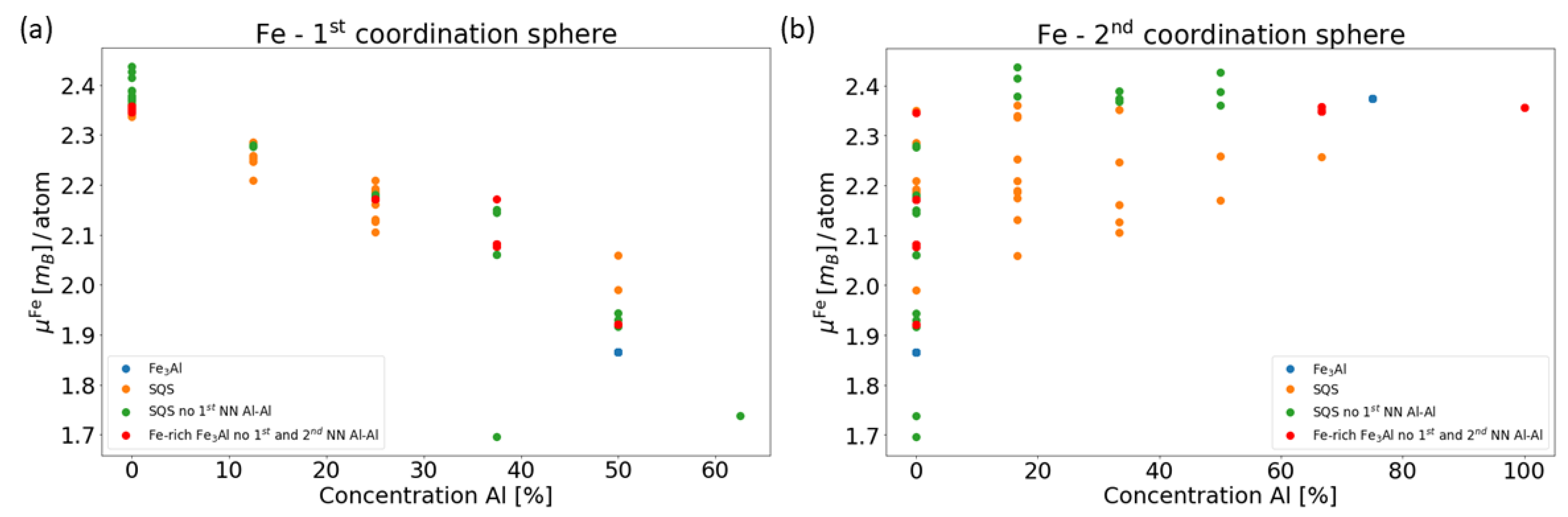
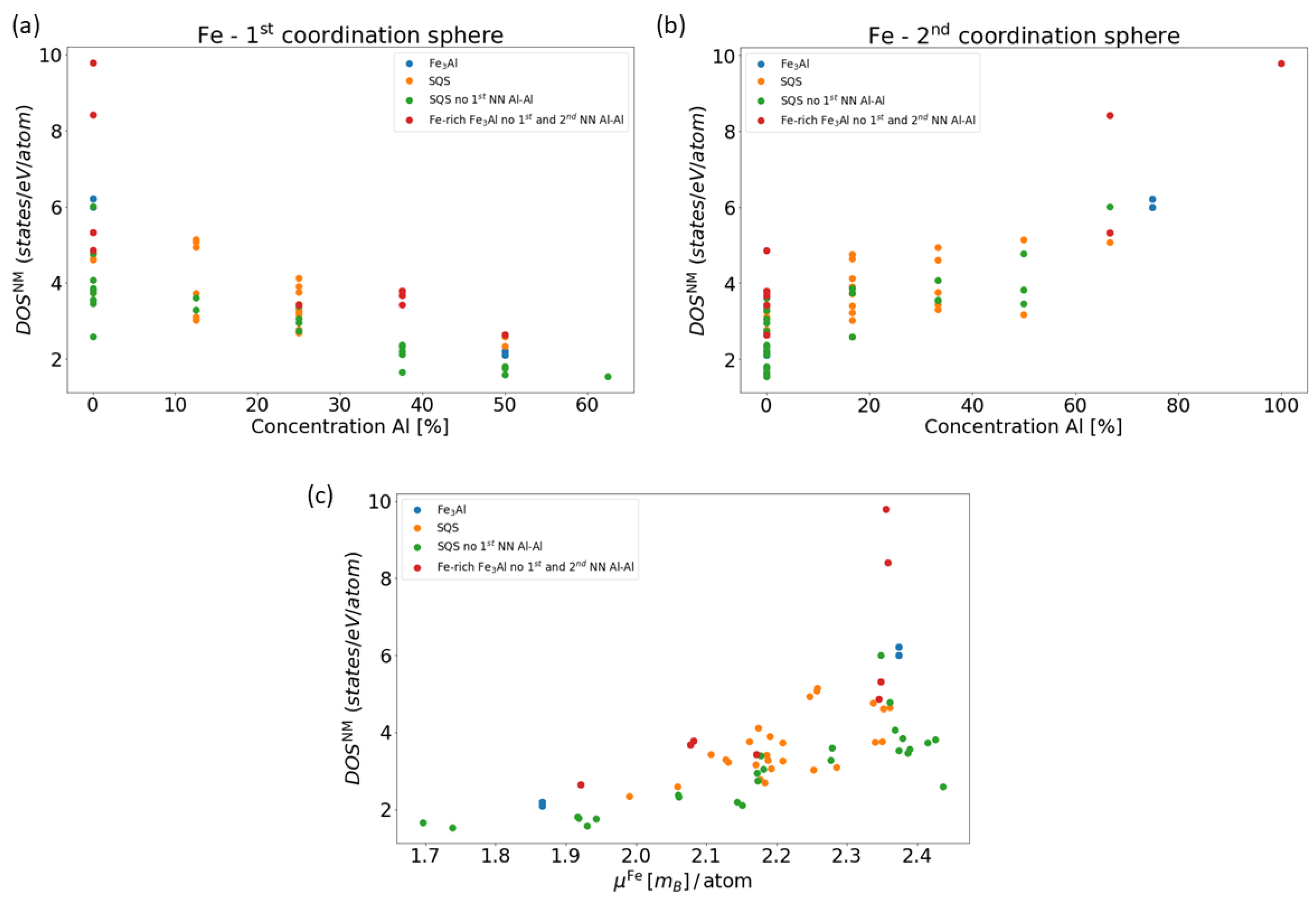
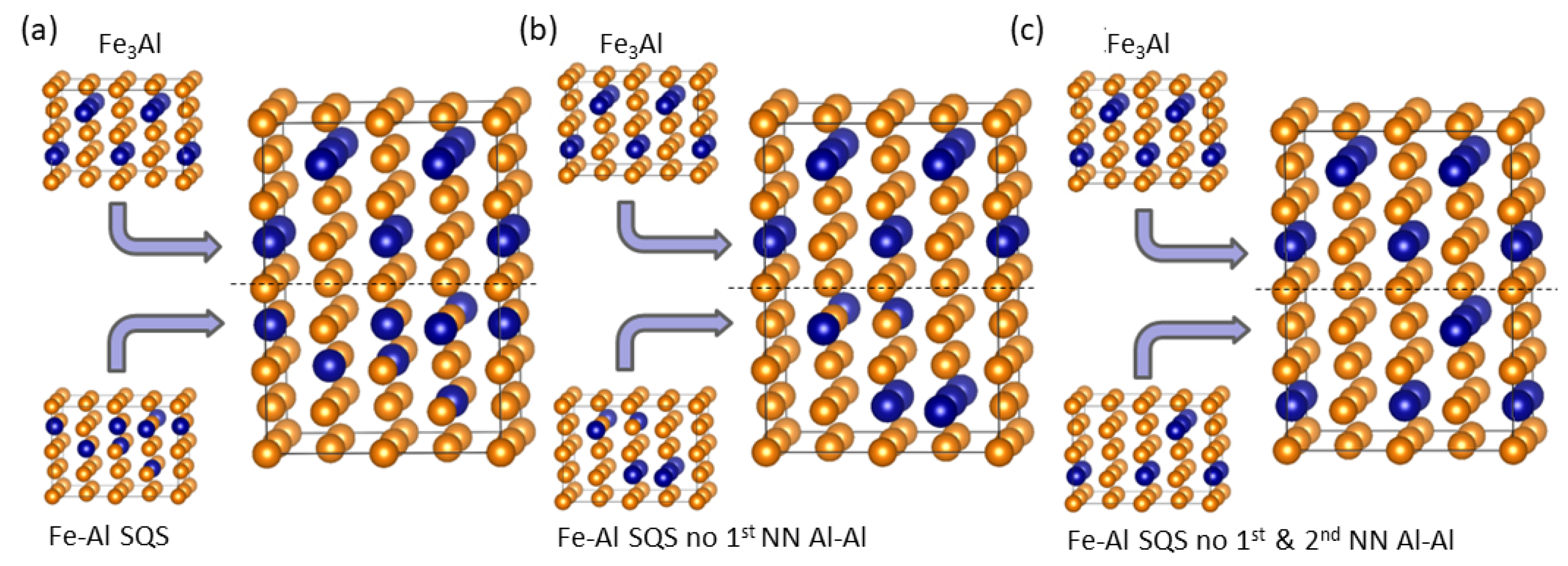
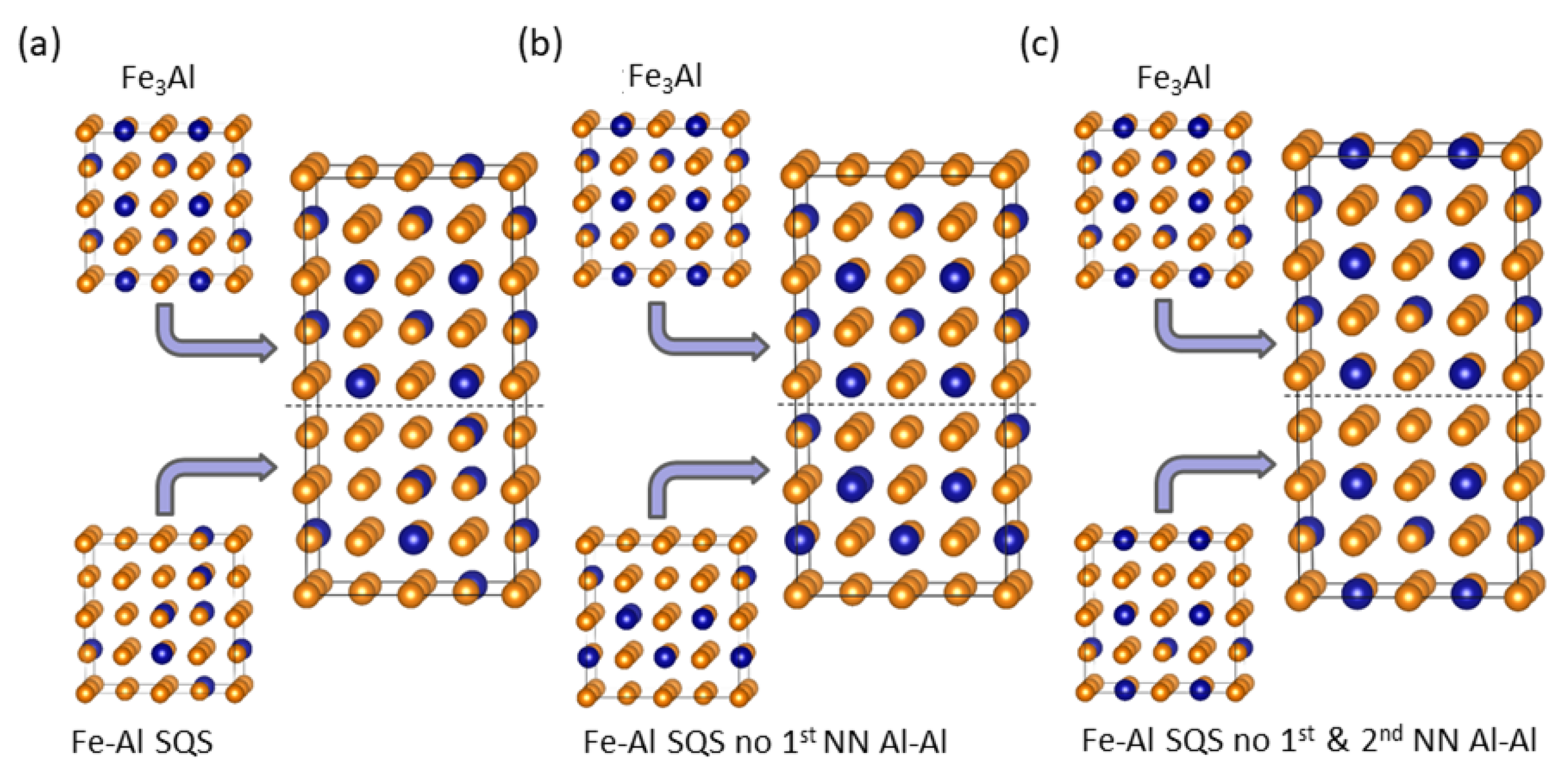
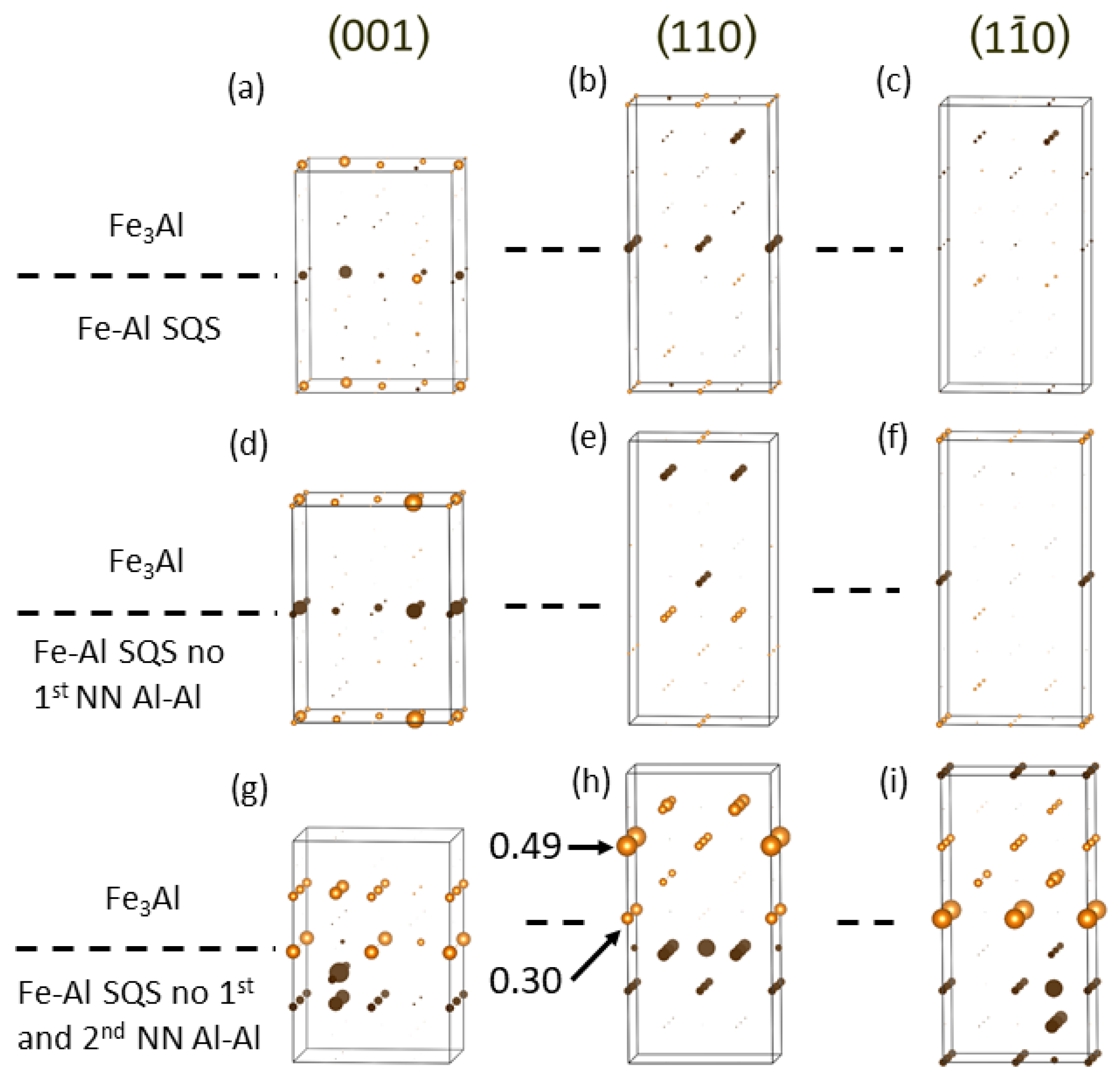
4. Results for Nanocomposites
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Fe-Al SQS | Fe-Al SQS no 1NN | Fe-Al SQS no 1&2NN | FeAl | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | /2 | 1 | 1 | /2 | 1 | 1 | /2 | 1 | 1 | /2 |
| 0.75 | 0.75 | 0.50 | 0.50 | 0.75 | 0.25 | 0.25 | 0.00 | 0.75 | 0.25 | 0.00 | 0.75 |
| 0.25 | 0.00 | 0.75 | 0.75 | 0.00 | 0.75 | 0.25 | 0.50 | 0.75 | 0.75 | 0.00 | 0.75 |
| 0.50 | 0.75 | 0.75 | 0.25 | 0.00 | 0.25 | 0.00 | 0.25 | 0.25 | 0.25 | 0.50 | 0.75 |
| 0.00 | 0.75 | 0.75 | 0.25 | 0.50 | 0.25 | 0.00 | 0.75 | 0.25 | 0.75 | 0.50 | 0.75 |
| 0.25 | 0.50 | 0.25 | 0.50 | 0.25 | 0.25 | 0.50 | 0.25 | 0.25 | 0.00 | 0.25 | 0.25 |
| 0.50 | 0.50 | 0.50 | 0.50 | 0.25 | 0.75 | 0.50 | 0.75 | 0.25 | 0.00 | 0.75 | 0.25 |
| 0.50 | 0.25 | 0.25 | 0.75 | 0.50 | 0.75 | 0.75 | 0.50 | 0.75 | 0.50 | 0.25 | 0.25 |
| 0.75 | 0.50 | 0.25 | 0.00 | 0.75 | 0.75 | 0.75 | 0.00 | 0.75 | 0.50 | 0.75 | 0.25 |
| 0.00 | 0.25 | 0.75 | 0.50 | 0.75 | 0.75 | 0.00 | 0.25 | 0.75 | 0.00 | 0.25 | 0.75 |
| 0.00 | 0.75 | 0.25 | 0.00 | 0.75 | 0.25 | 0.00 | 0.75 | 0.75 | 0.00 | 0.75 | 0.75 |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.25 | 0.25 | 0.50 | 0.25 | 0.75 | 0.50 | 0.25 | 0.75 |
| 0.00 | 0.25 | 0.25 | 0.75 | 0.00 | 0.25 | 0.50 | 0.75 | 0.75 | 0.50 | 0.75 | 0.75 |
| 0.25 | 0.00 | 0.25 | 0.25 | 0.50 | 0.75 | 0.25 | 0.00 | 0.25 | 0.25 | 0.00 | 0.25 |
| 0.50 | 0.75 | 0.25 | 0.75 | 0.50 | 0.25 | 0.75 | 0.00 | 0.25 | 0.75 | 0.00 | 0.25 |
| 0.75 | 0.75 | 0.00 | 0.25 | 0.00 | 0.75 | 0.25 | 0.50 | 0.25 | 0.25 | 0.50 | 0.25 |
| 0.25 | 0.50 | 0.75 | 0.00 | 0.25 | 0.75 | 0.75 | 0.50 | 0.25 | 0.75 | 0.50 | 0.25 |
| 0.75 | 0.50 | 0.75 | 0.75 | 0.75 | 0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0.00 | 0.50 | 0.00 | 0.50 | 0.50 | 0.50 | 0.50 | 0.00 | 0.00 | 0.50 | 0.00 | 0.00 |
| 0.50 | 0.25 | 0.75 | 0.00 | 0.00 | 0.00 | 0.00 | 0.50 | 0.00 | 0.00 | 0.50 | 0.00 |
| 0.75 | 0.00 | 0.25 | 0.75 | 0.75 | 0.00 | 0.50 | 0.50 | 0.00 | 0.50 | 0.50 | 0.00 |
| 0.25 | 0.25 | 0.50 | 0.00 | 0.50 | 0.00 | 0.00 | 0.00 | 0.50 | 0.00 | 0.00 | 0.50 |
| 0.50 | 0.00 | 0.50 | 0.25 | 0.25 | 0.50 | 0.50 | 0.00 | 0.50 | 0.50 | 0.00 | 0.50 |
| 0.00 | 0.00 | 0.50 | 0.50 | 0.00 | 0.50 | 0.00 | 0.50 | 0.50 | 0.00 | 0.50 | 0.50 |
| 0.50 | 0.50 | 0.00 | 0.00 | 0.00 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 |
| 0.25 | 0.25 | 0.00 | 0.50 | 0.50 | 0.00 | 0.25 | 0.25 | 0.00 | 0.25 | 0.25 | 0.00 |
| 0.75 | 0.25 | 0.00 | 0.25 | 0.25 | 0.00 | 0.75 | 0.25 | 0.00 | 0.75 | 0.25 | 0.00 |
| 0.25 | 0.75 | 0.00 | 0.75 | 0.25 | 0.00 | 0.25 | 0.75 | 0.00 | 0.25 | 0.75 | 0.00 |
| 0.75 | 0.00 | 0.75 | 0.25 | 0.75 | 0.00 | 0.75 | 0.75 | 0.00 | 0.75 | 0.75 | 0.00 |
| 0.50 | 0.00 | 0.00 | 0.50 | 0.00 | 0.00 | 0.25 | 0.25 | 0.50 | 0.25 | 0.25 | 0.50 |
| 0.75 | 0.25 | 0.50 | 0.75 | 0.25 | 0.50 | 0.75 | 0.25 | 0.50 | 0.75 | 0.25 | 0.50 |
| 0.25 | 0.75 | 0.50 | 0.25 | 0.75 | 0.50 | 0.25 | 0.75 | 0.50 | 0.25 | 0.75 | 0.50 |
| 0.00 | 0.50 | 0.50 | 0.00 | 0.50 | 0.50 | 0.75 | 0.75 | 0.50 | 0.75 | 0.75 | 0.50 |
References
- Sauthoff, G. Intermetallics; VCH Verlagsgesellschaft: Weinheim, Germany, 1995. [Google Scholar]
- Liu, C.T.; Stringer, J.; Mundy, J.N.; Horton, L.L.; Angelini, P. Ordered intermetallic alloys: An assessment. Intermetallics 1997, 5, 579–596. [Google Scholar] [CrossRef]
- Stoloff, N.S. Iron aluminides: Present status and future prospects. Mater. Sci. Eng. A 1998, 258, 1–14. [Google Scholar] [CrossRef]
- Liu, C.T.; Lee, E.H.; McKamey, C.G. An environmental-effect as the major cause for room-temperature embrittlement in FeAl. Scr. Metall. 1989, 23, 875–880. [Google Scholar] [CrossRef]
- Lynch, R.J.; Heldt, L.A.; Milligan, W.W. Effects of alloy composition on environmental embrittlement of B2 ordered iron aluminides. Scr. Metall. 1991, 25, 2147–2151. [Google Scholar] [CrossRef]
- Liu, C.T.; McKamey, C.G.; Lee, E.H. Environmental-effects on room-temperature ductility and fracture in Fe3Al. Scr. Metall. 1990, 24, 385–389. [Google Scholar] [CrossRef]
- Lynch, R.J.; Gee, K.A.; Heldt, L.A. Environmental embrittlement of single-crystal and thermomechanically processed B2-ordered iron aluminides. Scr. Metall. 1994, 30, 945–950. [Google Scholar] [CrossRef]
- Palm, M.; Inden, G.; Thomas, N. The Fe-Al-Ti system. J. Phase Equilib. 1995, 16, 209–222. [Google Scholar] [CrossRef]
- Palm, M.; Lacaze, J. Assessment of the Al-Fe-Ti system. Intermetallics 2006, 14, 1291–1303. [Google Scholar] [CrossRef]
- Palm, M.; Sauthoff, G. Deformation behaviour and oxidation resistance of single-phase and two-phase L21-ordered Fe-Al-Ti alloys. Intermetallics 2004, 12, 1345–1359. [Google Scholar] [CrossRef]
- Sundman, B.; Ohnuma, I.; Dupin, N.; Kattner, U.R.; Fries, S.G. An assessment of the entire Al-Fe system including D0(3) ordering. Acta Mater. 2009, 57, 2896–2908. [Google Scholar] [CrossRef]
- Kattner, U.; Burton, B. Al-Fe (Aluminium-Iron). In Phase Diagrams of Binary Iron Alloys; Okamoto, H., Ed.; ASM International: Geauga County, OH, USA, 1993; pp. 12–28. [Google Scholar]
- Allen, S.; Cahn, J. Mechanisms of phase-transformations within miscibility gap of Fe-rich Fe-Al alloys. Acta Metall. Mater. 1976, 24, 425–437. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Cheng, Y. The Formation and Dynamic Evolution of Antiphase Domain Boundary in FeAl Alloy: Computational Simulation in Atomic Scale. Mater. Res.-Ibero-Am. J. Mater. 2018, 21. [Google Scholar] [CrossRef]
- Balagurov, A.M.; Bobrikov, I.A.; Sumnikov, V.S.; Golovin, I.S. Antiphase domains or dispersed clusters? Neutron diffraction study of coherent atomic ordering in Fe3Al-type alloys. Acta Mater. 2018, 153, 45–52. [Google Scholar] [CrossRef]
- Murakami, Y.; Niitsu, K.; Tanigaki, T.; Kainuma, R.; Park, H.S.; Shindo, D. Magnetization amplified by structural disorder within nanometre-scale interface region. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Oguma, R.; Matsumura, S.; Eguchi, T. Kinetics of B2-and D03 type ordering and formation of domain structures in Fe-Al alloys. J. Phys. Condens. Matter 2008, 20, 275225. [Google Scholar] [CrossRef] [PubMed]
- Watson, R.E.; Weinert, M. Transition-metal aluminide formation: Ti, V, Fe, and Ni aluminides. Phys. Rev. B 1998, 58, 5981–5988. [Google Scholar] [CrossRef]
- Gonzales-Ormeno, P.; Petrilli, H.; Schon, C. Ab-initio calculations of the formation energies of BCC-based superlattices in the Fe-Al system. Calphad 2002, 26, 573. [Google Scholar] [CrossRef]
- Friák, M.; Neugebauer, J. Ab initio study of the anomalous volume-composition dependence in Fe-Al alloys. Intermetallics 2010, 18, 1316–1321. [Google Scholar] [CrossRef]
- Friák, M.; Oweisová, S.; Pavlů, J.; Holec, D.; Šob, M. An Ab Initio Study of Thermodynamic and Mechanical Stability of Heusler-Based Fe2AlCo Polymorphs. Materials 2018, 11, 1543. [Google Scholar] [CrossRef]
- Friák, M.; Holec, D.; Šob, M. Quantum-Mechanical Study of Nanocomposites with Low and Ultra-Low Interface Energies. Nanomaterials 2018, 8, 1057. [Google Scholar] [CrossRef]
- Friák, M.; Slávik, A.; Miháliková, I.; Holec, D.; Všianská, M.; Šob, M.; Palm, M.; Neugebauer, J. Origin of the Low Magnetic Moment in Fe2AlTi: An Ab Initio Study. Materials 2018, 11, 1732. [Google Scholar] [CrossRef]
- Šesták, P.; Friák, M.; Holec, D.; Všianská, M.; Šob, M. Strength and Brittleness of Interfaces in Fe-Al Superalloy Nanocomposites under Multiaxial Loading: An ab initio and Atomistic Study. Nanomaterials 2018, 8, 873. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Duan, S.; Ma, B. First-principles calculation of vibrational entropy for Fe-Al compounds. Phys. Rev. B 1998, 58, 9705–9709. [Google Scholar]
- Kulikov, N.I.; Postnikov, A.V.; Borstel, G.; Braun, J. Onset of magnetism in B2 transition-metal aluminides. Phys. Rev. B 1999, 59, 6824–6833. [Google Scholar] [CrossRef]
- Fähnle, M.; Drautz, R.; Lechermann, F.; Singer, R.; Diaz-Ortiz, A.; Dosch, H. Thermodynamic properties from ab-initio calculations: New theoretical developments, and applications to various materials systems. Phys. Status Solidi B Basic Solid State Phys. 2005, 242, 1159–1173. [Google Scholar] [CrossRef]
- Friák, M.; Deges, J.; Krein, R.; Frommeyer, G.; Neugebauer, J. Combined ab initio and experimental study of structural and elastic properties of Fe3Al-based ternaries. Intermetallics 2010, 18, 1310. [Google Scholar] [CrossRef]
- Kirklin, S.; Saal, J.E.; Hegde, V.I.; Wolverton, C. High-throughput computational search for strengthening precipitates in alloys. Acta Mater. 2016, 102, 125–135. [Google Scholar] [CrossRef]
- Airiskallio, E.; Nurmi, E.; Heinonen, M.H.; Vayrynen, I.J.; Kokko, K.; Ropo, M.; Punkkinen, M.P.J.; Pitkanen, H.; Alatalo, M.; Kollar, J.; et al. High temperature oxidation of Fe-Al and Fe-Cr-Al alloys: The role of Cr as a chemically active element. Corros. Sci. 2010, 52, 3394–3404. [Google Scholar] [CrossRef]
- Medvedeva, N.I.; Park, M.S.; Van Aken, D.C.; Medvedeva, J.E. First-principles study of Mn, Al and C distribution and their effect on stacking fault energies in fcc Fe. J. Alloy. Compd. 2014, 582, 475–482. [Google Scholar] [CrossRef]
- Čížek, J.; Lukáč, F.; Procházka, I.; Kužel, R.; Jirásková, Y.; Janičkovič, D.; Anwand, W.; Brauer, G. Characterization of quenched-in vacancies in Fe-Al alloys. Phys. B 2012, 407, 2659–2664. [Google Scholar] [CrossRef]
- Ipser, H.; Semenova, O.; Krachler, R. Intermetallic phases with D0(3)-structure: A statistical-thermodynamic model. J. Alloy. Compd. 2002, 338, 20–25. [Google Scholar] [CrossRef]
- Lechermann, F.; Welsch, F.; Elsässer, C.; Ederer, C.; Fähnle, M.; Sanchez, J.; Meyer, B. Density-functional study of Fe3Al: LSDA versus GGA. Phys. Rev. B 2002, 65, 132104. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Connetable, D.; Maugis, P. First principle calculations of the kappa-Fe3AlC perovskite and iron-aluminium intermetallics. Intermetallics 2008, 16, 345–352. [Google Scholar] [CrossRef]
- Lechermann, F.; Fähnle, M.; Meyer, B.; Elsässer, C. Electronic correlations, magnetism, and structure of Fe-Al subsystems: An LDA+U study. Phys. Rev. B 2004, 69, 165116. [Google Scholar] [CrossRef]
- Kellou, A.; Grosdidier, T.; Raulot, J.M.; Aourag, H. Atomistic study of magnetism effect on structural stability in Fe3Al and Fe3AlX (X = H, B, C, N, O) alloys. Phys. Status Solidi B Basic Solid State Phys. 2008, 245, 750–755. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Miháliková, I.; Slávik, A.; Friák, M.; Všianská, M.; Koutná, N.; Holec, D.; Šob, M. First-principles study of interface energies in Fe-Al-based superalloy nanocomposites. In Proceedings of the NANOCON 9th International Conference on Nanomaterials—Research & Application, Brno, Czech Republic, 18–20 October 2017; Tanger Ltd.: Ostrava, Czech Republic, 2018; pp. 69–74. [Google Scholar]
- Amara, H.; Fu, C.C.; Soisson, F.; Maugis, P. Aluminum and vacancies in α-iron: Dissolution, diffusion, and clustering. Phys. Rev. B 2010, 81, 174101. [Google Scholar] [CrossRef]
- Zunger, A.; Wei, S.; Ferreira, L.; Bernard, J. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef]
- Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef]
- Lyakhov, A.O.; Oganov, A.R.; Stokes, H.T.; Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013, 184, 1172–1182. [Google Scholar] [CrossRef]
- Oganov, A.R.; Lyakhov, A.O.; Valle, M. How Evolutionary Crystal Structure Prediction Works—And Why. Acc. Chem. Res. 2011, 44, 227–237. [Google Scholar] [CrossRef]
- Bose, S.K.; Kudrnovský, J.; Drchal, V.; Turek, I. Magnetism of mixed quaternary Heusler alloys: (Ni,T)2MnSn(T = Cu,Pd) as a case study. Phys. Rev. B 2010, 82, 174402. [Google Scholar] [CrossRef]
- Mayrhofer, P.H.; Fischer, F.D.; Boehm, H.J.; Mitterer, C.; Schneider, J.M. Energetic balance and kinetics for the decomposition of supersaturated Ti1-xAlxN. Acta Mater. 2007, 55, 1441–1446. [Google Scholar] [CrossRef]
- Wu, L.; Chen, M.; Li, C.; Zhou, J.; Shen, L.; Wang, Y.; Zhong, Z.; Feng, M.; Zhang, Y.; Han, K.; et al. Ferromagnetism and matrix-dependent charge transfer in strained LaMnO3-LaCoO3 superlattices. Mater. Res. Lett. 2018, 6, 501–507. [Google Scholar] [CrossRef]
- Koutná, N.; Holec, D.; Friák, M.; Mayrhofer, P.H.; Šob, M. Stability and elasticity of metastable solid solutions and superlattices in the MoN–TaN system: First-principles calculations. Mater. Des. 2018, 144, 310–322. [Google Scholar] [CrossRef]
- Jiang, M.; Xiao, H.Y.; Peng, S.M.; Yang, G.X.; Liu, Z.J.; Zu, X.T. A comparative study of low energy radiation response of AlAs, GaAs and GaAs/AlAs superlattice and the damage effects on their electronic structures. Sci. Rep. 2018, 8, 2012. [Google Scholar] [CrossRef]
- Wen, Y.N.; Gao, P.F.; Xia, M.G.; Zhang, S.L. Half-metallic ferromagnetism prediction in MoS2-based two-dimensional superlattice from first-principles. Mod. Phys. Lett. B 2018, 32, 1850098. [Google Scholar] [CrossRef]
- Friák, M.; Tytko, D.; Holec, D.; Choi, P.P.; Eisenlohr, P.; Raabe, D.; Neugebauer, J. Synergy of atom-probe structural data and quantum-mechanical calculations in a theory-guided design of extreme-stiffness superlattices containing metastable phases. New J. Phys. 2015, 17, 093004. [Google Scholar] [CrossRef]
- Dai, Q.; Eckern, U.; Schwingenschlog, U. Effects of oxygen vacancies on the electronic structure of the (LaVO3)(6)/SrVO3 superlattice: A computational study. New J. Phys. 2018, 20, 073011. [Google Scholar] [CrossRef]
- Jiang, M.; Xiao, H.; Peng, S.; Qiao, L.; Yang, G.; Liu, Z.; Zu, X. First-Principles Study of Point Defects in GaAs/AlAs Superlattice: The Phase Stability and the Effects on the Band Structure and Carrier Mobility. Nanoscale Res. Lett. 2018, 13, 301. [Google Scholar] [CrossRef]
- Chen, H.; Millis, A.J.; Marianetti, C.A. Engineering Correlation Effects via Artificially Designed Oxide Superlattices. Phys. Rev. Lett. 2013, 111, 116403. [Google Scholar] [CrossRef]
- Mottura, A.; Janotti, A.; Pollock, T.M. A first-principles study of the effect of Ta on the superlattice intrinsic stacking fault energy of L12-Co-3(Al,W). Intermetallics 2012, 28, 138–143. [Google Scholar] [CrossRef]
- Rosengaard, N.; Skriver, H. Ab-initio study of antiphase boundaries and stacking-faults in L12 and D022 compounds. Phys. Rev. B 1994, 50, 4848–4858. [Google Scholar] [CrossRef]
- Torres-Pardo, A.; Gloter, A.; Zubko, P.; Jecklin, N.; Lichtensteiger, C.; Colliex, C.; Triscone, J.M.; Stephan, O. Spectroscopic mapping of local structural distortions in ferroelectric PbTiO3/SrTiO3 superlattices at the unit-cell scale. Phys. Rev. B 2011, 84, 220102. [Google Scholar] [CrossRef]
- Chawla, V.; Holec, D.; Mayrhofer, P.H. Stabilization criteria for cubic AlN in TiN/AlN and CrN/AlN bi-layer systems. J. Phys. D Appl. Phys. 2013, 46, 045305. [Google Scholar] [CrossRef]
- Cooper, V.R.; Rabe, K.M. Enhancing piezoelectricity through polarization-strain coupling in ferroelectric superlattices. Phys. Rev. B 2009, 79, 180101. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, Q.; Bernholc, J. Si diffusion in gaas and si-induced interdiffusion in gaas/alas superlattices. Phys. Rev. B 1994, 49, 2985–2988. [Google Scholar] [CrossRef]
- Schmid, U.; Christensen, N.; Cardona, M.; Lukes, F.; Ploog, K. Optical anisotropy in GaAs/AlSs(110) superlattices. Phys. Rev. B 1992, 45, 3546–3551. [Google Scholar] [CrossRef]
- Gibson, Q.D.; Schoop, L.M.; Weber, A.P.; Ji, H.; Nadj-Perge, S.; Drozdov, I.K.; Beidenkopf, H.; Sadowski, J.T.; Fedorov, A.; Yazdani, A.; et al. Termination-dependent topological surface states of the natural superlattice phase Bi4Se3. Phys. Rev. B 2013, 88, 081108. [Google Scholar] [CrossRef]
- Park, C.; Chang, K. Structural and electronic-properties of GaP-AlP (001) superlattices. Phys. Rev. B 1993, 47, 12709–12715. [Google Scholar] [CrossRef]
- Romanyuk, O.; Hannappel, T.; Grosse, F. Atomic and electronic structure of GaP/Si(111), GaP/Si(110), and GaP/Si(113) interfaces and superlattices studied by density functional theory. Phys. Rev. B 2013, 88, 115312. [Google Scholar] [CrossRef]
- Abdulsattar, M.A. SiGe superlattice nanocrystal pure and doped with substitutional phosphorus single atom: Density functional theory study. Superlattices Microstruct. 2011, 50, 377–385. [Google Scholar] [CrossRef]
- Botti, S.; Vast, N.; Reining, L.; Olevano, V.; Andreani, L. Ab initio and semiempirical dielectric response of superlattices. Phys. Rev. B 2004, 70, 045301. [Google Scholar] [CrossRef]
- Rondinelli, J.M.; Spaldin, N.A. Electron-lattice instabilities suppress cuprate-like electronic structures in SrFeO3/OSrTiO3 superlattices. Phys. Rev. B 2010, 81, 085109. [Google Scholar] [CrossRef]
- Giorgetti, M.; della longa, S.; Benfatto, M. EXAFS and XANES simulations of Fe/Co hexacyanoferrate spectra by GNXAS and MXAN. J. Phys. Conf. Ser. 2009, 190, 012145. [Google Scholar] [CrossRef]
- Westre, T.E.; Cicco, A.; Filipponi, A.; Natoli, C.R.; Hedman, B.; Solomon, E.I.; Hodgson, K.O. Using GNXAS, a multiple-scattering EXAFS analysis, for determination of the FeNO angle in FeNO7 complexes. Phys. B Condens. Matter 1995, 208–209, 137–139. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miháliková, I.; Friák, M.; Jirásková, Y.; Holec, D.; Koutná, N.; Šob, M. Impact of Nano-Scale Distribution of Atoms on Electronic and Magnetic Properties of Phases in Fe-Al Nanocomposites: An Ab Initio Study. Nanomaterials 2018, 8, 1059. https://doi.org/10.3390/nano8121059
Miháliková I, Friák M, Jirásková Y, Holec D, Koutná N, Šob M. Impact of Nano-Scale Distribution of Atoms on Electronic and Magnetic Properties of Phases in Fe-Al Nanocomposites: An Ab Initio Study. Nanomaterials. 2018; 8(12):1059. https://doi.org/10.3390/nano8121059
Chicago/Turabian StyleMiháliková, Ivana, Martin Friák, Yvonna Jirásková, David Holec, Nikola Koutná, and Mojmír Šob. 2018. "Impact of Nano-Scale Distribution of Atoms on Electronic and Magnetic Properties of Phases in Fe-Al Nanocomposites: An Ab Initio Study" Nanomaterials 8, no. 12: 1059. https://doi.org/10.3390/nano8121059
APA StyleMiháliková, I., Friák, M., Jirásková, Y., Holec, D., Koutná, N., & Šob, M. (2018). Impact of Nano-Scale Distribution of Atoms on Electronic and Magnetic Properties of Phases in Fe-Al Nanocomposites: An Ab Initio Study. Nanomaterials, 8(12), 1059. https://doi.org/10.3390/nano8121059







