Molecular Dynamics Simulation on B3-GaN Thin Films under Nanoindentation
Abstract
1. Introduction
2. Method
2.1. Selection of Potentials
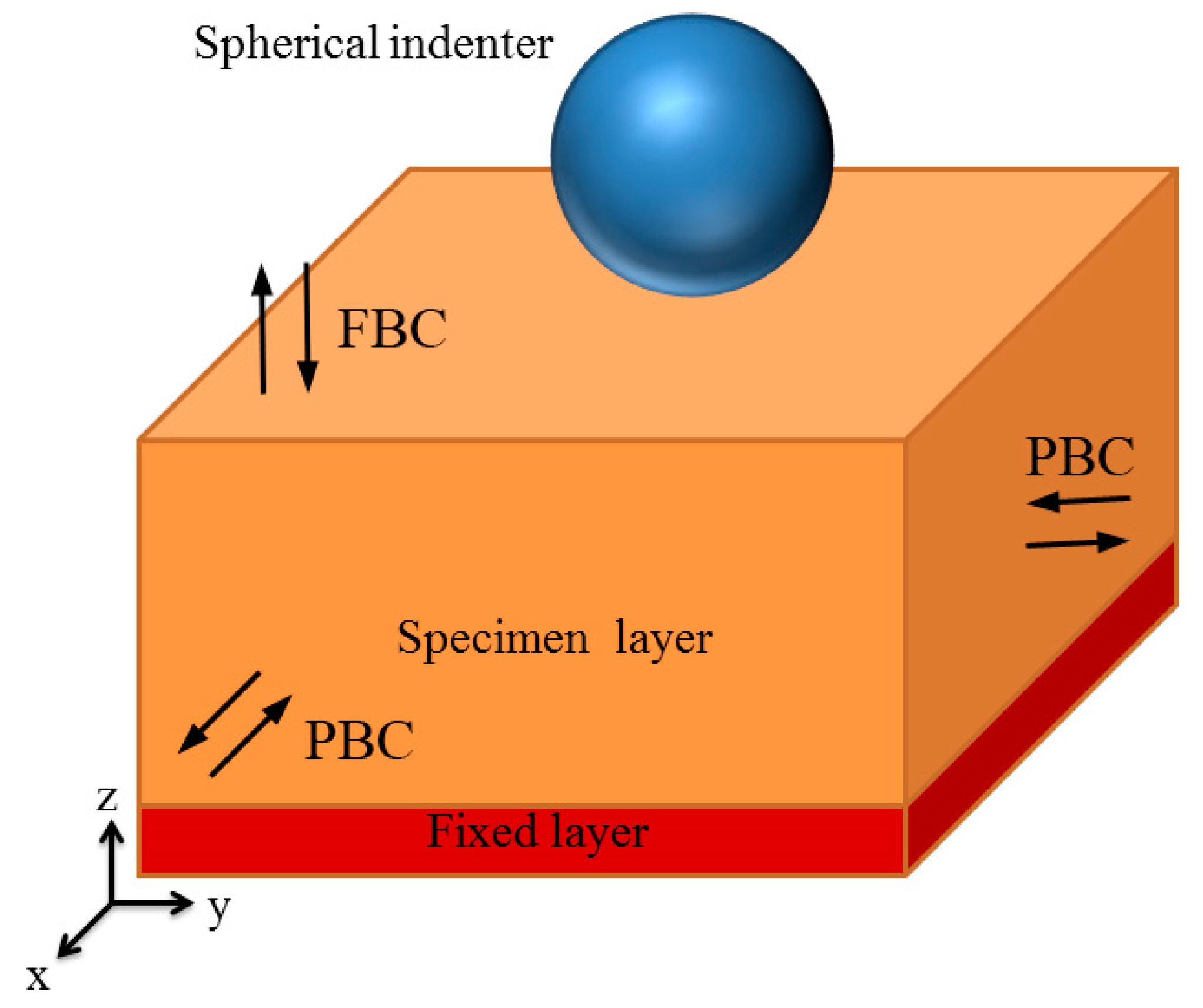
2.2. Simulation Details
2.3. Structure Identification
3. Results and Discussions
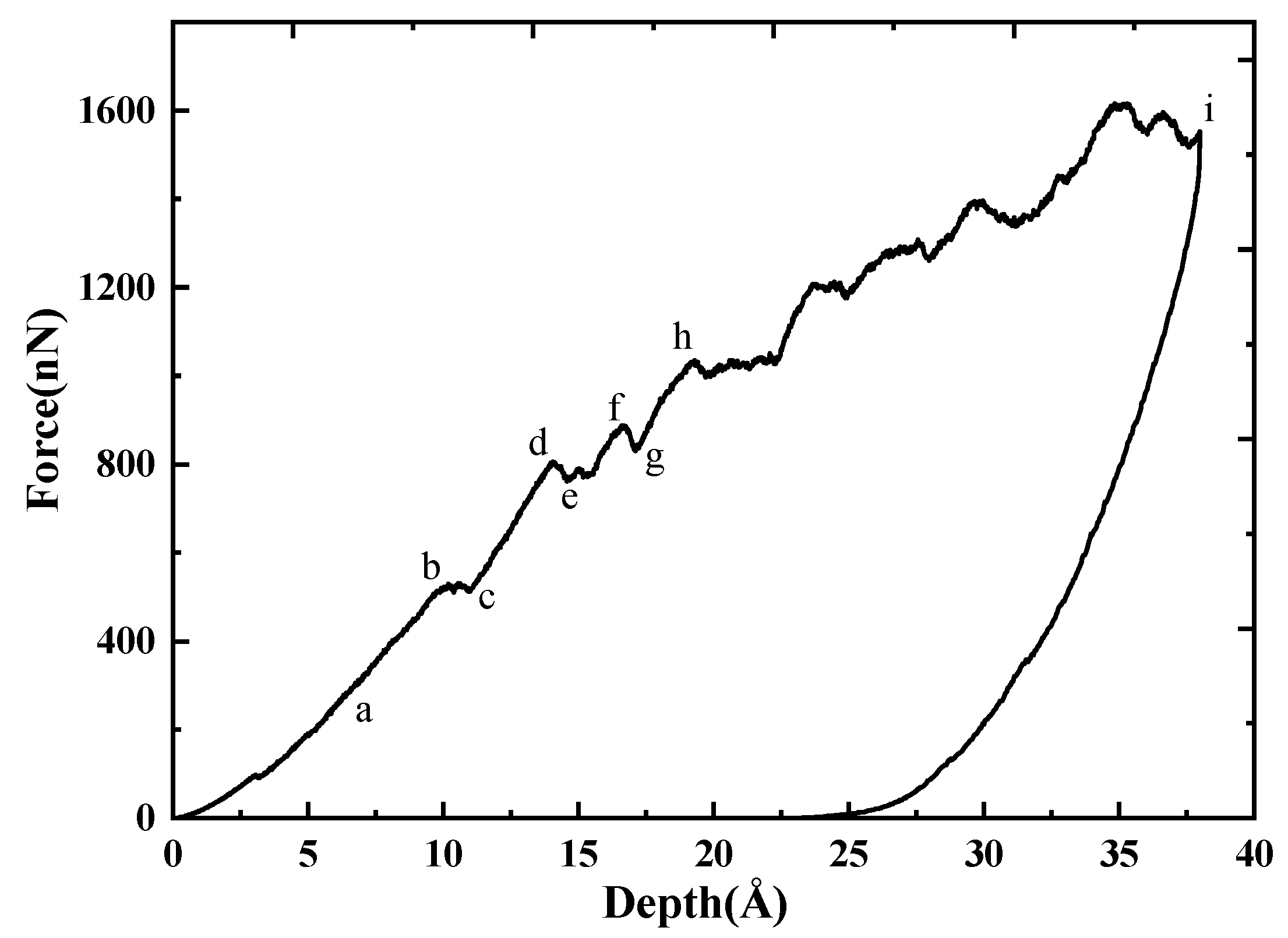
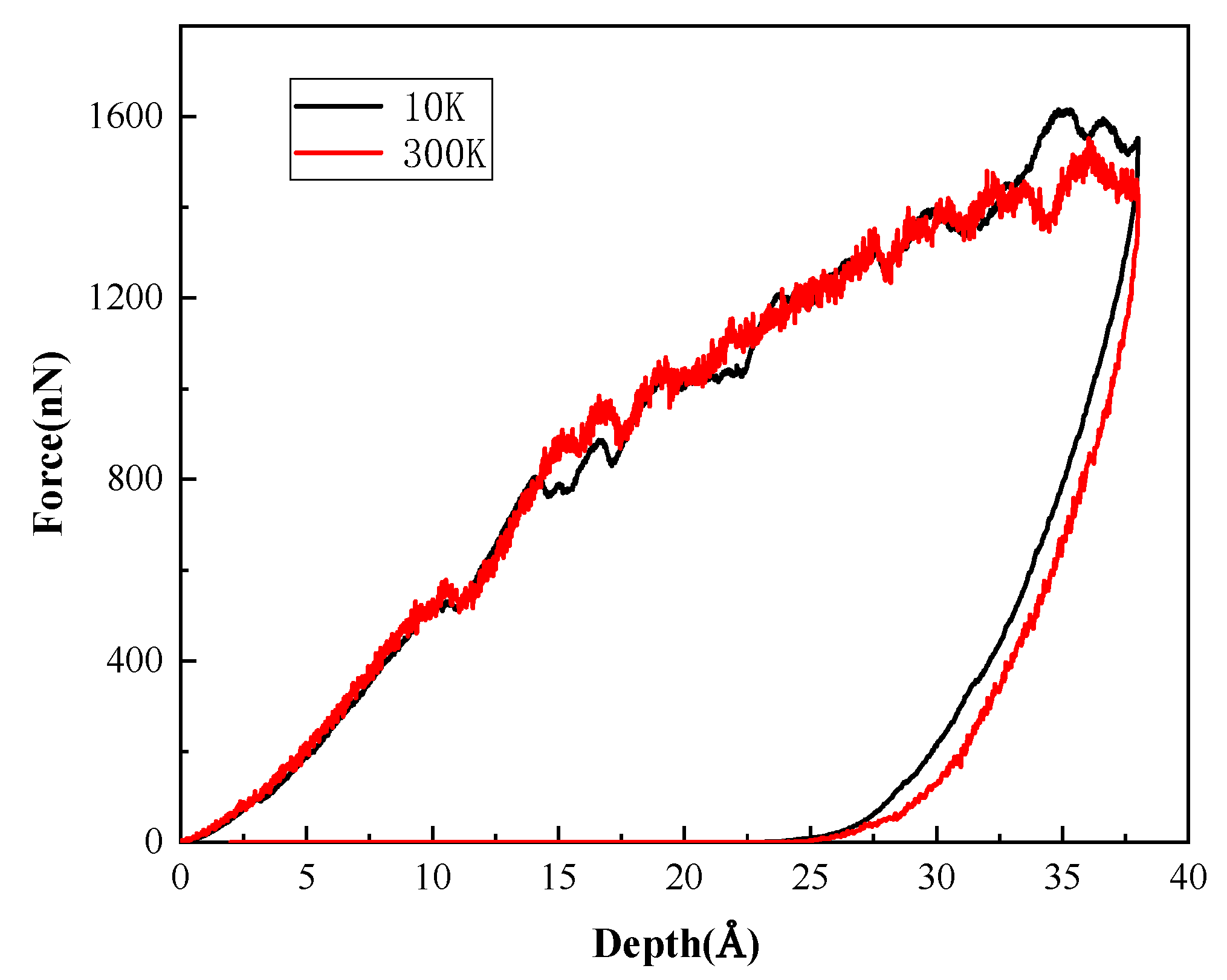
3.1. Deformational Behavior of GaN under Indentation
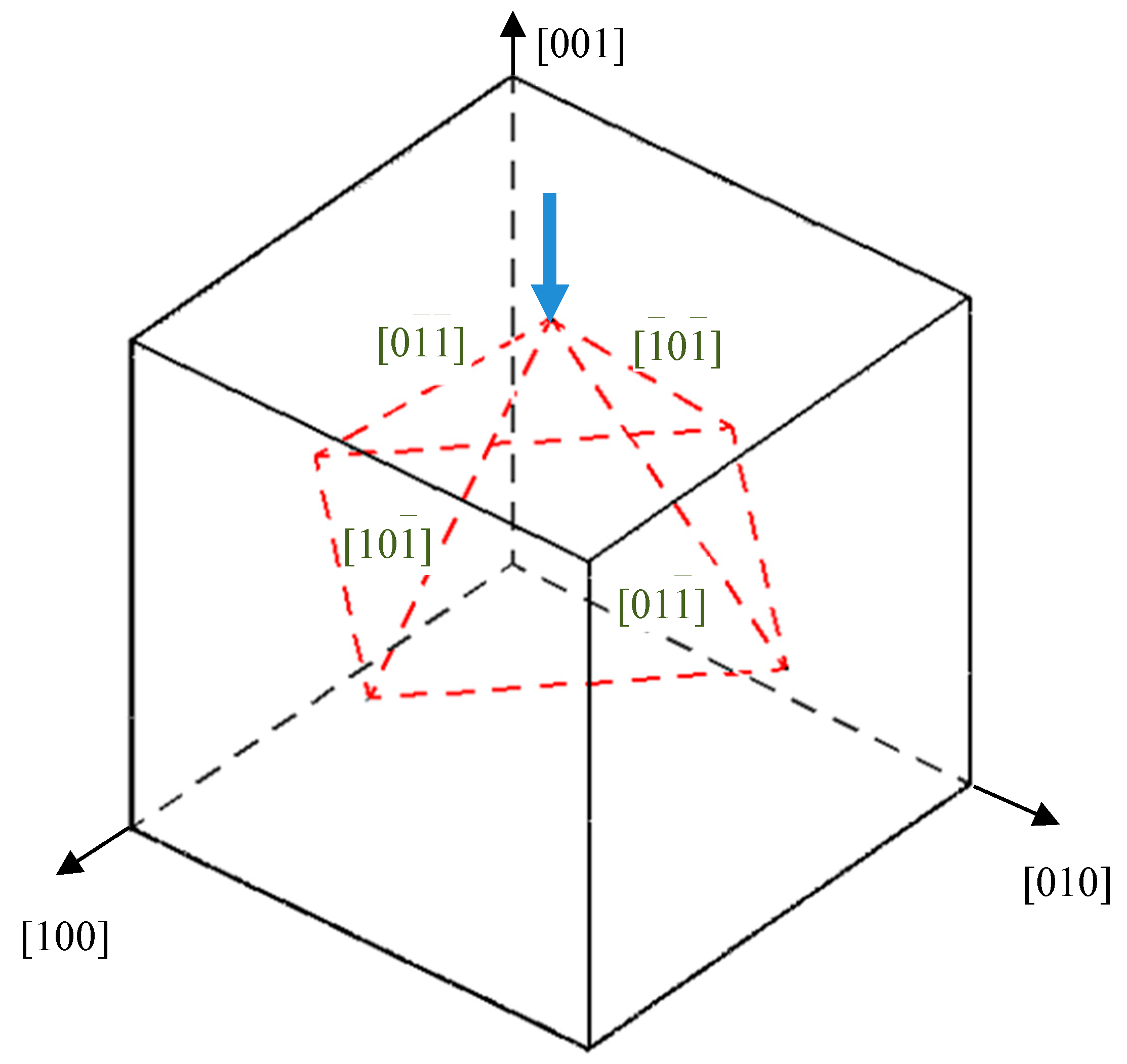
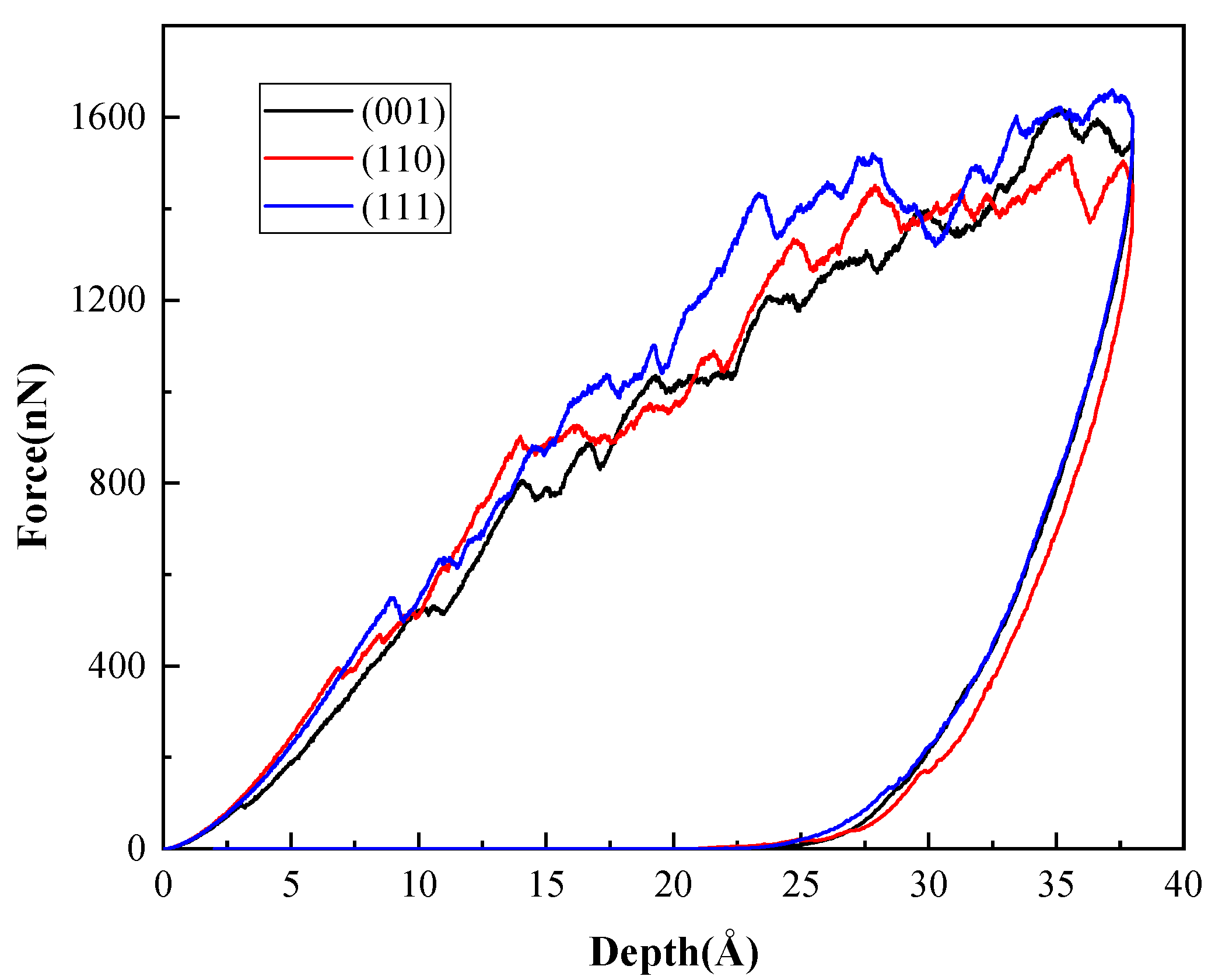
3.2. Anisotropy in B3-GaN
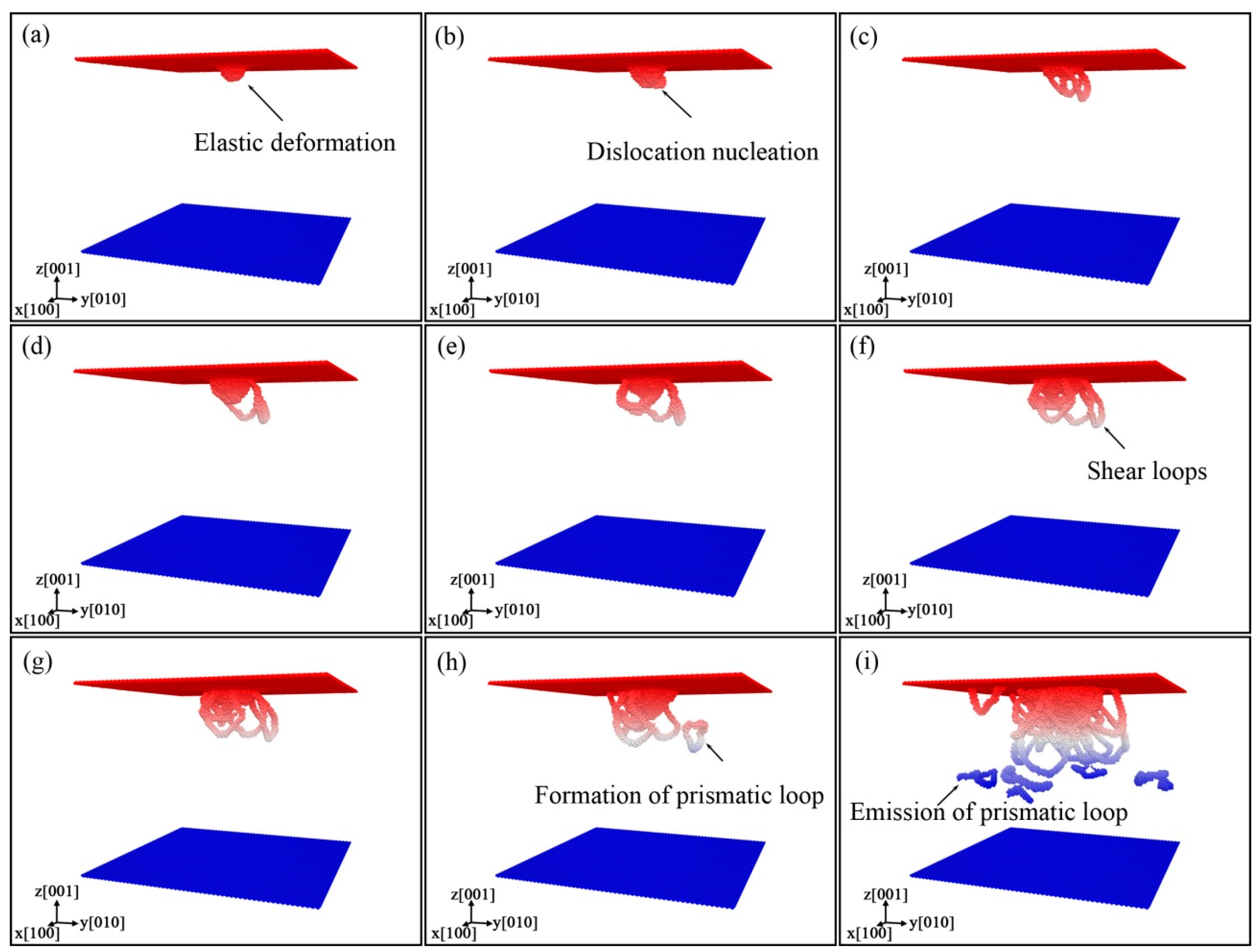
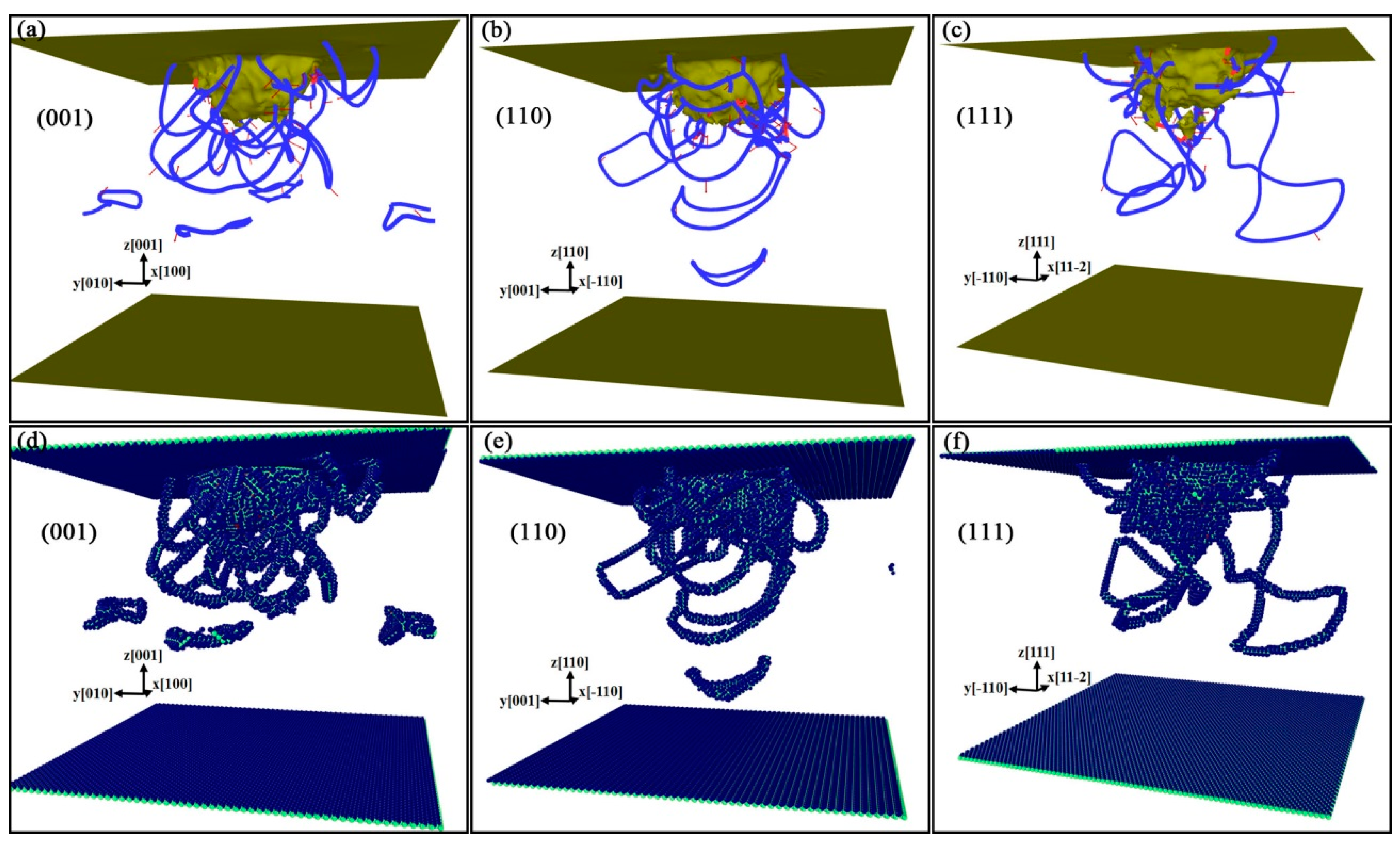
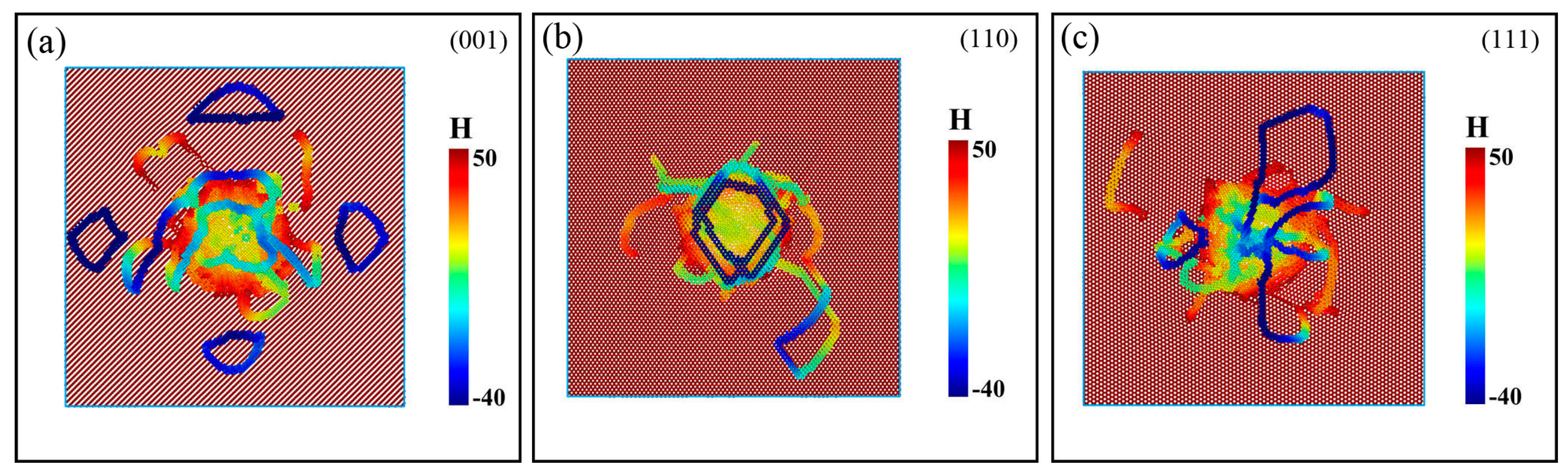
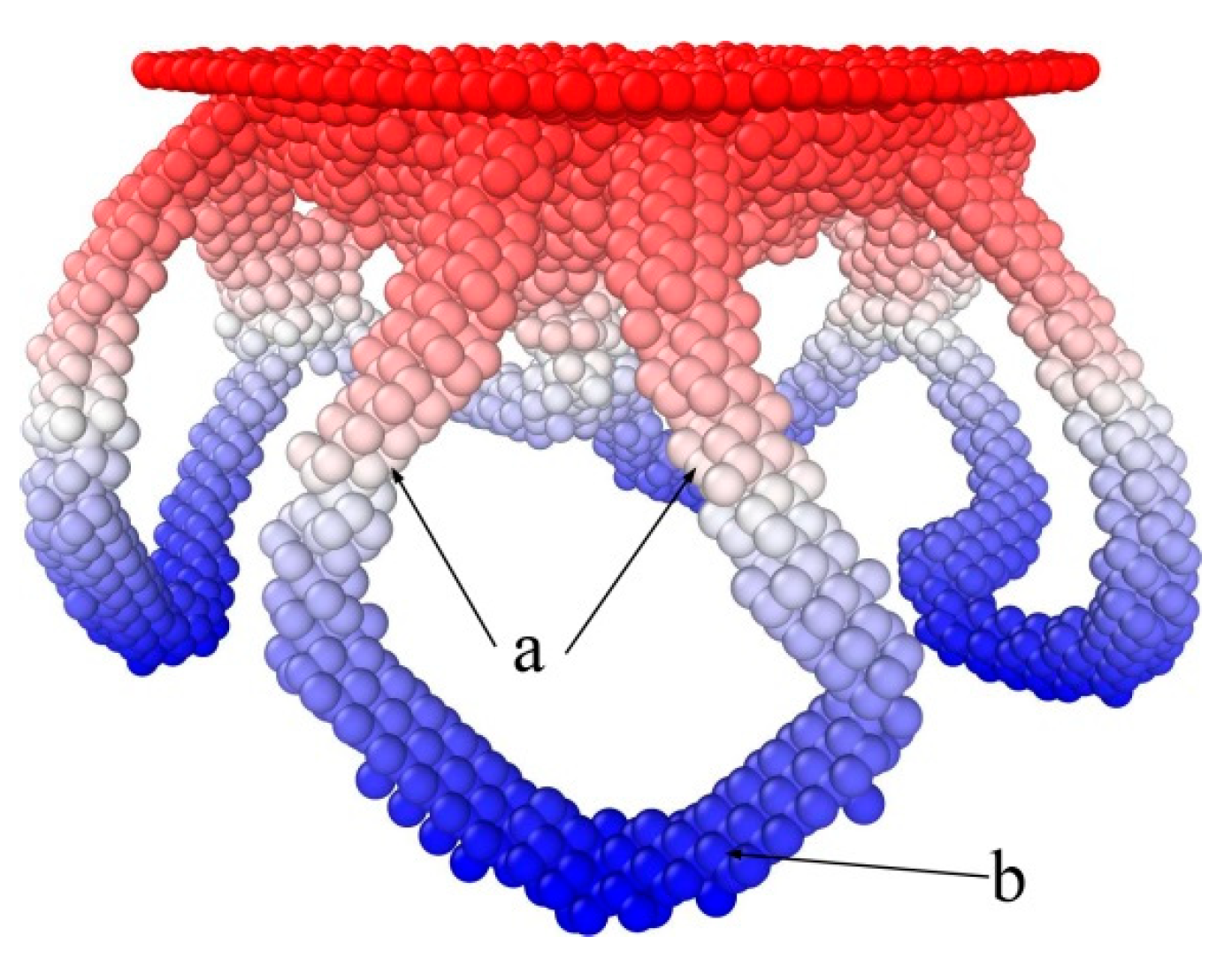
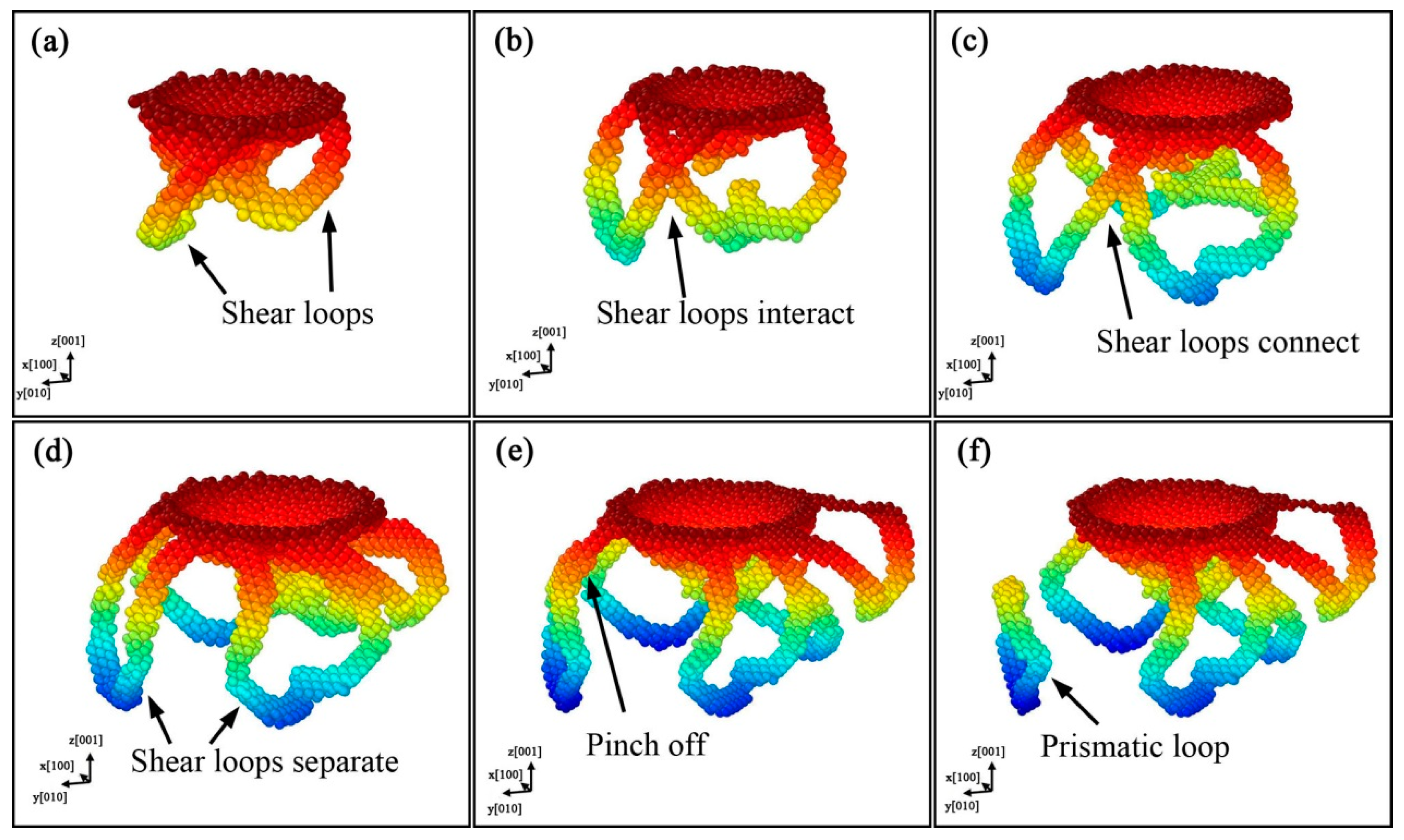
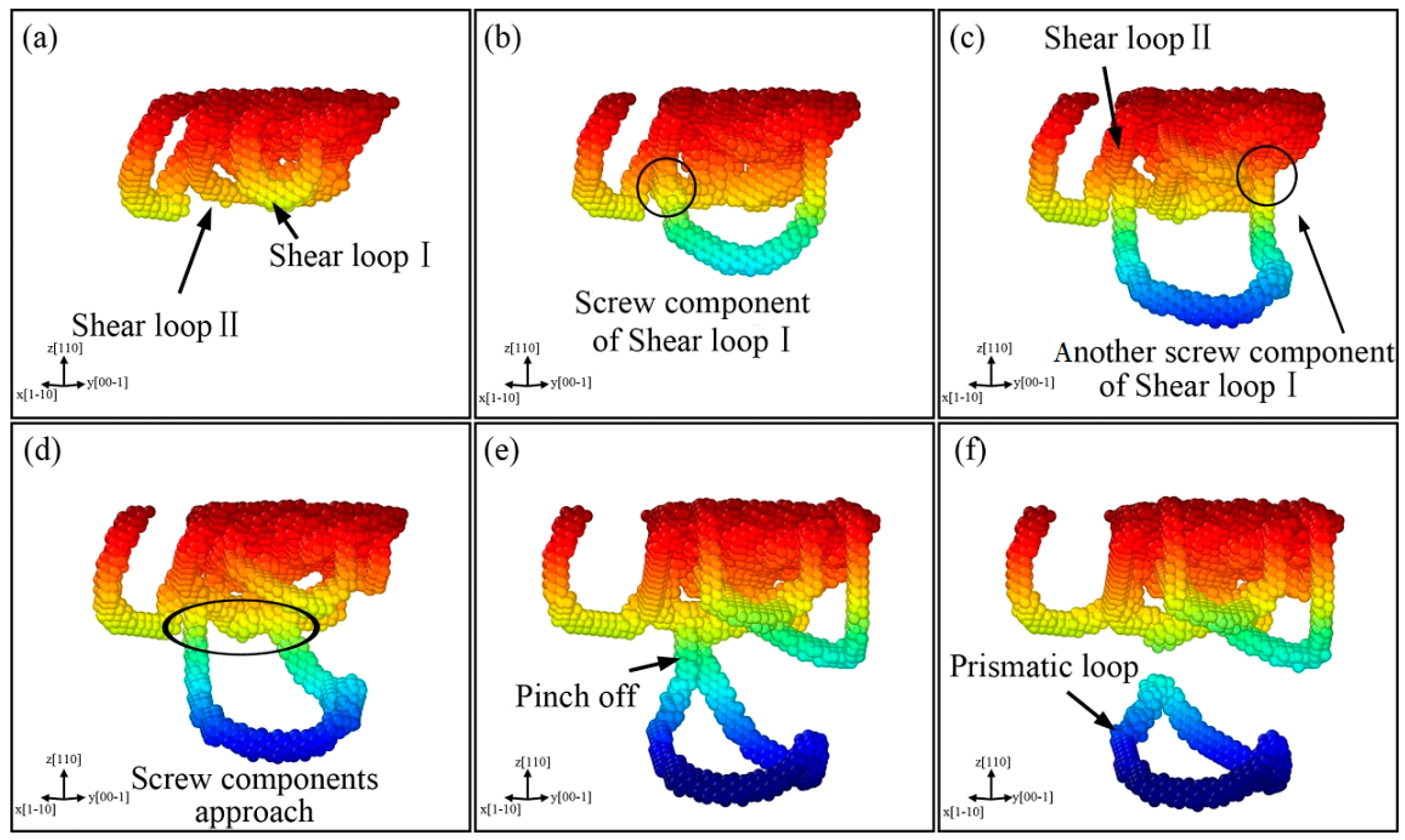
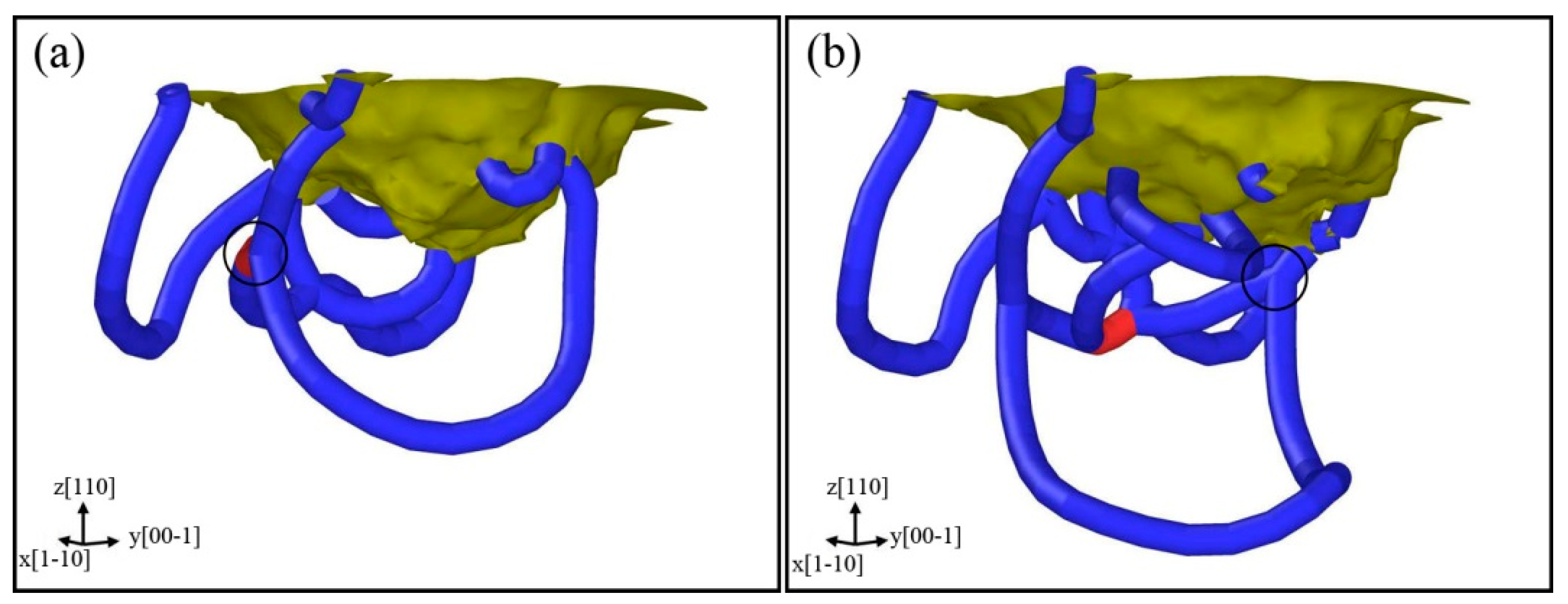
3.3. Formation and Propagation of Prismatic Loops
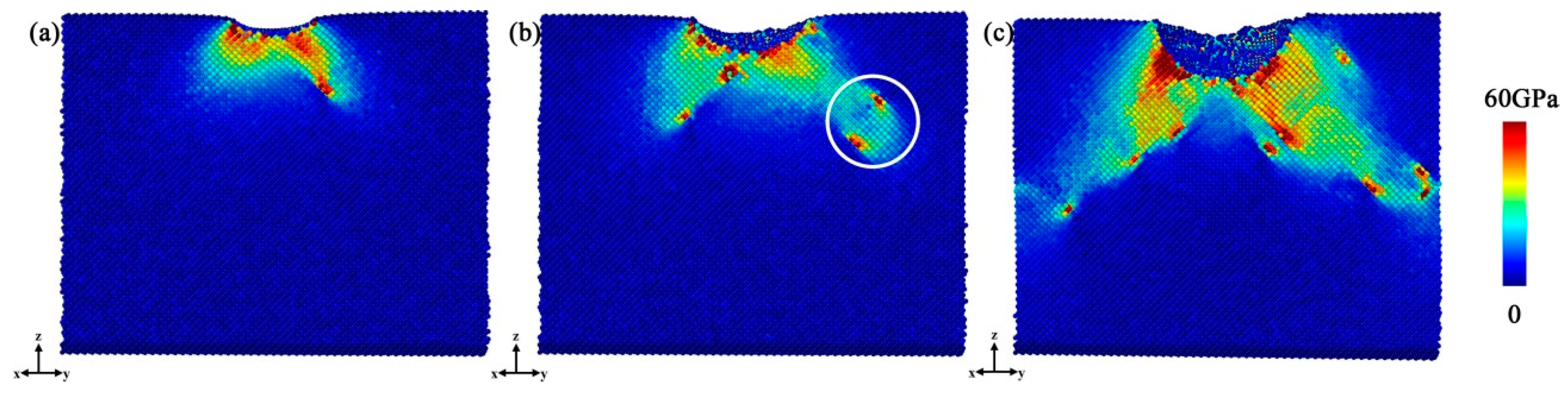
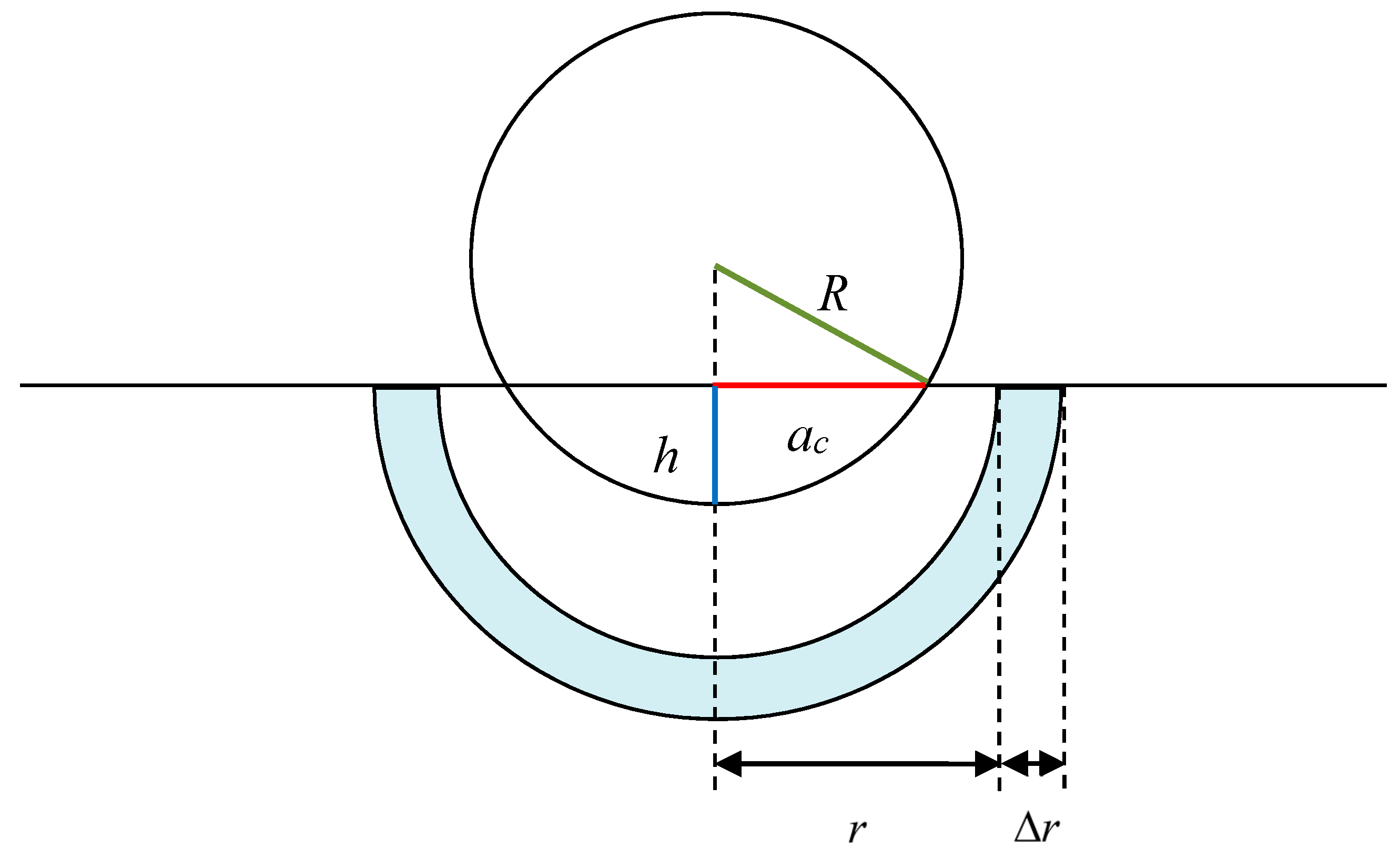
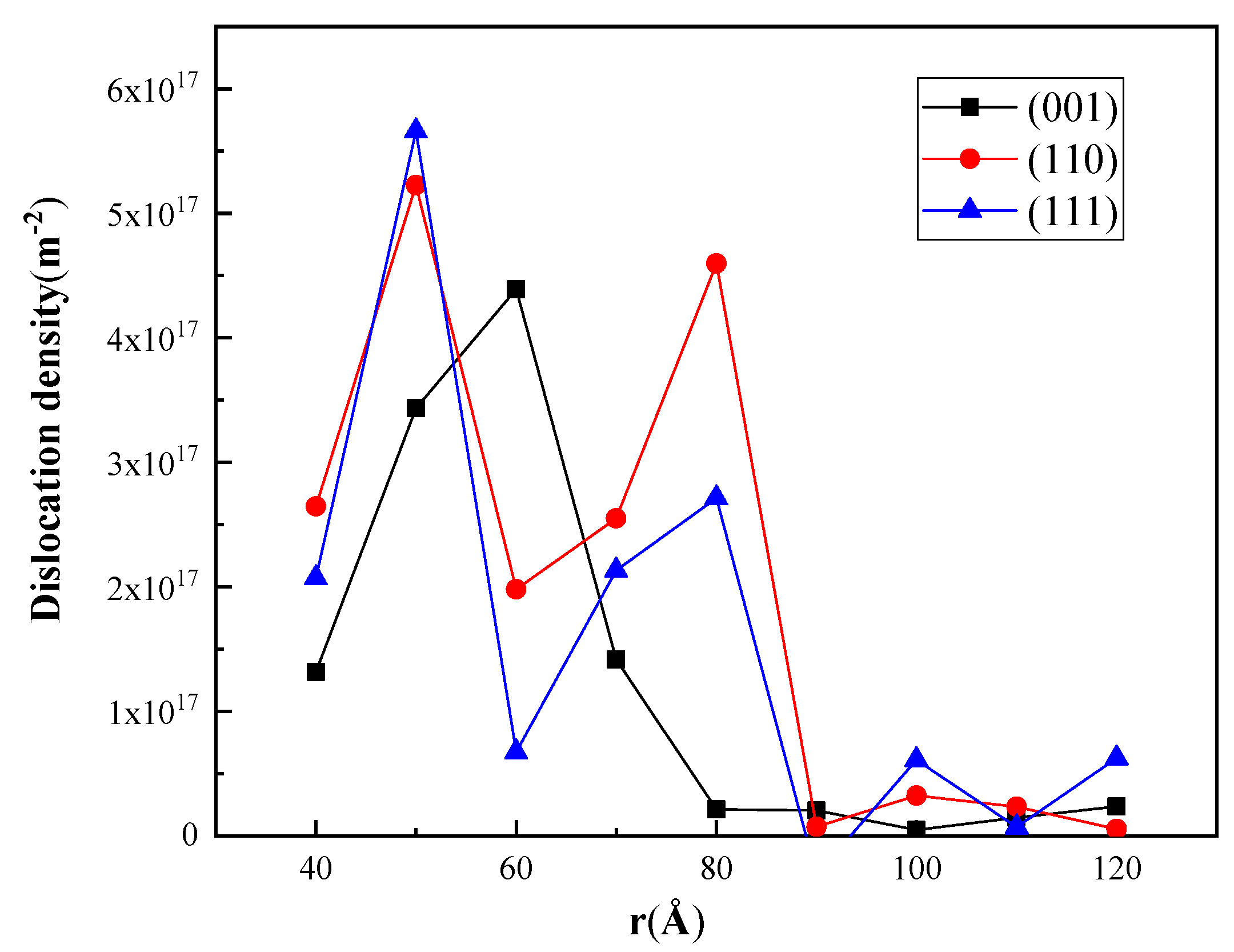
3.4. Dislocation Density
4. Conclusions
- The P-h curves for the indentation on the three planes exhibit anisotropy and show different depths at the onset of plasticity. (111) plane has the maximum hardness. The dislocation distributions analyzed by DXA and IDS show that only perfect dislocation with Burgers vector b = 1/2<110> can be found.
- Two mechanisms for the formation of prismatic loops were found. The “lasso”-like mechanism reveals that the screw components of a shear loop can attract each other and annihilate by cross-slip, finally a prismatic loop is formed. The extended “lasso”-like mechanism shows that two screw components of a shear loop can glide on another shear loop, and eventually a prismatic loop is also formed.
- The dislocation densities are different in the samples under the indentations on different oriented surface, and the corresponding size factors of the plastic zone in B3-GaN are similar to those in the fcc metals.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wittmer, M. Properties and microelectronic applications of thin films of refractory metal nitrides. J. Vac. Sci. Technol. A 1985, 3, 1797–1803. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, Y.; Sun, M.; Piedra, D.; Chowdhury, N.; Palacios, T. Materials and processing issues in vertical GaN power electronics. Mater. Sci. Semicond. Process. 2018, 78, 75–84. [Google Scholar] [CrossRef]
- Jiang, H.; Su, Y.; Zhu, J.; Lu, H.; Meng, X. Piezoelectric and pyroelectric properties of intrinsic GaN nanowires and nanotubes: Size and shape effects. Nano Energy 2018, 45, 359–367. [Google Scholar] [CrossRef]
- González, R.; López-Pérez, W.; González-García, Á.; Moreno-Armenta, M.G.; González-Hernández, R. Vacancy charged defects in two-dimensional GaN. Appl. Surf. Sci. 2018, 433, 1049–1055. [Google Scholar] [CrossRef]
- Paisley, M.J.; Sitar, Z.; Posthill, J.B.; Davis, R.F. Growth of cubic phase gallium nitride by modified molecular-beam epitaxy. J. Vac. Sci. Technol. A 1989, 7, 701–705. [Google Scholar] [CrossRef]
- Mu, F.; He, R.; Suga, T. Room temperature GaN-diamond bonding for high-power GaN-on-diamond devices. Scr. Mater. 2018, 150, 148–151. [Google Scholar] [CrossRef]
- Mishra, M.; Krishna, S.; Aggarwal, N.; Gundimeda, A.; Gupta, G. Electronic structure and chemical state analysis of nanoflowers decorated GaN and AlGaN/GaN heterostructure. J. Alloys Compd. 2017, 708, 385–391. [Google Scholar] [CrossRef]
- Herval, L.K.S.; de Godoy, M.P.F.; Wecker, T.; As, D.J. Investigation on interface-related defects by photoluminescence of cubic (Al) GaN/AlN multi-quantum wells structures. J. Lumin. 2018, 198, 309–313. [Google Scholar] [CrossRef]
- Gao, T.; Li, K.; Li, Y.; Hu, X.; Ren, L.; Luo, X.; Xie, Q. Crystalline structures and defects in liquid GaN during rapid cooling processes. Mater. Sci. Semicond. Process. 2018, 74, 46–50. [Google Scholar] [CrossRef]
- Barretta, R.; Fazelzadeh, S.A.; Feo, L.; Ghavanloo, E.; Luciano, R. Nonlocal inflected nano-beams: A stress-driven approach of bi-helmholtz type. Compos. Struct. 2018, 200, 239–245. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Weber, T.A. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B 1985, 31, 5262–5271. [Google Scholar] [CrossRef]
- Bere, A.; Serra, A. On the atomic structures, mobility and interactions of extended defects in GaN: Dislocations, tilt and twin boundaries. Philos. Mag. 2006, 86, 2159–2192. [Google Scholar] [CrossRef]
- Lei, H.P.; Chen, J.; Petit, S.; Ruterana, P.; Jiang, X.Y.; Nouet, G. Stillinger-weber parameters for In and N atoms. Superlattices Microstruct. 2006, 40, 464–469. [Google Scholar] [CrossRef]
- Sangiovanni, D.G.; Edström, D.; Hultman, L.; Petrov, I.; Greene, J.E.; Chirita, V. Ab initio and classical molecular dynamics simulations of N2 desorption from TiN (001) surfaces. Surf. Sci. 2014, 624, 25–31. [Google Scholar] [CrossRef]
- Sangiovanni, D.G.; Alling, B.; Steneteg, P.; Hultman, L.; Abrikosov, I.A. Nitrogen vacancy, self-interstitial diffusion, and frenkel-pair formation/dissociation in b1 TiN studied by ab initio and classical molecular dynamics with optimized potentials. Phys. Rev. B 2015, 91, 262–267. [Google Scholar] [CrossRef]
- Sangiovanni, D.G.; Edström, D.; Hultman, L.; Petrov, I.; Greene, J.E.; Chirita, V. Ti adatom diffusion on TiN (001): Ab initio and classical molecular dynamics simulations. Surf. Sci. 2014, 627, 34–41. [Google Scholar] [CrossRef]
- Edström, D.; Sangiovanni, D.G.; Hultman, L.; Chirita, V.; Petrov, I.; Greene, J.E. Ti and N adatom descent pathways to the terrace from atop two-dimensional TiN/TiN (001) islands. Thin Solid Films 2014, 558, 37–46. [Google Scholar] [CrossRef]
- Sangiovanni, D.G.; Mei, A.B.; Edstrom, D.; Hultman, L.; Chirita, V.; Petrov, I.; Greene, J.E. Effects of surface vibrations on interlayer mass transport: Ab initio molecular dynamics investigation of Ti adatom descent pathways and rates from TiN/TiN (001) islands. Phys. Rev. B 2018, 97, 035406. [Google Scholar] [CrossRef]
- Kim, K.; Lambrecht, W.R.; Segall, B. Elastic constants and related properties of tetrahedrally bonded Bn, AlN, GaN, and InN. Phys. Rev. B 1996, 53, 16310–16326. [Google Scholar] [CrossRef]
- Lei, T.; Moustakas, T.D.; Graham, R.J.; He, Y.; Berkowitz, S.J. Epitaxial growth and characterization of zinc-blende gallium nitride on (001) silicon. J. Appl. Phys. 1998, 71, 4933–4943. [Google Scholar] [CrossRef]
- Benkabou, F.; Aourag, H.; Becker, P.J.; Certier, M. Molecular dynamics study of zinc-blende GaN, AlN and InN. Mol. Simul. 2000, 23, 327–341. [Google Scholar] [CrossRef]
- Kim, K.; Lambrecht, W.R.; Segall, B. Electronic structure of GaN with strain and phonon distortions. Phys. Rev. B 1994, 50, 1502–1505. [Google Scholar] [CrossRef]
- Wang, S.Q.; Ye, H.Q. First-principles study on elastic properties and phase stability of iii-v compounds. Phys. Status Solidi B 2003, 240, 45–54. [Google Scholar] [CrossRef]
- Wright, A.F. Elastic properties of zinc-blende and wurtzite AlN, GaN, and InN. J. Appl. Phys. 1997, 82, 2833–2839. [Google Scholar] [CrossRef]
- Xiang, H.; Li, H.; Fu, T.; Huang, C.; Peng, X. Formation of prismatic loops in AlN and GaN under nanoindentation. Acta Mater. 2017, 138, 131–139. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with ovito-the open visualization tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Williams, B.E.; Glass, J.T. Characterization of diamond thin films: Diamond phase identification, surface morphology, and defect structures. J. Mater. Res. 1989, 4, 373–384. [Google Scholar] [CrossRef]
- Maras, E.; Trushin, O.; Stukowski, A.; Ala-Nissila, T.; Jonsson, H. Global transition path search for dislocation formation in Ge on Si (001). Comput. Phys. Commun. 2016, 205, 13–21. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Miyazaki, N.; Shiozaki, Y. Calculation of mechanical properties of solids using molecular dynamics method. JSME Int. J. Ser. A 1996, 39, 606–612. [Google Scholar] [CrossRef]
- Srolovitz, D.; Maeda, K.; Vitek, V.; Egami, T. Structural defects in amorphous solids statistical analysis of a computer model. Philos. Mag. A 1981, 44, 847–866. [Google Scholar] [CrossRef]
- Goel, S.; Beake, B.; Chan, C.W.; Faisal, N.H.; Dunne, N. Twinning anisotropy of tantalum during nanoindentation. Mater. Sci. Eng. A 2015, 627, 249–261. [Google Scholar] [CrossRef]
- Chen, H.P.; Kalia, R.K.; Nakano, A.; Vashishta, P. Multimillion-atom nanoindentation simulation of crystalline silicon carbide: Orientation dependence and anisotropic pileup. J. Appl. Phys. 2007, 102, 1409–1452. [Google Scholar] [CrossRef]
- Nabarro, F.R.N. Fifty-year study of the peierls-nabarro stress. Mater. Sci. Eng. A 1997, 234–236, 67–76. [Google Scholar] [CrossRef]
- Caceres, D.; Vergara, I.; Gonzalez, R.; Monroy, E.; Calle, F.; Munoz, E.; Omnes, F. Nanoindentation on alGaN thin films. J. Appl. Phys. 1999, 86, 6773–6778. [Google Scholar] [CrossRef]
- Kucheyev, S.O.; Bradby, J.E.; Williams, J.S.; Jagadish, C.; Toth, M.; Phillips, M.R.; Swain, M.V. Nanoindentation of epitaxial GaN films. Appl. Phys. Lett. 2000, 77, 3373–3375. [Google Scholar] [CrossRef]
- Navamathavan, R.; Moon, Y.T.; Kim, G.S.; Lee, T.G.; Hahn, J.H.; Park, S.J. ‘Pop-in’ phenomenon during nanoindentation in epitaxial GaN thin films on c-plane sapphire substrates. Mater. Chem. Phys. 2006, 99, 410–413. [Google Scholar] [CrossRef]
- Yu, G.; Ishikawa, H.; Egawa, T.; Soga, T.; Watanabe, J.; Jimbo, T.; Umeno, M. Mechanical properties of the GaN thin films deposited on sapphire substrate. J. Cryst. Growth 1998, 189–190, 701–705. [Google Scholar] [CrossRef]
- Nan, X.L.; Wang, H.Y.; Zhang, L.; Li, J.B.; Jiang, Q.C. Calculation of schmid factors in magnesium: Analysis of deformation behaviors. Scr. Mater. 2012, 67, 443–446. [Google Scholar] [CrossRef]
- Du, X.; Zhao, H.; Zhang, L.; Yang, Y.; Xu, H.; Fu, H.; Li, L. Molecular dynamics investigations of mechanical behaviours in monocrystalline silicon due to nanoindentation at cryogenic temperatures and room temperature. Sci. Rep. 2015, 5, 16275. [Google Scholar] [CrossRef] [PubMed]
- Remington, T.P.; Ruestes, C.J.; Bringa, E.M.; Remington, B.A.; Lu, C.H.; Kad, B.; Meyers, M.A. Plastic deformation in nanoindentation of tantalum: A new mechanism for prismatic loop formation. Acta Mater. 2014, 78, 378–393. [Google Scholar] [CrossRef]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part I. Theoretical. Proc. R. Soc. Lond. A 1934, 145, 362–387. [Google Scholar] [CrossRef]
- Hua, J.; Hartmaier, A. Determining burgers vectors and geometrically necessary dislocation densities from atomistic data. Model. Simul. Mater. Sci. Eng. 2010, 18, 045007. [Google Scholar] [CrossRef]
- Gao, Y.; Ruestes, C.J.; Tramontina, D.R.; Urbassek, H.M. Comparative simulation study of the structure of the plastic zone produced by nanoindentation. J. Mech. Phys. Solids 2015, 75, 58–75. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Nanoindentation; Springer: New York, NY, USA, 2004; pp. 339–352. [Google Scholar]
- Voyiadjis, G.Z.; Peters, R. Size effects in nanoindentation: An experimental and analytical study. Acta Mech. 2010, 211, 131–153. [Google Scholar] [CrossRef]
- Alhafez, I.A.; Ruestes, C.J.; Gao, Y.; Urbassek, H.M. Nanoindentation of hcp metals: A comparative simulation study of the evolution of dislocation networks. Nanotechnology 2016, 27, 045706. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Vehoff, H. Dependence of nanohardness upon indentation size and grain size—A local examination of the interaction between dislocations and grain boundaries. Acta Mater. 2007, 55, 849–856. [Google Scholar] [CrossRef]
- Begau, C.; Hua, J.; Hartmaier, A. A novel approach to study dislocation density tensors and lattice rotation patterns in atomistic simulations. J. Mech. Phys. Solids 2012, 60, 711–722. [Google Scholar] [CrossRef]
- Durst, K.; Backes, B.; Göken, M. Indentation size effect in metallic materials: Correcting for the size of the plastic zone. Scr. Mater. 2005, 52, 1093–1097. [Google Scholar] [CrossRef]
| Property | MD | Exp./Cal. | Error |
|---|---|---|---|
| Bulk modulus (GPa) | 205.79 | 201.00 a | 2.3% |
| Lattice constant (Å) | 4.51 | 4.5 b | 0.2% |
| Cohesive energy (eV) | 4.34 | 4.32 c | 0.4% |
| C11(GPa) | 318.21 | 296.00 d | 7.5% |
| C12(GPa) | 149.58 | 152.00 e | 1.6% |
| C44(GPa) | 122.83 | 155.00 f | 20.7% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Li, H.; Xiang, H.; Peng, X. Molecular Dynamics Simulation on B3-GaN Thin Films under Nanoindentation. Nanomaterials 2018, 8, 856. https://doi.org/10.3390/nano8100856
Chen C, Li H, Xiang H, Peng X. Molecular Dynamics Simulation on B3-GaN Thin Films under Nanoindentation. Nanomaterials. 2018; 8(10):856. https://doi.org/10.3390/nano8100856
Chicago/Turabian StyleChen, Chen, Haitao Li, Henggao Xiang, and Xianghe Peng. 2018. "Molecular Dynamics Simulation on B3-GaN Thin Films under Nanoindentation" Nanomaterials 8, no. 10: 856. https://doi.org/10.3390/nano8100856
APA StyleChen, C., Li, H., Xiang, H., & Peng, X. (2018). Molecular Dynamics Simulation on B3-GaN Thin Films under Nanoindentation. Nanomaterials, 8(10), 856. https://doi.org/10.3390/nano8100856




