Optimization of the Fano Resonance Lineshape Based on Graphene Plasmonic Hexamer in Mid-Infrared Frequencies
Abstract
1. Introduction
2. Method
3. Results and Discussion
3.1. The Extinction Spectrum of the Graphene Hexamer as a Function of R2
3.2. The Effect of the Chemical Potential of the Central Disk
3.3. The Effect of the Momentum Relaxation Time
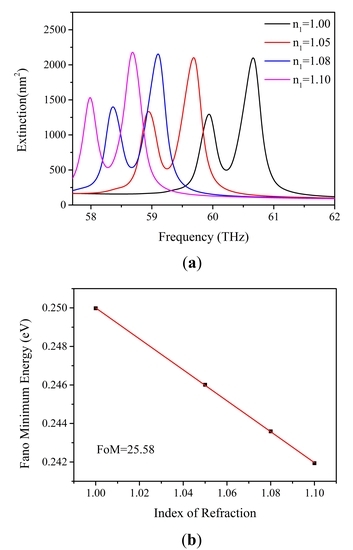
3.4. Sensing Effect of the Optimized Graphene Plasmonic Oligomer
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lal, S.; Link, S.; Halas, N.J. Nano-optics from sensing to waveguiding. Nat. Photonics 2007, 1, 641–648. [Google Scholar] [CrossRef]
- Schuller, J.A.; Barnard, E.S.; Cai, W.; Jun, Y.C.; White, J.S.; Brongersma, M.L. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Zohar, N.; Chuntonov, L.; Haran, G. The simplest plasmonic molecules: Metal nanoparticle dimers and trimers. J. Photochem. Photobiol. C Photochem. Rev. 2014, 21, 26–39. [Google Scholar] [CrossRef]
- Prodan, E.; Nordlander, P. Plasmon hybridization in spherical nanoparticles. J. Chem. Phys. 2004, 120, 5444–5454. [Google Scholar] [CrossRef] [PubMed]
- Brandl, D.W.; Mirin, N.A.; Nordlander, P. Plasmon modes of nanosphere trimers and quadrumers. J. Phys. Chem. B 2006, 110, 12302–12310. [Google Scholar] [CrossRef] [PubMed]
- Brown, L.V.; Sobhani, H.; Lassiter, J.B.; Nordlander, P.; Halas, N.J. Heterodimers: Plasmonic properties of mismatched nanoparticle pairs. ACS Nano 2010, 4, 819–832. [Google Scholar] [CrossRef] [PubMed]
- Shegai, T.; Li, Z.P.; Dadosh, T.; Zhang, Z.Y.; Xu, H.X.; Haran, G. Managing light polarization via plasmon-molecule interactions within an asymmetric metal nanoparticle trimer. Proc. Natl. Acad. Sci. USA 2008, 105, 16448–16453. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Cao, C.; Xu, X.L.; Liow, C.; Li, S.Z.; Tan, P.H.; Xiong, Q.H. Tailoring alphabetical metamaterials in optical frequency: Plasmonic coupling, dispersion, and sensing. ACS Nano 2014, 8, 3796–3806. [Google Scholar] [CrossRef] [PubMed]
- Gambhir, K.; Ray, B.; Mehrotra, R.; Sharma, P. Morphology dependent two photon absorption in plasmonic structures and plasmonic–organic hybrids. Opt. Laser Technol. 2017, 90, 201–210. [Google Scholar] [CrossRef]
- Fedotov, V.A.; Papasimakis, N.; Plum, E.; Bitzer, A.; Walther, M.; Kuo, P.; Tsai, D.P.; Zheludev, N.I. Spectral collapse in ensembles of metamolecules. Phys. Rev. Lett. 2010, 104, 223901. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Saliba, M.; Vogelgesang, R.; Giessen, H.; Alivisatos, A.P.; Liu, N. Transition from isolated to collective modes in plasmonic oligomers. Nano Lett. 2010, 10, 2721–2726. [Google Scholar] [CrossRef] [PubMed]
- Luk’yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef] [PubMed]
- Strelniker, Y.M.; Bergman, D.J. Transmittance and transparency of subwavelength-perforated conducting films in the presence of a magnetic field. Phys. Rev. B 2008, 77, 5. [Google Scholar] [CrossRef]
- Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-induced transparency in metamaterials. Phys. Rev. Lett. 2008, 101, 047401. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Leng, X.; Jiang, Y. Fano resonance in all-dielectric binary nanodisk array realizing optical filter with efficient linewidth tuning. Opt. Express 2015, 23, 6858–6866. [Google Scholar] [CrossRef] [PubMed]
- Dayal, G.; Chin, X.Y.; Soci, C.; Singh, R. High-qwhispering-gallery-mode-based plasmonic fano resonances in coupled metallic metasurfaces at near infrared frequencies. Adv. Opt. Mater. 2016, 4, 1295–1301. [Google Scholar] [CrossRef]
- Li, M.J.; Fang, H.; Li, X.M.; Yuan, X.C. Subgroup decomposition analyses of d-3h and d-4h plasmonic metamolecule fano resonance spectrum. Acta Phys. Sin. 2016, 65, 8. [Google Scholar] [CrossRef]
- Fan, J.A.; Bao, K.; Wu, C.; Bao, J.; Bardhan, R.; Halas, N.J.; Manoharan, V.N.; Shvets, G.; Nordlander, P.; Capasso, F. Fano-like interference in self-assembled plasmonic quadrumer clusters. Nano Lett. 2010, 10, 4680–4685. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.A.; Wu, C.; Bao, K.; Bao, J.; Bardhan, R.; Halas, N.J.; Manoharan, V.N.; Nordlander, P.; Shvets, G.; Capasso, F. Self-assembled plasmonic nanoparticle clusters. Science 2010, 328, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
- Giannini, V.; Francescato, Y.; Amrania, H.; Phillips, C.C.; Maier, S.A. Fano resonances in nanoscale plasmonic systems: A parameter-free modeling approach. Nano Lett. 2011, 11, 2835–2840. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, M.; Lei, D.Y.; Giannini, V.; Lukiyanchuk, B.; Ranjbar, M.; Liew, T.Y.; Hong, M.; Maier, S.A. Subgroup decomposition of plasmonic resonances in hybrid oligomers: Modeling the resonance lineshape. Nano Lett. 2012, 12, 2101–2106. [Google Scholar] [CrossRef] [PubMed]
- Lassiter, J.B.; Sobhani, H.; Fan, J.A.; Kundu, J.; Capasso, F.; Nordlander, P.; Halas, N.J. Fano resonances in plasmonic nanoclusters: Geometrical and chemical tunability. Nano Lett. 2010, 10, 3184–3189. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Kivshar, Y.S. Fano resonances in all-dielectric oligomers. Nano Lett. 2012, 12, 6459–6463. [Google Scholar] [CrossRef] [PubMed]
- Lassiter, J.B.; Sobhani, H.; Knight, M.W.; Mielczarek, W.S.; Nordlander, P.; Halas, N.J. Designing and deconstructing the fano lineshape in plasmonic nanoclusters. Nano Lett. 2012, 12, 1058–1062. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Dregely, D.; Vogelgesang, R.; Giessen, H.; Liu, N. Plasmonic oligomers: The role of individual particles in collective behavior. ACS Nano 2011, 5, 2042–2050. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Qiu, W.; Huang, Y.; Wang, J.X.; Kan, Q.; Pan, J.Q. Investigation of plasmonic whispering-gallery mode characteristics for graphene monolayer coated dielectric nanodisks. Opt. Lett. 2014, 39, 5527–5530. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.Q.; Henriksen, E.A.; Jiang, Z.; Hao, Z.; Martin, M.C.; Kim, P.; Stormer, H.L.; Basov, D.N. Dirac charge dynamics in graphene by infrared spectroscopy. Nat. Phys. 2008, 4, 532–535. [Google Scholar] [CrossRef]
- Zhang, H.; Virally, S.; Bao, Q.; Ping, L.; Massar, S.; Godbout, N.; Kockaert, P. Z-scan measurement of the nonlinear refractive. Opt. Lett. 2012, 37, 1856–1858. [Google Scholar] [CrossRef] [PubMed]
- Qiu, W.; Liu, X.; Zhao, J.; He, S.; Ma, Y.; Wang, J.-X.; Pan, J. Nanofocusing of mid-infrared electromagnetic waves on graphene monolayer. Appl. Phys. Lett. 2014, 104, 041109. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Nikitin, A.Y.; Garcia-Vidal, F.J.; Martin-Moreno, L. Analytical expressions for the electromagnetic dyadic green’s function in graphene and thin layers. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 11. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. Magneto-optical conductivity in graphene. J. Phys. Condens. Matter 2007, 19, 026222. [Google Scholar] [CrossRef]
- Llatser, I.; Kremers, C.; Cabellos-Aparicio, A.; Jornet, J.M.; Alarcón, E.; Chigrin, D.N. Graphene-based nano-patch antenna for terahertz radiation. Photonics Nanostruct. Fundam. Appl. 2012, 10, 353–358. [Google Scholar] [CrossRef]
- Amanatiadis, S.A.; Kantartzis, N.V.; Tsiboukis, T.D. A loss-controllable absorbing boundary condition for surface plasmon polaritons propagating onto graphene. IEEE Trans. Magn. 2015, 51, 4. [Google Scholar] [CrossRef]
- Tamagnone, M.; Gómez-Díaz, J.S.; Mosig, J.R.; Perruisseau-Carrier, J. Reconfigurable terahertz plasmonic antenna concept using a graphene stack. Appl. Phys. Lett. 2012, 101, 214102. [Google Scholar] [CrossRef]
- Vakil, A.; Engheta, N. Transformation optics using graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef] [PubMed]
- Qiu, W.; Huang, Y.; Chen, H.; Qiu, P.; Tang, Y.; Wang, J.-X.; Kan, Q.; Pan, J.-Q. Coupling of whispering-gallery modes in the graphene nanodisk plasmonic dimers. Plasmonics 2016, 12, 39–45. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, X.; Qiu, W.; Ma, Y.; Huang, Y.; Wang, J.X.; Qiang, K.; Pan, J.Q. Surface-plasmon-polariton whispering-gallery mode analysis of the graphene monolayer coated ingaas nanowire cavity. Opt. Express 2014, 22, 5754–5761. [Google Scholar] [CrossRef] [PubMed]
- Ju, L.; Geng, B.; Horng, J.; Girit, C.; Martin, M.; Hao, Z.; Bechtel, H.A.; Liang, X.; Zettl, A.; Shen, Y.R.; et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 2011, 6, 630–634. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Badioli, M.; Alonso-Gonzalez, P.; Thongrattanasiri, S.; Huth, F.; Osmond, J.; Spasenovic, M.; Centeno, A.; Pesquera, A.; Godignon, P.; et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 2012, 487, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Shi, B.; Cai, W.; Zhang, X.; Xiang, Y.; Zhan, Y.; Geng, J.; Ren, M.; Xu, J. Tunable band-stop filters for graphene plasmons based on periodically modulated graphene. Sci. Rep. 2016, 6, 26796. [Google Scholar] [CrossRef] [PubMed]
- Amanatiadis, S.; Kantartzis, N. Distortion of surface plasmon polariton propagation on graphene due to chemical potential variation. Appl. Phys. A 2016, 122. [Google Scholar] [CrossRef]
- Bouzianas, G.D.; Kantartzis, N.V.; Antonopoulos, C.S.; Tsiboukis, T.D. Optimal modeling of infinite graphene sheets via a class of generalized fdtd schemes. IEEE Trans. Magn. 2012, 48, 379–382. [Google Scholar] [CrossRef]
- Nayyeri, V.; Soleimani, M.; Ramahi, O.M. Modeling graphene in the finite-difference time-domain method using a surface boundary condition. IEEE Trans. Antennas Propag. 2013, 61, 4176–4182. [Google Scholar] [CrossRef]
- Ren, J.; Qiu, W.; Chen, H.; Qiu, P.; Lin, Z.; Wang, J.X.; Kan, Q.; Pan, J.Q. Electromagnetic field coupling characteristics in graphene plasmonic oligomers: From isolated to collective modes. Phys. Chem. Chem. Phys. 2017, 19, 14671–14679. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.B.; Zhu, W.; Xu, H.J.; Ni, Z.H.; Dong, Z.G.; Cui, T.J. Flexible transformation plasmonics using graphene. Opt. Express 2013, 21, 10475–10482. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Sarris, C.D. A perfectly matched layer for subcell fdtd and applications to the modeling of graphene structures. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1080–1083. [Google Scholar] [CrossRef]
- Shao, L.; Fang, C.; Chen, H.; Man, Y.C.; Wang, J.; Lin, H.Q. Distinct plasmonic manifestation on gold nanorods induced by the spatial perturbation of small gold nanospheres. Nano Lett. 2012, 12, 1424–1430. [Google Scholar] [CrossRef] [PubMed]
- Mirin, N.A.; Bao, K.; Nordlander, P. Fano resonances in plasmonic nanoparticle aggregates. J. Phys. Chem. A 2009, 113, 4028–4034. [Google Scholar] [CrossRef] [PubMed]
- Sherry, L.J.; Chang, S.-H.; Schatz, G.C.; Van Duyne, R.P.; Wiley, B.J.; Xia, Y. Localized surface plasmon resonance spectroscopy of single silver nanocubes. Nano Lett. 2005, 5, 2034–2038. [Google Scholar] [CrossRef] [PubMed]
- Hao, F.; Sonnefraud, Y.; Dorpe, P.V.; Maier, S.A.; Halas, N.J.; Nordlander, P. Symmetry breaking in plasmonic nanocavities: Subradiant lspr sensing and a tunable fano resonance. Nano Lett. 2008, 8, 3983–3988. [Google Scholar] [CrossRef] [PubMed]
- Liao, H.W.; Nehl, C.L.; Hafner, J.H. Biomedical applications of plasmon resonant metal nanoparticles. Nanomedicine 2006, 1, 201–208. [Google Scholar] [CrossRef] [PubMed]







© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Wang, G.; Qiu, W.; Lin, Z.; Chen, H.; Qiu, P.; Wang, J.-X.; Kan, Q.; Pan, J.-Q. Optimization of the Fano Resonance Lineshape Based on Graphene Plasmonic Hexamer in Mid-Infrared Frequencies. Nanomaterials 2017, 7, 238. https://doi.org/10.3390/nano7090238
Ren J, Wang G, Qiu W, Lin Z, Chen H, Qiu P, Wang J-X, Kan Q, Pan J-Q. Optimization of the Fano Resonance Lineshape Based on Graphene Plasmonic Hexamer in Mid-Infrared Frequencies. Nanomaterials. 2017; 7(9):238. https://doi.org/10.3390/nano7090238
Chicago/Turabian StyleRen, Junbo, Guangqing Wang, Weibin Qiu, Zhili Lin, Houbo Chen, Pingping Qiu, Jia-Xian Wang, Qiang Kan, and Jiao-Qing Pan. 2017. "Optimization of the Fano Resonance Lineshape Based on Graphene Plasmonic Hexamer in Mid-Infrared Frequencies" Nanomaterials 7, no. 9: 238. https://doi.org/10.3390/nano7090238
APA StyleRen, J., Wang, G., Qiu, W., Lin, Z., Chen, H., Qiu, P., Wang, J.-X., Kan, Q., & Pan, J.-Q. (2017). Optimization of the Fano Resonance Lineshape Based on Graphene Plasmonic Hexamer in Mid-Infrared Frequencies. Nanomaterials, 7(9), 238. https://doi.org/10.3390/nano7090238