A Novel Method to Determine the Thermal Conductivity of Interfacial Layers Surrounding the Nanoparticles of a Nanofluid
Abstract
:1. Introduction
2. Theoretical Background
2.1. Viscosity of Nanofluids
2.2. Thermal Conductivity of Nanofluids
3. Estimation of Interfacial Layer Thermal Conductivity
4. Simulation Results
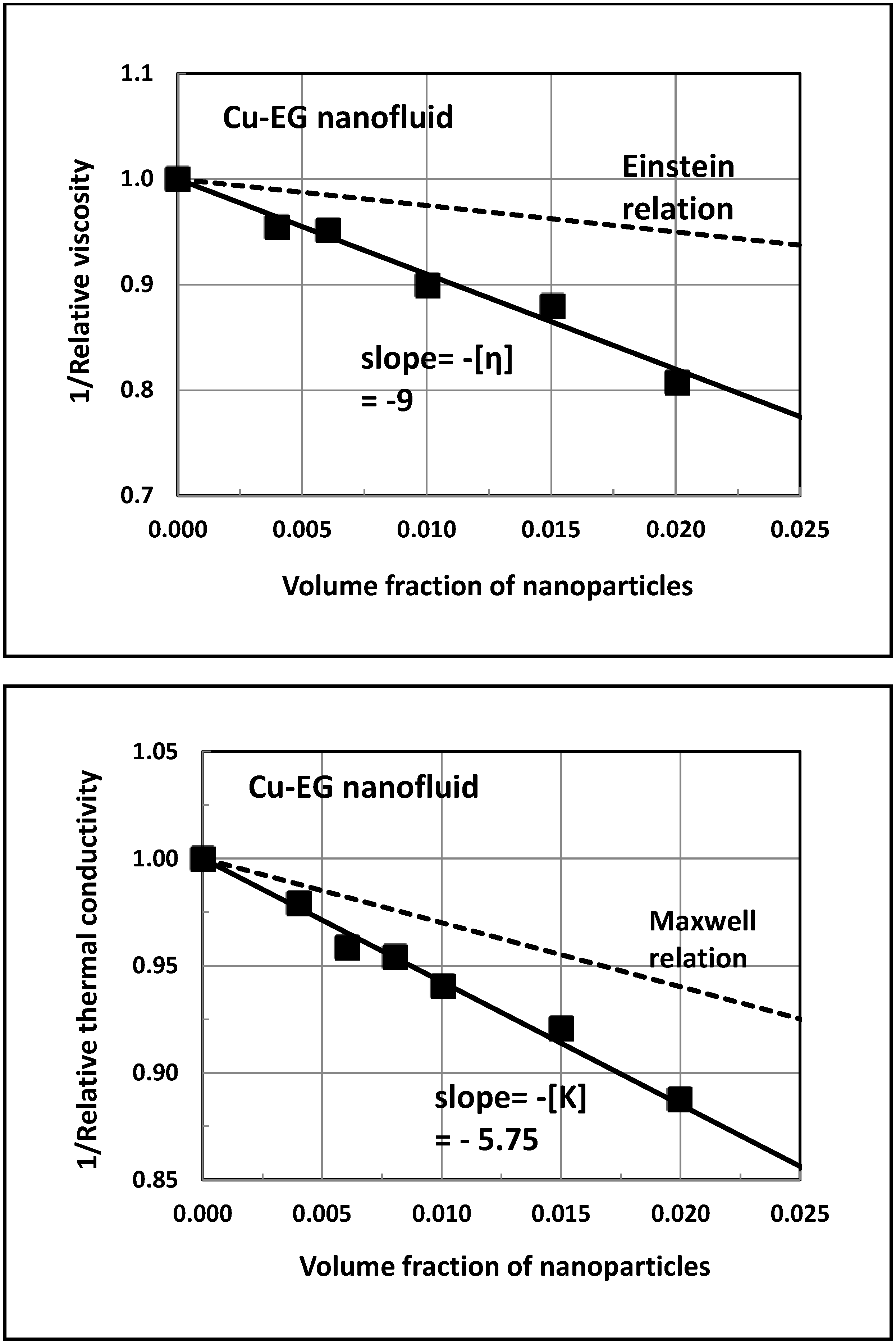
5. Experimental Validation

6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Das, S.K.; Choi, S.U.S.; Yu, W.; Pradeep, T. Nanofluids; Wiley: New York, NY, USA, 2008; pp. 1–37. [Google Scholar]
- Wang, Y.; Zheng, Y.; Zhang, L.; Wang, Q.; Zhang, D. Stability of nanosuspensions in drug delivery. J. Control. Release 2013, 172, 1126–1141. [Google Scholar] [CrossRef] [PubMed]
- Mahbubul, I.M.; Saidur, R.; Amalina, M.A. Latest developments on the viscosity of nanofluids. Int. J. Heat Mass Transf. 2012, 55, 874–885. [Google Scholar] [CrossRef]
- Duan, F.; Kwek, D.; Crivoi, A. Viscosity affected by nanoparticle aggregation in Al2O3-water nanofluids. Nanoscale Res. Lett. 2011, 6, 248–252. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Yang, B.; Hammouda, B. Thermal conductivity and viscosity of self-assembled alcohol/polyalphaolefin nanoemulsion fluids. Nanoscale Res. Lett. 2011, 6, 274–279. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Park, S.D.; Kang, S.; Bang, I.C.; Kim, J.H. Investigation of viscosity and thermal conductivity of SiC nanofluids for heat transfer applications. Int. J. Heat Mass Transf. 2011, 54, 433–438. [Google Scholar] [CrossRef]
- Namburu, P.K.; Kulkarni, D.P.; Misra, D.; Das, D.K. Viscosity of copper oxide nanoparticles dispersed in ethylene glycol and water mixture. Exp. Therm. Fluid Sci. 2007, 32, 397–402. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Desgranges, F.; Galanis, N.; Roy, G.; Mare, T.; Boucher, S. Viscosity data for Al2O3-water nanofluid-hysteresis: Is heat transfer enhancement using nanofluids reliable? Int. J. Therm. Sci. 2008, 47, 103–111. [Google Scholar] [CrossRef]
- Wang, X.Q.; Mujumdar, A.S. Heat transfer characteristics of nanofluids: A review. Int. J. Therm. Sci. 2007, 46, 1–19. [Google Scholar] [CrossRef]
- Wang, X.Q.; Mujumdar, A.S. A review on nanofluids. Braz. J. Chem. Eng. 2008, 25, 613–630. [Google Scholar]
- Chen, H.; Ding, Y.; He, T.; Tan, C. Rheological behavior of ethylene glycol based titania nanofluids. Chem. Phys. Lett. 2007, 444, 333–337. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Desgranges, F.; Roy, G.; Galanis, N.; Mare, T.; Boucher, S.; Angue Mintsa, H. Temperature and particle-size dependent viscosity data for water-based nanofluids—Hysteresis phenomenon. Int. J. Heat Fluid Flow 2007, 28, 1492–1506. [Google Scholar] [CrossRef]
- Yu, W.; Choi, S.U.S. The role of interfacial layers in the enhanced thermal conductivity of nanofluids: A renovated Maxwell model. J. Nanoparticle Res. 2003, 5, 167–171. [Google Scholar] [CrossRef]
- Pal, R. New models for the viscosity of nanofluids. J. Nanofluids 2014, 3, 260–266. [Google Scholar] [CrossRef]
- Einstein, A. Eine neue Bestimmung der Molekuldimension. Ann. Phys. (Leipzig) 1906, 19, 289–306. (in German). [Google Scholar] [CrossRef]
- Einstein, A. Berichtigung zu meiner Arbeit: Eine neue Bestimmung der Molekuldimension. Ann. Phys. (Leipzig) 1911, 34, 591–592. (in German). [Google Scholar] [CrossRef]
- Batchelor, G.K.; Green, J.T. The determination of the bulk stress in a suspension of spherical particles to order c2. J. Fluid Mech. 1972, 56, 401–427. [Google Scholar] [CrossRef]
- Okeke, G.; Witharana, S.; Antony, S.J.; Ding, Y. Computational analysis of factors influencing thermal conductivity of nanofluids. J. Nanoparticle Res. 2011, 13, 6365–6375. [Google Scholar] [CrossRef]
- Pal, R. New models for thermal conductivity of particulate composites. J. Reinf. Plast. Compos. 2007, 26, 643–651. [Google Scholar] [CrossRef]
- Pal, R. Electromagnetic, Mechanical, and Transport Properties of Composite Materials; CRC Press: Boca Raton, FL, USA, 2014; pp. 261–264. [Google Scholar]
- Yu, W.; Choi, S.U.S. The role of interfacial layers in the enhanced thermal conductivity of nanofluids: A renovated Hamilton-Crosser model. J. Nanoparticle Res. 2004, 6, 355–361. [Google Scholar] [CrossRef]
- Liang, Z.; Tsai, H.L. Thermal conductivity of interfacial layers in nanofluids. Phys. Rev. 2011, 83, 0416021–0416028. [Google Scholar]
- Yu, C.J.; Richter, A.G.; Datta, A.; Durbin, M.K.; Dutta, P. Molecular layering in a liquid on a solid substrate. Phys. B 2000, 283, 27–31. [Google Scholar] [CrossRef]
- Okeke, G.; Hammond, R.B.; Joseph Antony, S. Influence of size and temperature on the phase stability and thermophysical properties of anatase TiO2 nanoparticles: Molecular dynamics simulation. J. Nanoparticle Res. 2013, 15, 1584–1592. [Google Scholar] [CrossRef]
- Garboczi, E.J.; Schwartz, L.M.; Bentz, D.P. Modeling the influence of the interfacial zone the dc electrical conductivity of mortar. Adv. Cem. Based Mater. 1995, 2, 169–181. [Google Scholar] [CrossRef]
- Garg, J.; Poudel, B.; Chiesa, M.; Gordon, J.B.; Ma, J.J.; Wang, J.B.; Ren, Z.F.; Kang, Y.T.; Ohtani, H.; Nanda, J.; et al. Enhanced thermal conductivity and viscosity of copper nanoparticles in ethylene glycol nanofluid. J. Appl. Phys. 2008, 103, 074301–074306. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, R. A Novel Method to Determine the Thermal Conductivity of Interfacial Layers Surrounding the Nanoparticles of a Nanofluid. Nanomaterials 2014, 4, 844-855. https://doi.org/10.3390/nano4040844
Pal R. A Novel Method to Determine the Thermal Conductivity of Interfacial Layers Surrounding the Nanoparticles of a Nanofluid. Nanomaterials. 2014; 4(4):844-855. https://doi.org/10.3390/nano4040844
Chicago/Turabian StylePal, Rajinder. 2014. "A Novel Method to Determine the Thermal Conductivity of Interfacial Layers Surrounding the Nanoparticles of a Nanofluid" Nanomaterials 4, no. 4: 844-855. https://doi.org/10.3390/nano4040844
APA StylePal, R. (2014). A Novel Method to Determine the Thermal Conductivity of Interfacial Layers Surrounding the Nanoparticles of a Nanofluid. Nanomaterials, 4(4), 844-855. https://doi.org/10.3390/nano4040844



