Tailoring Metal Phthalocyanine/Graphene Interfaces for Highly Sensitive Gas Sensors
Abstract
1. Introduction
2. Computational Methods
3. Results and Discussion
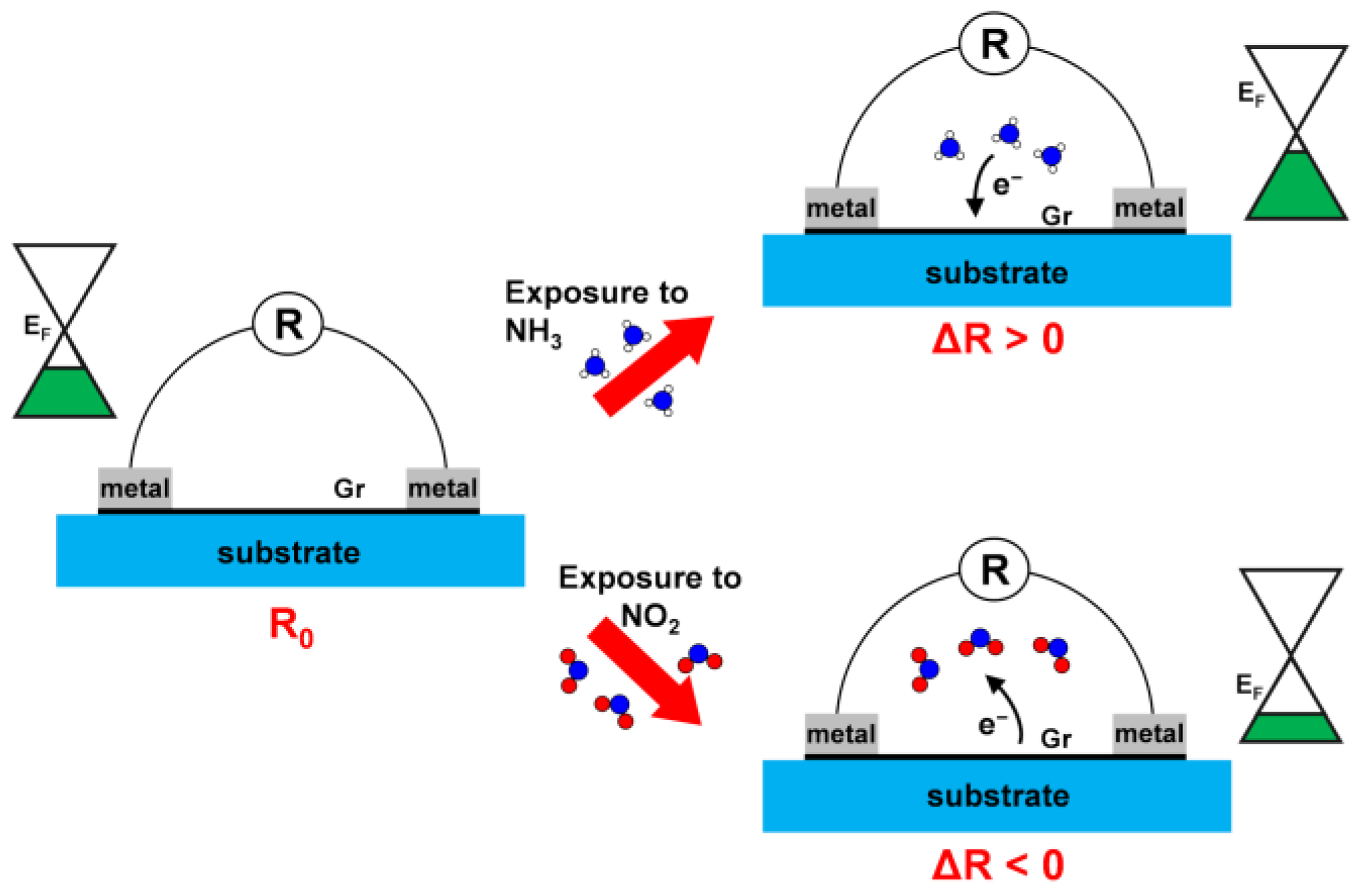
3.1. Working Principle of a Graphene-Based Chemiresistor in Gas Sensing
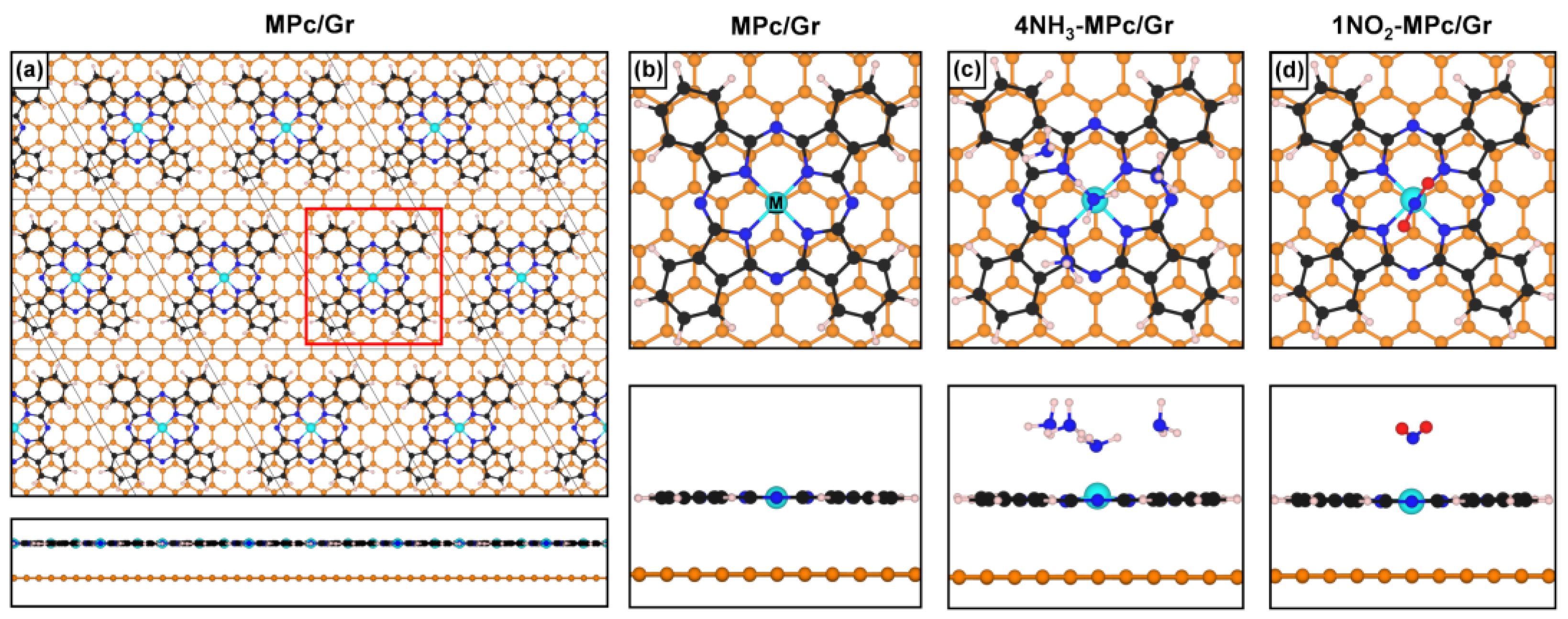
3.2. Influence of Metal Cation and Gr Charge State on the Electronic Properties of the MPc/Gr Interface
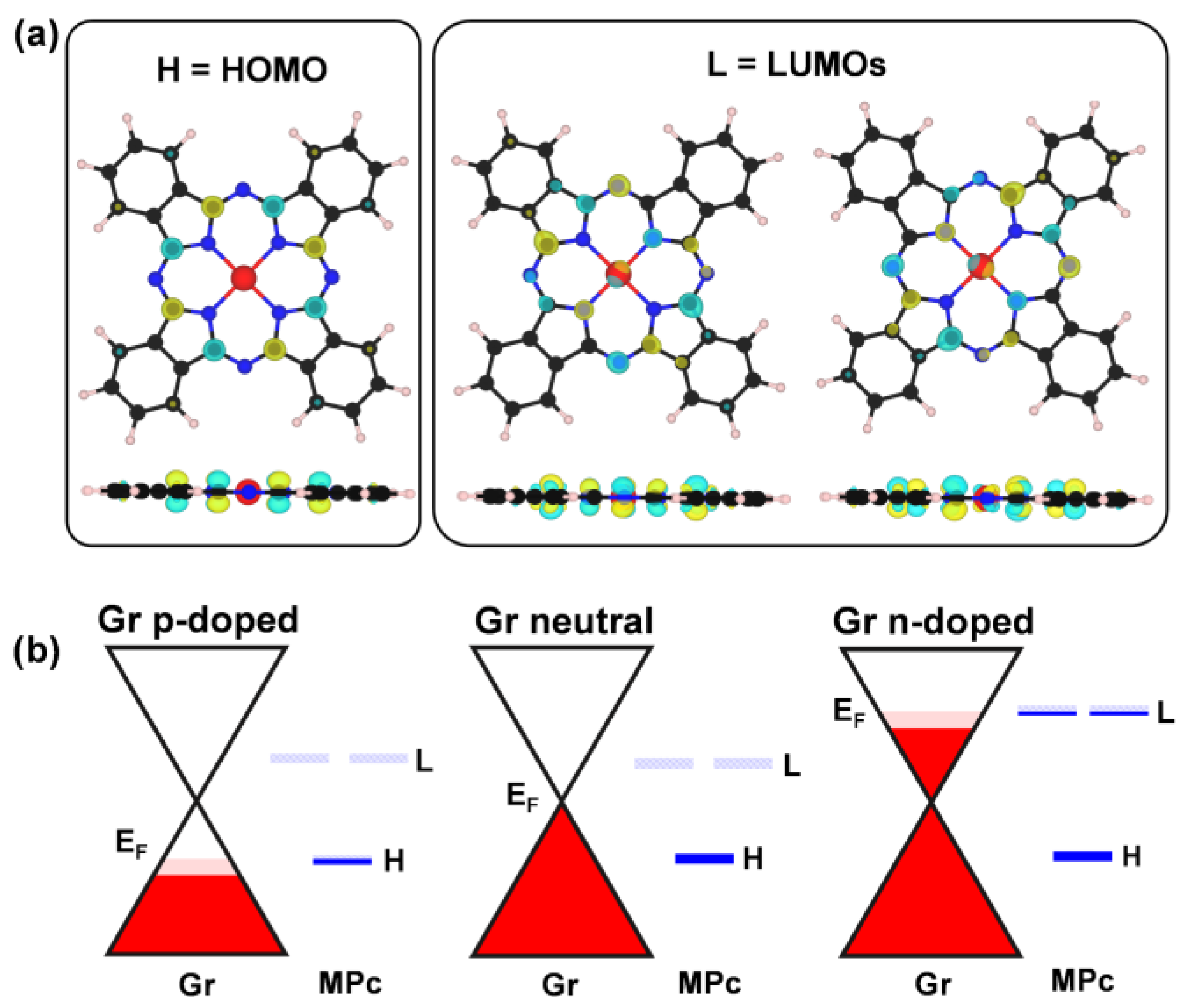
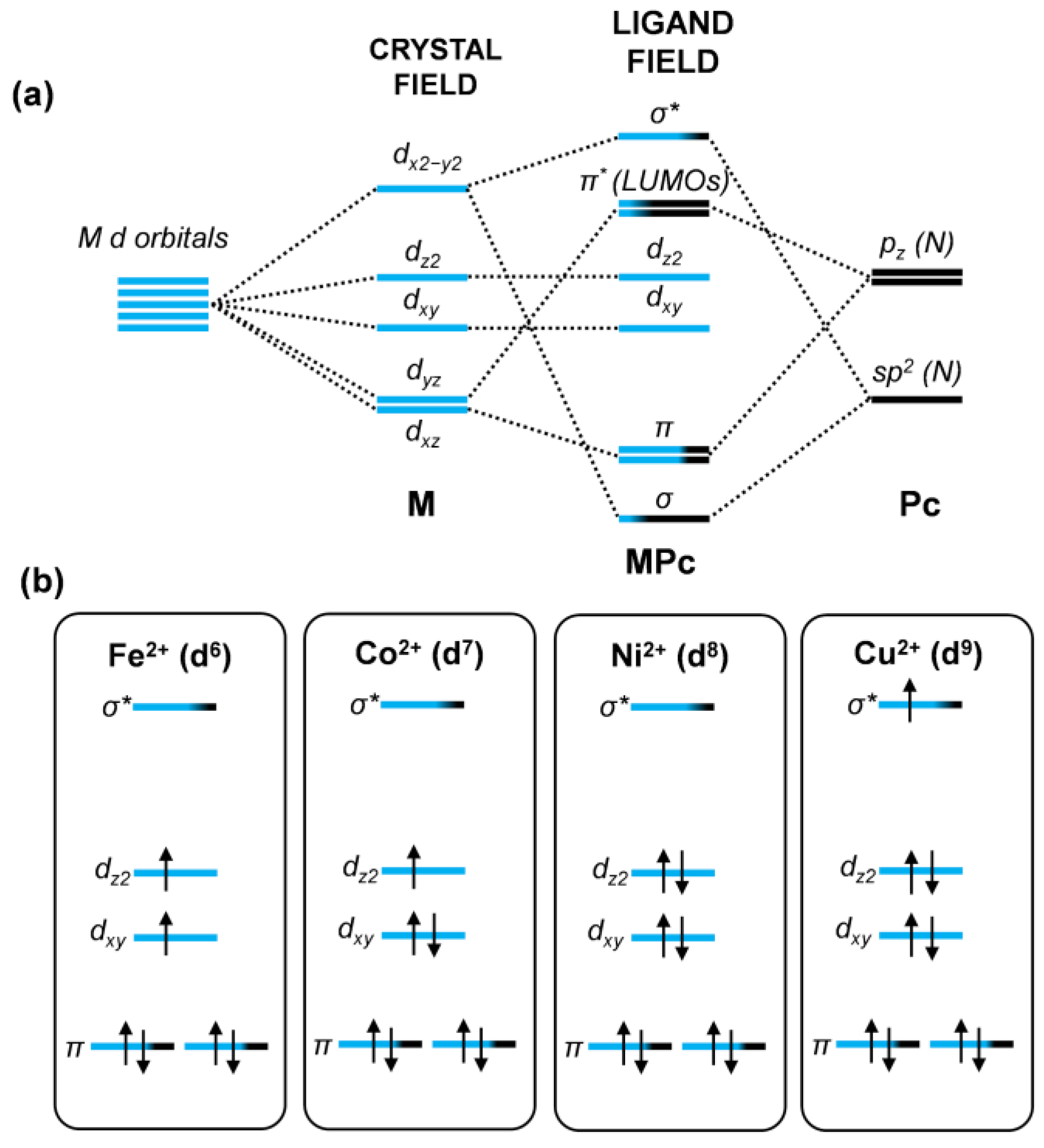
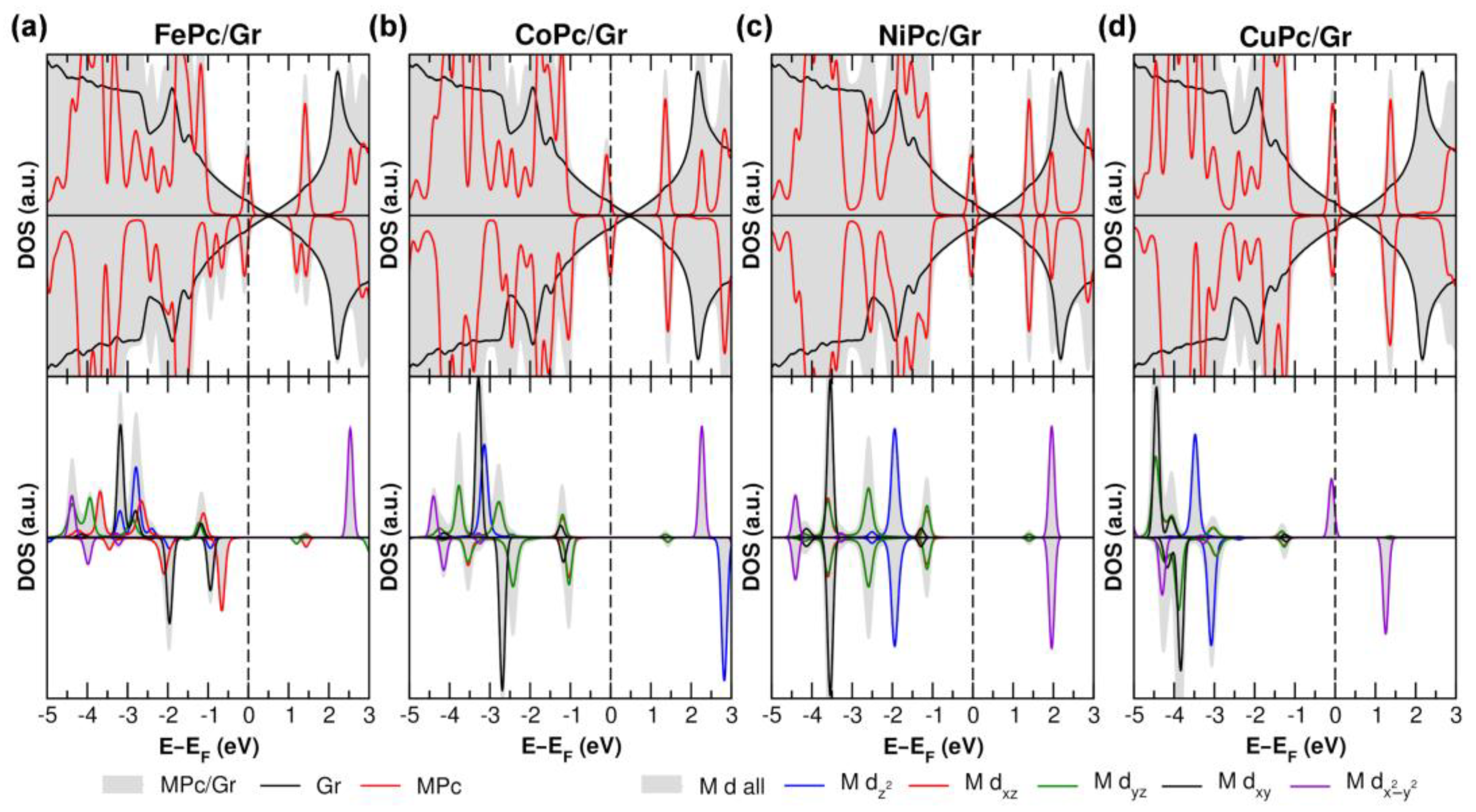
3.3. Interaction with Electron-Donor Gas: NH3 Adsorption on MPc/Gr
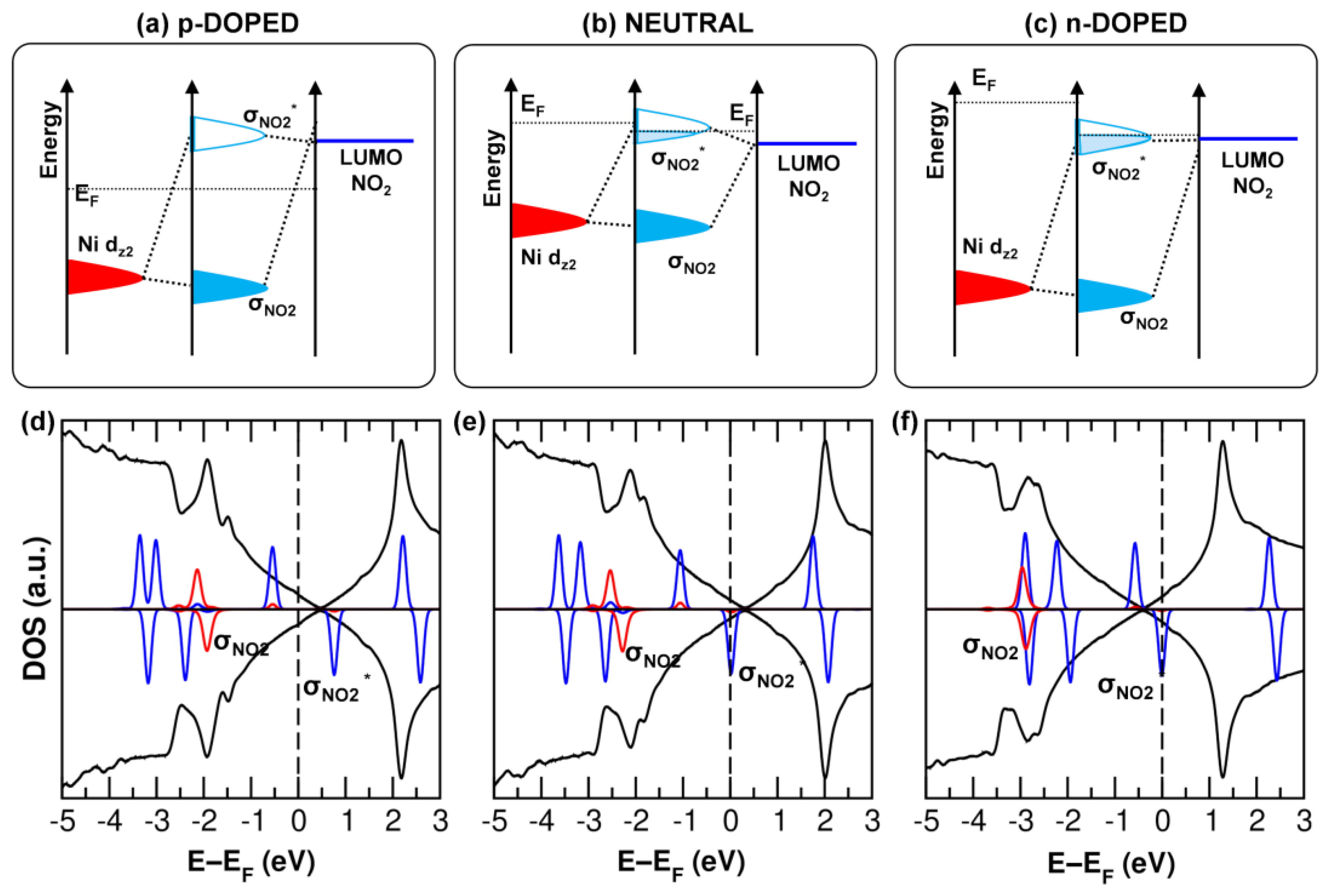
3.4. Interaction with Electron-Acceptor Gas: NO2 Adsorption on MPc/Gr
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Milone, A.; Monteduro, A.G.; Rizzato, S.; Leo, A.; Di Natale, C.; Kim, S.S.; Maruccio, G. Advances in materials and technologies for gas sensing from environmental and food monitoring to breath analysis. Adv. Sustain. Syst. 2023, 7, 2200083. [Google Scholar] [CrossRef]
- Ji, H.; Zeng, W.; Li, Y. Gas sensing mechanisms of metal oxide semiconductors: A focus review. Nanoscale 2019, 11, 22664–22684. [Google Scholar] [CrossRef] [PubMed]
- Tricoli, A.; Nasiri, N.; De, S. Wearable and miniaturized sensor technologies for personalized and preventive medicine. Adv. Funct. Mater. 2017, 27, 1605271. [Google Scholar] [CrossRef]
- Sharma, A.; Eadi, S.B.; Noothalapati, H.; Otyepka, M.; Lee, H.D.; Jayaramulu, K. Porous materials as effective chemiresistive gas sensors. Chem. Soc. Rev. 2024, 53, 2530–2577. [Google Scholar] [CrossRef]
- Dai, J.; Ogbeide, O.; Macadam, N.; Sun, Q.; Yu, W.; Li, Y.; Su, B.-L.; Hasan, T.; Huang, X.; Huang, W. Printed gas sensors. Chem. Soc. Rev. 2020, 49, 1756–1789. [Google Scholar] [CrossRef]
- Degler, D.; Weimar, U.; Barsan, N. Current understanding of the fundamental mechanisms of doped and loaded semiconducting metal-oxide-based gas sensing materials. ACS Sens. 2019, 4, 2228–2249. [Google Scholar] [CrossRef]
- Tang, X.; Debliquy, M.; Lahem, D.; Yan, Y.; Raskin, J.P. A review on functionalized graphene sensors for detection of ammonia. Sensors 2021, 21, 1443. [Google Scholar] [CrossRef]
- Chatterjee, S.G.; Chatterjee, S.; Ray, A.K.; Chakraborty, A.K. Graphene–metal oxide nanohybrids for toxic gas sensor: A review. Sens. Actuators B Chem. 2015, 221, 1170–1181. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, H.; Cai, Y.; Zhao, J.; Gao, Z.; Song, Y.Y. The challenges and opportunities for TiO2 nanostructures in gas sensing. ACS Sens. 2024, 9, 1644–1655. [Google Scholar] [CrossRef]
- Ottaviano, L.; Mastrippolito, D. The future ahead gas sensing with two-dimensional materials. Appl. Phys. Lett. 2023, 123, 050502. [Google Scholar] [CrossRef]
- Ko, J.K.; Park, I.H.; Hong, K.; Kwon, K.C. Recent advances in chemoresistive gas sensors using two-dimensional materials. Nanomaterials 2024, 14, 1397. [Google Scholar] [CrossRef] [PubMed]
- Llobet, E. Transition metal dichalcogenide based toxic gas sensing. Curr. Opin. Environ. Sci. Health 2024, 37, 100533. [Google Scholar] [CrossRef]
- Wu, H.; Zhong, S.; Bin, Y.; Jiang, X.; Cui, H. Ni-decorated WS2-WSe2 heterostructure as a novel sensing candidate upon C2H2 and C2H4 in oil-filled transformers: A first-principles investigation. Mol. Phys. 2025, e2492391. [Google Scholar] [CrossRef]
- Abbas, A.N.; Liu, B.; Chen, L.; Ma, Y.; Cong, S.; Aroonyadet, N.; Köpf, M.; Nilges, T.; Zhou, C. Black phosphorus gas sensors. ACS Nano 2015, 9, 5618–5624. [Google Scholar] [CrossRef]
- Han, D.; Han, X.; Zhang, X.; Wang, W.; Li, D.; Li, H.; Sang, S. Highly sensitive and rapidly responding room-temperature NH₃ gas sensor that is based on exfoliated black phosphorus. Sens. Actuators B 2022, 367, 132038. [Google Scholar] [CrossRef]
- Goel, N.; Kumar, M. Recent advances in ultrathin 2D hexagonal boron nitride based gas sensors. J. Mater. Chem. C 2021, 9, 1537–1549. [Google Scholar] [CrossRef]
- Recum, P.; Hirsch, T. Graphene-based chemiresistive gas sensors. Nanoscale Adv. 2024, 6, 11–31. [Google Scholar] [CrossRef]
- Wang, T.; Huang, D.; Yang, Z.; Xu, S.; He, G.; Li, X.; Zhang, L. A review on graphene-based gas/vapor sensors with unique properties and potential applications. Nano-Micro Lett. 2016, 8, 95–119. [Google Scholar] [CrossRef]
- Chakraborthy, A.; Nuthalapati, S.; Nag, A.; Afsarimanesh, N.; Alahi, M.E.E.; Altinsoy, M.E. A critical review of the use of graphene-based gas sensors. Chemosensors 2022, 10, 355. [Google Scholar] [CrossRef]
- Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef]
- Choi, S.H.; Yun, S.J.; Won, Y.S.; Oh, C.S.; Kim, S.M.; Kim, K.K.; Lee, Y.H. Large-scale synthesis of graphene and other 2D materials towards industrialization. Nat. Commun. 2022, 13, 1484. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.W.; Hung, S.C.; Yang, M.D.; Yeh, C.W.; Wu, C.H.; Chi, G.C.; Pearton, S.J. Oxygen sensors made by monolayer graphene under room temperature. Appl. Phys. Lett. 2011, 99, 24. [Google Scholar] [CrossRef]
- Yavari, F.; Castillo, E.; Gullapalli, H.; Ajayan, P.M.; Koratkar, N. High sensitivity detection of NO2 and NH₃ in air using chemical vapor deposition grown graphene. Appl. Phys. Lett. 2012, 100, 203120. [Google Scholar] [CrossRef]
- Alzate-Carvajal, N.; Luican-Mayer, A. Functionalized graphene surfaces for selective gas sensing. ACS Omega 2020, 5, 21320–21329. [Google Scholar] [CrossRef]
- Perilli, D.; Chesnyak, V.; Ugolotti, A.; Panighel, M.; Vigneri, S.; Armillotta, F.; Naderasli, P.; Stredansky, M.; Schied, M.; Lacovig, P.; et al. CO Adsorption on a Single-Atom Catalyst Stably Embedded in Graphene. Angew. Chem. 2025, 64, e202421757. [Google Scholar] [CrossRef]
- Dan, Y.; Lu, Y.; Kybert, N.J.; Luo, Z.; Johnson, A.C. Intrinsic response of graphene vapor sensors. Nano Lett. 2009, 9, 1472–1475. [Google Scholar] [CrossRef]
- Lv, R.; Chen, G.; Li, Q.; McCreary, A.; Botello-Méndez, A.; Morozov, S.V.; Terrones, M. Ultrasensitive gas detection of large-area boron-doped graphene. Proc. Natl. Acad. Sci. USA 2015, 112, 14527–14532. [Google Scholar] [CrossRef]
- Freddi, S.; Perilli, D.; Vaghi, L.; Monti, M.; Papagni, A.; Di Valentin, C.; Sangaletti, L. Pushing down the limit of NH₃ detection of graphene-based chemiresistive sensors through functionalization by thermally activated tetrazoles dimerization. ACS Nano 2022, 16, 10456–10469. [Google Scholar] [CrossRef]
- Georgakilas, V.; Otyepka, M.; Bourlinos, A.B.; Chandra, V.; Kim, N.; Kemp, K.C.; Hobza, P.; Zboril, R.; Kim, K.S. Functionalization of graphene: Covalent and non-covalent approaches, derivatives and applications. Chem. Rev. 2012, 112, 6156–6214. [Google Scholar] [CrossRef]
- Giovannetti, G.; Khomyakov, P.A.; Brocks, G.; Karpan, V.V.; van den Brink, J.; Kelly, P.J. Doping graphene with metal contacts. Phys. Rev. Lett. 2008, 101, 026803. [Google Scholar] [CrossRef]
- Qi, Y.; Rhim, S.H.; Sun, G.F.; Weinert, M.; Li, L. Epitaxial graphene on SiC (0001): More than just honeycombs. Phys. Rev. Lett. 2010, 105, 085502. [Google Scholar] [CrossRef] [PubMed]
- Rao, C.N.R.; Gopalakrishnan, K.; Govindaraj, A. Synthesis, properties and applications of graphene doped with boron, nitrogen and other elements. Nano Today 2014, 9, 324–343. [Google Scholar] [CrossRef]
- Szary, M.J. Unlocking the chemistry of graphene: The impact of charge carrier concentration on molecular adsorption on graphene. Appl. Surf. Sci. 2025, 679, 161175. [Google Scholar] [CrossRef]
- MacLeod, J.M.; Rosei, F. Molecular self-assembly on graphene. Small 2014, 10, 1038–1049. [Google Scholar] [CrossRef]
- Cuxart, M.G.; Perilli, D.; Tömekce, S.; Deyerling, J.; Haag, F.; Muntwiler, M.; Allegretti, F.; Di Valentin, C.; Auwärter, W. Spatial segregation of substitutional B atoms in graphene patterned by the moiré superlattice on Ir(111). Carbon 2023, 201, 881–890. [Google Scholar] [CrossRef]
- Garcia-Basabe, Y.; Cardoso, M.S.; da Silva Lima, B.; Mendoza, C.D.; Junior, F.L.F.; Larrude, D.G. Investigation into electronic interaction and work function tuning of phthalocyanine molecules and graphene interfaces. Phys. Chem. Chem. Phys. 2024, 26, 24438–24446. [Google Scholar] [CrossRef]
- Ren, J.; Meng, S.; Wang, Y.L.; Ma, X.C.; Xue, Q.K.; Kaxiras, E. Properties of copper (fluoro-) phthalocyanine layers deposited on epitaxial graphene. J. Chem. Phys. 2011, 134, 194706. [Google Scholar] [CrossRef]
- Uihlein, J.; Polek, M.; Glaser, M.; Adler, H.; Ovsyannikov, R.; Bauer, M.; Ivanovic, M.; Preobrajenski, A.B.; Generalov, A.V.; Chassé, T.; et al. Influence of graphene on charge transfer between CoPc and metals: The role of graphene–substrate coupling. J. Phys. Chem. C 2015, 119, 15240–15247. [Google Scholar] [CrossRef]
- Dieng, M.; Bensifia, M.; Borme, J.; Florea, I.; Abreu, C.M.; Jama, C.; Léonard, C.; Alpuim, P.; Pribat, D.; Yassar, A.; et al. Wet-chemical noncovalent functionalization of CVD graphene: Molecular doping and its effect on electrolyte-gated graphene field-effect transistor characteristics. J. Phys. Chem. C 2022, 126, 4522–4533. [Google Scholar] [CrossRef]
- de Souza, R.M.; Siani, P.; Schmidt, T.F.; Itri, R.; Dias, L.G. Methylene blue location in (hydroperoxized) cardiolipin monolayer: Implication in membrane photodegradation. J. Phys. Chem. B 2017, 121, 8512–8522. [Google Scholar] [CrossRef]
- de la Torre, B.; Švec, M.; Hapala, P.; Redondo, J.; Krejčí, O.; Lo, R.; Manna, D.; Sarmah, A.; Nachtigallová, D.; Tuček, J.; et al. Non-covalent control of spin-state in metal-organic complex by positioning on N-doped graphene. Nat. Commun. 2018, 9, 2831. [Google Scholar] [CrossRef] [PubMed]
- Calmeiro, J.M.; Tomé, J.P.; Lourenço, L.M. Supramolecular graphene–phthalocyanine assemblies for technological breakthroughs. J. Mater. Chem. C 2020, 8, 8344–8361. [Google Scholar] [CrossRef]
- Kumar, A.; Vashistha, V.K.; Das, D.K. Recent development on metal phthalocyanines based materials for energy conversion and storage applications. Coord. Chem. Rev. 2021, 431, 213678. [Google Scholar] [CrossRef]
- Gounden, D.; Nombona, N.; Van Zyl, W.E. Recent advances in phthalocyanines for chemical sensor, non-linear optics (NLO) and energy storage applications. Coord. Chem. Rev. 2020, 420, 213359. [Google Scholar] [CrossRef]
- Jiang, W.; Chen, X.; Wang, T.; Li, B.; Zeng, M.; Yang, J.; Hu, N.; Su, Y.; Zhou, Z.; Yang, Z. Enhancing room-temperature NO2 gas sensing performance based on a metal phthalocyanine/graphene quantum dot hybrid material. RSC Adv. 2021, 11, 5618–5628. [Google Scholar] [CrossRef]
- Motta, S.; Siani, P.; Levy, A.; Di Valentin, C. Exploring the drug loading mechanism of photoactive inorganic nanocarriers through molecular dynamics simulations. Nanoscale 2021, 13, 13000–13013. [Google Scholar] [CrossRef]
- Freddi, S.; Marzuoli, C.; Pagliara, S.; Drera, G.; Sangaletti, L. Targeting biomarkers in the gas phase through a chemoresistive electronic nose based on graphene functionalized with metal phthalocyanines. RSC Adv. 2023, 13, 251–263. [Google Scholar] [CrossRef]
- Cranston, R.R.; Lessard, B.H. Metal phthalocyanines: Thin-film formation, microstructure, and physical properties. RSC Adv. 2021, 11, 21716–21737. [Google Scholar] [CrossRef]
- Casotto, A.; Drera, G.; Perilli, D.; Freddi, S.; Pagliara, S.; Zanotti, M.; Schio, L.; Verdini, A.; Floreano, L.; Di Valentin, C.; et al. π-Orbital mediated charge transfer channels in a monolayer Gr–NiPc heterointerface unveiled by soft X-ray electron spectroscopies and DFT calculations. Nanoscale 2022, 14, 13166–13177. [Google Scholar] [CrossRef]
- Perilli, D.; Freddi, S.; Zanotti, M.; Drera, G.; Casotto, A.; Pagliara, S.; Schio, L.; Sangaletti, L.; Di Valentin, C. Design of highly responsive chemiresistor-based sensors by interfacing NiPc with graphene. Commun. Mater. 2024, 5, 254. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Dal Corso, A. Pseudopotentials periodic table: From H to Pu. Comput. Mater. Sci. 2014, 95, 337–350. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Brumboiu, I.E.; Haldar, S.; Luder, J.; Eriksson, O.; Herper, H.C.; Brena, B.; Sanyal, B. Influence of electron correlation on the electronic structure and magnetism of transition-metal phthalocyanines. J. Chem. Theory Comput. 2016, 12, 1772–1785. [Google Scholar] [CrossRef]
- Brumboiu, I.E.; Haldar, S.; Luder, J.; Eriksson, O.; Herper, H.C.; Brena, B.; Sanyal, B. Ligand effects on the linear response Hubbard U: The case of transition metal phthalocyanines. J. Phys. Chem. A 2019, 123, 3214–3222. [Google Scholar] [CrossRef]
- Pozzo, M.; Alfe, D.; Lacovig, P.; Hofmann, P.; Lizzit, S.; Baraldi, A. Thermal expansion of supported and freestanding graphene: Lattice constant versus interatomic distance. Phys. Rev. Lett. 2011, 106, 135501. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Why gold is the noblest of all the metals. Nature 1995, 376, 238–240. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, L.; Yang, Y.; Huang, Q.; Li, D.; Zeng, D. A review on two-dimensional materials for chemiresistive-and FET-type gas sensors. Phys. Chem. Chem. Phys. 2021, 23, 15420–15439. [Google Scholar] [CrossRef] [PubMed]
- Ellis, T.S.; Park, K.T.; Ulrich, M.D.; Hulbert, S.L.; Rowe, J.E. Interaction of metallophthalocyanines (MPc, M = Co, Ni) on Au(001): Ultraviolet photoemission spectroscopy and low energy electron diffraction study. J. Appl. Phys. 2006, 100, 093714. [Google Scholar] [CrossRef]
- Brena, B.; Puglia, C.; de Simone, M.; Coreno, M.; Tarafder, K.; Feyer, V.; Banerjee, R.; Göthelid, E.; Sanyal, B.; Oppeneer, P.M.; et al. Valence-band electronic structure of iron phthalocyanine: An experimental and theoretical photoelectron spectroscopy study. J. Chem. Phys. 2011, 134, 074312. [Google Scholar] [CrossRef] [PubMed]
- Evangelista, F.; Carravetta, V.; Stefani, G.; Jansik, B.; Alagia, M.; Stranges, S.; Ruocco, A. Electronic structure of copper phthalocyanine: An experimental and theoretical study of occupied and unoccupied levels. J. Chem. Phys. 2007, 126, 124709. [Google Scholar] [CrossRef]
- Sato, N.; Yoshida, H.; Tsutsumi, K. Unoccupied electronic states in phthalocyanine thin films studied by inverse photoemission spectroscopy. Synth. Met. 2003, 133, 673–674. [Google Scholar] [CrossRef]
- Nachtigallová, D.; Antalík, A.; Lo, R.; Sedlák, R.; Manna, D.; Tuček, J.; Ugolotti, J.; Veis, L.; Legeza, Ö.; Pittner, J.; et al. An Isolated Molecule of Iron(II) Phthalocyanin Exhibits Quintet Ground-State: A Nexus between Theory and Experiment. Chem.-Eur. J. 2018, 24, 13413–13417. [Google Scholar] [CrossRef]
- Schmid, M.; Kaftan, A.; Steinrück, H.P.; Gottfried, J.M. The electronic structure of cobalt(II) phthalocyanine adsorbed on Ag(111). Surf. Sci. 2012, 606, 945–949. [Google Scholar] [CrossRef]
- Bartolomé, J.; Monton, C.; Schuller, I.K. Magnetism of metal phthalocyanines. In Molecular Magnets: Physics and Applications; Springer: Berlin/Heidelberg, Germany, 2014; pp. 221–245. [Google Scholar]
- Marom, N.; Hod, O.; Scuseria, G.E.; Kronik, L. Electronic structure of copper phthalocyanine: A comparative density functional theory study. J. Chem. Phys. 2008, 128, 164107. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Hammer, B.; Morikawa, Y.; Nørskov, J.K. CO chemisorption at metal surfaces and overlayers. Phys. Rev. Lett. 1996, 76, 2141. [Google Scholar] [CrossRef]
- Szary, M.J. Toward high selectivity of sensor arrays: Enhanced adsorption interaction and selectivity of gas detection (N2, O2, NO, CO, CO2, NO2, SO2, AlH₃, NH₃, and PH₃) on transition metal dichalcogenides (MoS2, MoSe2, and MoTe2). Acta Mater. 2024, 274, 120016. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perilli, D.; Rizzi, A.M.; Di Valentin, C. Tailoring Metal Phthalocyanine/Graphene Interfaces for Highly Sensitive Gas Sensors. Nanomaterials 2025, 15, 691. https://doi.org/10.3390/nano15090691
Perilli D, Rizzi AM, Di Valentin C. Tailoring Metal Phthalocyanine/Graphene Interfaces for Highly Sensitive Gas Sensors. Nanomaterials. 2025; 15(9):691. https://doi.org/10.3390/nano15090691
Chicago/Turabian StylePerilli, Daniele, Alberto Maria Rizzi, and Cristiana Di Valentin. 2025. "Tailoring Metal Phthalocyanine/Graphene Interfaces for Highly Sensitive Gas Sensors" Nanomaterials 15, no. 9: 691. https://doi.org/10.3390/nano15090691
APA StylePerilli, D., Rizzi, A. M., & Di Valentin, C. (2025). Tailoring Metal Phthalocyanine/Graphene Interfaces for Highly Sensitive Gas Sensors. Nanomaterials, 15(9), 691. https://doi.org/10.3390/nano15090691






